Multi-Period Multi-Criteria Decision Making under Uncertainty: A Renewable Energy Transition Case from Germany
Abstract
1. Introduction
2. Literature Review: MP MADM Approaches
3. MP MADM Approach under Deep Uncertainty
3.1. Description of PROMETHEE
- The indifference threshold defines the largest that is considered negligible for the decision maker.
- The preference threshold defines the minimal that is required for a strict preference on a criterion.
- The reversal point represents the inflection point of the preference function (Type VI) and is derived from the normal distribution.
3.2. Extension of PROMETHEE to the MP Case with Scenarios (MP-PROMETHEE-S)
4. Case Study: Planning the Local Energy Transition in Jühnde
- Technical progress (power supply): This key factor represents the technical progress in terms of efficiency gains of already readily available power generation technologies.
- Governmental support: This represents the governmental support of power generation technologies, e.g., in terms of subsidies or R&D, as well as fostering awareness for energy efficiency in the public.
- Public contribution: This represents the behavior of the public in terms of acceptance of energy-efficient electrical appliances.
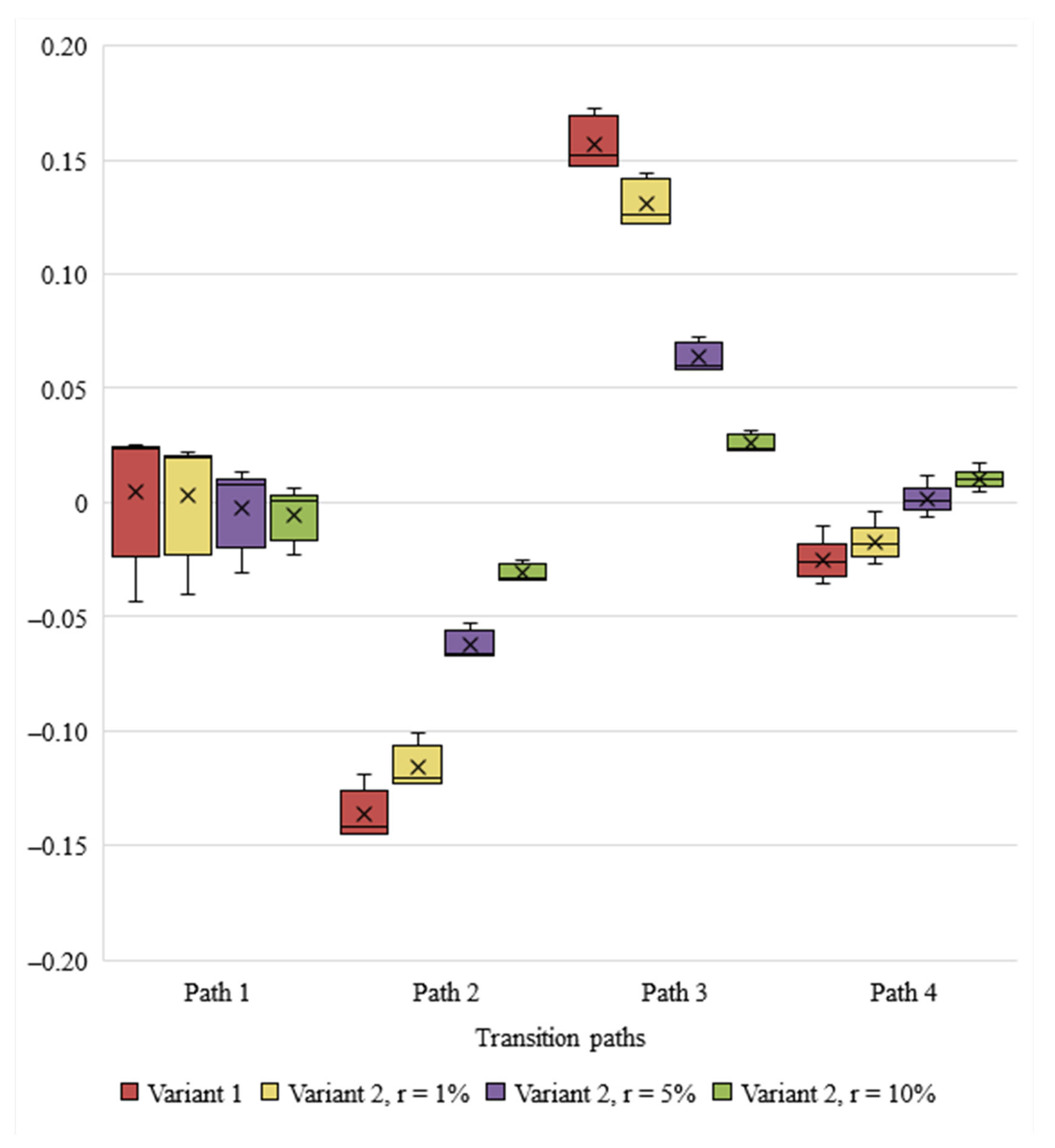
5. Discussion and Future Research Opportunities
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grunwald, A.; Dieckhoff, C.; Fischedick, M.; Höffler, F.; Mayer, C.; Weimer-Jehle, W. Consulting with Energy Scenarios: Requirements for Scientific Policy Advice; Monograph Series on Science-based Policy Advice: München, Germany, 2016. [Google Scholar]
- Weimer-Jehle, W.; Buchgeister, J.; Hauser, W.; Kosow, H.; Naegler, T.; Poganietz, W.-R.; Pregger, T.; Prehofer, S.; von Recklinghausen, A.; Schippl, J.; et al. Context scenarios and their usage for the construction of socio-technical energy scenarios. Energy 2016, 111, 956–970. [Google Scholar] [CrossRef]
- Fortes, P.; Alvarenga, A.; Seixas, J.; Rodrigues, A.M.A. Long-term energy scenarios: Bridging the gap between socio-economic storylines and energy modeling. Technol. Forecast. Soc. Chang. 2015, 91, 161–178. [Google Scholar] [CrossRef]
- Fitiwi, D.Z.; Lynch, M.; Bertsch, V. Enhanced network effects and stochastic modelling in generation expansion planning: Insights from an insular power system. Socio-Economic Plan. Sci. 2020, 71, 100859. [Google Scholar] [CrossRef]
- Harjanne, A.; Korhonen, J. Abandoning the concept of renewable energy. Energy Policy 2019, 127, 330–340. [Google Scholar] [CrossRef]
- Antunes, C.H.; Henriques, C.O. Multi-Objective Optimization and Multi-Criteria Analysis Models and Methods for Problems in the Energy Sector. In Multiple Criteria Decision Analysis: State of the Art Surveys, 2nd ed.; Greco, S., Ehrgott, M., Figueira, J., Eds.; Springer: New York, NY, USA, 2016; pp. 1067–1165. ISBN 978-1-4939-3093-7. [Google Scholar]
- Narayanamoorthy, S.; Ramya, L.; Kalaiselvan, S.; Kureethara, J.V.; Kang, D. Use of DEMATEL and COPRAS method to select best alternative fuel for control of impact of greenhouse gas emissions. Socio-Econ. Plan. Sci. 2020, 100996, 100996. [Google Scholar] [CrossRef]
- Kowalski, K.; Stagl, S.; Madlener, R.; Omann, I. Sustainable energy futures: Methodological challenges in combining scenarios and participatory multi-criteria analysis. Eur. J. Oper. Res. 2009, 197, 1063–1074. [Google Scholar] [CrossRef]
- Volkart, K.; Weidmann, N.; Bauer, C.; Hirschberg, S. Multi-criteria decision analysis of energy system transformation pathways: A case study for Switzerland. Energy Policy 2017, 106, 155–168. [Google Scholar] [CrossRef]
- Witt, T.; Dumeier, M.; Geldermann, J. Combining scenario planning, energy system analysis, and multi-criteria analysis to develop and evaluate energy scenarios. J. Clean. Prod. 2020, 242, 118414. [Google Scholar] [CrossRef]
- Løken, E. Use of multicriteria decision analysis methods for energy planning problems. Renew. Sustain. Energy Rev. 2007, 11, 1584–1595. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Khalifah, Z.; Zakuan, N.; Jusoh, A.; Nor, K.M.; Khoshnoudi, M. A review of multi-criteria decision-making applications to solve energy management problems: Two decades from 1995 to 2015. Renew. Sustain. Energy Rev. 2017, 71, 216–256. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res. 2017, 258, 607–616. [Google Scholar] [CrossRef]
- Janeiro, L.; Patel, M.K. Choosing sustainable technologies. Implications of the underlying sustainability paradigm in the decision-making process. J. Clean. Prod. 2015, 105, 438–446. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Wang, J.-J.; Jing, Y.-Y.; Zhang, C.-F.; Zhao, J.-H. Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
- Kilic, H.S.; Yalcin, A.S. Comparison of municipalities considering environmental sustainability via neutrosophic DEMATEL based TOPSIS. Socio-Economic Plan. Sci. 2021, 75, 100827. [Google Scholar] [CrossRef]
- Cuoghi, K.G.; Leoneti, A.B. A group MCDA method for aiding decision-making of complex problems in public sector: The case of Belo Monte Dam. Socio-Economic Plan. Sci. 2019, 68, 100625. [Google Scholar] [CrossRef]
- Manzini, F.; Islas, J.; Macías, P. Model for evaluating the environmental sustainability of energy projects. Technol. Forecast. Soc. Chang. 2011, 78, 931–944. [Google Scholar] [CrossRef]
- Yeo, M.; Kim, Y. Changes of the carbon dioxide emissions and the overshoot ratio resulting from the implementation of the 2nd Energy Master Plan in the Republic of Korea. Energy Policy 2016, 96, 241–250. [Google Scholar] [CrossRef]
- Li, W.; Yang, G.; Li, X.; Sun, T.; Wang, J. Cluster analysis of the relationship between carbon dioxide emissions and economic growth. J. Clean. Prod. 2019, 225, 459–471. [Google Scholar] [CrossRef]
- Mardani, A.; Liao, H.; Nilashi, M.; Alrasheedi, M.; Cavallaro, F. A multi-stage method to predict carbon dioxide emissions using dimensionality reduction, clustering, and machine learning techniques. J. Clean. Prod. 2020, 275, 122942. [Google Scholar] [CrossRef]
- Marra, A.; Colantonio, E. The path to renewable energy consumption in the European Union through drivers and barriers: A panel vector autoregressive approach. Socio-Economic Plan. Sci. 2020, 100958, 100958. [Google Scholar] [CrossRef]
- Dyer, J.S. Multiattribute Utility Theory (MAUT). In Multiple Criteria Decision Analysis: State of the Art Surveys, 2nd ed.; Greco, S., Ehrgott, M., Figueira, J., Eds.; Springer: New York, NY, USA, 2016; pp. 285–314. ISBN 978-1-4939-3093-7. [Google Scholar]
- Brans, J.-P.; Smet, Y. de. PROMETHEE Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys, 2nd ed.; Greco, S., Ehrgott, M., Figueira, J., Eds.; Springer: New York, NY, USA, 2016; pp. 187–219. ISBN 978-1-4939-3093-7. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy and Analytic Network Processes for the Measurement of Intangible Criteria and for Decision Making. In Multiple Criteria Decision Analysis: State of the Art Surveys, 2nd ed.; Greco, S., Ehrgott, M., Figueira, J., Eds.; Springer: New York, NY, USA, 2016; pp. 363–420. ISBN 978-1-4939-3093-7. [Google Scholar]
- Figueira, J.R.; Mousseau, V.; Roy, B. ELECTRE Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys, 2nd ed.; Greco, S., Ehrgott, M., Figueira, J., Eds.; Springer: New York, NY, USA, 2016; pp. 155–186. ISBN 978-1-4939-3093-7. [Google Scholar]
- Hämäläinen, R.P.; Seppäläinen, T.O. The analytic network process in energy policy planning. Socio-Econ. Plan. Sci. 1986, 20, 399–405. [Google Scholar] [CrossRef]
- Belton, V.; Stewart, T.J. Multiple Criteria Decision Analysis: An Integrated Approach, 2. Print; Kluwer Academic Publishers: Boston, MA, USA, 2003; ISBN 0-7923-7505-X. [Google Scholar]
- Yu, P.-L.; Chen, Y.-C. Dynamic multiple criteria decision making in changeable spaces: From habitual domains to innovation dynamics. Ann. Oper. Res. 2012, 197, 201–220. [Google Scholar] [CrossRef]
- Verbong, G.; Geels, F. Exploring sustainability transitions in the electricity sector with socio-technical pathways. Technol. Forecast. Soc. Chang. 2010, 77, 1214–1221. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Ram, C.; Montibeller, G. Exploring the impact of evaluating strategic options in a scenario-based multi-criteria framework. Technol. Forecast. Soc. Chang. 2013, 80, 657–672. [Google Scholar] [CrossRef]
- Durbach, I.N.; Stewart, T.J. Modeling uncertainty in multi-criteria decision analysis. Eur. J. Oper. Res. 2012, 223, 1–14. [Google Scholar] [CrossRef]
- French, S. Uncertainty and Imprecision: Modelling and Analysis. J. Oper. Res. Soc. 1995, 46, 70–79. [Google Scholar] [CrossRef]
- Van Der Pas, J.W.G.M.; Walker, W.E.; Marchau, V.A.W.J.; Van Wee, G.P.; Agusdinata, D.B. Exploratory MCDA for handling deep uncertainties: The case of intelligent speed adaptation implementation. J. Multi-Criteria Decis. Anal. 2010, 17, 1–23. [Google Scholar] [CrossRef]
- Stewart, T.J.; Durbach, I.N. Dealing with Uncertainties in MCDA. In Multiple Criteria Decision Analysis: State of the Art Surveys, 2nd ed.; Greco, S., Ehrgott, M., Figueira, J., Eds.; Springer: New York, NY, USA, 2016; pp. 467–496. ISBN 978-1-4939-3093-7. [Google Scholar]
- Zimmermann, H.-J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Kaya, I.; Çolak, M.; Terzi, F. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strat. Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Greco, S.; Matarazzo, B.; Slowinski, R. Rough sets theory for multicriteria decision analysis. Eur. J. Oper. Res. 2001, 129, 1–47. [Google Scholar] [CrossRef]
- van der Heijden, K. Scenarios: The Art of Strategic Conversation, 2nd ed.; Wiley: Chichester, UK, 2009; ISBN 0-470-02368-6. [Google Scholar]
- Goodwin, P.; Wright, G. The limits of forecasting methods in anticipating rare events. Technol. Forecast. Soc. Chang. 2010, 77, 355–368. [Google Scholar] [CrossRef]
- Gausemeier, J.; Fink, A.; Schlake, O. Scenario Management: An Approach to Develop Future Potentials. Technol. Forecast. Soc. Chang. 1998, 59, 111–130. [Google Scholar] [CrossRef]
- Spaniol, M.J.; Rowland, N.J. Defining scenario. Futures Foresight Sci. 2018, 1, e3. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Balash, P.; Nichols, C.; Victor, N. Multi-regional evaluation of the U.S. electricity sector under technology and policy uncertainties: Findings from MARKAL EPA9rUS modeling. Socio-Econ. Plan. Sci. 2013, 47, 89–119. [Google Scholar] [CrossRef]
- Bendoly, E.; Bachrach, D.G. A process-based model for priority convergence in multi-period group decision-making. Eur. J. Oper. Res. 2003, 148, 534–545. [Google Scholar] [CrossRef]
- Frini, A.; Guitouni, A.; Martel, J.-M. A general decomposition approach for multi-criteria decision trees. Eur. J. Oper. Res. 2012, 220, 452–460. [Google Scholar] [CrossRef]
- Frini, A. A multi-criteria multi-period approach for energy project selection in sustainable development con-text. In Proceedings of the 2014 First International Conference on Green Energy ICGE 2014, Sfax, Tunisia, 25–27 March 2014; pp. 65–71, ISBN 978-1-4799-3602-1. [Google Scholar]
- Frini, A.; Benamor, S. A TOPSIS multi-criteria multi-period approach for selecting projects in sustainable development context. In Proceedings of the 2015 International Conference on Industrial Engineering and Operations Management (IEOM), Dubai, United Arab Emirates, 3–5 March 2015; Volume Dubai, pp. 1–9. [Google Scholar]
- Frini, A.; Benamor, S. Making Decisions in a Sustainable Development Context: A State-of-the-Art Survey and Proposal of a Multi-period Single Synthesizing Criterion Approach. Comput. Econ. 2017, 52, 341–385. [Google Scholar] [CrossRef]
- Frini, A.; Ben Amor, S. MUPOM: A multi-criteria multi-period outranking method for decision-making in sustainable development context. Environ. Impact Assess. Rev. 2019, 76, 10–25. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Z.; Hu, J.; Liu, S. Systematic decision making: A extended multi-criteria decision making model. Technol. Econ. Dev. Econ. 2017, 23, 157–177. [Google Scholar] [CrossRef][Green Version]
- Banamar, I.; De Smet, Y. An extension of PROMETHEE II to temporal evaluations. Int. J. Multicrit. Decis. Mak. 2018, 7, 298. [Google Scholar] [CrossRef]
- Urli, B.; Frini, A.; Ben Amor, S. PROMETHEE-MP: A generalisation of PROMETHEE for multi-period evaluations under uncertainty. Int. J. Multicriteria Decis. Mak. 2019, 8, 13. [Google Scholar] [CrossRef]
- Witt, T.; Dumeier, M.; Geldermann, J. Multi-criteria Evaluation of the Transition of Power Generation Sys-tems. In Proceedings of the Multikriterielle Optimierung und Entscheidungsunterstützung, Tagungsband GOR Entscheidungstheorie und -Praxis 2018, Kaiserslautern, Germany, 1–2 March 2018; Küfer, K.-H., Ruzika, S., Halffmann, P., Eds.; Springer Gabler: Wiesbaden, Germany, 2019; pp. 121–141, ISBN 978-3-658-27041-4. [Google Scholar]
- Ziemba, P.; Jankowski, J.; Wątróbski, J. Dynamic Decision Support in the Internet Marketing Management. In Transactions on Computational Collective Intelligence XXIX; Nguyen, N.T., Kowalczyk, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 39–68. [Google Scholar]
- Webster, J.; Watson, R.T. Analyzing the Past to Prepare for the Future: Writing a literature Review. Manage Inform. Syst. Q. 2002, 26, 13–23. [Google Scholar]
- Denyer, D.; Tranfield, D. Producing a Systematic Review. In The Sage Handbook of Organizational Research Methods; Buchanan, D.A., Bryman, A., Eds.; Sage Publications Inc.: Thousand Oaks, CA, USA, 2011; pp. 671–689. ISBN 978-1-4462-0064-3. [Google Scholar]
- Jassbi, J.J.; Ribeiro, R.; Varela, L.R. Dynamic MCDM with future knowledge for supplier selection. J. Decis. Syst. 2014, 23, 232–248. [Google Scholar] [CrossRef]
- Campanella, G.; Ribeiro, R. A framework for dynamic multiple-criteria decision making. Decis. Support. Syst. 2011, 52, 52–60. [Google Scholar] [CrossRef]
- Kosow, H. New outlooks in traceability and consistency of integrated scenarios. Eur. J. Futur. Res. 2015, 3, 1–12. [Google Scholar] [CrossRef]
- Knoke, T.; Gosling, E.; Paul, C. Use and misuse of the net present value in environmental studies. Ecol. Econ. 2020, 174, 106664. [Google Scholar] [CrossRef]
- Dotoli, M.; Epicoco, N.; Falagario, M. Multi-Criteria Decision Making techniques for the management of public procurement tenders: A case study. Appl. Soft Comput. 2020, 88, 106064. [Google Scholar] [CrossRef]
- Schröder, T.; Lauven, L.-P.; Beyer, B.; Lerche, N.; Geldermann, J. Using PROMETHEE to assess bioenergy pathways. Central Eur. J. Oper. Res. 2018, 27, 287–309. [Google Scholar] [CrossRef]
- Munda, G. “Measuring Sustainability”: A Multi-Criterion Framework. Environ. Dev. Sustain. 2005, 7, 117–134. [Google Scholar] [CrossRef]
- Guitouni, A.; Martel, J.-M. Tentative guidelines to help choosing an appropriate MCDM method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Oberschmidt, J.; Geldermann, J.; Ludwig, J.; Schmehl, M. Modified PROMETHEE approach for assessing energy technologies. Int. J. Energy Sect. Manag. 2010, 4, 183–212. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Karangelis, F. Multi-criteria decision analysis and cost–benefit analysis of alternative scenarios for the power generation sector in Greece. Renew. Sustain. Energy Rev. 2007, 11, 716–727. [Google Scholar] [CrossRef]
- Tsoutsos, T.; Drandaki, M.; Frantzeskaki, N.; Iosifidis, E.; Kiosses, I. Sustainable energy planning by using multi-criteria analysis application in the island of Crete. Energy Policy 2009, 37, 1587–1600. [Google Scholar] [CrossRef]
- Doukas, H.C.; Andreas, B.M.; Psarras, J.E. Multi-criteria decision aid for the formulation of sustainable technological energy priorities using linguistic variables. Eur. J. Oper. Res. 2007, 182, 844–855. [Google Scholar] [CrossRef]
- French, S.; Geldermann, J. The varied contexts of environmental decision problems and their implications for decision support. Environ. Sci. Policy 2005, 8, 378–391. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P. Note-A Preference Ranking Organisation Method: The PROMETHEE Method for Multiple Criteria Decision-Making. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Montibeller, G.; Gummer, H.; Tumidei, D. Combining scenario planning and multi-criteria decision analysis in practice. J. Multi-Crit. Decis. Anal. 2006, 14, 5–20. [Google Scholar] [CrossRef]
- Stewart, T.J.; French, S.; Rios, J. Integrating multicriteria decision analysis and scenario planning—Review and extension. Omega 2013, 41, 679–688. [Google Scholar] [CrossRef]
- Durbach, I.N.; Stewart, T.J. Probability and Beyond: Including Uncertainties in Decision Analysis. In Behavioral Operational Research; White, L., Kunc, M., Burger, K., Malpass, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 75–91. ISBN 978-3-030-25404-9. [Google Scholar]
- Vadén, T.; Majava, A.; Toivanen, T.; Järvensivu, P.; Hakala, E.; Eronen, J. To continue to burn something? Technological, economic and political path dependencies in district heating in Helsinki, Finland. Energy Res. Soc. Sci. 2019, 58, 101270. [Google Scholar] [CrossRef]
- Kuper, G.; van Soest, D.P. Path-dependency and input substitution: Implications for energy policy modelling. Energy Econ. 2003, 25, 397–407. [Google Scholar] [CrossRef]
- Daystar, J.; Venditti, R.; Kelley, S.S. Dynamic greenhouse gas accounting for cellulosic biofuels: Implications of time based methodology decisions. Int. J. Life Cycle Assess. 2017, 22, 812–826. [Google Scholar] [CrossRef]
- Cropper, M.L.; Aydede, S.K.; Portney, P.R. Preferences for life saving programs: How the public discounts time and age. J. Risk Uncertain. 1994, 8, 243–265. [Google Scholar] [CrossRef]
- Bell, M.L.; Hobbs, B.F.; Ellis, H. The use of multi-criteria decision-making methods in the integrated assessment of climate change: Implications for IA practitioners. Socio-Economic Plan. Sci. 2003, 37, 289–316. [Google Scholar] [CrossRef]
- Weitzman, M.L. Why the Far-Distant Future Should Be Discounted at Its Lowest Possible Rate. J. Environ. Econ. Manag. 1998, 36, 201–208. [Google Scholar] [CrossRef]
- Ram, C. Scenario presentation and scenario generation in multi-criteria assessments: An exploratory study. Technol. Forecast. Soc. Chang. 2020, 151, 119850. [Google Scholar] [CrossRef]
- Lerche, N.; Wilkens, I.; Schmehl, M.; Eigner-Thiel, S.; Geldermann, J. Using methods of Multi-Criteria Decision Making to provide decision support concerning local bioenergy projects. Socio-Econ. Plan. Sci. 2019, 68, 100594. [Google Scholar] [CrossRef]
- Schär, S.; Geldermann, J. Adopting Multiactor Multicriteria Analysis for the Evaluation of Energy Scenarios. Sustainability 2021, 13, 2594. [Google Scholar] [CrossRef]
- Kim, S.-H.; Ahn, B.-S. Group decision making procedure considering preference strength under incomplete information. Comput. Oper. Res. 1997, 24, 1101–1112. [Google Scholar] [CrossRef]
- Mareschal, B.; Brans, J.P.; Macharis, C. The GDSS PROMETHEE procedure: A PROMETHEE-GAIA based procedure for group decision support. J. Decis. Syst. 1998, 7, 283–307. [Google Scholar]
- Haralambopoulos, D.; Polatidis, H. Renewable energy projects: Structuring a multi-criteria group decision-making framework. Renew. Energy 2003, 28, 961–973. [Google Scholar] [CrossRef]
- Nestle, U.; Kunz, C. Studienvergleich: Stromgestehungskosten Verschiedener Erzeugungstechnologien; Forschungsradar Energiewende–Metaanalyse: Berlin, Germany, 2014. [Google Scholar]
- Wissel, S.; Rath-Nagel, M.; Blesl, U.; Fahl, U.; Voß, A. Stromerzeugungskosten im Vergleich; Institut für Energiewirtschaft und Rationelle Energieanwendung: Stuttgart, Germany, 2008. [Google Scholar]
- Bundesverband der Energie- und Wasserwirtschaft, e.V. BDEW-Strompreisanalyse Januar 2021. Available online: https://www.bdew.de/service/daten-und-grafiken/bdew-strompreisanalyse/ (accessed on 28 May 2021).
- Statistisches Bundesamt. Index der Erzeugerpreise gewerblicher Produkte (Inlandsabsatz) nach dem Güterverzeichnis für Produktionsstatistiken: Lange Reihen der Fachserie 17, Reihe 2 von Januar 2005 bis April 2021. Available online: https://www.destatis.de/DE/Themen/Wirtschaft/Preise/Erzeugerpreisindex-gewerbliche-Produkte/Publikationen/Downloads-Erzeugerpreise/erzeugerpreise-lange-reihen-pdf-5612401.pdf?__blob=publicationFile (accessed on 28 May 2021).
- Genske, D.; Jödecke, T.; Ruff, A.; Porsche, L. Nutzung Städtischer Freiflächen für Erneuerbare Energien: Ein Projekt des FORSCHUNGSPROGRAMMS “Experimenteller Wohnungs- und Städtebau” (ExWoSt) des Bundesministeriums für Verkehr, Bau und Stadtentwicklung (BMVBS) und des Bundesamtes für Bauwesen und Raumordnung (BBR); Bundesamt für Bauwesen und Raumordnung: Bonn, Germany, 2009; ISBN 978-3-87994-044-8. [Google Scholar]
- Icha, P. Entwicklung der spezifischen Kohlendioxid-Emissionen des deutschen Strommix in den Jahren 1990–2016. Available online: https://www.umweltbundesamt.de/publikationen/entwicklung-der-spezifischen-kohlendioxid-3 (accessed on 28 May 2021).
- ED Netze GmbH. Lastprofile der ED Netze GmbH. Available online: https://www.ednetze.de/kunde/lieferanten/lastprofile-temperaturtabellen/ (accessed on 28 May 2021).
- 50Hertz Transmission GmbH. Zeitlicher Verlauf der EEG-Stromeinspeisung. Available online: http://www.50hertz.com/de/EEG/Veroeffentlichung-EEG-Daten/Verlauf-EEG-Stromeinspeisung (accessed on 27 October 2017).
- Weimer-Jehle, W.; Vögele, S.; Hauser, W.; Kosow, H.; Poganietz, W.-R.; Prehofer, S. Socio-technical energy scenarios: State-of-the-art and CIB-based approaches. Clim. Chang. 2020, 162, 1723–1741. [Google Scholar] [CrossRef]
- Weimer-Jehle, W. Cross-impact balances: A system-theoretical approach to cross-impact analysis. Technol. Forecast. Soc. Chang. 2006, 73, 334–361. [Google Scholar] [CrossRef]
- Weimer-Jehle, W. ScenarioWizard 4.3: Constructing Consistent Scenarios Using Cross-Impact Balance Analysis. Available online: http://www.cross-impact.org/ressourcen/ScenarioWizardManual_en.pdf (accessed on 5 August 2020).
- de Bruin, Y.B.; Lequarre, A.-S.; McCourt, J.; Clevestig, P.; Pigazzani, F.; Jeddi, M.Z.; Colosio, C.; Goulart, M. Initial impacts of global risk mitigation measures taken during the combatting of the COVID-19 pandemic. Saf. Sci. 2020, 128, 104773. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101922. [Google Scholar] [CrossRef] [PubMed]
- Kemp-Benedict, E. Converting qualitative assessments to quantitative assumptions: Bayes’ rule and the pundit’s wager. Technological Forecasting and Social Change 2010, 77, 167–171. [Google Scholar] [CrossRef]
- Madlener, R.; Alcott, B. Energy rebound and economic growth: A review of the main issues and re-search needs. Energy 2009, 34, 370–376. [Google Scholar] [CrossRef]
- Marttunen, M.; Lienert, J.; Belton, V. Structuring problems for Multi-Criteria Decision Analysis in practice: A literature review of method combinations. Eur. J. Oper. Res. 2017, 263, 1–17. [Google Scholar] [CrossRef]
- Witt, T. Transparency in Energy Scenario Studies: Survey of Different Approaches Combining Scenario Planning, Energy System Analysis, and Multi-criteria Analysis. In Proceedings of the 9th International Conference on Smart Cities and Green ICT Systems, Prague, Czech Republic, 2–4 May 2020; Klein, C., Helfert, M., Eds.; SCITEPRESS: Setúbal, Portugal, 2020; pp. 114–121. [Google Scholar]
- Comes, T.; Hiete, M.; Schultmann, F. An Approach to Multi-Criteria Decision Problems Under Severe Uncertainty. J. Multi-Crit. Decis. Anal. 2013, 20, 29–48. [Google Scholar] [CrossRef]
- Grant, R.M. Strategic planning in a turbulent environment: Evidence from the oil majors. Strat. Manag. J. 2003, 24, 491–517. [Google Scholar] [CrossRef]
- Schubert, D.K.J.; Thuß, S.; Möst, D. Does political and social feasibility matter in energy scenarios? Energy Res. Soc. Sci. 2015, 7, 43–54. [Google Scholar] [CrossRef]
- Li, F.G.; Trutnevyte, E.; Strachan, N. A review of socio-technical energy transition (STET) models. Technol. Forecast. Soc. Chang. 2015, 100, 290–305. [Google Scholar] [CrossRef]
- Alcamo, J. The SAS Approach: Combining Qualitative and Quantitative Knowledge in Environmental Sce-narios. In Environmental Futures: The Practice of Environmental Scenario Analysis, 1st ed.; Alcamo, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 123–150. ISBN 978-0-444-53293-0. [Google Scholar]
- Jhala, K.; Tasi, M.C.; Seltzer, S.E. Scenario Planning: Radiology Optimization for the New Era of Health Care Economics. J. Am. Coll. Radiol. 2020, 17, 190–193. [Google Scholar] [CrossRef] [PubMed]
- Edejer, T.T.-T.; Hanssen, O.; Mirelman, A.; Verboom, P.; Lolong, G.; Watson, O.J.; Boulanger, L.L.; Soucat, A. Projected health-care resource needs for an effective response to COVID-19 in 73 low-income and middle-income countries: A modelling study. Lancet Glob. Health 2020, 8, e1372–e1379. [Google Scholar] [CrossRef]
- Anderson, M.; Pitchforth, E.; Asaria, M.; Brayne, C.; Casadei, B.; Charlesworth, A.; Coulter, A.; Franklin, B.D.; Donaldson, C.; Drummond, M.; et al. LSE–Lancet Commission on the future of the NHS: Re-laying the foundations for an equitable and efficient health and care service after COVID-19. Lancet 2021, 397, 1915–1978. [Google Scholar] [CrossRef]
| References | MADM Algorithm | MP Aggregation | Uncertainty Consideration | Criteria Weights | Path Dependency | Specific Features |
|---|---|---|---|---|---|---|
| [47] | Generic | Not specified | No uncertainties | Dynamic | Not considered | Group decision-making |
| [48] | Generic | Decision tree | Probabilities of scenarios | Static | Modeled explicitly | |
| [49,50,51,52] | Single synthesizing criteria approach | Confidence levels of periods | Probabilities of scenarios | Static | Not considered | |
| [53] | Generic | Not specified | Not specified | Static | Modeled explicitly | |
| [54] | PROMETHEE II | Confidence levels of periods | No uncertainties | Static | Not considered | Varying thresholds in preference functions |
| [55] | PROMETHEE I | Confidence levels of periods | Monte Carlo simulations of performance scores | Static | Not considered | |
| [56] | PROMETHEE II | Arithmetic mean, weighted average (confidence levels of periods), mean of discounted net flows | No uncertainties | Static or dynamic | Modeled explicitly | Varying thresholds in preference functions are aggregated |
| [57] | PROMETHEE II | Arithmetic mean or weighted average | No uncertainties | Static or dynamic | Not considered | Weighting factor for MP aggregation can include a discount |
| This paper | PROMETHEE II | Arithmetic mean, mean of discounted net flows | Scenarios (without probabilities) | Static of dynamic | Modeled explicitly | Sensitivity analysis of discount factors |
| Power Supply | 2005 | 2010 | 2015 | 2020 | |
|---|---|---|---|---|---|
| Biogas power plant | 4816.68 (+4816.68) | 6811.31 (+1994.63) | 6811.31 | 6811.31 | |
| PV systems | 95.83 (+95.83) | 388.70 (+292.87) | 706.31 (+317.61) | 706.31 | |
| Wind power plant | - | - | - | - | |
| Ψ2 | Biogas power plant | 4816.68 (+4816.68) | 4816.68 | 4816.68 | 4816.68 |
| PV systems | - | - | 2700.94 (+2700.94) | 2700.94 | |
| Wind power plant | - | - | - | - | |
| Ψ3 | Biogas power plant | 4816.68 (+4816.68) | 4816.68 | 4816.68 | 4816.68 |
| PV systems | - | - | - | - | |
| Wind power plant | - | - | 2700.94 (+2700.94) | 2700.94 | |
| Biogas power plant | - | - | - | - | |
| PV systems | 95.83 (+95.83) | 95.83 | 1541.66 (+1445.83) | 2700.94 (+1159.28) | |
| Wind power plant | 4816.68 (+4816.68) | 4816.68 | 4816.68 | 4816.68 |
| A1: Hist | A2: + | A3: − | B1: Hist | B2: + | B3: − | C1: Hist | C2: + | C3: − | |
|---|---|---|---|---|---|---|---|---|---|
| A1: hist | 2 | 1 | 1 | 2 | 1 | 1 | |||
| A2: + | −1 | 1 | −1 | 1 | 1 | 1 | |||
| A3: − | 1 | 0 | 1 | 1 | 1 | 1 | |||
| B1: hist | 3 | 2 | −2 | 3 | 1 | 1 | |||
| B2: + | −1 | 3 | −3 | −1 | 3 | −2 | |||
| B3: − | 1 | −1 | 3 | −1 | −2 | 3 | |||
| C1: hist | 0 | 0 | 0 | 1 | 0 | 0 | |||
| C2: + | 0 | 0 | 0 | 0 | −1 | 0 | |||
| C3: − | 0 | 0 | 0 | 0 | 0 | −1 |
| Scenario | S1: Reference | S2: Best Case | S3: Worst Case | S4: Efficient Power Generation | S5: Lower Energy Demand | |
|---|---|---|---|---|---|---|
| Key Factor | ||||||
| A: Technical progress | Historic | Increased | Decreased | Increased | Historic | |
| B: Political support | Historic | Increased | Decreased | Historic | Historic | |
| C: Public contribution | Historic | Increased | Decreased | Historic | Increased | |
| Scenarios | Power from grid | Bioenergy | Ground-mounted PV | Wind energy | Power from grid | Bioenergy | Rooftop/ground-mounted PV | Wind energy | - | |
| S1: Reference Scenario | 2005 | 586 | 980 | 30 | 60 | 0.11 | 0.10 | 0.54 | 0.09 | 8021 |
| 2010 | 567 | 980 | 30 | 60 | 0.14 | 0.11 | 0.35 | 0.08 | 8021 | |
| 2015 | 511 | 980 | 30 | 60 | 0.13 | 0.11 | 0.21 | 0.08 | 8021 | |
| 2020 | 471 | 980 | 30 | 60 | 0.14 | 0.10 | 0.14 | 0.07 | 8021 | |
| S2: Best case | 2005 | 527.76 | 882.00 | 27.00 | 54.00 | 0.10 | 0.09 | 0.48 | 0.08 | 7860.58 |
| 2010 | 474.98 | 793.80 | 24.30 | 48.60 | 0.09 | 0.08 | 0.32 | 0.07 | 7703.37 | |
| 2015 | 427.49 | 741.42 | 21.87 | 43.74 | 0.08 | 0.07 | 0.19 | 0.06 | 7549.30 | |
| 2020 | 384.74 | 642.98 | 19.68 | 39.37 | 0.07 | 0.07 | 0.12 | 0.06 | 7398.32 | |
| S3: Worst case | 2005 | 645.04 | 1078.00 | 33.00 | 66.00 | 0.12 | 0.11 | 0.59 | 0.10 | 8181.42 |
| 2010 | 709.54 | 1185.80 | 36.30 | 72.60 | 0.14 | 0.12 | 0.39 | 0.11 | 8345.05 | |
| 2015 | 780.50 | 1304.38 | 39.93 | 79.86 | 0.15 | 0.13 | 0.23 | 0.12 | 8511.95 | |
| 2020 | 858.55 | 1434.82 | 43.92 | 87.85 | 0.17 | 0.15 | 0.15 | 0.13 | 8682.19 | |
| S4: Efficient power generation | 2005 | 547.67 | 960.4 | 29.4 | 58.8 | 0.11 | 0.10 | 0.54 | 0.09 | 8021 |
| 2010 | 555.46 | 941.19 | 28.81 | 57.62 | 0.14 | 0.11 | 0.35 | 0.08 | 8021 | |
| 2015 | 500.49 | 922.37 | 28.24 | 56.47 | 0.13 | 0.11 | 0.21 | 0.08 | 8021 | |
| 2020 | 462.01 | 903.92 | 27.67 | 55.34 | 0.14 | 0.10 | 0.14 | 0.07 | 8021 | |
| S5: Low energy demand in 2020 | 2005 | 586 | 980 | 30 | 60 | 0.11 | 0.10 | 0.54 | 0.09 | 8021 |
| 2010 | 567 | 980 | 30 | 60 | 0.14 | 0.11 | 0.35 | 0.08 | 8021 | |
| 2015 | 511 | 980 | 30 | 60 | 0.13 | 0.11 | 0.21 | 0.08 | 8021 | |
| 2020 | 471 | 980 | 30 | 60 | 0.14 | 0.10 | 0.14 | 0.07 | 6416.8 | |
| Year | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LCOE | Land Use | CO2 | SS | LCOE | Land Use | CO2 | SS | LCOE | Land Use | CO2 | SS | LCOE | Land Use | CO2 | SS | ||
| S1 | 2005 | 11.01 | 472.03 | 1823 | 61.25 | 10.51 | 472.03 | 1879 | 60.05 | 10.51 | 472.03 | 1879 | 60.05 | 10.29 | 28.90 | 1823 | 47.63 |
| 2010 | 12.01 | 667.57 | 465 | 89.77 | 11.61 | 472.03 | 1816 | 60.05 | 11.61 | 472.03 | 1816 | 60.05 | 11.36 | 28.90 | 1762 | 47.63 | |
| 2015 | 12.24 | 667.57 | 257 | 93.38 | 13.97 | 472.03 | 257 | 83.95 | 9.42 | 488.24 | 257 | 87.83 | 12.47 | 28.90 | 849 | 60.75 | |
| 2020 | 12.28 | 667.57 | 237 | 93.38 | 14.01 | 472.03 | 237 | 83.95 | 9.47 | 488.24 | 237 | 87.83 | 12.59 | 28.90 | 237 | 65.41 | |
| S2 | 2005 | 9.91 | 424.83 | 1556 | 62.50 | 9.44 | 424.83 | 1606 | 61.28 | 9.44 | 424.83 | 1606 | 61.28 | 9.24 | 26.01 | 1556 | 48.20 |
| 2010 | 10.13 | 583.22 | 239 | 93.47 | 9.05 | 424.83 | 1371 | 62.53 | 9.05 | 424.83 | 1,371 | 62.53 | 8.86 | 26.01 | 1326 | 48.77 | |
| 2015 | 10.57 | 583.22 | 14 | 95.06 | 12.60 | 424.83 | 14 | 86.08 | 8.07 | 436.64 | 14 | 90.18 | 10.61 | 26.01 | 509 | 62.62 | |
| 2020 | 10.63 | 583.22 | −46 | 95.54 | 12.71 | 424.83 | −46 | 86.78 | 8.08 | 436.64 | −46 | 90.92 | 11.32 | 26.01 | −46 | 67.60 | |
| S3 | 2005 | 12.12 | 519.24 | 2109 | 60.04 | 11.58 | 519.24 | 2170 | 58.87 | 11.58 | 519.24 | 2170 | 58.87 | 11.34 | 31.79 | 2109 | 47.07 |
| 2010 | 13.16 | 755.84 | 812 | 86.27 | 12.12 | 519.24 | 2504 | 57.72 | 12.12 | 519.24 | 2504 | 57.72 | 11.87 | 31.79 | 2436 | 46.51 | |
| 2015 | 13.69 | 755.84 | 776 | 88.31 | 15.38 | 519.24 | 776 | 81.80 | 11.69 | 540.81 | 776 | 85.32 | 13.90 | 31.79 | 1681 | 58.87 | |
| 2020 | 13.91 | 755.84 | 1000 | 86.58 | 15.57 | 519.24 | 1000 | 81.07 | 11.96 | 540.81 | 1000 | 84.45 | 14.13 | 31.79 | 1000 | 63.18 | |
| S4 | 2005 | 11.01 | 462.59 | 1786 | 61.25 | 10.51 | 462.59 | 1841 | 60.05 | 10.51 | 462.59 | 1841 | 60.05 | 10.29 | 28.32 | 1786 | 47.63 |
| 2010 | 12.01 | 650.39 | 456 | 89.77 | 11.61 | 462.59 | 1780 | 60.05 | 11.61 | 462.59 | 1780 | 60.05 | 11.36 | 28.32 | 1727 | 47.63 | |
| 2015 | 12.24 | 650.39 | 252 | 93.38 | 13.97 | 462.59 | 252 | 83.95 | 9.42 | 477.85 | 252 | 87.83 | 12.47 | 28.32 | 832 | 60.75 | |
| 2020 | 12.28 | 650.39 | 233 | 93.38 | 14.01 | 462.59 | 233 | 83.95 | 9.47 | 477.85 | 233 | 87.83 | 12.59 | 28.32 | 233 | 65.41 | |
| S5 | 2005 | 11.01 | 472.03 | 1823 | 61.25 | 10.51 | 472.03 | 1879 | 60.05 | 10.51 | 472.03 | 1879 | 60.05 | 10.29 | 28.90 | 1823 | 47.63 |
| 2010 | 12.01 | 667.57 | 465 | 89.77 | 11.61 | 472.03 | 1816 | 60.05 | 11.61 | 472.03 | 1816 | 60.05 | 11.36 | 28.90 | 1762 | 47.63 | |
| 2015 | 12.24 | 667.57 | 257 | 93.38 | 13.97 | 472.03 | 257 | 83.95 | 9.42 | 488.24 | 257 | 87.83 | 12.47 | 28.90 | 849 | 60.75 | |
| 2020 | 11.89 | 667.57 | −519 | 97.96 | 14.06 | 472.03 | −519 | 91.46 | 8.38 | 488.24 | −519 | 95.25 | 12.28 | 28.90 | −519 | 71.21 | |
| Criterion | Unit | Type | Weight | |||||
|---|---|---|---|---|---|---|---|---|
| LCOE | cent/kWh | Min | 0.25 | 0.91 | 2.19 | 4.02 | 0.91 | 1.14 |
| Land use | ha/a | Min | 0.25 | 127.73 | 111.44 | 144.81 | 124.41 | 127.73 |
| CO2 emissions | t/a | Min | 0.25 | 270.20 | 226.40 | 338.20 | 264.80 | 270.20 |
| Self-sufficiency | % | Max | 0.25 | 8.43 | 8.94 | 7.95 | 8.43 | 8.43 |
| Rank | Rank | Rank | Rank | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | −0.099 | 4 | 0.117 | 1 | 0.076 | 2 | 0.000 | 2 | |
| −0.021 | 2.5 | −0.086 | 3.5 | −0.194 | 3 | −0.278 | 4 | ||
| −0.021 | 2.5 | −0.086 | 3.5 | 0.390 | 1 | 0.306 | 1 | ||
| 0.141 | 1 | 0.055 | 2 | −0.271 | 4 | −0.028 | 3 | ||
| S2 | −0.085 | 4 | 0.000 | 2 | 0.049 | 2 | 0.020 | 2 | |
| −0.024 | 2.5 | −0.034 | 3.5 | −0.196 | 3 | −0.278 | 4 | ||
| −0.024 | 2.5 | −0.034 | 3.5 | 0.401 | 1 | 0.320 | 1 | ||
| 0.133 | 1 | 0.067 | 1 | −0.254 | 4 | −0.062 | 3 | ||
| S3 | −0.151 | 4 | 0.000 | 2 | 0.040 | 2 | −0.062 | 3 | |
| −0.008 | 2.5 | −0.045 | 3.5 | −0.176 | 3 | −0.247 | 4 | ||
| −0.008 | 2.5 | −0.045 | 3.5 | 0.410 | 1 | 0.334 | 1 | ||
| 0.168 | 1 | 0.090 | 1 | −0.274 | 4 | −0.025 | 2 | ||
| S4 | −0.099 | 4 | 0.117 | 1 | 0.076 | 2 | 0.000 | 2 | |
| −0.021 | 2.5 | −0.086 | 3.5 | −0.195 | 3 | −0.278 | 4 | ||
| −0.021 | 2.5 | −0.086 | 3.5 | 0.390 | 1 | 0.307 | 1 | ||
| 0.141 | 1 | 0.055 | 2 | −0.271 | 4 | −0.028 | 3 | ||
| S5 | −0.068 | 4 | 0.144 | 1 | 0.072 | 2 | −0.047 | 3 | |
| −0.026 | 2.5 | −0.089 | 3.5 | −0.194 | 3 | −0.258 | 4 | ||
| −0.026 | 2.5 | −0.089 | 3.5 | 0.390 | 1 | 0.333 | 1 | ||
| 0.120 | 1 | 0.034 | 2 | −0.267 | 4 | −0.029 | 2 | ||
| S1 | S2 | S3 | S4 | S5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LCOE | - | 10.85 | - | 8.02 | - | 4.25 | - | 10.84 | - | 8.91 |
| Land use | 35.16 | 9.66 | 36.27 | 2.36 | 35.63 | - | 35.18 | 9.66 | 35.89 | 9.18 |
| CO2 emissions | - | - | - | - | - | - | - | - | - | - |
| Self-sufficiency | 37.92 | 12.42 | - | 10.86 | - | 12.22 | 37.93 | 12.41 | 39.7 | 11.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witt, T.; Klumpp, M. Multi-Period Multi-Criteria Decision Making under Uncertainty: A Renewable Energy Transition Case from Germany. Sustainability 2021, 13, 6300. https://doi.org/10.3390/su13116300
Witt T, Klumpp M. Multi-Period Multi-Criteria Decision Making under Uncertainty: A Renewable Energy Transition Case from Germany. Sustainability. 2021; 13(11):6300. https://doi.org/10.3390/su13116300
Chicago/Turabian StyleWitt, Tobias, and Matthias Klumpp. 2021. "Multi-Period Multi-Criteria Decision Making under Uncertainty: A Renewable Energy Transition Case from Germany" Sustainability 13, no. 11: 6300. https://doi.org/10.3390/su13116300
APA StyleWitt, T., & Klumpp, M. (2021). Multi-Period Multi-Criteria Decision Making under Uncertainty: A Renewable Energy Transition Case from Germany. Sustainability, 13(11), 6300. https://doi.org/10.3390/su13116300






