Did Noise Pollution Really Improve during COVID-19? Evidence from Taiwan

Abstract

Background and objectives: The impacts of COVID-19 are like two sides of one coin. During 2020, there were many research papers that proved our environmental and climate conditions were improving due to lockdown or large-scale restriction regulations. In contrast, the economic conditions deteriorated due to disruption in industry business activities and most people stayed at home and worked from home, which probably reduced the noise pollution. Methods: To assess whether there were differences in noise pollution before and during COVID-19. In this paper, we use various statistical methods following odds ratios, Wilcoxon and Fisher’s tests and Bayesian Markov chain Monte Carlo (MCMC) with various comparisons of prior selection. The outcome of interest for a parameter in Bayesian inference is complete posterior distribution. Roughly, the mean of the posterior will be clear with point approximation. That being said, the median is an available choice. Findings: To make the Bayesian MCMC work, we ran the sampling from the conditional posterior distributions. It is straightforward to draw random samples from these distributions if they have regular shapes using MCMC. The case of over-standard noise per time frame, number of noise petition cases, number of industry petition cases, number of motorcycles, number of cars and density of vehicles are significant at α = 5%. In line with this, we prove that there were differences of noise pollution before and during COVID-19 in Taiwan. Meanwhile, the decreased noise pollution in Taiwan can improve quality of life.

1. Introduction

COVID-19 has caused tremendous, problematic situations in the world’s communities. These include poverty, that further disrupted sustainable livelihoods, hunger and disease, increasing socio-economic disparities attributable to educational disparities, alienation and foreign policy [1,2,3] and they affect the responses in critical policy areas, including public health directives and financial responses. In the presence of such obstacles, each nation uses its own strategies [4,5,6,7,8].

COVID-19 has a clear impact on all parties included in the Penta Helix model, including academia, government, industry, non-governmental organization (NGOs) and civic sectors of society, and social entrepreneurs, the agriculture sector [9], macro-economic factors [10] and social vulnerability [11]. There are positive environmental effects that can be witnessed, including the reduction in air emissions in the atmosphere [12,13,14,15,16] and also noise pollution, proven by outdoor and neighbor noise, acoustic measurements and complaints [17,18,19,20,21,22].

Noise pollution cannot be seen by the eye but still causes suffering. Noise pollution can be inferred when disturbance triggers different kinds of human health conditions. All noises or movements are measured in dB units. Previous studies have proven that noise pollution has a very strong impact on human health [23], including hearing loss [24], cardiovascular effects [25], anger and smoking addiction [26], and a negative impact on the physiology, behavior and fitness of marine organisms [27,28]. Noise pollution is a persistent response to sudden sound, and is damaging to health and the environment, including animals and plants. It generally involves outdoor annoyances from scooters, motorbikes and traffic noise [29,30,31,32], longitudinal annoyance [33], viaduct rail transit [34] and seaports [35]. Sounds under 70dB are considered to also likely impact living organisms, and exposure to these sounds tends to persist over a prolonged period, for example, if people work 8 h a day near to a major road. To overcome this, the WHO issued environmental noise guidelines for the European region [36].

Previous research used a dataset using 12 monitoring stations’ data in Dublin, Ireland [17], noise levels averaged over 14 days in Madrid [18] and the port of Koper and the adjacent residential areas in Koper and Ankaran [35]. The contribution of this article is to examine whether there are differences regarding noise pollution in Taiwan before and during COVID-19. In line with this, the Local Environmental Protection Bureaus, the Environmental Protection Administration (EPA), Executive Yuan, Taiwan launched a dataset that provides information on reports of people who felt disturbed by noise pollution originating from industrial activities, households and others. Therefore, we address the question of whether it is true that before and during COVID-19, there was a significance difference regarding noise reduction. Taiwan will only see lockdowns if 100 COVID cases perday. In line with this, for the objective of this research, we ran a Bayesian MCMC to calculate the posterior odds of the reported cases of noise pollution. The use of prior probability distributions represents a powerful mechanism for incorporating information from studies [37,38,39].

This article is organized as follows. In Section 2, we review the materials and methods for using Bayesian MCMC. The construction of Bayesian Markov chain Monte Carlo (MCMC) and evidence of noise reduction during COVID-19 are examined in Section 3 via simulation studies. Finally, Section 4 gives a summary and discussion.

2. Materials and Methods

2.1. Busy Areas of Taiwan and Sources of Noise Pollution

The most common source of noise pollution is motor vehicle noise and industrial parks. In line with this, the EPA reports that the primary sources for motor vehicle noise are engine noise, intake, emissions and wheels. In a previous inspection scheme, however, the noise from vehicles, intakes and exhaust was reduced considerably. Noise from city traffic should not be restricted to the control systems of cars with advances in automotive technology; the noise from tires has steadily gained prominence in relation to this. Recently enacted limits for noise reduction by the United Nations and EU and inspection procedures improved automotive acceleration noise test results significantly. The EPA referred to recent international rules to draft the current amendments to significantly decrease the effects of urban road pollution on communities and follow the Sustainable Development Goal (SDG) Indicators for Health and Pollution. The Environmental Protection Administration, ROC (Taiwan) focus on volatile organic air pollution control and emission Standards and, in particular, on the latest European noise guidelines (United Nations/ECE R51.03).

Taiwan has six industrial parks, Changhua Coastal Industrial Park, Hsinchu Industrial Park, Linhai Industrial Park, Nankang Software Park, Tai Yuen Hi-Tech Industrial Park and Taichung Gateway. Activities that take place in these areas have a high impact on noise pollution in Taiwan. Together with the increasing development of industry, industries are established at once and then spread throughout Taiwan. Throughout the early period, the government did not attempt to provide factory locations in industrial parks, and many industries grew mainly along major highways and also in distinct locations, due to an inability to use and manage land and the conditions properly.

Currently, there are four international airports in Taiwan: Taiwan Taoyuan International Airport, Kaohsiung International Airport, Taichung International Airport and Taipei Songshan Airport. Activities that occur at the airports also cause noise pollution from the roar of aircraft, which causes disturbances to people living in residential areas around the airports. Noise is an unpleasant part in the airport environment, induced by the running of the airport, in other words, the noise of aircraft engines. This activity triggers noise that impacts operations and residents who live close to the airport. The psychological effect of noise on humans is shock as well as inhibition of concentration and impaired conversational contact and may further affect work performance, including safe systems of work, as well as cause hearing problems and distress at a rather severe stage. The current measurement method uses the CNS-7129 noise meter, which is also known as a sound level meter, and is compliant with the national Taiwanese guidelines, or the aircraft noise level measuring meter IEC-1672 Class 1, which is compliant with the norms of the IEC. The calculated noise levels could be used to test the aircraft noise predictor readings such as the average sound DNL. The indicated techniques are used for assessing non-stationary noise in the airport environment and also for monitoring indoor DNL [40].

There are 151 Local Environmental Protection Bureaus in Taiwan that calculate time frames with over-standard environmental noise. Therefore, people living in the area can report their discomfort regarding noise pollution.

2.2. Bayesian Regression MCMC

In the heart of statistics analysis, the regression and prediction model is as a tool in decision making. In non-parametric contexts, the Gaussian process combines a Bayesian regression model with parameter metrics and a Gaussian process prior to having an optimal solution. A generative model can collect new information while mimicking the representations of currently available information.

In terms of statistics, this model can be defined as a procedure for sampling data. $a$ is derived from the data distribution, $p\left(a\right)$ is derived from the provided data collection $A=\left\{a\right\}$. Typically, we define a latent variable $l$ to describe the semantics of the data and $A$ to define the distribution $p\left(a\right),a|A$. Then, the latent variable $l$ is realized by the $p\left(l|a\right)$ when the data $a$ are given. This is the Bayesian statistics interpretation of latent variables, which we are focused on. The Bayesian method, which is beneficial in solving the generative model problem, offers several realistic approaches to exploring the latent space, such as sampling. Below is a thorough explanation of Bayesian statistics in Equation (1) [37].

$$E\left[f\right]=\int f\left(l\right) p\left(l\right)dl$$

(1)

The joint distribution $p\left(l,a\right)=p\left(l|a\right)p\left(a\right)$ is defined by the likelihood function $p\left(l|a\right)$ and the prior $p\left(a\right)$. The prior probability $p(a)$ captures our assumption about $a$, until reviewing the information. In most situations, the posterior distribution is required for the purpose of obtaining expectations, for example, in order to make predictions. Therefore, the fundamental problem we are trying to solve is finding expectations for some function $f\left(l\right)$ with respect to a probability distribution $p\left(l\right)$. In the case of a continuous variable $l$, our goal is to solve the expectation in Equation (2) [41].

$$p\left(l|a\right)=\frac{p\left(a,l\right)}{p\left(a\right)}$$

(2)

If $l$ is a discrete variable, the integral will be substituted. In many applications, the expectations are too complex to be empirically calculated using analytical methods. The key idea of the Monte Carlo approximation is to obtain independent samples $l^i$ from the distribution $p\left(l\right)$ and use them for approximation. Using the set of samples $l^i=1,2, \dots ,N$ and we can approximate the expectation in Equation (3) [42]:

$$\overline{f}=\frac{1}{N}{\displaystyle \sum }_{i=1}^{N}f\left(l^i\right)$$

(3)

We can easily confirm that the estimator f has a correct mean because $E\left[f\right]=E\left[f\right]$. The estimator converges to the actual expectation according to the ‘law of large numbers’, and we can assume high precision once given ten to twenty independent samples. The log of marginal likelihood of the model (LOGMARG), which is approximately $\frac{1}{2}BIC$, is as follows [43]:

$$\begin{gathered} BIC=-2\ln \left(\widehat{likelihood}\right)+\left(p+1\right)\ln \left(n\right) \\ likelihood=p\left(y_i|\alpha ,\beta , {\sigma }^2\right)=\mathcal{L}(\alpha , \beta ,{\sigma }^2) \end{gathered}$$

(4)

2.3. Dataset

This paper uses a dataset from Local Environmental Protection Bureaus, the EPA, Executive Yuan, Taiwan, from 2015 to the 4th quarter of 2020. We only focus on the dataset regarding complaints and petitions related to noise pollution. The dataset consists of the cases of over-standard noise per time frame, number of noise petitions, number of industry petitions, number of motorcycles, number of cars and density of vehicles. Meanwhile, we provide the nomenclature in Nomenclature.

3. Results

3.1. The Construction Steps of Bayesian MCMC

Therefore, we use a generic and powerful framework called Markov chain Monte Carlo (MCMC) which allows sampling from a large class of distributions and can manage the large dimensions of the sample space. Markov chain Monte Carlo (MCMC) is an algorithm in which the sample $l_i$ of the state $l$ is connected to the Markov chain and iteratively discovers the state space. The purpose of the algorithm is to let the sampled $l^i$ mimic the samples from the posterior $p\left(l|A\right)$, where $A$ is the set of data $s$. For simplicity, $l^i$ is assumed to be in discrete space in this section, where $l^i|\left\{z_1,z_2,\dots ,z_s\right\}$. The stochastic process zi is called a Markov process when it satisfies Equation (5).

$$p\left(l^i|l^1,l^2,\dots , l^{i-1}\right)=p\left(l^i|l^{i-1}\right)$$

(5)

The Markov chain in the MCMC algorithm should be unobservable and time-varying, which can be fulfilled when the chain satisfies the thorough balance condition of the Metropolis–Hastings algorithm, the most popular algorithm programmed to fulfill the comprehensive balance condition [38,39,44,45,46]. To bring these algorithms into effect, the proposal distribution must be well established. If the proposal distribution produces a significant number of rejected samples, the convergence speed is sluggish, as proven in Equation (6).

$$Z\left(l_f,l_c\right)=\min \frac{p\left(l_f\right)q\left(l_c|l_f\right)}{p\left(l_c\right)q\left(l_f|l_c\right)}$$

(6)

3.2. Evidence of Noise Pollution Reduction

Based on

Table 1. Information on noise reduction before and during COVID-19.

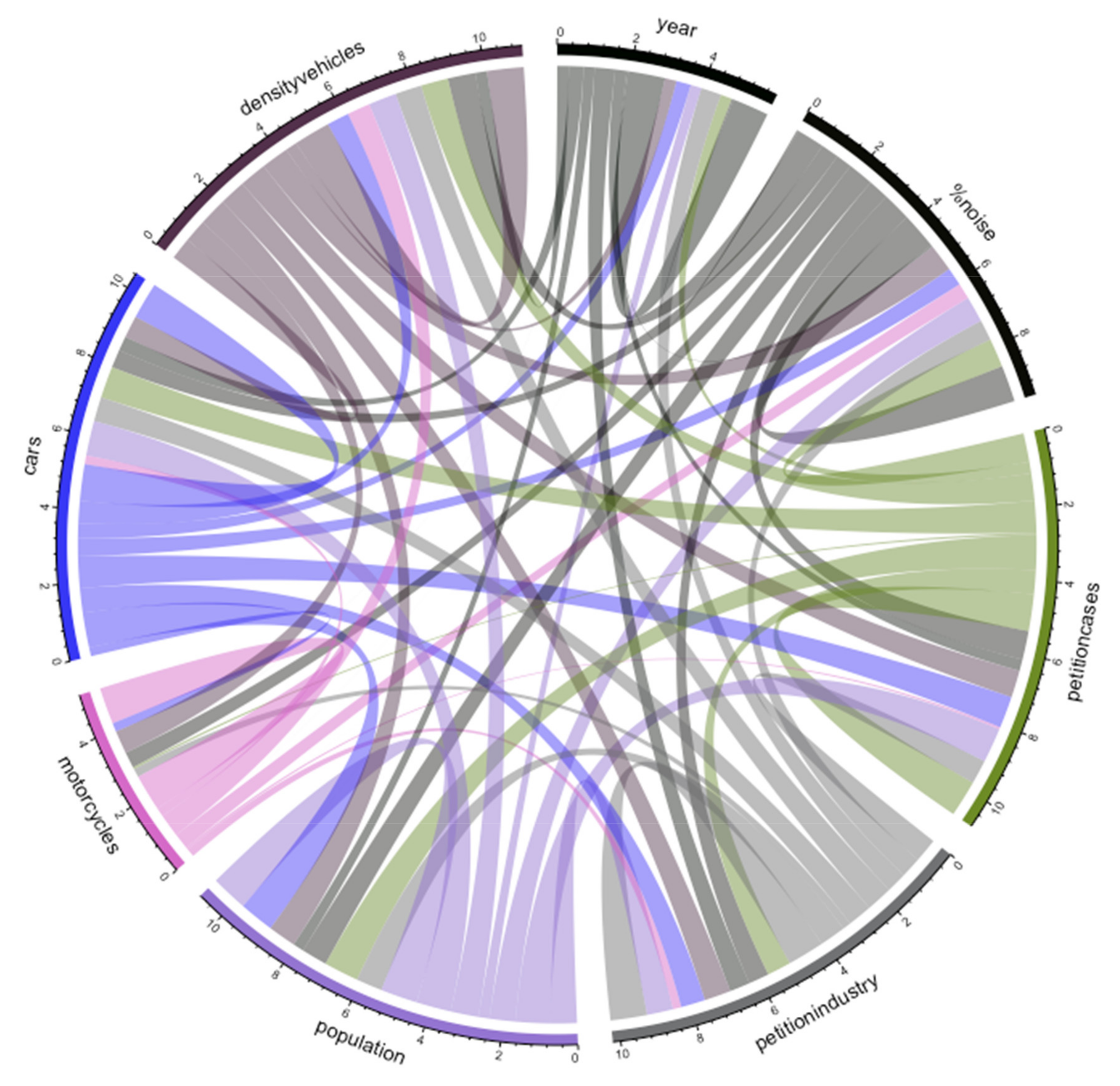
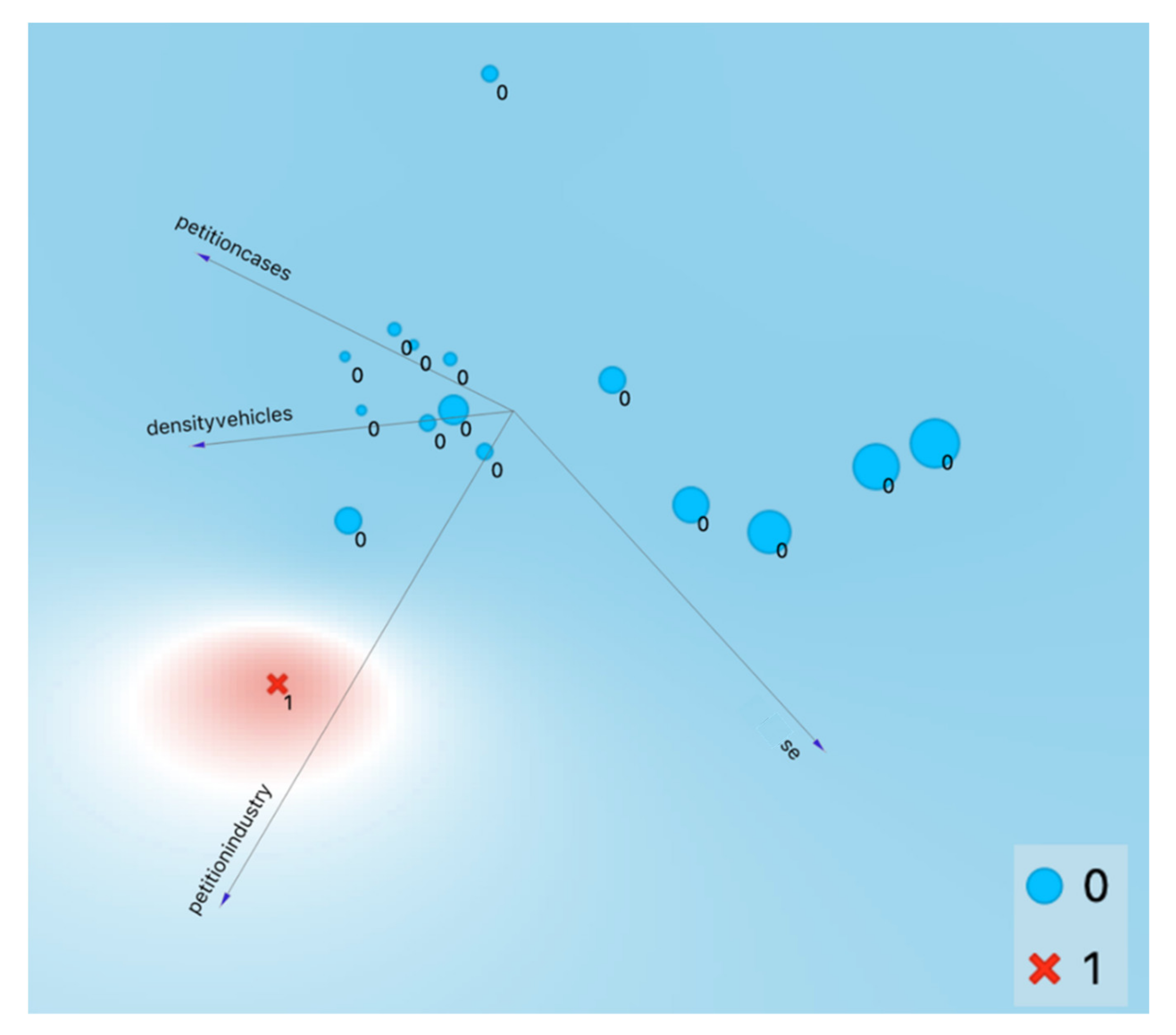
Descriptive		Cases of Over-Standard Noise per Time Frame	Petition Cases	Industry Petitions	Motorcycles	Cars	Density of Vehicles
Before COVID-19	Min.	2	39,636	25,445	13,195,265	6,667,542	549
	1st	3	58,722	29,201	13,719,027	6,769,454	587
	Median	4	81,368	32,034	13,968,198	7,287,146	595
	Mean	6	72,394	31,628	14,110,811	7,351,197	593
	3rd	9	87,076	33,998	14,425,164	7,869,013	606
	Max.	14	96,739	40,174	15,173,602	8,193,237	617
During COVID-19	Min.	6	85,457	31,142	13,992,922	8,118,885	611
	1st	6	87,926	33,400	14,020,632	8,137,473	612
	Median	7	90,394	35,658	14,048,343	8,156,061	613
	Mean	7	90,394	35,658	14,048,343	8,156,061	613
	3rd	7	92,863	37,916	14,076,053	8,174,649	615
	Max.	8	95,331	40,174	14,103,763	8,193,237	616
Statistical Test	p-value Wilcoxon test (before and during COVID19)	0.58680	0.00002	0.66670	0.50000	0.50000	0.66700
	Fisher’s test (before and during COVID-19)	0.43750	0.02564	0.00020	0.00050	0.00051	0.00050

, it can be seen that there was a significant difference in the cases of over-standard noise per time frame before and during COVID-19 according to the reduction in the number of noise pollution petition reports submitted by each household to the Environmental Protection Administration, Taiwan. The p-value of Wilcoxon’s and Fisher’s tests is significant at $\alpha =5\%.$ Meanwhile, there are also differences in the industry petitions of complaints about noise pollution. For vehicles, there is a significant difference in the values of motorcycles, cars and vehicle density both before and during the COVID-19 period. Since in Taiwan there was no lockdown nor large-scale restriction, then the number of cases of over-standard noise per time frame before and during COVID-19 should be the same. Yet, the density of vehicles was different before and during COVID-19. The petition cases represent the number of people in Taiwan who submit complaints about noise due to feeling depression because of noise around major cities. Household activities ran as usual, for example, people went to supermarkets or traditional markets to buy household groceries. In line with this, with the p-value of both Wilcoxon’s and Fisher’s tests, there is a significant difference in the values of motorcycles, cars and vehicle density both before and during the COVID-19 period.

Figure 1 represents the connections between various entities known as nodes and it can be seen that there is a significant connection between vehicles, connecting motorcycles and cars to the number of petitions. A label on the outer part of the circular layout represents each entity. There are significant differences, especially for the number of noise pollution disturbance petitions due to industrial activity. The highest correlation value between petition cases and the population is (0.95). It means that the people of Taiwan are very active in giving their opinion to the government. In addition, the correlation value between the population and the petitioning industry of (0.71). In represents, people who live in the manufacturing industry area and its surroundings also have active participation in reporting on noise pollution. This study also highlighted that all percentage noise values have negative values such as petition cases (−0.78), petition industry (−0.56), motorcycles (−0.43), cars (−0.49), and density vehicles (−0.75), respectively. All things considered during the COVID-19 pandemic there was a reduction in activity by the local people in Taiwan.

Figure 2 explains the linear projection with the labels before COVID-19 (0) and during COVID-19 (1). It is clear that there are differences in projection values, especially for the number of industrial petitions. The number of reports of discomfort due to noise pollution decreased during the COVID-19 pandemic. However, during the first month of COVID-19, most of industrial businesses temporarily closed. In addition, industrial noise control was carried out to prevent industrial noise and protect workers from the harmful effects of high-intensity noise exposure. Covering frequency components (partial or complete acoustic enclosure), acoustic barriers, noise shielding and noise lagging are some commonly implemented procedures. In addition, noise control can also be implemented administratively by regulating work patterns. A final measure is the use of personal protective equipment to reduce noise, such as earplugs and ear protection. All the statistical analyses proved there was a significant difference in noise pollution before and during COVID-19. However, during COVID-19, the Taiwan government’s policy and response was that no lockdown would be implemented [47]. Taiwan’s COVID-19 control has been a great accomplishment, mostly due to early moves to observe incoming travelers from Wuhan, China, and strict regulations for lockdown and facemasks. There was no lockdown in the nation and fewer than 1027 cases were recorded in April 2021.

3.3. Measuring Noise Pollution Using Bayesian MCMC

The Bayesian approach was developed by Bayes to assess a population’s initial distribution type prior [37,48,49]. The whole dataset would then be associated with information from the sample to estimate population parameters [39]. In

Table 2. Comparing prior selection Bayesian regression with best model *.

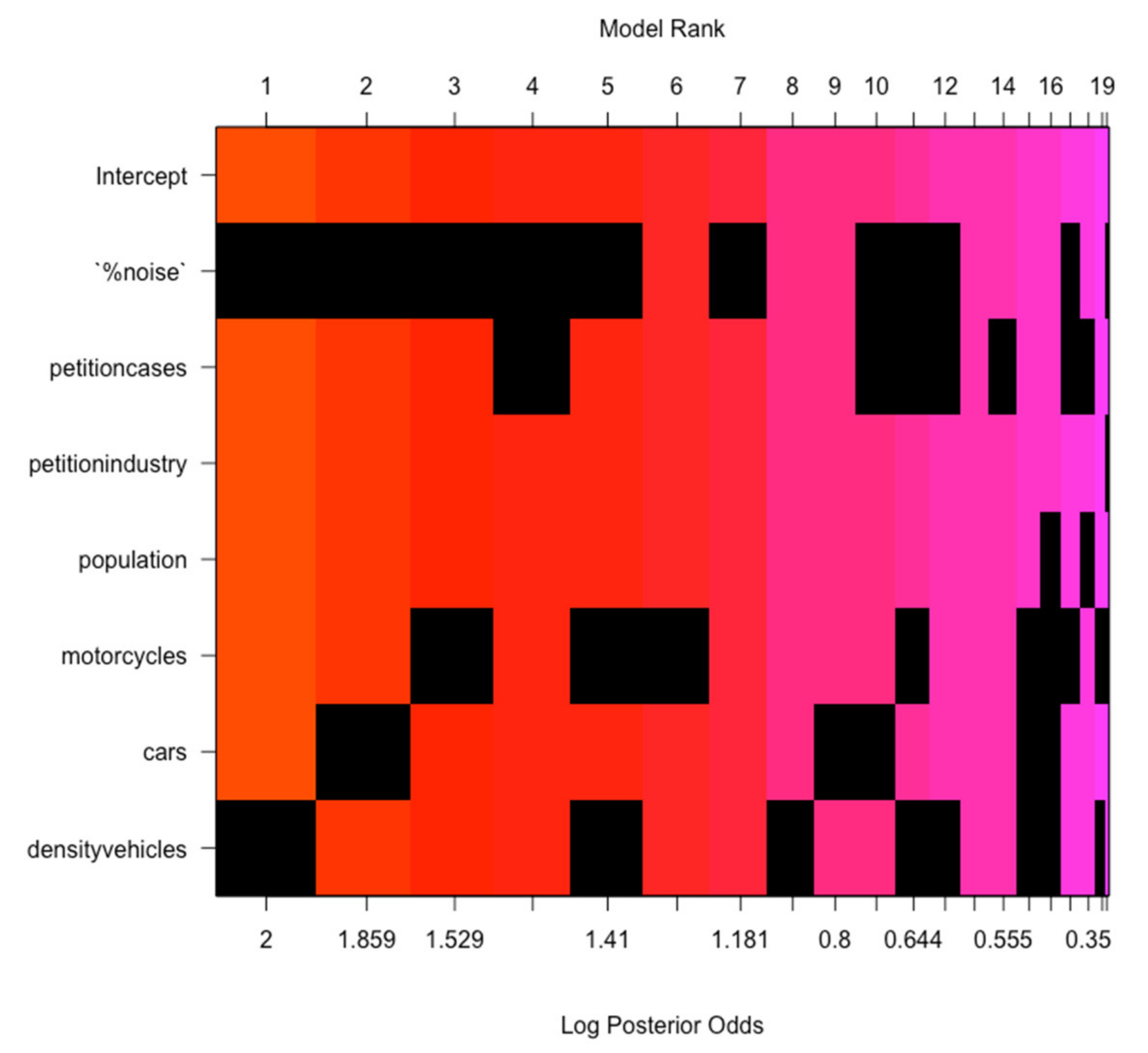
Prior	R2	Dim	LOGMARG	POSTROBS
AIC *	84.70%	6	2.845605	0.0644
g-prior	30.7%	2	1.131336	0.0785
ZS-null	30.7%	2	0.062679	0.0449
ZS-full	48.2%	4	3.190674	0.0316
Hyper-g	64.6%	6	0.820071	0.0304
Hyper-g-n	30.7%	2	0.613492	0.0414
Hyper-g-Laplace	40.86%	3	0.7213114	0.0465
Hyper-g-n	30.7%	2	0.6134929	0.0307
EB-local	64.70%	6	1.520647	0.0267
EB-global	64.70%	6	1.377268	0.0200

, regarding the noise pollution modeling, we show 10 different priors and the best prior is Bayesian-MCMC-AIC with R² 84.70%. If we look in more detail at Table 2, the prior setting for EB-local and EB-global has the same value. The objectives of the two priors are to find the global empirical Bayes estimates of g in Zellner’s g-prior and model probabilities [50].

Figure 3 explains the prior odds multiplied by the probability ratio equaling the posterior odds, according to the odds type of Bayes’ rule. We take the log of both sides of this equation to obtain a similar equation that uses addition rather than multiplication. The Bayesian MCMC with a prior AIC selection model can explain 84.70% of the noise reduction in Taiwan, which can be explained by the cases of over-standard noise per time frame, number of industry petition cases, motorcycles, cars and density of vehicles.

To some objective Bayesians, the prior represents neutral knowledge and the resulting posterior is to give the probability of a proposition arising from just the data. Various other priors have been developed. We believe that such a goal is naturally achieved via the likelihood approach which uses all the information in the data, as we shall discuss [51,52,53,54,55,56]. The core of Bayesian statistics is inference [37,49]. The inference is made up of three components. The first component is the prior distribution of parameters $\theta$, $\pi \left(\theta \right)$ representing the uncertainty of parameters before seeing data $D$ [24]. The second component is the likelihood $\pi \left(\theta \right)$ which represents the probability that we might have data $D$ given $\theta$. The last component is the posterior distribution $\theta$ after seeing data $D$. In line with this, $\pi (\theta |D)$ represents the updated belief or probability of $\theta$ after seeing data $D.$ With these three components, we can derive inference using Bayes’ rule, such that $\pi \left(\theta |D\right)=\frac{ \pi \left(\theta \right)\pi (D|\theta )}{\int \pi \left(\theta \right)\pi (D|\theta )d\theta }$ and we provide the calculation of posterior computation in Appendix A.

4. Conclusions

The main conclusion from this analysis is that there were differences before and during COVID-19 in Taiwan as evidenced by the Wilcoxon test and the Fisher test. The Bayesian model that provides high accuracy is the Bayesian-MCMC-AIC prior with R² 84.70%. The Environmental Protection Administration (EPA), Executive Yuan, Taiwan declared on 21 January 2010 the Environmental Sound Level Standard to preserve adequate noise levels. In compliance with Article 20(3) of the Noise Control Act, the EPA has proposed the Environmental Noise Measurement Methods. At the moment, large-scale noise management activities, including local councils, event promoters and local suppliers, are expected to take responsibility for noise reduction and regulation prior to and after activities to maintain a safe atmosphere. Preventive steps include the elimination of noise at the sound source, the modification of the sound propagation route and the preservation of levels of the reception of noise. Any individual in violation of noise reduction requirements will be liable to a fine of NTD 3000–30,000. Several city councils also advised activity planners and local suppliers that they would cooperate with the regulations. City municipalities have already adopted these guidelines into their autonomous rules on the protection of large-scale activities. In a nutshell, as in Taiwan’s pre-COVID-19 pandemic strategy, the Taiwan CDC, in coordination with the Central Epidemic Command Center (CECC), held the responsibility of controlling the pandemic. Taiwanese officials were alerted to the outbreak in China by established action networks, triggering an urgent response, including screening of all airline passengers. We do not know when COVID-19 will end, but between the dynamics that occur, we see a positive impact, especially concerning reducing noise pollution. COVID-19 has had a positive impact on the environment, and this paper has proven that reductions in the amount of noise pollution in Taiwan were related to the number of petition cases. Future research should examine types of emissions and GHG reduction.