Poverty and Physical Geographic Factors: An Empirical Analysis of Sichuan Province Using the GWR Model
Abstract
1. Introduction
2. Literature Review
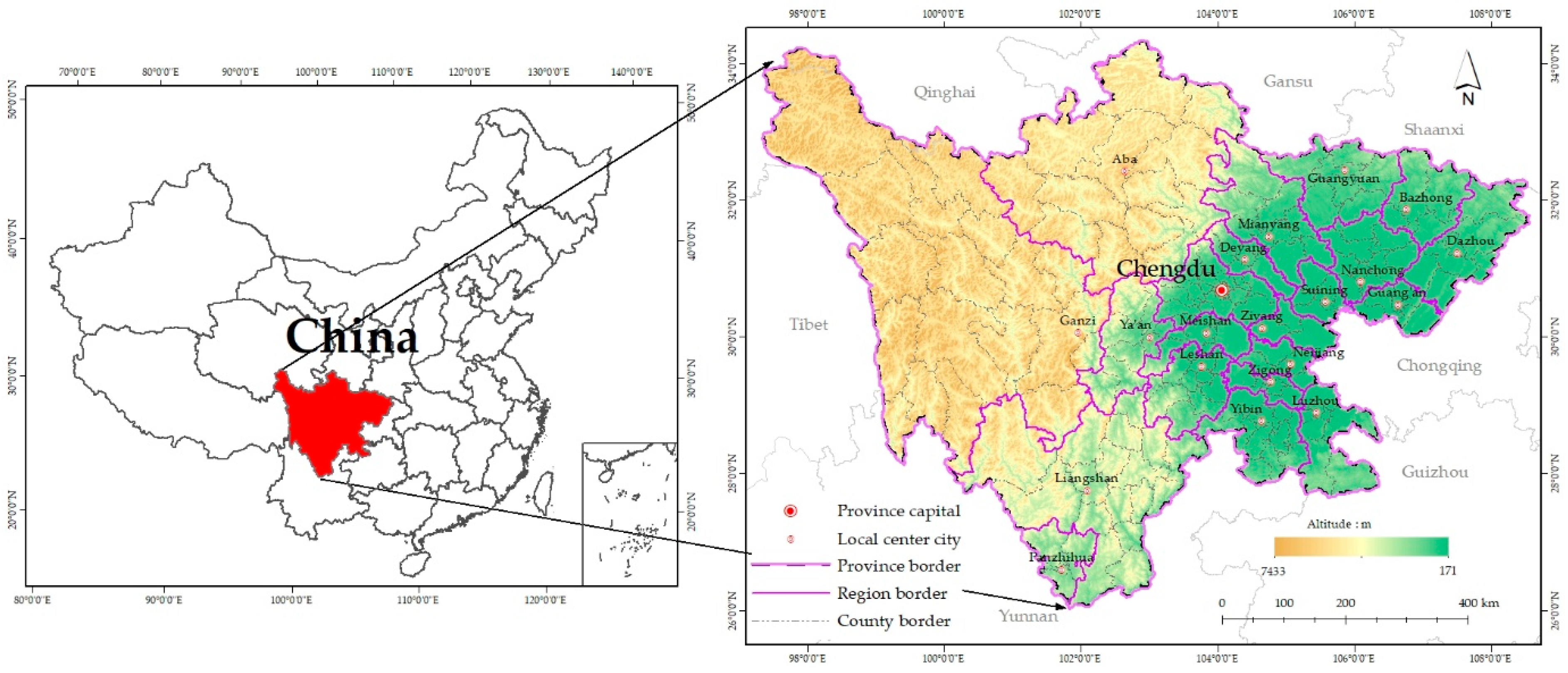
3. Study Area
4. Data
4.1. Variables Selection
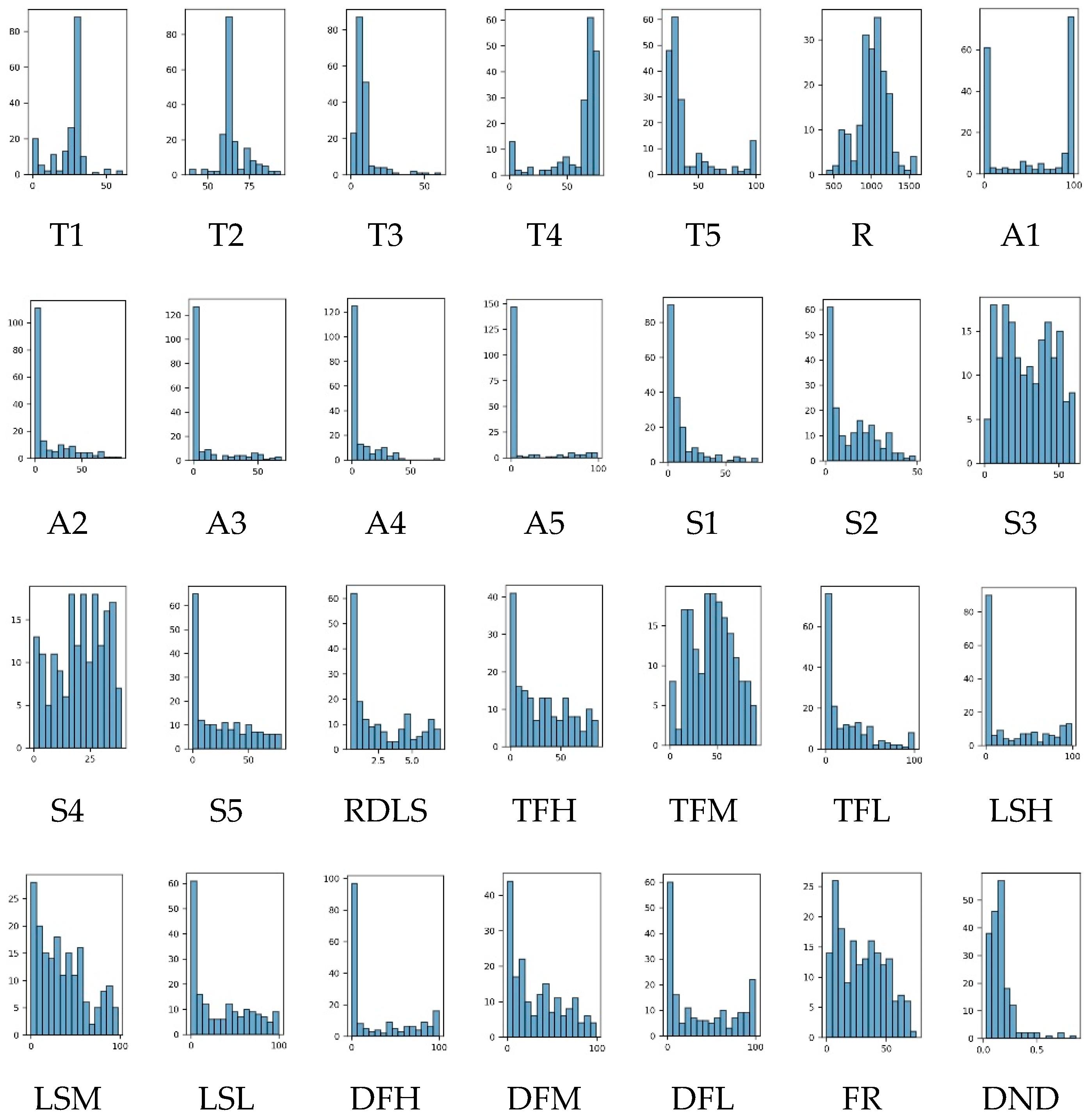
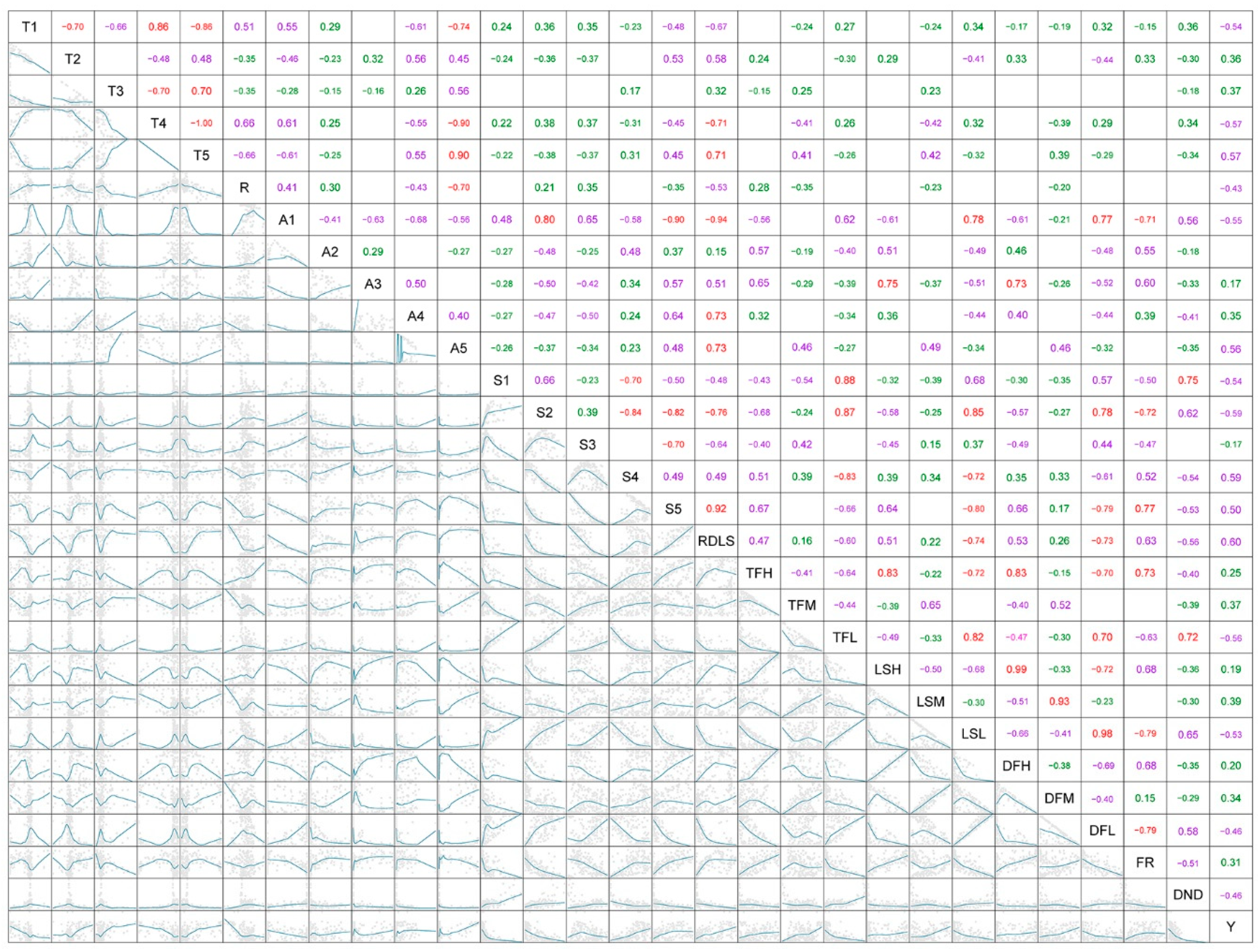
4.2. Variables Characteristics
5. Methods
5.1. Ordinary Least Squares Regression
5.2. GWR Model
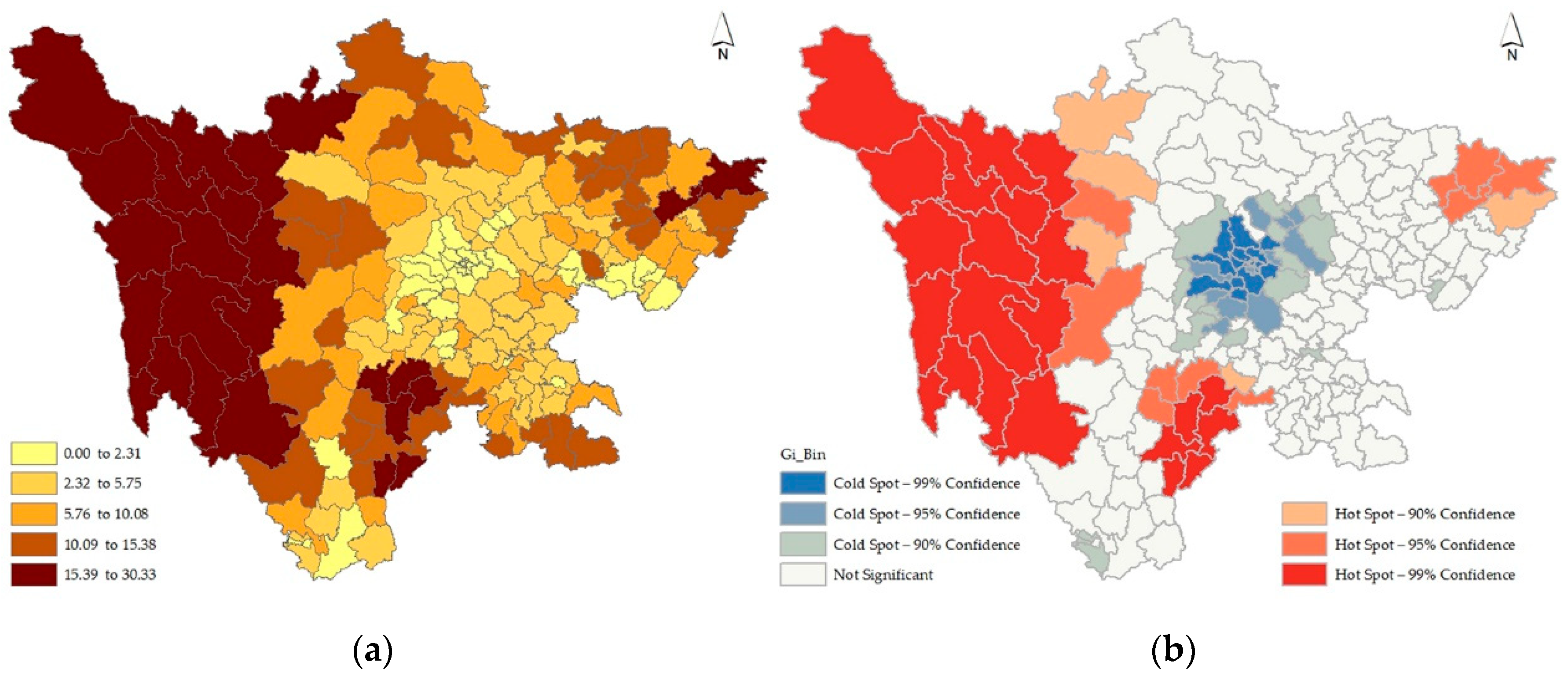
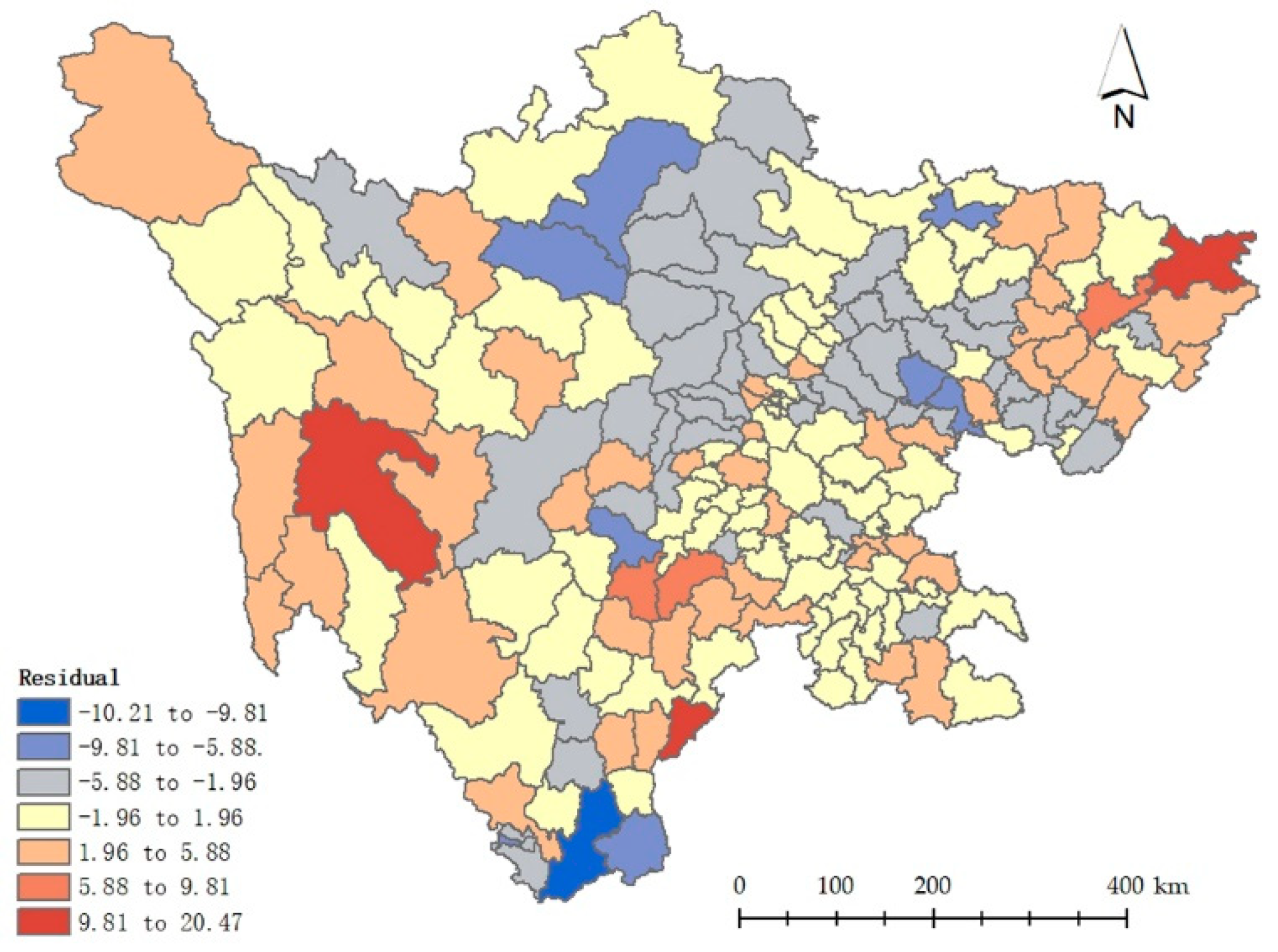
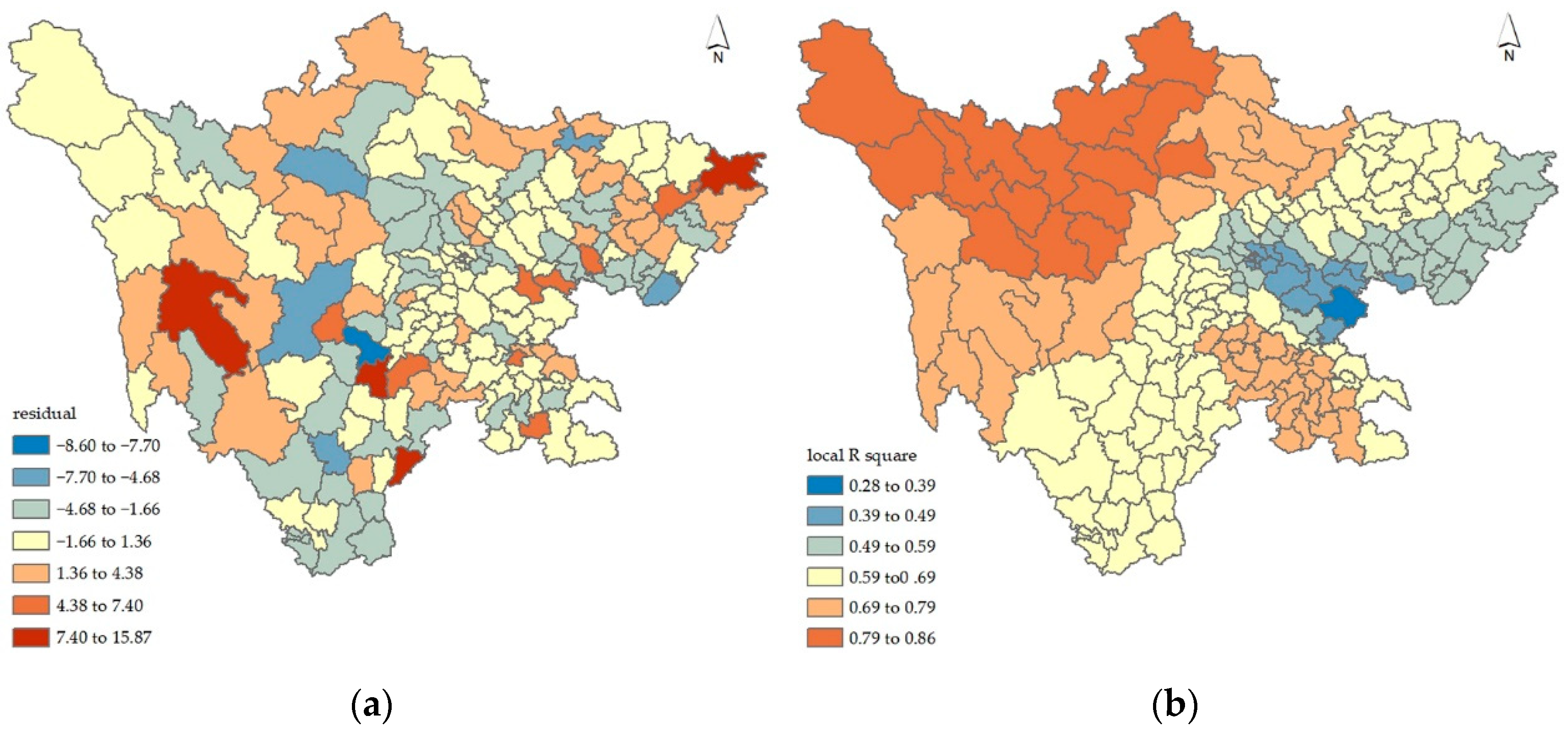
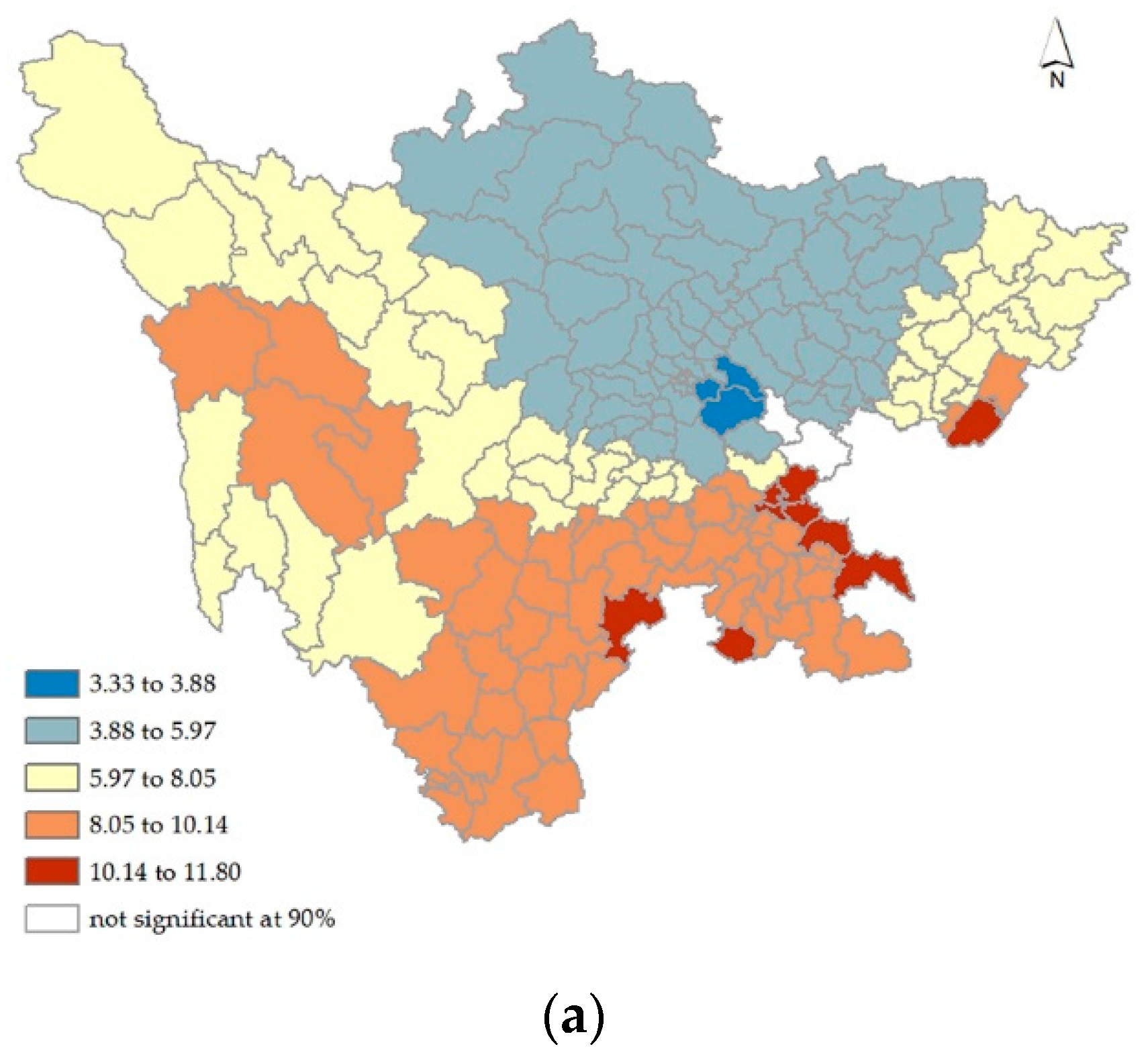
6. Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chinanews China Has Achieved Historic Achievements in the Five Years of Targeted Poverty Alleviation. Available online: https://www.chinanews.com/gn/2018/11-04/8667665.shtml (accessed on 1 September 2019).
- Bird, K.; Higgins, K.; Harris, D. Spatial Poverty Traps; Overseas Development Institute: London, UK, 2010. [Google Scholar]
- Montesquieu, C.d. The Spirit of Laws; Nourse and Vaillant: London, UK, 1748. [Google Scholar]
- Libby, O.G. Influences of Geographic Environment, on the Basis of Ratzel’s System of Anthropo-Geography. By Ellen Churchill Semple. (New York: Henry Holt and Company; London: Constable and Company. 1911. Pp. xvii, 683.). Am. Hist. Rev. 1912, 17, 355–357. [Google Scholar] [CrossRef]
- Huntington, E. Civilization and Climate; Yale University Press: London, UK, 1924. [Google Scholar]
- Thompson, J.H. What About a Geography of Poverty? Econ. Geogr. 1964, 40, i. [Google Scholar] [CrossRef]
- Elgie, R.A.; Ulch, C.L. The Geography of Poverty in the United States. Econ. Geogr. 1973, 49, 3. [Google Scholar] [CrossRef]
- Shaw, W. The Geography of United States Poverty: Patterns of Deprivation, 1980–1990; Garland Pub: New York, NY, USA, 1996; ISBN 9780815325369. [Google Scholar]
- Pringle, D.G.; Walsh, J.; Hennessy, M. Poor People, Poor Places: The Geography of Poverty and Deprivation in Ireland; Oak Tree Press: Dublin, Ireland, 1999; ISBN 1860761089. [Google Scholar]
- Shaw, M. Poor People, Poor Places: A Geography of Poverty and Deprivation in Ireland. J. Rural Stud. 2001, 17, 131–132. [Google Scholar] [CrossRef]
- Pacione, M. The geography of multiple deprivation in Scotland. Appl. Geogr. 1995, 15, 115–133. [Google Scholar] [CrossRef]
- Bramley, G.; Lancaster, S.; Gordon, D. Benefit Take-up and the Geography of Poverty in Scotland. Reg. Stud. 2000, 34, 507–519. [Google Scholar] [CrossRef]
- Jyotsna, J.; Mlartin, R. Spatial Poverty Traps? (Enlish); Policy Research Working Papers Series 1862; The World Bank: Washington, DC, USA, 1997. [Google Scholar]
- Jalan, J.; Ravallion, M. Geographic poverty traps? A micro model of consumption growth in rural China. J. Appl. Econom. 2002, 17, 329–346. [Google Scholar] [CrossRef]
- Straubhaar, T.; Suhrcke, M.; Urban, D.M. Divergence—Is It Geography? HWWA Discussion Papers 181; Hamburg Institute of International Economics (HWWA): Hamburg, Germany, 2002. [Google Scholar]
- Bloom, D.E.; Canning, D.; Sevilla, J. Geography and Poverty Traps. J. Econ. Growth 2003, 8, 355–378. [Google Scholar] [CrossRef]
- Paraguas, F.J.; Kamil, A.A. Spatial econometrics modeling of poverty. WSEAS Trans. Math. 2005, 4, 368. [Google Scholar]
- Deinne, C.E.; Ajayi, D.D. Spatial Dynamics of Urban Poverty in Delta State Nigeria. J. Poverty 2017, 22, 1–18. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Y.; Jiang, W. Spatial Correlation and Interaciton between Rocky Desertification and Poverty in Karst Mountainous Area in Guangxi. Resour. Ind. 2009, 11, 105–110. [Google Scholar]
- Wang, S.; Tian, J.; Wang, B.; Cheng, L.; Du, G. Regional Characteristics and Causes of Rural Poverty in Northeast China from the Perspective of Targeted Poverty Alleviation. Sci. Geogr. Sin. 2017, 37, 1449–1458. [Google Scholar]
- Zhao, Y.; Liu, X.; Guo, Y. Model Analysis for Spatial Poverty in the Poor Areas of Liupan Mountain in Ningxia Hui Autonomous Region Based on GIS. Res. Soil Water Conserv. 2014, 21, 94–99. [Google Scholar]
- Ma, Z.; Chen, X.; Jia, Z.; Lv, P. Poor people, or poor area? A geostatistical test for spatial poverty traps. Geogr. Res. 2018, 37, 1997–2010. [Google Scholar]
- Tong, X.; Liang, Q.; Wei, Y.; Liu, Q. Analysis of Influencing Factors of County Poverty in Guangxi Based on Geo Detector. Hunan Agric. Sci. 2018, 82–88. [Google Scholar] [CrossRef]
- Ding, J.; Leng, Z. Regional poverty analysis in a view of geography science. Acta Geogr. Sin. 2018, 73, 232–247. [Google Scholar]
- Liu, Y.; Liu, J.; Zhou, Y. Spatio-temporal patterns of rural poverty in China and targeted poverty alleviation strategies. J. Rural Stud. 2017, 52, 66–75. [Google Scholar] [CrossRef]
- Niu, T.; Chen, Y.; Yuan, Y. Measuring urban poverty using multi-source data and a random forest algorithm: A case study in Guangzhou. Sustain. Cities Soc. 2020, 54, 102014. [Google Scholar] [CrossRef]
- Haughton, J.; Khandker, S.R. Understanding the Determinants of Poverty. In Handbook on Poverty and Inequality; The World Bank: Washington, DC, USA, 2009; pp. 145–158. [Google Scholar]
- Xhafaj, E.; Nurja, I. Determination of the Key Factors that Influence Poverty through Econometric Models. Eur. Sci. J. 2014, 10, 65–72. [Google Scholar]
- Duarte, R. Socioeconomic Determinants of Poverty in Paraguay; Washington University in St. Louis: St. Louis, MO, USA, 2015. [Google Scholar]
- Petrucci, A.; Salvati, N.; Seghieri, C. Autologistic Regression Model for Poverty Mapping and Analysis. Metodoloski Zv. 2004, 1, 225–234. [Google Scholar]
- Achia, T.N.O.; Wangombe, A.; Khadioli, N. A logistic regression model to identify key determinants of poverty using demographic and health survey data. Eur. J. Soc. Sci. 2010, 13, 38–45. [Google Scholar]
- Karim, A.; Noy, I. Poverty and Natural Disasters: A Meta-Regression Analysis. Rev. Econ. Inst. Econ. Soc. Ist. 2016, 7, 1–26. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression-modelling spatial non-stationarity. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Quantitative Geography: Perspectives on Spatial Data Analysis; Sage: London, UK, 2000. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Benson, T.; Chamberlin, J.; Rhinehart, I. An Investigation of the Spatial Determinants of the Local Prevalence of Poverty in Rural Malawi. Food Policy 2005, 30, 532–550. [Google Scholar] [CrossRef]
- Dawson, T.; Sandoval, J.S.; Sagan, V.; Crawford, T.; Dawson, T.; Sandoval, J.S.O.; Sagan, V.; Crawford, T. A Spatial Analysis of the Relationship between Vegetation and Poverty. ISPRS Int. J. Geo-Inf. 2018, 7, 83. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.; Wu, D.; Zhao, L.; Ding, J. Spatial Patterns and Determinants of Rural Poverty: A Case of Guizhou Province, China. Sci. Geogr. Sin. 2017, 37, 217–227. [Google Scholar]
- Vaziri, M.; Acheampong, M.; Downs, J.; Rafee Majid, M. Poverty as a function of space: Understanding the spatial configuration of poverty in Malaysia for Sustainable Development Goal number one. GeoJournal 2019, 84, 1317–1336. [Google Scholar] [CrossRef]
- Guo, Y.; Chang, S.S.; Sha, F.; Yip, P.S.F. Poverty concentration in an affluent city: Geographic variation and correlates of neighborhood poverty rates in Hong Kong. PLoS ONE 2018, 13, 1–17. [Google Scholar] [CrossRef]
- Robinson, C.; Bouzarovski, S.; Lindley, S. Underrepresenting neighbourhood vulnerabilities? The measurement of fuel poverty in England. Environ. Plan. A Econ. Space 2018, 50, 1109–1127. [Google Scholar] [CrossRef]
- Lucas, K.; Philips, I.; Mulley, C.; Ma, L. Is transport poverty socially or environmentally driven? Comparing the travel behaviours of two low-income populations living in central and peripheral locations in the same city. Transp. Res. Part A Policy Pract. 2018, 116, 622–634. [Google Scholar] [CrossRef]
- Sichuan Yearbook Office. Sichuan Yearbook; Ma, X., Ed.; Sichuan Yearbook Society: Chengdu, China, 2017. [Google Scholar]
- Sichuan Statistical Bereau; NBS Survey Office in Sichuan. Sichuan Statistical Yearbook 2019; China Statistics Press: Beijing, China, 2019.
- Sichuan Statistics Bureau Population Statistics Bulletin of Sichuan Province in 2018. Available online: http://web.sctjj.cn/sjfb/tjgb/201903/t20190319_277120.html (accessed on 10 September 2019).
- Sichuan Provincial Committee of the Communist Party of China Decision on Commending Advanced Cities and Counties for Poverty Alleviation in 2016. Sichuan Dly. 2017. Available online: https://epaper.scdaily.cn/shtml/scrb/20170423/161450.shtml (accessed on 22 September 2019).
- Li, M.; Hou, C. 45 Poverty-Stricken Counties Reduced Poverty by 446,000 in Three Years. Sichuan Dly. 2017. Available online: https://epaper.scdaily.cn/shtml/scrb/20170816/171006.shtml (accessed on 22 September 2019).
- Gallup, J.L.; Sachs, J.D. Agriculture, climate, and technology: Why are the tropics falling behind? Am. J. Agric. Econ. 2000, 82, 731–737. [Google Scholar] [CrossRef]
- Yang, J. A GWR-Based Study on Impoveriishment Factors of Guizhou Province: A Case Study of Jianhe County; Guizhou University: Guiyang, China, 2018. [Google Scholar]
- Zhao, Y. Research on the Spatial Poverty Trap of Concentrated Contiguous Area with Particular Difficulties on Basis of the Geographic Capital; Ningxia University: Yinchuan, China, 2015. [Google Scholar]
- Akoglu, H. User’s guide to correlation coefficients. Turkish J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Garg, A.; Tai, K. Comparison of statistical and machine learning methods in modelling of data with multicollinearity. Int. J. Model. Identif. Control 2013, 18, 295. [Google Scholar] [CrossRef]
- Liu, R.X.; Kuang, J.; Gong, Q.; Hou, X.L. Principal component regression analysis with SPSS. Comput. Methods Programs Biomed. 2003, 71, 141–147. [Google Scholar] [CrossRef]
- Wong, D.W.-S.; Lee, J. Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Wong, D.W.S.; Wang, F. Spatial Analysis Methods. In Comprehensive Geographic Information Systems; Huang, B., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 125–147. [Google Scholar]
- Xu, Y.; Wang, L. GIS-based analysis of obesity and the built environment in the US. Cartogr. Geogr. Inf. Sci. 2015, 42, 9–21. [Google Scholar] [CrossRef]
- Lin, C.-H.; Wen, T.-H.; Lin, C.-H.; Wen, T.-H. Using Geographically Weighted Regression (GWR) to Explore Spatial Varying Relationships of Immature Mosquitoes and Human Densities with the Incidence of Dengue. Int. J. Environ. Res. Public Health 2011, 8, 2798–2815. [Google Scholar] [CrossRef]
- Mennis, J. Mapping the results of geographically weighted regression. Cartogr. J. 2006, 43, 171–179. [Google Scholar] [CrossRef]
- Matthews, S.A.; Yang, T.-C. Mapping the results of local statistics: Using geographically weighted regression. Demogr. Res. 2012, 26, 151–166. [Google Scholar] [CrossRef]
| Group | Variables | Description | Calculation | Units |
|---|---|---|---|---|
| Climate | T1 | Rate of days with max temp ≥ 28 °C | Days with max temperature ≥ 28 °C/365 | % |
| T2 | Rate of days with 10 °C < max temp < 28 °C | Days with 10 °C < max temperature < 28 °C/365 | % | |
| T3 | Rate of days with max temperature ≤ 10 °C | Days with max temperature ≤ 10 °C/365 | % | |
| T4 | Rate of days with 10 °C < min temp ≤ 28 °C | Days with 10 °C < min temperature ≤ 28 °C/365 | % | |
| T5 | Rate of days with min temp ≤ 10 °C | Days with min temperature ≤ 10 °C/365 | % | |
| R | annual average rainfall | get directly | mm | |
| Terrain | A1 | Rate of area with altitude 0 to 800 m | Area with altitude from 0 to 800 m/county area | % |
| A2 | Rate of area with altitude 800 to 1800 m | Area with altitude from 800–1800 m/county area | % | |
| A3 | Rate of area with altitude 1800 to 2800 m | Area with altitude from 1800–2800 m/county area | % | |
| A4 | Rate of area with altitude 2800 to 3600 m | Area with altitude from 2800–3600 m/county area | % | |
| A5 | Rate of area with altitude above 3600 m | Area with altitude above 3600 m/county area | % | |
| S1 | Rate of area with slope of 0–2° | Area with slope of 0–2°/county area | % | |
| S2 | Rate of area with slope of 2–5° | Area with slope of 2–5°/county area | % | |
| S3 | Rate of area with slope of 5–15° | Area with slope of 5–15°/county area | % | |
| S4 | Rate of area with slope of 15–25° | Area with slope of 15–25°/county area | % | |
| S5 | Rate of area with slope above 25° | Area with slope above 25°/county area | % | |
| RDLS | Relief degree of the land surface | Method comes from Feng [51] | ||
| Geological disasters | TFH | Area rate of torrential flood high-danger | Area of torrential flood high-danger/county area | % |
| TFM | Area rate of torrential flood medium-danger | Area of torrential flood medium-danger/county area | % | |
| TFL | Area rate of torrential flood low-danger | Area of torrential flood low-danger/county area | % | |
| LSH | Area rate of landslide high-danger | Area of landslide high-danger/county area | % | |
| LSM | Area rate of landslide medium-danger | Area of landslide medium-danger/county area | % | |
| LSL | Area rate of landslide low-danger | Area of landslide low-danger/county area | % | |
| DFH | Area rate of debris flow high-danger | Area of debris flow high-danger/county area | % | |
| DFM | Area rate of debris flow medium-danger | Area of debris flow medium-danger/county area | % | |
| DFL | Area rate of debris flow low-danger | Area of debris flow low-danger/county area | % | |
| Physical resources | FR | Forest coverage rate | Forest area/county area | % |
| DND | Drainage network density | Total length of drainage network/county area | km/km2 | |
| Y | Poverty rate | Poor population/county population | % |
| Variables | Min | Max | Mean | SD | Observations | |
|---|---|---|---|---|---|---|
| Dependent variable Y | 0 | 30.3 | 7.47 | 6.23 | 183 | |
| Independent variable | T1 | 0 | 61 | 25.32 | 11.45 | 183 |
| T2 | 39 | 94 | 65.1 | 8.66 | 183 | |
| T3 | 0 | 61 | 9.59 | 8.23 | 183 | |
| T4 | 0 | 78 | 60.7 | 21.08 | 183 | |
| T5 | 22 | 100 | 39.3 | 21.08 | 183 | |
| R | 409 | 1599 | 1019.5 | 206.26 | 183 | |
| A1 | 0 | 100 | 55.34 | 44.35 | 183 | |
| A2 | 0 | 92 | 14.36 | 21.73 | 183 | |
| A3 | 0 | 68 | 9.77 | 17.87 | 183 | |
| A4 | 0 | 75 | 6.63 | 11.84 | 183 | |
| A5 | 0 | 99 | 12.64 | 27.85 | 183 | |
| S1 | 0 | 78 | 10.7 | 15.38 | 183 | |
| S2 | 1 | 49 | 14.22 | 12.32 | 183 | |
| S3 | 0 | 61 | 29.38 | 16.53 | 183 | |
| S4 | 0 | 39 | 20.67 | 10.89 | 183 | |
| S5 | 0 | 79 | 24.98 | 24.11 | 183 | |
| RDLS | 0.5 | 7.08 | 2.65 | 2.14 | 183 | |
| TFH | 0 | 87 | 32.31 | 26.29 | 183 | |
| TFM | 0 | 92 | 44.78 | 22.55 | 183 | |
| TFL | 0 | 100 | 22.84 | 26.67 | 183 | |
| LSH | 0 | 99 | 30.07 | 35.29 | 183 | |
| LSM | 0 | 98 | 36.62 | 27.14 | 183 | |
| LSL | 0 | 100 | 33.3 | 32.15 | 183 | |
| DFH | 0 | 100 | 28.56 | 36.31 | 183 | |
| DFM | 0 | 99 | 33.27 | 28.76 | 183 | |
| DFL | 0 | 100 | 38.12 | 36.63 | 183 | |
| FR | 0 | 75 | 29.09 | 19.24 | 183 | |
| DND | 0 | 0.87 | 0.16 | 0.12 | 183 | |
| Variable | Coefficient | StdError | p-Value | VIF |
|---|---|---|---|---|
| Intercept | 0.307 | 4.045 | 0.93948 | — |
| T2 | 0.174 | 0.044 | 0.00015 | 1.72 |
| T3 | 0.179 | 0.042 | 0.00003 | 1.34 |
| R | −0.009 | 0.002 | 0.00000 | 1.43 |
| A4 | −0.064 | 0.034 | 0.05941 | 1.81 |
| S1 | −0.085 | 0.027 | 0.00222 | 2.04 |
| S4 | 0.221 | 0.038 | 0.00000 | 2.00 |
| Moran’s I (residuals) | 0.26 | — | — | — |
| R2 | 0.60 | — | — | — |
| Adjusted R2 | 0.59 | — | — | — |
| AICc | 1036.37 | — | — | — |
| Variable | Min | 25% Quartile | 50% Quartile | 75% Quartile | Max |
|---|---|---|---|---|---|
| Intercept | 3.33 | 5.18 | 6.98 | 8.61 | 11.80 |
| T2 | −2.72 | −0.44 | 0.42 | 1.11 | 2.59 |
| T3 | −1.38 | 1.06 | 1.67 | 2.85 | 4.40 |
| R | −3.22 | −2.38 | −1.17 | −0.15 | 1.52 |
| A4 | −2.42 | −0.74 | −0.10 | 2.05 | 9.72 |
| S1 | −2.65 | −1.48 | −1.35 | −1.05 | −0.43 |
| S4 | −0.39 | 0.93 | 1.80 | 2.27 | 2.78 |
| Moran’s I (residuals) | 0.02 | - | - | - | - |
| R2 | 0.76 | - | - | - | - |
| Adjusted R2 | 0.71 | - | - | - | - |
| AICc | 990.88 | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Mai, X.; Shen, G. Poverty and Physical Geographic Factors: An Empirical Analysis of Sichuan Province Using the GWR Model. Sustainability 2021, 13, 100. https://doi.org/10.3390/su13010100
He X, Mai X, Shen G. Poverty and Physical Geographic Factors: An Empirical Analysis of Sichuan Province Using the GWR Model. Sustainability. 2021; 13(1):100. https://doi.org/10.3390/su13010100
Chicago/Turabian StyleHe, Xindong, Xianmin Mai, and Guoqiang Shen. 2021. "Poverty and Physical Geographic Factors: An Empirical Analysis of Sichuan Province Using the GWR Model" Sustainability 13, no. 1: 100. https://doi.org/10.3390/su13010100
APA StyleHe, X., Mai, X., & Shen, G. (2021). Poverty and Physical Geographic Factors: An Empirical Analysis of Sichuan Province Using the GWR Model. Sustainability, 13(1), 100. https://doi.org/10.3390/su13010100





