Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals
Abstract
1. Introduction
2. The Modeling Approach
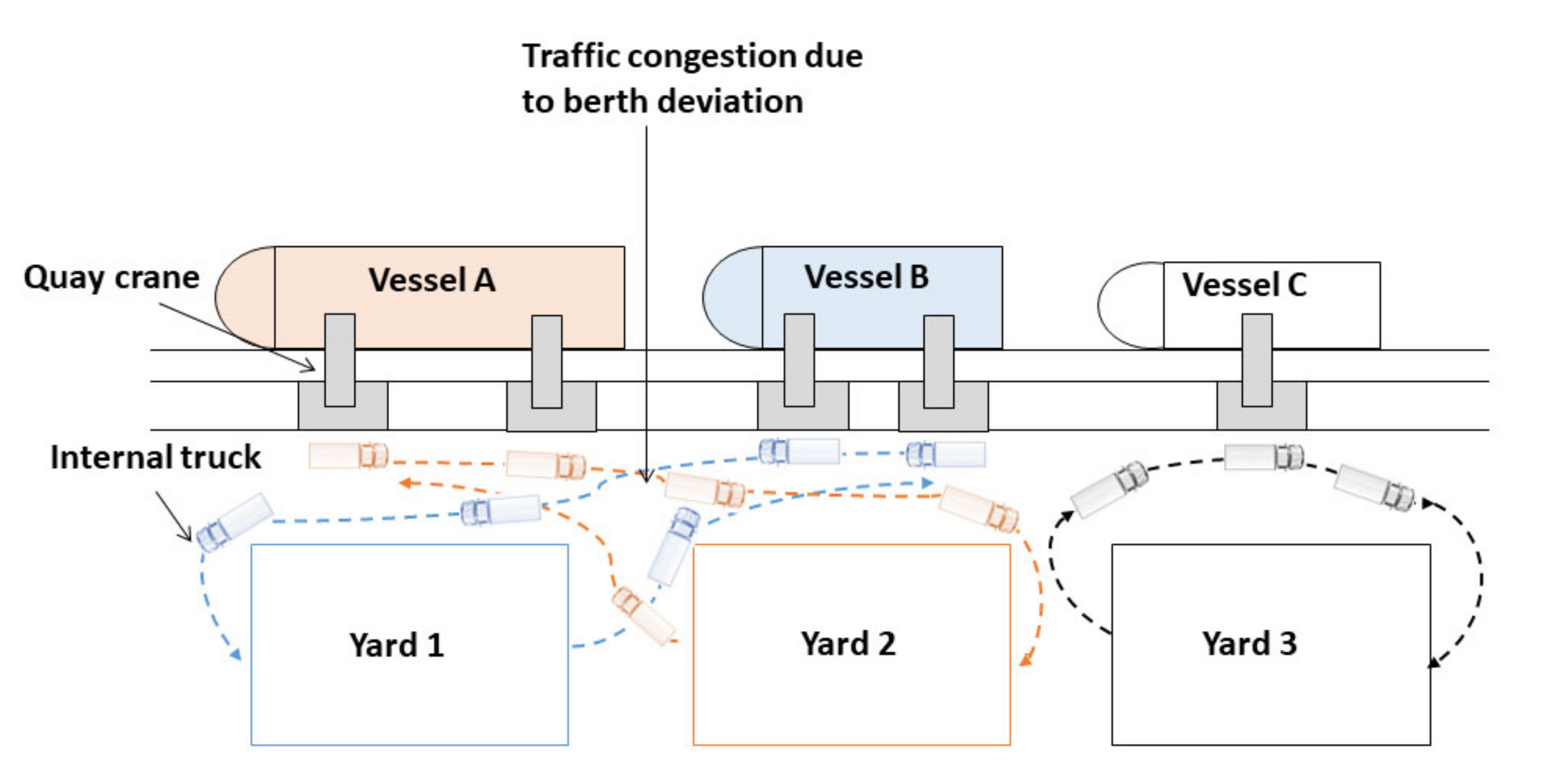
2.1. Problem Description
2.2. Description of the Developed Model
2.2.1. Model Assumption
- The planning horizon is partitioned into equal time periods, and each period is one hour;
- The berth is discretized by being divided into equally sized segments of 50 m;
- The service of each vessel starts directly after berthing and cannot be stopped until the vessel‘s workload is fully handled;
- It is assumed that water depth along the berth is suitable for arriving vessels;
- Minimum and maximum numbers of QCs are determined for each vessel, and a vessel cannot be moored until the minimum number of QCs are ready to handle its containers;
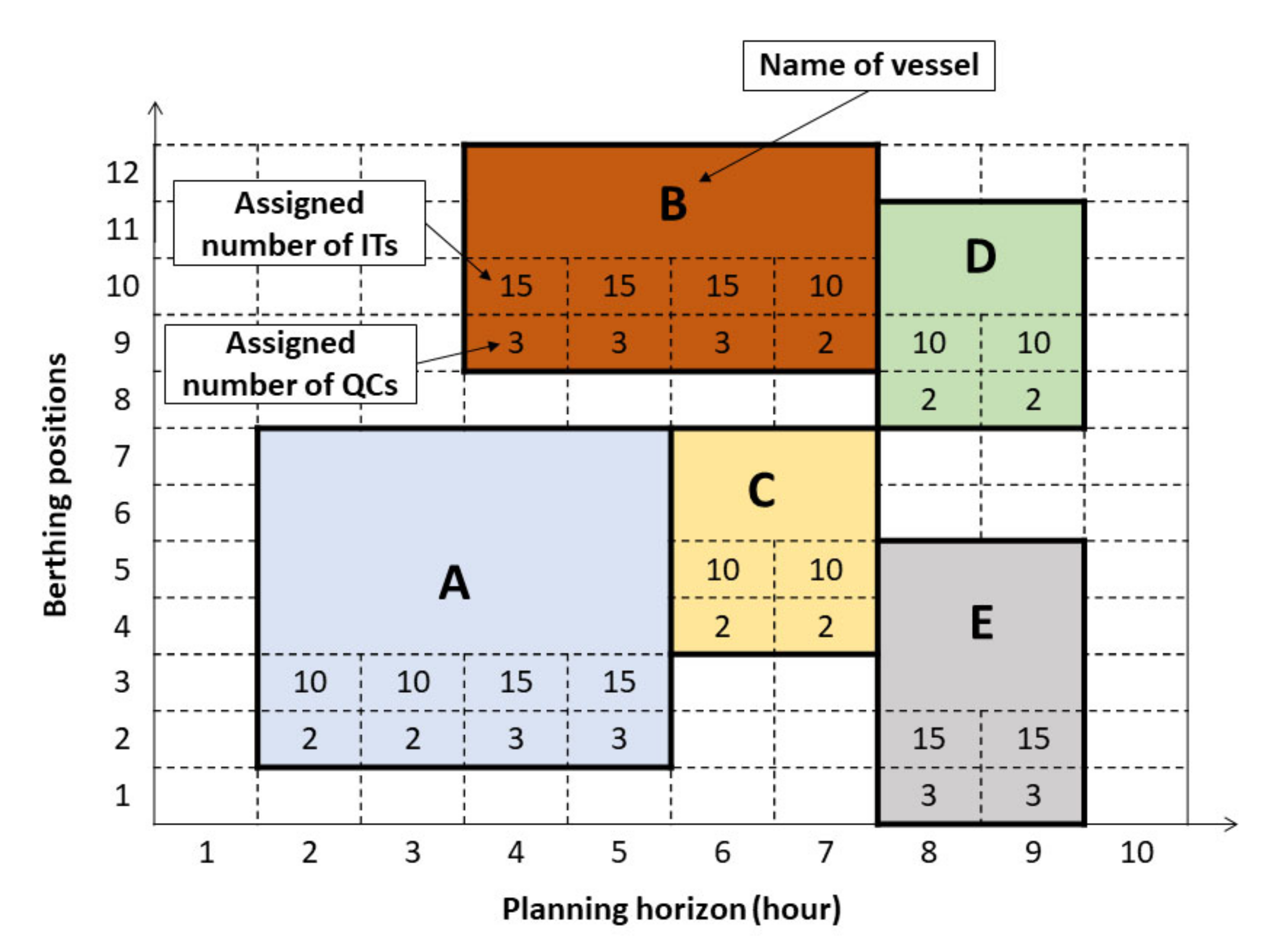
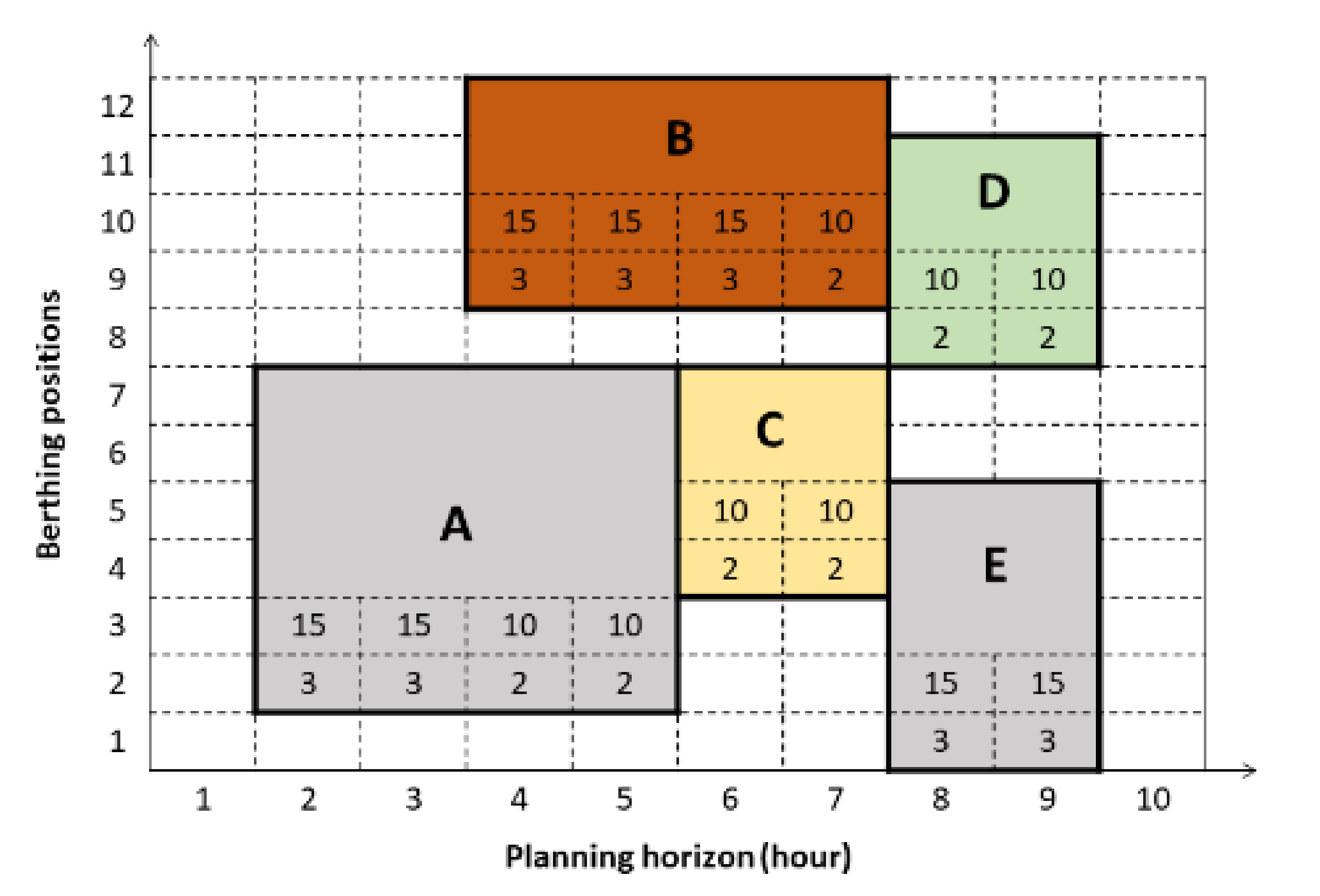
- The change in the number of QCs serving each vessel is restricted to one change at most, as was done in Reference [33]. It is worth noting that strategies for the QC assignments include time-invariant QC assignments, time-variant QC assignments, and limited time-variant QC assignments. Time-invariant QC assignments imply that the number of QCs serving each vessel must be the same during the service of the vessel [16,34], while time-variant QC assignments imply that the number of QCs can be varied dynamically according to the assignable range of QCs allowed for the vessel [12,15,17]. Note that varying the number of QCs serving the vessel is sometimes essential for improving the utilization of QCs as well as the service times of vessels. This is because some QCs serving vessels are reallocated to start operations on other vessels. However, many changes cause a long setup time, which is unacceptable in reality. Therefore, a well-balanced tradeoff is limited time-variant QC assignments, in which the variation in the number of QCs is limited. Referring to vessel B in Figure 2, it can be noted that the assigned numbers of QCs change only one time during service in time period 7. Therefore, the service duration of the vessel is divided into two stages. A stage is the number of successive time periods, and the number of QCs assigned to the vessel does not change during the same stage. A new stage starts whenever a change in the number of QCs serving the vessel occurs. Referring to Figure 2, it can be noted that vessel B has two stages. The first stage runs from time period 4 to time period 6, while the second stage starts in time period 7, in which the assigned number of QCs changes from 3 to 2;
- Minimum and maximum numbers of ITs are specified for each QC so that the waiting times of the QCs and ITs are suitable. For more details on how such numbers are determined, we refer the reader to the work of Murty et al. [20], in which the authors developed a queuing network model to capture the interactions between QCs, ITs, and yard cranes. Their model can be used to determine the numbers of ITs assigned to each QC such that that the waiting times of the QCs and ITs are minimized.
2.2.2. Notations
- SETs:
- V: Set of arriving vessels, V= {1,2,...,n} (indexed by v);
- T: Set of time periods in the planning horizon, T = {1,2,...,H} (indexed by t).
- Parameters:
- : The length of vessel v, in which a safe distance between vessels is included;
- : The time at which vessel v is expected to arrive at the terminal, called the expected arrival time;
- : The time at which vessel v is expected to depart from the terminal, called the expected departure time;
- : The nearest berthing position to the storage yard of containers on vessel v, called the desired berthing position;
- : The available number of berthing positions;
- : The number of time periods in the planning horizon;
- : The total number of available QCs;
- : The total number of available ITs;
- : The workload of vessel v, expressed in numbers of containers in a 20-ft equivalent unit (TEU);
- : Maximum number of QCs that can serve vessel v;
- : Minimum number of QCs that can serve vessel v;
- : Maximum number of ITs that can work with each quay crane;
- : Minimum number of ITs that should work with each quay crane;
- : Feasible range of ITs that can work with each quay crane, ;
- : The penalty cost incurred if there is a deviation between the allocated berthing position, , and of vessel v (unit: $/unit distance deviation);
- : The energy consumption cost of vessel v per hour in idle mode (unit: $/ hour);
- : The penalty cost incurred if the departure of vessel v is later than its expected departure time (unit: $/hour);
- : The average time needed to serve the ITs at the QCs;
- 2 : The average time needed by the ITs to travel between the quayside and the yard;
- : The average time needed to serve the ITs at the yard crane;
- β : The berth deviation factor;
- : A sufficiently large constant.
- Decision variables:
- : 1, if vessel v is berthed at berthing position j at time period t, and 0 otherwise;
- : An integer, the number of QCs serving vessel v in time period t if i ITs are assigned to each QC, i∊ R;
- : 1, if vessel v is processed in time period t, and 0 otherwise;
- : 1, if there is any decrease or increase in the number of QCs serving vessel v in time period t compared to its preceding time period (t ‒ 1), and 0 otherwise;
- : Integer, the first berthing position of vessel v;
- : An integer, the berthing time of vessel v;
- : An integer, the completion time of vessel v, which is the largest t at which = 1 plus 1;
- : An integer, the deviated distance of vessel v between the desired berthing position of vessel v and its berthing position, ;
- : An integer, the delayed berthing of vessel v, ;
- : An integer, the delayed departure of vessel v, ;
- : 1, if j and t are equal to the first berthing position and berthing time of vessel v, respectively, and 0 otherwise.
2.2.3. Estimation of the Vessel Handling Time
- I.
- The assigned number of QCs;
- II.
- The assigned number of ITs serving each QC; and
- III.
- The distance between the vessel’s berthing position and the storage yard for the containers on the vessel.
2.2.4. Formulation of Objective Functions
2.2.5. The Mathematical Model
3. The Lagrangian Solution Method
3.1. The Lagrangian Relaxation for the Developed Model
3.2. The Overall Procedures for the Subgradient Optimization Method
- Step 1:
- Initialize the upper bound (ZUB) as a large value and the multipliers and as 0.
- Step 2:
- The lower and upper bounds of the optimal solution objective are calculated as follows:
- Step 2.2: For each vessel v, solve LDv using initial values of the multipliers. The procedures for solving LDv will be presented in Section 3.3. The lower bound of the solution objective (ZLB) is formed by (34), and the largest lower bound is updated,.
- Step 2.3: If the solution obtained using (36) violates the relaxed constraints, a feasibility restoration method is used to solve the infeasibilities and calculate the upper bound (ZUB). Afterwards, update the lowest upper bound,.
- Step 3:
- Evaluate the subgradients as well as the step sizes to calculate the multipliers and.
- Step 4:
- The multipliers and, for the next iteration, are calculated as follows:
- Step 5:
- Return to step 2.
3.3. The Overall Procedures for the Subgradient Optimization Method
- Step 1:
- Assign an initial value to the minimum objective value, e.g., 15,000, and set j = 1 and t = 1.
- Step 2:
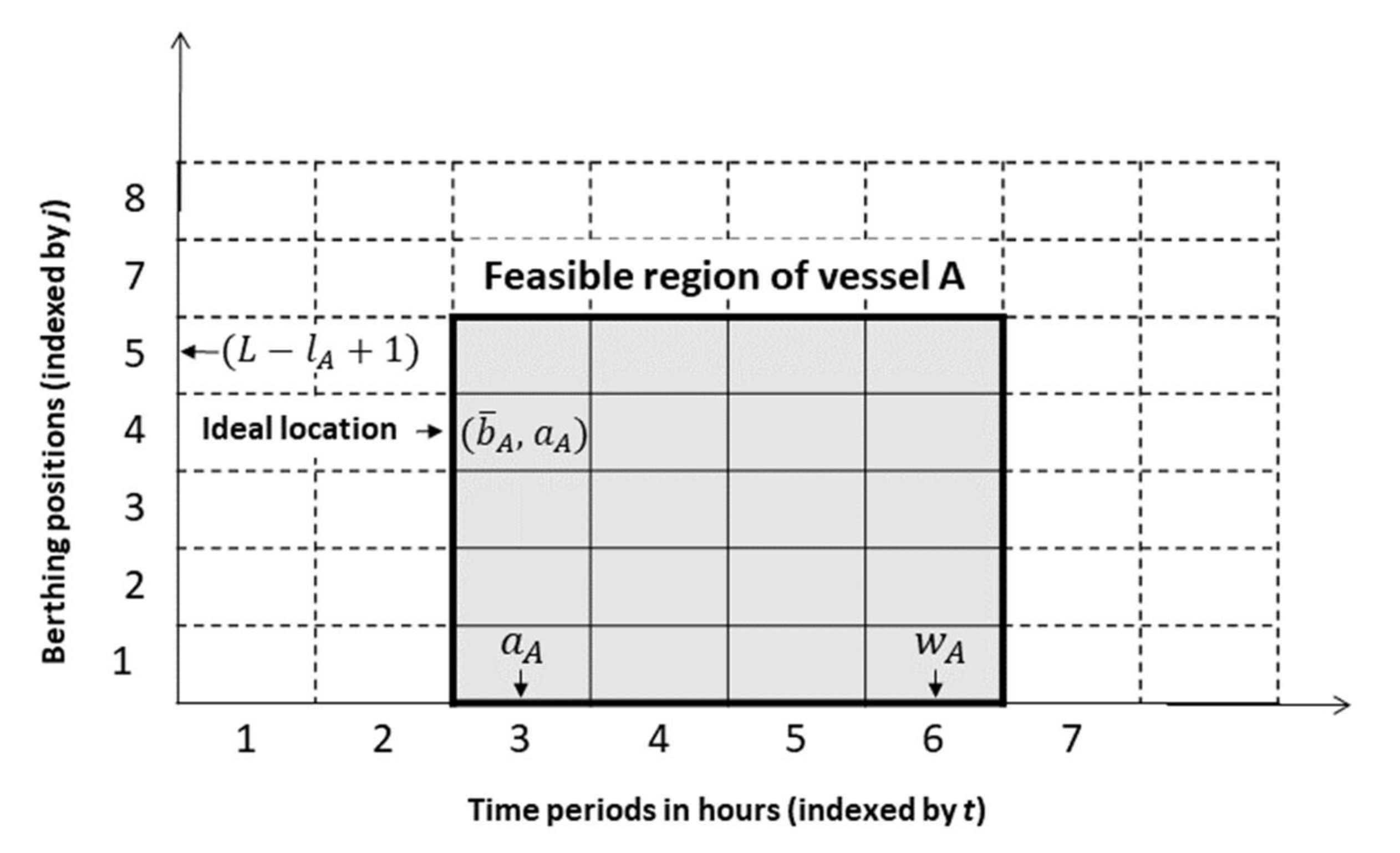
- This step aims to determine the coordinates of the left lower corner (reference corner) of the vessel rectangle in the time–space diagram, i.e., and . The minimum value of the berthing cost (is used to decide on the best values of and . Note that if and are searched for in each grid in the feasible region, this would increase the computational time. Therefore, instead of trying all grids in the feasible region, and are searched for in the grids around ( because the optimal values of and may be close or equal to and , respectively. For this, and are searched for time period by time period, starting from At each time period, the following steps are performed.
- Step 2.1:
- Select the next grid, starting from through. If the berthing cost in the grid is lower than the minimum objective value, go to step 3. Otherwise, go back to the beginning of step 2.1 until all berthing positions fromthrough are tried once, and then go to step 2.2. It is important to point out that the minimum objective value is iteratively updated in step 3 based on the vessel schedule (berthing time, berthing position, completion time, and assignments of QCs and ITs). Therefore, if the berthing cost is higher than the minimum objective value, this implies that berthing the vessel in the grid corresponding to this berthing cost will not yield an objective value better than the current minimum objective value. Therefore, this grid is excluded, and the next grid is tried. In this way, step 3 is not performed for all the grids in the feasible region, and thus computational time can be saved.
- Step 2.2:
- Select the next grid, starting from) to 1. If the berthing cost in the grid is lower than the minimum objective value, go to step 3. Otherwise, go back to the beginning of step 2.2 until all berthing positions from to 1 are tried once, and then go to step 2.
- Step 3:
- The reference corner of the rectangle corresponding to vessel v is located at (j,t), which is determined by step 2. Hereafter, in this step, the QCs and ITs are allocated to vessel v. To stimulate limited time-variant quay crane assignments, the service of the vessel is divided into two stages. The first and second stages are designated by and, respectively. To try all feasible combinations of the QCs and ITs that can be allocated to vessel v, the following steps are performed.
- Step 3.1:
- If all combinations of (, ),, and are tried once, go back to step 2. Otherwise, select the next combination of (, ) and set = 1, where is the first stage at which QCs are assigned to vessel v and ITs are assigned to each QC.
- Step 3.2:
- For all combinations of (, ),, and , select the next combination of (,) and set to the rounded value of max , where is the second stage at which vessel v is assigned QCs and ITs are assigned to each QC so as to completely handle . If t + t1 + t2 - 1 ≤ H, then obtain the objective value of (39) corresponding to the schedule just identified for the combination of {j, t, t1, q1, i1, t2, q2, i2}, and update the minimum objective value. If two or more schedules have the minimum objective value, random selection is used to select the vessel’s schedule from these schedules. Otherwise, go to step 3.2 until all combinations (, ) have been tried once.
- Step 3.3:
- If , increase t1 by one and go to step 3.2. Otherwise, go to step 3.1.
3.4. Feasibility Restoration and Solution Refinement
- Step 1:
- Sort vessels sequentially in increasing orders of and set v = 0 and Fe = In = ∅, where Fe and In are feasible and infeasible sets, respectively.
- Step 2:
- Increase v by 1 and perform step 2 if v ≤ n. Otherwise, go to step 3. In this step, the obtained solution of the vth vessel is checked for any violation of the relaxed constraints, given that the solutions for the preceding vessels in Fe are known. If there is no violation of the relaxed constraints, the vth vessel is inserted into Fe. Otherwise, the vth vessel is inserted into In. Return the beginning of this step.
- Step 3:
- Sort vessels in In sequentially in increasing orders of, and then the next vessel in In is selected. The procedures in Section 3.3 are used to find the least-cost feasible schedule for the selected vessel that results in no violation of the relaxed constraints, provided that the solutions of vessels in Fe are given. Afterwards, the selected vessel is deleted from In and is inserted into Fe. Redo step 3 until In contains no vessels.
- Step 4:
- After a feasible solution is constructed by performing the previous steps, the feasible solution is refined. As noted, the solution is composed of a set of vessels. Each vessel has its own cost that contributes to the overall quality of the obtained solution. Therefore, if the schedules of vessels with relatively higher costs are refined, the overall solution cost may be improved. A straightforward procedure is applied as follows: Sort vessels sequentially in decreasing order of their individual cost. For the first 20% of vessels at the top of the list, perform the same procedure of solving the decomposed primal problems. It is important to point out that a percentage of 20% is selected because if this percentage were higher, more vessels will have to carry out the procedure of solving, which would lead to an increased computational time.
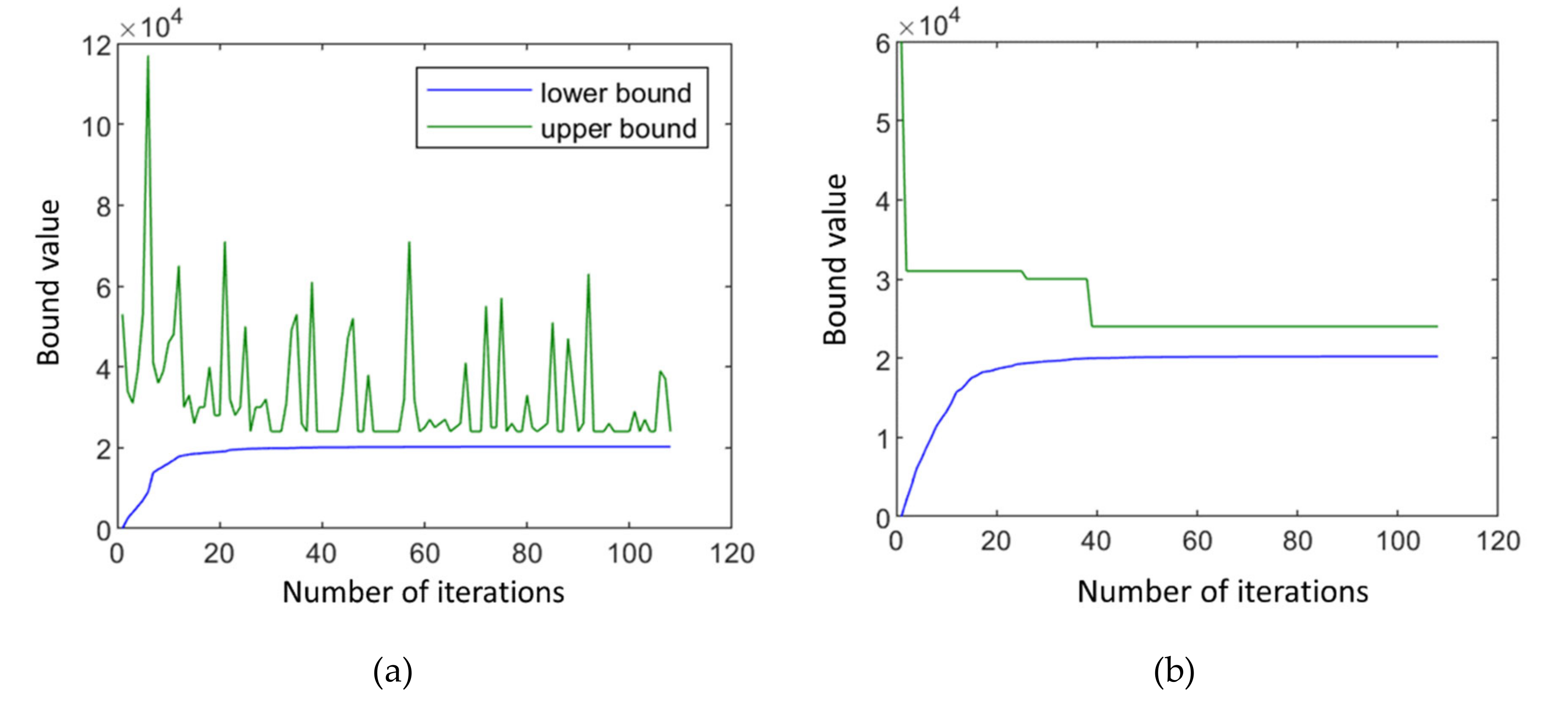
3.5. An Illustrative Example
4. Numerical Experiments
4.1. Generating Test Instances
4.2. Comparison to Cplex Results
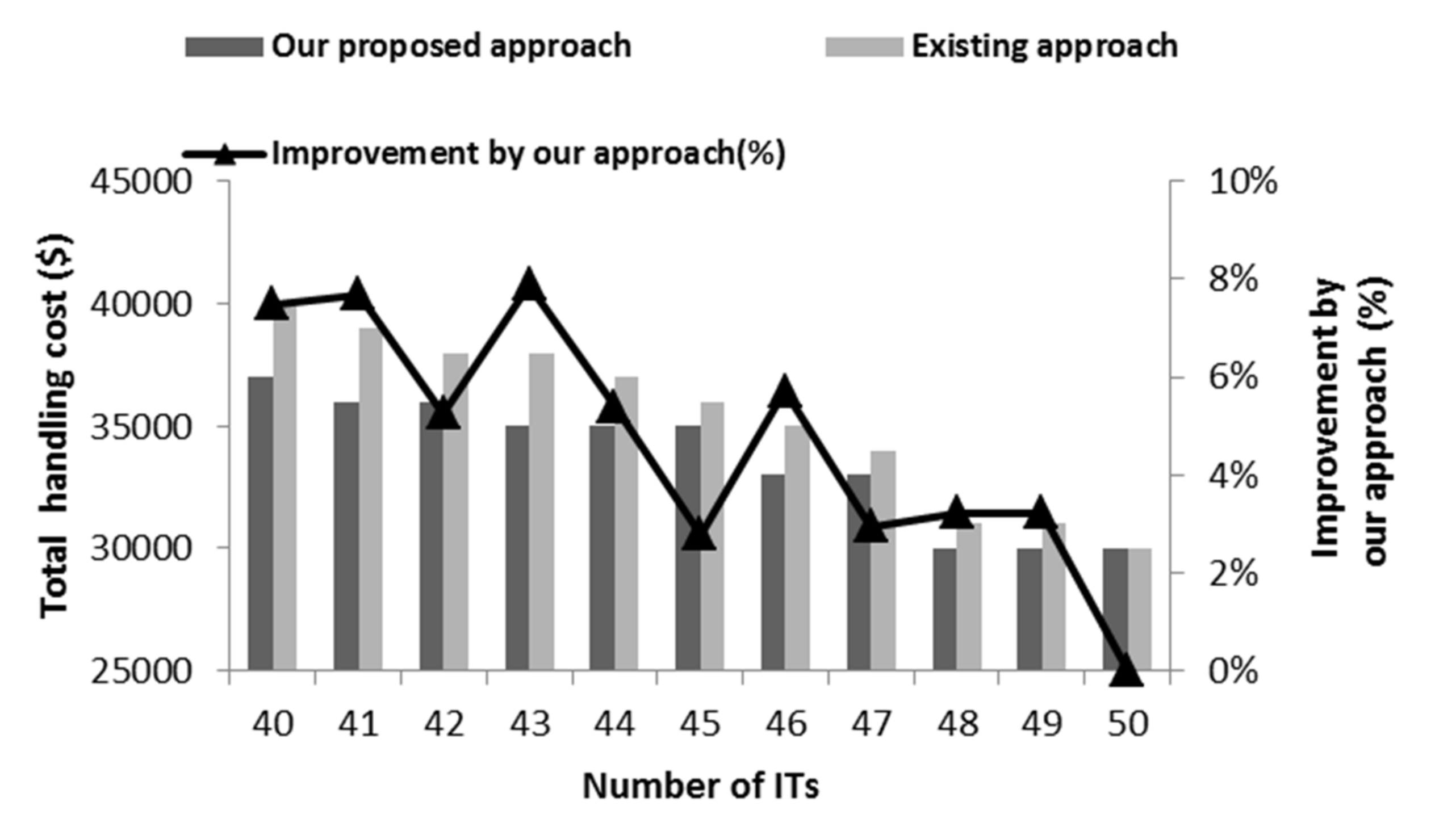
4.3. Solving Instances with Large Sizes
4.4. Significance of the Proposed New Integration Framework
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Juan, W.; Asariotis, R.; Assaf, M.; Ayala, G.; Benamara, H.; Chantrel, D.; Hoffmann, J.; Premti, A.; Rodríguez, L.; Youssef, F. Review of Maritime Transport; UNCTAD: New York, NY, USA, 2019; ISBN 978-92-1-112958-8. [Google Scholar]
- Cao, J.; Shi, Q.; Lee, D.-H. Integrated Quay Crane and Yard Truck Schedule Problem in Container Terminals. Tsinghua Sci. Technol. 2010, 15, 467–474. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W.; Wang, S. Integrated internal truck, yard crane and quay crane scheduling in a container terminal considering energy consumption. Expert Syst. Appl. 2015, 42, 2464–2487. [Google Scholar] [CrossRef]
- He, J.; Zhang, W.; Huang, Y.; Yan, W. A simulation optimization method for internal trucks sharing assignment among multiple container terminals. Adv. Eng. Inform. 2013, 27, 598–614. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 1–15. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Jan, K. Transport operations in container terminals: Literature overview, trends, research directions and classification scheme. Eur. J. Oper. Res. 2014, 236, 675–689. [Google Scholar] [CrossRef]
- Lee, D.; Qiu, H.; Miao, L. Quay crane scheduling with non-interference constraints in port container terminals. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 124–135. [Google Scholar] [CrossRef]
- Acciaro, M.; Vanelslander, T.; Sys, C.; Ferrari, C.; Roumboutsos, A.; Giuliano, G.; Lam, J.S.L.; Kapros, S. Environmental sustainability in seaports: A framework for successful innovation. Marit. Policy Manag. 2014, 41, 480–500. [Google Scholar] [CrossRef]
- Huang, G.Q.; Pratap, S.; Zhang, M.; Shen, C.L.D. A multi-objective approach to analyse the effect of fuel consumption on ship routing and scheduling problem. Int. J. Shipp. Transp. Logist. 2019, 11, 161. [Google Scholar] [CrossRef]
- Abdel-Fattah, A.; El-Tawil, A.; Harraz, N. An Integrated Operational Research and System Dynamics Approach for Planning Decisions in Container Terminals. Int. J. Ind. Sci. Eng. 2013, 7, 273–279. [Google Scholar]
- Golias, M.M.; Saharidis, G.K.; Boile, M.; Theofanis, S.; Ierapetritou, M.G. The berth allocation problem: Optimizing vessel arrival time. Marit. Econ. Logist. 2009, 11, 358–377. [Google Scholar] [CrossRef]
- Meisel, F.; Bierwirth, C. Heuristics for the integration of crane productivity in the berth allocation problem. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 196–209. [Google Scholar] [CrossRef]
- He, J. Berth allocation and quay crane assignment in a container terminal for the trade-off between time-saving and energy-saving. Adv. Eng. Inform. 2016, 30, 390–405. [Google Scholar] [CrossRef]
- Lokuge, P.; Alahakoon, D. Improving the adaptability in automated vessel scheduling in container ports using intelligent software agents. Eur. J. Oper. Res. 2007, 177, 1985–2015. [Google Scholar] [CrossRef]
- Park, Y.M.; Kim, K.H. A scheduling method for Berth and Quay cranes. OR Spectr. 2003, 25, 1–23. [Google Scholar] [CrossRef]
- Türkogulları, Y.B.; Taskın, Z.C.; Aras, N.; Altınel, I.K. Optimal berth allocation and time-invariant quay crane assignment in container terminals. Eur. J. Oper. Res. 2014, 235, 88–101. [Google Scholar] [CrossRef]
- Ursavas, E. A decision support system for quayside operations in a container terminal. Decis. Support Syst. 2014, 59, 312–324. [Google Scholar] [CrossRef]
- Chang, D.; Fang, T.; He, J.; Lin, D. Defining Scheduling Problems for Key Resources in Energy-Efficient Port Service Systems. Sci. Program. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Chang, D.; Jiang, Z.; Yan, W.; He, J. Integrating berth allocation and quay crane assignments. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 975–990. [Google Scholar] [CrossRef]
- Murty, K.G.; Liu, J.; Wan, Y.W.; Linn, R. A decision support system for operations in a container terminal. Decis. Support Syst. 2005, 39, 309–332. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.B. Functional integration approach for the berth allocation, quay crane assignment and specific quay crane assignment problems. Comput. Ind. Eng. 2016, 102, 458–466. [Google Scholar] [CrossRef]
- Vahdani, B.; Mansour, F.; Soltani, M.; Veysmoradi, D. Bi-objective optimization for integrating quay crane and internal truck assignment with challenges of trucks sharing. Knowl.-Based Syst. 2019, 163, 675–692. [Google Scholar] [CrossRef]
- Schulz, S.A.; Luthans, K.W.; Messersmith, J.G.; Harvey, M.; Kiessling, T.; Randall, W.S.; Nowicki, D.R.; Deshpande, G. Psychological capital A new tool for driver retention. Int. J. Phys. Distrib. Logist. Manag. 2014, 44, 621–634. [Google Scholar] [CrossRef]
- The Port of Hong Kong Handbook & Directory. Available online: http://www.mardep.gov.hk/en/publication/pdf/porthk.pdf (accessed on 13 November 2014).
- Wang, Z.X.; Chan, F.T.S.; Chung, S.H.; Niu, B. A decision support method for internal truck employment. Ind. Manag. Data Syst. 2014, 114, 1378–1395. [Google Scholar] [CrossRef]
- Notteboom, T. Dock labour systems in North-West European seaports: How to meet stringent market requirements? In Proceedings of the International Forum on Shipping, Ports and Airports (IFSPA), Hong Kong, China, 27–30 May 2012; pp. 1–21. [Google Scholar]
- Petering, M.E.H. Decision support for yard capacity, fleet composition, truck substitutability, and scalability issues at seaport container terminals. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 85–103. [Google Scholar] [CrossRef]
- Karam, A.; Attia, E.-A. Integrating collaborative and outsourcing strategies for yard trucks assignment in ports with multiple container terminals. Int. J. Logist. Syst. Manag. 2019, 32, 372–394. [Google Scholar] [CrossRef]
- Karam, A.; ElTawil, A.B.; Harraz, N.A. Simultaneous assignment of quay cranes and internal trucks in container terminals. Int. J. Ind. Syst. Eng. 2016, 24, 107–125. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.B. A Lagrangian relaxation approach for the integrated quay crane and internal truck assignment in container terminals. Int. J. Logist. Syst. Manag. 2016, 24, 113–136. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.B. A new method for allocating berths, quay cranes and internal trucks in container terminals. In Proceedings of the 2015 International Conference on Logistics, Informatics and Service Science, Barcelona, Spain, 27–29 July 2015; pp. 31–36. [Google Scholar]
- Kang, S.; Medina, J.C.; Ouyang, Y. Optimal operations of transportation fleet for unloading activities at container ports. Transp. Res. Part B Methodol. 2008, 42, 970–984. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, L.; Zhang, Z.; Shi, L.; Armstrong, A.J. The allocation of berths and quay cranes by using a sub-gradient optimization technique. Comput. Ind. Eng. 2010, 58, 40–50. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.; Li, Z. An optimization approach for coupling problem of berth allocation and quay crane assignment in container terminal. Comput. Ind. Eng. 2012, 63, 243–253. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J.N. Introduction to Linear Optimization; Athena Scientific: Belmont, TN, USA, 1997; ISBN 1886529191. [Google Scholar]
- Geoffrion, A.M. Lagrangian relaxation for integer programming. In Proceedings of the 50 Years of integer programming 1958–2008, Aussois, France, 7–11 January 2008; pp. 243–281. [Google Scholar]
- Imai, A.; Nishimura, E.; Papadimitriou, S. The dynamic berth allocation problem for a container port. Transp. Res. Part B Methodol. 2001, 35, 401–417. [Google Scholar] [CrossRef]

| Class | ||||
|---|---|---|---|---|
| Feeder | U (3, 4) + 1** | U (150, 450) | 1 | 2 |
| Medium | U (4, 6) + 1 | U (450, 1400) | 2 | 4 |
| Jumbo | U (6, 7) + 1 | U (1400, 1900) | 4 | 6 |
| Instance # (No. of Vessels) | CPLEX | The Heuristic Algorithm | |||||
|---|---|---|---|---|---|---|---|
| The Average Values | |||||||
| Optimal Solution | Lower Bound | CPU*(min.) | Upper Bound (UB) | Lower Bound (LB) | CPU (min.) | ||
| 1(3) | 4000 | - | 2.24 | 4000 | 3510 | 0.5236 | 12.2 |
| 2(4) | 3000 | - | 5.43 | 3000 | 2307.5 | 0.791310 | 23.08 |
| 3(4) | 2000 | - | 19.27 | 2000 | 1112.1 | 0.616287 | 44.39 |
| 4(4) | 4000 | - | 6.54 | 4000 | 3902.2 | 0.895599 | 2.45 |
| 5(4) | 2000 | - | 0.23 | 2000 | 2000 | 0.031226 | 0 |
| 6(4) | 3000 | - | 15.54 | 3000 | 2886.6 | 0.505049 | 3.78 |
| 7(4) | 4000 | - | 4.15 | 4000 | 3790 | 1.118004 | 5.25 |
| 8(5) | 7000 | - | 20.13 | 7000 | 6234.7 | 1.51 | 10.93 |
| 9a(5) | - | 5771.12 | 39.89 | 8000 | 7634.91 | 2.01 | 4.56 |
| 10a(5) | - | - | 13.56 | 8000 | 7512 | 2.384742 | 6.10 |
| 11a(5) | - | - | 42.32 | 9000 | 8464.4 | 1.085400 | 5.95 |
| Instance # (Size) | The Worst | The Best | The Average | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LB* | UB* | Gap % | LB | UB | Gap% | LB | UB | CPU (Min.) | Gap % | |
| 1 (20) | 25.39 | 27 | 5.97 | 25.99 | 26 | 0.03 | 25.64 | 26.4 | 10.14 | 2.89 |
| 2 (20) | 28.46 | 31 | 8.19 | 28.86 | 29 | 0.49 | 28.7 | 29.8 | 10.84 | 3.7 |
| 3 (20) | 8.16 | 9 | 9.29 | 8.55 | 9 | 5.01 | 8.38 | 9 | 4.26 | 6.87 |
| 4 (20) | 24.3 | 27 | 10.01 | 24.45 | 27 | 9.44 | 24.34 | 27 | 6.08 | 9.83 |
| 5 (20) | 17.93 | 23 | 22.05 | 18.36 | 21 | 12.59 | 18.15 | 22 | 5.82 | 17.5 |
| 6 (20) | 29.37 | 40 | 26.58 | 30.19 | 33 | 8.52 | 29.95 | 37.6 | 9.1 | 20.36 |
| 7 (20) | 22.71 | 27 | 15.89 | 22.9 | 23 | 0.45 | 22.82 | 24 | 21.5 | 4.93 |
| 8 (20) | 24.11 | 28 | 13.89 | 24.64 | 26 | 5.25 | 24.35 | 27 | 10.2 | 9.8 |
| 9 (20) | 18.63 | 23 | 19 | 19.72 | 21 | 6.1 | 19.22 | 22 | 4.8 | 12.65 |
| 10 (20) | 23.14 | 24 | 3.6 | 23.91 | 24 | 0.38 | 23.6 | 24 | 5.22 | 1.66 |
| 11 (25) | 32.3 | 40 | 19.24 | 32.69 | 37 | 11.64 | 32.45 | 38.4 | 16.57 | 15.5 |
| 12 (25) | 34.12 | 43 | 20.64 | 34.56 | 36 | 4 | 34.27 | 38.6 | 14.86 | 11.23 |
| 13 (25) | 42.77 | 62 | 31.02 | 42.95 | 51 | 15.79 | 42.85 | 58.8 | 14.74 | 27.13 |
| 14 (25) | 21.82 | 30 | 27.28 | 21.86 | 24 | 8.9 | 21.83 | 25.4 | 6.02 | 14.04 |
| 15 (25) | 35.77 | 43 | 16.82 | 36.11 | 41 | 11.93 | 35.91 | 41.4 | 15.92 | 13.26 |
| 16 (25) | 19.39 | 22 | 11.86 | 20.09 | 21 | 4.35 | 19.82 | 21.6 | 7.12 | 8.22 |
| 17 (25) | 34.71 | 36 | 3.58 | 34.94 | 35 | 0.19 | 34.8 | 35.4 | 8.5 | 1.69 |
| 18 (25) | 30.41 | 38 | 19.98 | 30.75 | 34 | 9.57 | 30.59 | 35.8 | 14.86 | 14.55 |
| 19 (25) | 25.8 | 31 | 16.78 | 26 | 26 | 0 | 25.92 | 27.4 | 7.28 | 5.41 |
| 20 (25) | 44.02 | 67 | 34.3 | 44.24 | 51 | 13.3 | 44.09 | 55.4 | 17.65 | 20.4 |
| 21 (30) | 41.1 | 49 | 16.13 | 41.96 | 44 | 4.65 | 41.52 | 46.2 | 12.64 | 10.13 |
| 22 (30) | 43.46 | 75 | 42.05 | 43.68 | 59 | 25.96 | 43.59 | 67.8 | 37.15 | 35.71 |
| 23 (30) | 44.18 | 51 | 13.37 | 44.18 | 47 | 5.99 | 44.18 | 49.8 | 9.46 | 11.28 |
| 24 (30) | 42.74 | 65 | 34.2 | 42.94 | 53 | 19.0 | 42.84 | 58.4 | 46.15 | 26.6 |
| 25 (30) | 32.24 | 60 | 46.26 | 32.67 | 49 | 33.32 | 32.46 | 54.6 | 29.17 | 40.56 |
| 26 (30) | 50.4 | 59 | 14.58 | 51.5 | 52 | 0.96 | 51.02 | 56.2 | 22.64 | 9.22 |
| 27 (30) | 61.23 | 69 | 11.26 | 61.8 | 64 | 3.44 | 61.51 | 67.8 | 31.55 | 9.28 |
| 28 (30) | 44.48 | 61 | 27.08 | 45.9 | 51 | 9.99 | 45.18 | 59.8 | 22.46 | 24.44 |
| 29 (30) | 45.99 | 74 | 37.86 | 45.88 | 68 | 32.53 | 45.03 | 71.8 | 46.15 | 37.34 |
| 30 (30) | 42.99 | 75 | 42.69 | 41.91 | 71 | 40.97 | 42.06 | 74.6 | 29.17 | 41.62 |
| Average | 33.07 | 43.63 | 20.72 | 33.47 | 38.43 | 10.16 | 33.24 | 41.13 | 16.60 | 15.66 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karam, A.; Eltawil, A.; Hegner Reinau, K. Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability 2020, 12, 3202. https://doi.org/10.3390/su12083202
Karam A, Eltawil A, Hegner Reinau K. Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability. 2020; 12(8):3202. https://doi.org/10.3390/su12083202
Chicago/Turabian StyleKaram, Ahmed, Amr Eltawil, and Kristian Hegner Reinau. 2020. "Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals" Sustainability 12, no. 8: 3202. https://doi.org/10.3390/su12083202
APA StyleKaram, A., Eltawil, A., & Hegner Reinau, K. (2020). Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability, 12(8), 3202. https://doi.org/10.3390/su12083202





