1. Introduction
The economic sustainability and social development of most countries depend directly on the reliable and lasting behavior of their infrastructure [
1]. Infrastructures have special relevance because they strongly influence economic activity, growth, and employment. However, these activities have a significant impact on the environment, have irreversible effects, and can compromise the present and future of society. It is known that construction is a carbon-intensive industry [
2]; therefore, the minimization of emissions is increasingly important to reduce the environmental impact of construction projects. Looking further, we find that cement is one of the materials that generates large amounts of emissions. A large amount of emissions is mainly due to the calcination process of the limestone together with the high energy demand necessary for its production [
3]. Therefore, the optimization of structures that use large amounts of cement is critical. Consequently, it is essential to develop lines of research in sustainable construction [
4,
5], energy consumption [
6,
7], and in the study of the cycle of the CO
emissions made by concrete structures [
8]. The great challenge is to have an infrastructure capable of maximizing its social benefit without compromising its sustainability [
9].
The standard procedure [
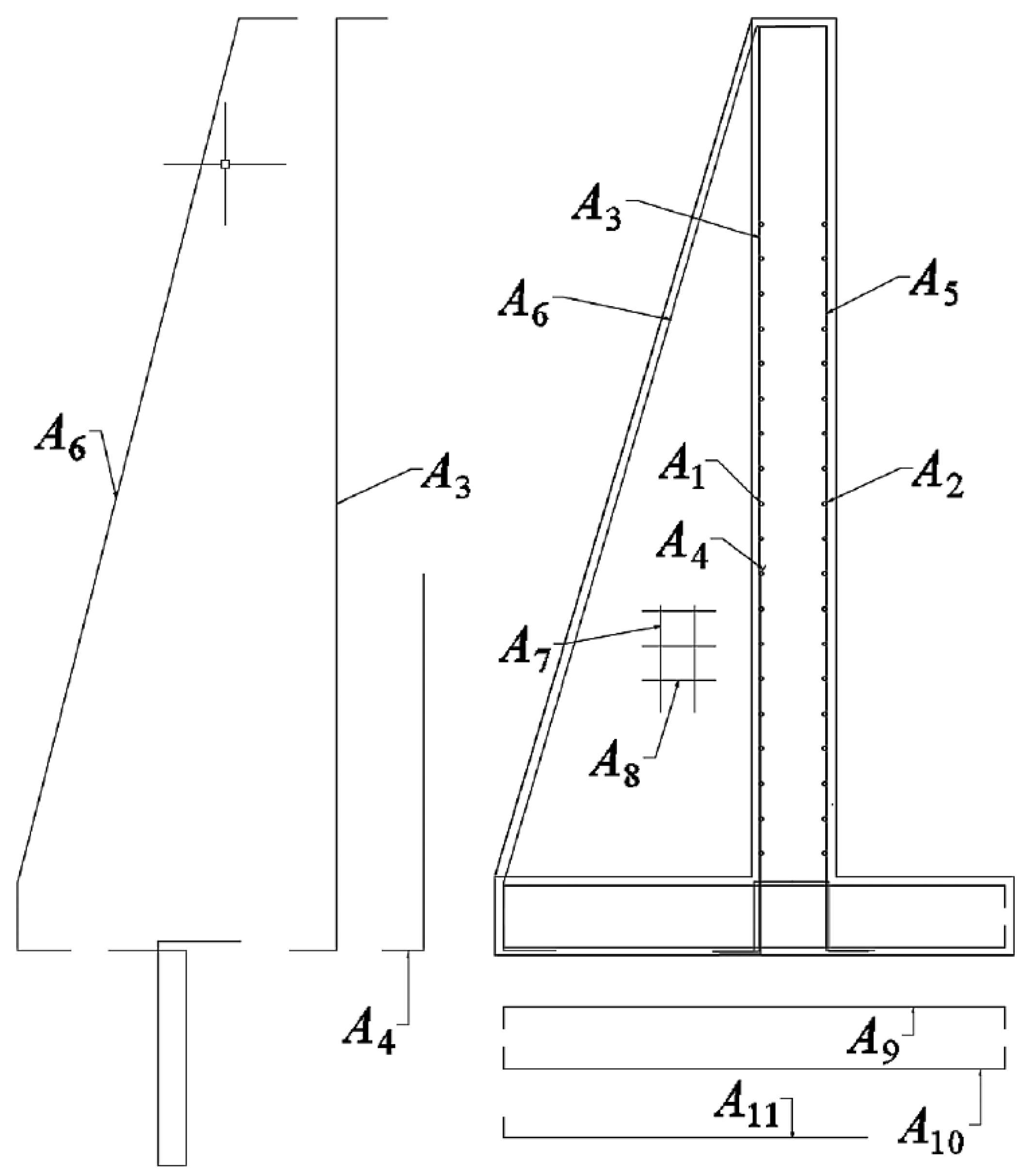
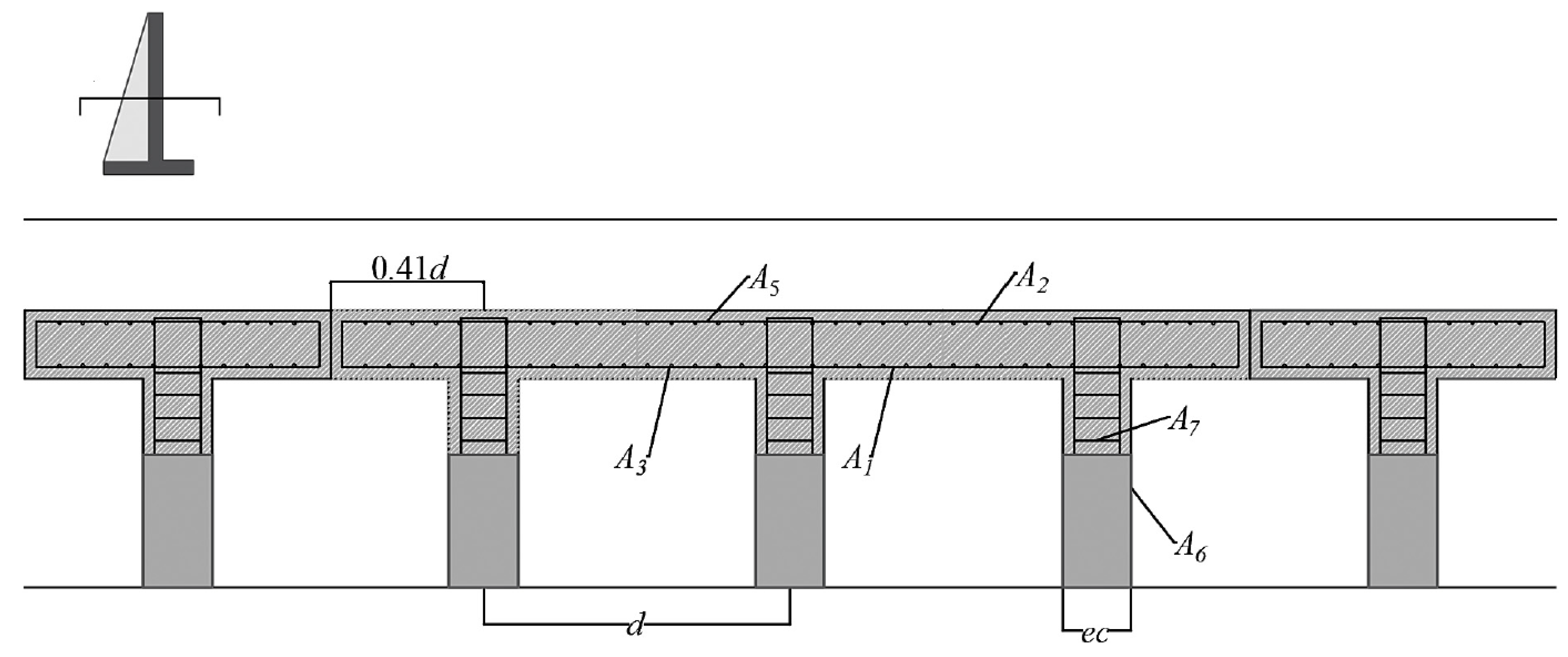
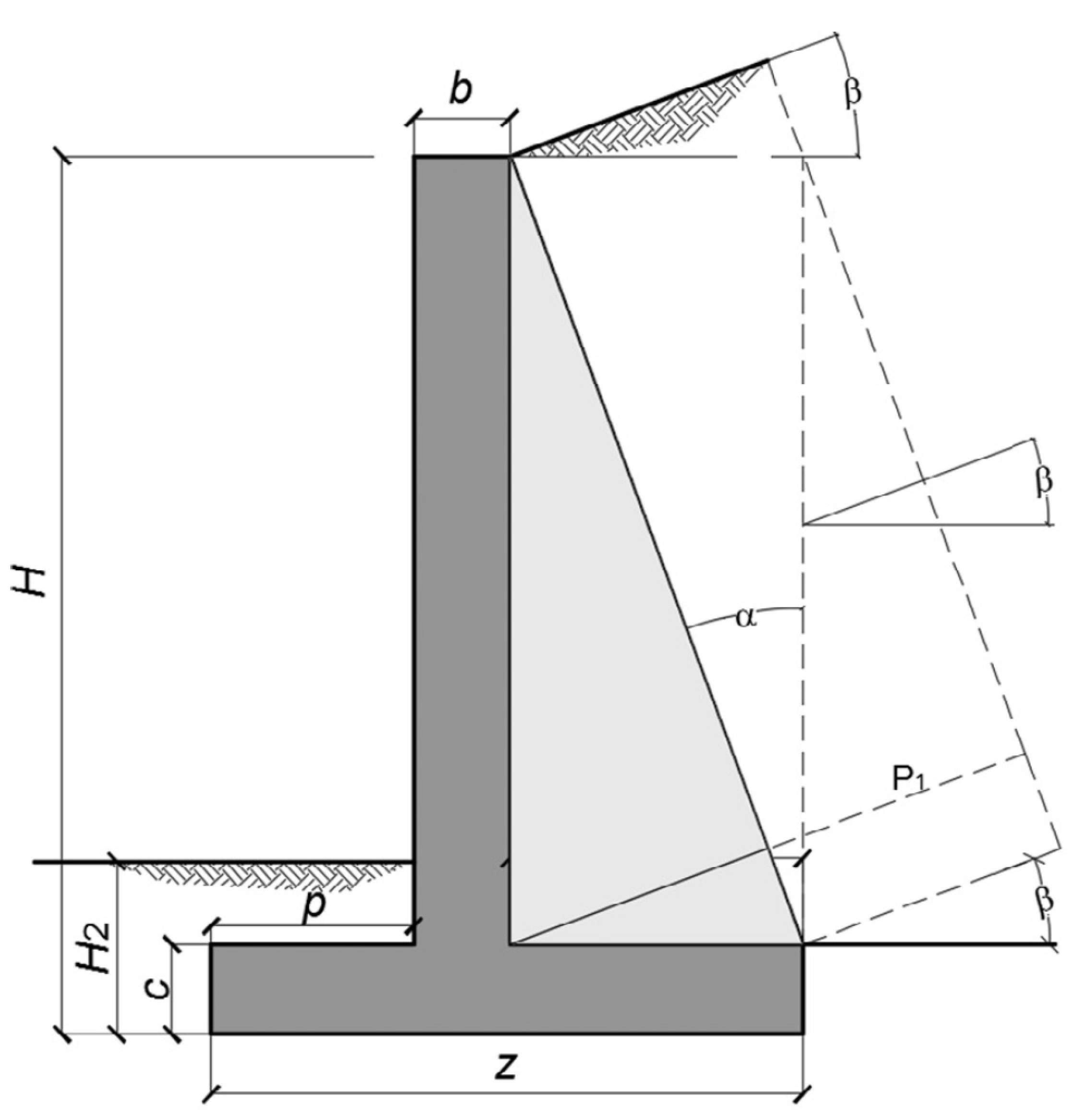
10] to perform the economic estimation of structures is based on a trial-and-error approach. This approach is necessary because the dimensions of the cross-section and the material grades are defined a priori. This involves analyzing the stresses and calculating the effort required in each material configuration. This standard procedure is slow and expensive. Particularly in the case of a wall, there are a number of parameters that must be taken into account, such as boundary conditions, the type of filling, the friction base angles, load capacity of the base of the ground, and surcharge loads.
On the other hand, the emissions of CO
constitute an important portion of the contribution to the global warming process of the planet. In particular, approximately 40%–50% of global GHG emissions are generated by construction [
11]. In addition, the cement industry releases 5% of global GHG emissions [
12]. Therefore, sustainability and specifically the use of high-carbon-footprint products in structural engineering is a relevant line of research. At present, the consumption of CO
has been investigated by considering it as an objective function within an optimization problem. Particularly in [
13], the optimization of CO
consumption in walls was analyzed using the harmony search algorithm. In [
14], the impact of CO
on cantilever retaining walls was studied. A CO
and cost analysis in precast–prestressed concrete road bridges was developed in [
11]. The study of a sustainable prototype for reinforced concrete columns was proposed in [
15]. In this study, heuristic methods of optimization of CO
emissions were applied. In [
16], the importance of the criteria that define social sustainability was analyzed. These criteria considered the complete life of infrastructure. The social sustainability of infrastructure projects was tackled in [
17] through the use of Bayesian methods. In [
18], an optimization was studied based on the cost criterion of reinforced concrete-retaining walls. The study considered using different types of load capacity estimates. The life cycle assessment of earth-retaining walls was analyzed in [
19,
20]. In [
21], a stochastic analysis of the emissions of CO
was developed and applied to construction sites. The relevance of carbon emissions and low-emission window films on energy spending was studied in [
22] and applied to an existing UK hotel building. In [
23], a methodology was built for the investigation of carbon emissions in a hospital building, which allowed the generation of an information model and an evaluation of its life cycle. In [
24], an optimization of reinforced concrete columns was optimized considering several environmental impact assessment parameters.
To solve large-scale and highly non-linear optimization problems, metaheuristic algorithms, which have demonstrated their efficiency and versatility, have been used [
25]. There has been a lot of research in the area of metaheuristics in recent years, and a large number of algorithms have been developed.
Most of these algorithms have been inspired by physical, chemical, and biological systems [
26]. As examples of these heuristic search algorithms that belong to this category, we find particle swarm optimization (PSO), harmony search (HS) [
27], threshold acceptance (TA), simulated annealing (SA) [
28,
29], threshold acceptance (TA), genetic algorithms (GA), ant colonies (ACO), genetic algorithms (GA), whale optimization (WO), cuckoo search (CS), and black hole (BH), among others. The use of metaheuristic algorithms in sustainability and construction has been used, for example, in [
30], where they applied heuristic methods to the study of reinforced concrete road vaults; in addition, a metaheuristic was applied to the problem of decision making in [
31]. In [
32], a mathematical model was developed with the goal of improving environmental economic policies. This model was applied to a protection zone. A survey of the social sustainability evaluation applied to the infrastructures was developed in [
33]. However, we must consider that many of the metaheuristics work in continuous spaces. Researchers have been developing techniques to obtain discrete or binary versions of these metaheuristics. For more details on binarization techniques, the reader can consult [
34,
35,
36].
In this article, inspired by the aforementioned, we explore the application of a binary black hole algorithm to solve the optimization of counterfort retaining walls. The contributions of this work are detailed below:
An adaptation of the BH optimization technique to work in discrete environments. Naturally, BH works in continuous spaces. Here, an adaptation is proposed using the concept of optimal approach velocity and a min–max normalization, which allows the velocity to be transformed into a transition probability.
The application of the discrete version of BH to the counterfort retaining walls optimization problem. This optimization considers the objective function, the costs, and the CO separately.
The impact of the relevant design variables is studied, both in costs and in CO emission.
In
Section 2, the optimization problem, the variables involved, and the restrictions are defined. The algorithm that executes the optimization is detailed in
Section 3. The experiments and results obtained are shown in
Section 4. Finally, in
Section 5, the conclusions and new lines of research are summarized.
5. Conclusions
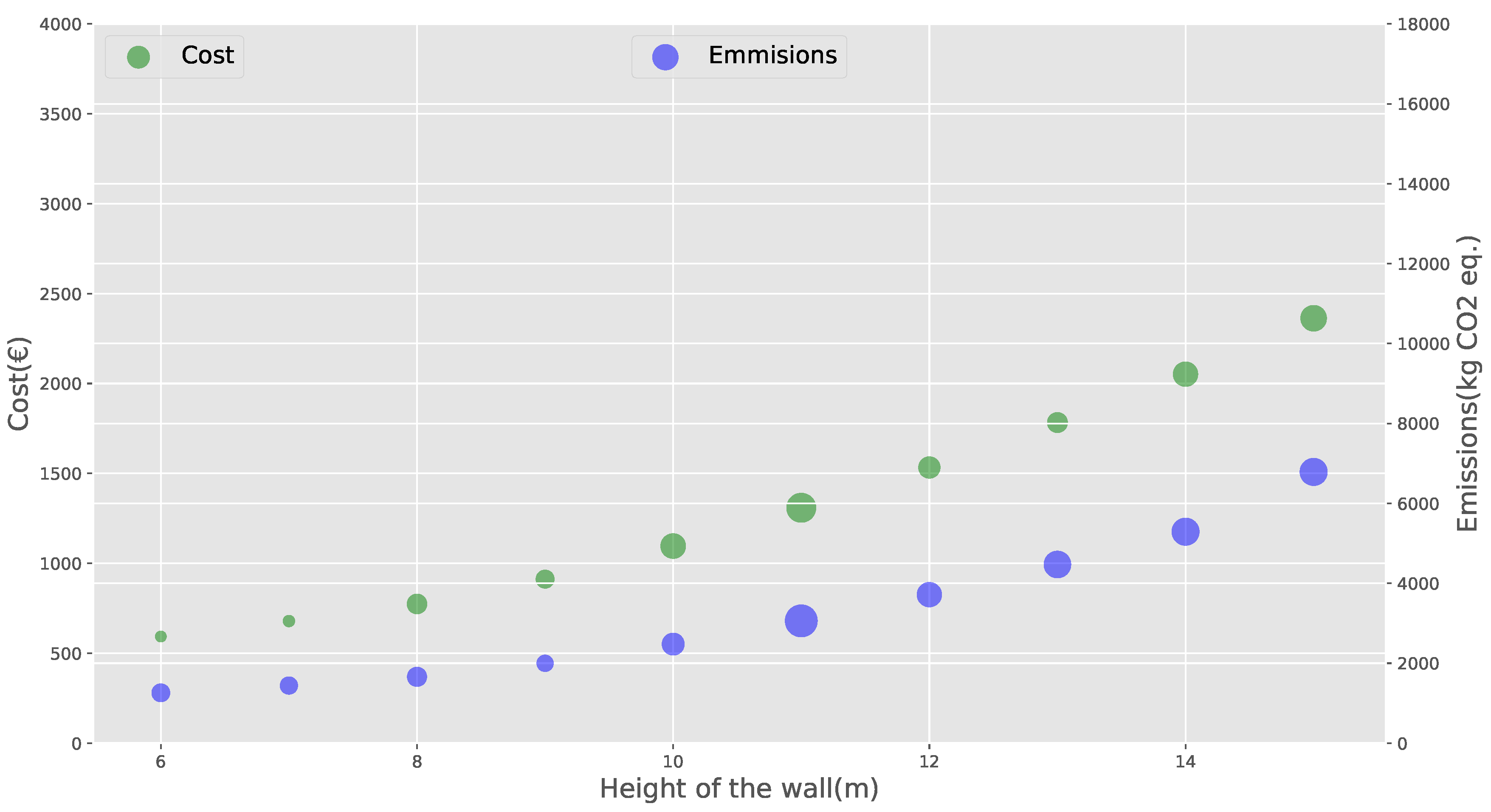
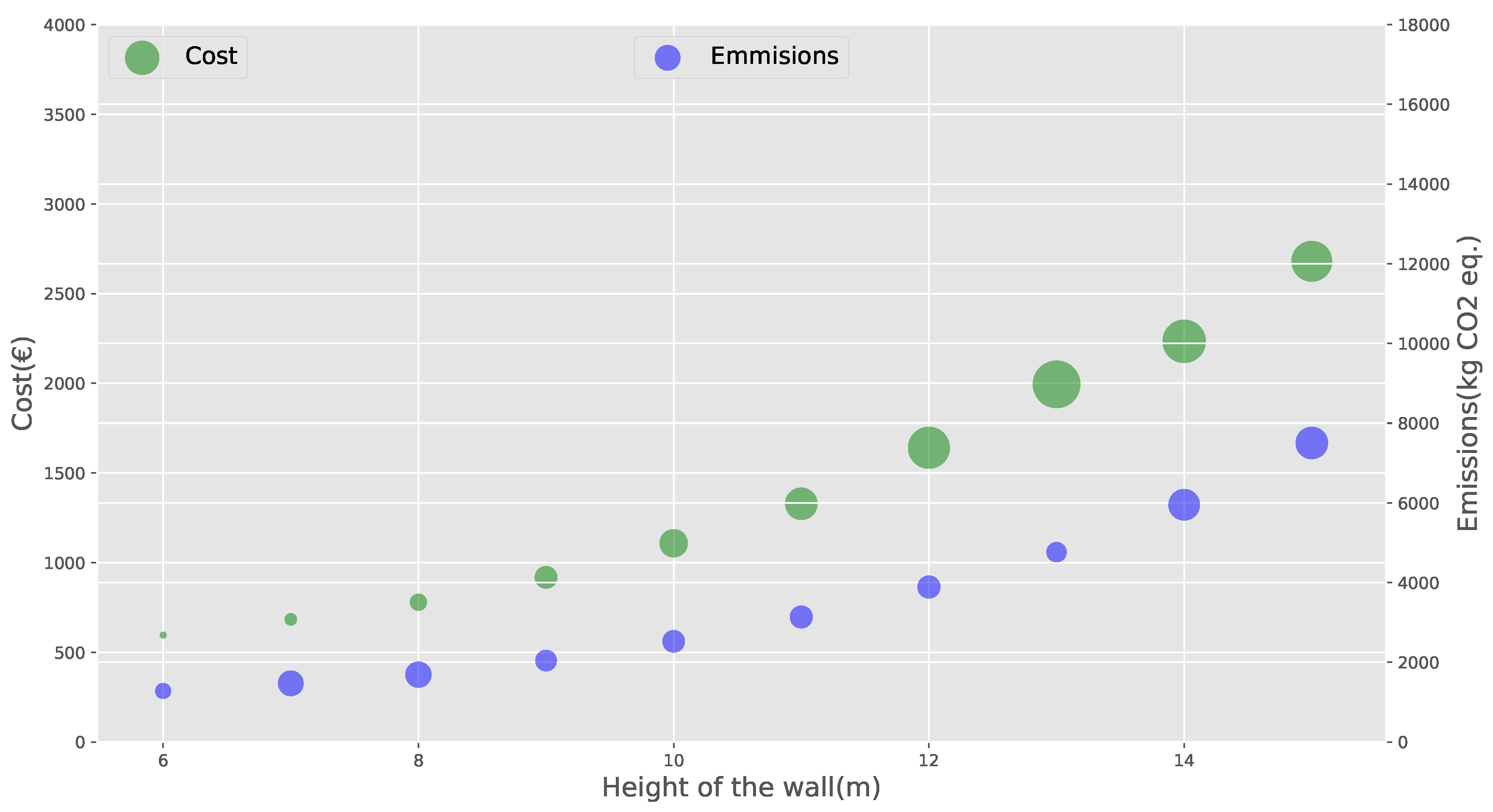
This article studies a parametric optimization of a buttressed earth-retaining wall using a discrete black hole algorithm. The analysis was developed considering two objective functions: One function that optimizes the cost of the structure and another that minimizes CO
emissions. In the different experiments, the height of the wall was varied, and we subsequently compared the results of both optimizations. Working with the target of reducing emissions provides stabilized results while maintaining the economic target. The results obtained with the BH heuristic also suggest that there is a relationship between cost and equivalent CO
emissions. For small heights of 6 and 7 m, the optimal CO
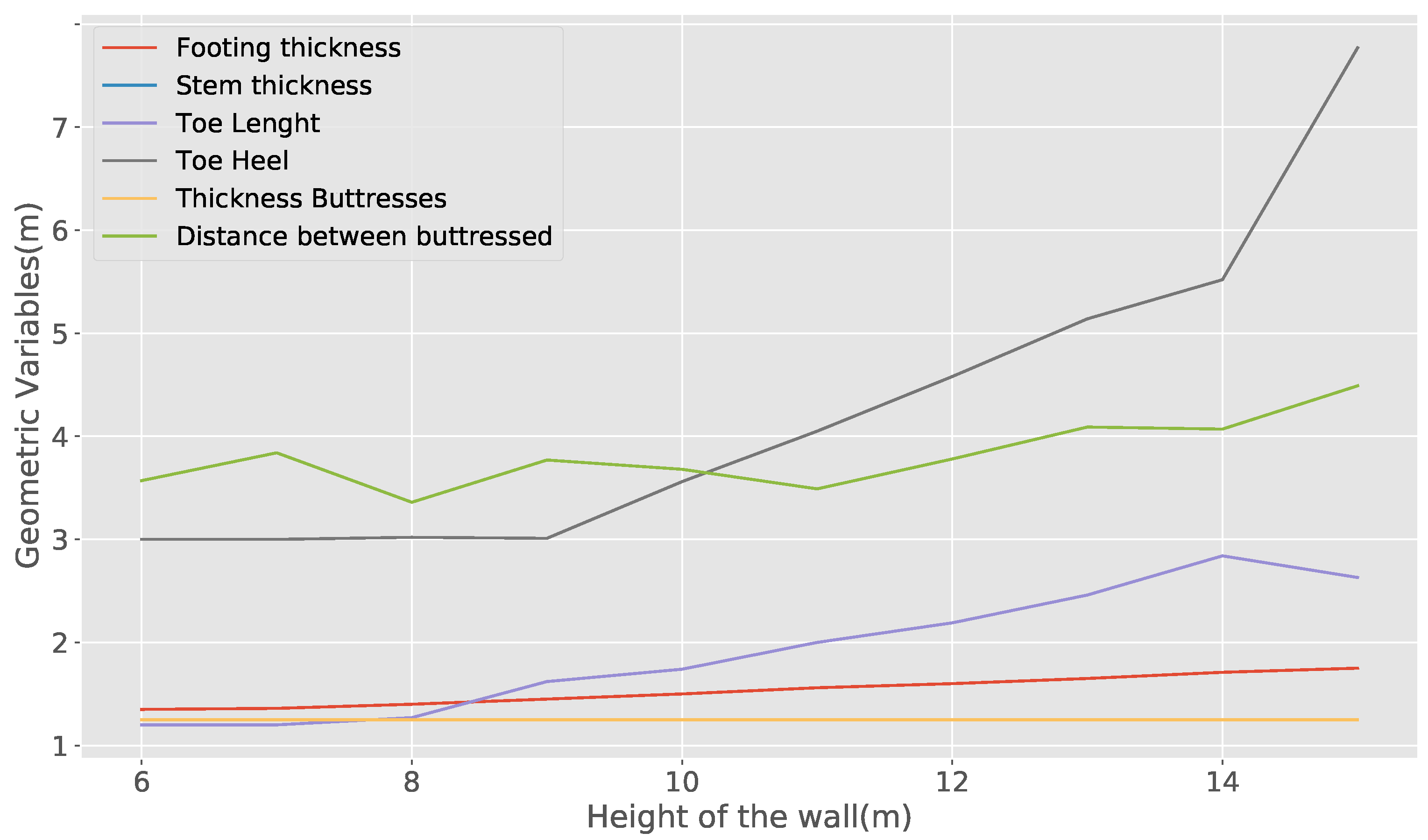
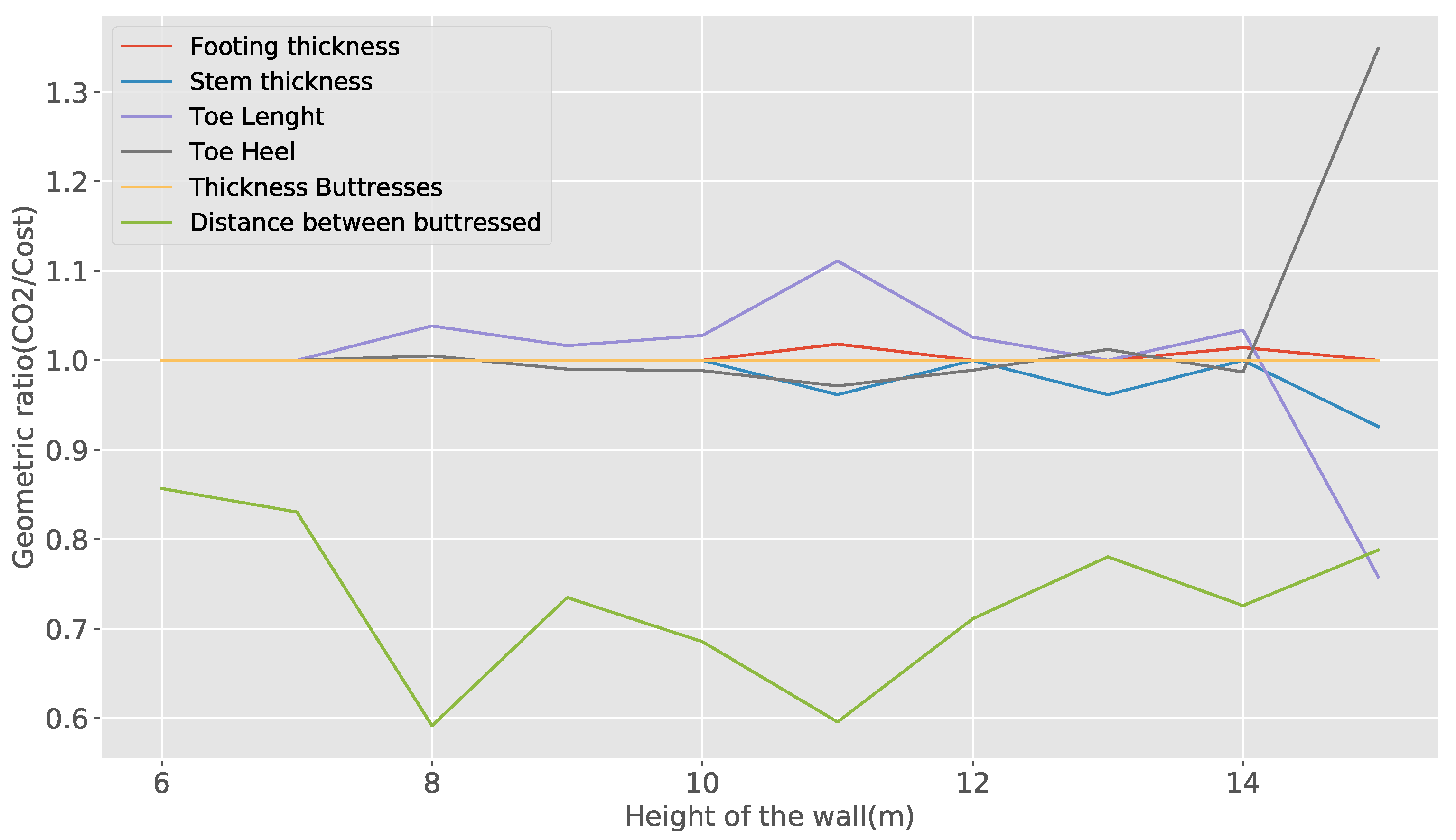
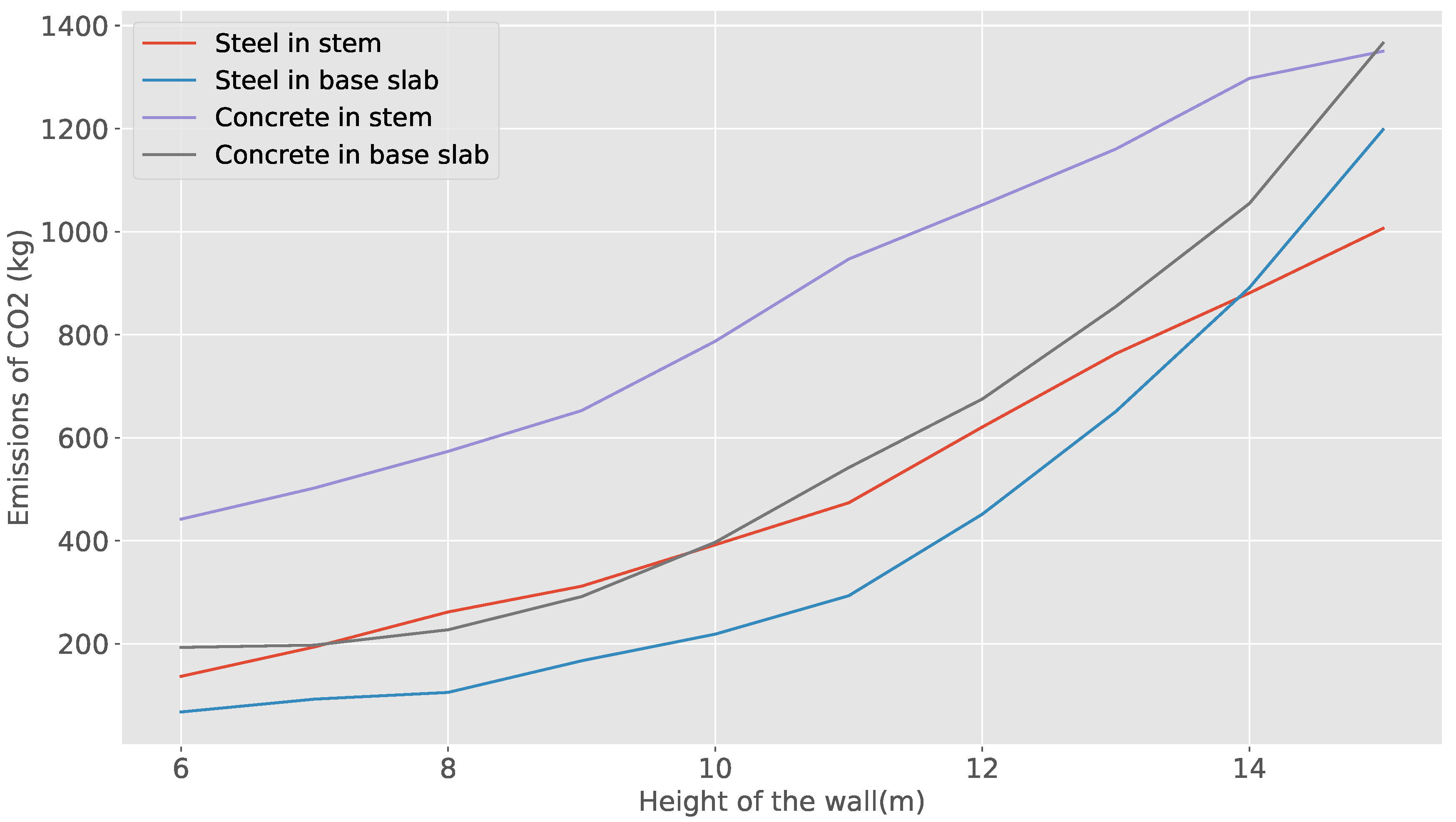
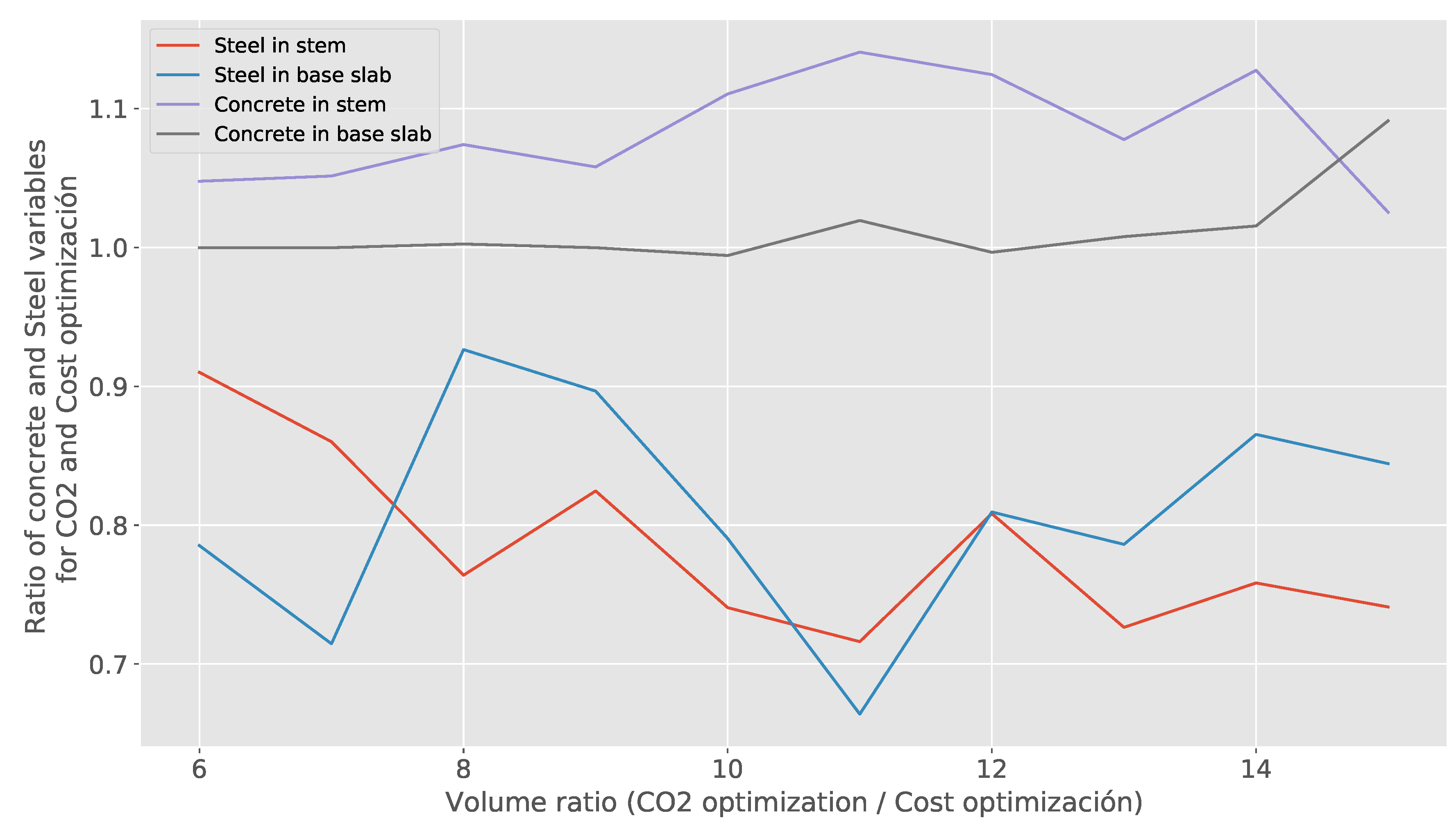
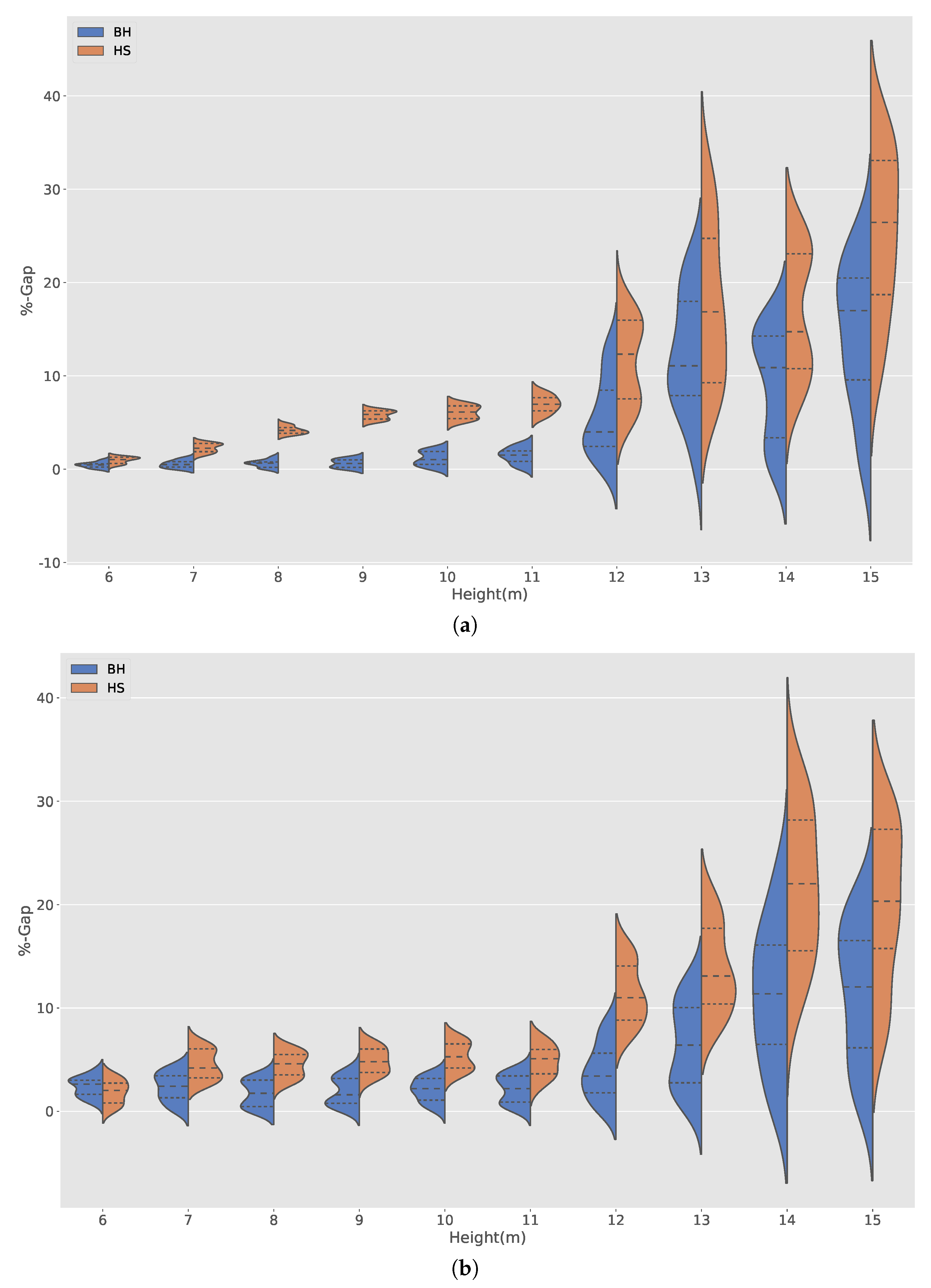
emission and structure costs do not deviate much from each other. As the wall grows, this difference increases, reaching a maximum at 11 m, where the emission deviates 6.16% and the cost 7.49%. When we analyze the main cause of this difference, it is found that it is related to the use of steel and cement. Solutions that minimize emissions prefer to use more concrete and less steel than those that optimize cost. Regarding the design variables, for optimal solutions, most of the values are very similar in both optimizations, with the exception of the variable of distance between buttresses, whose emission optimization value is always less than that obtained from cost optimization. For high heights (15 m), there is an inversion between the toe and heel length variables. As a result of the second analysis, in both optimizations and for the different wall heights, the concrete and the resulting steel in all cases are the C25/30 and BS500. When analyzing the dispersion results of the solutions for the different heights of the wall, it is observed that the dispersion of the solutions (
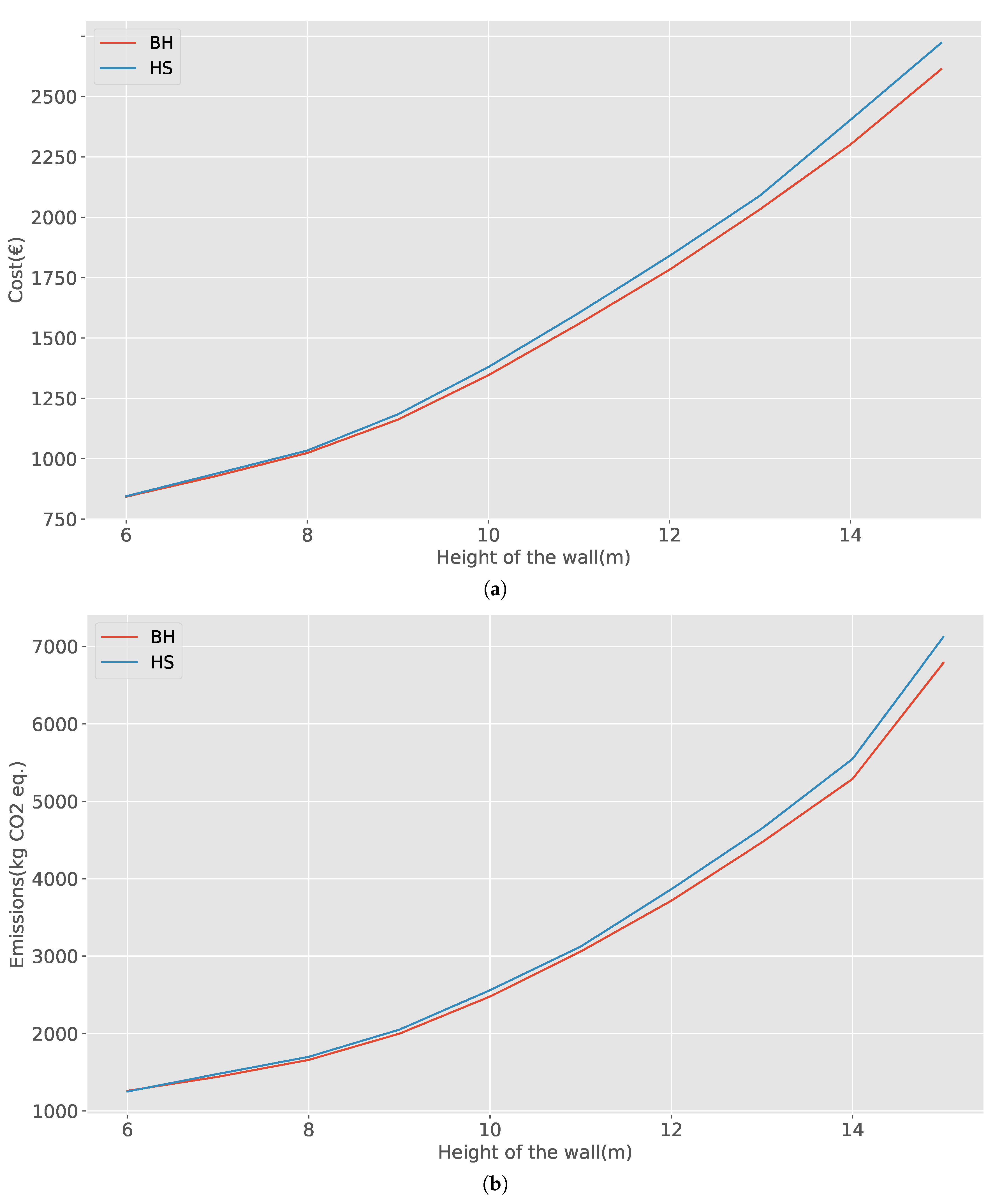
Figure 11a,b) increases. This increase is considerable from the height of 12 m onwards. The above is an indication that our optimization problem is becoming more difficult as the height of the wall increases. This is consistent with the fact that at higher heights, it is more difficult to obtain stability of the wall concerning overturning and sliding. Finally, when we compare BH with HS, we observe that as we increase the height, BH performs better than HS, arriving at the height of 14 m at a difference of 4.67% in favor of BH in the optimization of emissions and 4.74% in cost minimization.
As a new line of research, it is interesting to explore robust optimization. Consider the optimization of the wall, but incorporating different values of some of the design variables within the optimization, as well as edge conditions, such as natural disasters. This makes the optimization problem much more difficult to address. Aiming at the latter, hybrid techniques can be used where metaheuristic algorithms are integrated with machine learning [
46,
47] techniques in order to improve the quality and convergence time of the solutions. This allows the tackling of more difficult problems, such as robust optimization in reasonable execution times.