Analysis of the State-Dependent Queueing Model and Its Application to Battery Swapping and Charging Stations
Abstract
1. Introduction
2. Literature Review
3. Mathematical Model Analysis and Application
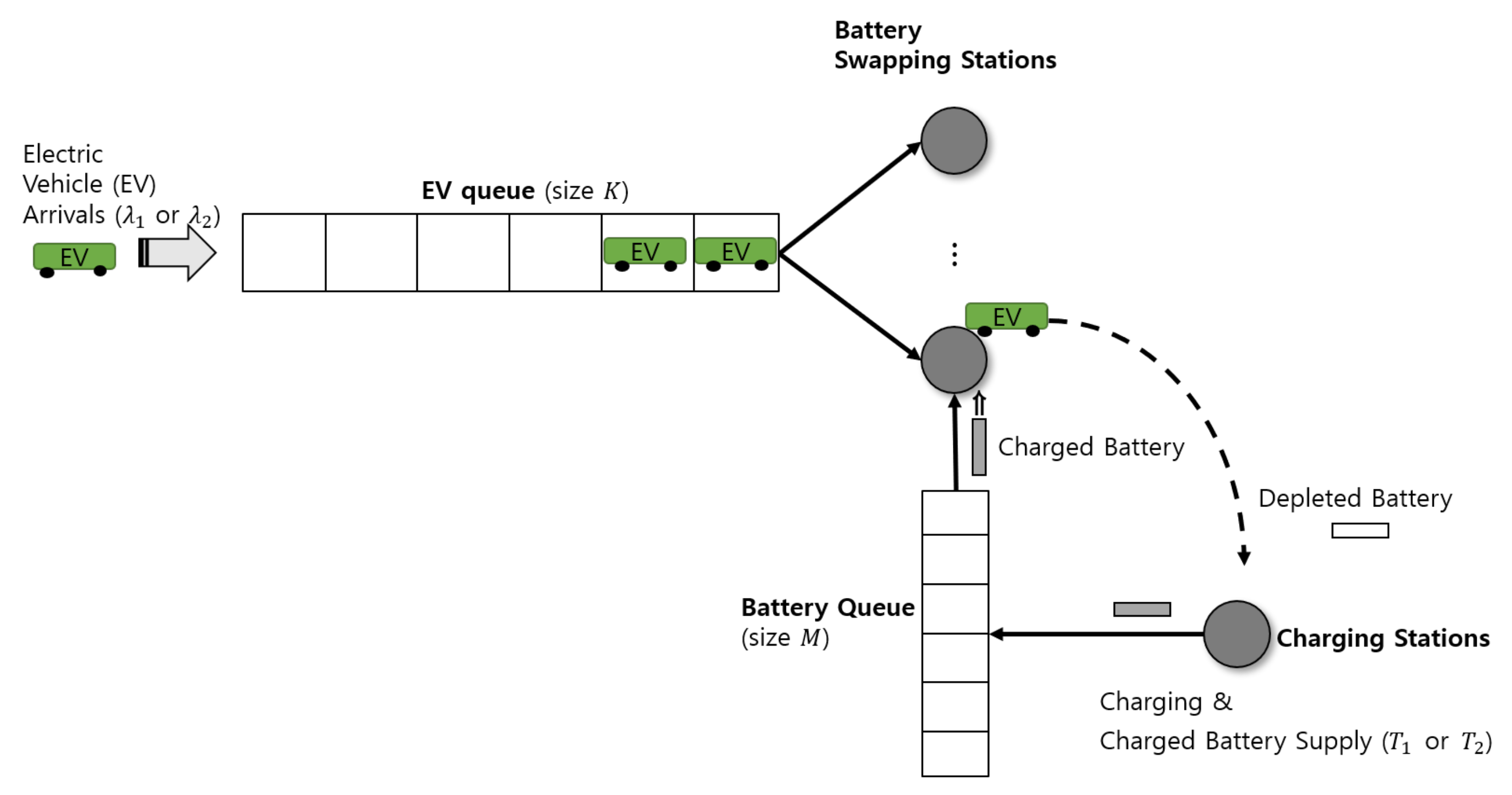
3.1. Model Description
3.2. Analysis of an Arrival First Model
- If , an EV-arrival rate is , and a battery-supply interval is . Note that arrival rates and supply intervals are adjusted according to the number of EVs in the EV queue immediately after a battery-supply event.
- If , an EV-arrival rate is set to , and a battery-supply interval is . Note that the “AF” policy is assumed.
- If , an EV-arrival rate is , and a battery-supply interval is set to .
3.3. Analysis of a Supply First Model
4. Numerical Examples
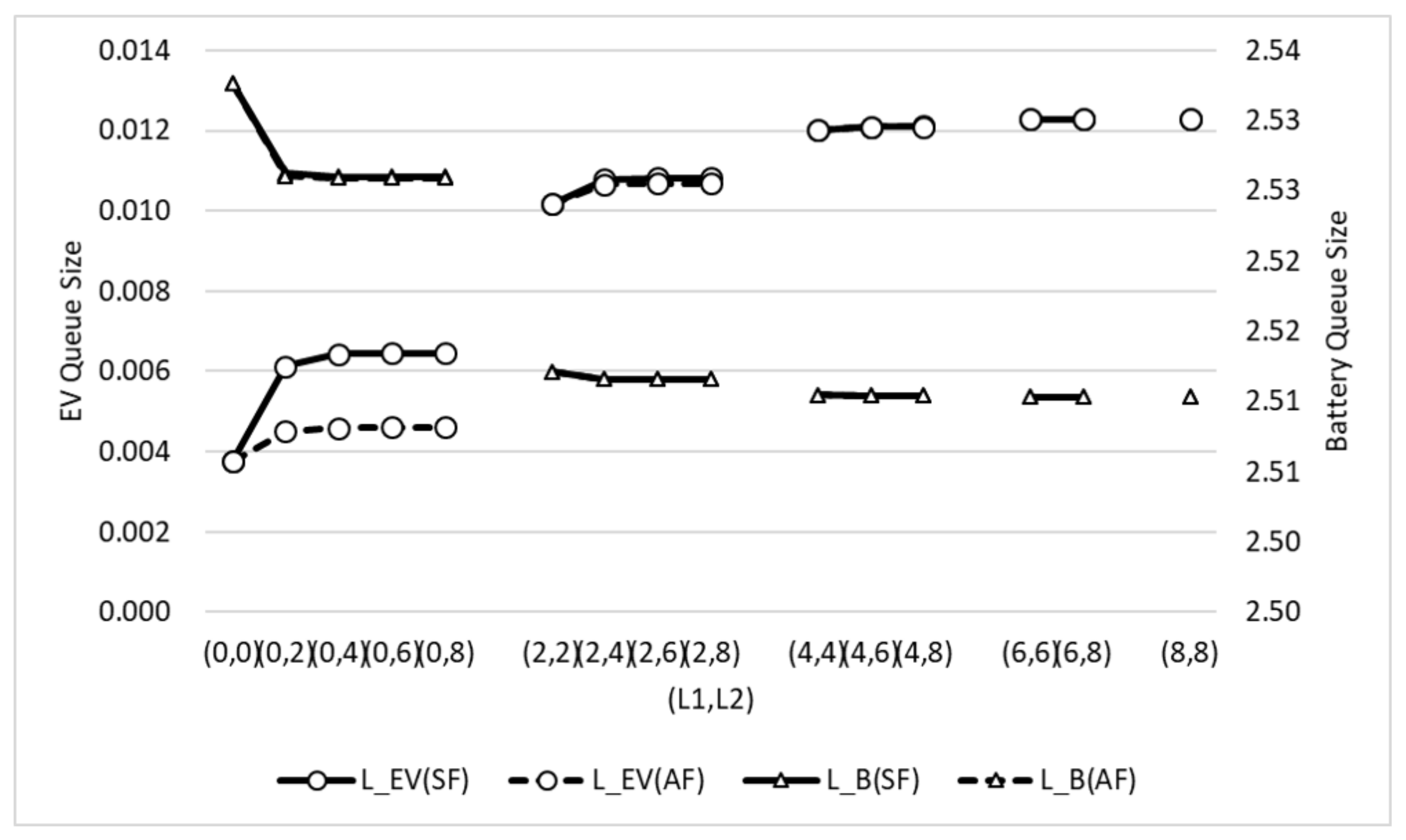
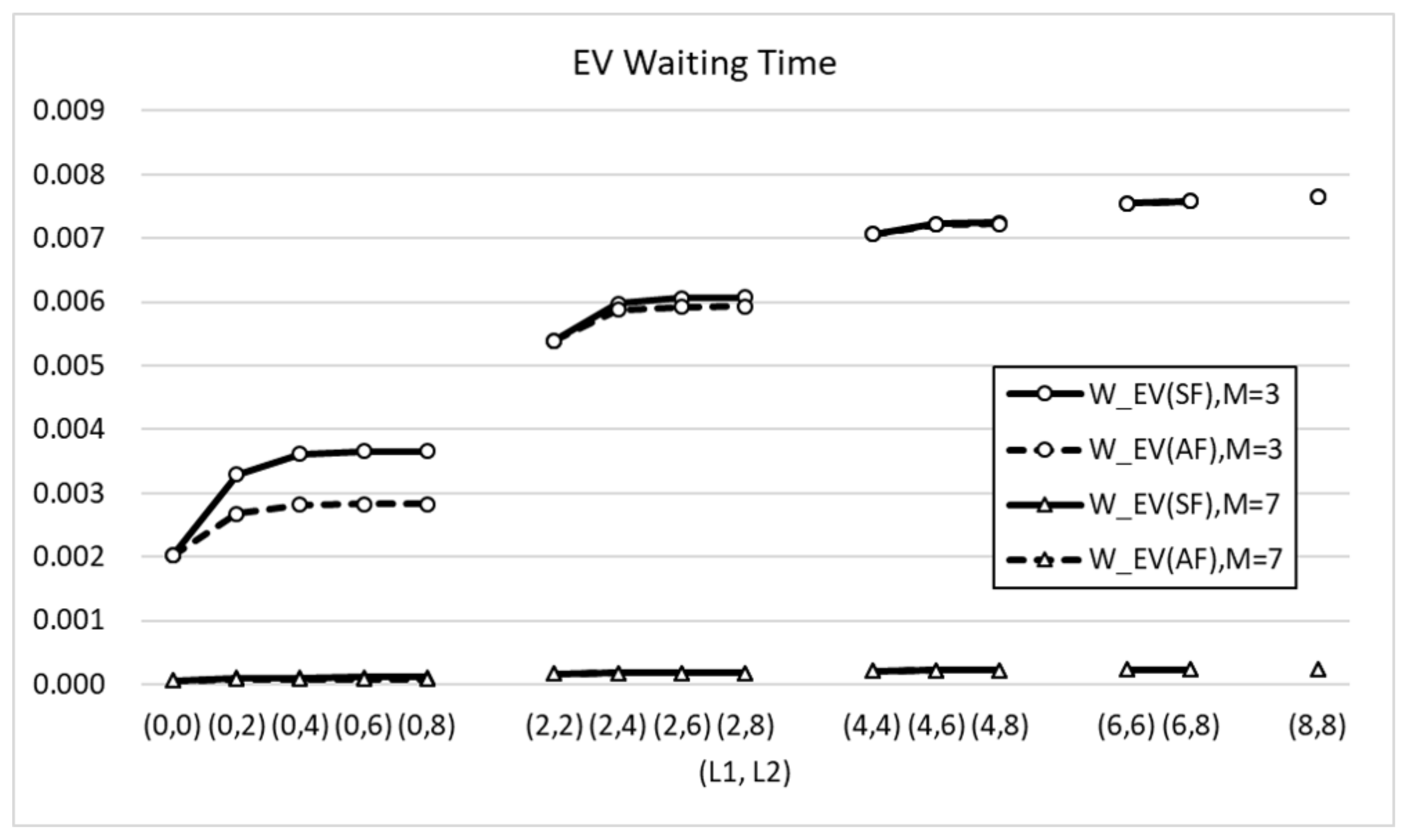
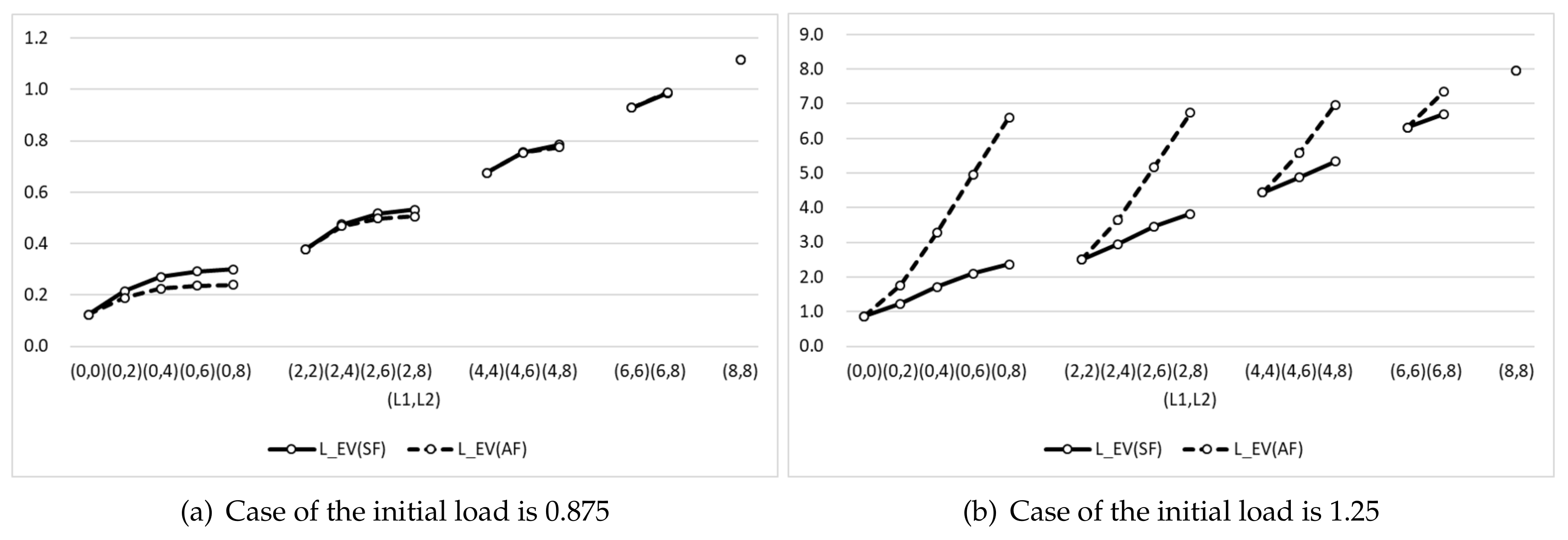
4.1. System Performance
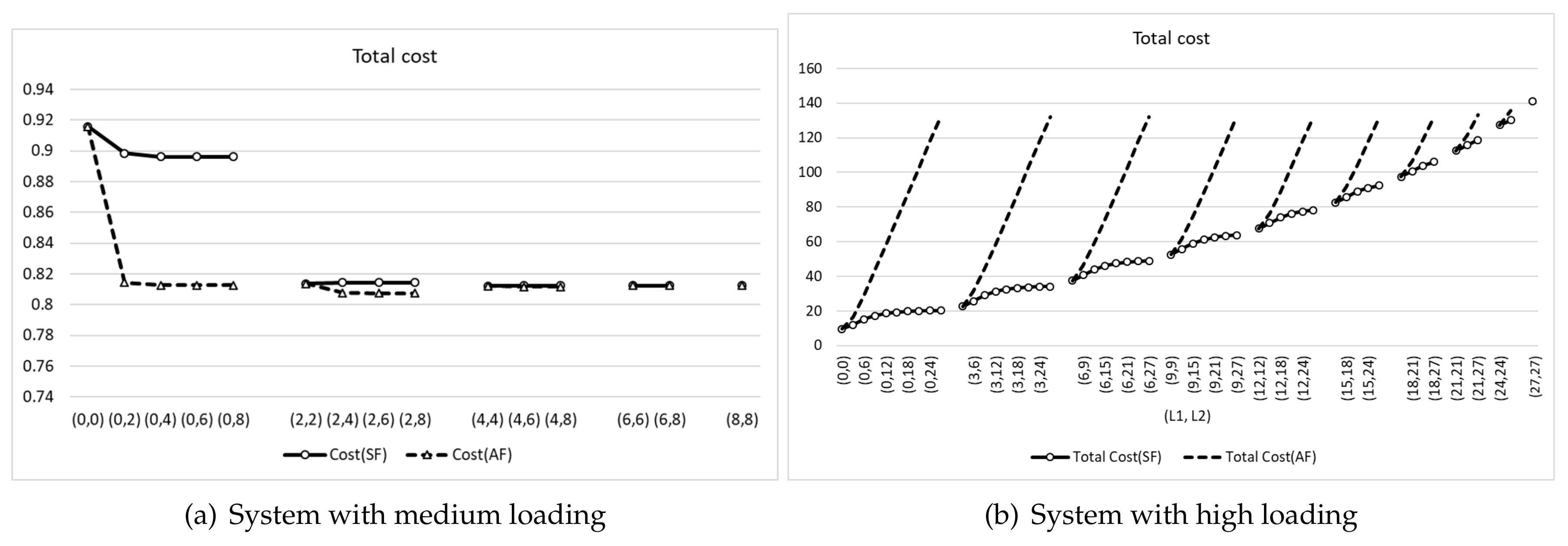
4.2. Cost Analysis of the Operation of a Battery Swapping and Charging Station
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Gupta, V.; Kumar, R.; Panigrahi, B. Electric Vehicle Charging Management–Battery Charging vs. Swapping in Densely Populated Environments. Available online: https://smartgrid.ieee.org/newsletters/october-2019/electric-vehicle-charging-management-battery-charging-vs-swapping-in-densely-populated-environments (accessed on 5 November 2019).
- Varga, B.O.; Sagoian, A.; Mariasiu, F. Prediction of electric vehicle range: A comprehensive review of current issues and challenges. Energies 2019, 12, 946. [Google Scholar] [CrossRef]
- Adegbohun, F.; Von Jouanne, A.; Lee, K.Y. Autonomous battery swapping system and methodologies of electric vehicles. Energies 2019, 12, 667. [Google Scholar] [CrossRef]
- Tillemann, L. The Faster, Cheaper, Better Way to Charge Electric Vehicles. Available online: https://www.wired.com/story/the-faster-cheaper-better-way-to-charge-electric-vehicles (accessed on 5 November 2019).
- Forbes India. Battery Swapping: The Future of Electric Vehicle Charging. Available online: http://www.forbesindia.com/blog/technology/battery-swapping-the-future-of-electric-vehicle-charging (accessed on 5 November 2019).
- Tan, X.; Sun, B.; Wu, Y.; Tsang, D.H. Asymptotic performance evaluation of battery swapping and charging station for electric vehicles. Perform. Eval. 2018, 119, 43–57. [Google Scholar] [CrossRef]
- Turner, J. New directions in communications(or which way to the information age?). IEEE Commun. Mag. 1986, 24, 8–15. [Google Scholar] [CrossRef]
- Tan, X.; Sun, B.; Tsang, D.H. Queueing network models for electric vehicle charging station with battery swapping. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; pp. 1–6. [Google Scholar]
- Lee, D.H.; Yang, W.S. The N-policy of a discrete time Geo/G/1 queue with disasters and its application to wireless sensor networks. Appl. Math. Model. 2013, 37, 9722–9731. [Google Scholar] [CrossRef]
- De Cuypere, E.; De Turck, K.; Fiems, D. A queueing model of an energy harvesting sensor node with data buffering. Telecommun. Syst. 2018, 67, 281–295. [Google Scholar] [CrossRef]
- Nicolaou, A.; Temene, N.; Sergiou, C.; Georgiou, C.; Vassiliou, V. Utilizing Mobile Nodes for Congestion Control in Wireless Sensor Networks. arXiv 2019, arXiv:1903.08989. [Google Scholar]
- Jamian, J.; Mustafa, M.; Mokhlis, H.; Baharudin, M. Simulation study on optimal placement and sizing of battery switching station units using artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 592–601. [Google Scholar] [CrossRef]
- Raviv, T. The battery switching station scheduling problem. Oper. Res. Lett. 2012, 40, 546–550. [Google Scholar] [CrossRef]
- Zou, B.; Xu, X.; De Koster, R. Evaluating battery charging and swapping strategies in a robotic mobile fulfillment system. Eur. J. Oper. Res. 2018, 267, 733–753. [Google Scholar] [CrossRef]
- Nishimura, S.; Jiang, Y. An M/G/l vacation model with two service modes. Probab. Eng. Inf. Sci. 1995, 9, 355–374. [Google Scholar] [CrossRef]
- Dudin, A. Optimal control for an M x/G/1 queue with two operation modes. Probab. Eng. Inf. Sci. 1997, 11, 255–265. [Google Scholar] [CrossRef]
- Choi, D.I. MAP/G/1/K queue with multiple thresholds on buffer. Commun. Korean Math. Soc. 1999, 14, 611–625. [Google Scholar]
- Dudin, A.N.; Nishimura, S. Optimal control for a BMAP/G/1 queue with two service modes. Math. Probl. Eng. 1999, 5, 255–273. [Google Scholar] [CrossRef]
- Banik, A. Some aspects of stationary characteristics and optimal control of the BMAP/ G- G/ 1/ N (∞) oscillating queueing system. Appl. Stoch. Model. Bus. Ind. 2015, 31, 204–230. [Google Scholar] [CrossRef]
- Gupta, U.; Samanta, S.; Goswami, V. Analysis of a discrete-time queue with load dependent service under discrete-time Markovian arrival process. J. Korean Stat. Soc. 2014, 43, 545–557. [Google Scholar] [CrossRef]
- Li, H.; Zhu, Y. M (n)/G/1/N queues with generalized vacations. Comput. Oper. Res. 1997, 24, 301–316. [Google Scholar]
- Li, H.; Zhu, Y.; Yang, P. Computational analysis of M (n)/G/1/N queues with setup time. Comput. Oper. Res. 1995, 22, 829–840. [Google Scholar] [CrossRef]
- Choi, D.; Lim, D. Performance Analysis of Novel Overload Control with Threshold Mechanism. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Lee, J.; Un, C. Performance of dynamic rate leaky bucket algorithm. Electron. Lett. 1993, 29, 1560–1561. [Google Scholar] [CrossRef]
- Choi, B.; Choi, D. Discrete-time analysis of the leaky bucket scheme with threshold-based token generation intervals. IEE Proc.-Commun. 1996, 143, 105–111. [Google Scholar] [CrossRef]
- Choi, D.; Choi, B.; Sung, D. Performance analysis of priority leaky bucket scheme with queue-length-threshold scheduling policy. IEE Proc. Commun. 1998, 145, 395–401. [Google Scholar] [CrossRef]
- Choi, D.; Lee, S. Performance analysis of the leaky bucket scheme with queue length dependent arrival rates. Bull. Korean Math. Soc. 2006, 43, 657. [Google Scholar] [CrossRef]
- Choi, D. Queueing analysis for traffic control with combined control of dynamic MMPP arrivals and token rates. J. Korea Soc. Ind. Appl. Math. 2013, 17, 103–113. [Google Scholar] [CrossRef]
- Lee, T.T. M/G/1/N queue with vacation time and exhaustive service discipline. Oper. Res. 1984, 32, 774–784. [Google Scholar] [CrossRef]
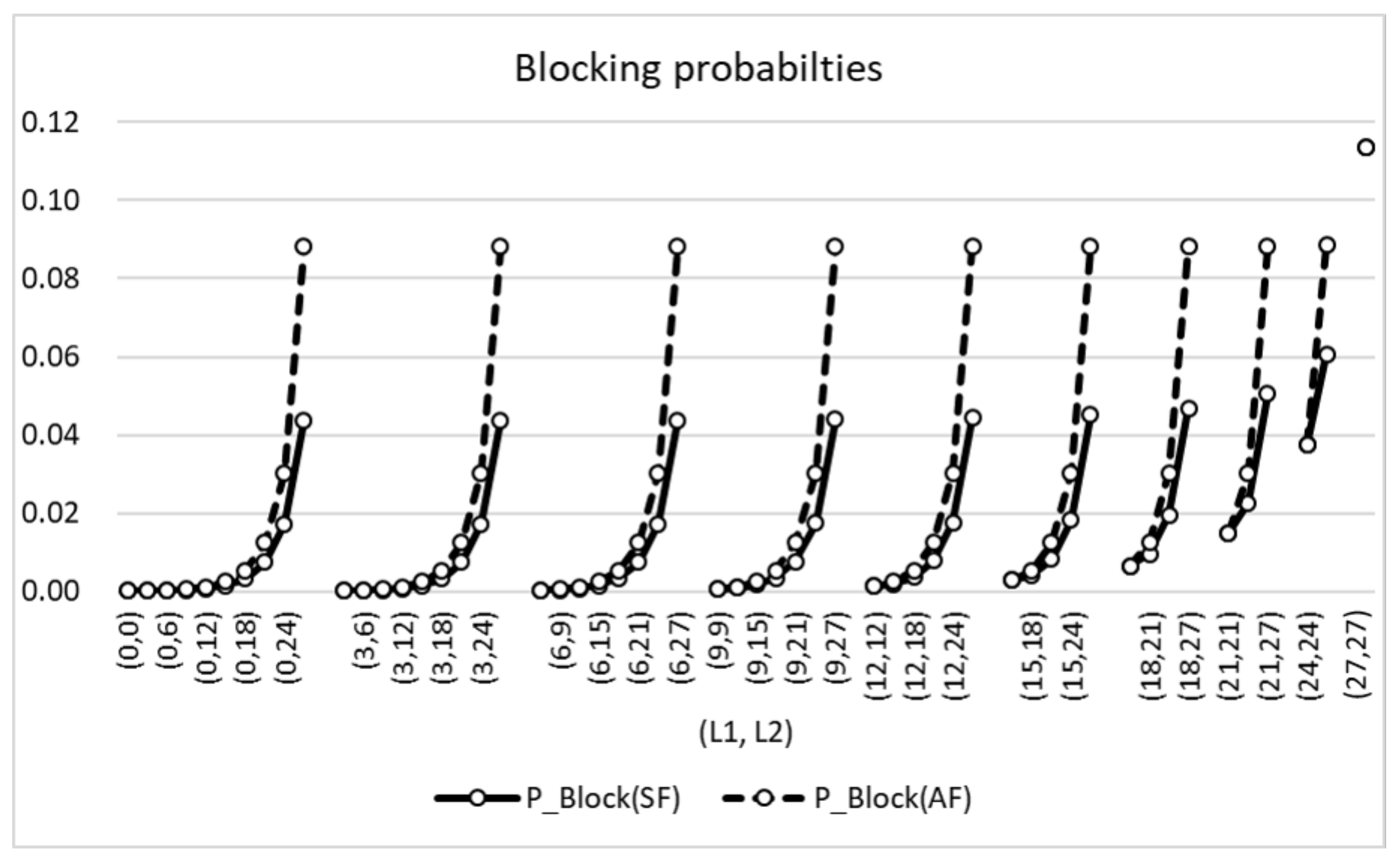
| P(a BSCS is in Mode 1) | ||
|---|---|---|
| SF Policy | AF Policy | |
| 0.9927 | 0.9927 | |
| 0.9922 | 0.9922 | |
| 0.9998 | 0.9998 | |
| 1 | 1 | |
| Policy | EV Blocking Cost | Holding Cost | Holding Cost | |||
|---|---|---|---|---|---|---|
| EV | Battery | Mode 1 | Mode 2 | Mode 3 | ||
| Supply First | 10 | 5 | 0.1 | 0.5 | 5 | 10 |
| Arrival First | 10 | 5 | 0.1 | 0.5 | 2 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.I.; Lim, D.-E. Analysis of the State-Dependent Queueing Model and Its Application to Battery Swapping and Charging Stations. Sustainability 2020, 12, 2343. https://doi.org/10.3390/su12062343
Choi DI, Lim D-E. Analysis of the State-Dependent Queueing Model and Its Application to Battery Swapping and Charging Stations. Sustainability. 2020; 12(6):2343. https://doi.org/10.3390/su12062343
Chicago/Turabian StyleChoi, Doo Il, and Dae-Eun Lim. 2020. "Analysis of the State-Dependent Queueing Model and Its Application to Battery Swapping and Charging Stations" Sustainability 12, no. 6: 2343. https://doi.org/10.3390/su12062343
APA StyleChoi, D. I., & Lim, D.-E. (2020). Analysis of the State-Dependent Queueing Model and Its Application to Battery Swapping and Charging Stations. Sustainability, 12(6), 2343. https://doi.org/10.3390/su12062343





