Contract Design for Enhancing Green Food Material Production Effort with Asymmetric Supply Cost Information
Abstract
1. Introduction
2. Literature Review
2.1. Contract Coordination in the Supply Chain under Cost Information Asymmetry
2.2. Contract Coordination in the Green Supply Chain under Green Cost Information Asymmetry
3. Model Descriptions
- The food supplier has the full information of the food producer’s green processing and green sale cost.
- Consumers’ green product demand can be completely met during the sale period.
- There is no overstock after completely meeting the consumers’ green product demands.
- Both the food producer and the food supplier are risk-neutral and aim to maximize their expected profits.
4. Wholesale Price Contract under Information Symmetry
5. Contract under Information Asymmetry
5.1. Wholesale Price Contract under Information Asymmetry
5.2. Impact of Information Sharing on Supplier’s Decision under Information Asymmetry
5.3. Combining a Wholesale Price Contract and a Green Cost Sharing Contract under an Information Asymmetry Situation
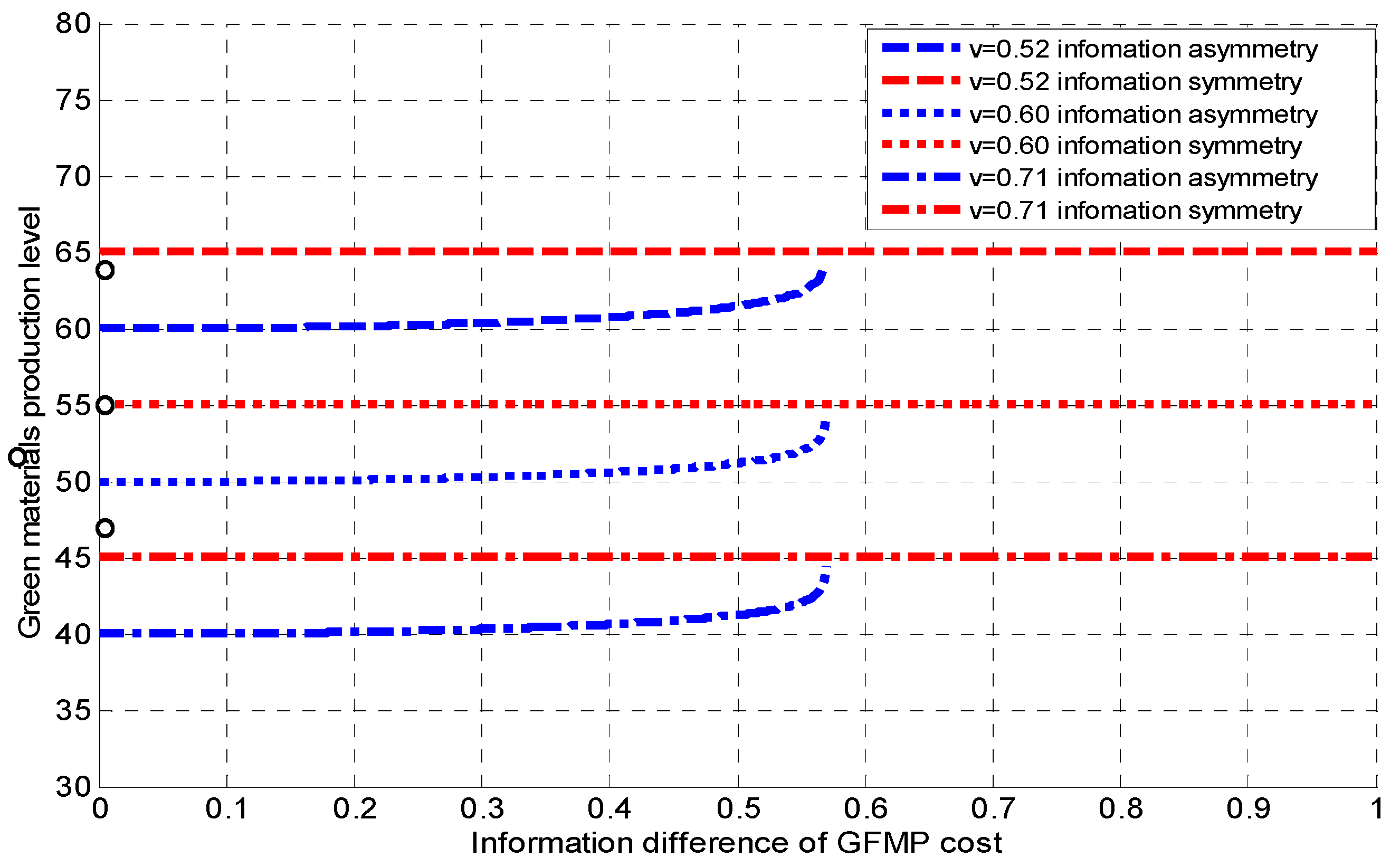
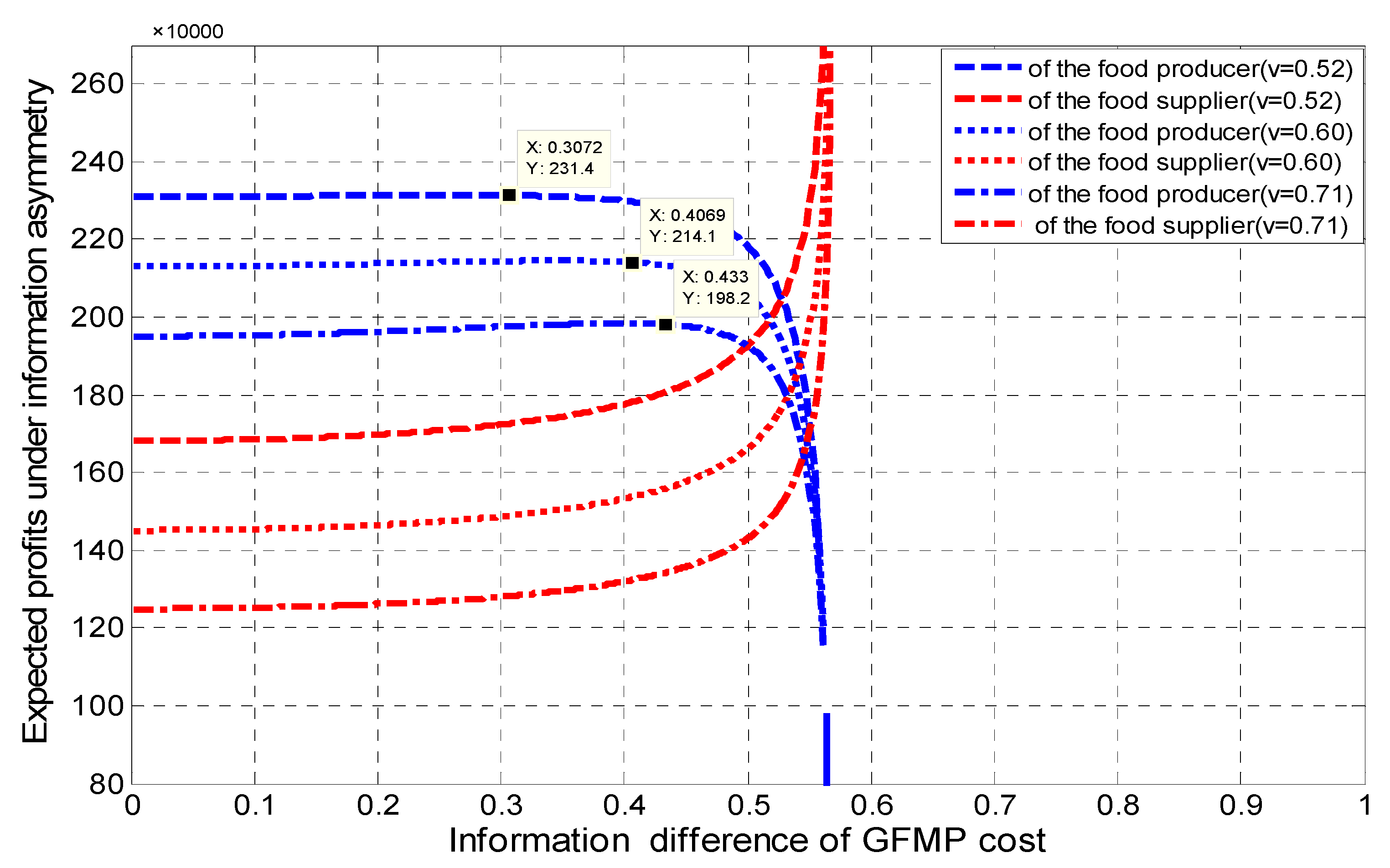
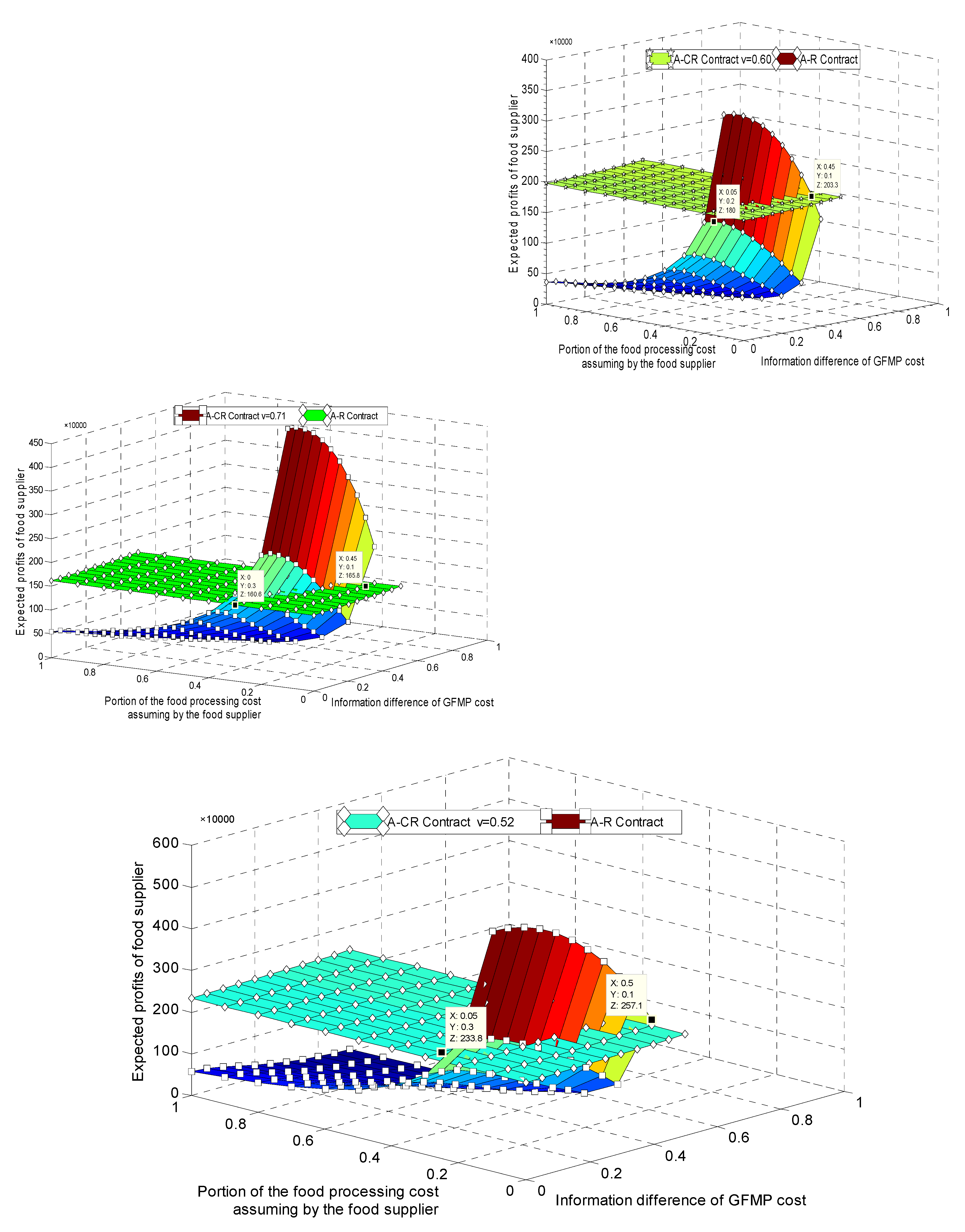
5.4. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Poof of Theorem 1
Appendix B. Poof of Theorem 2
Appendix C. Poof of Theorem 3
Appendix D. Proof of Theorem 4
Appendix E. Proof of Theorem 5
Appendix F. Proof of Theorem 6
References
- Wang, Z.; Mathiyazhagan, K.; Xu, L.; Diabat, A. A decision making trial and evaluation laboratory approach to analyze the barriers to Green Supply Chain Management adoption in a food packaging company. J. Clean. Prod. 2016, 117, 19–28. [Google Scholar] [CrossRef]
- Pham, T.P.; Kaushik, R.; Parshetti, G.K.; Mahmood, R.; Balasubramanian, R. Food waste-To-Energy conversion technologies: Current status and future directions. Waste Manag. 2015, 38, 399–408. [Google Scholar] [CrossRef] [PubMed]
- Moser, A.K. Consumers′ purchasing decisions regarding environmentally friendly products: An empirical analysis of German consumers. J. Retail. Consum. Serv. 2016, 31, 389–397. [Google Scholar] [CrossRef]
- Peterson, S.B.; Michalek, J.J. Cost-Effectiveness of plug-in hybrid electric vehicle battery capacity and charging infrastructure investment for reducing US gasoline consumption. Energy Policy 2013, 52, 429–438. [Google Scholar] [CrossRef]
- Prakash, G.; Pathak, P. Intention to buy eco-Friendly packaged products among young consumers of India: A study on developing nation. J. Clean. Prod. 2017, 141, 385–393. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, Q.; Cui, L. A decision-Making model for remanufacturers: Considering both consumers’ environmental preference and the government subsidy policy. Resour. Conserv. Recycl. 2018, 128, 176–186. [Google Scholar] [CrossRef]
- Zhu, Q.; Sarkis, J.; Lai, K.-H. Institutional-based antecedents and performance outcomes of internal and external green supply chain management practices. J. Purch. Supply Manag. 2013, 19, 106–117. [Google Scholar] [CrossRef]
- Resende-Filho, M.A.; Hurley, T.M. Information asymmetry and traceability incentives for food safety. Int. J. Prod. Econ. 2012, 139, 596–603. [Google Scholar] [CrossRef]
- Royera, A.; Ménard, C.; Gouina, D.-M. Reassessing marketing boards as hybrid arrangements: Evidence from Canadian experiences. Agric. Econ. 2016, 47, 105–116. [Google Scholar] [CrossRef]
- Rousseau, S.; Vranken, L. Green market expansion by reducing information asymmetries: Evidence for labeled organic food products. Food Policy 2013, 40, 31–43. [Google Scholar] [CrossRef]
- Chkanikova, O.; Lehner, M. Private eco-Brands and green market development: Towards new forms of sustainability governance in the food retailing. J. Clean. Prod. 2015, 107, 74–84. [Google Scholar] [CrossRef]
- Grekova, K.; Calantone, R.J.; Bremmers, H.J.; Trienekens, J.H.; Omta, S.W.F. How environmental collaboration with suppliers and customers influences firm performance: Evidence from Dutch food and beverage processors. J. Clean. Prod. 2016, 112, 1861–1871. [Google Scholar] [CrossRef]
- McCarthy, D.; Matopoulos, A.; Davies, P. Life cycle assessment in the food supply chain: A case study. Int. J. Logist. Res. Appl. 2015, 18, 140–154. [Google Scholar] [CrossRef]
- Song, C.; Zhuang, J. Modeling a Government-Manufacturer-Farmer game for food supply chain risk management. Food Control 2017, 78, 443–455. [Google Scholar] [CrossRef]
- Rueda, X.; Garrett, R.D.; Lambin, E.F. Corporate investments in supply chain sustainability: Selecting instruments in the agri-Food industry. J. Clean. Prod. 2017, 142, 2480–2492. [Google Scholar] [CrossRef]
- Rouvière, E.; Royer, A. Public Private Partnerships in food industries: A road to success? Food Policy 2017, 69, 135–144. [Google Scholar] [CrossRef]
- Ringsberg, H. Perspectives on food traceability: A systematic literature review. Supply Chain Manag. An Int. J. 2014, 19, 558–576. [Google Scholar] [CrossRef]
- Gunasekaran, A.; Subramanian, N.; Rahman, S. Green supply chain collaboration and incentives: Current trends and future directions. Transp. Res. Part E-Logist. Transp. Rev. 2015, 74, 1–10. [Google Scholar] [CrossRef]
- Chen, K.; Zhao, H.; Xiao, T. Outsourcing contracts and ordering decisions of a supply chain under multi-dimensional uncertainties. Comput. Ind. Eng. 2019, 130, 127–141. [Google Scholar] [CrossRef]
- Kim, S.-H.; Netessine, S. Collaborative Cost Reduction and Component Procurement Under Information Asymmetry. Manag. Sci. 2013, 59, 189–206. [Google Scholar] [CrossRef]
- Resende-Filho, M.A.; Buhr, B.L. A Principal-Agent Model for Evaluating the Economic Value of a Traceability System: A Case Study with Injection-site Lesion Control in Fed Cattle. Am. J. Agric. Econ. 2008, 90, 1091–1102. [Google Scholar] [CrossRef]
- Sun, S.; Wang, X. Promoting traceability for food supply chain with certification. J. Clean. Prod. 2019, 217, 658–665. [Google Scholar] [CrossRef]
- Stranieri, S.; Cavaliere, A.; Banterle, A. Voluntary traceability standards and the role of economic incentives. Br. Food J. 2016, 118, 1025–1040. [Google Scholar] [CrossRef]
- Zhang, M.; Jin, Y.; Qiao, H.; Zheng, F. Product quality asymmetry and food safety: Investigating the “one farm household, two production systems” of fruit and vegetable farmers in China. China Econ. Rev. 2017, 45, 232–243. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, S.; Zhang, M.; Sun, H.; He, L. A Closed-Loop Supply Chain with Competitive Dual Collection Channel under Asymmetric Information and Reward–Penalty Mechanism. Sustainability 2018, 10, 2131. [Google Scholar] [CrossRef]
- Xu, H.; Yao, N.; Tong, S. Sourcing under cost information asymmetry when facing time-Sensitive customers. Int. J. Prod. Econ. 2013, 144, 599–609. [Google Scholar] [CrossRef]
- Xing, G.; Qian, D.; Guo, J.E. Research on the Participant Behavior Selections of the Energy Performance Contracting Project Based on the Robustness of the Shared Savings Contract. Sustainability 2016, 8, 730. [Google Scholar] [CrossRef]
- Zhang, X.; Zeephongsekul, P. Asymmetric supply chain models implementable with a mechanism design. Appl. Math. Model. 2016, 40, 10719–10739. [Google Scholar] [CrossRef]
- Kerkkamp, R.B.O.; van den Heuvel, W.; Wagelmans, A.P.M. Two-Echelon lot-Sizing with asymmetric information and continuous type space. Omega 2019, 87, 158–176. [Google Scholar] [CrossRef]
- Mahadevan, B.; Hazra, J.; Jain, T. Services outsourcing under asymmetric cost information. Eur. J. Oper. Res. 2017, 257, 456–467. [Google Scholar] [CrossRef]
- Cao, E.; Ma, Y.; Wan, C.; Lai, M. Contracting with asymmetric cost information in a dual-Channel supply chain. Oper. Res. Lett. 2013, 41, 410–414. [Google Scholar] [CrossRef]
- Esmaeili, M.; Zeephongsekul, P. Seller–Buyer models of supply chain management with an asymmetric information structure. Int. J. Prod. Econ. 2010, 123, 146–154. [Google Scholar] [CrossRef]
- Corbett, C.J.; Zhou, D.; Tang, C.S. Designing Supply Contracts: Contract Type and Information Asymmetry. Manag. Sci. 2004, 50, 550–559. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Tao, F.; Wang, J.C. Designing optimal and practical volume discounting contracts for the dominant retailer with information asymmetry. Int. Trans. Oper. Res. 2017, 24, 1405–1433. [Google Scholar] [CrossRef]
- Wang, X.; Guo, H.; Yan, R.; Wang, X. Achieving optimal performance of supply chain under cost information asymmetry. Appl. Math. Model. 2018, 53, 523–539. [Google Scholar] [CrossRef]
- Nosoohi, I.; Nookabadi, A.S. Outsource planning with asymmetric supply cost information through a menu of option contracts. Int. Trans.Oper. Res. 2019, 26, 1422–1450. [Google Scholar] [CrossRef]
- Chen, X.; Li, B.; An, S. Option contract design for supply chains under asymmetric cost information. Kybernetes. 2019, 48, 835–860. [Google Scholar] [CrossRef]
- Zheng, B.; Yang, C.; Yang, J.; Zhang, M. Pricing, collecting and contract design in a reverse supply chain with incomplete information. Comput. Ind. Eng. 2017, 111, 109–122. [Google Scholar] [CrossRef]
- Yang, R.; Tang, W.; Dai, R.; Zhang, J. Contract design in reverse recycling supply chain with waste cooking oil under asymmetric cost information. J. Clean. Prod. 2018, 201, 61–77. [Google Scholar] [CrossRef]
- Wang, Q.; He, L. Incentive Strategies for Low-Carbon Supply Chains with Asymmetric Information of Carbon Reduction Efficiency. Int. J. Environ. Res. Public Health 2018, 15, 736. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Quan, B.T.; Yang, J.B. Decision analysis and coordination of two-Stage supply chain considering cost information asymmetry of corporate social responsibility. J. Clean. Prod. 2019, 228, 1073–1087. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, G.; Qi, F.; Li, H. Research on coordination mechanism for fresh agri-Food supply chain with option contracts. Kybernetes 2019, 48, 1134–1156. [Google Scholar] [CrossRef]
- Swami, S.; Shah, J. Channel coordination in green supply chain management. J. Oper. Res. Soc. 2017, 64, 336–351. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Zhao, S. Cost-Sharing models for green product production and marketing in a food supply chain. Ind. Manag. Data Syst. 2018, 118, 654–682. [Google Scholar] [CrossRef]
- Gleim, M.R.; Smith, J.S.; Andrews, D.; Cronin, J.J. Against the Green: A Multi-Method Examination of the Barriers to Green Consumption. J. Retail. 2013, 89, 44–61. [Google Scholar] [CrossRef]
- Lin, P.-C.; Huang, Y.-H. The influence factors on choice behavior regarding green products based on the theory of consumption values. J. Clean. Prod. 2012, 22, 11–18. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; You, J. Consumer environmental awareness and channel coordination with two substitutable products. Eur. J. Oper. Res. 2015, 241, 63–73. [Google Scholar] [CrossRef]
- Hardesty, S.D.; Leff, P. Determining marketing costs and returns in alternative marketing channels. Renew. Agric. Food Syst. 2009, 25, 24–34. [Google Scholar] [CrossRef]
- Foster, G.; Gupta, M. Marketing, cost management and management accounting. J. Manag. Account. 1994, 6, 36. [Google Scholar]

| Parameter | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 0.71 | 310,000 | 5 | 0.55 | 0.45 | 45 | 35 | 0.65 | 2 | 80 | 1 |
| Value | 0.60 | 310,000 | 5 | 0.55 | 0.45 | 45 | 35 | 0.65 | 2 | 80 | 1 |
| Value | 0.52 | 310,000 | 5 | 0.55 | 0.45 | 45 | 35 | 0.65 | 2 | 80 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhu, Q. Contract Design for Enhancing Green Food Material Production Effort with Asymmetric Supply Cost Information. Sustainability 2020, 12, 2119. https://doi.org/10.3390/su12052119
Li X, Zhu Q. Contract Design for Enhancing Green Food Material Production Effort with Asymmetric Supply Cost Information. Sustainability. 2020; 12(5):2119. https://doi.org/10.3390/su12052119
Chicago/Turabian StyleLi, Xiaoying, and Qinghua Zhu. 2020. "Contract Design for Enhancing Green Food Material Production Effort with Asymmetric Supply Cost Information" Sustainability 12, no. 5: 2119. https://doi.org/10.3390/su12052119
APA StyleLi, X., & Zhu, Q. (2020). Contract Design for Enhancing Green Food Material Production Effort with Asymmetric Supply Cost Information. Sustainability, 12(5), 2119. https://doi.org/10.3390/su12052119





