Improvement of the Performance Balance between Thermal Comfort and Energy Use for a Building Space in the Mid-Spring Season
Abstract
1. Thermal Systems in Buildings
2. Methodology
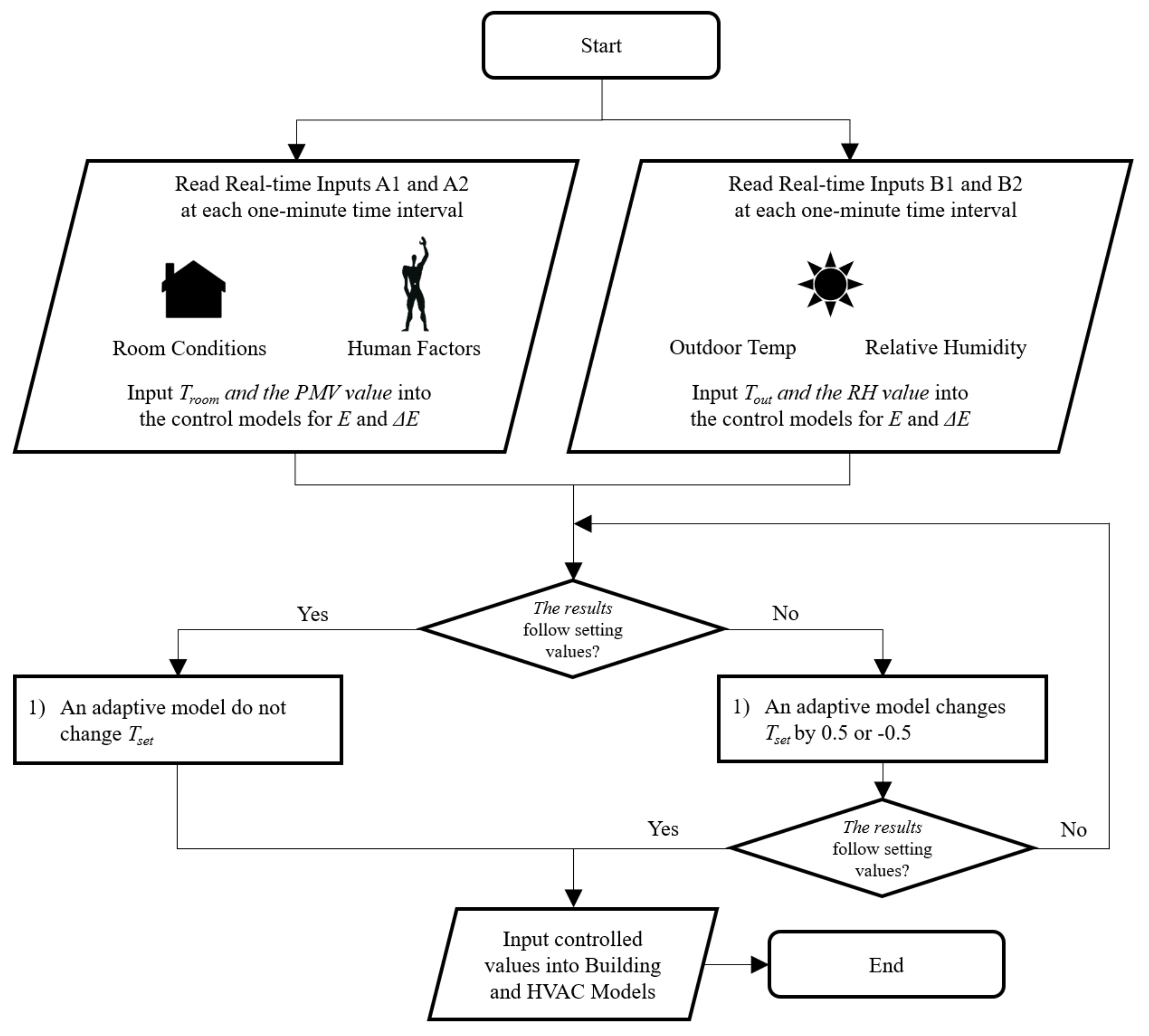
2.1. Overall Framework
- (1)
- A thermal transfer model calculates the heating and cooling energy transfer based on the characteristics of a small commercial office, occupant, and outdoor temperature conditions.
- (2)
- After the determination of the thermal energy transfer, the optimized supply air conditions go to the building space model to define thermal comfort levels by the PMV index at each one-minute time interval.
- (3)
- Based on the result, when the PMV level is over or under the setting range (−0.5 < x < 0.5), an equipped adaptive model changes Tset by ±0.5 for cooling or heating.
- (4)
- If the PMV level is still over or under the setting range (x < −0.5 or 0.5 < x), an adaptive model additionally adds values for Tset.
- (5)
- If the PMV level is still over or under the setting values, the adaptive model repeats the previous process. If not in any point, it stops the adaptive process and bypass the signals.
2.2. Heat Transfer Model
2.3. PMV and PPD Models
2.4. Three Different Controllers
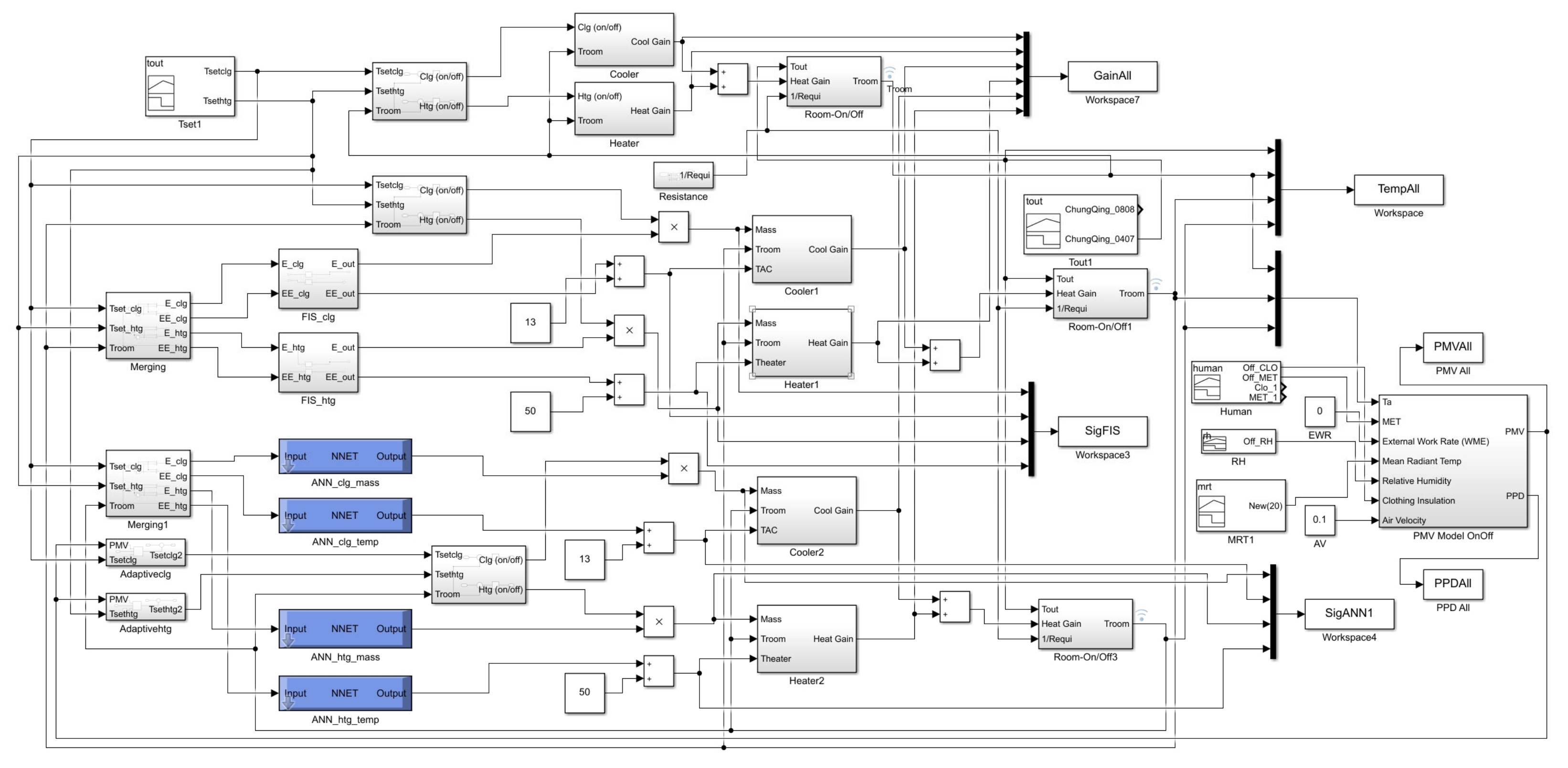
2.5. Simulation Model
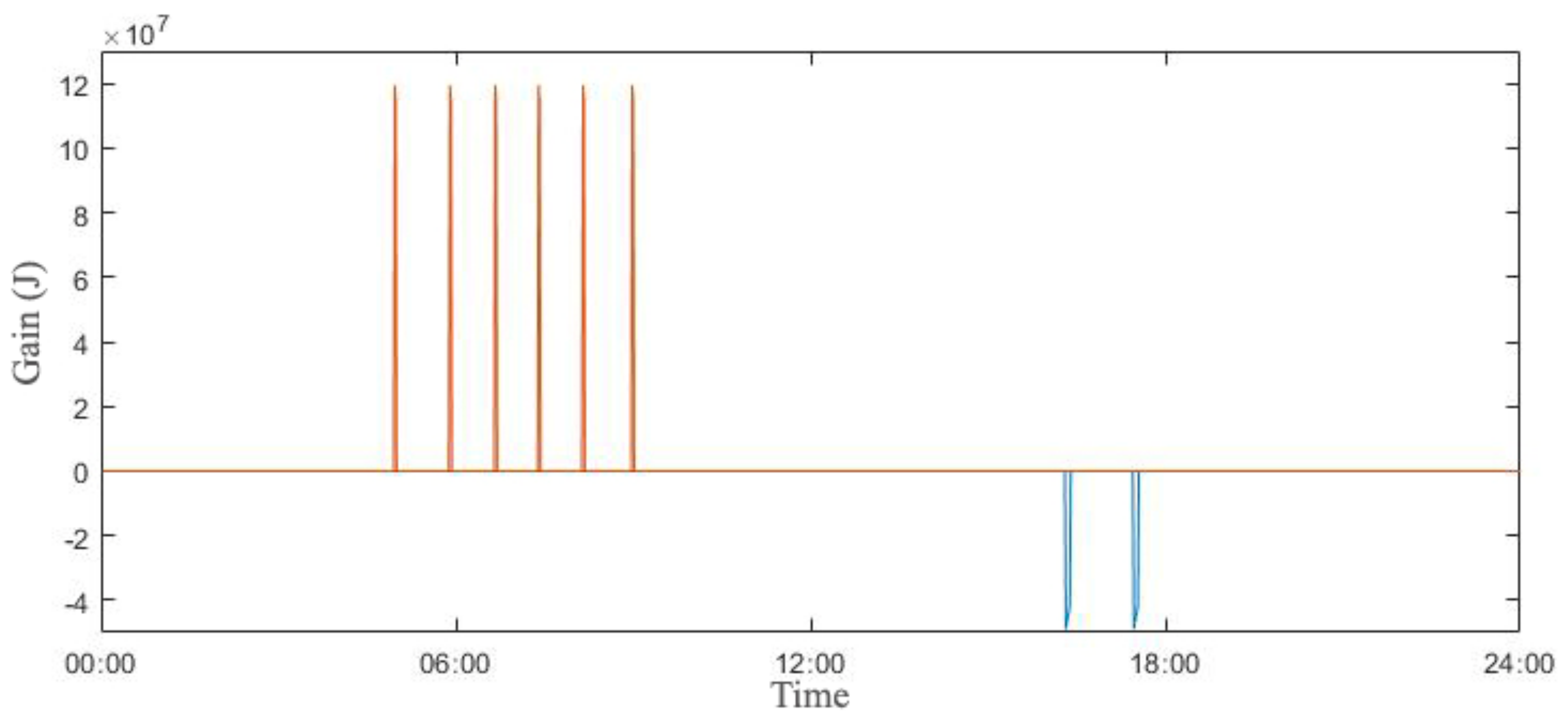
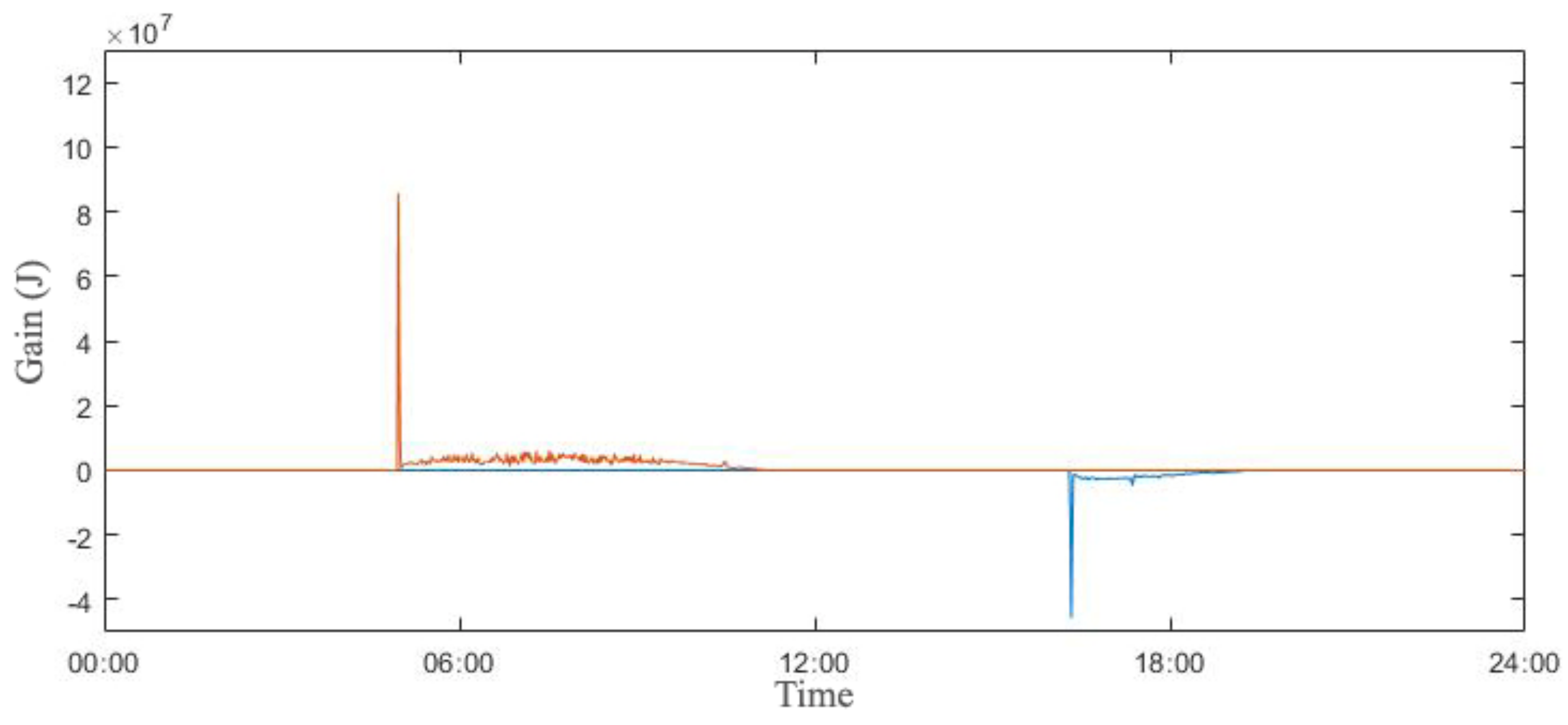
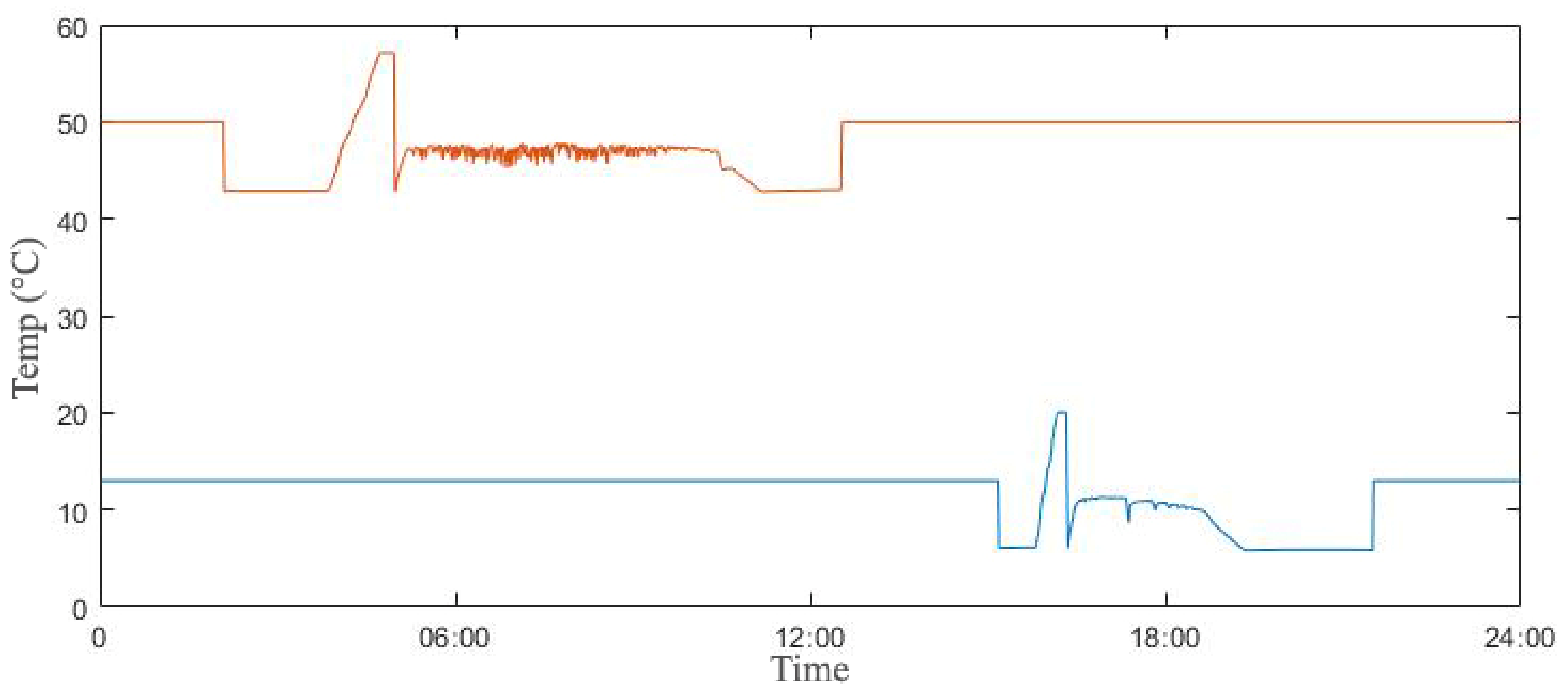
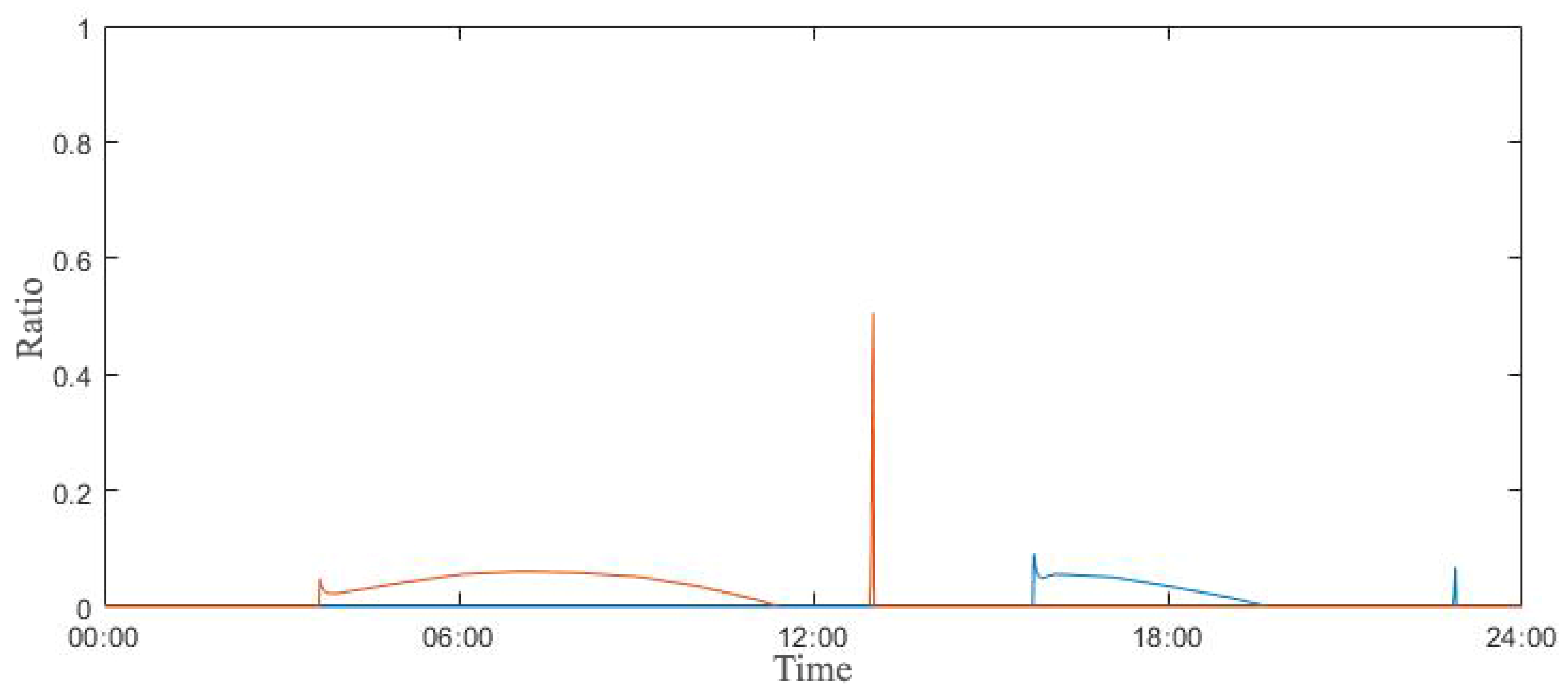
3. Results
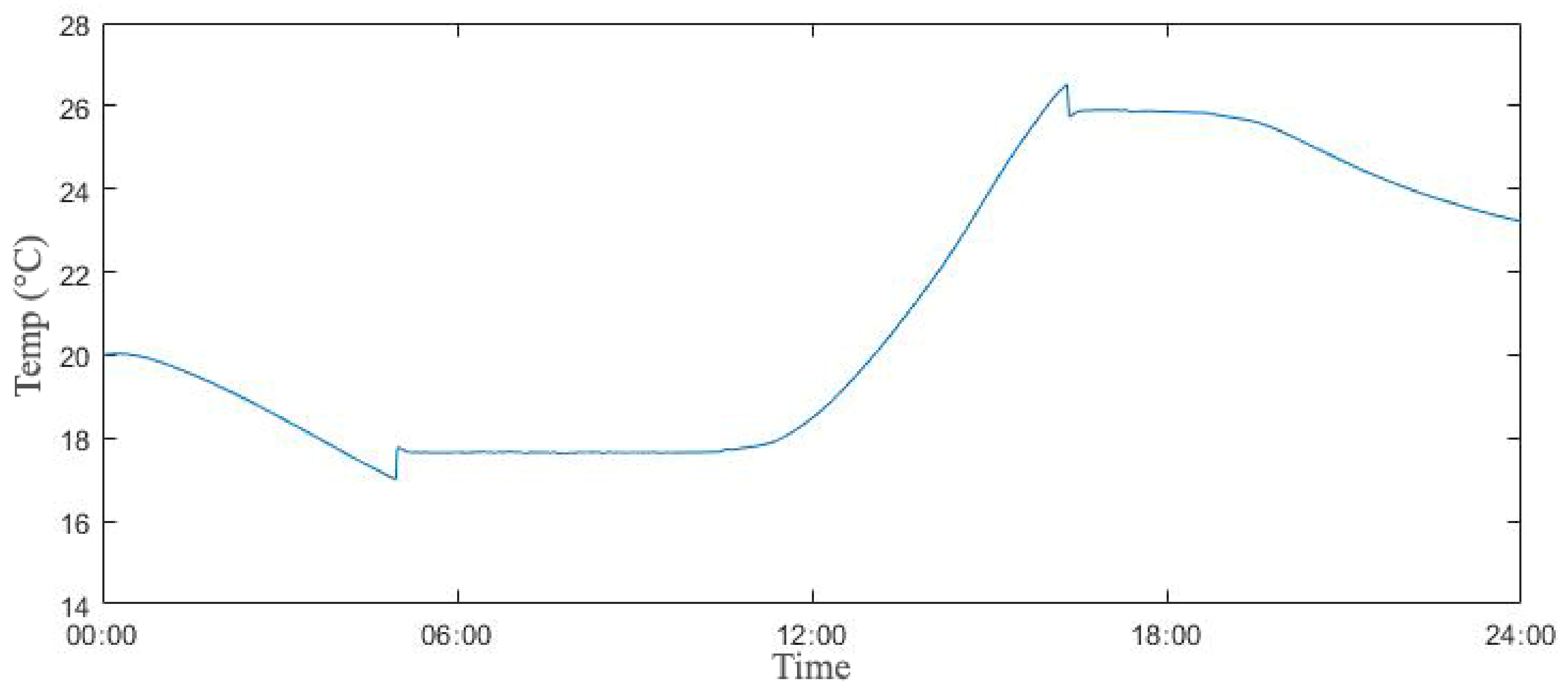
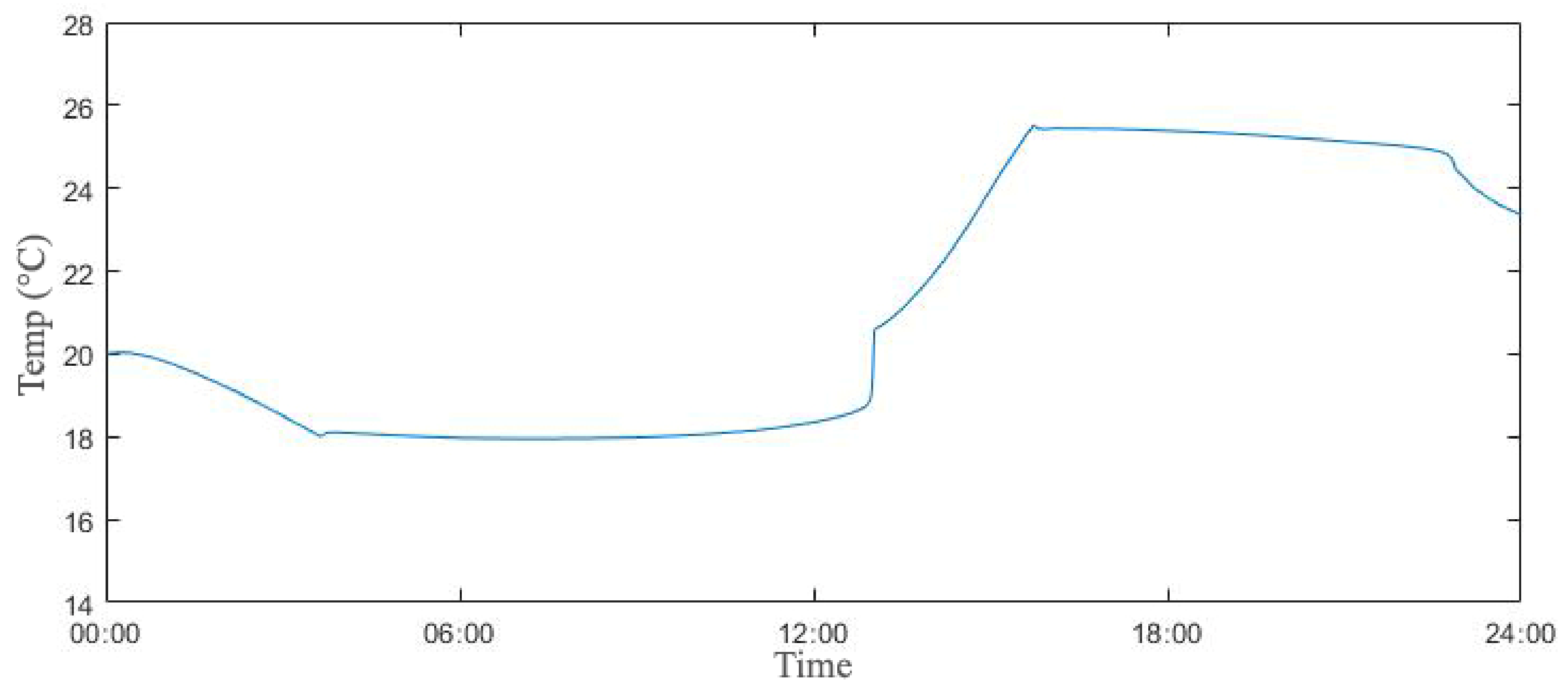
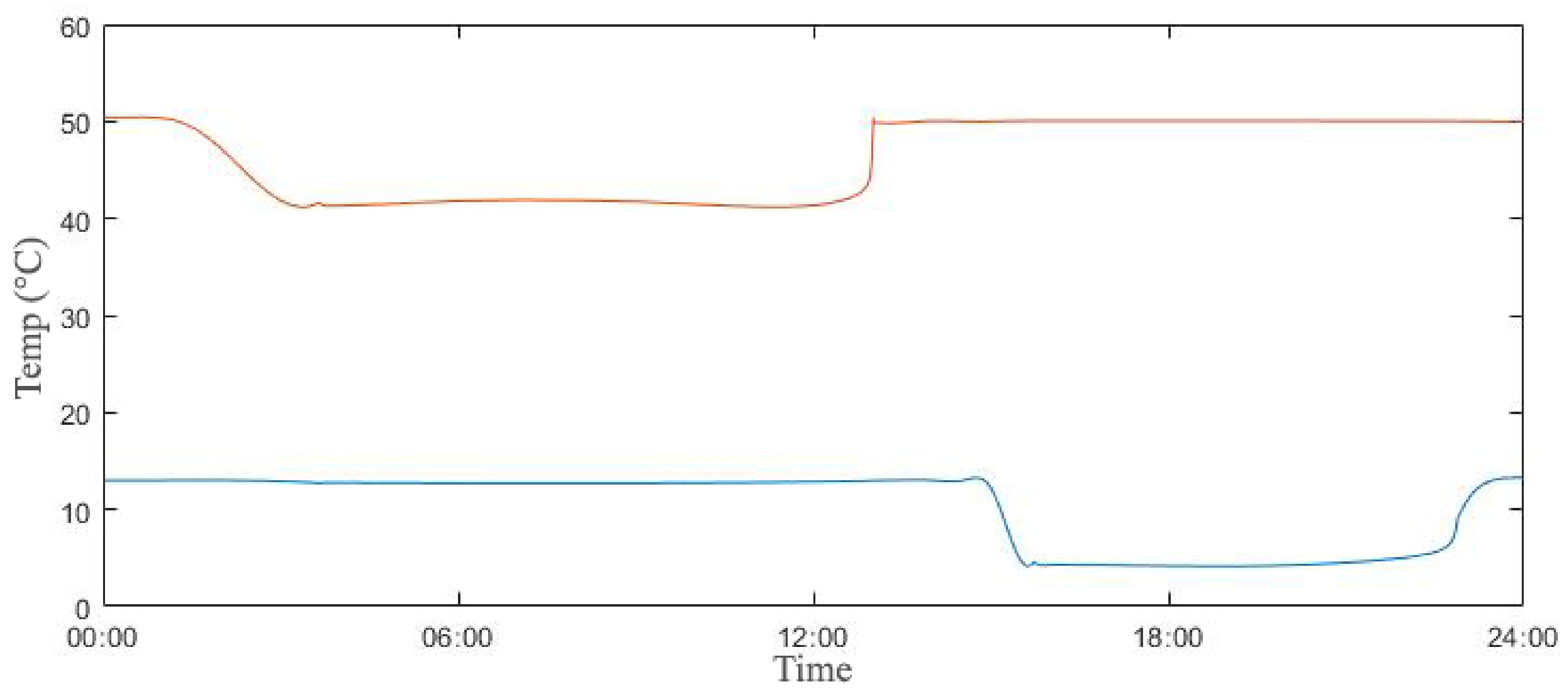
3.1. Room Temperature
3.2. Energy Demand
4. Discussion
4.1. Sustainability in Thermal Comfort and Energy Transfer
4.2. Strengths and Weaknesses of the Proposed Model
5. Conclusions
Funding
Conflicts of Interest
Nomenclature
| A | surface area (m2) | mroomair | mass of room air (kg) |
| Cv | specific heat capacity at constant volume (J/kg·K) | qmet,heat | metabolic rate (W/m2) |
| Cp | specific heat capacity at constant pressure (J/kg·K) | Qloss | convection and transmission heat loss (J) |
| D | depth of material (m) | Qgain | convection and transmission heat gain (J) |
| E | error | R | thermal resistance (m2·K/W) |
| ΔE | derivative of error | Ta | air temperature (°C) |
| fcl | ratio of clothed surface area | Tcl | average surface temperature of clothed body (°C) |
| hc | convection heat transfer coefficient (W/m2·K) | Theater | air temperature entered into room (°C) |
| hin | convection heat transfer coefficient inside (W/m2·K) | Tout | outdoor temperature |
| hout | convection heat transfer coefficient outside (W/m2·K) | Troom | room temperature (°C) |
| Icl | clothing insulation (m2·C/W) | Tset | thermostat set-point temperature (°C) |
| k | transmission coefficient (W/m·K) | va | air speed (m/s) |
| M | metabolic rate (W/m2) | u | internal energy (J) |
| ṁht | mass flow-rate from heater (kg/h) | W | work (J) |
| ṁin | mass flow-rate into room (kg/h) | Wa | air humidity ratio |
| ṁout | mass flow-rate out from room (kg/h) | Wsk | saturated humidity ratio at the skin temperature |
References
- Blasco, C.; Montreal, J.; Benítez, I.; Lluna, A. Modelling and PID Control of HVAC System According to Energy Efficiency and Comfort Criteria. In Sustainability in Energy and Buildings; Springer: Berlin/Heidelberg, Germany, 2012; Volume 12, pp. 365–374. [Google Scholar]
- Wemhoff, A. Calibration of HVAC equipment PID coefficients for energy conservation. Energy Build. 2012, 45, 60–66. [Google Scholar] [CrossRef]
- WaTalib, R.; Nablim, N.; Choi, W. Optimization-Based Data-Enabled Modeling Technique for HVAC Systems Components. Buildings 2020, 10, 163. [Google Scholar] [CrossRef]
- Paris, B.; Eynard, J.; Grieu, S.; Polit, M. Hybrid PID-fuzzy control scheme for managing energy resources in buildings. Appl. Soft Comput. 2011, 11, 315–319. [Google Scholar] [CrossRef]
- Talebi, A.; Hatami, A. Online fuzzy control of HVAC systems considering demand response and users’ comfort. Energy Sources Part B Econ. Plan. Policy 2020. [Google Scholar] [CrossRef]
- Fazzolari, M.; Alcala, R.; Nojima, Y.; Ishibuchi, H.; Herrera, F. A Review of the Application of Multiobjective Evolutionary Fuzzy Systems: Current Status and Further Directions. Fuzzy Syst. 2013, 21, 45–65. [Google Scholar] [CrossRef]
- Zhang, J.; Ou, J.; Sun, D. Study on Fuzzy Control for HVAC Systems; ASHRAE: Peachtree Corners, GA, USA, 2003; pp. 13–36. [Google Scholar]
- Alcala, R. Fuzzy Control of HVAC Systems Optimized by Genetic Algorithms. Appl. Intell. 2003, 18, 155–177. [Google Scholar] [CrossRef]
- Killian, M.; Kozek, M. Implementation of cooperative Fuzzy model predictive control for an energy-efficient office building. Energy Build. 2018, 158. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141. [Google Scholar] [CrossRef]
- Kwater, T.; Topczewska, J. Forecasting the Utility Value of Hucul Horses by Means of Artificial Intelligence. Sustainability 2020, 12, 7989. [Google Scholar] [CrossRef]
- Rijal, H.B.; Humphreys, M.A.; Nicol, J.F. Adaptive model and the adaptive mechanisms for thermal comfort in Japanese dwellings. Energy Build 2019, 202, 109371. [Google Scholar] [CrossRef]
- Simanic, B.; Nordquist, B.; Bagge, H.; Johansson, D. Influence of User-Related Parameters on Calculated Energy Use in Low-Energy School Buildings. Energies 2020, 13, 2985. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, S.; Chung, D. Analysis of energy and control efficiencies of fuzzy logic and artificial neural network technologies in the heating energy supply system responding to the changes of user demands. Appl. Energy 2017, 190. [Google Scholar] [CrossRef]
- Moon, J.; Ahn, J. Improving sustainability of ever-changing building spaces affected by users’ fickle taste: A focus on human comfort and energy use. Energy Build. 2020, 208. [Google Scholar] [CrossRef]
- Singh, M.K.; Attia, S.; Mahapatra, S.; Teller, J. Assessment of thermal comfort in existing pre-1945 residential building stock. Energy 2016, 98, 122–134. [Google Scholar] [CrossRef]
- Kim, S.; Shin, H.; Ahn, J. Energy performance analysis of airport terminal buildings by use of architectural, operational information and benchmark metrics. J. Air Transp. Manag. 2020, 83. [Google Scholar] [CrossRef]
- Kariminia, S.; Shamshirband, S.; Hashim, R.; Saberi, A.; Petković, D.; Roy, C.; Motamedi, S. A simulation model for visitors’ thermal comfort at urban public squares using non-probabilistic binary-linear classifier through soft-computing methodologies. Energy 2016, 101, 568–580. [Google Scholar] [CrossRef]
- Ahn, J.; Chung, D.; Cho, S. Performance analysis of space heating smart control models for energy and control effectiveness in five different climate zones. Build. Environ. 2017, 115. [Google Scholar] [CrossRef]
- Park, S.; Cho, S.; Ahn, J. Improving the quality of building spaces that are planned mainly on loads rather than residents: Human comfort and energy savings for warehouses. Energy Build. 2018, 178. [Google Scholar] [CrossRef]
- Kurte, K.; Munk, J.; Kotevska, O.; Amasyali, K.; Smith, R.; McKee, E.; Du, Y.; Cui, B.; Kuruganti, T.; Zandi, H. Evaluating the Adaptability of Reinforcement Learning Based HVAC Control for Residential Houses. Sustainability 2020, 12, 7727. [Google Scholar] [CrossRef]
- Sung, L.; Ahn, J. Comparative Analyses of Energy Efficiency between on-Demand and Predictive Controls for Buildings’ Indoor Thermal Environment. Energies 2020, 13, 1089. [Google Scholar] [CrossRef]
- Attia, S. Spatial and Behavioral Thermal Adaptation in Net Zero Energy Buildings: An Exploratory Investigation. Sustainability 2020, 12, 7961. [Google Scholar] [CrossRef]
- Ahn, J. Performance analyses of Temperature Controls by a Network-Based Learning Controller for an Indoor Space in a Cold Area. Sustainability 2020, 12, 8515. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, S. Anti-logic or common sense that can hinder machine’s energy performance: Energy and comfort control models based on artificial intelligence responding to abnormal indoor environments. Appl. Energy 2017, 204. [Google Scholar] [CrossRef]
- Lee, S.; Joe, J.; Karava, P.; Bilionis, I.; Tzempelikos, A. Implementation of a self-tuned HVAC controller to satisfy occupant thermal preferences and optimize energy use. Energy Build 2019, 194, 301–316. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 2018. [Google Scholar]
- Engineering Toolbox. Recommended Indoor Temperatures Summer and Winter. Engineering Toolbox. 2016. Available online: http://www.engineeringtoolbox.com (accessed on 11 November 2016).
- ASHRAE. ASHRAE Standard 55-2004; ASHRAE: Atlanta, GA, USA, 2004. [Google Scholar]
- Petković, D.; Protić, M.; Shamshirband, S.; Akib, S.; Raos, M.; Marković, D. Evaluation of the most influential parameters of heat load in district heating systems. Energy Build. 2015, 104, 264–274. [Google Scholar] [CrossRef]
- Graupe, D. Principle of Artificial Neural Networks; World Scientific Publishing Co. Pte. Ltd: Singapore, 2013; ISBN 978-981-4522-73-1. [Google Scholar]
- Priddy, K.; Keller, P. Artificial Neural Networks: An. Introduction; SPIE Press: Bellingham, WA, USA, 2005; ISBN 0-8194-5987-9. [Google Scholar]




| Geometry | Value | |
|---|---|---|
| Building type | - | Commercial Office |
| Building space | Width × Depth × Height | 25.50 × 22.50 × 3.55 (m) |
| Wall | Area | 362.10 (m2) |
| Thickness | 0.2 (m) | |
| Thermal Resistance | 1.60 × 10−6 (h∙°C/J) | |
| Window | Area | 6.00 (m2) |
| Thickness | 0.01 (m) | |
| Thermal Resistance | 5.94 × 10−7 (h∙°C/J) | |
| Control-Type | PMV (Avg. of Abs.) | Efficiency (%) |
|---|---|---|
| Thermostat | 2.47 | - |
| FIS | 2.49 | +0.81 |
| ANN | 2.12 | −14.17 |
| Control-Type | Energy Transfer (kWh/m2∙Year) | Efficiency (%) | ||
|---|---|---|---|---|
| For Cooling | For Heating | Total | ||
| Thermostat | 197.55 | 612.31 | 809.86 | - |
| FIS | 158.21 | 653.71 | 811.92 | +2.54 |
| ANN | 133.69 | 709.01 | 842.70 | +4.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, J. Improvement of the Performance Balance between Thermal Comfort and Energy Use for a Building Space in the Mid-Spring Season. Sustainability 2020, 12, 9667. https://doi.org/10.3390/su12229667
Ahn J. Improvement of the Performance Balance between Thermal Comfort and Energy Use for a Building Space in the Mid-Spring Season. Sustainability. 2020; 12(22):9667. https://doi.org/10.3390/su12229667
Chicago/Turabian StyleAhn, Jonghoon. 2020. "Improvement of the Performance Balance between Thermal Comfort and Energy Use for a Building Space in the Mid-Spring Season" Sustainability 12, no. 22: 9667. https://doi.org/10.3390/su12229667
APA StyleAhn, J. (2020). Improvement of the Performance Balance between Thermal Comfort and Energy Use for a Building Space in the Mid-Spring Season. Sustainability, 12(22), 9667. https://doi.org/10.3390/su12229667




