Economic and Social Sustainability: The Influence of Oligopolies on Inequality and Growth
Abstract
1. Introduction
2. Literature Review
3. The Model
3.1. Production and Distribution
3.2. Barriers to Entry
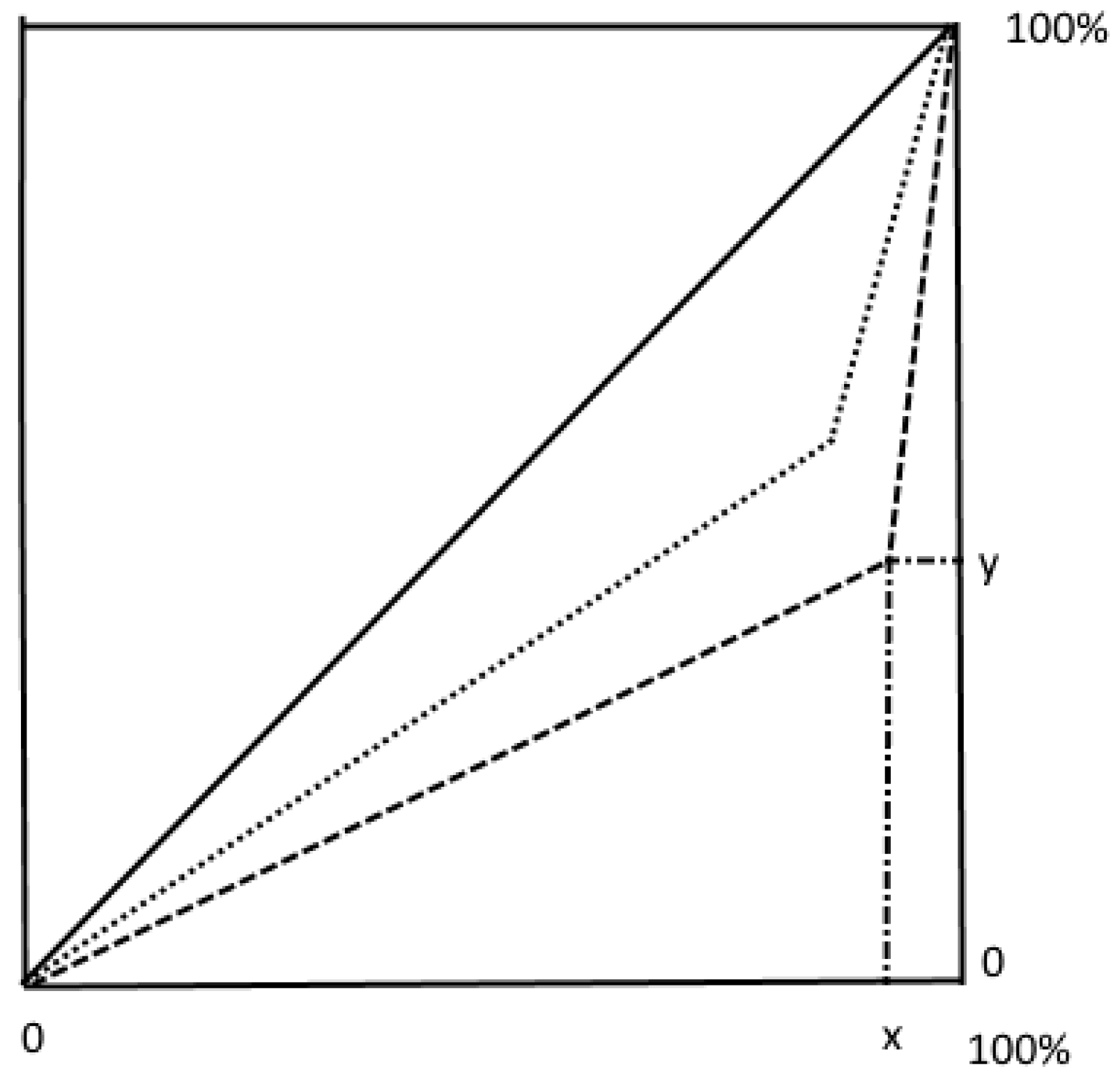
3.3. Distribution of Income
3.4. Households
4. The Development of the Economy
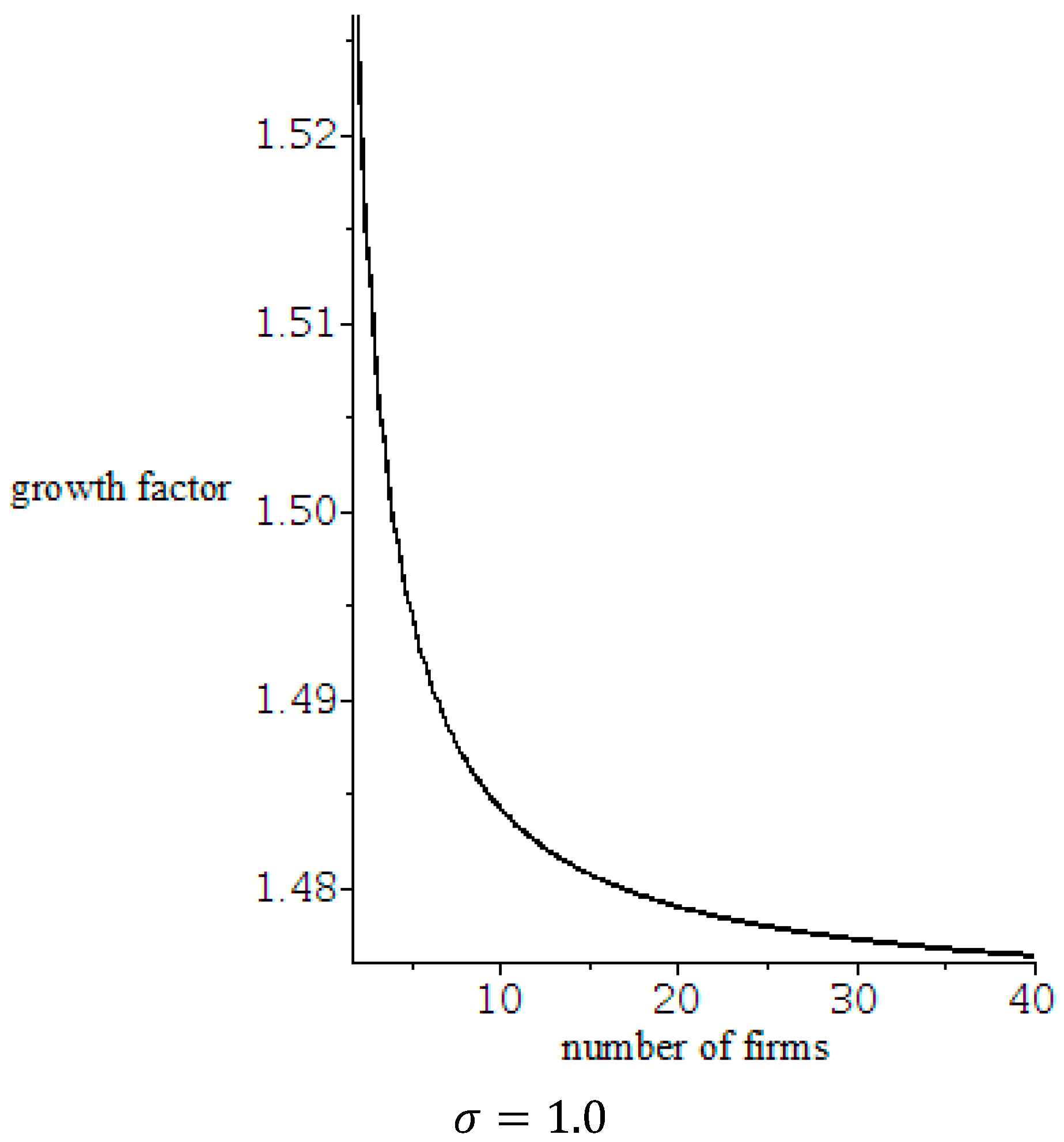
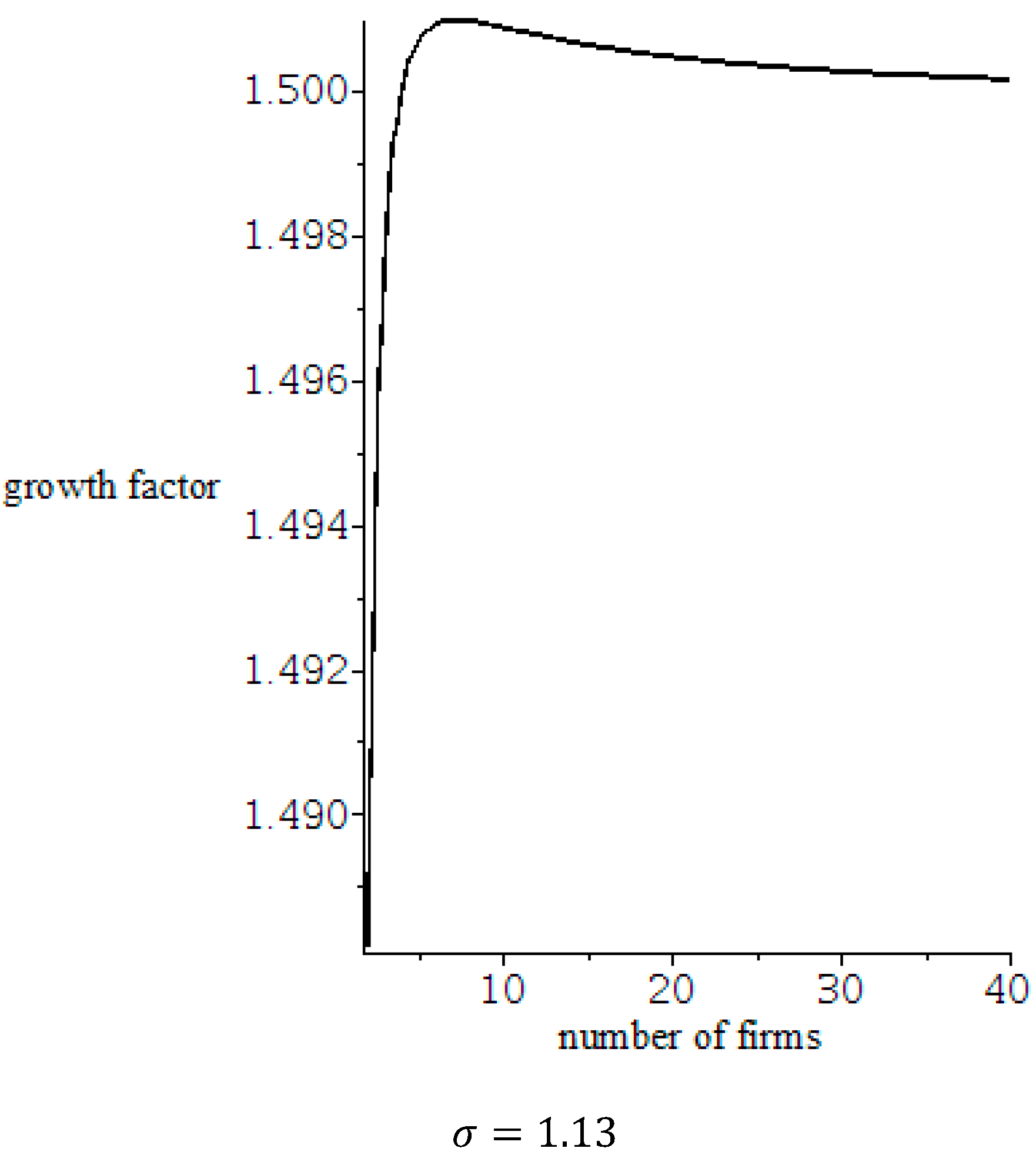
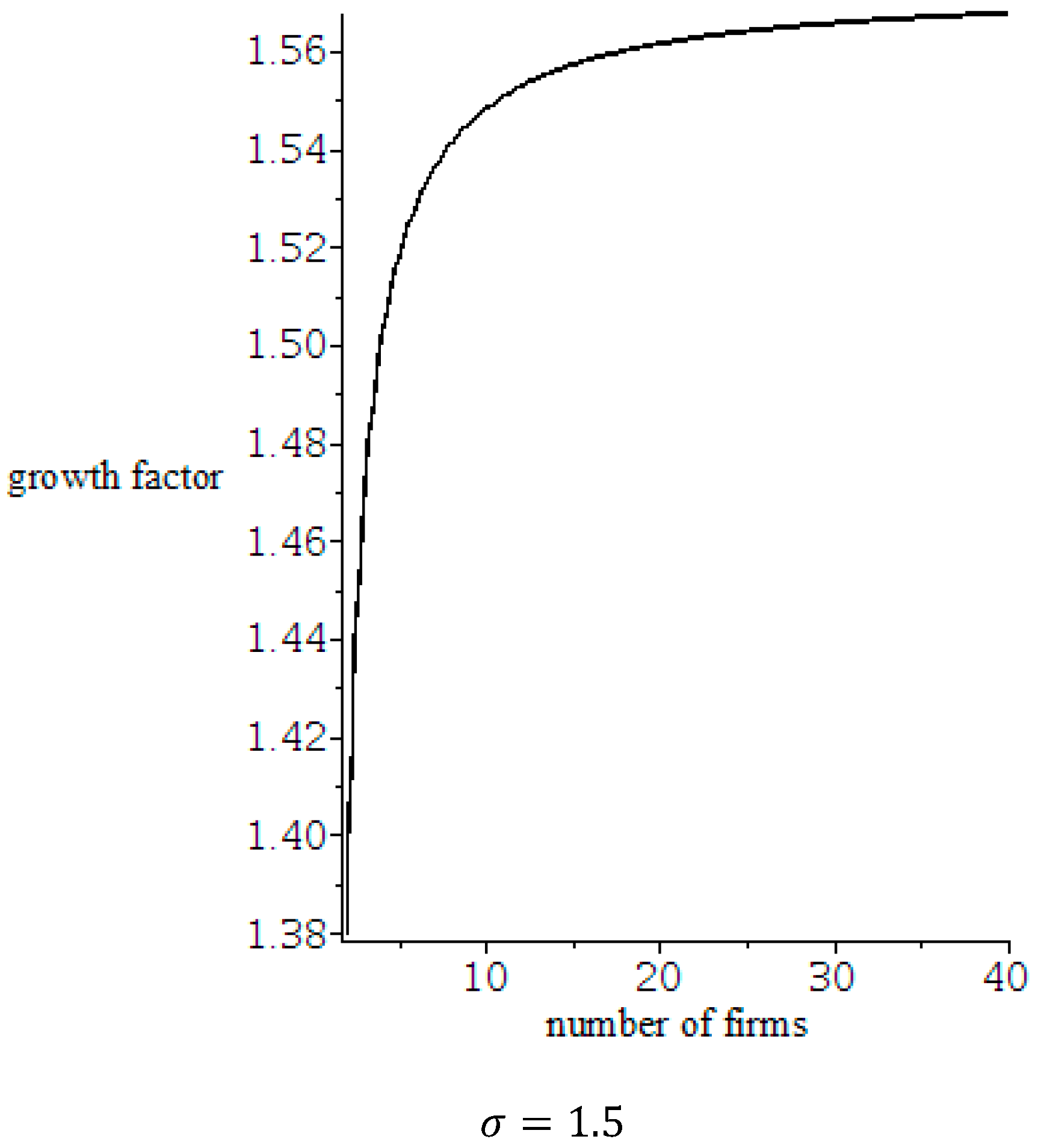
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baumgärtner, S.; Quaas, M.F. What is sustainability economics? Ecol. Econ. 2010, 69, 445–450. [Google Scholar] [CrossRef]
- Ota, T. Economic growth, income inequality and environment: Assessing the applicability of the Kuznets hypotheses to Asia. Palgrave Commun. 2017, 3. [Google Scholar] [CrossRef]
- Baumgärtner, S.; Drupp, M.A.; Meya, J.N.; Munz, J.M.; Quaas, M.F. Income inequality and willingness to pay for environmental public goods. J. Environ. Econ. Manag. 2017, 85, 35–61. [Google Scholar] [CrossRef]
- Vasconcelos, V.V.; Santos, F.C.; Pacheco, J.M.; Levin, S.A. Climate policies under wealth inequality. Proc. Natl. Acad. Sci. USA 2014, 111, 2212–2216. [Google Scholar] [CrossRef] [PubMed]
- Tavoni, A.; Dannenberg, A.; Kallis, G.; Löschel, A. Inequality, communication, and the avoidance of disastrous climate change in a public goods game. Proc. Natl. Acad. Sci. USA 2011, 108, 11825–11829. [Google Scholar] [CrossRef] [PubMed]
- De Neve, J.-M.; Powdthavee, N. Income Inequality Makes Whole Countries Less Happy, Harvard Business Review. 2016. Available online: https://hbr.org/2016/01/income-inequality-makes-whole-countries-less-happy (accessed on 16 October 2020).
- Oswald, A.J. Happiness and Economic Performance. Econ. J. 1997, 107, 1815–1831. [Google Scholar] [CrossRef]
- Hagerty, M.R.; Veenhoven, R. Wealth and Happiness Revisited—Growing National Income Does Go with Greater Happiness. Soc. Indic. Res. 2003, 64, 1–27. [Google Scholar] [CrossRef]
- Easterlin, R.A. Does Economic Growth Improve the Human Lot? Some Empirical Evidence. In Nations and Households in Economic Growth; Elsevier BV: Amsterdam, The Netherlands, 1974; pp. 89–125. [Google Scholar]
- Fajnzylber, P.; Lederman, D.; Loayza, N.V. Inequality and Violent Crime. J. Law Econ. 2002, 45, 1–39. [Google Scholar] [CrossRef]
- Blanchard, O.J.; Nordhaus, W.D.; Phelps, E.S. The Medium Run. Brook. Pap. Econ. Act. 1997, 1997, 89. [Google Scholar] [CrossRef]
- Elsby, M.W.L.; Hobijn, B.; Şahin, A. The Decline of the U.S. Labor Share. Brook. Pap. Econ. Act. 2013, 2013, 1–63. [Google Scholar] [CrossRef]
- Karabarbounis, L.; Neiman, B. The Global Decline of the Labor Share. Q. J. Econ. 2013, 129, 61–103. [Google Scholar] [CrossRef]
- Karabarbounis, L.; Neiman, B. Accounting for Factorless Income. NBER Macroecon. Annu. 2019, 33, 167–228. [Google Scholar] [CrossRef]
- Piketty, T. Capital in the Twenty-First Century; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Dao, M.C.; Das, M.; Koczan, Z.; Lian, W. Why Is Labor Receiving a Smaller Share of Global Income? Theory and Empirical Evidence. IMF Work. Pap. 2017, 17. [Google Scholar] [CrossRef]
- Autor, D.; Dorn, D.; Katz, L.F.; Patterson, C.; Van Reenen, J. Concentrating on the Fall of the Labor Share. Am. Econ. Rev. 2017, 107, 180–185. [Google Scholar] [CrossRef]
- Autor, D.; Dorn, D.; Katz, L.F.; Patterson, C.; Van Reenen, J. The Fall of the Labor Share and the Rise of Superstar Firms*. Q. J. Econ. 2020, 135, 645–709. [Google Scholar] [CrossRef]
- Barkai, S. Declining Labor and Capital Shares. J. Financ. 2020. [Google Scholar] [CrossRef]
- Barkai, S.; Benzell, S.G. 70 Years of US Corporate Profits; Stigler Center for the Study of the Economy and the State University of Chicago Booth School of Business: Chicago, IL, USA, 2018; Available online: https://research.chicagobooth.edu/stigler/research/-/media/8ee68ec563aa4c70aa94897ee04f68b6.ashx (accessed on 11 November 2020).
- Van Reenen, J.; Patterson, C. Research: The Rise of Superstar Firms Has Been Better for Investors than for Employees; Harvard Business Review: Brighton, MA, USA, 2017. [Google Scholar]
- Solow, R.M. A Contribution to the Theory of Economic Growth. Q. J. Econ. 1956, 70, 65. [Google Scholar] [CrossRef]
- Diamond, P.A. National debt in a neoclassical growth model. Am. Econ. Rev. 1965, 55, 1126–1150. [Google Scholar]
- Romer, P.M. Dynamic Competitive Equilibria with Externalities, Increasing Returns and Unbounded Growth. Ph.D. Thesis, University of Chicago, Chicago, IL, USA, 1983. [Google Scholar]
- Romer, P.M. Increasing Returns and Long-Run Growth. J. Politi Econ. 1986, 94, 1002–1037. [Google Scholar] [CrossRef]
- Mankiw, N.G.; Romer, D.; Weil, D.N. A Contribution to the Empirics of Economic Growth. Q. J. Econ. 1992, 107, 407–437. [Google Scholar] [CrossRef]
- Romer, P.M. Endogenous Technological Change. J. Politi. Econ. 1990, 98, S71–S102. [Google Scholar] [CrossRef]
- Mankiw, N. Imperfect competition and the Keynesian cross. Econ. Lett. 1988, 26, 7–13. [Google Scholar] [CrossRef]
- Solow, R.M. Technical Change and the Aggregate Production Function. Rev. Econ. Stat. 1957, 39, 312. [Google Scholar] [CrossRef]
- Peretto, P.F. Endogenous market structure and the growth and welfare effects of economic integration. J. Int. Econ. 2003, 60, 177–201. [Google Scholar] [CrossRef]
- Melitz, M.J.; Ottaviano, G.I.P. Market Size, Trade, and Productivity. Rev. Econ. Stud. 2008, 75, 295–316. [Google Scholar] [CrossRef]
- Rebelo, S. Long-Run Policy Analysis and Long-Run Growth. J. Politi. Econ. 1991, 99, 500–521. [Google Scholar] [CrossRef]
- Schumpeter, J. Capitalism, Socialism, and Democracy; Harper: New York, NY, USA, 1942. [Google Scholar]
- Cohen, W.M.; Klepper, S. A Reprise of Size and R & D. Econ. J. 1996, 106, 925. [Google Scholar] [CrossRef]
- Aghion, P.; Howitt, P. A Model of Growth Through Creative Destruction. Economics 1992, 60, 323. [Google Scholar] [CrossRef]
- Acs, Z.J.; Audretsch, D.B. Testing the Schumpeterian hypothesis. East. Econ. J. 1988, 14, 129–140. [Google Scholar]
- Aghion, P.; Bechtold, S.; Cassar, L.; Herz, H. The Causal Effects of Competition on Innovation: Experimental Evidence. J. Law Econ. Organ. 2018, 34, 162–195. [Google Scholar] [CrossRef]
- Scherer, F.M. Market structure and employment of scientists and engineers. Am. Econ. Rev. 1967, 57, 524–531. [Google Scholar]
- Scherer, F.M.; Ross, D. Industrial Market Structure and Economic Performance; Houghton Mifflin: Boston, MA, USA, 1990. [Google Scholar]
- Aghion, P.; Bloom, N.; Blundell, R.; Griffith, R.; Howitt, P. Competition and Innovation: An Inverted-U Relationship. Q. J. Econ. 2005, 120, 701–728. [Google Scholar] [CrossRef]
- OECD. Directorate for Financial and Enterprise Affairs Competition Committee, Market Concentration: Issues Paper by the Secretariat. DAF/COMP/WD (2018) 46. 2018. Available online: https://one.oecd.org/document/DAF/COMP/WD(2018)46/en/pdf (accessed on 10 November 2020).
- Bajgar, M.; Berlingieri, G.; Calligaris, S.; Criscuolo, C.; Timmis, J. Industry Concentration in Europe and North America. Available online: https://www.oecd-ilibrary.org/docserver/2ff98246-en.pdf?expires=1605067382&id=id&accname=guest&checksum=AE987B06BFE8A19F0A5EDD84C53819EC (accessed on 11 November 2020).
- Diez, F.; Fan, J.; Villegas-Sánchez, C. Global Declining Competition. IMF Work. Pap. 2019, 19. [Google Scholar] [CrossRef]
- Guinea, O.; Erixon, F. Standing up for Competition: Market Concentration, Regulation, and Europe’s Quest for a New Industrial Policy, ECIPE Occasional Paper 01/2019. Available online: https://ecipe.org/wp-content/uploads/2019/03/ECI_19_OccasionalPaper_Competition_01_2019-1.pdf (accessed on 10 November 2020).
- Van Reenen, J. Increasing Differences between Firms: Market Power and the Macro-Economy. Centre of European Policy. Available online: https://www.kansascityfed.org/~/media/files/publicat/sympos/2018/papersandhandouts/jh%20john%20van%20reenen%20version%2020.pdf (accessed on 10 November 2020).
- Syverson, C. Macroeconomics and Market Power: Context, Implications, and Open Questions. J. Econ. Perspect. 2019, 33, 23–43. [Google Scholar] [CrossRef]
- Shapiro, C. Protecting Competition in the American Economy: Merger Control, Tech Titans, Labor Markets. J. Econ. Perspect. 2019, 33, 69–93. [Google Scholar] [CrossRef]
- Basu, S. Are Price-Cost Markups Rising in the United States? A Discussion of the Evidence. J. Econ. Perspect. 2019, 33, 3–22. [Google Scholar] [CrossRef]
- Autor, D.; Dorn, D.; Katz, L.F.; Patterson, C.; Van Reenen, J. Concentrating on the Fall of the Labor Share; National Bureau of Economic Research: Cambridge, MA, USA, 2017; Available online: https://www.nber.org/system/files/working_papers/w23108/w23108.pdf (accessed on 11 November 2020).
- Cavalleri, M.C.; Eliet, A.; McAdam, P.; Petroulakis, F.; Soares, A.; Vansteenkiste, I. Concentration, Market Power and Dynamism in the Euro Area ECB Working Paper Series No 2253; European Central Bank: Frankfurt, Germany, 2019. [Google Scholar]
- Berry, S.; Gaynor, M.; Morton, F.S. Do Increasing Markups Matter? Lessons from Empirical Industrial Organization. J. Econ. Perspect. 2019, 33, 44–68. [Google Scholar] [CrossRef]
- Lamoreaux, N.R. The Problem of Bigness: From Standard Oil to Google. J. Econ. Perspect. 2019, 33, 94–117. [Google Scholar] [CrossRef]
- Ge, J.; Luo, J.; Yuan, Y. Misallocation in Chinese Manufacturing and Services: A Variable Markup Approach. China World Econ. 2019, 27, 74–103. [Google Scholar] [CrossRef]
- Hall, R. New Evidence on the Markup of Prices over Marginal Costs and the Role of Mega-Firms in the US Economy; National Bureau of Economic Research: Cambridge, MA, USA, 2018; Available online: https://www.nber.org/system/files/working_papers/w24574/w24574.pdf (accessed on 11 November 2020).
- Azar, J.; Marinescu, I.; Steinbaum, M. Measuring Labor Market Power Two Ways. AEA Pap. Proc. 2019, 109, 317–321. [Google Scholar] [CrossRef]
- De Loecker, J.; Eeckhout, J. The Rise of Market. Power and the Macroeconomic Implications; National Bureau of Economic Research: Cambridge, MA, USA, 2017; Available online: https://www.nber.org/system/files/working_papers/w23687/w23687.pdf (accessed on 10 November 2020).
- Poschke, M. The Firm Size Distribution across Countries and Skill-Biased Change in Entrepreneurial Technology. Am. Econ. J. Macroecon. 2018, 10, 1–41. [Google Scholar] [CrossRef]
- Ogilvie, S. The Economics of Guilds. J. Econ. Perspect. 2014, 28, 169–192. [Google Scholar] [CrossRef]
- Ogilvie, S.; Carus, A. Institutions and Economic Growth in Historical Perspective. Handb. Econ. Growth 2014, 2, 403–513. [Google Scholar] [CrossRef]
- Smith, A. An Inquiry into the Nature and Causes of the Wealth of Nations. In The Glasgow Edition of the Works and Correspondence of Adam Smith and An Inquiry into the Nature and Causes of the Wealth of Nations; Libery Fund: Indianapolis, IN, USA, 1776. [Google Scholar] [CrossRef]
- Demsetz, H. Barriers to entry. Am. Econ. Rev. 1982, 72, 47–57. [Google Scholar]
- Bain, J.S. Industrial Organization; Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Ferguson, J.M. Advertising and Competition: Theory, Measurement, Fact; Ballinger: Cambridge, UK, 1974. [Google Scholar]
- Stigler, G.J. The Organization of Industry; Richard D. Irwin: Homewood, IL, USA, 1968. [Google Scholar]
- Karakaya, F. Barriers to entry in industrial markets. J. Bus. Ind. Mark. 2002, 17, 379–388. [Google Scholar] [CrossRef]
- Djankov, S. The Regulation of Entry: A Survey. World Bank Res. Obs. 2009, 24, 183–203. [Google Scholar] [CrossRef]
- Pigou, A.C. The Economics of Welfare, 4th ed.; Macmillan: London, UK, 1938. [Google Scholar]
- Stigler, G.J. The Theory of Economic Regulation. Bell J. Econ. Manag. Sci. 1971, 2, 3–21. [Google Scholar] [CrossRef]
- Acemoglu, K.D. Oligarchic versus Democratic Societies. J. Eur. Econ. Assoc. 2008, 6, 1–44. [Google Scholar] [CrossRef]
- Morck, R.; Yeung, B. Family Control and the Rent-Seeking Society. Entrep. Theory Pr. 2004, 28, 391–409. [Google Scholar] [CrossRef]
- Djankov, S.; La Porta, R.; López-De-Silanes, F.; Shleifer, A. The Regulation of Entry. Q. J. Econ. 2002, 117, 1–37. [Google Scholar] [CrossRef]
- Shleifer, A.; Vishny, R.W. Corruption. Q. J. Econ. 1993, 108, 599–617. [Google Scholar] [CrossRef]
- Klapper, L.; Laeven, L.; Rajan, R. Entry regulation as a barrier to entrepreneurship. J. Financ. Econ. 2006, 82, 591–629. [Google Scholar] [CrossRef]
- Fisman, R.; Sarria-Allende, V. Regulation of Entry and the Distortion of Industrial Organization. J. Appl. Econ. 2010, 13, 91–111. [Google Scholar] [CrossRef]
- Ciccone, A.; Papaioannou, E. Red Tape and Delayed Entry. J. Eur. Econ. Assoc. 2007, 5, 444–458. [Google Scholar] [CrossRef]
- Djankov, S.; La Porta, R.; López-De-Silanes, F.; Shleifer, A. Courts. Q. J. Econ. 2003, 118, 453–517. [Google Scholar] [CrossRef]
- Dreher, A.; Gassebner, M. Greasing the wheels? The impact of regulations and corruption on firm entry. Public Choice 2013, 155, 413–432. [Google Scholar] [CrossRef]
- Becht, M.; Mayer, C.; Wagner, H.F. Where do firms incorporate? Deregulation and the cost of entry. J. Corp. Financ. 2008, 14, 241–256. [Google Scholar] [CrossRef]
- Kaplan, D.S.; Piedra, E.; Seira, E. Entry regulation and business start-ups: Evidence from Mexico. J. Public Econ. 2011, 95, 1501–1515. [Google Scholar] [CrossRef]
- Bruhn, M. License to Sell: Business Start-Up Reform in Mexico; Policy Research Working Paper 4538; World Bank: Washington, DC, USA, 2008. [Google Scholar]
- Yakovlev, E.; Zhuravskaya, E. Deregulation of Business. Available online: https://www.researchgate.net/publication/4800749_Deregulation_of_Business (accessed on 11 November 2020).
- Cabral, L. Good turnover and bad turnover: Barriers to business and productivity. Econ. Lett. 2014, 125, 179–181. [Google Scholar] [CrossRef]
- McGowan, D. Do entry barriers reduce productivity? Evidence from a natural experiment. Econ. Lett. 2014, 125, 97–100. [Google Scholar] [CrossRef]
- Djankov, S.; La Porta, R.; López-De-Silanes, F.; Shleifer, A. The Regulation of Entry; National Bureau of Economic Research: Cambridge, MA, USA, 2000; Available online: https://www.nber.org/system/files/working_papers/w7892/w7892.pdf (accessed on 11 November 2020).
- Mahmood, I.P.; Lee, C.-Y. Business groups: Entry barrier–innovation debate revisited. J. Econ. Behav. Organ. 2004, 54, 513–531. [Google Scholar] [CrossRef]
- Ganapati, S. Growing Oligopolies, Prices Output and Productivity. Available online: https://www.sganapati.com/files/Ganapati_2019_OligopoliesPricesQuantities_AEJmicro.pdf (accessed on 11 November 2020).
- Bessen, J. Information Technology and Industry Concentration; Law and Economic Paper No. 17–41; Boston University: Boston, MA, USA, 2017. [Google Scholar]
- Zingales, L. A Capitalism for the People: Recapturing the Lost Genius of American Prosperity (an excerpt). J. Econ. Sociol. 2015, 16, 14–19. [Google Scholar] [CrossRef]
- Zingales, L. Towards a Political Theory of the Firm. J. Econ. Perspect. 2017, 31, 113–130. [Google Scholar] [CrossRef]
- Ennis, S.F.; Gonzaga, P.; Pike, C. Inequality: A Hidden Cost of Market Power. SSRN Electron. J. 2017. [Google Scholar] [CrossRef]
- Ennis, S.; Kim, Y. Market Power and Wealth Distribution. In A Step Ahead: Competition Policy for Shared Prosperity and Inclusive Growth; World Bank: Washington, DC, USA, 2017; pp. 133–153. [Google Scholar]
- Høj, J.; Jimenez, M.; Maher, M.; Nicoletti, G.; Wise, M. Product Market Competition in the OECD Countries: Taking Stock and Moving Forward; OECD Economics Department Working Papers; OECD: Paris, France, 2007. [Google Scholar]
- Etzioni, A. The Capture Theory of Regulations—Revisited. Society 2009, 46, 319–323. [Google Scholar] [CrossRef]
- Mukoyama, T.; Popov, L. The political economy of entry barriers. Rev. Econ. Dyn. 2014, 17, 383–416. [Google Scholar] [CrossRef][Green Version]
- Stauvermann, P. Does globalization lead to a rat race of national labor-market institutions? Panoeconomicus 2013, 60, 73–87. [Google Scholar] [CrossRef]
- Uhlig, H.; Yanagawa, N. Increasing the capital income tax may lead to faster growth. Eur. Econ. Rev. 1996, 40, 1521–1540. [Google Scholar] [CrossRef]
- Cournot, A. Researches into the Mathematical Principles of the Theory Wealth; Bacon, N.T., Ed.; Macmillan: New York, NY, USA, 1838. [Google Scholar]
- Bertrand, J. Review. J. Savants 1883, 68, 499–508. [Google Scholar]
- Von Stackelberg, H. Marktform und Gleichgewicht; Peacock, A.T., Ed.; William Hodge: London, UK, 1934. [Google Scholar]
- Novshek, W. Cournot Equilibrium with Free Entry. Rev. Econ. Stud. 1980, 47, 473–486. [Google Scholar] [CrossRef]
- Tirole, J. The Theory of Industrial Organization; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Pepall, L.; Richards, D.; Norman, G. Industrial Organization-Contemporary Theory and Empirical Applications, 5th ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Rasmussen, E. Games and Information: An Introduction to Game Theory, 4th ed.; Basil Blackwell: Cambridge, UK, 2007. [Google Scholar]
- Friedman, J. Oligopoly Theory; Cambridge University Press (CUP): Cambridge, UK, 1983. [Google Scholar]
- Fudenberg, D.; Tirole, J. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Kopel, M. Simple and complex adjustment dynamics in Cournot duopoly models. Chaos Solitons Fractals 1996, 7, 2031–2048. [Google Scholar] [CrossRef]
- Maskin, E.; Tirole, J. A theory of dynamic oligopoly, III. Eur. Econ. Rev. 1987, 31, 947–968. [Google Scholar] [CrossRef]
- Edgeworth, F.Y. The Pure Theory of Monopoly. In Papers Relating to Political Economy; McMillan: London, UK, 1925; Volume I, pp. 111–142. [Google Scholar]
- Kreps, D.M.; Scheinkman, J.A. Quantity Precommitment and Bertrand Competition Yield Cournot Outcomes. Bell J. Econ. 1983, 14, 326. [Google Scholar] [CrossRef]
- Levine, D.P. Economic Studies: Contributions to the Critique of Economic Theory; Routledge: London, UK, 1977. [Google Scholar]
- Stauvermann, P.J. Endogenous Growth in OLG Models; Gabler: Wiesbaden, Germany, 1997. (In German) [Google Scholar]
- Grossman, G.M.; Yanagawa, N. Asset bubbles and endogenous growth. J. Monet. Econ. 1993, 31, 3–19. [Google Scholar] [CrossRef]
- Olson, M. The Logic of Collective Action: Public Goods and the Theory of Groups; Harvard University Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Bernheim, B.D.; Whinston, M.D. Menu Auctions, Resource Allocation, and Economic Influence. Q. J. Econ. 1986, 101, 1–31. [Google Scholar] [CrossRef]
- Deininger, K.; Squire, L. A New Data Set Measuring Income Inequality. World Bank Econ. Rev. 1996, 10, 565–591. [Google Scholar] [CrossRef]
- King, I.; Ferguson, D. Dynamic inefficiency, endogenous growth, and Ponzi games. J. Monet. Econ. 1993, 32, 79–104. [Google Scholar] [CrossRef]
- Dollar, D.; Kraay, A. Growth is Good for the Poor. J. Econ. Growth 2002, 7, 195–225. [Google Scholar] [CrossRef]
- Benchekroun, H.; Van Long, N. Efficiency inducing taxation for polluting oligopolists. J. Public Econ. 1998, 70, 325–342. [Google Scholar] [CrossRef]
- Lambertini, L. Oligopoly, the Environment and Natural Resources; Informa UK Limited: London, UK, 2013. [Google Scholar]
- Carraro, C.; Soubeyran, A. Environmental taxation, market share, and profits in oligopoly. Environ. Policy Market. Struct. 1996, 4, 23–44. [Google Scholar] [CrossRef]
- Requate, T. Environmental Policy under Imperfect Competition: A Survey; Economics Working Paper 2005-12; Department of Economics, Kiel University: Kiel, Germany, 2005; pp. 1–100. [Google Scholar]
- Persson, T.; Tabellini, G. Is Inequality Harmful for Growth? Theory and Evidence Am. Econ. Rev. 1991, 84, 600–621. [Google Scholar] [CrossRef]
- Alesina, A.; Rodrik, D. Distributive Politics and Economic Growth. Q. J. Econ. 1994, 109, 465–490. [Google Scholar] [CrossRef]
- D’Aspremont, C.; Ferreira, R.D.S. Oligopolistic vs. monopolistic competition: Do intersectoral effects matter? Econ. Theory 2015, 62, 299–324. [Google Scholar] [CrossRef][Green Version]
- D’Aspremont, C.; Ferreira, R.D.S. The Dixit–Stiglitz economy with a ‘small group’ of firms: A simple and robust equilibrium markup formula. Res. Econ. 2017, 71, 729–739. [Google Scholar] [CrossRef][Green Version]
- D’Aspremont, C.; Ferreira, R.D.S. Exploiting separability in a multisectoral model of oligopolistic competition. Math. Soc. Sci. 2020, 106, 51–59. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, R.R.; Stauvermann, P.J. Economic and Social Sustainability: The Influence of Oligopolies on Inequality and Growth. Sustainability 2020, 12, 9378. https://doi.org/10.3390/su12229378
Kumar RR, Stauvermann PJ. Economic and Social Sustainability: The Influence of Oligopolies on Inequality and Growth. Sustainability. 2020; 12(22):9378. https://doi.org/10.3390/su12229378
Chicago/Turabian StyleKumar, Ronald R., and Peter J. Stauvermann. 2020. "Economic and Social Sustainability: The Influence of Oligopolies on Inequality and Growth" Sustainability 12, no. 22: 9378. https://doi.org/10.3390/su12229378
APA StyleKumar, R. R., & Stauvermann, P. J. (2020). Economic and Social Sustainability: The Influence of Oligopolies on Inequality and Growth. Sustainability, 12(22), 9378. https://doi.org/10.3390/su12229378




