Comparative Analysis of Data Detection Techniques for 5G Massive MIMO Systems
Abstract
1. Introduction
2. Background
2.1. Successive over Relaxation
2.2. Gauss–Seidel Detector
2.3. Jacobi Method
2.4. Approximate Message Passing
3. Proposed Methods
- Step 1: Compute the initial solution as
- Step 2: Apply the SOR, GS, or JA methods where , as
- -
- If SOR:
- -
- If GS:
- -
- If JA:
- Step 3: Apply the AMP algorithm as shown in (8), where .
| Algorithm 1:Initialize the AMP using the SOR method |
| Input: Output: Estimated signal Initialization: , , Initial estimations: Iteration: for j = 2 : 1 : n Apply the AMP algorithm using (6)–(8) end Return . |
| Algorithm 2:Initialize the AMP detector using the GS method |
| Input: Output: Estimated signal Initialization: , , Initial estimations: Iteration: for j = 2 : 1 : n Apply the AMP algorithm using (6)–(8) end Return . |
| Algorithm 3:Initialize the AMP detector using the JA method |
| Input: Output: Estimated signal Initialization: , , Initial estimations: Iteration: for j = 2 : 1 : n Apply the AMP algorithm using (6)–(8) end Return . |
4. Complexity Analysis
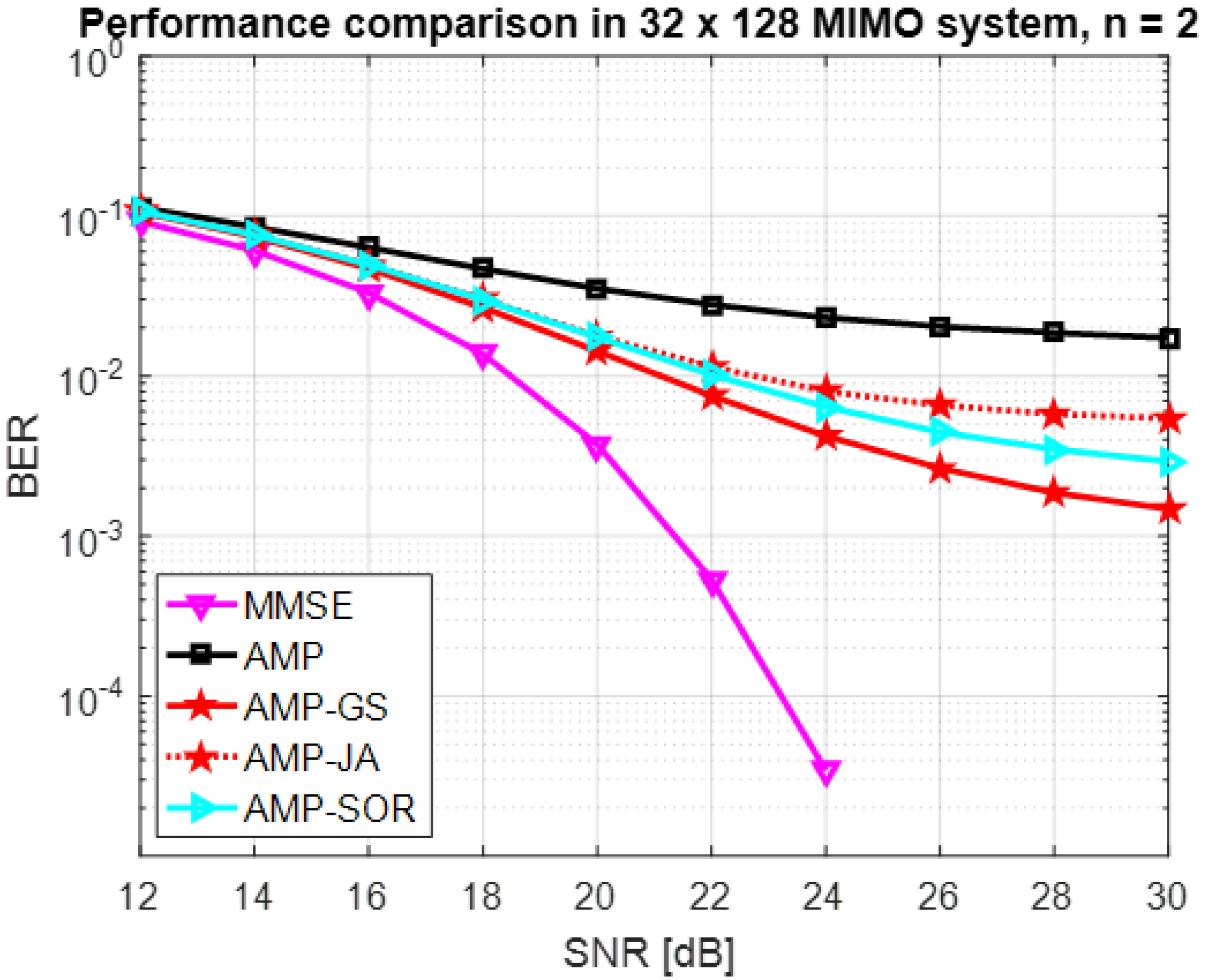
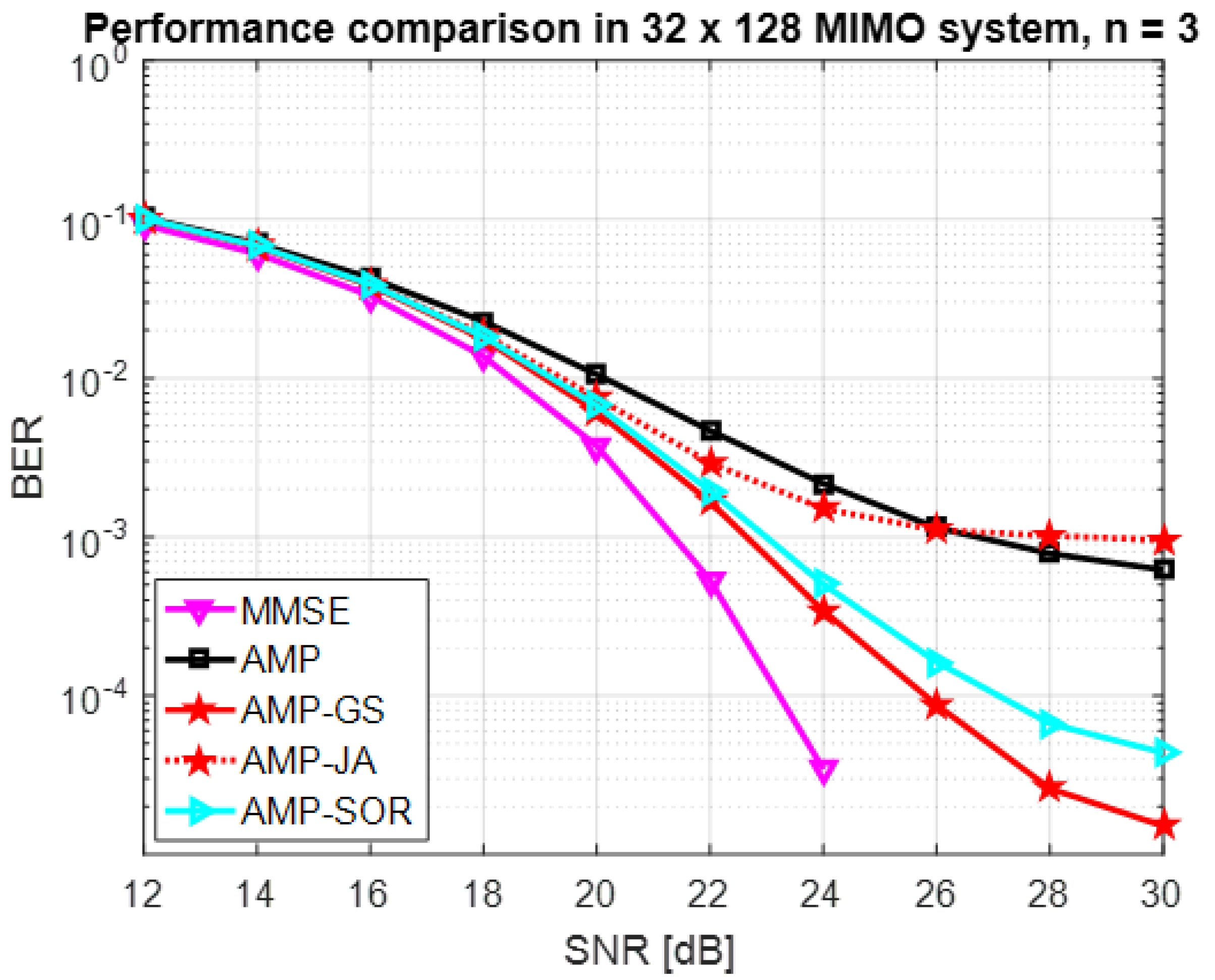
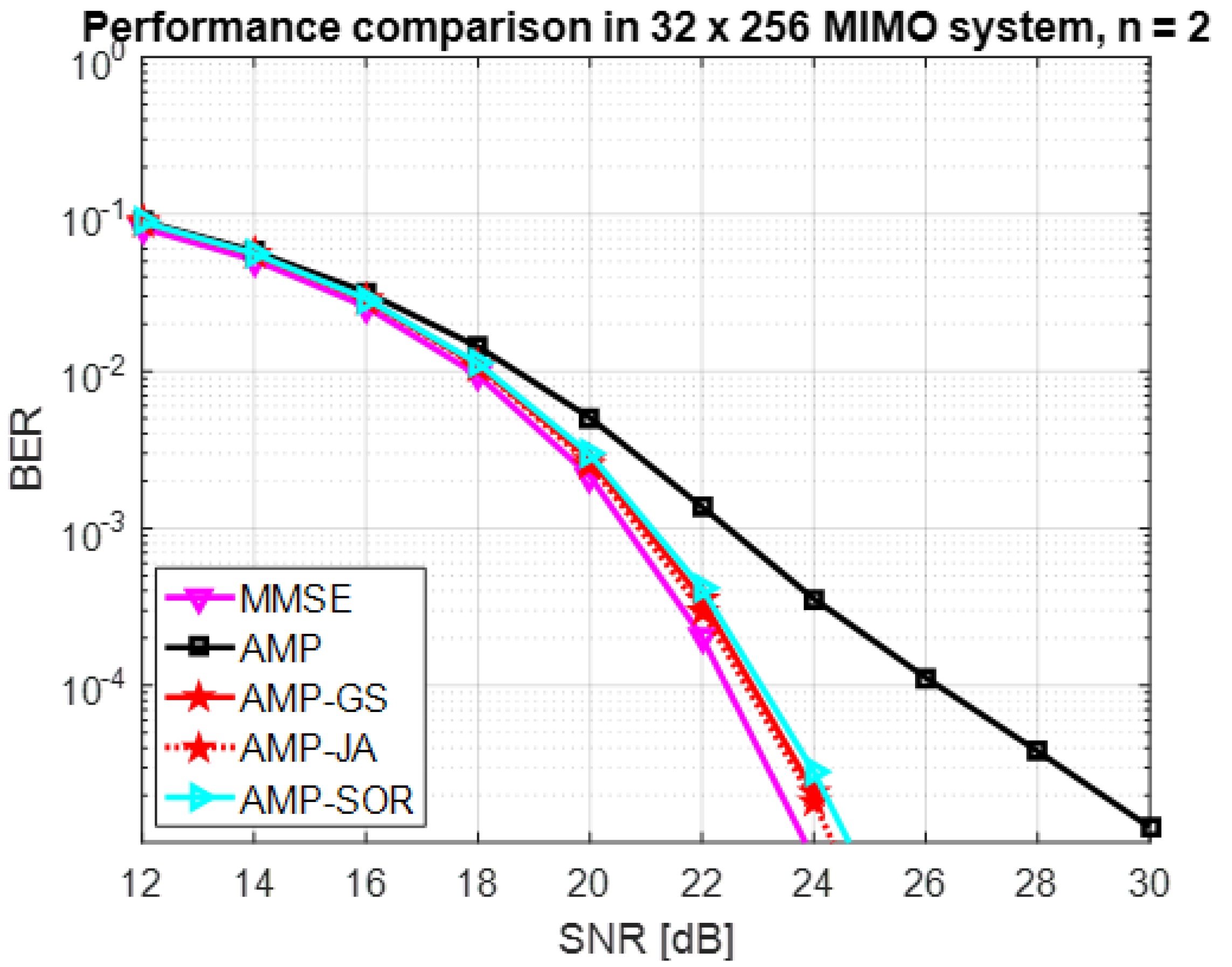
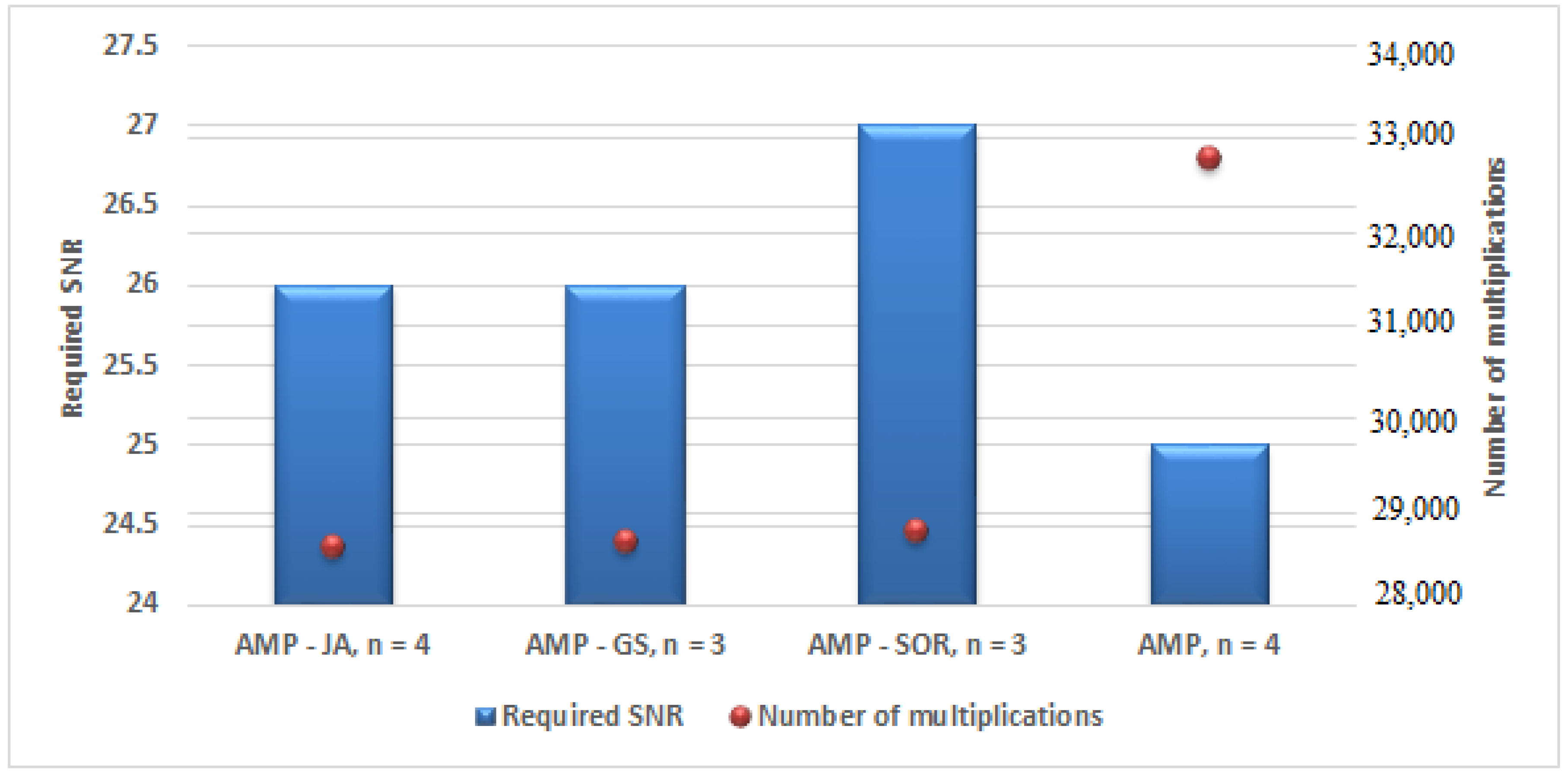
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cisco. Cisco Visual Networking Index: Forecast and Trends, 2017–2022. White Pap. 2018, 1, 1–38. [Google Scholar]
- Zhang, D.; Liu, Y.; Dai, L.; Bashir, A.K.; Nallanathan, A.; Shim, B. Performance Analysis of FD-NOMA-Based Decentralized V2X Systems. IEEE Trans. Commun. 2019, 67, 5024–5036. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Kelechi, A.H.; Albreem, M.A.; Chaudhry, S.A.; Zia, M.S.; Kim, S. Sixth Generation (6G) Wireless Networks: Vision, Research Activities, Challenges and Potential Solutions. Symmetry 2020, 12, 676. [Google Scholar] [CrossRef]
- Han, Y.; Rao, B.D.; Lee, J. Massive Uncoordinated Access with Massive MIMO: A Dictionary Learning Approach. IEEE Trans. Wirel. Commun. 2020, 19, 1320–1332. [Google Scholar] [CrossRef]
- Nomikos, N.; Michailidis, E.T.; Trakadas, P.; Vouyioukas, D.; Zahariadis, T.; Krikidis, I. Flex-NOMA: Exploiting Buffer-Aided Relay Selection for Massive Connectivity in the 5G Uplink. IEEE Access 2019, 7, 88743–88755. [Google Scholar] [CrossRef]
- Salah, W.A.; Albreem, M.A.; Alsayid, B.; Zneid, B.A.; Alkhasawneh, M.; Al-Mofleh, A.; Sneineh, A.A.; Al-Aish, A.A. Electric vehicle technology impacts on energy. Int. J. Power Electron. Drive Syst. 2019, 10, 1. [Google Scholar]
- Zhou, S.; Xu, W.; Zhang, H.; You, X. Hybrid precoding for millimeter wave massive MIMO with analog combining. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Michailidis, E.T.; Nomikos, N.; Trakadas, P.; Kanatas, A.G. Three-Dimensional Modeling of mmWave Doubly Massive MIMO Aerial Fading Channels. IEEE Trans. Veh. Technol. 2020, 69, 1190–1202. [Google Scholar] [CrossRef]
- Lee, B.M.; Yang, H. Massive MIMO for Industrial Internet of Things in Cyber-Physical Systems. IEEE Trans. Ind. Inf. 2018, 14, 2641–2652. [Google Scholar] [CrossRef]
- Albreem, M.A.M. 5G wireless communication systems: Vision and challenges. In Proceedings of the 2015 International Conference on Computer, Communications, and Control Technology (I4CT), Kuching, Malaysia, 21–23 April 2015; pp. 493–497. [Google Scholar] [CrossRef]
- Albreem, M.A.M.; El-Saleh, A.; Isa, M.; Salah, W.; Juso, M. Green internet of things: An overivew. In Proceedings of the 2017 IEEE 4th International Conference on Smart Instrumentation, Measurement and Application (ICSIMA), Putrajaya, Malaysia, 28–30 November 2017; pp. 1–6. [Google Scholar]
- Zhang, W.; Wang, C.; Ge, X.; Chen, Y. Enhanced 5G Cognitive Radio Networks Based on Spectrum Sharing and Spectrum Aggregation. IEEE Trans. Commun. 2018, 66, 6304–6316. [Google Scholar] [CrossRef]
- Chen, C.; Zhong, W.; Yang, H.; Du, P. On the Performance of MIMO-NOMA-Based Visible Light Communication Systems. IEEE Photonics Technol. Lett. 2018, 30, 307–310. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Wang, Z. Channel estimation for mmWave massive MIMO based access and backhaul in ultra-dense network. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kumar, A. Detection in 5G Mobile Communication System Using Hybrid Technique. Natl. Acad. Sci. Lett. 2020. [Google Scholar] [CrossRef]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef]
- Yin, H.; Gesbert, D.; Filippou, M.; Liu, Y. A Coordinated Approach to Channel Estimation in Large-Scale Multiple-Antenna Systems. IEEE J. Sel. Areas Commun. 2013, 31, 264–273. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO Detection Techniques: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Albreem, M.A.M.; El-Saleh, A.A.; Juntti, M. On Approximate Matrix Inversion Methods for Massive MIMO Detectors. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Ancona, Italy, 19–21 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, S.; Hanzo, L. Fifty years of MIMO detection: The road to large-scale MIMOs. IEEE Commun. Surv. Tutor. 2015, 17, 1941–1988. [Google Scholar] [CrossRef]
- Shahabuddin, S.; Islam, M.H.; Shahabuddin, M.S.; Albreem, M.A.; Juntti, M. Matrix Decomposition for Massive MIMO Detection. arXiv 2020, arXiv:2009.11172. [Google Scholar]
- Xiong, Y.; Wei, N.; Zhang, Z. A Low-Complexity Iterative GAMP-Based Detection for Massive MIMO with Low-Resolution ADCs. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Albreem, M.A.; Vasudevan, K. Efficient Hybrid Linear Massive MIMO Detector Using Gauss–Seidel And Successive Over-Relaxation. Int. J. Wirel. Inf. Netw. 2020, 27, 551–557. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, J.; Wang, Z. An Improved Gauss-Seidel Algorithm and Its Efficient Architecture for Massive MIMO Systems. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1194–1198. [Google Scholar] [CrossRef]
- Esswie, A.A.; El-Absi, M.; Dobre, O.A.; Ikki, S.; Kaiser, T. A novel FDD massive MIMO system based on downlink spatial channel estimation without CSIT. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Nhat Cuong, C.; Thi Hong, T.; Duc Khai, L. Hardware Implementation of the Efficient SOR-Based Massive MIMO Detection for Uplink. In Proceedings of the 2019 IEEE-RIVF International Conference on Computing and Communication Technologies (RIVF), Danang, Vietnam, 20–22 March 2019; pp. 1–6. [Google Scholar]
- Xie, T.; Dai, L.; Gao, X.; Dai, X.; Zhao, Y. Low-complexity SSOR-based precoding for massive MIMO systems. IEEE Commun. Lett. 2016, 20, 744–747. [Google Scholar] [CrossRef]
- Gao, X.; Dai, L.; Hu, Y.; Wang, Z.; Wang, Z. Matrix inversion-less signal detection using SOR method for uplink large-scale MIMO systems. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 3291–3295. [Google Scholar]
- Zhang, Y.; Yu, A.; Tan, X.; Zhang, Z.; You, X.; Zhang, C. Adaptive Damped Jacobi Detector and Architecture for Massive MIMO Uplink. In Proceedings of the 2018 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Chengdu, China, 26–30 October 2018; pp. 203–206. [Google Scholar]
- Yu, A.; Jing, S.; Tan, X.; Wu, Z.; Yan, Z.; Zhang, Z.; You, X.; Zhang, C. Efficient Successive Over Relaxation Detectors for Massive MIMO. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2128–2139. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, C.; Xue, Y.; Xu, S.; You, X. Efficient architecture for soft-output massive MIMO detection with Gauss-Seidel method. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1886–1889. [Google Scholar]
- Zeng, J.; Lin, J.; Wang, Z. Low Complexity Message Passing Detection Algorithm for Large-Scale MIMO Systems. IEEE Wirel. Commun. Lett. 2018, 7, 708–711. [Google Scholar] [CrossRef]
- Liu, L.; Yuen, C.; Guan, Y.L.; Li, Y.; Su, Y. Convergence Analysis and Assurance for Gaussian Message Passing Iterative Detector in Massive MU-MIMO Systems. IEEE Trans. Wirel. Commun. 2016, 15, 6487–6501. [Google Scholar] [CrossRef]
- Zhang, Z.; Cai, X.; Li, C.; Zhong, C.; Dai, H. One-Bit Quantized Massive MIMO Detection Based on Variational Approximate Message Passing. IEEE Trans. Signal Process. 2018, 66, 2358–2373. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, J. Approximate Message Passing Detection for Beam-Index Spatial Modulation in Massive MIMO. In Proceedings of the 2019 IEEE VTS Asia Pacific Wireless Communications Symposium (APWCS), Singapore, 28–30 August 2019; pp. 1–5. [Google Scholar]
- Bayati, M.; Montanari, A. The Dynamics of Message Passing on Dense Graphs, with Applications to Compressed Sensing. IEEE Trans. Inf. Theory 2011, 57, 764–785. [Google Scholar] [CrossRef]

| Method | Number of Multiplications |
|---|---|
| AMP | |
| AMP-SOR | |
| AMP-GS | |
| AMP-JA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albreem, M.A.; Kumar, A.; Alsharif, M.H.; Khan, I.; Choi, B.J. Comparative Analysis of Data Detection Techniques for 5G Massive MIMO Systems. Sustainability 2020, 12, 9281. https://doi.org/10.3390/su12219281
Albreem MA, Kumar A, Alsharif MH, Khan I, Choi BJ. Comparative Analysis of Data Detection Techniques for 5G Massive MIMO Systems. Sustainability. 2020; 12(21):9281. https://doi.org/10.3390/su12219281
Chicago/Turabian StyleAlbreem, Mahmoud A., Arun Kumar, Mohammed H. Alsharif, Imran Khan, and Bong Jun Choi. 2020. "Comparative Analysis of Data Detection Techniques for 5G Massive MIMO Systems" Sustainability 12, no. 21: 9281. https://doi.org/10.3390/su12219281
APA StyleAlbreem, M. A., Kumar, A., Alsharif, M. H., Khan, I., & Choi, B. J. (2020). Comparative Analysis of Data Detection Techniques for 5G Massive MIMO Systems. Sustainability, 12(21), 9281. https://doi.org/10.3390/su12219281







