Non-Monotone Projected Gradient Method in Linear Elasticity Contact Problems with Given Friction

Abstract

We are focusing on the algorithms for solving the large-scale convex optimization problem in linear elasticity contact problems discretized by Finite Element method (FEM). The unknowns of the problem are the displacements of the FEM nodes, the corresponding objective function is defined as a convex quadratic function with symmetric positive definite stiffness matrix and additional non-linear term representing the friction in contact. The feasible set constraints the displacement subject to non-penetration conditions. The dual formulation of this optimization problem is well-known as a Quadratic Programming (QP) problem and can be considered as a most basic non-linear optimization problem. Understanding these problems and the development of efficient algorithms for solving them play the crucial role in the large-scale problems in practical applications. We shortly review the theory and examine the behavior and the efficiency of Spectral Projected Gradient method modified for QP problems (SPG-QP) on the solution of a toy example in MATLAB environment.

1. Introduction

One of the key components of the structural design is the contact problem. This problem is crucial, for example, during the design process of steel components, namely welded and screwed contacts. From the mathematical point of view, we are dealing with variational equalities and variational inequalities [1]. Since the problem is analytically solvable only for simple geometries, the typical approach is to discretize the problem and using the Finite Element Method (FEM, [2,3]). Using the reformulation of the problem by the so-called Ritz–Galerkin method and under certain assumptions, one can mathematically prove that the solution of the discretized problem is the approximation of the contiguous one. Additionally, the error converges asymptotically to zero with the density increase in the used mesh [1,3]. The advantage of the method is the possibility of the formulation of the problem as the (constrained) energy functional minimization problem. In the case of the linear elasticity, this corresponding problem is the Quadratic programming (QP) problem [4].

QP problems belong among to the most important optimization problems in practical applications; for example, in the case of the least square methods for regression analysis with the Euclidean distance [5], the solution of the problems with symmetric positive definite system matrix [6,7], Support Vector Machine (SVM, [8,9]), the inner subproblem of more complex (non-linear) optimization problems [10,11], and the numerical solution of variational inequalities in the linear elasticity contact problems [1,4,12,13].

In our case, the Hessian matrix represents the stiffness matrix and the linear term of the objective function is the force density vector. The unknown is the vector of the displacements in the FEM nodes. In the case of contact problems, the non-penetration conditions of the bodies and obstacles are defining the feasible set of the corresponding optimization problem with the linear inequality constraints. Additionally, if we consider also a friction between the bodies and/or the obstacles, the original contiguous problem captures this property by the new term influencing the solution displacement. For example, in the case of the linear elasticity contact problem with the Tresca (given) friction, the discretized minimization problem of the energy functional with the additional non-linear term representing the response of displacement caused by friction and constraints representing the non-penetration, can be reformulated using the dualization into the QP problem with bound and separable quadratic inequality constraints [1,12,14].

Although the QP problems belong to the basic non-linear optimization problems necessary for understanding non-linear optimization theory in general, there does not exist the best algorithm for solving problems from different applications, especially when one introduces the Dirichlet boundary conditions by equality constraints and/or uses non-overlapping domain decomposition methods, such as the Finite Element Tearing and Interconnecting Method (FETI, [4,15,16,17,18,19,20,21]). The contact problems of linear elasticity are characterized by the bounded spectrum independent of the used mesh [22]. The utilization of this property has been proven and practically applied/demonstrated only in the case of active-set algorithms, namely the MPRGP algorithm (Modified Proportioning with Reduced Gradient Projections, [4,8,12,23,24]). Another approach is to use Interior-Point (IP, [25]) method—we eliminate the inequality constraints using barrier functions and solve the sequence of resulting saddle-point problems. In this paper, we examine the projected gradient descent method [26,27,28], especially SPG-QP (Spectral Projected Gradients [29] for QP [5]).

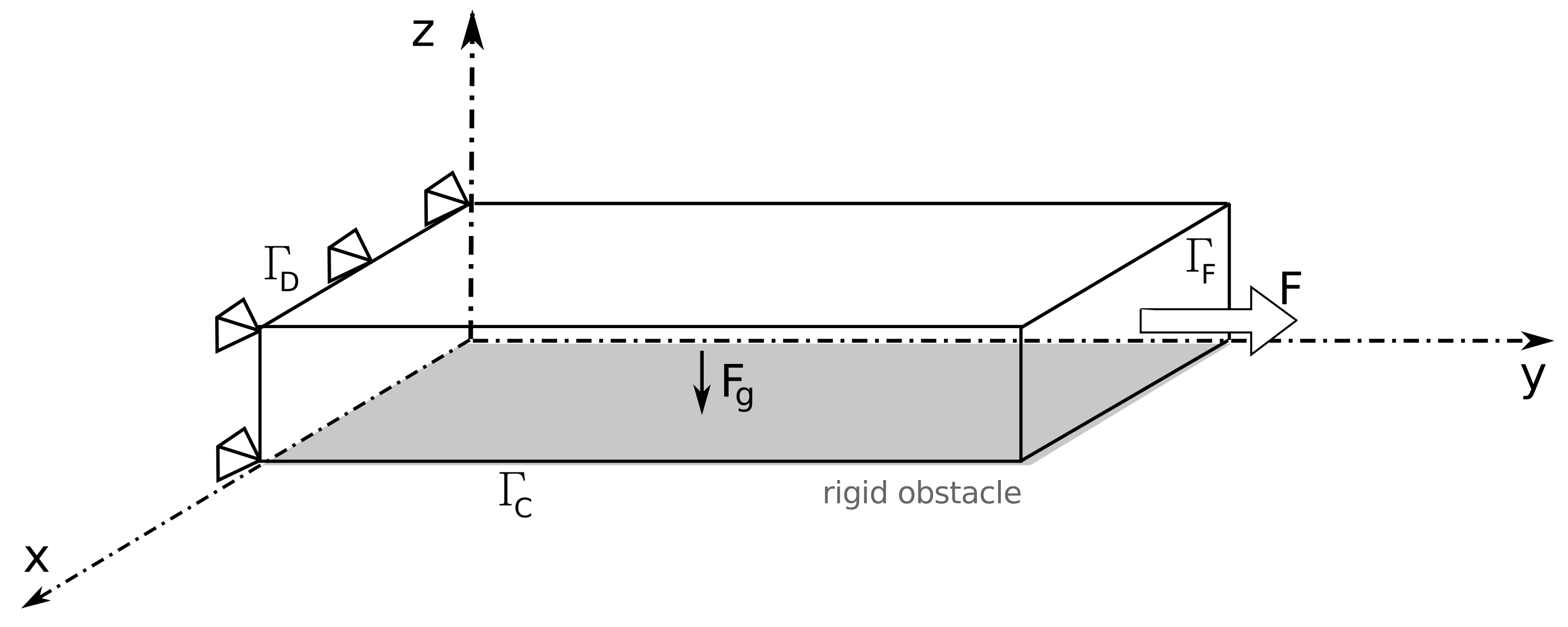
2. Problem Definition

As a simple benchmark, we consider the block of homogeneous material $\mathsf{\Omega }$ with fixed zero displacement on boundary ${\mathsf{\Gamma }}_D$ and imposed traction forces F on ${\mathsf{\Gamma }}_F$. The part ${\mathsf{\Gamma }}_C$ denotes the part of boundary that may get into contact with a rigid obstacle. The block is attracted to the obstacle as consequence of the gravity force $F_g$, see Figure 1.

We solve the discretized form of the problem using FEM (see [2,3,30]), which leads to the optimization problem

$${\mathit{u}}^{*}:=arg\underset{\mathit{u}\in {\mathsf{\Omega }}_C}{min}f\left(\mathit{u}\right)+j_h\left(\mathit{u}\right),$$

(1)

where $N\in \mathbb{N}$ is a number of used FEM nodes, $n=3N$ is a number of primal variables, $m_c\le N$ is a number of FEM nodes in ${\mathsf{\Gamma }}_C$, the terms of the objective function are defined as

$$f\left(\mathit{u}\right):=\frac{1}{2}{\mathit{u}}^T\mathit{K}\mathit{u}-{\mathit{f}}^T\mathit{u},j_h\left(\mathit{u}\right):=\sum _{i=1}^{m_c}{\psi }_i{\parallel {\mathit{T}}_i\mathit{u}\parallel }_2,$$

and

• $\mathit{u}\in {\mathbb{R}}^n$ is a vector of unknown displacements in FEM nodes;
• ${\mathsf{\Omega }}_C\subset {\mathbb{R}}^n$ is a set of feasible (non-penetrated) displacements;
• $\mathit{K}\in {\mathbb{R}}^{n,n}$ is a symmetric positive definite (SPD) stiffness matrix (the Dirichlet boundary condition is implemented by the modification of the stiffness matrix);
• $\mathit{f}\in {\mathbb{R}}^n$ is a vector of forces density resulting from the stresses imposed on the structure during a displacement (the discretized form of $\mathit{F}$ and ${\mathit{F}}_g$);
• $j_h:{\mathbb{R}}^n\to \mathbb{R}$ is a numerical integration of functional describing the friction forces in the weak formulation of the problem;
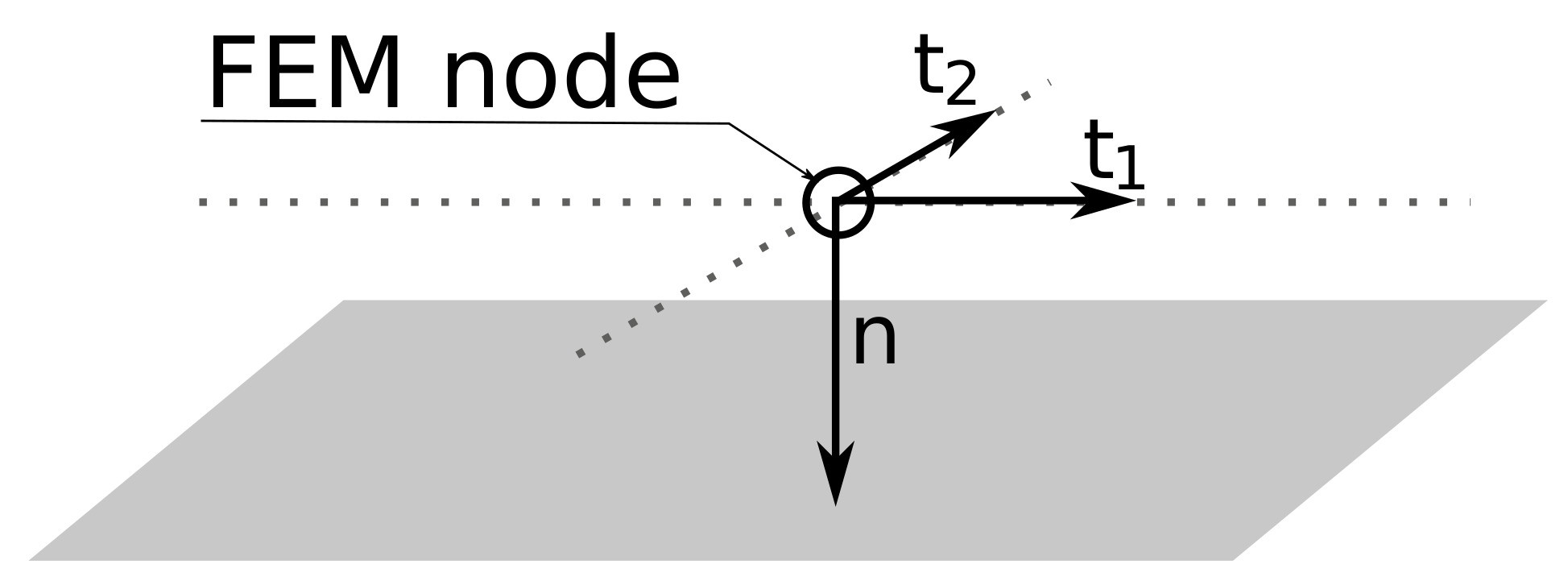
• ${\mathit{T}}_i\in {\mathbb{R}}^{2,n},i=1,\dots ,m_c$ are basis vectors formed by appropriately placed multiples of the unit tangential vectors in such a way that the jump of tangential displacement in i-th FEM node is given by ${\mathit{T}}_i\mathit{u}$;
• ${\psi }_i\in {\mathbb{R}}^{+},i=1,\dots ,m$ are slip bound coefficients associated with ${\mathit{T}}_i$.

Since our problem has a simple geometry, see Figure 2, we set $\mathit{n}:=[0,0,-1]$ as the unit normal contact vector and ${\mathit{t}}_1:=[1,0,0],{\mathit{t}}_2:=[0,1,0]$ as the tangential vectors for every FEM node in ${\mathsf{\Gamma }}_C$.

For every contact node (i-th node of ${\mathsf{\Gamma }}_C$) ${\mathit{T}}_i\in {\mathbb{R}}^{2,n}$ is given by a zero matrix with 1 in the first row on appropriate x-coordinate of i-th node and in the second row on appropriate y-coordinate of i-th node. Consequently, the matrix composed as

$$\mathit{T}:=\left[\begin{array}{c}{\mathit{T}}_1\\ ⋮\\ {\mathit{T}}_{m_c}\end{array}\right]\in {\mathbb{R}}^{2m_c,n}$$

is a full rank matrix.

We can modify the non-differentiable term $j_h$ in (1) into equivalent form (see [1])

$$j_h\left(\mathit{u}\right)=\sum _{i=1}^{m_c}\underset{\parallel {\mathit{\tau }}_i{\parallel }_2\le {\psi }_i}{max}{\mathit{\tau }}_i^T{\mathit{T}}_i\mathit{u},$$

(2)

where ${\mathit{\tau }}_i\in {\mathbb{R}}^2$ are regulation variables. We denote the function and the vector

$$L(\mathit{u},\mathit{\tau }):=f\left(\mathit{u}\right)+{\mathit{\tau }}^T\mathit{T}\mathit{u},\mathit{\tau }=\left[\begin{array}{c}{\mathit{\tau }}_1\\ ⋮\\ {\mathit{\tau }}_{m_c}\end{array}\right]\in {\mathbb{R}}^{2m_c},$$

(3)

and we write constraints $\parallel {\mathit{\tau }}_i{\parallel }_2\le {\psi }_i$ in (2) in the form

$$\sqrt{{\left[{\mathit{\tau }}_i\right]}_1^2+{\left[{\mathit{\tau }}_i\right]}_2^2}\le {\psi }_i,i=1,\dots ,m_c.$$

(4)

After the substitution into (1), we get

$$\underset{\mathit{u}\in {\mathsf{\Omega }}_C}{min}f\left(\mathit{u}\right)+j_h\left(\mathit{u}\right)=\underset{\mathit{u}\in {\mathsf{\Omega }}_C}{min}\underset{\mathit{\tau }\in {\mathrm{\Lambda }}_{\mathit{\tau }}}{max}L(\mathit{u},\mathit{\tau }),$$

(5)

where we denoted ${\mathrm{\Lambda }}_{\mathit{\tau }}\subset {\mathbb{R}}^{2m_c}$ as a feasible set defined by constraints (4). We consider $L(\mathit{u},\mathit{\tau })$ as a Lagrange function and $\mathit{\tau }$ as a vector of the Lagrange multipliers (in notation (3)) and we use the duality theorem (see Dostál [4]) to reformulate problem (5) into

$$\underset{\mathit{u}\in {\mathsf{\Omega }}_C}{min}\underset{\mathit{\tau }\in {\mathrm{\Lambda }}_{\mathit{\tau }}}{max}L(\mathit{u},\mathit{\tau })=\underset{\mathit{\tau }\in {\mathrm{\Lambda }}_{\mathit{\tau }}}{max}\underset{\mathit{u}\in {\mathsf{\Omega }}_C}{min}L(\mathit{u},\mathit{\tau }).$$

(6)

We include condition $\mathit{u}\in {\mathsf{\Omega }}_C$ by creating new Lagrange multipliers

$$\underset{\mathit{\tau }\in {\mathrm{\Lambda }}_{\mathit{\tau }}}{max}\underset{\mathit{u}\in {\mathsf{\Omega }}_C}{min}L(\mathit{u},\mathit{\tau })=\underset{\mathit{\tau }\in {\mathrm{\Lambda }}_{\mathit{\tau }},{\mathbf{\lambda }}_C\ge 0}{max}\underset{\mathit{u}\in {\mathbb{R}}^n}{min}L(\mathit{u},\mathit{\tau })+{\mathbf{\lambda }}_C^T(\mathit{B}\mathit{u}-\mathit{c}),$$

(7)

where matrix $\mathit{B}\in {\mathbb{R}}^{m_c,n}$ and vector $\mathit{c}\in {\mathbb{R}}^{m_c}$ are constructed in such way that

$${\mathsf{\Omega }}_C=\{\mathit{u}\in {\mathbb{R}}^n:\mathit{B}\mathit{u}\le \mathit{c}\}.$$

(8)

Due to geometry in our problem we can construct $\mathit{B}$ simply; $\mathit{B}$ is zero matrix with $-1$ in every i-th row (which is corresponding to i-th node in ${\mathsf{\Gamma }}_C$) on appropriate z-coordinate of i-th node (see the choice of normal vectors for nodes in ${\mathsf{\Gamma }}_C$ in Figure 2). Using these values, the set (8) consists of the feasible displacements which do not penetrate the rigid obstacle.

Problem (6) is equivalent to the saddle point problem

$$({\mathit{u}}^{*},{\mathbf{\lambda }}^{*}):=arg\underset{\mathbf{\lambda }\in \mathrm{\Lambda }}{max}\underset{\mathit{u}\in {\mathbb{R}}^n}{min}f\left(\mathit{u}\right)+{\mathbf{\lambda }}^T(\widehat{\mathit{B}}\mathit{u}-\widehat{\mathit{c}}),$$

(9)

where

$$\mathbf{\lambda }:=\left[\begin{array}{c}\mathit{\tau }\\ {\mathbf{\lambda }}_C\end{array}\right],\widehat{\mathit{B}}:=\left[\begin{array}{c}\mathit{T}\\ \mathit{B}\end{array}\right],\widehat{\mathit{c}}:=\left[\begin{array}{c}\mathit{0}\\ \mathit{c}\end{array}\right]$$

and

$$\mathrm{\Lambda }:=\{[\mathit{\tau },{\mathbf{\lambda }}_C]\in {\mathbb{R}}^{3m_c}:\sqrt{{\mathit{\tau }}_{2i-1}^2+{\mathit{\tau }}_{2i}^2}\le {\psi }_i,i=1,\dots ,m_c,{\mathbf{\lambda }}_C\ge \mathbf{0}\}.$$

(10)

We derive the dual problem corresponding to (9). From the first KKT condition (since stiffness matrix is SPD, we can use standard inversion $K^{-1}$) we get

$$\mathit{K}\mathit{u}-\mathit{f}+{\widehat{\mathit{B}}}^T\mathbf{\lambda }=0\Rightarrow \mathit{u}={\mathit{K}}^{-1}\left(\mathit{f}-{\widehat{\mathit{B}}}^T\mathbf{\lambda }\right)$$

(11)

and substitute into Lagrange function (7). After the simplifications, we get

$$L(\mathit{u},\mathbf{\lambda })=L\left({\mathit{K}}^{-1}(\mathit{f}-{\widehat{\mathit{B}}}^T\mathbf{\lambda }),\mathbf{\lambda }\right)=-\frac{1}{2}{\mathbf{\lambda }}^T\widehat{\mathit{B}}{\mathit{K}}^{-1}{\mathit{T}}^T\mathbf{\lambda }+{\mathbf{\lambda }}^T\widehat{\mathit{B}}{\mathit{K}}^{-1}\mathit{f}-\frac{1}{2}{\mathit{f}}^T{\mathit{K}}^{-1}\mathit{f}.$$

We obtain the function of only one variable $\mathbf{\lambda }$. Since we want to find maximizer (see saddle-point problem (9)), we omit the constant term and change signs and ${\mathbf{\lambda }}^{*}$ solves equivalent minimization problem

$${\mathbf{\lambda }}^{*}=arg\underset{\mathbf{\lambda }\in \mathrm{\Lambda }}{min}\mathsf{\Theta }\left(\mathbf{\lambda }\right),\mathsf{\Theta }\left(\mathbf{\lambda }\right):=\frac{1}{2}{\mathbf{\lambda }}^T\mathit{A}\mathbf{\lambda }-{\mathbf{\lambda }}^T\mathit{b},$$

(12)

where we denoted

$$\mathit{A}:=\widehat{\mathit{B}}{\mathit{K}}^{-1}{\widehat{\mathit{B}}}^T,\mathit{b}:=\widehat{\mathit{B}}{\mathit{K}}^{-1}\mathit{f}.$$

(13)

After solving the minimization problem (12), the corresponding solution ${\mathit{u}}^{*}$ of primal problem (1) can be evaluated using (11).

Obviously, $\mathit{A}\in {\mathbb{R}}^{3m_c,3m_c}$ is SPD and problem (12) is the QP problem with separable quadratic constraints combinated with bound constraints. Such a problem always has a unique solution [4].

3. Numerical Solution

To solve the problem (12), we use the Spectral Projected Gradient method (SPG, [29]), which is a projection gradient method for solving the general minimization problems

$$\overline{\mathit{x}}:=arg\underset{\mathit{x}\in \mathsf{\Theta }}{min}f\left(\mathit{x}\right).$$

The method is based on the Barzilai–Borwein (BB, [31,32]) step-size

$${\mathit{x}}_{\mathrm{it}+\frac{1}{2}}=P_{\mathsf{\Theta }}({\mathit{x}}_{\mathrm{it}}-{\alpha }_{\mathrm{it}}\nabla f\left({\mathit{x}}_{\mathrm{it}}\right)),{\alpha }_{\mathrm{it}}:=\frac{\langle {\mathit{x}}_{\mathrm{it}}-{\mathit{x}}_{\mathrm{it}-1},{\mathit{x}}_{\mathrm{it}}-{\mathit{x}}_{\mathrm{it}-1}\rangle }{\langle {\mathit{x}}_{it}-{\mathit{x}}_{\mathrm{it}-1},\nabla f\left({\mathit{x}}_{\mathrm{it}}\right)-\nabla f\left({\mathit{x}}_{\mathrm{it}-1}\right)\rangle },$$

where $\nabla f\left(\mathit{x}\right)\in {\mathbb{R}}^n$ is a gradient of objective function $f:{\mathbb{R}}^n\to \mathbb{R}$ and $P_{\mathsf{\Theta }}:{\mathbb{R}}^n\to \mathsf{\Theta }$ is the projection onto closed convex feasible set $\mathsf{\Theta }\subset {\mathbb{R}}^n$. However, since this procedure does not necessarily provide the decreasing sequence of function values (see [33]), an additional step is introduced

$${\mathit{x}}_{\mathrm{it}+1}={\mathit{x}}_{\mathrm{it}}+{\beta }_{\mathrm{it}}{\mathit{d}}_{\mathrm{it}},{\mathit{d}}_{\mathrm{it}}={\mathit{x}}_{\mathrm{it}+\frac{1}{2}}-{\mathit{x}}_{\mathrm{it}},$$

where ${\mathit{d}}_{\mathrm{it}}\in {\mathbb{R}}^n$ is called spectral projected gradient. The appropriate step-size ${\beta }_{\mathrm{it}}\in (0,\infty )$ is computed using the iterative Grippo–Lampariello–Lucidi line-search method (GLL, [34]) to satisfy so-called generalized Armijo condition

$$f({\mathit{x}}_{\mathrm{it}}+{\beta }_{\mathrm{it}}{\mathit{d}}_{\mathrm{it}})<f_{max}+\mathit{\tau }{\beta }_{\mathrm{it}}\langle \nabla f\left({\mathit{x}}_{\mathrm{it}}\right),{\mathit{d}}_{\mathrm{it}}\rangle .$$

(14)

Here, $\mathit{\tau }\in (0,1)$ represents a safeguarding parameter and

$$f_{max}:=max\{f\left({\mathit{x}}_{\mathrm{it}-j}\right):0\le j\le min\{\mathrm{it},m-1\}\}$$

with predefined constant $m\in \mathbb{N}$. Because of the enforcement of condition (14), the algorithm generates the sequence of approximations with a decrease in objective function in every m iterations and the algorithm is converging to the minimizer.

Recently, [5] introduced the simplification of the method in the case of the quadratic optimization problem. If the objective function is quadratic, one can derive the analytical formula for the computation of step-size, which satisfies (14)

$${\beta }_{\mathrm{it}}\in \left[{\sigma }_1,min\{{\sigma }_2,\widehat{\beta }\}\right]$$

with safeguarding parameters $0<{\sigma }_1<{\sigma }_2<1$ and

$$\widehat{\beta }=(1-\mathit{\tau })\overline{\beta }+\sqrt{{(1-\mathit{\tau })}^2{\overline{\beta }}^2+2\xi },\xi =\frac{f_{max}-f\left({\mathit{x}}_{\mathrm{it}}\right)}{\langle \mathit{A}{\mathit{d}}_{\mathrm{it}},{\mathit{d}}_{\mathrm{it}}\rangle },\overline{\beta }=-{\displaystyle \frac{\langle \nabla f\left({\mathit{x}}_{\mathrm{it}}\right),{\mathit{d}}_{\mathrm{it}}\rangle }{\langle \mathit{A}{\mathit{d}}_{\mathrm{it}},{\mathit{d}}_{\mathrm{it}}\rangle }},$$

where $\mathit{A}={\nabla }^{2}f\left({\mathit{x}}_{\mathrm{it}}\right)\in {\mathbb{R}}^{n,n}$ is a Hessian matrix of quadratic objective function $f:{\mathbb{R}}^n\to \mathbb{R}$. The algorithm can be written with only single matrix-vector multiplication during one iteration, see Algorithm 1.

Algorithm 1: SPG for QP problems (SPG-QP, [5])

Given a quadratic objective function $f\left(\mathit{x}\right)=\frac{1}{2}{\mathit{x}}^T\mathit{A}\mathit{x}-{\mathit{b}}^T\mathit{x}$ with $\mathit{A}\in {\mathbb{R}}^{n,n}$SPD and $\mathit{b}\in {\mathbb{R}}^n$, closed convex feasible set $\mathsf{\Theta }\subset {\mathbb{R}}^n$, initial approximation ${\mathit{x}}_0\in \mathsf{\Theta }$, projection onto feasible set $P_{\mathsf{\Theta }}\left(\mathit{x}\right)$, parameters $m\in \mathbb{N},\mathit{\tau }\in (0,1)$, safeguarding parameters ${\sigma }_1,{\sigma }_2\in \mathbb{R}:0<{\sigma }_1<{\sigma }_2<1$, precision $\epsilon >0$, and initial step-size ${\alpha }_0>0$.   ${\mathit{g}}_0:=\mathit{A}{\mathit{x}}_0-\mathit{b}$   $f_0:=1/2\langle {\mathit{g}}_0-\mathit{b},{\mathit{x}}_0\rangle$   set index of iteration $it:=0$   while stopping criterium is not safisfied    ${\mathit{d}}_{it}:=P_{\mathsf{\Theta }}({\mathit{x}}_{it}-{\alpha }_{it}{\mathit{g}}_{it})-{\mathit{x}}_{it}$    compute matrix-vector multiplication $\mathit{A}{\mathit{d}}_{it}$    compute multiple dot-product $\langle {\mathit{d}}_{it},\{{\mathit{d}}_{it},\mathit{A}{\mathit{d}}_{it},{\mathit{g}}_{it}\}\rangle$    $f_{max}:=max\{f\left({\mathit{x}}_{it-j}\right):0\le j\le min\{it,m-1\}\}$    $\xi :=(f_{max}-f\left({\mathit{x}}_{it}\right))/\langle {\mathit{d}}_{it},\mathit{A}{\mathit{d}}_{it}\rangle$    $\overline{\beta }:=-\langle {\mathit{g}}_{it},{\mathit{d}}_{it}\rangle /\langle {\mathit{d}}_{it},\mathit{A}{\mathit{d}}_{it}\rangle$    $\widehat{\beta }:=\tau \overline{\beta }+\sqrt{{\tau }^2{\overline{\beta }}^2+2\xi }$    choose ${\beta }_{it}\in [{\sigma }_1,min\{{\sigma }_2,\widehat{\beta }\}]$    ${\mathit{x}}_{it+1}:={\mathit{x}}_{it}+{\beta }_{it}{\mathit{d}}_{it}$    ${\mathit{g}}_{it+1}:={\mathit{g}}_{it}+{\beta }_{it}\mathit{A}{\mathit{d}}_{it}$    $f_{it+1}:=f\left({\mathit{x}}_{it}\right)+{\beta }_{it}\langle {\mathit{d}}_{it},{\mathit{g}}_{it}\rangle +\frac{1}{2}{\beta }_{it}^2\langle {\mathit{d}}_{it},\mathit{A}{\mathit{d}}_{it}\rangle$    ${\alpha }_{it+1}:=\langle {\mathit{d}}_{it},{\mathit{d}}_{it}\rangle /\langle {\mathit{d}}_{it},\mathit{A}{\mathit{d}}_{it}\rangle$    $it:=it+1$   endwhile  Return the approximation of solution ${\mathit{x}}_{it}$ and the number of performed iterations $\mathrm{it}$.

We used the presented Spectral Projected Gradient method for QP for solving the dual problem (12) with variable $\mathbf{\lambda }\in {\mathbb{R}}^{m_c}$, objective function $\mathsf{\Theta }:{\mathbb{R}}^{3m_c}\to \mathbb{R}$, and feasible set (10) defined by separable quadratic constraints and bound constraints.

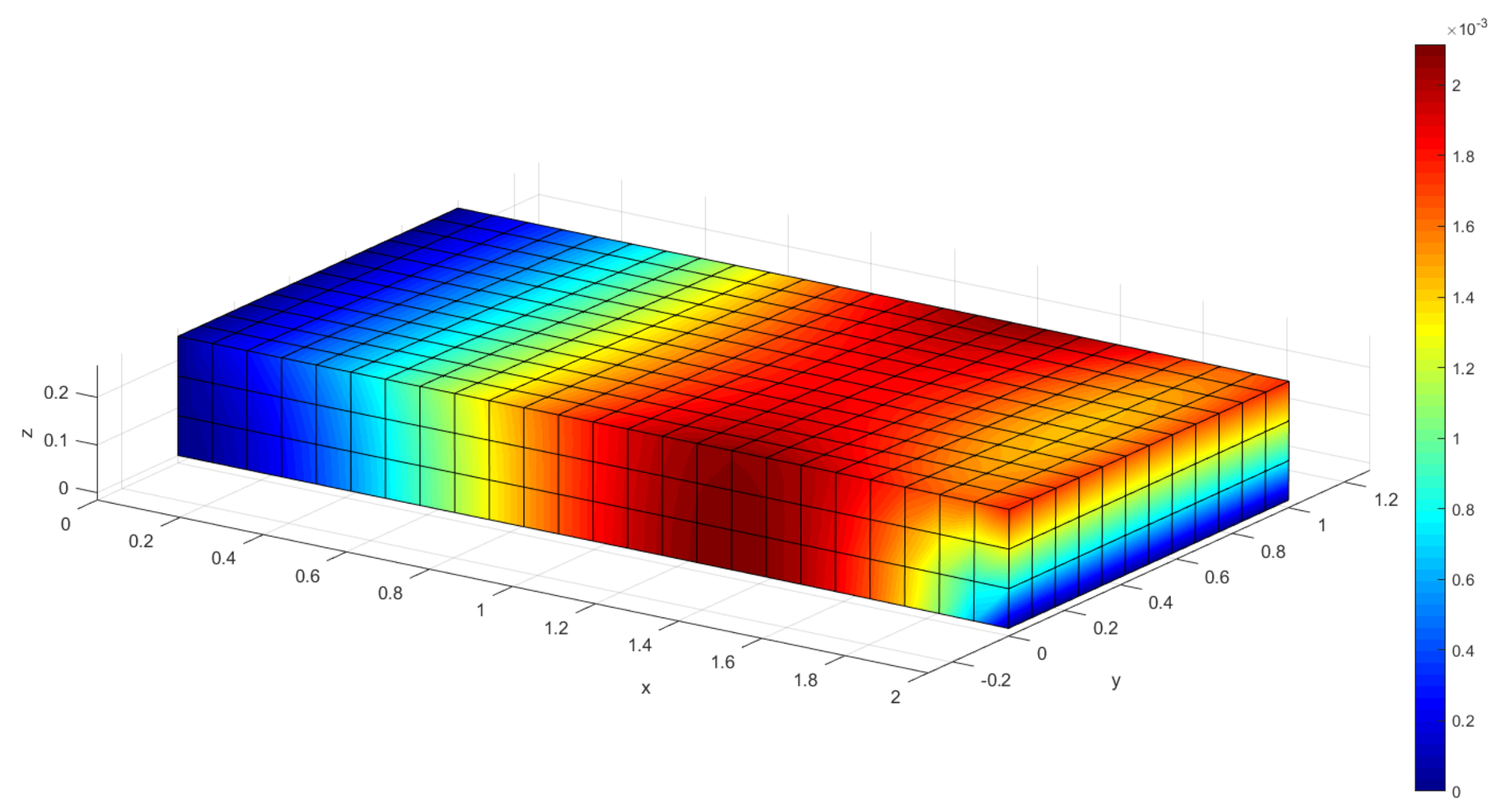
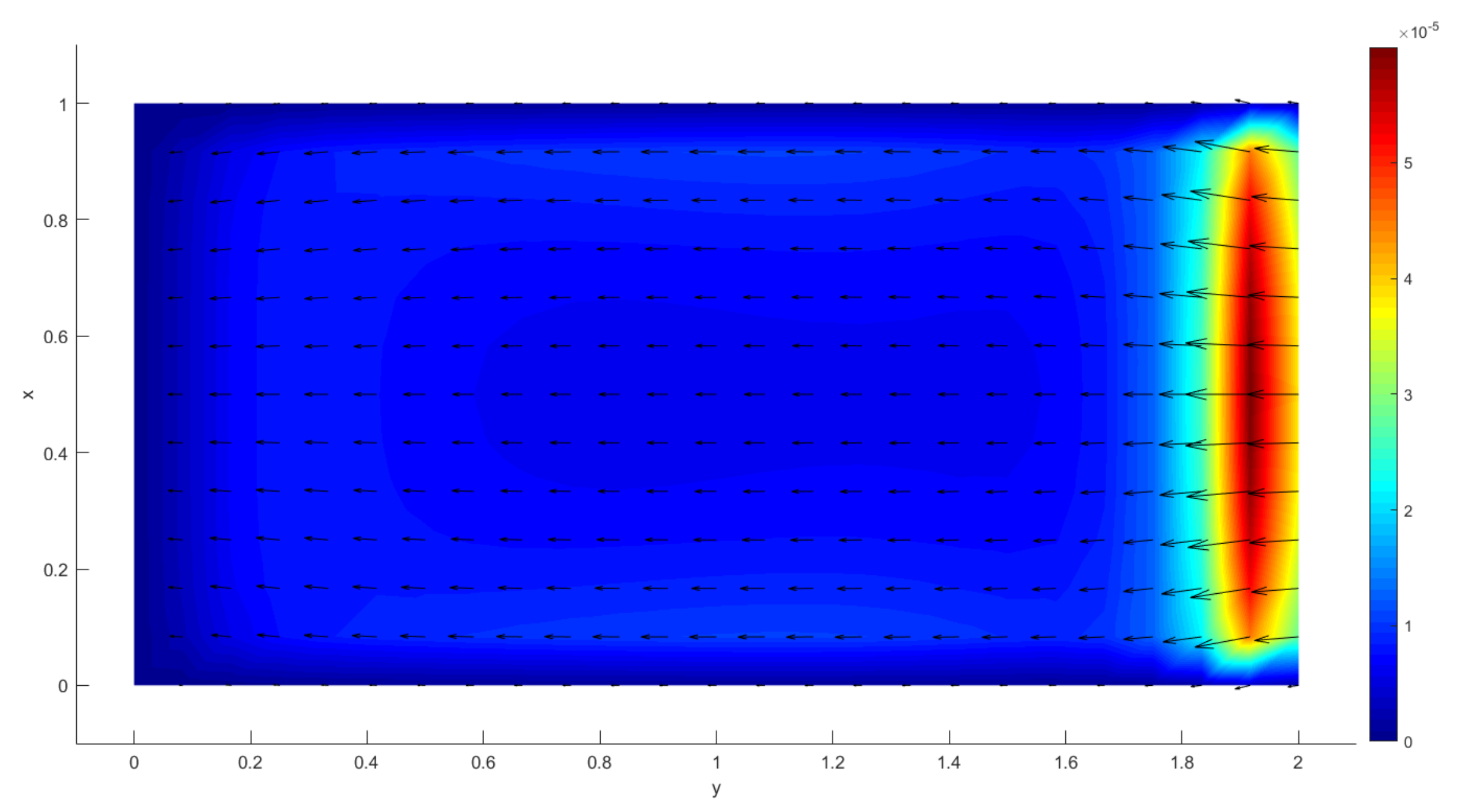
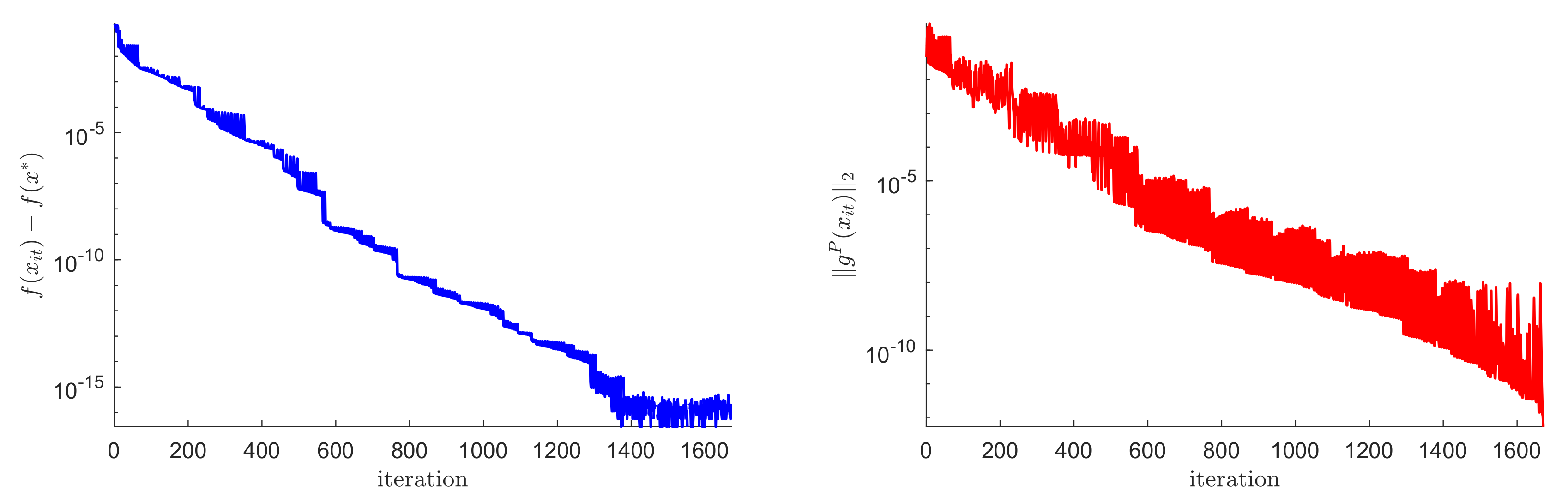
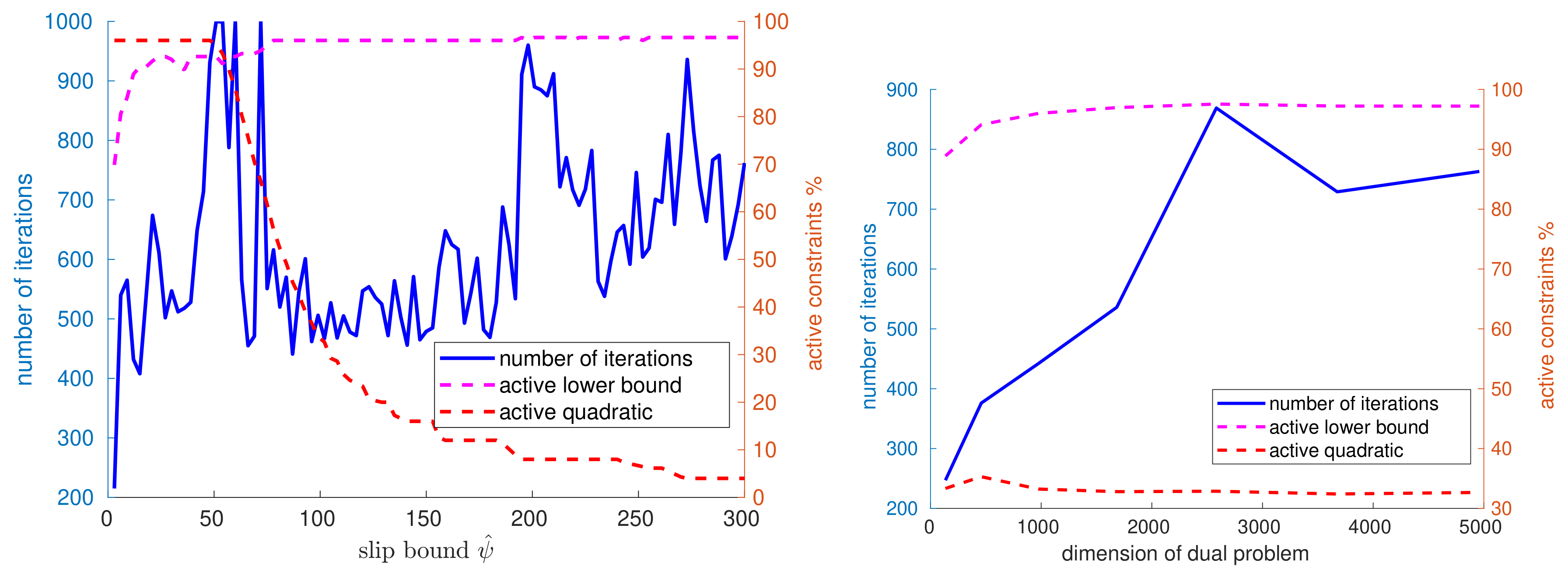
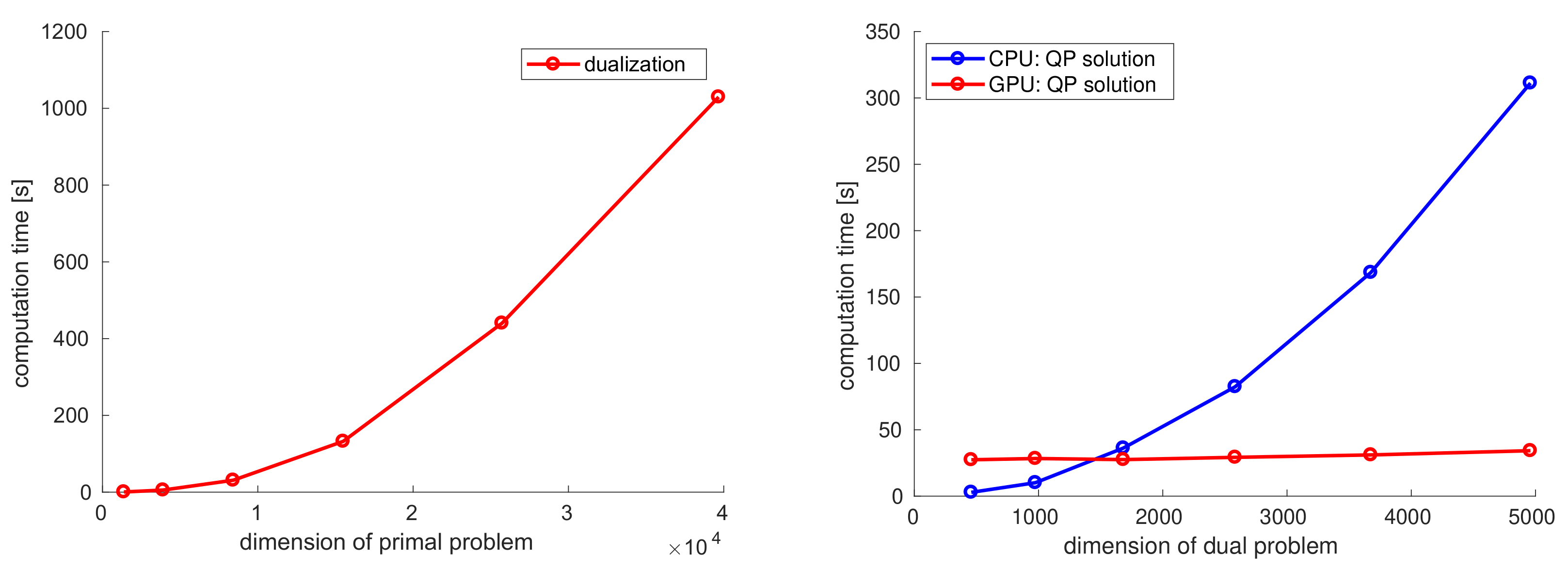
4. Results

We implement and solve the problem introduced in Section 2 using MATLAB. For the FEM discretization, we adopt the open-source library presented in [35]. Instead of evaluating and computing the inverse of the matrix in the dualization (13), we solve the system of linear equations with multiple right-hand side vectors. In MATLAB, we evaluate

$$\mathit{Y}=\mathit{K}\backslash \widehat{\mathit{B}};\mathit{A}=\widehat{\mathit{B}}\ast \mathit{Y};\mathit{b}={\mathit{Y}}^T\ast \mathit{f}.$$

(15)

In our numerical experiment, we consider steel brick with $E=2\times {10}^5\left[\mathrm{MPa}\right],\mu =0.33,\rho =7.85\times {10}^{-2}[\mathrm{kg}·{\mathrm{m}}^{-3}]$ of size $2\times 1\times 0.25\left[\mathrm{m}\right]$ in contact with the rigid obstacle. The displacement and the friction are caused by the force $F=[450,0,0]\left[\mathrm{MPa}\right]$. We consider given (Tresca) friction between the brick and the obstacle. To discretize the problem, we construct regular grid with the number of FEM nodes in axis equal to $N_x=25,N_y=13,N_z=4$. In total, we obtain $N=1300$ FEM nodes, the primal problem of dimension $n=3900$, the number of FEM nodes in contact $m_c=325$, and dual problem of 975 unknowns. The feasible set of dual problem is composed from 325 bound constraints and 325 separable quadratic constraints.

We implemented SPG-QP in MATLAB and set the parameters of the Armijo criterion to recommended values $m=10,\tau =0.9$ and initial approximation equal to the (feasible) zero vector. The first BB step-size is equal to steepest descent (Cauchy) step-size. We solved the problem (see Figure 3 and Figure 4) with the coefficient of friction (slip bound) ${\psi }_i=100S_i\left[\mathrm{MPa}\right]$, where $S_i$ is the contact surface corresponding to i-th node. Figure 5 demonstrates the decrease in the Euclidean norm of scaled projected gradient

$${\mathit{g}}_{\overline{\alpha }}^P\left(\mathit{x}\right):=\frac{1}{\overline{\alpha }}\left(P_{\mathsf{\Theta }}(\mathit{x}-\overline{\alpha }\nabla f\left(\mathit{x}\right))-\mathit{x}\right),$$

where $\overline{\alpha }\in \left(0,1/{\lambda }_{max}^{\mathit{A}}\right]$ (see [36]) and ${\lambda }_{max}^{\mathit{A}}$ is an upper estimation of the largest eigenvalue of the Hessian matrix $\mathit{A}$, which we compute using Gershgorin circle theorem. The norm of the projected gradient is used as a stopping criterion of the algorithm—i.e., we stop the algorithm if

$$\sqrt{\langle {\mathit{d}}_{\mathrm{it}},{\mathit{d}}_{\mathrm{it}}\rangle }<\epsilon .$$

In the SPG-QP algorithm, we decided to choose the largest possible ${\beta }_{\mathrm{it}}$ to perform the steps in as large a manner as possible. This approach has been suggested by Fletcher [33].

Figure 6 shows the dependency of the number of iterations on the value of friction coefficient (the size of quadratic constraints) and the size of the problem. In the first case, we solve the problem of dimension $N=1300$ and absolute error $\epsilon ={10}^{-6}$ for the norm of scaled projected gradient. In the second case, we are solving the problem with friction coefficient $\widehat{\psi }=100\left[\mathrm{MPa}\right]$ while varying the problem size using the same stopping criterion.

To improve the performance of the solution process, we utilize the GPU capability of the MATLAB. In our case, we compute on GeForce RTX 2080 Ti (4352 cuda cores, $11GB$ GDDR6 memory) and compare with Intel Core i9-7900X in MATLAB R2017a. Since our code is highly vectorized, the only prerequisite to perform the computation on GPU is to transfer the data using MATLAB command gpuArray. The overloaded MATLAB operations perform the matrix and vector operations on GPU. To analyze the performance of this approach, we fix the number of iterations of the SPG-QP algorithm to be equal to ${10}^4$ and measure the computational time. From the results presented in Figure 7, it is clear that the main computational bottleneck is not the solution of dual QP problem, but the dualization—i.e., the solution of the system of linear Equations (15). The results suggest the suitability of used gradient projected method on GPU; however, the problem has to be sufficiently large to efficiently use this architecture. The performance of SPG-QP is limited by the matrix–vector multiplication with dense dual Hessian matrix, which is the most time-consuming operation. Consequently, the time complexity of the method scales quadratically with the dimension of dual problem, see Figure 7.

5. Conclusions

We examined SPG-QP algorithm for solving the strictly convex QPQC in the solution of linear elasticity contact problem with given friction. The results demonstrate the suitability of the algorithm for this type of problems. However, with the increasing size of the primal problem, we observe the increase in the computational complexity of the corresponding Hessian matrix inverse (which has polynomial complexity, in general). We suggested using domain decomposition methods, for instance the Finite Element Tearing and Interconnecting method (FETI). This extension will be the topic of our upcoming research.