1. Introduction
In the last decade, resource shortages and environmental problems have received more and more attention in both academia and industry. With the rapid technological development, the replacement of electronic products is very fast, with more and more different models, which makes the used products difficult to deal with, causing a lot of waste of resources and pollution. Waste electrical and electronic equipment (WEEE), such as LCD TVs, mobile phones, and so on, contains a lot of toxic chemicals, which pollute land and groundwater and threaten human health and even survival. In order to solve the problems of resources and pollution, the concept of the extended warranty period (EPR) has been proposed to recycle the used products and incentivize the manufacturer to fulfill their social responsibility. EPR policies indicate that the producer’s responsibility not only refers to production, but should extend to the entire product life cycle, including product disposal, recycling, and remanufacturing processes. Many governments worldwide explore various forms of EPR polices with financial intervention. For instance, Japan has implemented the “Household Appliance Recycling Act” since 2002. Furthermore, the European Union (EU) enacted the Electronic Equipment Directive in 2003, which emphasizes penalties. In 2003, the Cailifornia government provided manufacturers of electronic products with pre-payments to promote remanufacturing and waste recycling, and intervened in the manufacturing through taxation; in addition, the recyclers were given subsidies for recycling of waste products. Based the above policies, China issued the Waste Electrical and Electronic Equipment Recycling Management Regulation in 2011, forcing manufacturers to collect used products actively. These polices are all penalty-based, which means that manufacturers will be penalized if they fail to achieve the recycling or reuse targets set by governments. However, this may motivate companies to just recycle the minimum required amount without any incentive to do more.
Recently, some researchers proposed a reward-penalty mechanism (RPM) [
1,
2], which combines penalty and rewards. If the actual quantity of recycling is higher than the target recycling quantity, the government will reward the manufactures; otherwise, the government penalizes the manufactures, which can urge enterprises to participate in recycling and remanufacturing activities of used products. Compared to other government policies, the RPM can save government expenditure and is more flexible. However, the current discussion is based on a traditional business setting, where only the physical channel is considered. Nowadays, e-commerce is playing an important role in businesses, and is changing the traditional supply chain structure [
3]. The online channel provides manufactures the opportunity to directly face the market and consumers. For instance, consumers can purchase all Apple products through the online store. Huawei has established VMall.com to sell its products online. Meanwhile, consumers who are unwilling to purchase online can buy the products through an authorized physical store offline. Establishing the dual-channel pattern model can shorten the distance between manufacturing and market demand, which can also enlarge the market demand through a service improvement. Moreover, dual channels can also help in waste collection and the sale of remanufactured/recycled products. Some manufactures have begun to collect used products to solve the concerns of resource consumption and environmental pollution using different channels. In Huawei’s VMall platform, it provides a “trade-in” program, which encourages consumers to return their used products when purchasing new ones by rewarding with discounts or credits. Meanwhile, some third-party companies are also undertaking the tasks of recycling used Huawei phones, such as LE RECYCLING, JD, and so on. Authorized offline stores of Huawei also collect used products and sell the products to the consumers who favor physical stores. Similarly, Apple has also established a dual-channel closed-loop supply chain to sell new products and collect used ones through online and offline stores.
Due to the prevalence of dual-channel closed-loop supply chains, it is worth investigating the effects of policies in this new setting. However, it is still unclear what the impact of the RPM on dual-channel closed-loop supply chains is. In this paper, we will explore how the RPM scheme affects the decisions of supply chain members and social welfare, as well as how the government should design the RPM scheme. In particular, we aim to answer the following questions:
- (1)
How does the government RPM scheme affect the optimal decisions of the supply chain members of the dual-channel supply chain?
- (2)
When should the manufacturer develop dual channels to sell products? How does the government RPM affect the relationship between the online channel and retailer channel?
- (3)
How does the government set the parameters of RPMs to maximize the total social welfare?
This paper has four contributions to the literature. First, to the best of our knowledge, this paper is the first to investigate the government RPM in the dual-channel closed-loop supply chain (CLSC), and the dual channel supply is prevalent in practice. Second, we analyze the impact of government financial intervention, and we are surprised to find that it can relieve the conflict of the online and offline channels. Third, we study the impact of the government RPM’s intensity on supply chain decisions, and find that as the government RPM intensity increases, the online price, retailer price, and wholesale price decrease and the collection rate increases. Fourth, we provide a method for the government to set the optimal RPM to maximize social welfare.
The remainder of the paper is organized as follows. In the next section, we provide a literature review related our research. We describe the problem and develop our model in
Section 3.
Section 4 solves the equilibrium decisions in the dual-channel CLSC. We provide the analysis of the impact of the government RPM on the total social welfare in
Section 5. How the government sets the optimal RPM to maximize the social welfare is analyzed in
Section 6.
Section 7 summarizes our main findings and implications, and outlines the limitations of our work and directions for future research.
2. Literature Review
Our work is related to three streams of literature. The first stream is about dual-channel supply chains, the second one is about CLSC management, and the last one is about the impact of governmental financial intervention on the decisions of CLSC supply chains.
Previous studies on the dual-channel supply chain (DCSC) mainly focus on pricing strategies, channel conflicts, and coordinate mechanisms. Chiang et al. (2003) [
4] study the role of direct marketing on the dual-channel supply chain. They developed a pricing model between a manufacturer and an independent retailer, and found that indirect marketing improved all the supply chain member’s profits. However, to the retailer, the introduction of indirect marketing can decrease the wholesale price set by the manufacture whilst increasing the whole market demand, which indicates the channel conflict between the online manufacturer and the offline retailer. Later, Huang and Swamianathan (2009) [
5] investigated the optimal pricing strategies in DCSCs based on a deterministic demand model where the channel demands depend on the sales price, which is widely accepted by supply chain researchers. Tsay and Agrawal (2004) [
6] constructed a model to capture the key attributes of a DCSC and proposed several ways to resolve channel conflict. Based on the above work, Dumrongsiri et al. (2008) [
7] considered a DCSC with demand impacted by both sales prices and service quality. Then, Chen et al. (2012) [
8] used a Stackelberg game model to study the pricing strategies and coordination mechanism between a dual-channel manufacturer and an offline retailer, where the manufacturer is the leader and the retailer is the follower. They find that two-part tariff and revenue sharing contracts can coordinate the dual-channel supply chain. Xu et al. (2014) [
9] studied the risk attitudes between the manufacturer and the retailer that can affect the supply chain members’ optimal decisions. They compared the risk-decentralized and centralized supply chain system under the mean-variance model, and found that the competition will decrease the supply chain efficiency. They established a dual-channel coordinating contract under a mean variance model to avoid risk. The previous literature proposes a lot of solutions for the dual-channel coordination mechanism to solve channel conflict, such as channel priority policy, service quality and decisions, complementary products, and so on [
3,
10,
11,
12]. However, the above literature mainly discusses the dual-channel construction, coordinate mechanism of channel conflict, and pricing strategies in the forward supply chain without considering the reverse supply chain.
The stream of literature about closed-loop supply chains focuses mainly on optimal decisions in both forward and reverse supply chains to improve the environmental performance and the profits of the supply chain members. A number of analyses have identified which player in the supply chain is the most efficient in collecting used products for the manufacturer [
13]. One of the well-known studies was developed by Savaskan et al. (2004) [
14], which compares three options of the manufacturer: manufacturer collections, retailer collections, and third-party collections. They find that ceteris paribus, the player who is closer to the customer, such as the retailer, is the most effective collector. In addition, they show that simple coordination mechanisms can be designed such that the collection effort of the retailer and the supply chain profits are attained at the same level as in a centrally coordinated system. Savaskan and Van (2006) [
15] further extend the model to include competition among retailers and show that the manufacturer should entrust the collection activities of used products to the retailers under certain conditions. Ferrer and Swaminathan (2006) [
16] study the decisions between the retailer and the manufacturer and their Nash equilibrium in the duopoly environment. They find that the remanufacturing activities are profitable for the manufacturer by reducing the unit cost of production from the recycled products. Based on the above closed-loop model and collecting modes, some researchers have studied the reward policy to improve the collection efficiency and the profits of the whole supply chain system. For instance, Saha et al. (2016) [
17] established a dual-channel supply chain model to study the system performance, pricing strategies, and remanufacturing policies of the supply chain members. They proposed a three-way discount mechanism for the manufacturer to incentivize the efficiency of the reward-driven supply chain in the dual-channel setting. Then, the research was expanded to the incentive strategies, revenue sharing, collection policies, and coordination mechanism between the manufacturer and the retailer [
18,
19,
20,
21]. However, this literature does not discuss how government intervention influences the pricing strategies, coordination mechanism, and collection activities of a supply chain system, which is the main focus of this paper. We will discuss the most efficient collection mode, the manufacturer collection model, and the third-party collection model under the government RPM scheme.
The last stream of literature is about the effects of government intervention on the CLSC members. Government also plays an important role in coordinating the supply chain members and improving the performance of collection activities to ease environment problems [
22]. Aksen et al. (2009) [
10] developed two bilevel programming models to guide the government to choose the appropriate mode to subsidize manufacturers, and to establish companies’ subsidization agreement with the government, who imposes a minimum collection rate on cores. Heydari et al. (2017) [
23] explored the government’s role in reverse and closed-loop chain coordination. They compared the effects of different government interventions on the supply chain members’ decisions, and also compared tax exemption and subsidies to the manufacturer and the retailer, respectively. They found that government intervention for the manufacturer is more effective and economic than for the retailer. In addition, they also concluded that the government subsidy is more feasible than the government tax exemption. The government intervention improves the profits and performance of the supply chain; meanwhile, the new product price for the customer is lower than the condition without government intervention, which indicates that it also benefits the consumers. Ma et al. (2013) [
24] consider the government subsidy from the customer side, which means that when the customer purchases the products, they can receive the subsidy paid by the government. This can improve the product quantity and market demand. They find that the government customer subsidy can improve the scale of the supply chain and the profits of all the supply members, and benefits the costumer. Zhang et al. (2018) [
2] studied the government RPM based on dynamic game theory and principle–agent theory. They proposed three game models, two competitive manufacturers, and a recycler without any RPM, with only a carbon emission RPM or the government collection RPM and carbon emission RPM simultaneously. They found that the carbon emission RPM decreases supply chain performance and collection quantity; meanwhile, the intensity of the government collection RPM increases the supply chain’s profit, the members’ profits, and the collection quantity. Therefore, they advise that the government should decrease the carbon emission RPM and increase the collection RPM appropriately in order to improve the environmental performance. Wang et al. (2019) [
25] compared the decisions of supply members in different power structures under a government reward–penalty mechanism. They found that the member that has more power in the supply chain always bears more responsibility with respect to the government reward–penalty mechanism. The above research mainly focuses on the simplest supply chain structure with one channel. Differently from the above, our work focuses on the model of a dual-channel closed-loop supply chain and the study of the impact of a government RPM.
From the review of the literature, we can see that although the government RPM’s influences on collection activities have been extensively studied, how the government RPM influences the dual-channel closed-loop supply chain is not clear. In addition, the existing literature does not discuss how the government should optimize the RPM scheme. To the best of our knowledge, this is the first work to explore the impact of a government RPM on a dual-channel supply chain and to provide a method of obtaining the optimal RPM settings for the government.
3. Problem Description and Model Setup
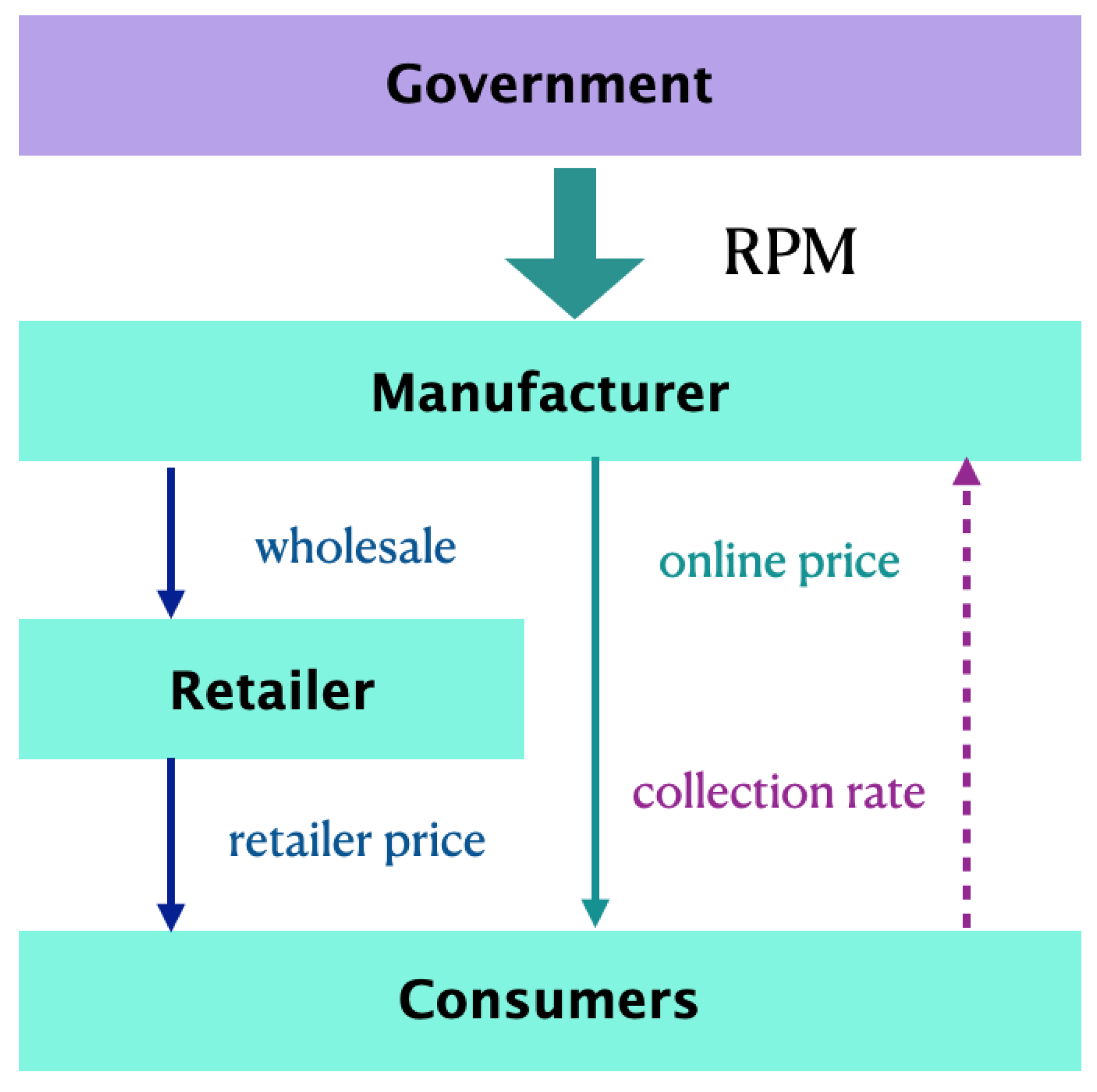
We consider a dual-channel closed-loop supply chain, as depicted in
Figure 1. The supply chain consists of one manufacturer and one retailer. The manufacturer produces new products with unit cost
c, and sells the product through two channels, the direct channel at price
and the retailer channel at wholesale price
w. The retailer then sells the product at price
to customers. The manufacturer can achieve residual value
s of the used products from consumers [
1,
15,
26]. Meanwhile, the government will implement an RPM scheme for the individual manufacturer according to its collection rate of the used products from consumers, which is consistent with Wang et al. [
25].
Following Huang and Swaminathan (2009) [
5], Xu et al. (2014) [
9], and Aksen et al. (2009) [
10], we assume that the corresponding market demand functions for the manufacturer and the retailer are expressed as
and
, where
denotes the online market demand, whilst
denotes the offline market channel market demand,
a is the potential market size, and
is consumers’ loyalty to online channel;
denotes the price elasticity for the online price and
r represents the degree to which the products sold through two channels are fungible. We assume
, which indicates that the effect of ownership price is greater than the effect of cross-price.
We only consider the scenario of the manufacturer collecting model. It has been proven that the direct collection model is the most profitable and efficient for the supply chain compared to entrusting third parties or retailers to collect used products. In practice, many companies have developed online platforms to collect used products from consumers, such as trade-in programs on Apple’s and Huawei’s websites. We denote the collection rate
, which indicates the effort of the manufacturer on the reverse channel. It will incur the cost
for the manufacturer to collect used products, where
k denotes a scaling parameter. We assume that the used product is at the end of the product life cycle for the consumers, and the manufacturer can extract the valuable components from the recycled products, which can be used for remanufacturing. The used product collection function can be expressed as
, which corresponds to the function used by Xie et al. (2018) [
20] and Savaskan et al. (2004) [
14].
The government implements an RPM scheme that requires a target collection rate to recycle/remanufacture. If the real collection rate is below the threshold, the manufacturer will be penalized at , while if above the threshold, the manufacturer will be awarded at . We name m the intensity of the government RPM.
We assume that there is a Stackelberg game between the manufacturer and the retailer. The decision process is as follows: (1) The government decides the recycling target and RPM intensity, then (2) the manufacturer determines its online sales price
, wholesale price
w, and the effort of collection
. (3) Then, the retailer purchases new products at wholesale
w from the manufacturer, and sells the products at price
to customers. In our model, we assume that all members are risk-neutral, without regard to risk preference or risk aversion. Their targets are to earn the maximum profits. The related parameters are shown in
Table 1.
Meanwhile, the superscript “*” denotes the optimal value of the variables and expressions, and the superscripts “MD” and “MT” respectively represent the parameters corresponding to the manufacturer collection model and the third-party collection model.
4. Model Analysis
We first consider the manufacturer collection model in a Stackelberg game framework between a dual-channel manufacturer and an offline retailer. Given the government RPM, the manufacturer first sets the wholesale price for the retailer, the online price for the consumer, and the collection effort. After observing the manufacturer’s wholesale price, the retailer sets the offline price. The profit functions of the dual-channel manufacturer and the offline retailer are as follows:
Using backward induction, we solve the model recursively based on their first-order condition. The optimal online price, online market volume, wholesale price, and collection rate of the dual-channel manufacturer as well as the offline retailing price are obtained and summarized in Proposition 1. All related proofs of
Section 4 are put in
Appendix A.
Proposition 1. We denote the critical value of the consumer’s loyalty to the online channel between the dual sales channel and single online sales channel of the manufacturer. When , the manufacturer should sell products through dual channels. When , the manufacturer should sell products only through the online channel, where . In this paper, we focus on the dual-channel supply chain under a government RPM to recycle used products. Therefore, we only provide the optimal decisions of the supply chain members as follows. In this section, we derive managerial insights by analyzing the optimal decisions of the supply chain members, which are shown in Proposition 1. To guarantee the convexity of the optimization, is required.
Proposition 2. We find that , which means that the critical value increases in m.
Proposition 2 suggests that the government RPM can improve the robustness of the dual-channel supply chain by extending the upper bound of the consumer’s preference for the direct sales channel. Moreover, the government improves the competitive advantage of the retailer channel.
Proposition 3. In the dual-channel supply chain, , , , , and . The optimal online price and retailer price decrease in m. The optimal collection rate, online market demand, and offline market demand increase in m.
Proposition 3 indicates that the government RPM scheme can effectively improve the collection rate of the used products from consumers. Meanwhile, with more residual value of the collected used products, the RPM scheme achieves the purpose of reducing unit production cost. The manufacturer enjoys a cost advantage in the forward channel, using a lower price to incentivize market demand of the new products both in the online and retail sales channels. Thus, the influence of government RPM on the reverse channel can improve the economic performance of the forward channel by moderating production cost.
In the following, we analyze the impact of the government RPM scheme on the manufacturer’s profitability.
Proposition 4. There exists a critical value of the government RPM intensity of the manufacturer’s profit. When , the profit of the manufacturer decreases in m; when , the profit of manufacturer increases in m. The value of is as follows. From Proposition 4, we find that is decided by . The government financial intervention should not hurt manufacturers’ profits. Thus, there exists a trade-off between this consideration and expenditure of the target collection rate of RPM. must be satisfied in the consideration. Therefore, we can obtain the maximum and optimal through . Interestingly, , which indicates the number relationship between the optimal RPM parameter settings of the intensity and target collection rate. Thus, if we can get the optimal value of RPM intensity while maximizing the total social welfare, we can obtain the optimal target collection rate of the RPM. Based on this, we provide a method of optimizing the RPM scheme of the whole closed-loop supply chain system.
Proposition 5. We find that , which indicates that the optimal collection rate of used products increases with α, the consumers’ loyalty to the online channel.
Proposition 5 indicates that the bigger the share of the online market, the higher the collection rate of the used products. In reality, the higher collection rate indicates the lower production cost with more residual value from the used products, which will also incur higher recycling cost. Meanwhile, without the retailer sharing the profit from selling new products, the manufacturer enjoys a more profitable operation structure in the online channel, which will increase the collection effort to further reduce production cost. Therefore, the effort in the reverse channel of the manufacturer will move into a more competitive direction of the forward channel.
5. Optimal Government Policy for the RPM
In this section, we further investigate how the government should design the RPM scheme including the intensity and the target quantity. While in reality, a government may have different goals when implementing financial intervention, thus we convert them into an index called total social welfare comprised of consumer surplus, supply chain profit, environmental impact and government expenditure.
5.1. Social Welfare
In this subsection, we assume that the government implements the RPM to maximize the total social welfare, which consists of consumer surplus, total profits of the supply chain system, environmental impact, and government RPM expenditure [
27].
(1) Consumer surplus (CS): Consumer surplus is an economic indicator to measure the benefits from the consumers’ perspective [
28,
29]. In the dual-channel supply chain, the total consumer surplus is divided into two parts: the online market and offline market consumer surplus. In the online channel, the largest online price is
, which is not disturbed by the retailer channel. The retailer is simply taking a share of the online market demand without affecting the highest online price accepted by consumers. From the perspective of online market segmentation, the online market demand
is a linear function of
. Thus, we denote
as consumer surplus of the online market, where
. Similarly, we denote
as consumer surplus of offline market, where
. Therefore, the total consumer surplus of the dual channel supply chain,
, can be calculated as follows:
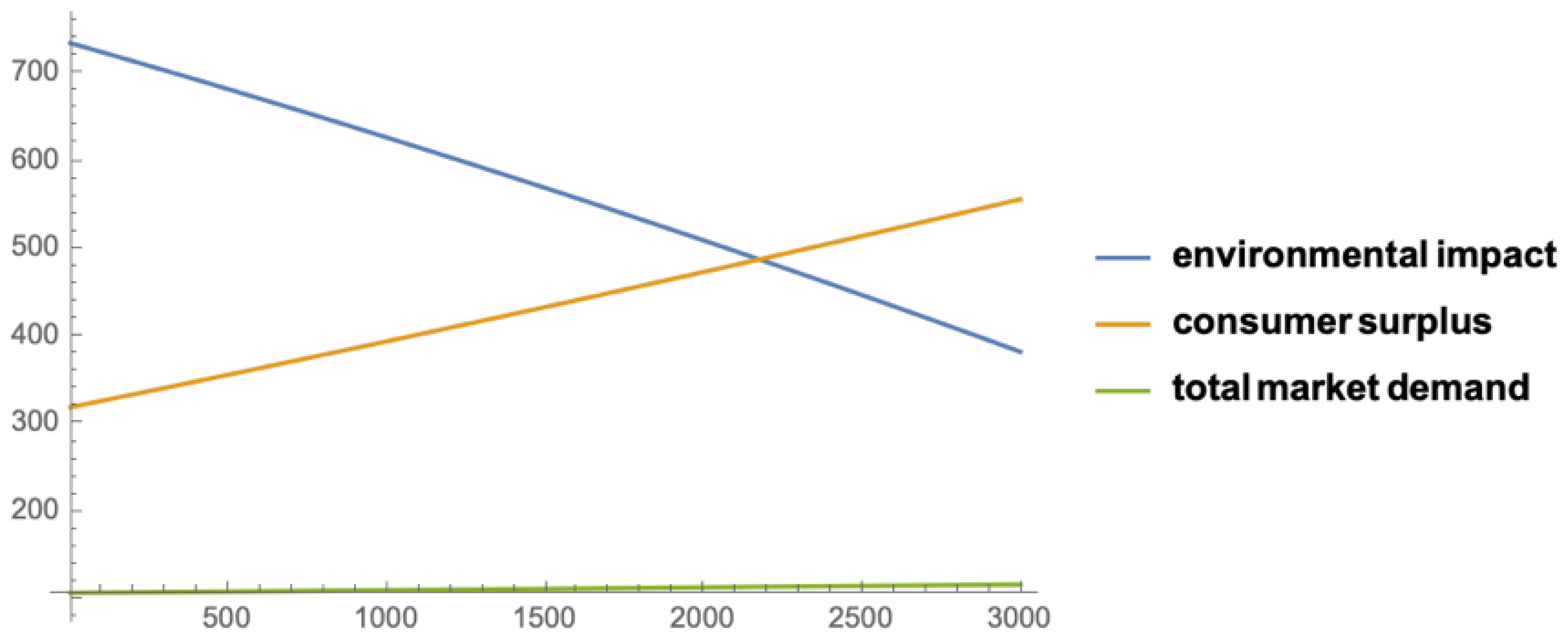
In order to analyze the consumer surplus, we develop a numerical example with the data in
Table 2, which describes the relationship between
m, the intensity of the government RPM, and consumer surplus. From
Figure 2, we can see that the consumer surplus is a monotonically increasing function of
m.
(2) Total profit of the supply chain: The total profit is equal to the manufacturer’s profit plus the retailer’s profit, which can be formulated as follows.
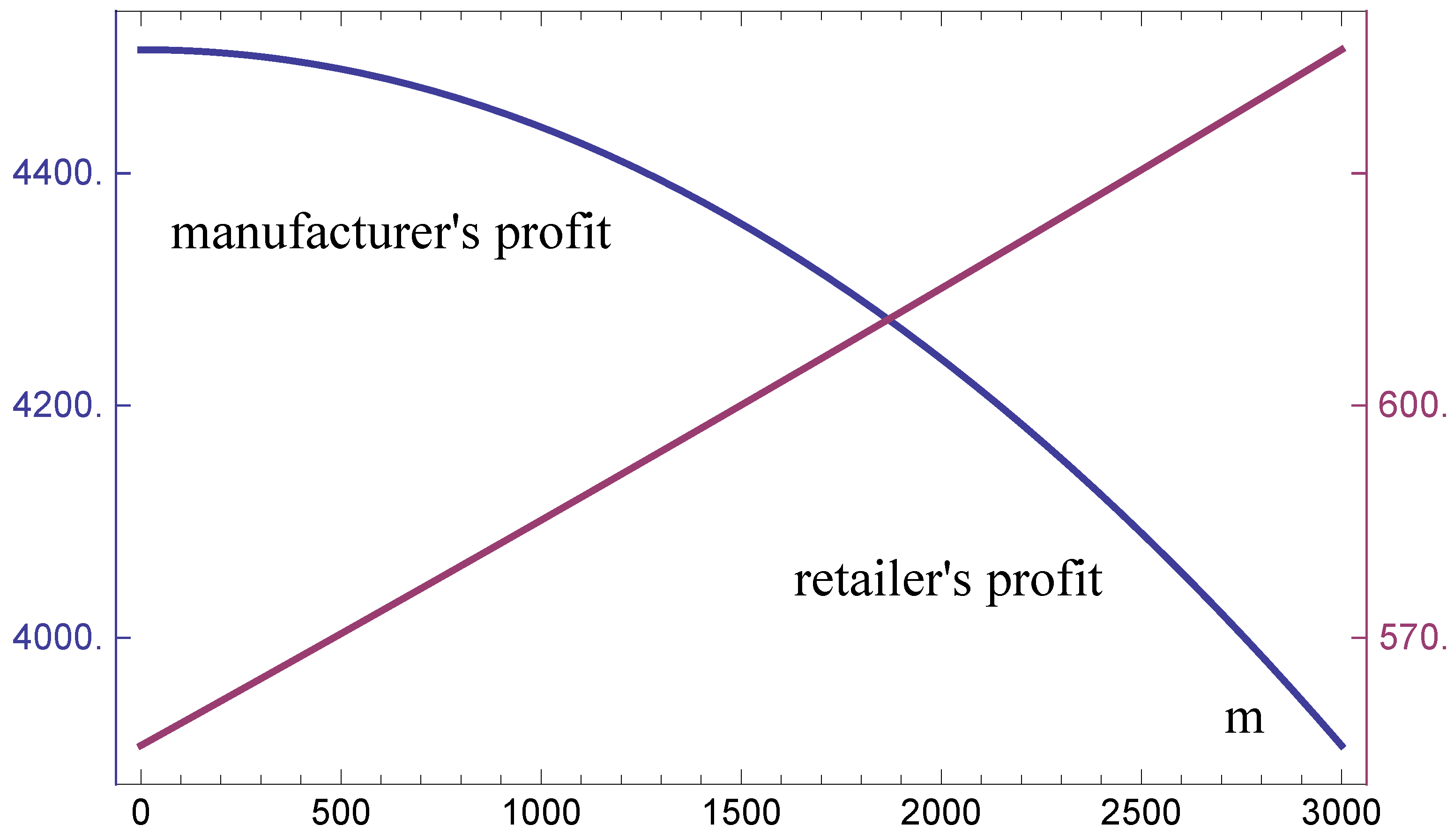
We also investigate how the government affects the manufacturer’s profit without RPM expenditure, as well as the retailer’s profit. In order to visually describe the number relationship of the profits with respect to
m, we develop a numerical example, as shown in
Figure 3. We can obtain that the profit of the manufacturer without government RPM expenditure decreases with
m, which indicates that the government RPM scheme incurs a higher collection cost. However, a higher collection rate will further decrease the production cost for the manufacturer, which will make the retailer enjoy lower wholesale. Thus, from
Figure 3, the retailer’s profit increases with
m. Interestingly, the RPM expenditure scheme has two effects that are opposite to the operation performance of the manufacturer and retailer. In other words, the government RPM can improve the competitive advantage of the retailer and promote stability of dual-channel supply chain, which is consistent with Proposition 2.
(3) Environmental impact (
E): Following [
30], we convert the environmental impact into monetary terms. We use
, a general parameter including pollution as well as resource and energy savings, to denote the unit monetary environmental impact of new products because the manufacturer can extract valuable components from used products recycled from consumers, which will be thrown away to the environment through a strict disposal process. In order to simplify the model’s parameters, we assume that the recycled products have no negative impacts on the environment. the environmental impact can be formulated as follows:
Through a numerical example, we further analyze how the intensity of the government RPM affects the total market demand and environmental impact, as shown in
Figure 2. We can obtain that the total market demand increases with
m and the negative environmental impact decreases with
m, which is induced by the higher collection rate of the used products encouraged by the government RPM scheme. Therefore, the government can improve market performance and decrease the environmental impact through the RPM scheme, which is what government financial intervention is all about.
(4) Government expenditure (
G): The government designs the RPM for enterprises to protect the environment, which incentivizes the manufacturer to collect used products through financial intervention. From the public welfare perspective, the government is only concerned with overall externalities and government surplus. The government expenditure on RPM can be formulated as follows [
25].
Finally, the total social welfare is formulated as follows, which is consistent with the literature [
31].
Before getting the optimal government RPM, we first analyze the optimal intensity of the RPM
m to maximize the performance of the total social welfare. Then, corresponding to Proposition 4, we can obtain the optimal target quantity of the RPM
to maximize the profits of the system supply chain and the approximate government financial expenditure. Therefore, we can get the optimal RPM decision of the government.
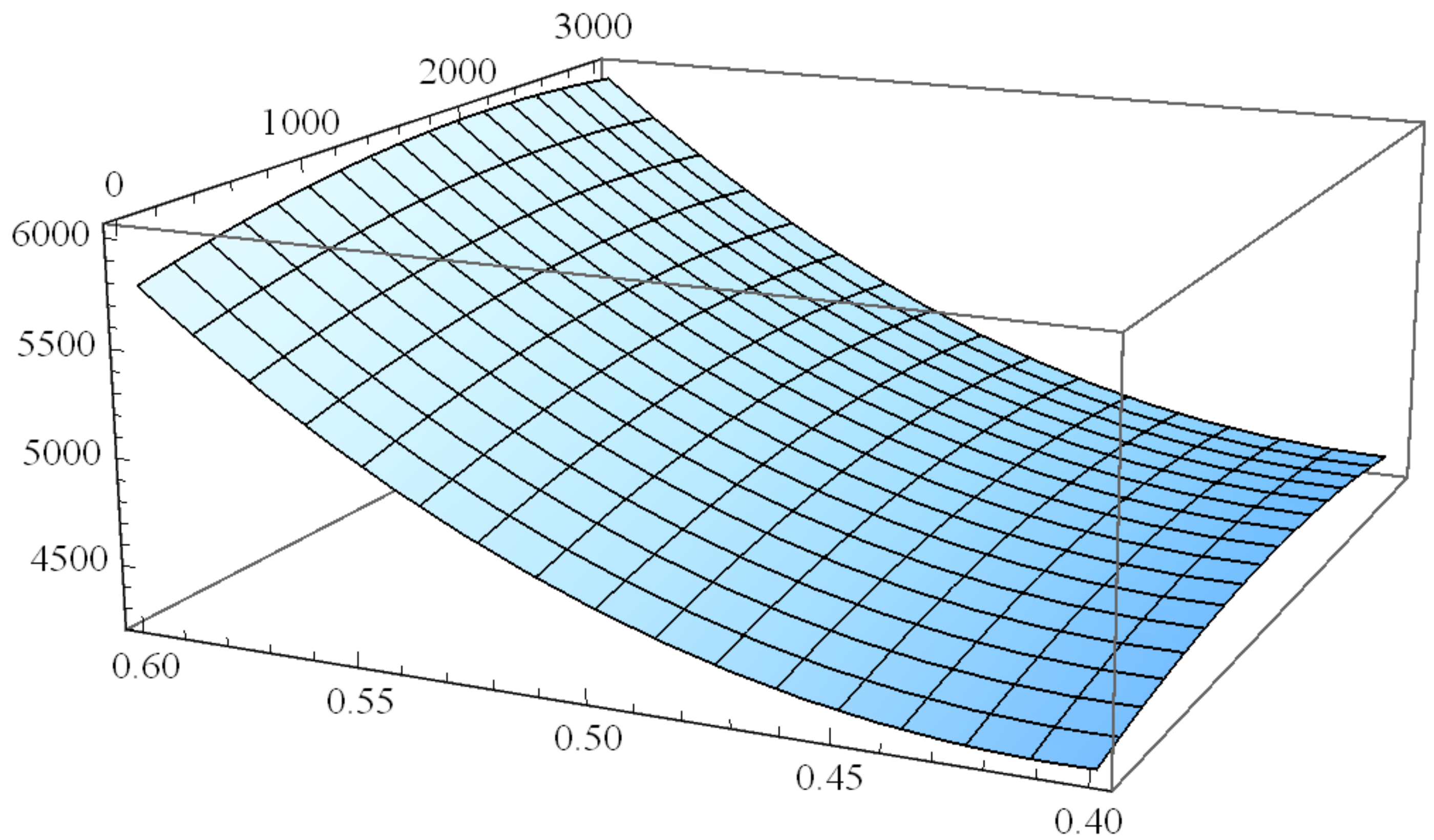
5.2. The Impact of Government RPM Intensity on Total Social Welfare
In this subsection, we investigate the impact of government RPM intensity on the total social welfare. However, for the optimal , it is too difficult to get an analytical solution. Therefore, we use a numerical analysis to illustrate the existence and value of the optimal . In addition, a sensitive analysis of the proposed model parameters is conducted. Meanwhile, we also investigate the models with different values of consumer loyalty to the online sales channel. The following parameter values are used for the analysis: , , , , , , , , and .
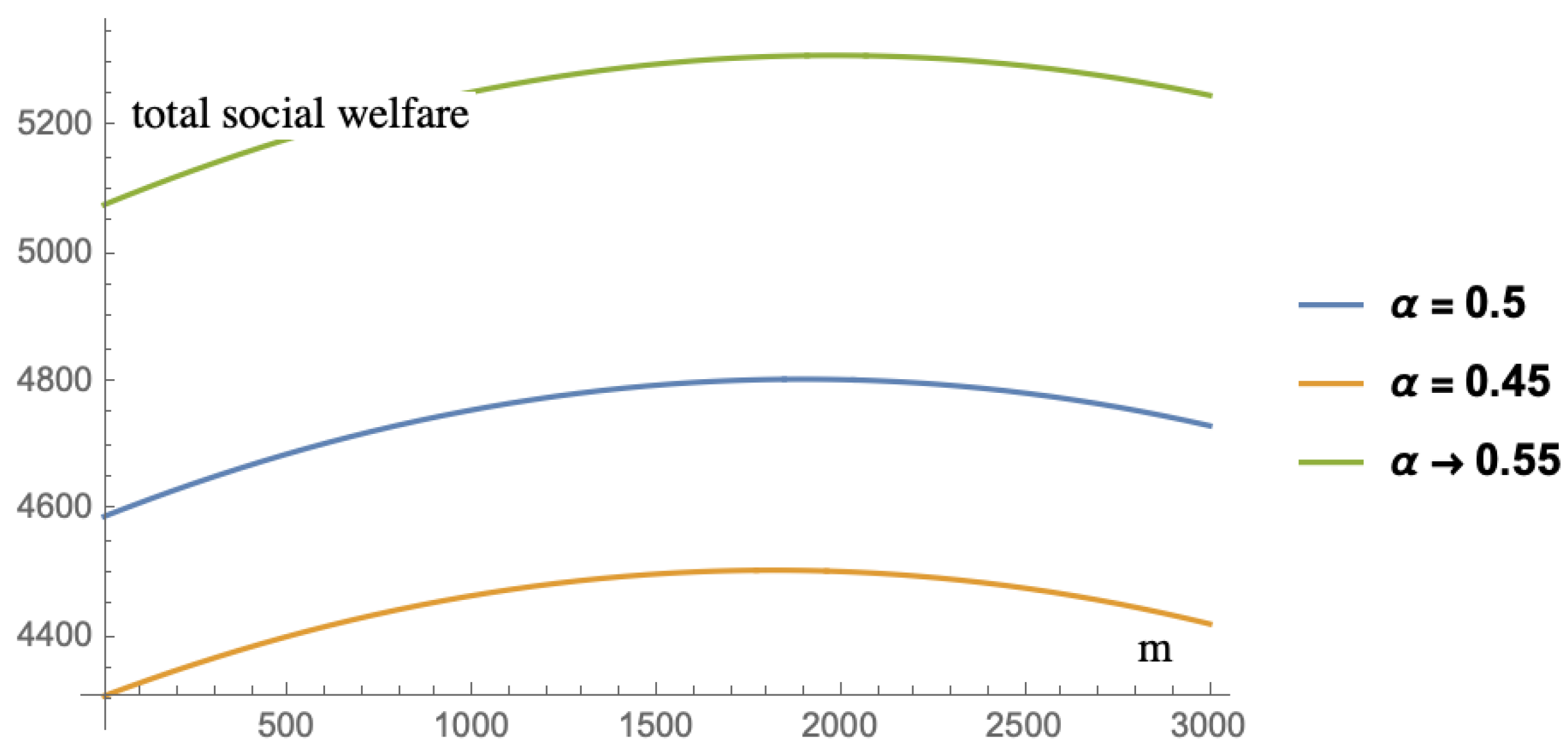
Figure 4 shows the change of total social welfare with respect to the government RPM intensity. We can see that the total social welfare is a concave function of
m. Therefore, there exists an optimal
to maximize the social welfare. The optimal
means that the government RPM makes the optimal intensity decision for the supply chain system, environmental impact, consumer surplus, and the government expenditure. The interpretation of this finding is that the RPM promotes the increase of social welfare by collecting used products, such that the production cost of manufacturers proposed in Proposition 4 and environmental impact are decreased, while the intensity of the RPM increases first. However, when
m exceeds the peak of the curve, the RPM will not increase this effect. In addition, we also find that the consumer loyalty to the online channel will change the position of the extreme value of the curve, which contains the position of the
and the maximum value of social welfare. In order to find out how the consumer loyalty affects the curve, we further study the relationships among the total social welfare, the intensity of the government RPM, and the consumer loyalty to the online channel using the above data.
It can be seen from
Figure 5 that the value of
decreases as
s increases, which means that when the consumers prefer to buy the products online more and more, the government can make the intensity of the RPM lower. In addition, the total social welfare falls as
s increases, which indicates that the online channel will bring lower social welfare and the dual channels will bring lower social welfare, which is caused by the competition and channel conflict.
6. Optimal Design of the RPM Scheme
In this section, we show how the government should design the RPM scheme. From
Section 5.2, we can determine the optimal
, where
, and the social welfare reaches the maximum value. Then, from Proposition 4,
, so we can get the optimal
, the target collection rate of the government RPM. Therefore, we have achieved the optimal decision set, (
,
). Under this condition, government financial intervention maximizes the social welfare and the profits of the supply chain system with approximate government expenditure.
In order to show the process of getting the optimal government RPM visually, we provide numerical examples with the parameters in
Table 2. Through the numerical analysis, we get the government RPM with different consumer loyalty to the online channel, which is shown in
Table 3. In addition, for the government’s adoption of the optimal RPM to incentivize the enterprise to collect used products and maximize the total social welfare in the dual-channel CLSC, the optimal decisions and profits of the supply chain members are provided in
Table 4.
7. Conclusions and Future Research
This paper establishes a closed-loop supply chain model considering the financial intervention of the government’s RPM in the recycling activities of enterprises for the first time. We analyze the influence of the government’s RPM on the optimal decisions of the members of the closed-loop supply chain and the two forward channels. We found that the government’s RPM enhances the stability of the dual-channel supply chain and can increase the recovery rate. In addition, we provide an optimal RPM scheme for the government to maximize the social welfare of the whole supply chain system.
This paper has not only important theoretical significance, but also has important practical guidance. In the aspect of theory, this paper extends the research on closed-loop supply chain management. Previous studies mainly discussed the influence of government financial intervention on single-channel decision-making and social welfare. However, companies at the present stage have developed dual-channel sales of products. For example, Huawei has set up a Huawei mall to sell products online while entrusting offline retail-experience stores to sell products. In the Huawei mall, consumers can participate in recycling activities, such as a trade-in program. In fact, this business model has become widely adopted by electronic product enterprises. Therefore, it is necessary to study the efficiency of the government RPM in this business model and its impact on social welfare, and we find that the government can reduce the channel conflict between the manufacturer and the retailer by strengthening the profits of the reverse channel. Furthermore, we provide a method to achieve the optimal RPM scheme, where we first calculated the optimal RPM intensity using social welfare, and then derived the amount of recovery according to the intensity.
Our research is not exempt from limitations that require further investigation. First, we assume that all the players have full information, which is not the case in practice. Therefore, further study should explore the situation of information asymmetry among the supply chain members. Second, we assume that the demand function is deterministic. Considering the fuzziness, uncertainty, and quality sensitivity associated with market demand, uncertainty should be modeled in future research. Third, we assume that the recycled/remanufactured products have no difference from the new products with new materials, which could be relaxed to model consumers’ different perceptions in future research.