Analysis of Tail Dependence between Sovereign Debt Distress and Bank Non-Performing Loans
Abstract
1. Introduction
2. Econometric Methodology
2.1. Granger Causality Tests
2.2. Kendall’s Tau Coefficient
2.3. Copula Function and Tail Dependence
- (1)
- The domain of is [0,1] × [0,1]
- (2)
- C(u, 1) = C(1, u) = u, C(v, 1) = C(1, v) = v, ∀u, v ∈ [0,1]
- (3)
- has zero fundamentals and is incremented in two dimensions
2.3.1. Student’s t Copula
2.3.2. Clayton Copula
2.3.3. Joe Copula
2.4. Gaussian Copula Regression Method
3. Definition of Variables and Data Description
3.1. Variables and Data Description
3.2. Descriptive Statistics
4. Empirical Results and Discussion
4.1. Granger Results
4.2. Kendall’s Tau Results
4.3. Copula Results
4.4. Gaussian Copula Regression Method Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Monetary Fund. Sovereign Debt Restructurings and the Domestic Economy Experience in Four Recent cases; Policy Development and Review Department: Washington, DC, USA, 2002. [Google Scholar]
- Reinhart, C.M.; Rogoff, K.S. From financial crash to debt crisis. Am. Econ. Rev. 2011, 101, 1676–1706. [Google Scholar] [CrossRef]
- Moody’s Analysis. European Sovereign Debt and Banking Crises: Contagion, Spillovers and Causality; Moody’s Investors Service: New York, NY, USA, 2014. [Google Scholar]
- Alter, A.; Beyer, A. The dynamics of spillover effects during the European sovereign debt turmoil. J. Bank Financ. 2014, 42, 134–153. [Google Scholar] [CrossRef]
- Angeloni, C.; Wolff, W. Are banks affected by their holdings of government debt? Int. Econ. Rev. 2012, 7, 1–23. [Google Scholar]
- Zaghini, A. The Impact of Sovereign Credit Risk on Bank Funding Conditions; CGFS Papers; Bank for International Settlement: Basel, Switzerland, 2011; ISBN 92-9131-879-5. [Google Scholar]
- Kleinow, J.; Moreira, F. Systemic risk among European banks: A copula approach. J. Int. Financ. Mark. Inst. Money. 2016, 42, 27–42. [Google Scholar] [CrossRef]
- Reinhart, C.M.; Rogoff, K.S. The Aftermath of Financial Crises. Am. Econ. Rev. 2009, 99, 466–472. [Google Scholar] [CrossRef]
- Reinhart, C.M.; Rogoff, K.S. Growth in a time of debt. Am. Econ. Rev. 2010, 100, 573–578. [Google Scholar] [CrossRef]
- Louzis, D.P.; Vouldis, A.T.; Metaxas, V.L. Macroeconomic and bank-specific determinants of non-performing loans in Greece: A comparative study of mortgage, business and consumer loan portfolios. J. Bank. Finan. 2012, 36, 1012–1027. [Google Scholar] [CrossRef]
- Makri, V.; Tsagkanos, A.; Bellas, A. Determinants of non-performing loans: The case of eurozone. Panoeconomicus 2014, 61, 193–206. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Ugolini, A. Systemic risk in European sovereign debt markets: A CoVaR-copula approach. J. Int. Money Finan. 2015, 51, 214–244. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Ugolini, A. A vine-copula conditional value-at-risk approach to systemic sovereign debt risk for the financial sector. N. Am. Econ. Financ. 2015, 32, 98–123. [Google Scholar] [CrossRef]
- Berger, A.N.; De Young, R. Problem loans and cost efficiency in commercial banks. J. Bank. Financ. 1997, 21, 849–870. [Google Scholar] [CrossRef]
- Ellul, A.; Yerramilli, V. Stronger risk controls, lower risk: Evidence from U.S. bank holding companies. J. Financ. 2013, 68, 1757–1803. [Google Scholar] [CrossRef]
- Hu, J.L.; Li, Y.; Chiu, Y.H. Ownership and nonperforming loans: Evidence from Taiwan’s banks. Dev. Econ. 2010, 42, 405–420. [Google Scholar] [CrossRef]
- Vithessonthi, C. Deflation, bank credit growth, and non-performing loans: Evidence from Japan. Int. Rev. Financ. Anal. 2016, 45, 295–305. [Google Scholar] [CrossRef]
- Maddaloni, A. Bank risk-taking, securitization, supervision, and low interest rates: Evidence from the euro-area and the u.s. lending standards. Rev. Financ. Stud. 2010, 24, 2121–2165. [Google Scholar] [CrossRef]
- Klein, N. Non-Performing Loans in CESEE: Determinants and Impact on Macroeconomic Performance; IMF Working Paper No. 13/72; International Monetary Fund: Washington, DC, USA, 2013. [Google Scholar]
- Ozili, P.K. Non-performing loans and financial development: New evidence. J. Risk Financ. 2019, 20, 1526–5943. [Google Scholar] [CrossRef]
- Beck, R.; Jakubik, P.; Piloiu, A. Key determinants of non-performing loans: New evidence from a global sample. Open Econ. Rev. 2015, 26, 525–550. [Google Scholar] [CrossRef]
- Kuzucu, N.; Kuzucu, S. What Drives Non-Performing Loans? Evidence from Emerging and Advanced Economies during Pre- and Post-Global Financial Crisis. Emerg. Mark. Financ. Trade 2019, 55, 1694–1708. [Google Scholar] [CrossRef]
- Kaminsky, G.L.; Reinhart, C.M.; Végh, C.A. When it rains, it pours: Procyclical capital flows and macroeconomic policies. NBER Macroecon. Ann. 2004, 19, 11–53. [Google Scholar] [CrossRef]
- Clichici, D.; Tatiana, C. The impact of macroeconomic factors on non-performing loans in the republic of moldova. J. Financ. Monet. Econ. 2014, 1, 73–78. [Google Scholar]
- Anastasiou, D.; Louri, H.; Tsionas, E.G. Determinants of non-performing loans: Evidence from euro-area countries. Financ. Res. Lett. 2016, 18, 116–119. [Google Scholar]
- Koju, L.M.; Koju, R.; Wang, S.Y. Macroeconomic and Bank-Specific Determinants of Non-Performing Loans: Evidence from Nepalese Banking System. J. Cent. Bank. Theory Prac. 2018, 7, 111–138. [Google Scholar] [CrossRef]
- Ghosh, A. Banking-industry specific and regional economic determinants of non-performing loans: Evidence from us states. J. Financ. Stab. 2015, 20, 93–104. [Google Scholar] [CrossRef]
- Espinoza, R.A.; Prasad, A. Nonperforming Loans in the GCC Banking System and Their Macroeconomic Effects; IMF Working Papers; International Monetary Fund: Washington, DC, USA, 2010. [Google Scholar]
- Us, V. Dynamics of non-performing loans in the Turkish banking sector by an ownership breakdown: The impact of the global crisis. Financ. Res. Lett. 2016, 20, 109–117. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.M.; Kim, J.M. Sustainable Visual Analysis for Bank Non-Performing Loans and Government Debt Distress. Sustainability 2020, 12, 131. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Miguel, P.; Sansonavarro, M. Granger causality between debt and growth: Evidence from oecd countries. Int. Rev. Econ. Financ. 2015, 35, 66–77. [Google Scholar]
- Laszlo, K. Exports and growth: Granger causality analysis on OECD countries with a panel data approach. Econ. Model. 2006, 23, 978–992. [Google Scholar]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Anastasopoulos, A.; Segot, T.L. Testing for financial contagion: New evidence from the Greek crisis and yuan devaluation. Res. Int. Bus. Financ. 2018, 45, 499–511. [Google Scholar] [CrossRef]
- Fung, W.K.; Hu, Y.Q. Probability and Statistics. In Statistical DNA Forensics: Theory, Methods and Computation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kaminsky, G.L.; Pablo, V.G. Systemic and idiosyncratic sovereign debt crises. J. Eur. Econ. Assoc. 2016, 14, 80–114. [Google Scholar] [CrossRef]
- Kim, J.M.; Jung, H. Can asymmetric conditional volatility imply asymmetric tail dependence? Econ. Model. 2017, 64, 409–418. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Walpole, R.E.; Myers, R.H. Probability and statistics for engineers and scientists. Technometrics 2006, 74, 348–349. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Joe, H. Multivariate models and dependen dence concepts. Technometrics 1997, 40, 353. [Google Scholar]
- He, Y.; Zhang, X.; Zhang, L. Variable selection for high dimensional gaussian copula regression model: An adaptive hypothesis testing procedure. Comput. Stat. Data Anal. 2018, 124, 132–150. [Google Scholar] [CrossRef]
- Kim, J.M.; Jung, H. Relationship between oil price and exchange rate by fda and copula. Appl. Econ. 2018, 50, 2486–2499. [Google Scholar] [CrossRef]
- Masarotto, G.; Varin, C. Gaussian Copula Regression in R. J. Stat. Softw. 2017, 77, 1–26. [Google Scholar] [CrossRef]
- Song, P.X.K. Multivariate Dispersion Models Generated from Gaussian Copula. Scand. J. Stat. 2000, 27, 305–320. [Google Scholar] [CrossRef]
- Masarotto, G.; Varin, C. Gaussian Copula Marginal Regression. Electron. J. Stat. 2012, 6, 1517–1549. [Google Scholar] [CrossRef]
- Rime, B.; Mathur, I. Capital requirements and bank behaviour: Empirical evidence for Switzerland. J. Bank Financ. 2001, 25, 789–805. [Google Scholar] [CrossRef]
- Were, M.; Wambua, J. What factors drive interest rate spread of commercial banks? empirical evidence from Kenya. Rev. Deve. Financ. 2014, 4, 73–82. [Google Scholar] [CrossRef]
- Afonso, A.; Jalles, J.T. Fiscal volatility, financial crises and growth. Appl. Econ. Lett. 2012, 19, 1821–1826. [Google Scholar] [CrossRef]
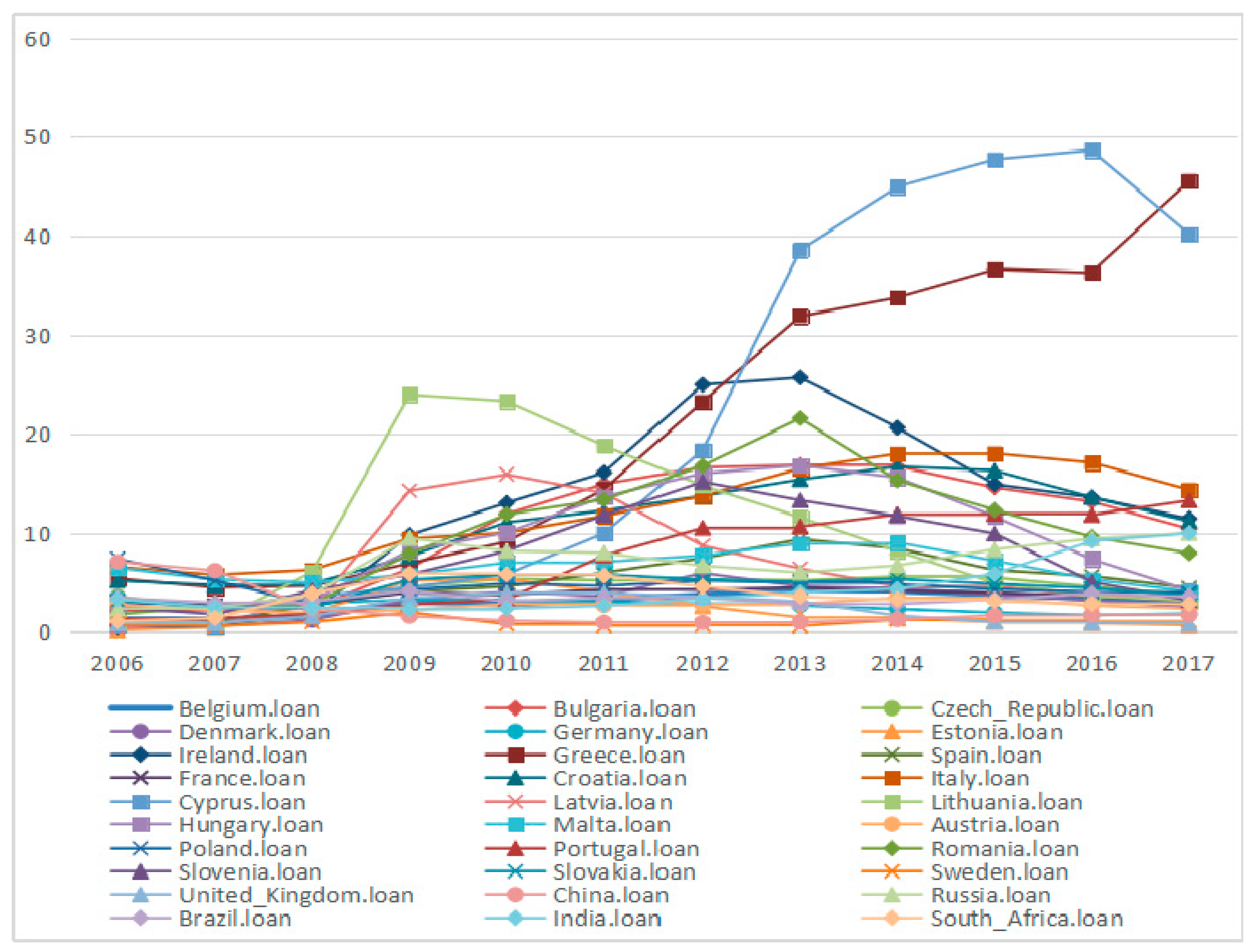
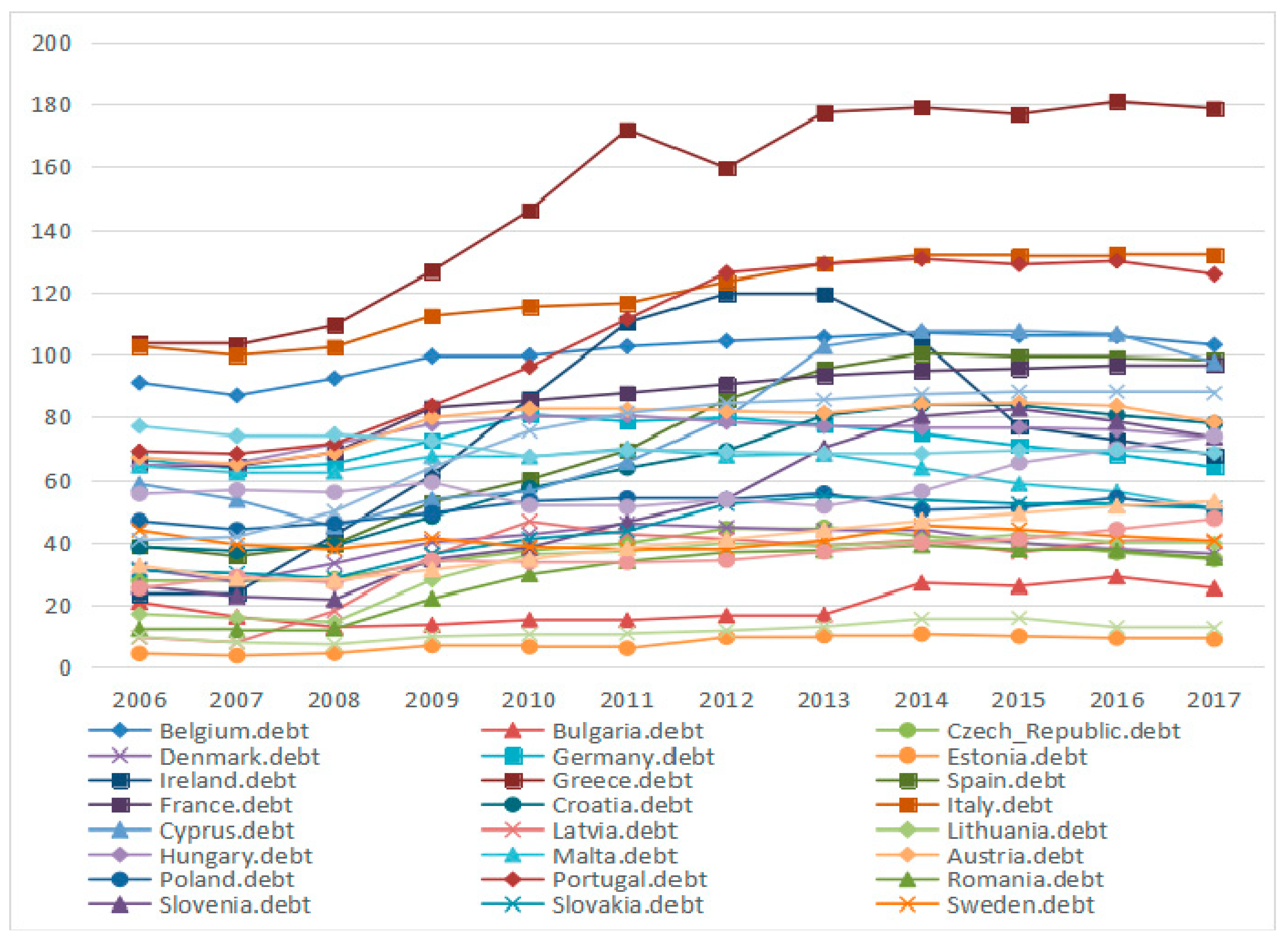
| Variable | Definition | Source |
|---|---|---|
| Non-performing loans (NPLs) | The ratio of non-performing loans to total loans. | Eurostat, International Monetary Fund (IMF) |
| Sovereign debt | The general government gross debt to GDP ratio. | Eurostat, IMF |
| Gross domestic product (GDP) | GDP has a significant negative impact on NPLs, because the growth of GDP creates more jobs, which increases income of borrowers and reduces NPLs. Therefore, the level of NPLs will rise when the economy slows down. | IMF |
| Inflation rate | It is represented by a percentage change in regional consumer price index (CPI) and low liquidity level is conducive to economic growth, while high liquidity rate weakens borrowers’ solvency by reducing their real income, thus increasing NPLs. | IMF |
| Government fiscal expenditure | Government fiscal expenditure refers to the funds expended by the government. Economic growth through fiscal expenditure and government investment, as well as more central government deficits and money supply has been greatly limited after the economic crisis. Meanwhile, insufficient fiscal revenue will offset the growth of tax revenue. When the government faces a budget deficit, it will generate public debt. | IMF |
| Government fiscal revenue | Government revenue is the income available to fund the activities of a government. High fiscal revenue usually means the government controls a large share of financial resources has the ability to repay bank loans, while fiscal distress implies that fiscal revenue cannot satisfy government’s expenditures. | IMF |
| Mean | Median | Minimum | Maximum | St.D | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|
| Belgium | 2.9642 | 3.1900 | 1.1600 | 4.2400 | 1.0694 | −0.6117 | 2.0734 |
| Bulgaria | 10.7067 | 12.545 | 2.1000 | 16.8800 | 5.9127 | −0.4996 | 1.6586 |
| Czech Republic | 4.4858 | 4.8950 | 2.3700 | 5.6100 | 1.1010 | −0.7795 | 2.2255 |
| Denmark | 3.1392 | 3.4800 | 0.4000 | 5.9500 | 1.6898 | −0.3115 | 2.2255 |
| Germany | 2.6633 | 2.7800 | 1.6900 | 3.4000 | 0.5744 | −0.4537 | 1.9127 |
| Estonia | 2.1083 | 1.4300 | 0.2000 | 5.3800 | 1.8157 | 0.8590 | 2.2676 |
| Ireland | 12.7833 | 13.3300 | 0.5300 | 25.7100 | 8.6392 | −0.0637 | 2.0023 |
| Greece | 21.0450 | 18.8500 | 4.5000 | 45.5700 | 15.1776 | 0.2151 | 1.4648 |
| Spain | 5.0642 | 5.1200 | 0.7000 | 9.3800 | 2.7234 | −0.1510 | 2.1743 |
| France | 3.6867 | 3.8700 | 2.7000 | 4.5000 | 0.6312 | −0.3824 | 1.6509 |
| Croatia | 11.0725 | 11.7350 | 4.7500 | 16.7100 | 4.4540 | −0.3116 | 1.6736 |
| Italy | 12.3108 | 12.7450 | 5.7800 | 18.0600 | 4.6595 | −0.1378 | 1.5490 |
| Cyprus | 21.9842 | 14.1800 | 0.6000 | 48.6800 | 20.1756 | 0.2544 | 1.2686 |
| Latvia | 6.6000 | 4.6200 | 0.5000 | 15.9300 | 5.4205 | 0.6585 | 1.9852 |
| Lithuania | 10.0508 | 7.1350 | 1.0000 | 23.9900 | 8.3663 | 0.5788 | 1.8944 |
| Hungary | 9.3150 | 9.1400 | 2.3000 | 16.8300 | 5.4712 | 0.0334 | 1.5220 |
| Malta | 6.5892 | 6.7450 | 4.1000 | 9.05000 | 1.5497 | 0.1544 | 2.0655 |
| Austria | 2.6900 | 2.7250 | 1.9000 | 3.4700 | 0.4563 | 0.1258 | 2.4942 |
| Poland | 4.7175 | 4.7400 | 2.8200 | 7.4000 | 1.0769 | 0.8988 | 4.8279 |
| Portugal | 7.3750 | 9.1250 | 1.3000 | 13.3000 | 4.8475 | 0.1852 | 1.2605 |
| Romania | 10.3367 | 10.7600 | 1.8000 | 21.6000 | 6.1126 | 0.1340 | 2.1850 |
| Slovenia | 7.7317 | 7.0000 | 1.8000 | 15.1800 | 4.5795 | 0.2129 | 1.6299 |
| Slovakia | 4.4883 | 4.9850 | 2.5000 | 5.8000 | 1.2140 | −0.6285 | 1.9133 |
| Sweden | 0.9758 | 0.9000 | 0.6000 | 2.0000 | 0.3941 | 1.4469 | 4.7866 |
| United Kingdom | 2.1617 | 1.6250 | 0.8100 | 3.9600 | 1.3342 | 0.3073 | 1.3017 |
| China | 2.3125 | 1.6350 | 0.9500 | 7.1000 | 2.0789 | 1.6631 | 4.0742 |
| Russia | 6.8017 | 7.3650 | 2.4000 | 10.0000 | 2.6596 | −0.5731 | 2.0161 |
| Brazil | 3.3600 | 3.3800 | 2.8500 | 4.2100 | 0.4157 | 0.6093 | 2.5971 |
| India | 4.3675 | 3.3350 | 2.3000 | 9.9800 | 2.6547 | 1.2948 | 3.2111 |
| South Africa | 3.6742 | 3.4350 | 1.1000 | 5.9000 | 1.5988 | −0.0098 | 2.0376 |
| Mean | Median | Minimum | Maximum | St.D | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|
| Belgium | 100.3583 | 102.8500 | 87.0000 | 107.0000 | 6.6701 | −0.8902 | 2.4051 |
| Bulgaria | 19.6333 | 16.8500 | 13.0000 | 29.0000 | 5.7362 | 0.4649 | 1.6080 |
| Czech Republic | 36.4417 | 37.1000 | 27.5000 | 44.9000 | 6.2432 | −0.2141 | 1.7903 |
| Denmark | 39.0333 | 40.0500 | 27.3000 | 46.1000 | 5.9322 | −0.6277 | 2.2842 |
| Germany | 71.9000 | 71.8000 | 63.7000 | 80.9000 | 6.3577 | 0.0684 | 1.5050 |
| Estonia | 7.6083 | 8.0000 | 3.7000 | 10.7000 | 2.5300 | −0.2885 | 1.5525 |
| Ireland | 75.7500 | 74.8500 | 23.6000 | 119.6000 | 34.0440 | −0.2120 | 1.8718 |
| Greece | 151.1000 | 165.8500 | 103.1000 | 180.8000 | 31.9020 | −0.5597 | 1.6123 |
| Spain | 72.8917 | 77.6000 | 35.6000 | 100.4000 | 26.4605 | −0.2630 | 1.4036 |
| France | 85.1750 | 89.2000 | 64.5000 | 97.0000 | 12.4362 | −0.7907 | 2.0593 |
| Croatia | 63.3833 | 66.6000 | 37.3000 | 84.0000 | 18.6716 | −0.2974 | 1.4865 |
| Italy | 119.0583 | 119.9500 | 99.8000 | 132.0000 | 12.6018 | −0.3452 | 1.5921 |
| Cyprus | 77.8750 | 72.7000 | 45.1000 | 107.5000 | 24.8807 | 0.0977 | 1.2836 |
| Latvia | 33.3000 | 39.5500 | 8.0000 | 46.8000 | 13.3813 | −1.1015 | 2.5721 |
| Lithuania | 32.5500 | 38.0000 | 14.6000 | 42.6000 | 10.6798 | −0.8592 | 1.9943 |
| Hungary | 74.8750 | 76.6500 | 64.5000 | 80.5000 | 5.2343 | −1.0305 | 2.8415 |
| Malta | 63.3583 | 64.1500 | 50.8000 | 70.1000 | 5.7175 | −0.9038 | 2.9411 |
| Austria | 78.3167 | 81.6000 | 65.0000 | 84.6000 | 7.0776 | −1.0123 | 2.3322 |
| Poland | 50.8000 | 50.8500 | 44.2000 | 55.7000 | 3.5868 | −0.4349 | 2.0792 |
| Portugal | 105.8917 | 118.5500 | 68.4000 | 130.6000 | 26.2724 | −0.4422 | 1.4574 |
| Romania | 28.8333 | 34.5000 | 11.9000 | 39.1000 | 11.0311 | −0.7188 | 1.7858 |
| Slovenia | 52.4583 | 50.2000 | 21.8000 | 82.6000 | 23.7567 | −0.0003 | 1.3967 |
| Slovakia | 43.8500 | 47.3000 | 28.5000 | 54.7000 | 10.0848 | −0.4233 | 1.5416 |
| Sweden | 40.8500 | 40.6500 | 37.8000 | 45.5000 | 2.6586 | 0.4120 | 1.8766 |
| United Kingdom | 72.9333 | 82.9000 | 40.8000 | 88.2000 | 18.7544 | −0.8410 | 2.0280 |
| China | 35.6000 | 34.3000 | 25.4000 | 47.6000 | 6.7618 | 0.1938 | 2.1800 |
| Russia | 11.5417 | 11.3500 | 7.4000 | 15.9000 | 2.6569 | 0.1562 | 2.2124 |
| Brazil | 58.4508 | 56.1300 | 51.2700 | 74.0400 | 7.4771 | 1.0211 | 2.7483 |
| India | 70.7583 | 69.5500 | 67.5000 | 77.1000 | 3.0125 | 0.9404 | 2.5640 |
| South Africa | 39.9167 | 39.6000 | 27.8000 | 53.1000 | 9.0799 | 0.0783 | 1.5803 |
| Country | Debt → NPLs | NPLs → Debt | ||||
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | k = 3 | k =1 | k = 2 | k = 3 | |
| Belgium | 0.0690 | 0.0928 | 0.1287 | 0.0621 | 0.06772 | 0.2773 |
| Bulgaria | 0.1033 | 0.4841 | 0.9006 | 0.0085 ** | 0.0767 | 0.3815 |
| Czech Republic | 0.0398 * | 0.0362 * | 0.1691 | 0.1746 | 0.2878 | 0.2525 |
| Denmark | 0.0056 ** | 0.598 | 0.9068 | 0.0001 *** | 0.0133 * | 0.0907 |
| Germany | 0.0011 ** | 0.1085 | 0.0445 * | 0.0928 | 0.0587 | 0.2920 |
| Estonia | 0.4735 | 0.2668 | 0.1499 | 0.1239 | 0.3308 | 0.1546 |
| Ireland | 0.7105 | 0.0138 * | 0.2595 | 0.2626 | 0.6566 | 0.7956 |
| Greece | 0.0102 * | 0.0347 * | 0.1988 | 0.9357 | 0.5671 | 0.2092 |
| Spain | 0.0028 ** | 0.5248 | 0.1932 | 0.0024 ** | 0.0358 * | 0.1492 |
| France | 0.4955 | 0.8559 | 0.6277 | 0.1203 | 0.2864 | 0.7300 |
| Croatia | 0.1952 | 0.1818 | 0.1523 | 0.9109 | 0.8177 | 0.7420 |
| Italy | 0.3479 | 0.0128 * | 0.1527 | 0.1608 | 0.0003 *** | 0.2963 * |
| Cyprus | 0.0003 *** | 0.5192 | 0.6840 | 0.0042 ** | 0.0109 * | 0.8223 |
| Latvia | 0.9098 | 0.3147 | - | 0.8794 | 0.3847 | 0.0400 * |
| Lithuania | 0.0089 ** | 0.0042 ** | 0.0638 | 0.1923 | 0.3646 | 0.6983 |
| Hungary | 0.6667 | 0.9697 | 0.6400 | 0.4286 | 0.2949 | 0.3772 |
| Malta | 0.0177 * | 0.0599 | 0.3195 | 0.02565 | 0.6050 | 0.2901 |
| Austria | 0.01399 * | 0.0352 * | 0.031 * | 0.1153 | 0.3596 | 0.8432 |
| Poland | 0.4803 | 0.6403 | 0.6308 | 0.6490 | 0.2583 | 0.4747 |
| Portugal | 0.0014 ** | 0.2132 | 0.4841 | 0.0279 * | 0.4442 | 0.8346 |
| Romania | 0.0245 * | 0.1286 | 0.5888 | 0.036 * | 0.0515 | 0.3409 |
| Slovenia | 0.4660 | 0.2373 | 0.0443 * | 0.8733 | 0.8929 | 0.8374 |
| Slovakia | 0.0089 ** | 0.0171 * | 0.1097 | 0.2338 | 0.7354 | 0.7900 |
| Sweden | 0.0044 ** | 0.3647 | 0.8736 | 0.0052 ** | 0.1596 | 0.0232 * |
| United Kingdom | 0.4964 | 0.6775 | 0.8912 | 0.0009 *** | 0.0268 * | 0.4423 |
| China | 0.0948 | 0.0870 | 0.4707 | 0.7309 | 0.7335 | 0.0995 |
| Russia | 0.6297 | 0.5957 | 0.0577 | 0.8246 | 0.6897 | 0.2555 |
| Brazil | 0.2648 | 0.0435 * | 0.3470 | 0.1724 | 0.1267 | 0.3427 |
| India | 0.0074 ** | 0.2449 | 0.3934 | 0.8505 | 0.5818 | 0.2473 |
| South Africa | 0.0047 ** | 0.0022 ** | 0.1917 | 0.0094 ** | 0.0615 | 0.9620 |
| Mean of NPLs | Mean of Debt | |
|---|---|---|
| Panel A: Kendall’s Tau within European Countries | ||
| 25 EU countries | 0.4742 | 0.5815 |
| Belgium-24 EU countries | 0.4390 | 0.6167 |
| Bulgaria-24 EU countries | 0.4695 | 0.3874 |
| Czech Republic-24 EU countries | 0.4292 | 0.4951 |
| Denmark-24 EU countries | 0.4475 | 0.3667 |
| Germany-24 EU countries | −0.0679 | 0.2402 |
| Estonia-24 EU countries | 0.2619 | 0.5377 |
| Ireland-24 EU countries | 0.4351 | 0.4182 |
| Greece-24 EU countries | 0.2847 | 0.5571 |
| Spain-24 EU countries | 0.4592 | 0.6435 |
| France-24 EU countries | 0.4425 | 0.5350 |
| Croatia-24 EU countries | 0.4328 | 0.6147 |
| Italy-24 EU countries | 0.3719 | 0.5701 |
| Cyprus-24 EU countries | 0.3231 | 0.5619 |
| Latvia-24 EU countries | 0.3388 | 0.3293 |
| Lithuania-24 EU countries | 0.2956 | 0.5814 |
| Hungary-24 EU countries | 0.4758 | 0.2210 |
| Malta-24 EU countries | 0.3593 | 0.0442 |
| Austria-24 EU countries | 0.3469 | 0.4761 |
| Poland-24 EU countries | 0.0438 | 0.4184 |
| Portugal-24 EU countries | 0.2968 | 0.6035 |
| Romania-24 EU countries | 0.4594 | 0.6086 |
| Slovenia-24 EU countries | 0.4517 | 0.5915 |
| Slovakia-24 EU countries | 0.3841 | 0.5610 |
| Sweden-24 EU countries | 0.1051 | 0.2437 |
| United Kingdom-24 EU countries | 0.2969 | 0.5610 |
| Panel B: Kendall’s Tau between BRICS and European Countries | ||
| 5 BRICS countries | 0.0141 | 0.2582 |
| China-25 EU countries | −0.3992 | 0.4438 |
| Russia-25 EU countries | 0.1456 | 0.5874 |
| Brazil-25 EU countries | −0.0064 | 0.0387 |
| India-25 EU countries | 0.0700 | −0.3436 |
| South Africa-25 EU countries | 0.2498 | 0.5006 |
| Country | t Copula | Rotated Clayton Copula | Joe Copula | |||
|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | Lower | Upper | |
| Belgium | 0.4045 | 0.4045 | 0 | 0.8047 | 0 | 0.8115 |
| Bulgaria | 0.0015 | 0.0015 | 0 | 0.3241 | 0 | 0.3892 |
| Czech Republic | 0.0917 | 0.0917 | 0 | 0.5971 | 0 | 0.6215 |
| Denmark | 0.7460 | 0.7460 | 0 | 0.7905 | 0 | 0.8002 |
| Germany | 0.0011 | 0.0011 | 0 | 0.2882 | 0 | 0.3599 |
| Estonia | 0.0001 | 0.0001 | 0 | 0.0000 | 0 | 0.0001 |
| Ireland | 0.8778 | 0.8778 | 0 | 0.9231 | 0 | 0.9237 |
| Greece | 0.2977 | 0.2977 | 0 | 0.7800 | 0 | 0.7887 |
| Spain | 0.1112 | 0.1112 | 0 | 0.6620 | 0 | 0.6751 |
| France | 0.1909 | 0.1909 | 0 | 0.1300 | 0 | 0.1185 |
| Croatia | 0.8252 | 0.8252 | 0 | 0.9011 | 0 | 0.9020 |
| Italy | 0.2979 | 0.2979 | 0 | 0.7379 | 0 | 0.7514 |
| Cyprus | 0.2074 | 0.2074 | 0 | 0.8356 | 0 | 0.8412 |
| Latvia | 0.6543 | 0.6543 | 0 | 0.7781 | 0 | 0.7830 |
| Hungary | 0.0620 | 0.0620 | 0 | 0.5273 | 0 | 0.5548 |
| Malta | 0.4359 | 0.4359 | 0 | 0.5465 | 0 | 0.5850 |
| Austria | 0.0817 | 0.0817 | 0 | 0.7646 | 0 | 0.7698 |
| Poland | 0.1781 | 0.1781 | 0 | 0.0000 | 0 | 0.0001 |
| Portugal | 0.7246 | 0.7246 | 0 | 0.7089 | 0 | 0.7266 |
| Romania | 0.1218 | 0.1218 | 0 | 0.6658 | 0 | 0.6762 |
| Slovenia | 0.0083 | 0.0083 | 0 | 0.3696 | 0 | 0.4003 |
| Slovakia | 0.0057 | 0.0057 | 0 | 0.2229 | 0 | 0.2468 |
| Sweden | 0.0096 | 0.0096 | 0 | 0.5883 | 0 | 0.6172 |
| Russia | 0.0048 | 0.0048 | 0 | 0.2807 | 0 | 0.3127 |
| Brazil | 0.0043 | 0.0043 | 0 | 0.5227 | 0 | 0.5571 |
| Country | Intercept | Debt | Expenditure | GDP | Revenue | Inflation |
|---|---|---|---|---|---|---|
| Bulgaria | 44.8120 * (18.9509) | −0.2404 (0.3626) | 0.4717 (0.5271) | 0.5576 (0.4915) | −1.2776 * (0.6131) | −1.2742 * (0.6076) |
| Cyprus | 1.7552 *** (0.0024) | 0.7646 *** (0.0715) | −0.7424 (0.5010) | 0.1576 (0.5022) | −0.2369 (0.5877) | −0.5485 (0.8323) |
| Croatia | 53.0771 *** (0.0004) | 0.2805 *** (0.0093) | 0.3155 *** (0.0562) | 0.0338 (0.0412) | −1.0389 *** (0.062) | −0.2666 *** (0.07863) |
| Greece | −118.6 *** (0.0065) | 0.2387 ** (0.0903) | 0.5013 (0.2686) | 1.2320 ** (0.3769) | 1.8230 *** (0.5232) | −0.3670 (0.6392) |
| Italy | −76.6442 *** (0.0014) | 0.22266 *** (0.02853) | 0.2701 (0.2545) | 0.2415 * (0.1127) | 1.0594 *** (0.2863) | −0.3310 (0.2282) |
| Malta | 28.7748 * (11.5029) | 0.3301 *** (0.0796) | −0.0692 (0.2348) | 0.3674 *** (0.0684) | 0.4126 (0.3108) | −0.1790 (0.2387) |
| Portugal | −4.1232 (12.4124) | 0.1813 *** (0.0146) | 0.3222 * (0.1385) | 0.0537 (0.1089) | 0.1857 (0.2245) | −0.0917 (0.1744) |
| Romania | −12.5478 (20.7407) | 0.6090 *** (0.0893) | −1.1359 (0.8139) | −0.3779 (0.2783) | 1.3277 * (0.5304) | 1.1883 ** (0.4413) |
| Spain | −27.9760 ** (10.5332) | 0.0699 *** (0.0135) | 0.3601 (0.1946) | −0.2669 (0.1958) | 0.3274 * (0.1546) | 0.0860 (0.1712) |
| Slovenia | −131.3625 *** (21.3408) | 0.1401 *** (0.033) | 0.1843 (0.1469) | −0.4206 ** (0.1370) | 3.0411 *** (0.5862) | 0.8356 (0.4637) |
| Belgium | −19.6475 *** (0.9114) | 0.04560 *** (0.0096) | 0.2127 *** (0.0235) | 0.0205 (0.0221) | 0.1381 ** (0.0279) | −0.1122 *** (0.0212) |
| France | −42.1100 *** (0.0005) | −0.0807 *** (0.0096) | 0.7195 *** (0.0678) | 0.0410 (0.0713) | 0.2384 *** (0.0697) | 0.0857 (0.0971) |
| Ireland | −9.76100 (5.3245) | 0.2519 *** (0.0139) | −0.2364 *** (0.0689) | 0.0107 (0.0699) | 0.4172 * (0.2016) | −1.0583 * (0.4138) |
| United Kingdom | −35.2600 *** (0.0009) | −0.0104 * (0.0051) | 0.6023 *** (0.0418) | 0.0595 (0.0528) | 0.3763 *** (0.0433) | 0.00591 (0.0802) |
| Austria | −38.1600 *** (0.0003) | 0.0000 (0.9981) | 0.2473 *** (0.0000) | 0.2690 *** (0.0275) | 0.5744 *** (0.0412) | −0.0910 *** (0.0469) |
| Czech Republic | 23.0463 *** (0.0009) | 0.2120 *** (0.0147) | 0.0625 (0.0389) | 0.0931 *** (0.0281) | −0.7161 *** (0.0456) | −0.2335 *** (0.0445) |
| Germany | 18.3133 *** (0.0004) | 0.0187 * (0.0090) | 0.1316 *** (0.0363) | −0.0854 *** (0.0225 | −0.5232 *** (0.0312) | 0.2074 ** (0.0780) |
| Hungary | −155.4512 *** (40.5536) | 0.8237 *** (0.2018) | 1.1118 * (0.5583) | 0.5173 (0.3618) | 1.0447 (0.6036) | 0.1635 (0.4481) |
| Poland | −49.4549 * (19.4889) | 0.1730 (0.1054) | 0.5021* (0.1993) | 0.0908 (0.2431) | 0.6117 (0.3446) | −3.7770 * (0.1628) |
| Slovakia | −4.06700 (3.3320) | 0.0981 *** (0.0171) | 0.4829 *** (0.0775) | 0.0273 (0.0385) | −0.4233 *** (0.0788) | 0.1052 (0.0874) |
| Denmark | −21.8500 * (1094) | 0.0696 (0.0787) | 0.4173 * (0.1649) | 0.0754 (0.0830) | −0.0008 (0.1549) | −0.1979 (0.1464) |
| Sweden | −0.0660 (3.0839) | 0.1284 *** (0.0226) | 0.0373 (0.0594) | −0.0792 *** (0.0212) | −0.1271 * (0.0508) | 0.3247 *** (0.0950) |
| Estonia | −48.8265 ** (18.7886) | 0.0166 (0.3587) | −0.4439 (0.7987) | −0.0130 (0.1615) | 1.6916 (1.0694) | 0.5242 (0.3737) |
| Latvia | −212.5658 *** (39.9114) | −0.1794 (0.0922) | 3.2445 *** (0.3430) | 0.6411 *** (0.1166) | 2.7942 ** (0.9595) | 0.6060 *** (0.1792) |
| Lithuania | 12.7869 (35.3126) | 0.1462 (0.1060) | 2.0778 *** (0.3039) | −0.1690 (0.1391) | −2.4429 * (0.9685) | −0.3245 (0.3397) |
| China | 14.7477 (8.7543) | 0.1116 (0.1435) | 0.1928 (0.5110) | −0.0441 (0.4064) | −0.8561 * (0.3772) | 0.08932 (0.1556) |
| Russia | 43.9618 (25.632) | −0.1486 (0.1724) | 0.0552 (0.3749) | −0.1515 (0.1686) | −1.0344 ** (0.3970) | −0.1898 (0.1067) |
| Brazil | −7.6525 (4.7255) | 0.0515 * (0.0227) | 0.0048 (0.1067) | −0.1513 ** (0.0466) | 0.2473 ** (0.0774) | −0.0237 (0.0685) |
| India | 1.2336 (20.9252) | −0.2745 (0.1432) | 1.1337 (0.61111) | −0.0997 (0.2197) | −0.0520 (−0.5827) | −0.8655 *** (0.1773) |
| South Africa | 4.9088 *** (0.0009) | −0.133 *** (0.0188) | 1.0070 *** (0.0887) | 0.2845 ** (0.1061) | −1.0491 *** (0.1153) | 0.2123 * (0.0845) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Liu, Y.-M.; Kim, J.-M.; Zhong, R.; Ren, G.-Q. Analysis of Tail Dependence between Sovereign Debt Distress and Bank Non-Performing Loans. Sustainability 2020, 12, 747. https://doi.org/10.3390/su12020747
Liu L, Liu Y-M, Kim J-M, Zhong R, Ren G-Q. Analysis of Tail Dependence between Sovereign Debt Distress and Bank Non-Performing Loans. Sustainability. 2020; 12(2):747. https://doi.org/10.3390/su12020747
Chicago/Turabian StyleLiu, Li, Yu-Min Liu, Jong-Min Kim, Rui Zhong, and Guang-Qian Ren. 2020. "Analysis of Tail Dependence between Sovereign Debt Distress and Bank Non-Performing Loans" Sustainability 12, no. 2: 747. https://doi.org/10.3390/su12020747
APA StyleLiu, L., Liu, Y.-M., Kim, J.-M., Zhong, R., & Ren, G.-Q. (2020). Analysis of Tail Dependence between Sovereign Debt Distress and Bank Non-Performing Loans. Sustainability, 12(2), 747. https://doi.org/10.3390/su12020747







