1. Introduction
Incentive policies are the main deciding factors in achieving sustainable development, which mainly include tax incentives [
1], financial incentives [
2], monetary incentives [
3], and reward incentives [
4]. The Organization for Economic Co-operation and Development (OECD) pointed out that proper incentive policies could promote sustainable corporate growth [
5]. The European Union and its member states provide different incentives to make local sustainable development more attractive [
6]. Incentives were also demonstrated to facilitate sustainable urban development across the United States [
7]. Despite recommendations to use incentives to promote sustainable development, it was mentioned that policy makers only focused on the effectiveness of incentive policies and did not pay enough attention to the synergy of their transmission mechanism [
8,
9,
10]. Studying the transmission mechanism of incentive policies designed to achieve sustainability and appraising their effectiveness could help policy makers better understand the efficiency of different solution options. Consequently, decision-makers would benefit from the scientific analysis of the formulation and improvement of relevant strategies.
Studying the transmission mechanism of incentive policies for sustainable development has become increasingly more important. The transmission mechanism for incentives refers to the interactions and conduction laws of various incentive policies among different regions or cities through proliferation [
11]. In this study, a transmission mechanism for incentives is elaborated by the transmission path and transmission intensity of each incentive among the cities and regions to reveal the transmission laws. However, existing research mainly uses incentive policies as the carriers of influencing factors to analyze their external influence on industries and markets. For example, Kozlova et al. [
12] analyzed the profitability of energy markets based on incentives for renewable energy. Zhang et al. [
13] observed consumers’ intention to purchase electric vehicles influenced by a sustainable subsidy policy. Pleger et al. [
14] suggested increasing public acceptance of market-based spatial-planning policies by proposing effective sustainable policy frameworks. Nevertheless, none of the above studies fully considered the internal role of incentive policies. There should be a comprehensive analysis of the proliferation mode and broadcast role of incentive policies in the process of formulation.
To fill this gap, this paper proposes the structure of a transmission-weighted complex network (TWCN) and an experimental design to analyze the interactions and conduction laws of sustainable incentive policies between cities and regions. Complex networks represent a new multidisciplinary method for studying intricate systems [
15], which can investigate the topological properties of systems through statistical calculations of correlation features [
16]. Therefore, this research attempts to answer the question of how to use complex networks to analyze interactions and conduction behaviors of incentive policies transferred between cities and regions. First, based on a systematic review of the incentive policy text, we evaluated the system of intercity incentives and how they interrelate in a small-world network. Next, the structure of the TWCN is proposed to explore the transmission mechanism of interregional incentive policies from the perspective of transmission path and intensity. Third, we take incentives for prefabricated building or industrialized/manufactured construction (IMC) as an empirical case to systematically verify the functions and behaviors of the TWCN of incentive policies, find potential problems in policy formulation, and provide improvements. Prefabricated building or IMC, including residential, commercial, heavy civil, and industrial construction, help to reduce wasted time and materials and promote sustainable operation in the construction industry. Sources of research data on incentive policies for IMC are mainly policy documents published on the official websites of local governments and the Ministry of Housing and Urban-Rural Development from 2010 to 2018. Finally, to verify the reliability and feasibility of the TWCN design, we tested and evaluated the research results through the use of correlation analysis and cluster analysis methods.
This research contributes to the body of knowledge in the following aspects: (1) construction of a complex network based on the establishment of a relationship matrix, (2) analysis of the conduction paths of incentive policies among cities and regions based on the strength of the network nodes, (3) determination of accurate clustering coefficients to calculate and analyze the transmission intensity of incentive policies, and (4) comparison of the analysis results with the external effects to evaluate the results. The following sections include a literature review of the research background in studies on incentive policies for influencing factors. The literature review uncovers the research question of how to describe the interactions among the network nodes of the TWCN. The related areas of small-world and scale-free network areas provide theoretical support for the TWCN framework. The methodology section provides details of the relationship matrix, statistical parameters, and hypotheses. The data collection, analysis, and outcome evaluation sections systematically elaborate the functions and behaviors of the TWCN of incentive policies for IMC. The conclusion section explains the implications for practice and society with recommendations for future research.
2. Background
2.1. Previous Research on Transmission Mechanisms of Incentives
To further accelerate sustainable development and promote the transformation and upgrading of the sustainable industry, governments in various regions and areas have taken relevant measures and issued pertinent guidelines and supporting policies. However, certain problems occur in sustainable development. For example, inconsistent standardization levels, high construction costs, and imperfect technical systems of prefabricated building or IMC around the world [
17,
18,
19]. Even though the encouragement and guidance provided by various municipal administrations in financial, land and tax incentives have a positive influence on upholding the development of IMC, decision-makers and business practitioners are unsure how the sophisticated system of policies could benefit the markets in various locations. Judging from the incentive policies announced or published in various places for IMC, the policy measures are incomplete, the system has flaws, and the different incentive policies issued by different local governments are similar regardless of their geographical location, which indicates that there is a “transmission” effect among policy contents. Hence, it is important to understand the feasibility and transmission mechanism of sustainable incentives in complex networks.
Previous research discussed incentive policies for sustainable development, with a broad range of topics such as development status, policy formulation, implementation, and evaluation. Researchers built theories on how incentive policies promote innovation development by analyzing the status quo and existing problems of industry (or industry development). For example, Song et al. [
20] analyzed the situation and experience of the photovoltaic industry and proposed a series of incentive strategies to help enhance development of the industry. Zou et al. [
21] analyzed the development of China’s green building and found that local economic fundamentals and subsidy-based incentive policies can explain the presence of green buildings. Scholars have considered the influence of incentive policies in the process of policy making from various factors. For example, Burns et al. [
22] analyzed incentive subsidies from the economic and financial perspective and stated that they could bring great potential to the solar photovoltaic market. Kirakozian et al. [
23] believed that the influence of emotional factors and social interactions should also be considered in the process of formulating incentive policies. Scholars also established a welfare policy network to establish the core position of the policy in the decision-making process and achieve the goal of supporting policy formulation [
24]. With regard to the policy implementation phase, Aquila et al. [
25] analyzed the pros and cons of incentives along with their potential and vulnerability in the process of employment. Zhang et al. [
26] established a new dynamic energy policy system to regulate the behaviors of participants in technological progress and avoid subsidy frauds. Scholars have conducted comparative evaluations and analyses on how to stimulate the implementation of incentive policies and identified the problems [
27].
Previous research on sustainable incentive policies mainly applied methods such as game theory, stock model and system dynamics. Game theory is applicable to different subjects or policies. For example, researchers optimized incentives for green energy and energy-chain efficiency reform by formulating a game model between government, manufacturers and customers [
28,
29]. William et al. used the cooperative game theory framework to study the potential impacts of different policy strategies with a stimulation of green infrastructure installation. They recommended the types of policies that could be used to motivate private landowners to adopt green infrastructure [
30]. Zhao et al. established an evolutionary game model to study the possible responses of enterprises to the implementation of incentive policies related to carbon emission labeling. They used system dynamics to simulate game scenarios [
31]. Stock (or inventory) models help to examine the impacts of relevant incentive policies on the main players. For example, Sarker established a consignment inventory policy model for supply-chain systems and classified the systems from different perspectives to understand the operational mechanisms of different consignment policies [
32]. In addition, an analysis of the influence of incentive contracts on entrepreneurs helped to select the amount of retained equity so that all competitors could reach equity equilibrium [
33]. System dynamics is widely used for the evaluation of incentive policies because of the availability of proprietary software. For example, a sensitivity analysis was conducted to evaluate the rationality and effectiveness of incentive policies for the photovoltaic industry. Guo et al. established a system dynamics model for the incentive policies and considered the changes of economic and technical factors for model simulation [
34]. Another research project analyzed the effects of incentives related to the intermittent and uncertain nature of wind-power generation on investment decisions by establishing a relevant system dynamics model [
35].
2.2. Complex Networks
There are several commonly used models for studying complex networks, small-world networks and scale-free networks and random networks. Newman and Watts proposed a small-world network model to build a connection between regular and random networks [
36]. They studied the distribution of vertices, the average shortest distance, and the degree correlation using a small-world network. Later improvements on the model included combinations of complex algorithms and models. For example, Senkerik et al. studied the diversity of population development processes by combining complex networks with chaotic-driven heuristic algorithms to construct diversity [
37]. Huang established an epidemic model based on complex networks and analyzed the spread of malware by studying vulnerable nodes of weak and strong protections [
38]. Wang et al. launched complex networks of interactive transmissions to study the evolution of global imports of crude oil based on countries. Their research introduced dynamic topological indicators and long-term global recursive graphs to study global evolution and analyze the dependencies of countries on crude-oil imports [
39]. Another improvement on the complex network method is two-stage network construction, which can analyze the relationships between listed companies and the stability of large companies [
40]. To enlarge the boundaries, researchers introduced a scale-free network model. The application of the scale-free network model to the conduction paths of heterogeneous wireless-sensor networks was successful and the established network could effectively improve the sensor performance and balance the energy consumption of network nodes [
41,
42]. Another example of a scale-free network is a visual network system based on weighted joint crimes to analyze the evolutionary relationship between criminals which can provide better decision making for analysts with artificial intelligence [
43]. These studies provide theoretical support for this research and ideas for network design.
There are also many studies about dynamic of complex network in order to analyze the interaction of different polices. In particular, the pining control, which drives a networked system to a coherent state, can be used to the address cluster synchronization control problem for the reduction of network burden and improvement of cluster synchronization efficiency [
44,
45,
46]. Compared to the classical method, the pinning controllability could be better characterized by the coupling range and convergence speed in analytical and practical ways [
47]. Moreover, a comparison with other networks at the same scale identifies whether a network has the characteristics of a small-world network, comparing the average path length (L) and average clustering coefficient (C) of two networks [
48]. The average path length reflects the degree of remoteness between two nodes. It is calculated by adding the shortest distance between any two points in the network to obtain the average value. The average clustering coefficient of the entire network is the arithmetic mean of the clustering coefficient of all nodes.
In past research, scholars used different governments, enterprises and clients as the research subjects to carry out game theories of sustainable incentive policies, established the inventory model, and built a system dynamics model to analyze the influences of the incentive policies on decision-making. Furthermore, most of the transmission research on incentive policies only focus on the influences of interest rates among different regions or countries [
49,
50]. All the above studies have explored the external impact of incentive policies but have not fully considered the internal conduction laws between different incentive policies. This knowledge gap represents the lack of a description of the transmission mechanism among cities and regions (intercity or internode) of a complex network of sustainable incentive policies. Hence, this research seeks to answer the question of how to use small-world and scale-free network methods to analyze the functions and behaviors of incentive policies transferred between cities and regions. Therefore, this paper proposes to explore the transmission mechanism of incentives from the perspective of complex networks.
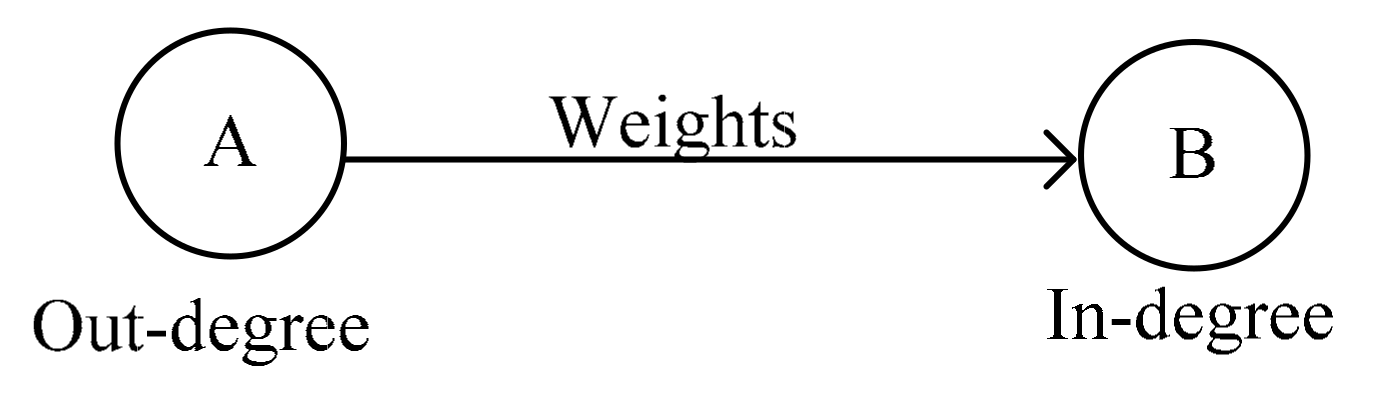
The transmission path of incentives among regions or cities is analyzed to reveal its transmission laws. Therefore, this study analyzes the transmission path of an incentive policy by comparing the strength of the node. The strength of the node is reflected by the reference quantity and cited quantity of policy documents. As shown in
Figure 1, nodes
A and
B both propose the same incentive policy. There must be a policy transmission relationship between the two nodes. Node
A issues the policy earlier than node
B. Therefore, the incentive policy proposed by node
A is referenced by node
B. The outbound value of node
A is equal to the ingress value of node
B. The greater the output value of node
A, the greater its reference rate in the incentive policy transmission in the network. Conversely, the greater the ingress value of node
B, the higher its incentive rate in the network. If a complex network is composed of N nodes, there are always incoming and outgoing relationships similar to the one between
A and
B for those nodes, which eventually form a chain of conduction paths. [
51]
The transmission intensity of incentives among regions or cities is analyzed to reveal its degree of spatial agglomeration. In this research, the clustering coefficient value reflects the spatial concentration of incentive policies. The clustering coefficient refers to the coefficient of the degree of node aggregation. If the value of the clustering coefficient of a node is larger, the effect of the incentive policy in the region (or city) is more significant. On the contrary, the smaller the clustering coefficient value, the weaker the influence of the incentive policy. Additionally, classification and decomposition of incentive policies can disclose the spatial agglomeration of various policies, thus deeply exploring the policy characteristics introduced in different regions.
3. Methodology
3.1. Data Collection
Prefabricated building or IMC are more energy-efficient, sustainable, productive, and cost-effective, and less wasteful than traditional in situ construction, which is an important transformation direction for sustainable development of the construction industry. Despite the many proven advantages over conventional site-built construction, the adoption of prefabricated building is slow in the face of dire challenges in the construction industry [
52]. Policy makers in cities of China have formulated many incentive policies for sustainable development of prefabricated building. As of 2018, policies were issued by 181 cities in China to promote the sustainable development of prefabricated building. Looking carefully at the documents on the incentives, there is a high degree of similarity among the policies issued.
Table 1 lists the top 24 most frequently used incentives and frequency of cities. Meanwhile, we find that policy makers actually learned from other cities’ policies in the process of formulation by field investigation and interviews. Therefore, we take the interaction of incentive policies among cities as a case for the TWCN to observe how they are transmitted.
The data source for IMC includes a discussion of implementation opinions, official government websites, and the Ministry of Housing and Urban–Rural Development. The keywords for policy search include implementation opinions, operation plans, and development strategies of assembly-type building, building industrialization, and industrial modernization to retrieve relevant policy documents. In this study, 415 policy documents from 2010 to 2018 were extracted at the provincial and municipal level, with a focus on data on the incentive policy parts. This research adopted the induction method and grounded theory to classify and sort original text data and form a systematic theoretical code. After classification and coding, the TWCN system had 2923 items from 181 nodes regarding IMC incentive policies.
Table 2 shows the specific results from data collection after the following detailed steps:
Extract the keywords from the collected incentive policy texts to form initial codes. The synonyms mentioned in the documents are merged repeatedly and sorted to form the theoretical codes, which become the IMC incentive policy elements.
Sort and classify the extracted theoretical codes. The main purpose is to combine similar factors. For example, value-added and deed taxes are grouped into tax policies; provident fund loans and bond financing are grouped into financial policies.
Continuously screen the incentive policy texts until there are no new theoretical codes. This follows the saturation principle of grounded theory.
Organize theoretical coding data and build a coding system of incentive policy elements. After statistical analysis using Cronbach’s alpha, this step divides the incentive policies into seven aspects (shown in
Table 2), including tax, finance, land, administration, construction, and research–development–training (RDT), and the number of key elements and nodes are counted.
In the policy formulation process, policy makers often refer to and draw on relevant policy plans and policy concepts from other countries, regions, or departments. Therefore, this study makes the following assumption: the government departments that formulated the IMC incentive policies referred to previous relevant IMC incentives. The study used the Java program to calculate the relationship matrix among intercity IMC incentive policies, and UCINET to analyze the relationship matrix.
Figure 2 shows an example of the relationship matrix for the connections between geographical locations when they adopt a particular IMC incentive policy. In this case, the policy is 3–5% floor area ratio in the tax policy. The topological structure of the transmission network for this incentive policy is shown in the figure.
3.2. Design of TWCN Model
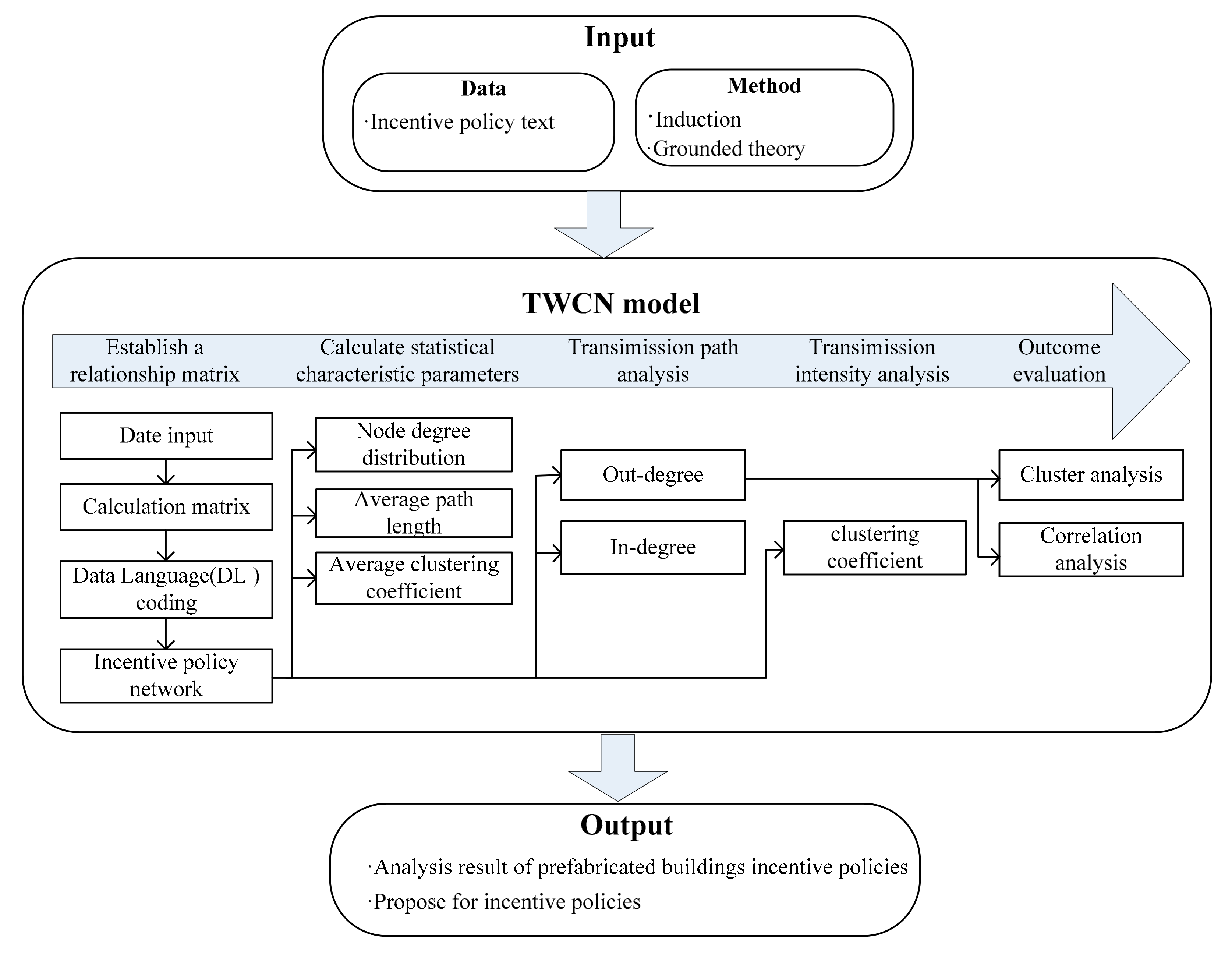
To explore the mechanisms of incentive policies, we designed a research method based on the path and intensity of policy transmission.
Figure 3 shows the structure of the proposed TWCN. The first step of the proposed solution is to collect data on the incentive policies, which is then processed using the induction method and rooted theory. The next step is to construct the TWCN through the established relationship matrix, followed by statistical feature analysis. After the analysis, the research continues with the transmission characteristics and rules of the incentive policies based on an analysis of their conduction paths and intensities. Meanwhile, correlation and cluster analysis methods are used to evaluate the effects of TWCN to verify its reliability. The results of TWCN research are suitable for decision making with reasonable recommendations.
3.3. Theoretical Details
Function
G(
Vn,
En,
Wn) for TWCN includes city node set
Vn = {
vi,
I = 1, 2, 3,
…,
n}, city contact edge set
Em = {
e(i, j),
i,
j = 1, 2, 3,
…,
m}, and network weight set
Wn = {
w(i, j),
i,
j = 1, 2, 3,
…,
n}. Node
vi represents the city and edge
e(i, j) represents the transmission relationship between the same incentive policy elements. The weights on the edges of the network (edge weight
w(i, j)) represent the numbers of incentive policy transmission entries among cities. There are interactive transmissions among multiple incentive policies in many cities. The following matrix constructs the relationships between intercity incentive policies (
w(i, j))
Equation (1) calculates the average of nodes
<k>, which is the average of all the nodes in the network.
where
n is the number of nodes and
is the number of nodes connected to the
ith node.
Distribution function calculates the node degree distribution, which is an important geometric feature in a complex network. It represents the ratio of the number of nodes with node degree k to total nodes. The degree of probability of any node is exactly k. The degree distribution of a complex network is close to the scale-free distribution in reality: .
Equations (2)–(7) calculate the characteristics of a small-world network. Equation (2) calculates the average path length where
is the shortest distance of the sum of the weights on the path between nodes
and
. Equation (3) is the average clustering coefficient, where
represents the aggregation coefficient of node
. Equations (4) and (5) compare the target network with other random networks, all of which have the same scale. The target network is a small-world network when Equations (4) and (5) are satisfied. Equations (6) and (7) calculate
and
, respectively, which represent the average path length and average clustering coefficient of random networks at the same scale.
Equations (8) and (9) analyze the transmission path for TWCN. There are two parameters, outward strength and inward strength. Outward strength or output strength (
) refers to the number of nodes connected by the arrow direction from the
ith node. Input strength (
) refers to the number of nodes with the arrow direction connecting to the
ith node.
where
represents the strength of the
th node and
is the weight of node
relative to node
.
Equation (10) analyzes the transmission intensity. Assuming that node
has
edges connected to other nodes in a complex network, the node has a median of
. The maximum value of the number of sides of the node and the corresponding node is expressed as
, then
. The actual number of edges of the node is
. The agglomeration coefficient of a node is the ratio of the actual number
and the maximum number of edges
, which is represented by
.
3.4. Hypothesis
To verify the validity and rationality of the TWCN design, we selected the strength value of the transmission network of sustainable incentive policies as the dependent variable for the evaluation of results. The strength can reflect the cited situation of the incentive policy in the process of transmission. The greater the value of the out-degree, the more significant the effect of the incentive policy (or the target node) on the other nodes. The next hypothesis test is to select the external indicator that affects the research object as the independent variable. Bivariate correlation analysis between the external indicators and the achievement evaluation indicators can explain whether there is a linear relationship between the two. The goal is to extract the indicators with significant correlation as the final external factors of the evaluation. The subsequent spatial agglomeration clusters the final external factors from previous statistical tests and finds the collection characteristics. The cluster characteristics become the input to compare with the TWCN analysis results. If the analysis results from both TWCN and clustering analysis are the same, it proves that the TWCN research method is reliable and sensible.
4. Results
4.1. Characteristic Analysis of the IMC incentive policies
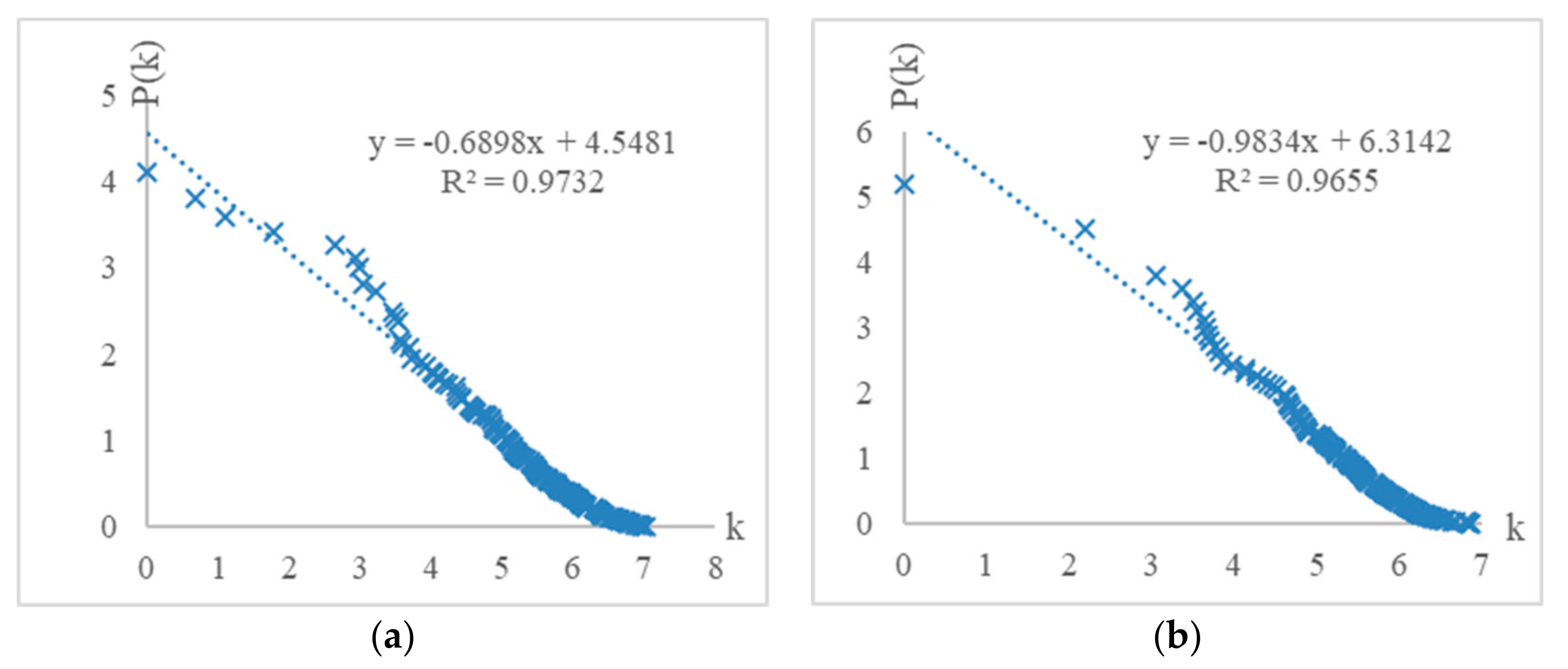
The statistical characteristics were analyzed with regard to node strength distribution and small-world characteristics of the TWCN for IMC incentive policies. The TWCN exhibits a long-tail characteristic in the logarithmic coordinates of the nodes’ distribution curves of out-degree and in-degree, which obeys the power law distribution.
Figure 4a shows the out-degree distribution of node strengths of the TWCN;
Figure 4b shows in-degree distribution of node strengths of the TWCN. Hence, incentive policies created by a few initiators (i.e., regions or cities) are cited by the rest. Furthermore, the complex network has scale-free characteristics.
To determine whether a network has the characteristics of a small-world network, we compared the average path length
L and average clustering coefficient
C with two random networks
and
at the same scale.
Table 3 shows the calculation results. The clustering coefficient of the complex network is 0.508, which is higher than that of the same size stochastic network (0.401). The average path length is 1.476, which is close to 1.214, the value for the same size stochastic network. Therefore, the TWCN network has the small-world characteristics.
4.2. Transmission Path Based on Degree Distribution
The strength of connections between TWCN nodes reflects the features of the transmission path. The out-degree and in-degree, respectively, represent the reference quantity and cited quantity of IMC incentive policies.
Table 4 shows examples of the calculation results, which are divided into sections, with the number of nodes counted.
Based on the transmission path analysis of IMC incentive policies, there are 127 nodes with fewer than 400 out-degree intervals, indicating that more than 70% of the 181 network nodes have a low quote rate. There are 13 nodes with more than 800 out-degree intervals, among which the eastern coastal areas (such as Jiangsu and Zhejiang Provinces) have seven nodes, indicating that these are the principal nodes in the transmission process. There are 101 nodes with fewer than 300 in-degree intervals. Among them, the eastern and central regions have more nodes, 34 and 22, respectively, compared to other regions. There are 64 nodes with 300 to 600 in-degree intervals. Among them, the eastern coastal and central regions have 12 and 16 nodes, respectively. Overall, the IMC incentive policies in the eastern coastal and central regions are more active than those in the northern and western areas. Among the 16 nodes with more than 600 in-degrees intervals, the northern region has five nodes. However, the out-degree values of these five nodes are less than 400, indicating that policy innovation in the region is low. In the western region (such as Guizhou and Gansu) and northeast region (such as Heilongjiang) the out-degrees are mainly less than 400 and in-degrees are mainly less than 300, indicating that these regions are less influenced by IMC incentive policies. In addition, the local governments of these regions are unwilling to implement such policies.
To identify the transmission routes, the following analysis integrated the key incentive elements in
Table 2 and the distribution of out-degree and in-degree nodes in
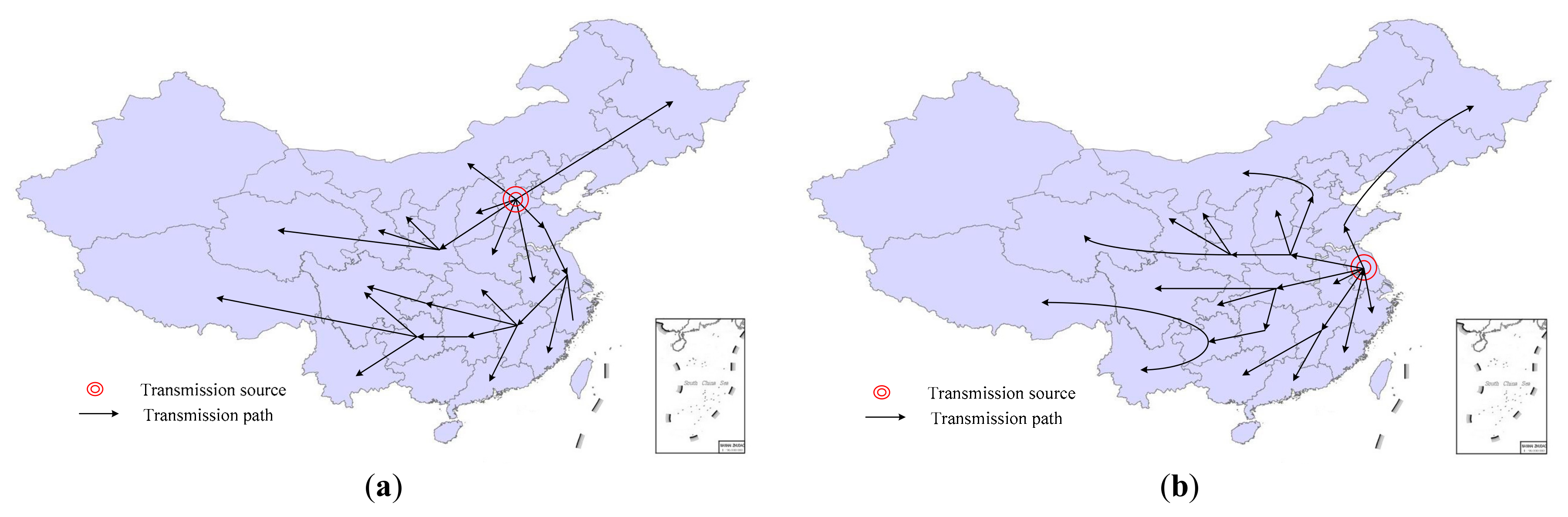
Table 4. Projects awarded is one of the most frequently quoted incentive policies for fiscal subsidy. The data show that this aspect was first mentioned in Shanghai and then disseminated to 26 provinces and cities (shown in
Figure 5a). Jiangsu Province was the earliest initiator of total investment in IMC in progress measurement (shown in
Figure 5b). It also has supporting policies of rural and affordable housing renovation projects. Shanghai was the first city to propose the policy of special funding for energy conservation of buildings (shown in
Figure 5c). Hunan was the first province to propose including the IMC incremental charge in the construction cost (shown in
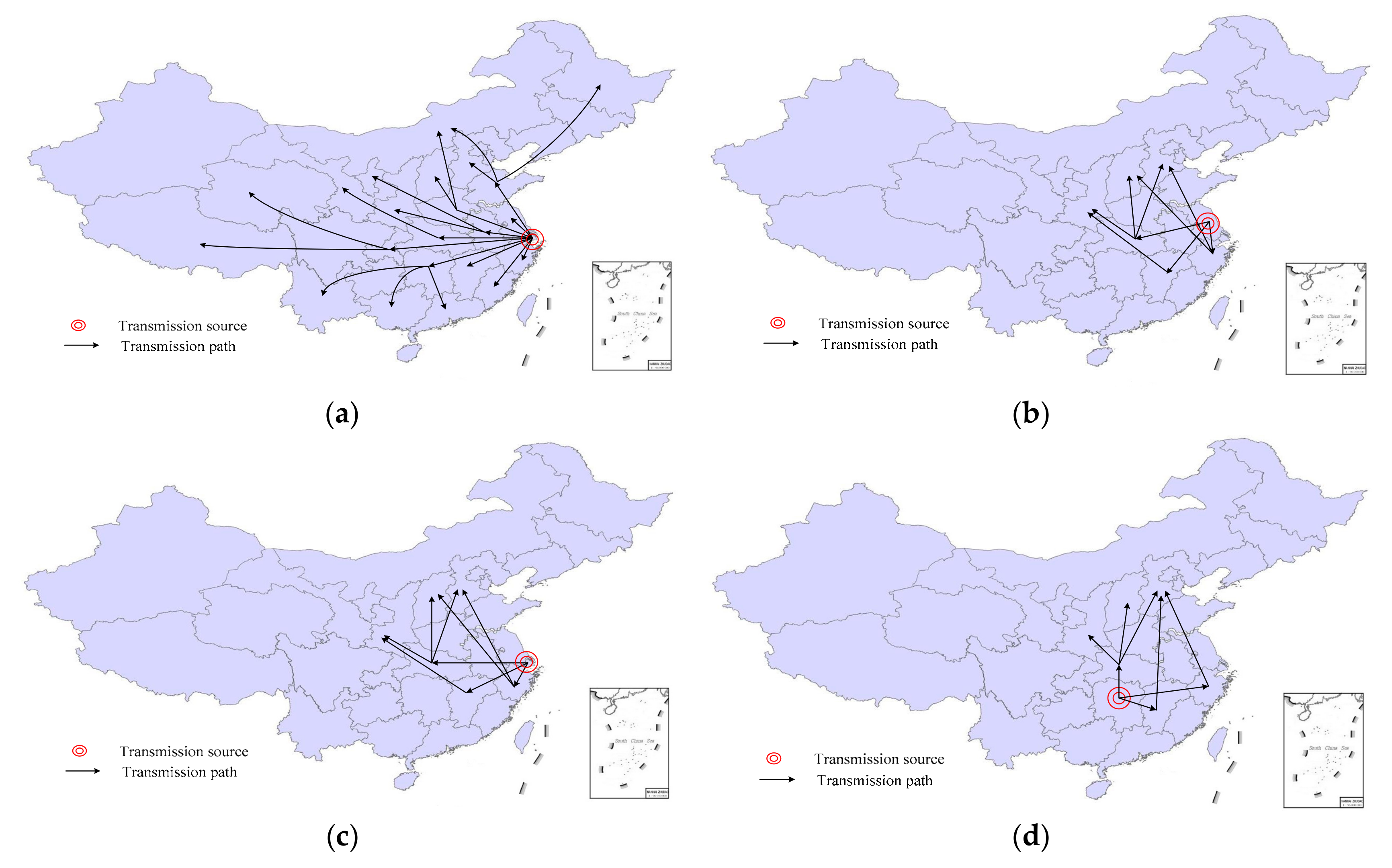
Figure 5d). The transmission routes of IMC policies started from these initiators and spread to the neighboring coastal regions of Zhejiang, Hubei, and Jiangxi Provinces, which introduced them and then conveyed them to the northern region (e.g., Hebei and Shanxi Provinces) and western region (e.g., Shaanxi Province). For other financial types of incentive policies, Shandong Province was the first to propose the policies of base award (
Figure 5e), subsidy (
Figure 5f), and prefunding supervision (
Figure 5g). Afterward, 19 provinces and cities referred to base awards and subsidies. However, only Hubei, Jiangxi, Sichuan, Guizhou, and Guangdong Provinces referred to the supervision policy of prefunding (
Figure 5f). The transmission routes continued with Jiangxi Province (
Figure 5g), which was the first to emphasize a preferential policy to attract investment. Then northeastern regions such as Heilongjiang and Liaoning Provinces cited this policy and western regions such as Sichuan and Tibet followed.
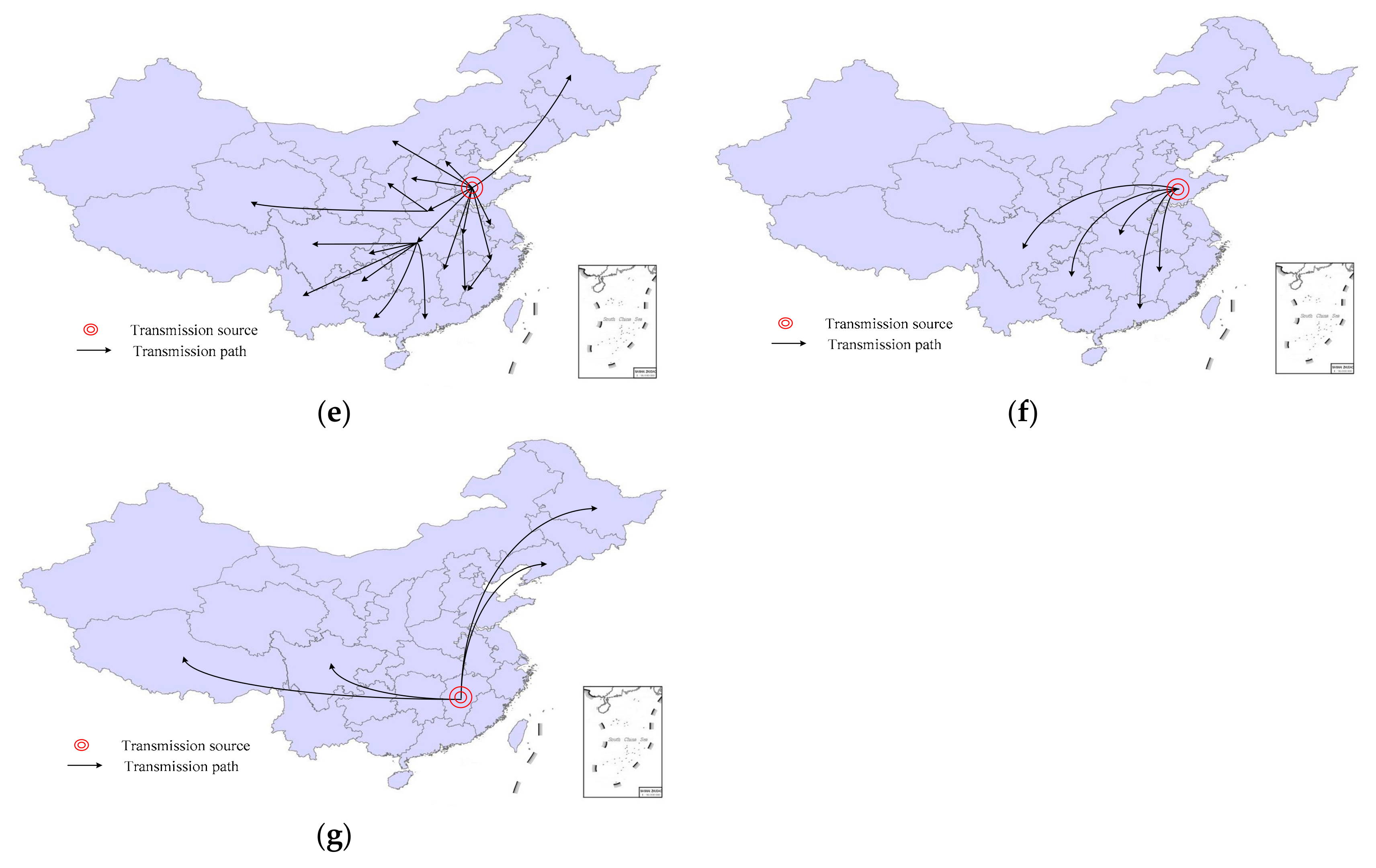
Another way to recognize the transmission routes is by analyzing incentive policies related to land use. Jiangsu was the first province to propose incentive policies by giving priority to land-use indices, such as a 3% plot ratio incentive, land supply by transfer, and land transfer installment payment, in addition to land supply allocation, bidding, auction, and hanging out shingles for land supply.
Figure 6a shows that these policies are cited the most frequently by following provinces and cities in their subsequent incentive policies. For example, after seeing the satisfactory results of land-use policies, Hunan first introduced a 5% plot ratio (
Figure 6b), which was later cited by Sichuan, Qinghai, Shaanxi, and other western regions to further strengthen the basis of the 3% plot ratio reward proposed by Jiangsu.
Figure 6c shows that Zhejiang was the first province to recommend the land supply plan policy, which was subsequently cited by 26 provinces and cities. Nevertheless, the policy does not include an implementation plan. To improve operability, Shanghai started excluding construction areas for precast exterior wall panels (
Figure 6d), accompanied by eastern coastal areas (such as Jiangsu and Shandong) and northern regions (such as Hebei and Beijing).
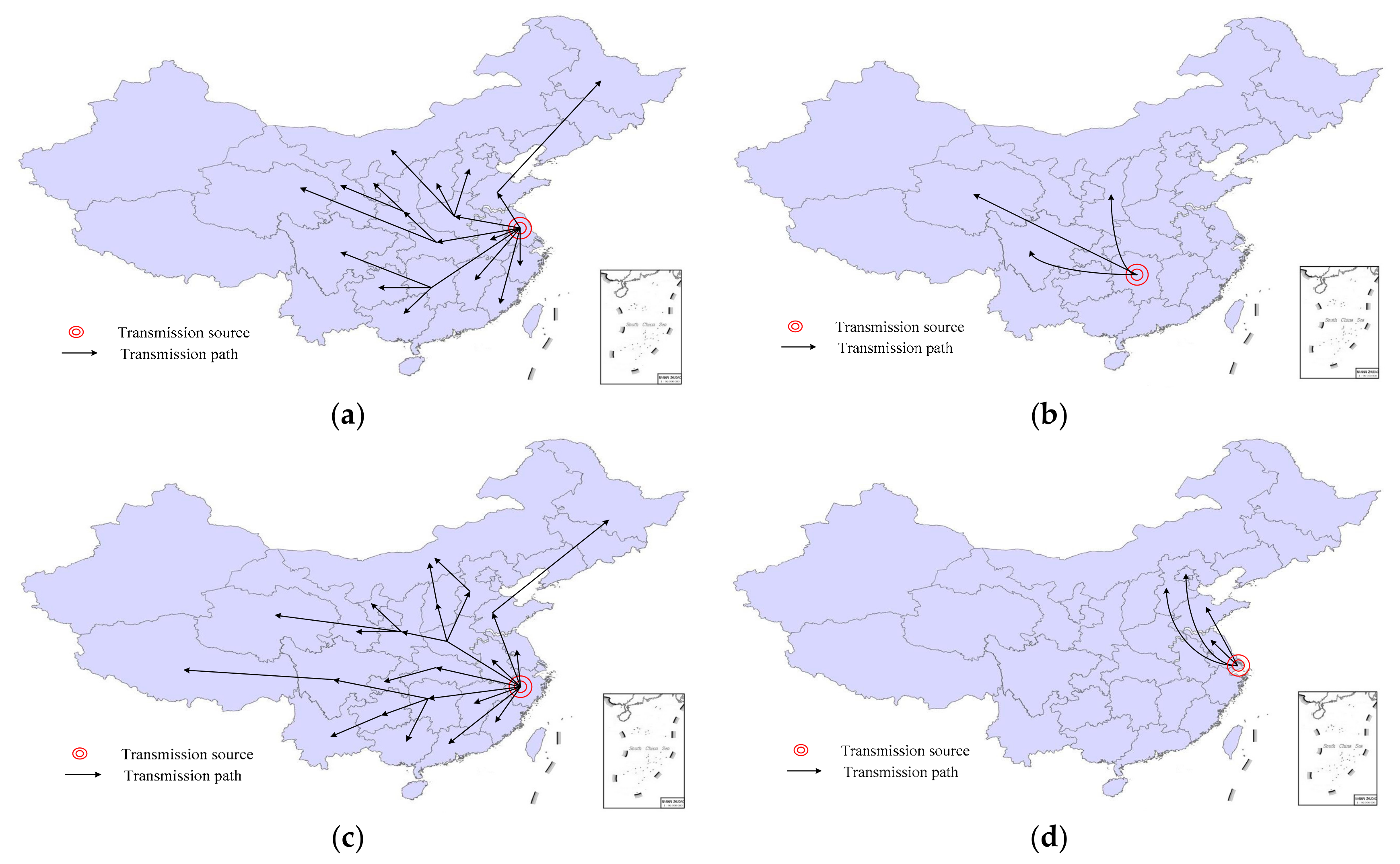
The adoption of taxation policies is vigorous due to their generalizability.
Figure 7a shows the transmission paths of VAT refund policies for new wall materials, which have the highest citation rate of all incentive policies. For example, Hebei Province first made a motion on a taxation policy for new wall materials, which was then cited by 26 other provinces and cities.
Figure 7b shows that other taxation policies with high citation rates were initiated in Jiangsu Province; for example, preferential treatment for high-tech enterprises, deductions for research and development expenses, quality margin discounts, farmers’ salary margin discounts, decoration cost tax discounts, performance bond benefits, performance bond discounts, wall reform fund/bulk cement fund discounts, and urban infrastructure construction preferential fees benefits. Overall, the transmission paths of IMC incentive policies show how sustainable incentive strategies proliferate from initiation to transformative practice. The data show that the policies first appeared in the eastern coastal areas (such as Jiangsu, Shanghai, and Zhejiang) and gradually expanded to the western and northern regions.
4.3. Transmission Intensity Based on Clustering Coefficient
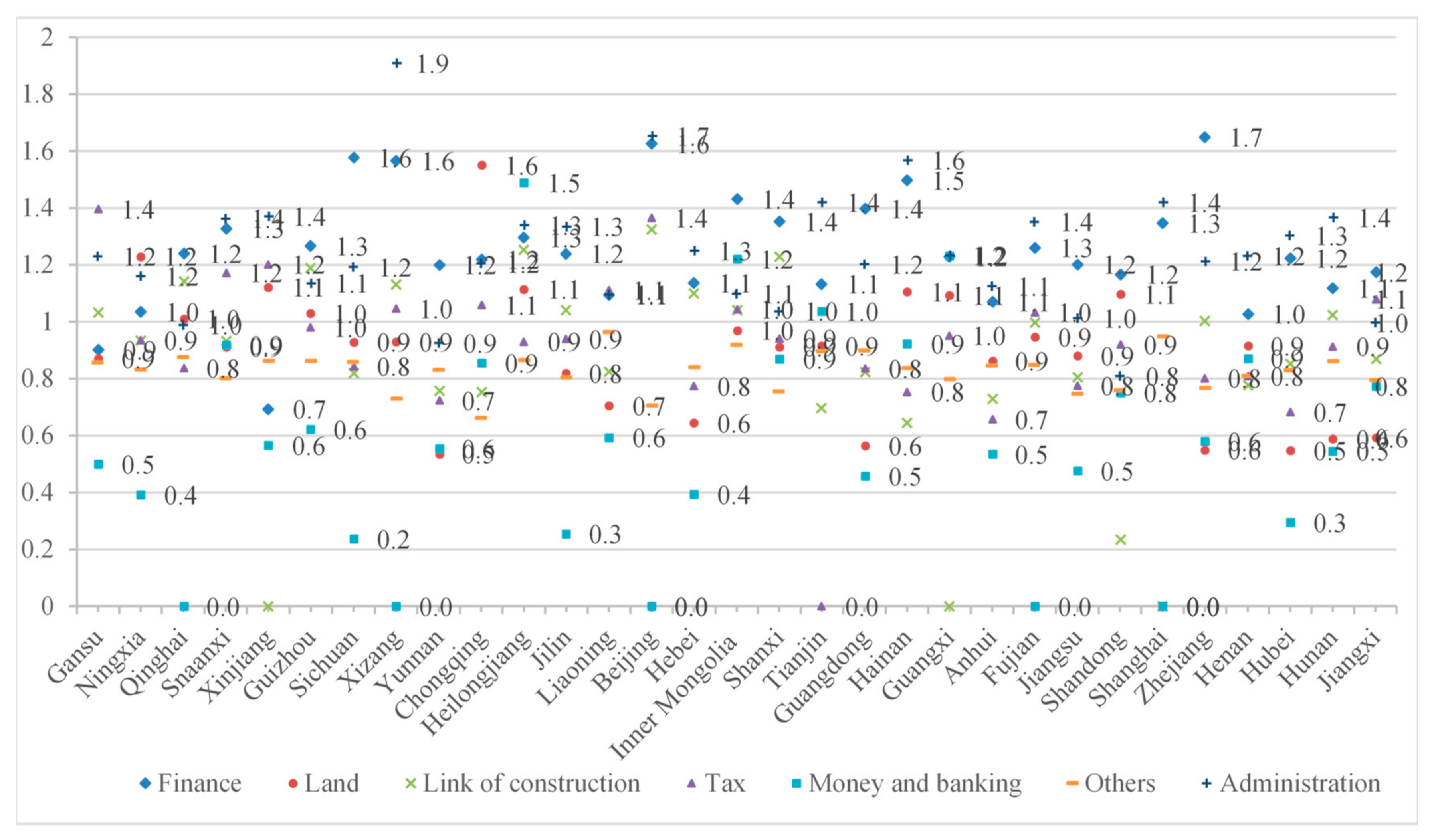
The clustering coefficient of TWCN reflects the tight connection between adjacent nodes. The larger the value, the more frequent the interaction among nodes, leading to greater intensity of incentive policies. Due to the policy hierarchy, the introduction of policy documents by various regional governments is affected by the application of provincial and ministerial policy documents. To analyze transmission intensity, we used the mean method to deal with the calculated clustering coefficient value of each node, which is categorized under provinces, municipalities, or autonomous regions.
Figure 8 shows the transmission clustering coefficients of IMC incentive policies, confirming that fiscal and taxation policies have relatively larger clustering coefficients (0.6–1.4) than the rest of the coefficients illustrated in
Figure 4a. The connections between these nodes are relatively more frequent than the rest as well, indicating that all provinces and cities in China pay more attention to these types of incentive policies than other types. Furthermore,
Figure 8 shows that the clustering coefficients of finance, link of construction, and RDT policies are smaller than the rest, mainly concentrated between 0 and 1. These clustering coefficients specify that the connections between nodes are weak, indicating that the governments of these areas are less willing to issue incentive policies for IMC. Hence, the implementation of these policies is very limited in these areas.
The following spatial agglomeration features of IMC incentive policies describe the small-world transmission mechanism of the network.
Figure 9 utilizes GIS visualization results to map the relative agglomeration characteristics of the various types of incentive policies in geographic regions. Based on policy coding in
Figure 9 and
Table 2, the following discussion explains the key incentives in the transmission process.
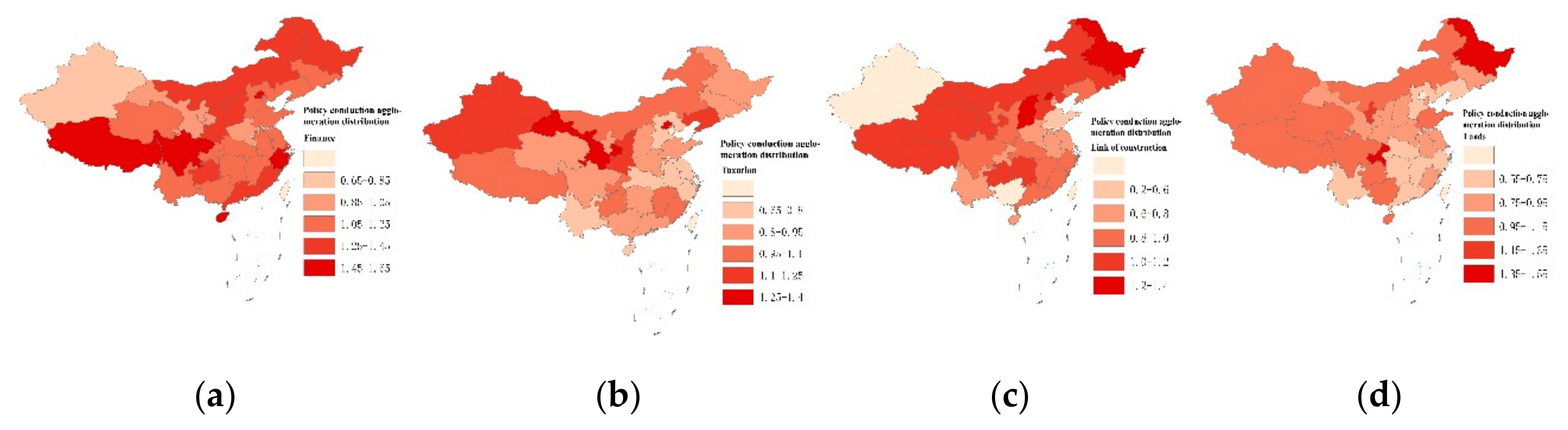
Figure 9a shows the spatial agglomeration of fiscal policy. Guangdong Province and other eastern coastal areas, together with Henan and other central areas, as well as northern areas, have greater transmission intensity than the rest of China. Examples of the most cited fiscal policies include rewarding or subsidizing IMC projects, enterprises, and bases; encouraging investments to integrate component parts into total construction; giving preference to high-tech enterprises (especially prefabricated building enterprises); specifying funds for the construction of building energy conservation; and providing financial support for rural and affordable housing projects.
Further analysis of
Figure 9b shows that as far as the tax policies are concerned, most areas show great transmission intensity and more than 30 kinds of taxes are investigated. Especially the eastern coastal areas, such as Jiangsu and Shandong Provinces, together with the western regions, such as Shaanxi and Yunnan Provinces, demonstrate high transmission intensity. Examples of repeatedly cited tax incentives include preferential treatment for high-tech enterprises, deduction of research and development expenses, tax discounts for quality margins, discounts for farmers’ salary margins, discounts for new wall materials, discounts for decoration costs, discounts for performance bonds, and discounts for wall reform fund/bulk cement funds.
Figure 9c shows the spatial agglomeration of construction link policies. This type of incentive mainly involves the stages of inviting and bidding, construction, and operation. The transmission intensity in Hunan, Henan, Hebei, and Liaoning is strong. Among them, Hunan has mainly issued incentives in terms of obtaining commercial licenses for housing sales in advance, invitations to bid, and priorities in bidding. Henan, Hebei, and Liaoning have mainly focused on incentives for transportation and exemption of shutdown for taking turns on pollution days. For example, some small industrial plants are forced to shut down on certain weekdays to reduce the pollution in the surrounding areas. Usually these plants take turns temporarily closing for one or two days a week. The exemption policy allows IMC companies to continue production and construction, which helps to improve productivity and reduce wasted time.
Figure 9d shows the spatial agglomeration of land policies. Chongqing has the greatest impact on the policy transmission process. Guangdong, Yunnan, the northwestern areas, and the eastern areas have less impact on policy transmission. Beijing and Shanghai have little impact on policy transmission. The land policies are mainly reflected in building area, plot ratio, and way-of-land granting.
Figure 9e shows the spatial agglomeration of financial policies (specifically loans and banking). Heilongjiang, Inner Mongolia, Guangxi, and Shanxi have a significant impact on policy transmission. On the other hand, Qinghai, Tibet, Beijing, Fujian, and Shanghai have almost no impact on this type of policy. Incentives in financial policies involve consumer credit and corporate credit. Consumer credit includes preferential treatment for concessional loans, mortgage loans, loan quotas, and interest rates. Corporate credit supports lending and opens up green channels for finance.
Figure 9f shows the spatial agglomeration of administrative policies. Policies with a substantial amount of citations mainly support appraising enterprises that adopt prefabricated building, optimizing the approval procedure in applications for declaration, and giving certain support to the application of qualifications.
Figure 9g shows the spatial agglomeration of other RDT policies. This type of policy encourages enterprises to strive for higher-level funds, train talent, and add new laboratories and construction for R&D platforms. RDT policies are cited on numerous occasions in the transmission process of IMC incentive policies. However, this type of incentive policy lacks details and criteria, with no specific practical measures proposed in the entire nation; hence, it has low operability.
4.4. Outcome Evaluation
For verification and validity of the TWCN analysis results, the outcome evaluation of this research starts with an analysis of the out-degree results of IMC incentive policies using the TWCN analysis to generate indicators of achievement evaluation. We selected 13 cities according to their geographical location, as shown in
Table 5, and created corresponding nodes in the TWCN. Then we calculated the out-degrees of the 13 selected cities and analyzed the transmission effects of their incentive policies. The first and second columns of
Table 5 show the results of the high output values; the third and fourth columns show the medium-level values; and the fifth and sixth show the medium-to low-level values. Based on the spatial agglomeration of these 13 nodes, the out-degree value of the IMC incentive policy is generally concentrated in the eastern region (e.g., Wuhan in
Table 5), followed by the central region (e.g., Kaifeng), and the smallest in the northwestern (e.g., Baotou), southwestern (e.g., Guiyang), and northern (e.g., Ankang) regions. The transmission path of incentive policies goes from the eastern region with a large output value to the central region, and then to the northwestern, southwestern, and northern regions. The TWCN analysis of the selected data verifies the same results as the transmission paths identified in
Section 4.3.
This paper uses the strength of the nodes obtained from the TWCN analysis as the dependent variable, and the indicators related to the development of IMC as independent variables. The first hypothesis states that the development degree of IMC in each region is positively correlated with the intensity of the incentive policy. In other words, the better the development of prefabricated building, the greater the cited rate of the local incentive policy. To verify the accuracy and confirm the analysis results, we continued the calculation using the TWCN based on the previously selected 13 cities. Moreover, since the announcement of the Guidelines for the Office of the State Council on the Development of Prefabricated Building by the State Council on 27 September 2016, local governments have successively issued instructions on the implementation of IMC or assembly buildings in response to the call of the state. The guidelines and instructions acknowledge that the development of IMC is an important part of the transformation and upgrade of the construction industry in China at this stage. Yet, the IMC practices started relatively late. The statistics of relevant data are still incomplete and uncomprehensive. In the existing official statistics, IMC is included in the statistics of relevant indicators of the construction industry. Therefore, this research uses the relevant indicators of the construction industry as variables to explain IMC development.
Table 6 shows the relevant index data, including the total output value of the construction industry (X1), the added value of the construction industry (X2), the number of construction enterprises (X3), the construction area of the construction enterprise (X4), and the completed area of the construction enterprise (X5) as explanatory variables. The prefabricated building node out-degree strength (Y) is analyzed by the explanatory variables.
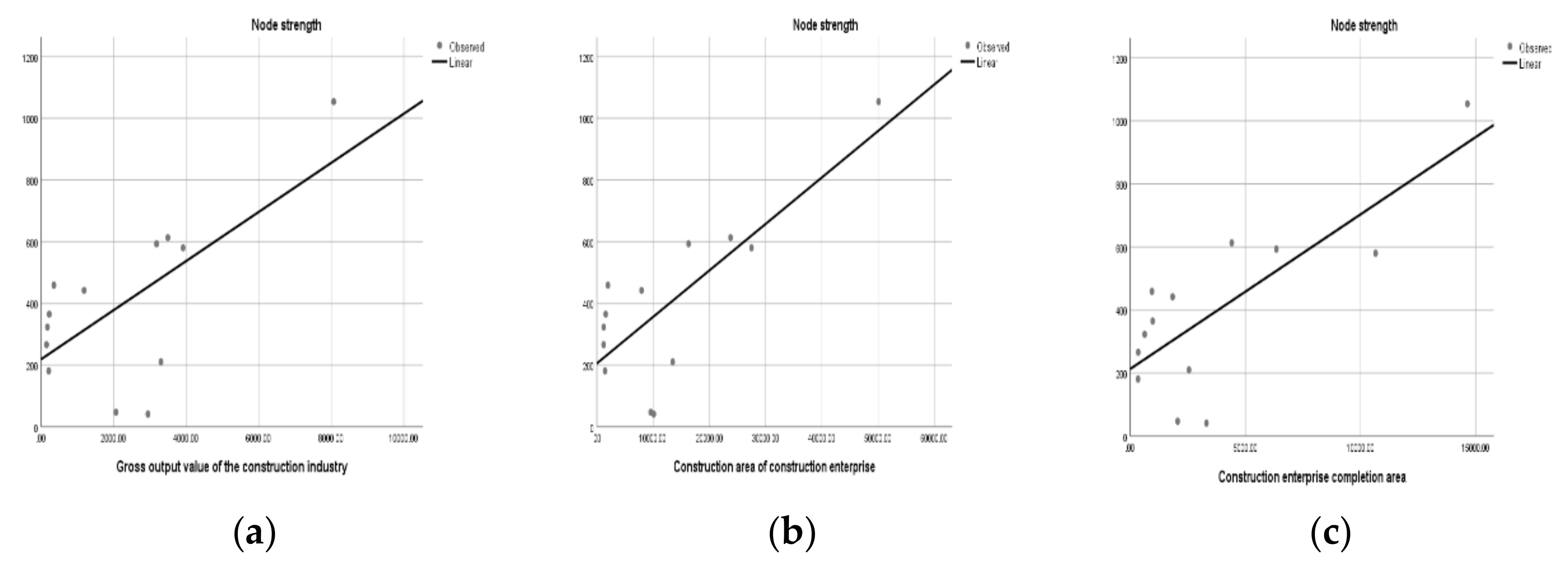
Table 7 shows the correlation analysis of each factor with the strength of the transmission node of the incentive policies. When the significance level is 0.05, the sig. values are 0.659, 0.777, and 0.779, corresponding to the total output values of the construction industry (X1), the construction housing area of the construction enterprise (X4), and the completed area of the construction enterprise (X5), respectively. The correlation level is significant. The values of the indicators added value of the construction industry (X2) and number of construction enterprises (X3) are 0.351 and 0.410, respectively, which do not meet the requirements of the critical values of the correlation coefficient. Therefore, this research uses the indicators total output value of the construction industry (X1), the construction housing area of the construction enterprise (X4), and the completed area of the construction enterprise (X5) to explain the node strength of the incentive policies.
To find the node strength, this research uses the bivariate correlation coefficients on the total output value of the construction industry (X1), the construction area of the construction enterprise (X4), and the completed area of the construction enterprise (X5) for the influence of incentive policies.
Table 8 shows the results of linear fitting performed by SPSS 25.0 software. R
2 of the linear fitting model of X1, X4, and X5 is 0.434, 0.604, and 0.608, respectively. The corresponding sig. values are all below 0.05, which indicates that the correlation level is significant. The resulting linear fit curves are shown in
Figure 10 for the completed area of the construction enterprise, the construction housing area of the construction enterprise, and the total output value of the construction industry as the independent variables. The strengths of IMC incentive policies are positively correlated. The incentive policies encourage the growth of the construction area, completed area, and total output value of the construction industry.
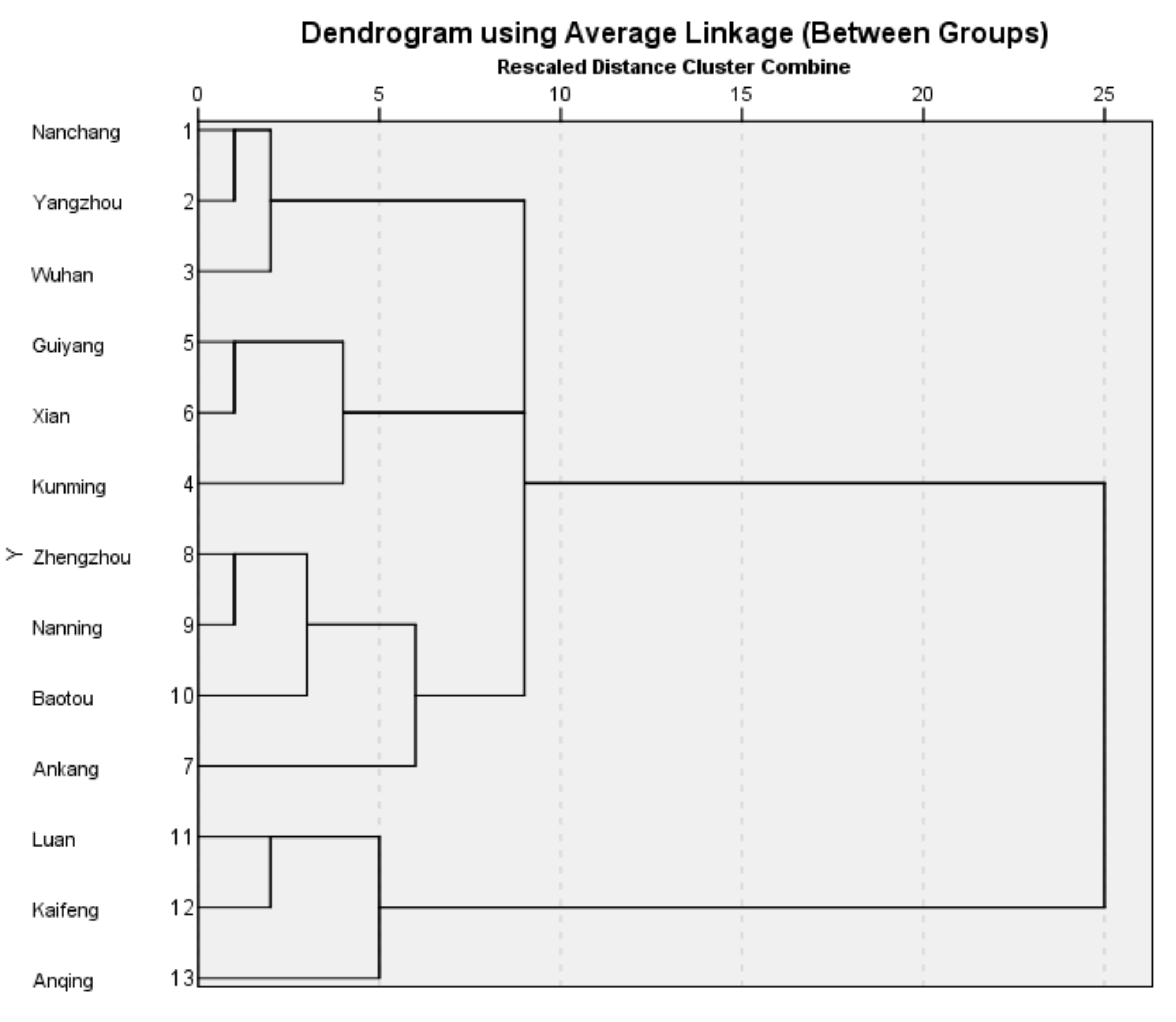
This research implements cluster analysis to verify that the spatial agglomeration of the selected 13 nodes for IMC development is consistent with the results of complex network analysis.
Table 9 shows the calculation results of the analysis carried out on indicators X1, X4, and X5. Based on the results in
Table 9, the results of cluster analysis are divided into four categories. Nanchang, Yangzhou, and Wuhan are in the first category. They are mainly in the eastern areas, in Hubei, Jiangsu, and Jiangxi Provinces. The cities of Lu’an, Kaifeng, and Anqing are in the second category. They are in the central area, in Anhui and Henan Provinces. Zhengzhou, Nanning, Ankang, and Baotou are in the third category. Kunming, Guiyang, and Xi’an are in the fourth category. The third and fourth categories are in the southwestern, northwestern, and northern regions (Shaanxi, Guizhou, Yunnan, and Inner Mongolia). According to the out-of-range value in
Table 2 and
Figure 11, the clustering result is larger in the first category because the intensity is greater than 500. The clustering result is decreased in the second category with a concentration between 300 and 500. For the clustering results in the third and fourth categories, the outswing values are mainly concentrated below 300. Therefore, from the results of cluster analysis of geographical regions, incentive policies for IMC are declining according to region, with the largest in the east, the second largest in the central region, and the least in the northwest, southwest, and north. The previous complex network analysis results are consistent with the correlation analysis of the samples, which confirms the scientific validity and rationality of the TWCN method.
5. Discussion
Based on the transmission mechanism of IMC incentive policies, this research scrutinizes the macro and micro perspectives of transmission path and intensity for sustainable industrial policies. From a macro perspective, the TWCN establishes a law of regional differentiation based on the issuing time and the contents of intercity IMC incentive policies through complex network analysis. Meanwhile, among the 293 prefecture-level cities in China, 33% cities have not released incentive policy documents for IMC. In particular, the western regions (such as Gansu, Ningxia, Qinghai, Tibet, and Xinjiang) and northeastern regions (such as Heilongjiang and Jilin) have only issued provincial-level or relevant documents in their provincial capitals. This indicates that these areas are still in the wait-and-see stage regarding the development of prefabricated building or IMC. Their incentive policies have not been issued yet. However, in the eastern coastal areas (such as Jiangsu, Zhejiang, and Shandong) and other central areas (such as Anhui, Henan, and Hunan), basically all cities have issued relevant documents on IMC incentive policies. At present, there are still noticeably insufficient IMC incentive policies in various provinces and cities in China. It is necessary to formulate policies with operable details for different stages of development in different regions. In areas suitable for promotion, the suggestion is to pinpoint pilot areas for active promotion and systematically increase the proportion of prefabricated building or IMC in newly built residential buildings. Another suggestion is to encourage and conduct pilot projects in potential areas to gradually realize nationwide coverage of IMC.
At the level of transmission intensity, we explored the spatial agglomeration characteristics of incentive policies from the aspects of finance, taxation, land, money and banking, link of construction, and administration. We diagnosed the key incentive elements of different policy content in each geographical area. The TWCN analysis shows that there are specific policy incentives and penalties for financial, taxation, land, and RDT aspects. This is attractive to enterprises or individuals who are IMC stakeholders. Particularly, the TWCN analysis shows greater policy transmission intensity of financial and tax incentives, land area, and plot ratio awards than other incentive policies. As for financial and administrative policies, there are insufficient indicators in China. The characteristics of specific rewards and penalties are difficult to achieve due to the unclear indicators proposed by governments, which indicates that local governments do not value these incentives as important. The suggestion is that the governments should further elaborate IMC incentive policies and measures and establish relevant incentive measures for financial and administrative aspects. Then, policy makers can strengthen and refine the aspects of standards and systems, administrative examination and approval, publicity and training of incentive content to promote IMC. Concurrently, researchers and policy makers should carefully examine the specific values for quantifiable indicators before proposing or announcing them; for example, the precise proportion of the loan quota for consumer provident funds and the exact value of incentives or subsidies given for fabricated buildings.
We explored the transmission process of IMC incentive policies through a comparative analysis of the strength of the complex network to determine the spatial transmission paths. The results show that there is a high rate of transmission of IMC policies in finance, taxation, and land. These policies were introduced in the eastern coastal areas (e.g., Jiangsu, Shanghai, and Zhejiang) and then gradually spread to the surrounding areas, including the central, western, and northern areas. The policy contents of various regions (e.g., Liaoning, Jilin, Heilongjiang, Inner Mongolia, Shanxi, and Guangxi) focus on finance, administration, and links of construction. This indicates that these regions have issued relevant policy documents but failed to achieve the incentive effects. For areas where the development of prefabricated building is lagging behind, the suggestion is to learn from the experience of areas with better development. Attention should be focused on detailed incentive policies, including economic incentives such as finance and taxation and practical subsidies. In addition, regions should study their local conditions to formulate relevant incentives. For example, cities in the west can consider national preferential policies for their development; areas with high pollution in winter (such as Hebei and Henan) may give preferential treatment for nonstop work.
6. Conclusions
This paper proposes the TWCN design, which is an analytical method for complex networks based on textual data of sustainable incentive policies. The research focused on the question of what the internal conduction laws are between incentive policies. To examine IMC incentive policies in China, we first formulated factor codes by text analysis based on the collected incentive texts of the past 10 years. Then, we implemented the factor codes as experimental data to create connections. The next step was to program the experimental data to establish the complex network model for the transmission mechanism of IMC incentive policies. By calculating the node strength, clustering coefficient, and other statistical characteristics, we deeply analyzed the transmission mechanism of IMC incentive policies from the aspects of transmission path and transmission intensity. In order to verify the validity and rationality of the experimental method, we used the TWCN analysis results as independent variables, and the correlation index of the IMC development as the dependent variable. The results from the selected samples are consistent with the TWCN analysis results, which confirms the reliability of the method. It is feasible to use the TWCN method to study the transmission of sustainable incentive policies.
The design of the TWCN sheds light on the transmission mechanism of incentive policies between cities and fills the theoretical gap of quantitative description of the dynamic paths of strategy influences. We proposed a novel research idea for text and content analysis and proved its feasibility at both the micro and macro level. In addition to evaluating the effects of new industrial incentive policies, the TWCN is suitable to study the transmission laws of interest rates for monetary policies, stock exchange rates for market monitoring, and exchange price differences for exploration of business opportunities. From the practical value perspective, using cities as observation points to study the transmission of sustainability policies can help to find the elements that policy makers focus on when introducing relevant procedures. Studying the transmission paths of sustainable incentive policies can reveal the laws of how different types of policies disseminate geographically. When decision makers formulate the relevant mechanisms of rewards and penalties, they can implement the TWCN to recognize the performance and functions of existing policies. Using existing local and outside policies as references, decision makers can expansively consider the actual conditions and propose effective strategies to ensure the sustainability of policies. Additionally, the TWCN analysis discloses unsatisfactory situations in incentive policies for research, development, and training (RDT) for sustainability in industries. Government funding agencies could foster the sustainable development of IMC by investing in research grants and encouraging researchers and educators to explore the related areas.
As with any study, the article at hand suffers from several limitations that are worth consideration for further research activities. First, we collected data on the relevant policies, guidelines, and regulations published on official governments websites in the past 10 years. Future research should ensure the comprehensiveness of data collection and take into account the openness of policies announced by government departments. One possible expansion of data availability is to study the incentive policies by in-depth interviews to gain a complete understanding of the intentions. Secondly, we studied the transmission path and intensity of incentive policies between cities in China based on TWCN. However, the differences in economic, environmental, political and social factors of individual cities were not taken into account when establishing the relationships among cities and regions. Thus, we would consider the above factors to optimize the model of TWCN in further research. Thirdly, this paper used published policy texts as the research data, but it is difficult to make a reasonable prediction for cities that have not issued the policy. As the volume of research data increases, TWCN network nodes will increase greatly. Future research will introduce the complex network evolution models or related algorithms to construct a dynamic TWCN model to study the dynamic transmission characteristic of incentive policies among cities and regions.
Furthermore, building upon and extending the research finding in the context of prefabricated building, future research could also expand the sample data on incentives of other countries, especially between close neighboring countries where develop similar incentive policies. Moreover, it should be noted that this study focuses on the transmission of incentive policy content between cities and regions. In future research, we would also consider interactions between different actors such as policy makers and implementers/practitioners to explore social network characteristics due to knowledge sharing in policy making, and then research the influence of consolidating arenas for knowledge sharing and discussion at the policy level among different regions.
Author Contributions
Writing—Conceptualization, Funding Acquisition, Project Administration, Resources, Data Curation, L.L.; Writing—Original Draft Preparation, L.F.; Conceptualization, Methodology, Supervision, Validation, X.G.; Writing—Review and Editing, Methodology, and Verification, H.X.; Review, Editing, Supervision, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received support from the National Key R&D Program of China (No. 2018YFD1100202), the Ministry of Education Humanistic and Social Science Program of China (No. 19YJC630080), the General Project of Shaanxi Province Soft Science Research Program (No. 2019KRM197), the Key Research Base of Philosophy and Social Science of Education Department of Shaanxi Province (No. 17JZ048), and the Shaanxi Key Research Base of Co-construction and Sharing for Human Settlement Environment and Good Life of the New Era.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shazmin, S.A.A.; Sipan, I.; Sapri, M. Property tax assessment incentives for green building: A review. Renew. Sustain. Energy Rev. 2016, 60, 536–548. [Google Scholar] [CrossRef]
- Maki, A.; Burns, R.J.; Ha, L.; Rothman, A.J. Paying people to protect the environment: A meta-analysis of financial incentive interventions to promote proenvironmental behaviors. J. Environ. Psychol. 2016, 47, 242–255. [Google Scholar] [CrossRef]
- Liebe, U.; Gewinner, J.; Diekmann, A. What is missing in research on non-monetary incentives in the household energy sector? Energy Policy 2018, 123, 180–183. [Google Scholar] [CrossRef]
- Jones, C.A.; Clark, E.M.; Weintraub, A.; Zia, A. Personalized Adaptive Rewards Versus Incentives to Motivate Sustainable Healthy Behavioral Change- A Neo-Maslowian Conceptual Model. Value Health 2016, 19, A823–A824. [Google Scholar] [CrossRef]
- Ravšelj, D.; Aristovnik, A. The Impact of Private Research and Development Expenditures and Tax Incentives on Sustainable Corporate Growth in Selected OECD Countries. Sustainability 2018, 10, 2304. [Google Scholar] [CrossRef]
- Thornton, G.; Franz, M.; Edwards, D.; Pahlen, G.; Nathanail, P. The challenge of sustainability: Incentives for brownfield regeneration in Europe. Environ. Sci. Policy 2007, 10, 116–134. [Google Scholar] [CrossRef]
- Cease, B.; Kim, H.A.; Kim, D.; Ko, Y.; Cappel, C. Barriers and incentives for sustainable urban development: An analysis of the adoption of LEED-ND projects. J. Environ. Manag. 2019, 244, 304–312. [Google Scholar] [CrossRef]
- Adekanye, O.G.; Davis, A.; Azevedo, I.L. Federal policy, local policy, and green building certifications in the U.S. Energy Build. 2019, 209. [Google Scholar] [CrossRef]
- Si, S.Y.; Lyu, M.J.; Lin Lawell, C.-Y.C.; Chen, S. The effects of energy-related policies on energy consumption in China. Energy Econ. 2018, 76, 202–227. [Google Scholar] [CrossRef]
- Diane, K. Petroleum industry tax incentives and energy policy implications: A comparison between Australia, Malaysia, Indonesia and Papua New Guinea. Energy Policy 2019, 126, 212–222. [Google Scholar] [CrossRef]
- Grazhevska, N.; Virchenko, A. Special Features of the Ukrainian Fiscal Policy Transmission Mechanism under Increasing Macroeconomic Instability. Procedia Econ. Financ. 2014, 16, 680–689. [Google Scholar] [CrossRef]
- Kozlova, M.; Collan, M.; Luukka, P. Renewable energy in emerging economies: Shortly analyzing the Russian incentive mechanisms for renewable energy investments. In Proceedings of the International Research Conference, GSOM Emerging Markets Conference: Business and Government Perspectives, St. Petersburg, Russia, 14–17 October 2015. [Google Scholar]
- Zhang, X.; Bai, X.; Shang, J. Is subsidized electric vehicles adoption sustainable: Consumers’ perceptions and motivation toward incentive policies, environmental benefits, and risks. J. Clean. Prod. 2018, 192, 71–79. [Google Scholar] [CrossRef]
- Pleger, L.E.; Lutz, P.; Sager, F. Public acceptance of incentive-based spatial planning policies: A framing experiment. Land Use Policy 2018, 73, 225–238. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Charakopoulos, A.Κ.; Karakasidis, T.E.; Papanicolaou, P.N.; Liakopoulos, A. The application of complex network time series analysis in turbulent heated jets. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 024408. [Google Scholar] [CrossRef] [PubMed]
- Steinhardt, D.A.; Manley, K. Adoption of prefabricated housing—The role of country context. Sustain. Cities Soc. 2016, 22, 126–135. [Google Scholar] [CrossRef]
- Jaillon, L.; Poon, C.S. Sustainable construction aspects of using prefabrication in dense urban environment: A Hong Kong case study. Constr. Manag. Econ. 2008, 26, 953–966. [Google Scholar] [CrossRef]
- Yuan, Z.M.; Sun, C.S.; Wang, Y.W. Design for Manufacture and Assembly-oriented parametric design of prefabricated buildings. Autom. Constr. 2018, 88, 13–22. [Google Scholar] [CrossRef]
- Song, A.; Lu, L.; Liu, Z.; Wong, M.S. A study of incentive policies for building-integrated photovoltaic technology in Hong Kong. Sustainability 2016, 8, 769. [Google Scholar] [CrossRef]
- Zou, Y.H.; Zhao, W.X.; Zhong, R.J. The spatial distribution of green buildings in China: Regional imbalance, economic fundamentals, and policy incentives. Appl. Geogr. 2017, 88, 39–47. [Google Scholar] [CrossRef]
- Burns, J.E.; Kang, J.S. Comparative economic analysis of supporting policies for residential solar PV in the United States: Solar Renewable Energy Credit (SREC) potential. Energy Policy 2012, 44, 217–225. [Google Scholar] [CrossRef]
- Kirakozian, A. One without the other? Behavioural and incentive policies for household waste management. J. Econ. Surv. 2016, 30, 526–551. [Google Scholar] [CrossRef]
- Coscieme, L.; Sutton, P.; Mortensen, L.F.; Kubiszewski, I.; Costanza, R.; Trebeck, K.; Pulselli, F.M.; Giannetti, B.F.; Fioramonti, L. Overcoming the Myths of Mainstream Economics to Enable a New Wellbeing Economy. Sustainability 2019, 11, 4374. [Google Scholar] [CrossRef]
- Aquila, G.; Pamplona, E.D.O.; Queiroz, A.R.D.; Junior, P.R.; Fonseca, M.N. An overview of incentive policies for the expansion of renewable energy generation in electricity power systems and the Brazilian experience. Renew. Sustain. Energy Rev. 2017, 70, 1090–1098. [Google Scholar] [CrossRef]
- Zhang, X.; Bai, X. Incentive Policies from 2006 to 2016 and New Energy Vehicle Adoption in 2010–2020 in China. Soc. Sci. Electron. Publ. 2017, 70, 24–43. [Google Scholar] [CrossRef]
- Schwilch, G.; Lemann, T.; Berglund, Ö.; Camarotto, C.; Cerdà, A.; Daliakopoulos, I.N.; Kohnová, S.; Krzeminska, D.; Marañón, T.; Rietra, R.; et al. Assessing impacts of soil management measures on Ecosystem Services. Sustainability 2018, 10, 4416. [Google Scholar] [CrossRef]
- Liang, X.; Yu, T.; Hong, J.; Shen, G.Q. Making incentive policies more effective: An agent-based model for energy-efficiency retrofit in China. Energy Policy 2019, 126, 177–189. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Luo, X.; Fu, H.; Wang, M.; Li, L. Impact of Different Policy Instruments on Diffusing Energy Consumption Monitoring Technology in Public Buildings: Evidence from Xi’ an, China. J. Clean. Prod. 2020. [Google Scholar] [CrossRef]
- William, R.; Garg, J.; Stillwell, A.S. A game theory analysis of green infrastructure stormwater management policies. Water Resour. Res. 2017, 53, 8003–8019. [Google Scholar] [CrossRef]
- Zhao, R.; Zhou, X.; Han, J.; Liu, C. For the sustainable performance of the carbon reduction labeling policies under an evolutionary game simulation. Technol. Forecast. Soc. Chang. 2016, 112, 262–274. [Google Scholar] [CrossRef]
- Sarker, B.R. Consignment stocking policy models for supply chain systems: A critical review and comparative perspectives. Inter. J. Prod. Econ. 2014, 155, 52–67. [Google Scholar] [CrossRef]
- Kihlstrom, R.E.; Matthews, S.A. Managerial incentives in an entrepreneurial stock market model. J. Financ. Intermediat. 1990, 1, 57–79. [Google Scholar] [CrossRef][Green Version]
- Guo, X.; Guo, X. China’s photovoltaic power development under policy incentives: A system dynamics analysis. Energy 2015, 93, 589–598. [Google Scholar] [CrossRef]
- Alishahi, E.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. A system dynamics approach for investigating impacts of incentive mechanisms on wind power investment. Renew. Energy 2012, 37, 310–317. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Watts, D.J. Renormalization Group Analysis of the Small-world Network Model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Senkerik, R.; Viktorin, A.; Pluhacek, M.; Janostik, J.; Davendra, D. On the influence of different randomization and complex network analysis for differential evolution. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar] [CrossRef]
- Huang, S. Global dynamics of a network-based WSIS model for mobile malware propagation over complex networks. Phys. A Stat. Mech. Appl. 2018, 503, 293–303. [Google Scholar] [CrossRef]
- Wang, M.; Tian, L.; Du, R. Research on the interaction patterns among the global crude oil import dependency countries: A complex network approach. Appl. Energy 2016, 180, 779–791. [Google Scholar] [CrossRef]
- An, F.; Gao, X.; Guan, J.; Li, H.; Liu, Q. An evolution analysis of executive-based listed company relationships using complex networks. Phys. A Stat. Mech. Appl. 2016, 447, 276–285. [Google Scholar] [CrossRef]
- Zhang, L.; Qu, J.; Fan, J. Topology Evolution Based on the Complex Networks of Heterogeneous Wireless Sensor Network. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID) IEEE, Hangzhou, China, 10–11 December 2016. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Y.; Liu, J.; Liu, X. Energy scheduling for a three-level integrated energy system based on energy hub models: A hierarchical Stackelberg game approach. Sustain. Cities Soc. 2020, 52. [Google Scholar] [CrossRef]
- Seidler, P.; Haider, J.; Kodagoda, N. Design for Intelligence Analysis of Complex Systems: Evolution of Criminal Networks. In Proceedings of the 2016 European Intelligence and Security Informatics Conference, Uppsala, Sweden, 17–19 August 2016. [Google Scholar] [CrossRef]
- Liu, L.F.; Liu, K.; Xiang, H.Y.; Liu, Q. Pinning impulsive cluster synchronization of complex dynamical network. Phys. A Stat. Mech. Appl. 2019, 123580. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, W.N.; Li, X.L.; Sun, Y.Q. Dynamic event-triggered approach for cluster synchronization of complex dynamical networks with switching via pinning control. Neurocomputing 2019, 340, 32–41. [Google Scholar] [CrossRef]
- Lu, H.Q.; Hu, Y.; Guo, C.Q.; Zhou, W.N. Cluster synchronization for a class of complex dynamical network system with randomly occurring coupling delays via an improved event-triggered pinning control approach. J. Frankl. Inst. 2019. [Google Scholar] [CrossRef]
- Zhou, M.Y.; Li, X.Y.; Xiong, W.M.; Liao, H. The coupling strength versus convergence speed in pinning control. Nonlinear Dyn. 2019, 96, 1055–1066. [Google Scholar] [CrossRef]
- Wu, J.; Watts, D.J. Small worlds: The dynamics of networks between order and randomness. ACM SIGMOD Rec. 2002, 31, 74–75. [Google Scholar] [CrossRef]
- Karakitsos, E. The Transmission of Monetary Policy in Interdependent Economies: An Empirical Investigation of the US and Europe. In Money and Banking; Palgrave Macmillan UK: London, UK, 1993. [Google Scholar] [CrossRef]
- Lee, S.; Bowdler, C. Banking Sector Globalization and Monetary Policy Transmission: Evidence from Asian Countries. J. Int. Money Financ. 2018, 93, 101–116. [Google Scholar] [CrossRef]
- Fu, H.; Wang, M.; Li, P.; Jiang, S.; Hu, W.; Guo, X.; Cao, M. Tracing Knowledge Development Trajectories of the Internet of Things Domain: A Main Path Analysis. IEEE Trans. Ind. Inf. 2019, 15, 6531–6540. [Google Scholar] [CrossRef]
- Eckelman, M.J.; Brown, C.; Troup, L.N.; Wang, L.; Webster, M.D.; Hajjara, J.F. Life cycle energy and environmental benefits of novel design-for-deconstruction structural systems in steel buildings. Build. Environ. 2018, 143, 421–430. [Google Scholar] [CrossRef]
Figure 1.
Node conduction diagram.
Figure 1.
Node conduction diagram.
Figure 2.
Example of transmission topology.
Figure 2.
Example of transmission topology.
Figure 3.
Structure of transmission-weighted complex network (TWCN) design.
Figure 3.
Structure of transmission-weighted complex network (TWCN) design.
Figure 4.
(a) Out-degree and (b) in-degree distribution of the transmission-weighted complex network (TWCN).
Figure 4.
(a) Out-degree and (b) in-degree distribution of the transmission-weighted complex network (TWCN).
Figure 5.
Transmission paths of fiscal incentive policy: (a) project award; (b) total investment of industrialized/manufacturing construction (IMC) in progress measurement and rural/affordable housing renovation; (c) special fund for building energy conservation; (d) fabricated incremental cost included in construction cost; (e) base award; (f) subsidy and prefunding supervision; (g) investment attraction.
Figure 5.
Transmission paths of fiscal incentive policy: (a) project award; (b) total investment of industrialized/manufacturing construction (IMC) in progress measurement and rural/affordable housing renovation; (c) special fund for building energy conservation; (d) fabricated incremental cost included in construction cost; (e) base award; (f) subsidy and prefunding supervision; (g) investment attraction.
Figure 6.
Transmission paths of land use policies: (a) 3% plot ratio; (b) 5% plot ratio; (c) land supply plan; (d) excluding construction area for precast exterior wall panels.
Figure 6.
Transmission paths of land use policies: (a) 3% plot ratio; (b) 5% plot ratio; (c) land supply plan; (d) excluding construction area for precast exterior wall panels.
Figure 7.
Transmission paths of tax incentive policies: (a) VAT refund for new wall materials; (b) other preferential tax policies.
Figure 7.
Transmission paths of tax incentive policies: (a) VAT refund for new wall materials; (b) other preferential tax policies.
Figure 8.
Transmission clustering coefficients of IMC incentive policies.
Figure 8.
Transmission clustering coefficients of IMC incentive policies.
Figure 9.
Spatial agglomeration of IMC incentive policies: (a) financial; (b) tax; (c) link of construction; (d) land; (e) money and banking; (f) administration; (g) RDT.
Figure 9.
Spatial agglomeration of IMC incentive policies: (a) financial; (b) tax; (c) link of construction; (d) land; (e) money and banking; (f) administration; (g) RDT.
Figure 10.
Fitting results of policy node strength for (a) construction industry total output value and assembly building; (b) construction site area and prefabricated building; (c) building construction enterprise completed area and fabricated building.
Figure 10.
Fitting results of policy node strength for (a) construction industry total output value and assembly building; (b) construction site area and prefabricated building; (c) building construction enterprise completed area and fabricated building.
Figure 11.
Cluster analysis results.
Figure 11.
Cluster analysis results.
Table 1.
Numbers of incentives in cities. VAT, value-added tax; R&D, research and development.
Table 1.
Numbers of incentives in cities. VAT, value-added tax; R&D, research and development.
| Incentives | Frequency of Cities | Incentives | Frequency of Cities | Incentives | Frequency of Cities |
|---|
| Project awards or subsidies | 127 | Quality margin offer | 48 | Consumer differentiated credit support | 35 |
| Adopt assembly type, give first-rate support | 95 | Enterprise award | 43 | Land transfer | 33 |
| Prioritize land use indicators | 93 | Farmers’ wage security | 41 | Included in land supply plan | 32 |
| VAT levied on new wall materials | 83 | Land protection for construction | 39 | Invitation to tender | 32 |
| 3% plot ratio | 82 | Land transfer method | 38 | Qualification support | 32 |
| Consumer provident fund loan limit | 80 | Base bonus | 37 | Bond financing | 31 |
| Preferential policies for high-tech enterprises | 52 | Special funds for energy-efficient building | 37 | Arbitrage | 30 |
| R&D funding support | 49 | Financial green channels | 36 | Personnel training | 27 |
| …… | | …… | | …… | |
Table 2.
Coding system of incentive policy elements. RDT, research–development–training.
Table 2.
Coding system of incentive policy elements. RDT, research–development–training.
| N | First Level | Meaning | Second-Level Classification |
|---|
| 1 | Tax (37) | Refers to tax concessions paid by enterprises or individuals through tax reduction and exemption | Value-added taxes (VATs) refunded upon collection (83), preferential treatment for high-tech enterprises (78), research and development expense deduction (60), quality margin discount (48), farmers’ salary margin discount (41) |
| 2 | Banking (26) | Refers to government’s financial allocation to reward or subsidize enterprises, projects, and production bases | Project award compensation (127), total investment in parts and components of construction included in progress measurement (60), preferential treatment for high-tech enterprises (52), research and development fund support (49), enterprise award compensation (43) |
| 3 | Land (20) | Refers to government-provided construction land policy guarantee | Prioritized land use index (93), 3% floor area ratio award (82), construction land guarantee (39), land supply by transfer (38), installment payment of land transfer fee (37) |
| 4 | Finance (17) | Refers to financial institutions providing credit, financing, etc., to enterprises or consumers | Consumer provident fund loan line (80), opening a green channel (36), consumer differentiated credit support (35), certain credit support for base/project/enterprise (32), bond financing (31) |
| 5 | Administration (7) | Refers to administrative support provided by government for enterprises, such as examination and approval procedures, qualification management, and credit bonuses | Signs included in admission system (12), priority given to pre-evaluation support (95), optimized approval procedures (56), qualification support given (32), credit bonus given (16) |
| 6 | Construction link (21) | Refers to government’s support for logistics, bidding, etc., in bidding, construction, operation and other aspects | Logistics and transportation support for ultra-large and ultra-wide construction (83), encouragement of general contracting mode (44), inviting public bidding (32), application for pre-sale permit for commercial housing in advance with construction site reaching ±0.000 and capital more than 25% of total investment (24), priority can be given to pre-sale permit for commercial housing to achieve design image progress (17) |
| 7 | RDT (16) | Refers to provision of talent training, scientific and technological achievement transformation, laboratory construction, and other incentives | Encourage striving for higher-level funds (27), personnel training (27), inclusion support (22), laboratory construction support (22), achievement transformation support (20) |
Table 3.
Comparison of small-world and TWCN networks.
Table 3.
Comparison of small-world and TWCN networks.
| | Number of Nodes | Total Number of Edges | Average Clustering Coefficient | Average Path Length |
|---|
| Small-world network | 181 | 15,487 | 0.508 | 1.476 |
| Stochastic network | 181 | 15,487 | 0.401 | 1.214 |
Table 4.
Node distribution of out-degree and in-degree intervals.
Table 4.
Node distribution of out-degree and in-degree intervals.
| Out-Degree Intervals | Node Examples | | In-Degree Intervals | Node Examples | Total Nodes |
|---|
| >800 | Jiangsu Province, Wuhan, Zhejiang Province, Yunnan Province, Shaoxing, Nanjing, Suqian, Changzhou, Jiangxi Province, Chuzhou | 13 | >600 | Panjin City, Chengde City, Xuchang City, Guyuan City, Baotou City, Luoyang City, Qiannan City, Jinzhou City, Jiangmen, Erdos City | 16 |
| 400–800 | Rizhao, Xuzhou, Suzhou, Hebei Province, Zhuha, Ningxia Hui Autonomous Region, Taizhou, Fuzhou, Huzhou, Zhengzhou. | 41 | 300–600 | Yinchuan City, Baiyin City, Bijie City, Yuxi City, Guiyang City, Zhangzhou City, Zhumadian City, Siping City, Zhanjiang | 64 |
| <400 | Yueyang, Gansu Province, Xiangyang, Tongchuan, Guizhou Province, Changchun, Anqing, Lvliang, Tongling, Jiyuan | 127 | <300 | Foshan, Dalian, Yangquan, Hebi, Hangzhou, Haikou, Zhangjiakou, Changde, Yiyang, Hainan Province | 101 |
Table 5.
City-level output values using TWCN.
Table 5.
City-level output values using TWCN.
| Node | Out-Degrees | Node | Out-Degrees | Node | Out-Degrees |
|---|
| Wuhan | 1054 | Kaifeng | 459 | Ankang | 266 |
| Zengzhou | 613 | Nanning | 442 | Xi’an | 210 |
| Nanchang | 593 | Anqing | 365 | Baotou | 181 |
| Yangzhou | 580 | Lu’an | 323 | Guiyang | 47 |
| | | | | Kunming | 41 |
Table 6.
Relevant indicator data.
Table 6.
Relevant indicator data.
| Node | y1 | X1 | X2 | X3 | X4 | X5 |
|---|
| (100 Million Yuan) | (100 Million Yuan) | (Unit) | (10,000 m2) | (10,000 m2) |
|---|
| Wuhan | 1054 | 8067.78 | 1087.41 | 1376 | 50,084.32 | 14,635.43 |
| Zhengzhou | 613 | 3494.5 | 566.2 | 1654 | 23,771.98 | 4409.32 |
| Nanchang | 593 | 3183.86 | 551.58 | 731 | 16,308.6 | 6343.53 |
| Yangzhou | 580 | 3915 | 340.34 | 657 | 27495 | 10,650.2 |
| Kaifeng | 459 | 352.37 | 125.02 | 302 | 1976.48 | 946.38 |
| Nanning | 442 | 1185.21 | 409.61 | 422 | 7955.52 | 1842.88 |
| Anqing | 365 | 223.24 | 101.87 | 291 | 1583.7 | 976.8 |
| Luan | 323 | 173.08 | 93.6 | 137 | 1229 | 631 |
| Ankang | 266 | 149.23 | 115.44 | 136 | 1220.91 | 349.47 |
| Xi’an | 210 | 3304.54 | 938.3 | 1055 | 13,491.49 | 2553.1 |
| Baotou | 181 | 210.26 | 8.75 | 113 | 1466.25 | 343.44 |
| Guiyang | 47 | 2064.71 | 502.61 | 320 | 9579.57 | 2062.15 |
| Kunming | 41 | 2945.82 | 707.44 | 1307 | 10,132.03 | 3313.49 |
Table 7.
Correlation analysis.
Table 7.
Correlation analysis.
| | Y | X | X2 | X3 | X4 | X5 |
|---|
Y
(Unit) | Pearson correlation | 1 | 0.659 * | 0.351 | 0.410 | 0.777 ** | 0.779 ** |
| Sig. (2-tailed) | | 0.014 | 0.239 | 0.164 | 0.002 | 0.002 |
X1
(100 million yuan) | Pearson correlation | 0.659 * | 1 | 0.871 ** | 0.785 ** | 0.972 ** | 0.921 ** |
| Sig. (2-tailed) | 0.014 | | 0.000 | 0.001 | 0.000 | 0.000 |
X2
(100 million yuan) | Pearson correlation | 0.351 | 0.871 ** | 1 | 0.817 ** | 0.753 ** | 0.637 * |
| Sig. (2-tailed) | 0.239 | 0.000 | | 0.001 | 0.003 | 0.019 |
X3
(Unit) | Pearson correlation | 0.410 | 0.785 ** | 0.817 ** | 1 | 0.720 ** | 0.582 * |
| Sig. (2-tailed) | 0.164 | 0.001 | 0.001 | | 0.006 | 0.037 |
X4
(10,000 m2) | Pearson correlation | 0.777 ** | 0.972 ** | 0.753 ** | 0.720 ** | 1 | 0.958 ** |
| Sig. (2-tailed) | 0.002 | 0.000 | 0.003 | 0.006 | | 0.000 |
X5
(10,000 m2) | Pearson correlation | 0.779 ** | 0.921 ** | 0.637 * | 0.582 * | 0.958 ** | 1 |
| Sig. (2-tailed) | 0.002 | 0.000 | 0.019 | 0.037 | 0.000 | |
Table 8.
Fitting results.
Table 8.
Fitting results.
| Dependent Variable: Node Strength (Y) |
|---|
| | Model Summary | Parameter Estimates |
|---|
| Equation | R Square | F | df1 | df2 | Sig. | Constant | b1 |
|---|
| Linear of X1 | 0.434 | 8.444 | 1 | 11 | 0.014 | 218.763 | 0.080 |
| Linear of X4 | 0.604 | 16.782 | 1 | 11 | 0.002 | 205.128 | 0.015 |
| Linear of X5 | 0.608 | 17.032 | 1 | 11 | 0.002 | 212.844 | 0.049 |
Table 9.
Cluster membership.
Table 9.
Cluster membership.
| Case | 4 Clusters | 3 Clusters | Case | 4 Clusters | 3 Clusters |
|---|
| Wuhan | 1 | 1 | Anqing | 4 | 3 |
| Nanchang | 1 | 1 | Luan | 3 | 3 |
| Yangzhou | 1 | 1 | Guiyang | 2 | 2 |
| Xian | 2 | 2 | Kunming | 2 | 2 |
| Baotou | 2 | 2 | Nanning | 2 | 2 |
| Zhengzhou | 2 | 2 | Ankang | 1 | 1 |
| Kaifeng | 3 | 3 | | | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).