Sustainable Traffic Management in an Urban Area: An Integrated Framework for Real-Time Traffic Control and Route Guidance Design
Abstract
1. Introduction and Motivation
- The design of decision/control variables for network control and link control;
- The day-to-day updating behavior of users under the route guidance information system;
- The development of the whole framework based on combinations of TC and RG.
2. State of Play and Research Goals
- The route choice, the learning process modeling, and the traveler reactions to information;
- The anticipatory route guidance problem, which affects the consistency between the experienced travel times and the provided information, as well as accurate information design;
- How traveler behaviors affect network convergence and the stability of the achieved solution.
3. Solution Approach and Implementation
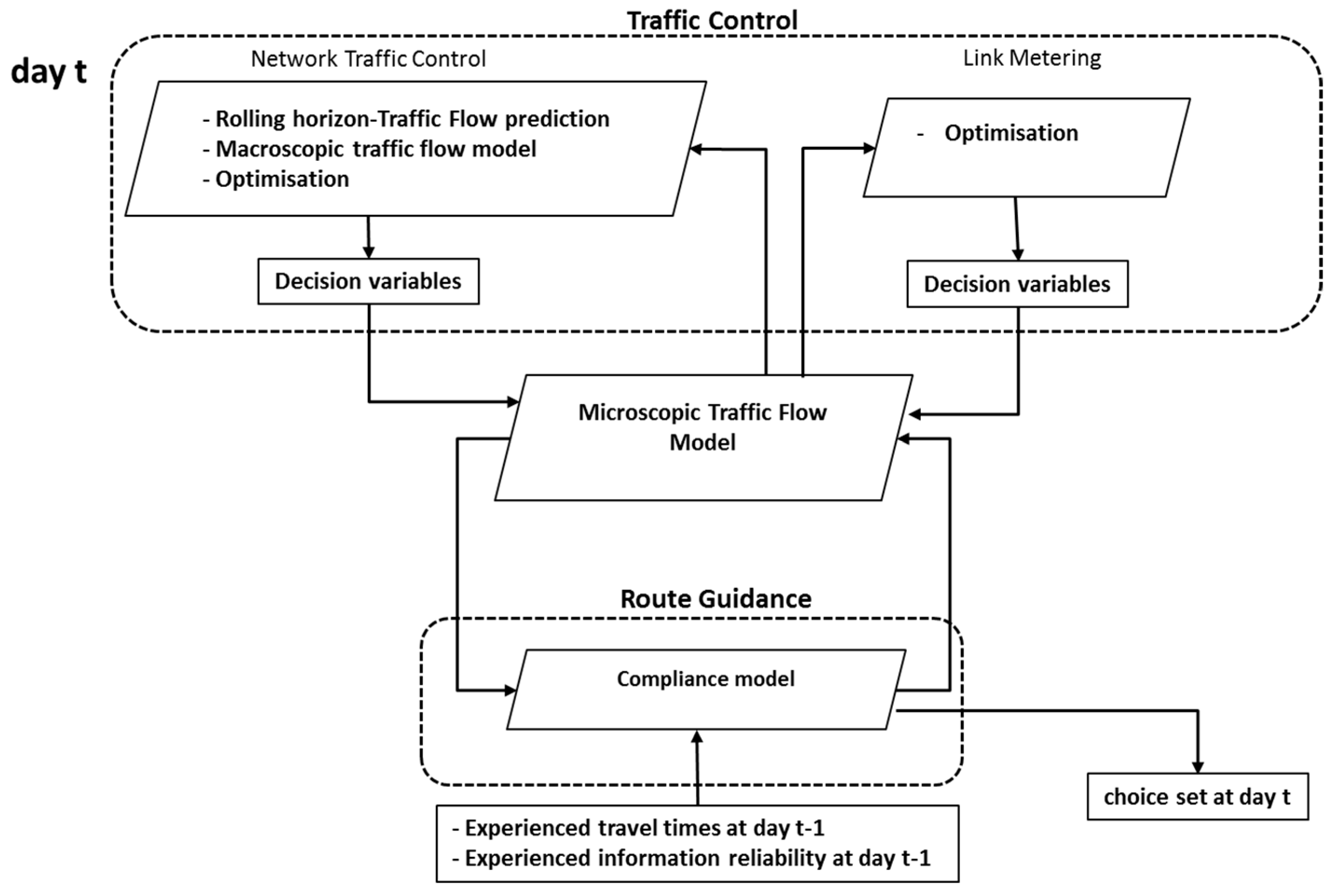
3.1. General Overview
- (1)
- A within-day module for TC;
- (2)
- A choice model which implicitly simulates the RG effect in terms of compliance within the RG module;
- (3)
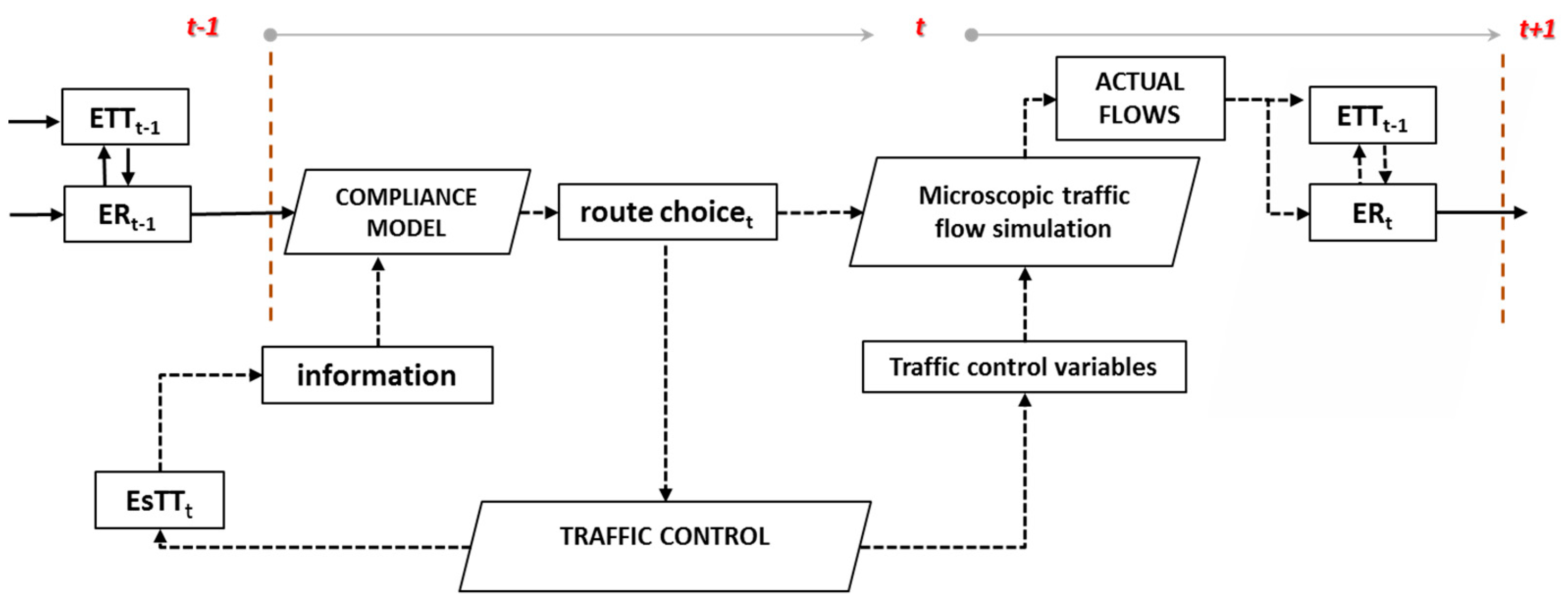
- An iterative procedure for anticipatory route guidance which is able to model the consistency between user behavior and traffic signal decision variables, the consistency between information (EsTTt) and user behavior (ETTt − 1), and focus on information reliability (ERt − 1);
- (4)
- A microscopic traffic flow model able to jointly simulate the effect of users’ preferences and decision variable optimizations.
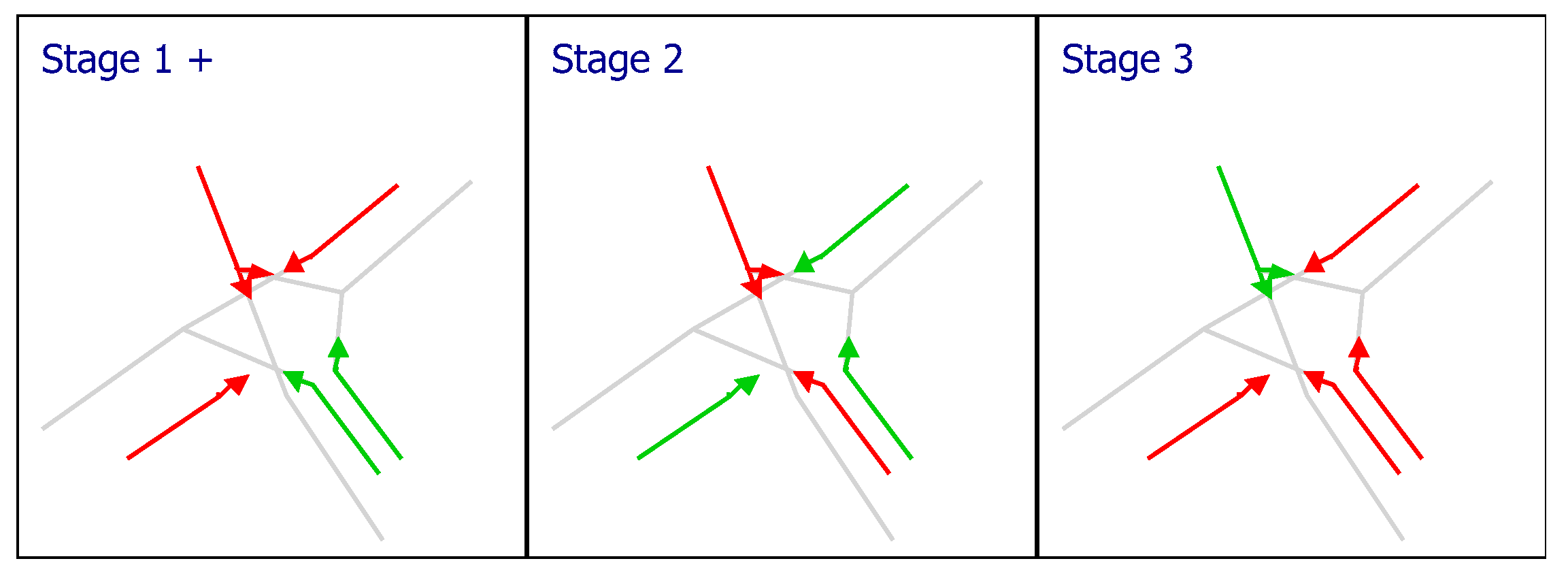
3.2. Traffic Control
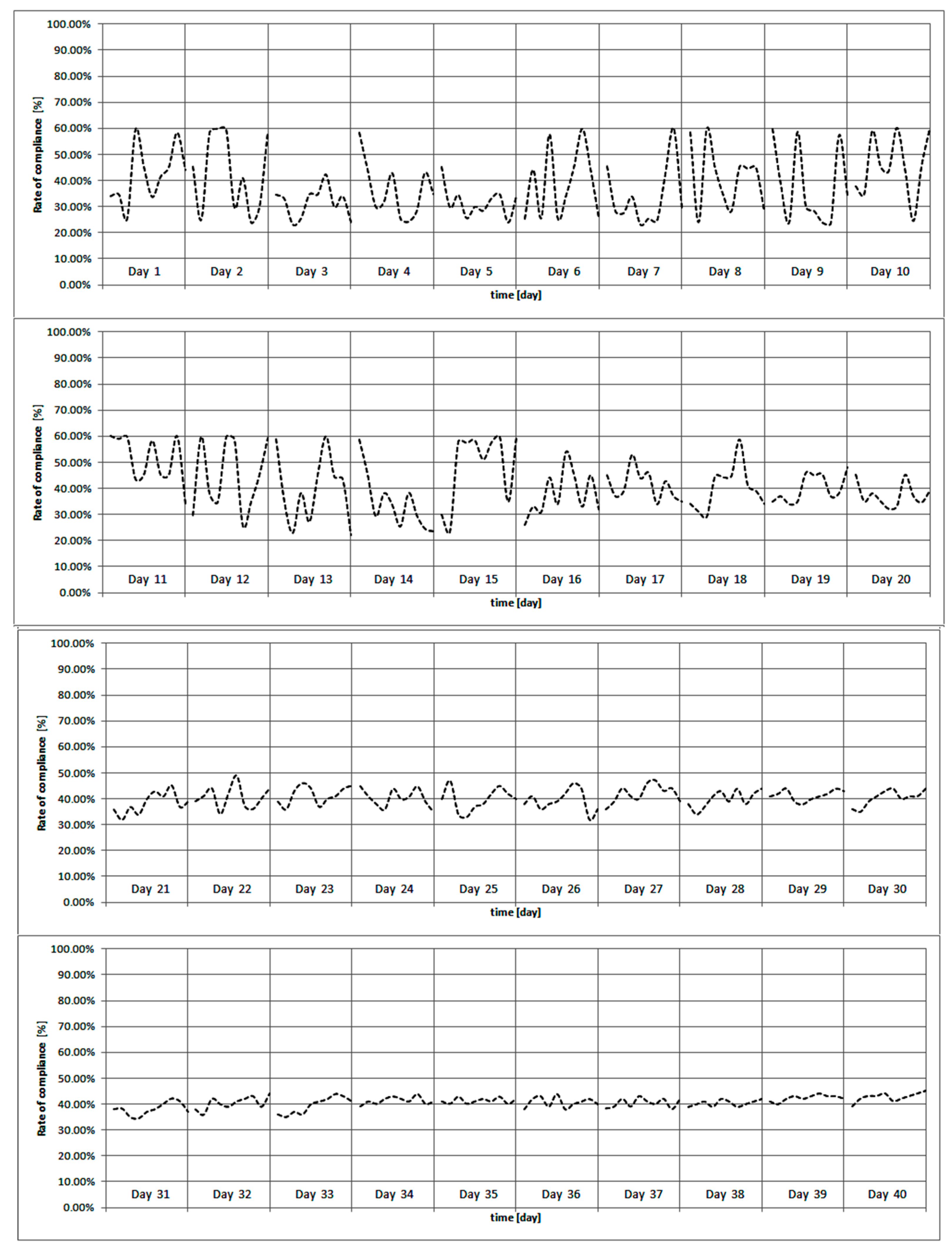
3.3. Day-to-Day Behavioral Modelling
- AtLeastOneUnrel: A binary variable that equals 1 if the information system has not been reliable in the previous three days, otherwise zero;
- SuggRouteIncr: The difference between the suggested route actual travel time at day t − 1 and the average value of the actual travel times of all routes suggested during the previous five days;
- Consec: An attribute synthesizing the consistency between the most chosen route by the traveler during the previous 5 days and the route suggested during day t (the current day);
- NotPreferredSugg: A performance measure over the last five days of the suggested route if different (then not preferred) from the route chosen by the traveler during the previous day;
- FreqChosen: An attribute summarizing the consistency between the frequency of choice of the suggested route with respect to the previous five days;
- FreqConc: An attribute representing the consistency between choices made by a traveler and the suggested information with respect to the previous five days.
3.4. Day-to-Day Behavioral Modelling
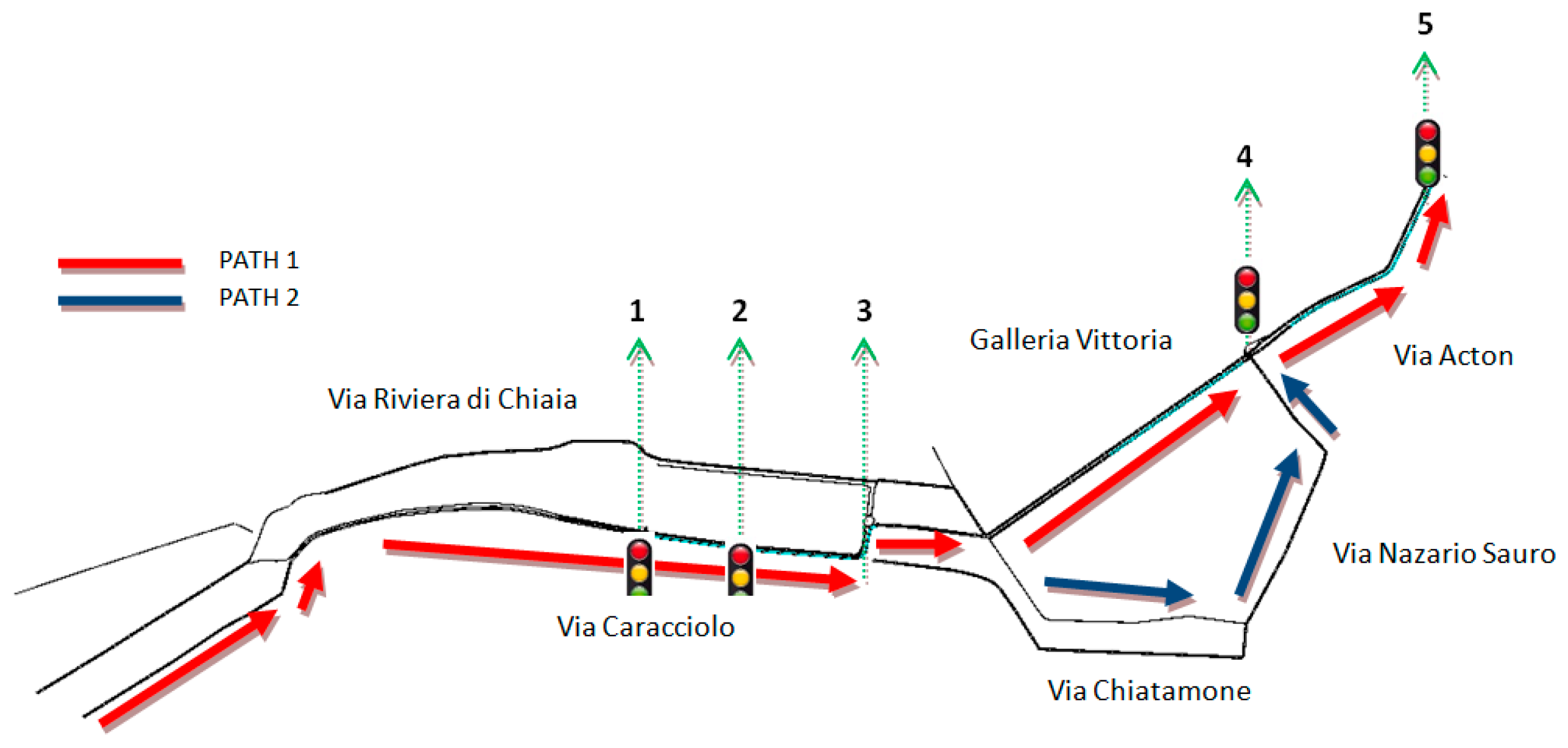
4. Application
5. Numerical Results and Discussion
- Do nothing (DN), which is the current scenario, in which travelers are not provided with information;
- Forced rerouting (FR), where the whole system simulates a forced rerouting strategy (to alternative route 2) and this is implemented when the length of the queue observed directly in the tunnel is higher than a specific value. This scenario refers to the case in which users are provided with prescriptive information, but the alternative route is temporarily closed off to drivers;
- Modeled compliance (MC), where the proposed TC-RG framework is implemented and a disaggregate compliance model is applied in order to reproduce the users’ outcomes coherently with their reaction to the information. It must be clarified that the most relevant users are considered systematic. The resulting compliance of this scenario is evaluated though the provided analyses;
- Parametric high compliance (PC-H), in which the value of compliance is equal to 60%. This scenario is intended to act as a sensitivity analysis, in the case of a high rate of compliance. This scenario corresponds to the case of highly accurate information, and, therefore, high rates of compliant users are expected.
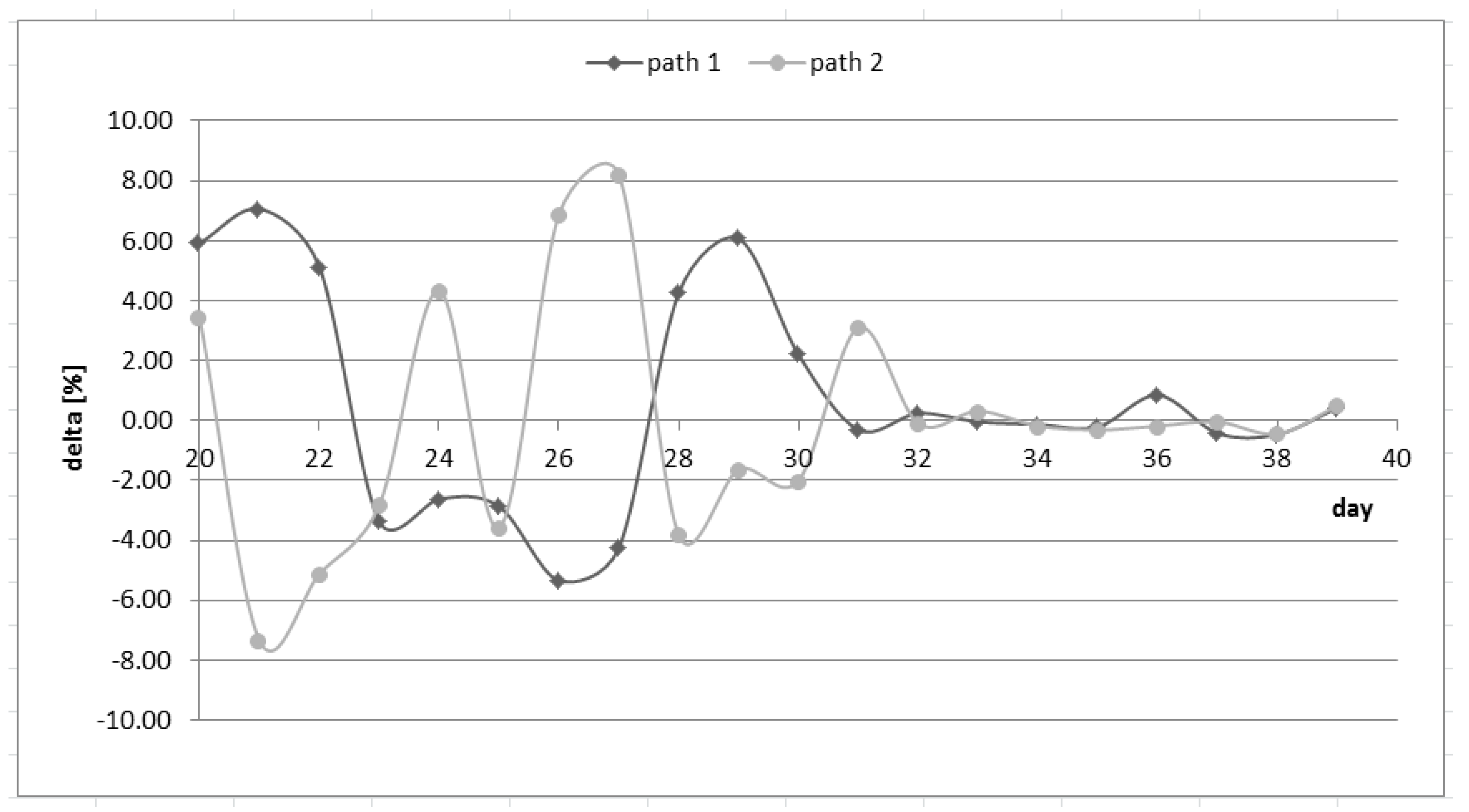
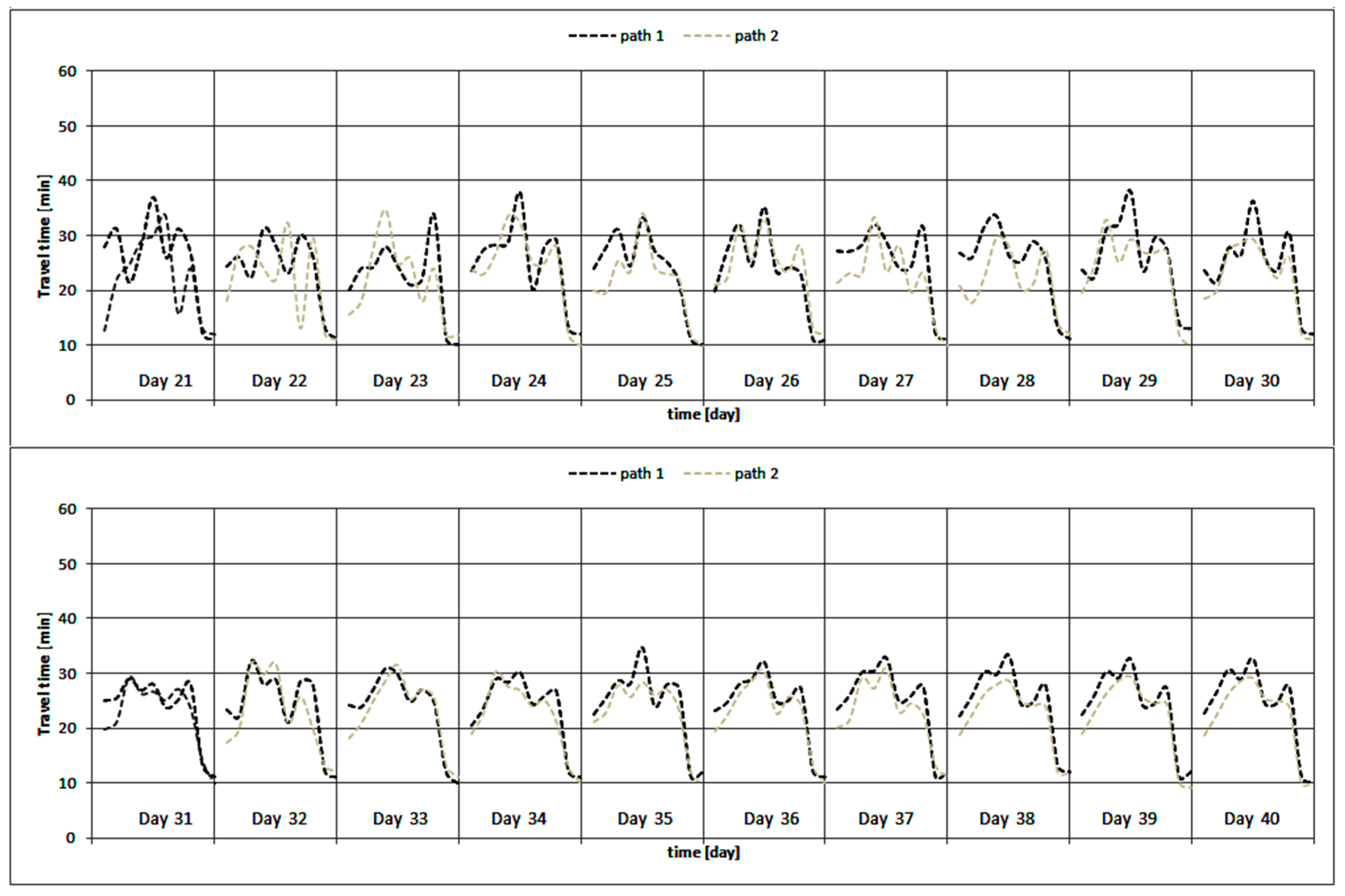
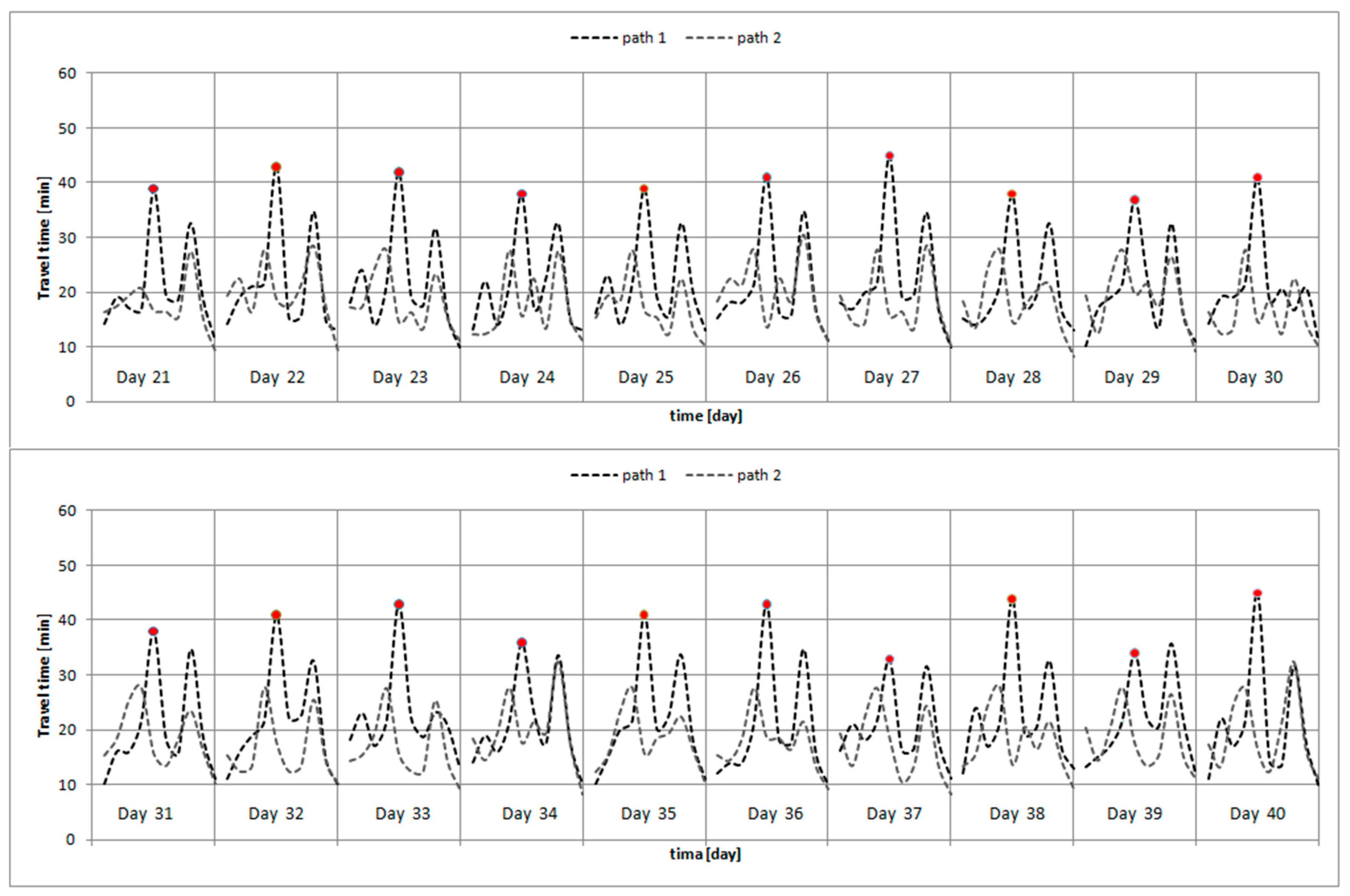
5.1. DN Scenario versus MC Scenario: Benefits of the Modeled Compliance Scenario
- The do nothing [DN] scenario;
- The modeled compliance [MC] scenario;
5.2. Further Analyses: FR and PC-H Scenarios
- forced rerouting [FR];
- parametric high compliance [PC-H].
5.3. Environmental Impact Analysis: Emissions and Fuel Consumption Evaluation
6. Conclusions and Future Perspectives
- (i)
- The whole framework proposed is able to provide more effective results then other frameworks, as observed through the values of the considered performance indicators;
- (ii)
- The TC-RG approach is able to guarantee system convergence and the stability of the achieved solution;
- (iii)
- In accordance with the literature (e.g., [13]), the analysis of the compliance evolution over the analyzed days clearly shows a consistent value of compliance in the case of system stabilization.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- IEA. “Tracking Transport”. IEA: Paris. Available online: https://www.iea.org/reports/tracking-transport-2019 (accessed on 14 January 2020).
- De Luca, S.; Di Pace, R.; Marano, V. Modelling the adoption intention and installation choice of an automotive after-market mild-solar-hybridization kit. Transp. Res. Part C Emerg. Technol. 2015, 56, 426–445. [Google Scholar] [CrossRef]
- Vandecasteele, I.; Baranzelli, C.; Siragusa, A.; Aurambout, J.P.; Alberti, V.; Alonso Raposo, M.; Batista e Silva, F. The Future of Cities– Opportunities, Challenges and the Way Forward; EUR 29752 EN; Publications Office: Luxembourg, 2019. [Google Scholar]
- De Luca, S.; Papola, A. Evaluation of travel demand management policies in the urban area of Naples. WIT Trans. Built Environ. 2001, 52, 10. [Google Scholar]
- Gozalvez, J.; Sepulcre, M.; Bauza, R. IEEE 802.11p vehicle to infrastructure communications in urban enviroments. IEEE Commun. Mag. 2012, 50, 176–183. [Google Scholar] [CrossRef]
- Melo, S.; Macedo, J.; Baptista, P. Guiding cities to pursue a smart mobility paradigm: An example from vehicle routing guidance and its traffic and operational effects. Res. Transp. Econ. 2017, 65, 24–33. [Google Scholar] [CrossRef]
- Mascia, M.; Hu, S.; Han, K.; North, R.; Van Poppel, M.; Theunis, J.; Beckx, C.; Litzenberger, M. Impact of traffic management on black carbon emissions: A microsimulation study. Netw. Spat. Econ. 2017, 17, 269–291. [Google Scholar] [CrossRef]
- Allsop, R.E. SIGCAP: A computer program for assessing the traffic capacity of signal-controlled road junctions. Traffic Eng. Control 1976, 17, 338–341. [Google Scholar]
- Robertson, D.I. TRANSYT: A Traffic Network Study Tool; TRRL Report 1969, LR253; Transport and Road Research Laboratory: London, UK, 1969. [Google Scholar]
- Geroliminis, N.; Haddad, J.; Ramezani, M. Optimal perimeter control for two urban regions with macroscopic fundamental diagrams: A model predictive approach. IEEE Trans. Intell. Transp. Syst. 2013, 14, 348–359. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Di Pace, R.; Bifulco, G.N.; Shiftan, Y. The impact of travel information’s accuracy on route-choice. Transp. Res. Part C Emerg. Technol. 2013, 26, 146–159. [Google Scholar] [CrossRef]
- Srinivasan, K.; Mahmassani, H. Modeling inertia and compliance mechanisms in route choice behavior under real-time information. Transp. Res. Rec. J. Transp. Res. Board 2000, 1725, 45–53. [Google Scholar] [CrossRef]
- Bifulco, G.N.; Cantarella, G.E.; Simonelli, F.; Velonà, P. Advanced traveller information systems under recurrent traffic conditions: Network equilibrium and stability. Transp. Res. Part B Methodol. 2016, 92, 73–87. [Google Scholar] [CrossRef]
- Abdelghany, K.; Valdes, D.; Abdelfatah, A.; Mahmassani, H. Real-Time Dynamic Traffic Assignment and Path-Based Signal Coordination; Application to Network Traffic Management. Transp. Res. Rec. J. Transp. Res. Board 1999, 1667, 67–76. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Bierlaire, M.; Burton, D.; Koutsopoulos, H.N.; Mishalani, R. Network state estimation and prediction for real-time traffic management. Netw. Spat. Econ. 2001, 1, 293–318. [Google Scholar] [CrossRef]
- Liu, R.; Van Vliet, D.; Watling, D. Microsimulation models incorporating both demand and supply dynamics. Transp. Res. Part A Policy Pract. 2006, 40, 125–150. [Google Scholar] [CrossRef]
- Memoli, S.; Cantarella, G.E.; de Luca, S.; Di Pace, R. Network signal setting design with stage sequence optimisation. Transp. Res. Part B 2017, 100, 20–42. [Google Scholar] [CrossRef]
- De Luca, S.; Di Pace, R.; Memoli, S.; Storani, F. A hybrid traffic control framework for urban network management. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Kotsialos, A.; Papageorgiou, M.; Middelham, F. Local and optimal coordinated ramp metering for freeway networks. J. Intell. Transp. Syst. 2005, 9, 187–203. [Google Scholar] [CrossRef]
- Papamichail, I.; Papageorgiou, M. Traffic-Responsive Linked Ramp Metering Control. IEEE Trans. Intell. Transp. Syst. 2008, 9, 111–121. [Google Scholar] [CrossRef]
- Mahmassani, H.; Hu, T.; Jayakrishnan, R. Dynamic traffic assignment and simulation for advanced network informatics (DynaSMART). In Urban Traffic Networks: Dynamic Flow Modeling and Control; Springer: Berlin, NY, USA, 1995. [Google Scholar]
- Ben-Akiva, M.; Koutsopoulos, H.N.; Antoniou, C.; Balakrishna, R. Traffic Simulation with DynaMIT. In Fundamentals of Traffic Simulation; Barceló, J., Ed.; Springer: New York, NY, USA, 2010; pp. 363–398. [Google Scholar]
- Vincent, R.A.; Peirce, J.R.; Webb, P.J. MOVA Traffic Control Manual; Transport and Road Research Laboratory: London, UK, 1990. [Google Scholar]
- Varaiya, P. Max pressure control of a network of signalized intersections. Transp. Res. Part C Emerg. Technol. 2013, 36, 177–195. [Google Scholar] [CrossRef]
- Hunt, P.B.; Robertson, D.I.; Bretherton, R.D.; Winton, R.I. SCOOT—A Traffic Responsive Method of Coordinating Signals; RRL Report LR 1041; Road Research Laboratory: London, UK, 1981. [Google Scholar]
- Luk, J.Y.K. Two traffic-responsive area traffic control methods: SCAT and SCOOT. Traffic Eng. Control 1984, 25, 14–22. [Google Scholar]
- Dinopoulou, V.; Diakaki, C.; Papageorgiou, M. Application and evaluation of the signal traffic control strategy TUC in Chania. J. Intell. Transp. Syst. 2005, 9, 133–143. [Google Scholar] [CrossRef]
- Mauro, V. UTOPIA—Urban Traffic Control—Main Concepts. In Proceedings of the the EU–China ITS Workshop, Beijing, China, 18–19 April 2002; pp. 18–19. [Google Scholar]
- Wood, K.; Bretherton, D.; Maxwell, A.; Smith, K.; Bowen, G. Improved Traffic Management and Bus Priority with SCOOT; TRL Staff Paper PA 3860/02; Transport Research Laboratory: London, UK, 2002. [Google Scholar]
- Luk, J.; Green, D. Balancing Traffic Density in a Signalised Network; Austroads Research Report AP-R369/10; Austroads: Sydney, Australia, 2010. [Google Scholar]
- Geroliminis, N.; Sun, J. Properties of a well-defined macroscopic fundamental diagram for urban traffic. Transp. Res. Part B Methodol. 2011, 45, 605–617. [Google Scholar] [CrossRef]
- Ramezani, M.; Haddad, J.; Geroliminis, N. Dynamics of heterogeneity in urban networks: Aggregated traffic modeling and hierarchical control. Transp. Res. Part B Methodol. 2015, 74, 1–19. [Google Scholar] [CrossRef]
- Jang, K.; Kim, H.; Jang, I.G. Traffic signal optimization for oversaturated urban networks: Queue growth equalization. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2121–2128. [Google Scholar] [CrossRef]
- Kucharski, R.; Gentile, G. Simulation of rerouting phenomena in Dynamic Traffic Assignment with the Information Comply Model. Transp. Res. Part B Methodol. 2018, 126, 414–441. [Google Scholar] [CrossRef]
- Gao, S.; Frejinger, E.; Ben-Akiva, M. Adaptive route choices in risky traffic networks: A prospect theory approach. Transp. Res. C 2010, 18, 727–740. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; De Palma, A.; Isam, K. Dynamic network models and driver information systems. Transp. Res. Part A Gen. 1991, 25, 251–266. [Google Scholar] [CrossRef]
- Jayakrishnan, R.; Mahmassani, H.S.; Hu, T.Y. An evaluation tool for advanced traffic information and management systems in urban networks. Transp. Res. Part C Emerg. Technol. 1994, 2, 129–147. [Google Scholar] [CrossRef]
- Unnikrishnan, A.; Waller, S.T. User equilibrium with recourse. Netw. Spat. Econ. 2009, 9, 575. [Google Scholar] [CrossRef]
- Bottom, J.; Ben-Akiva, M.; Bierlaire, M.; Chabini, I.; Koutsopoulos, H.; Yang, Q. Investigation of route guidance generation issues by simulation with DynaMIT. In Proceedings of the 14th International Symposium on Transportation and Traffic Theory, Jerusalem, Israel, 20–23 July 1999. [Google Scholar]
- Bottom, J.A. Consistent Anticipatory Route Guidance. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Crittin, F.; Bierlaire, M. New algorithmic approaches for the anticipatory route guidance generation problem. In Proceedings of the Swiss Transport Research Conference (No. TRANSP-OR-CONF-2006-056), Ascona, Switzerland, 1–3 March 2001. [Google Scholar]
- Dong, J.; Mahmassani, H.; Lu, C.C. How reliable is this route?: Predictive travel time and reliability for anticipatory traveler information systems. Transp. Res. Rec. J. Transp. Res. Board 2006, 1980, 117–125. [Google Scholar] [CrossRef]
- Zhang, D.; Nagurney, A. On the local and global stability of a travel route choice adjustment process. Transp. Res. Part B Methodol. 1996, 30, 245–262. [Google Scholar] [CrossRef]
- Lo, H.; Bie, J. Stability domains of traffic equilibrium: Directing traffic system evolution to equilibrium. In Proceedings of the First International Symposium on Dynamic Traffic Assignment (DTA), Leeds, UK, 21–23 June 2006. [Google Scholar]
- Bie, J.; Lo, H.K. Stability and attraction domains of traffic equilibria in a day-to-day dynamical system formulation. Transp. Res. Part B 2010, 44, 90–107. [Google Scholar] [CrossRef]
- Cantarella, G.E. Day-to-day dynamic models for intelligent transportation systems design and appraisal. Transp. Res. Part C Emerg. Tech. 2013, 29, 117–130. [Google Scholar] [CrossRef]
- Han, L.; Sun, H.; Wu, J.; Zhu, C. Day-to-day evolution of the traffic network with Advanced Traveler Information System. Chaos Solitons Fractals 2011, 44, 914–919. [Google Scholar] [CrossRef]
- Bifulco, G.N.; Cantarella, G.E.; Simonelli, F. Design of signal setting and advanced traveler information systems. J. Intell. Transp. Syst. 2014, 18, 30–40. [Google Scholar] [CrossRef]
- Watling, D.P.; Cantarella, G.E. Model representation & decision-making in an ever-changing world: The role of stochastic process models of transportation systems. Netw. Spat. Econ. 2015, 15, 843–882. [Google Scholar]
- Daganzo, C.F. The Cell-Transmission Model. Part II: Network Traffic. Transp. Res. Part B Methodol. 1995, 29, 79–93. [Google Scholar] [CrossRef]
- Pace, R.D. A traffic control framework for urban networks based on within-day dynamic traffic flow models. Transp. A Transp. Sci. 2019, 1–36. [Google Scholar] [CrossRef]
- Keyvan-Ekbatani, M.; Gao, X.; Gayah, V.V.; Knoop, V.L. Traffic-responsive signals combined with perimeter control: Investigating the benefits. Transp. B Transp. Dyn. 2019, 7, 1402–1425. [Google Scholar] [CrossRef]
- Hoogendoorn, S.P. Travel Simulator Laboratory, TSL Website, 2004. http://www.tsl.tudelft.nl.
- McFadden, D.; Train, K. Mixed MNL models for discrete response. J. Appl. Econom. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Bifulco, G.N.; Cantarella, G.E.; de Luca, S.; Di Pace, R. Analysis and modelling the effects of information accuracy on travellers’ behavior. In Proceedings of the 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 2098–2105. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent Development and Applications of SUMO—Simulation of Urban MObility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Wiedemann, R.; Reiter, U. Microscopic traffic simulation: The simulation system MISSION, background and actual state. In CEC Project ICARUS (V1052) Final Report, Vol 2, Appendix A. Brussels, CEC; CEC: Brussels, Belgium, 1992. [Google Scholar]
- Ma, J.; Dong, H.; Zhang, H.M. Calibration of Micro Simulation with Heuristic Optimization Methods. Trans. Res. Rec. 2007, 1999, 208–217. [Google Scholar] [CrossRef]
- Highways Agency. Design Manual for Roads and Bridges: Volume Contents Pages and Alpha-Numeric Index. Available online: http://www.standardsforhighways.co.uk/ha/standards/dmrb/ (accessed on 17 January 2020).
- TfL (Transport for London). Traffic Modelling Guidelines: TfL Traffic Manager and Network Performance Best Practice Version 3.0; Transport for London: London, UK, 2010; Available online: http://bailey.persona-pi.com/Public-Inquiries/Brent%20Cross/I-During%20Inquiry/AA-GEN/AA.INQ.28%20TfL%20Traffic%20Modelling%20Guidelines%20Version%203%200%20September%202010%20ex.pdf (accessed on 17 January 2020).
- SUMO Emissions and Fuel Consumption Models. Available online: https://sumo.dlr.de/docs/Models/Emissions/HBEFA-based.html (accessed on 1 January 2020).
- HBEFA Model. Available online: https://www.hbefa.net/e/index.html (accessed on 1 January 2020).
- ACI. Available online: http://www.aci.it/laci/studi-e-ricerche/dati-e-statistiche/annuario-statistico.html (accessed on 1 January 2020).
| Holding Model | ||
|---|---|---|
| Pseudo-ρ2 | 0.387 | |
| Final log-likelihood | −1088.787 | |
| (Var[])1 | 1.55 (7.75) | |
| Compliant | Not-Compliant | |
| ASA | +1.07 (+4.17) | |
| AtLeastOneUnrel | +0.87 (+1.50) | |
| SuggRouteIncr | +0.80 (+1.16) | |
| NotPreferredSugg | +1.48 (+4.78) | |
| FreqConc | +1.47 (+4.88) | |
| Consec | +2.64 (+5.42) | |
| Path | f [veh/h] |
|---|---|
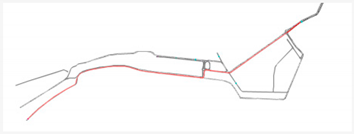 | 1375 [→] |
 | 650 [→] |
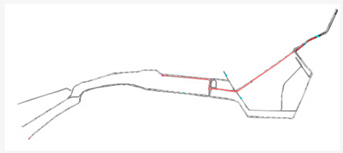 | 970 [←] |
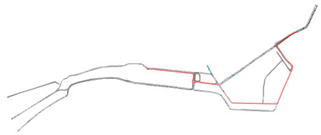 | 285 [←] |
| Path 1 | Path 2 |
|---|---|
| −23.15% | −16.53% |
| Section 1 | Section 2 | Section 3 | Section 4 | Section 5 |
|---|---|---|---|---|
| −88.70% | −75.28% | −84.46% | −68.13% | −32.18% |
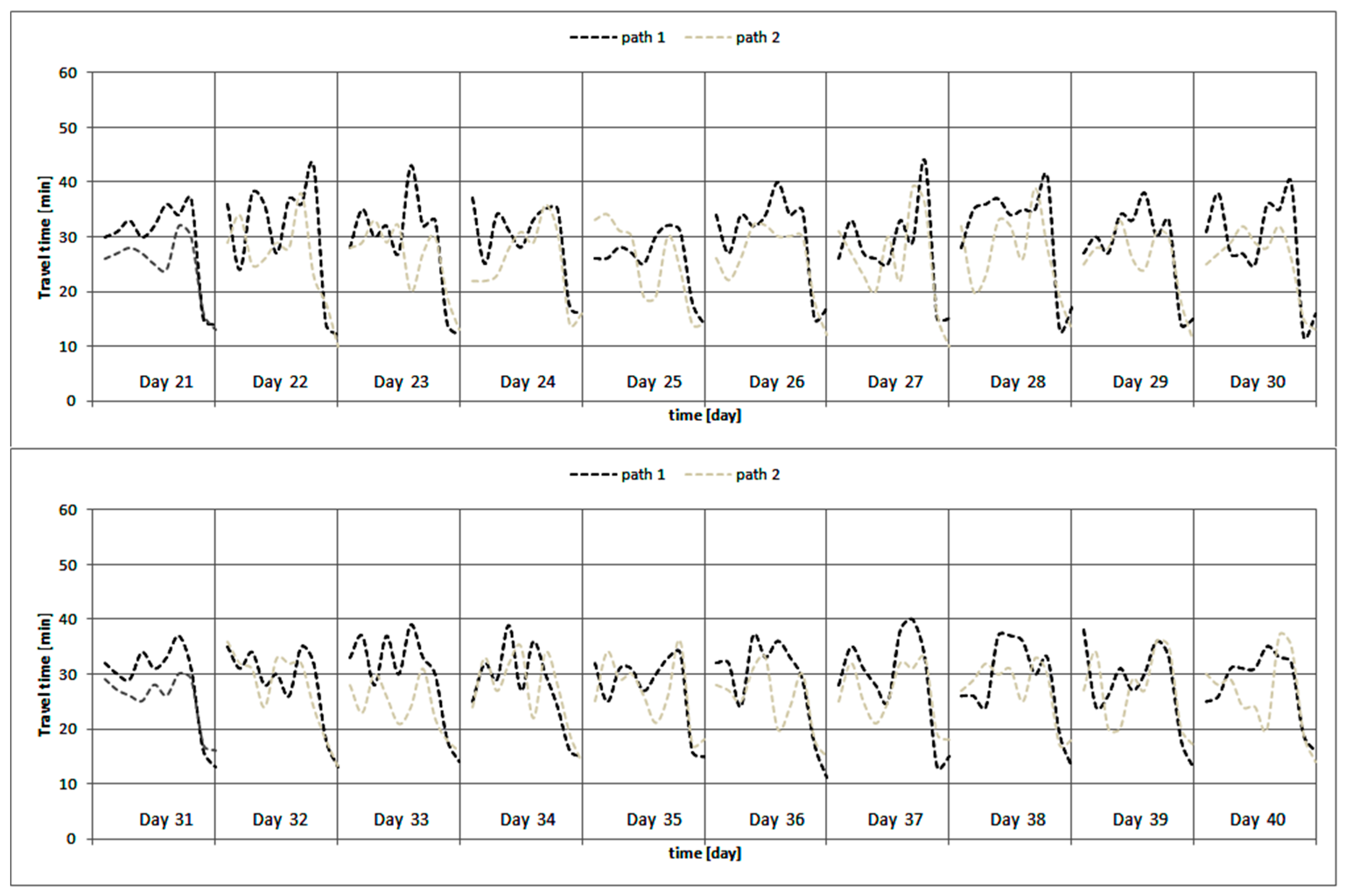
| day | TT path 1 [min] | St.dev. | TTpath 2 [min] | St.dev. |
|---|---|---|---|---|
| 20 | 26.86 | 2.91 | 22.42 | 2.03 |
| 21 | 25.27 | 2.20 | 21.65 | 1.83 |
| 22 | 23.48 | 2.24 | 23.24 | 1.92 |
| 23 | 22.28 | 2.16 | 24.43 | 1.84 |
| 24 | 23.03 | 2.21 | 25.12 | 2.02 |
| 25 | 23.63 | 2.48 | 24.03 | 1.70 |
| 26 | 24.31 | 2.18 | 24.89 | 1.84 |
| 27 | 25.61 | 2.44 | 23.18 | 1.65 |
| 28 | 26.70 | 1.92 | 21.28 | 1.78 |
| 29 | 25.57 | 1.75 | 22.09 | 1.65 |
| 30 | 24.01 | 1.40 | 22.45 | 1.29 |
| 31 | 23.48 | 1.41 | 22.90 | 1.30 |
| 32 | 23.56 | 1.39 | 22.19 | 1.28 |
| 33 | 23.54 | 1.38 | 22.21 | 1.29 |
| 34 | 23.51 | 1.37 | 22.14 | 1.26 |
| 35 | 23.54 | 1.39 | 22.18 | 1.30 |
| 36 | 23.59 | 1.36 | 22.25 | 1.32 |
| 37 | 23.39 | 1.40 | 22.29 | 1.29 |
| 38 | 23.49 | 1.41 | 22.30 | 1.34 |
| 39 | 23.60 | 1.37 | 22.40 | 1.27 |
| 40 | 23.50 | 1.39 | 22.29 | 1.31 |
| ID SCENARIO | Path 1 | Path 2 |
|---|---|---|
| MC | −23.15% | −16.53% |
| PC-H | −15.26% | 0.82% |
| [PC-H] | [MC] | ||
|---|---|---|---|
| Emissions | CO | −30.3% | −50.0% |
| CO2 | −39.8% | −59.9% | |
| NOX | −28.3% | −59.8% | |
| HC | −44.4% | −50.0% | |
| PMx | −25.0% | −50.0% | |
| Mean | −33.6% | −53.9% | |
| Fuel consumed | −40.0% | −50.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Luca, S.; Di Pace, R.; Memoli, S.; Pariota, L. Sustainable Traffic Management in an Urban Area: An Integrated Framework for Real-Time Traffic Control and Route Guidance Design. Sustainability 2020, 12, 726. https://doi.org/10.3390/su12020726
de Luca S, Di Pace R, Memoli S, Pariota L. Sustainable Traffic Management in an Urban Area: An Integrated Framework for Real-Time Traffic Control and Route Guidance Design. Sustainability. 2020; 12(2):726. https://doi.org/10.3390/su12020726
Chicago/Turabian Stylede Luca, Stefano, Roberta Di Pace, Silvio Memoli, and Luigi Pariota. 2020. "Sustainable Traffic Management in an Urban Area: An Integrated Framework for Real-Time Traffic Control and Route Guidance Design" Sustainability 12, no. 2: 726. https://doi.org/10.3390/su12020726
APA Stylede Luca, S., Di Pace, R., Memoli, S., & Pariota, L. (2020). Sustainable Traffic Management in an Urban Area: An Integrated Framework for Real-Time Traffic Control and Route Guidance Design. Sustainability, 12(2), 726. https://doi.org/10.3390/su12020726








