Optimizing the Rail Profile for High-Speed Railways Based on Artificial Neural Network and Genetic Algorithm Coupled Method
Abstract
:1. Introduction
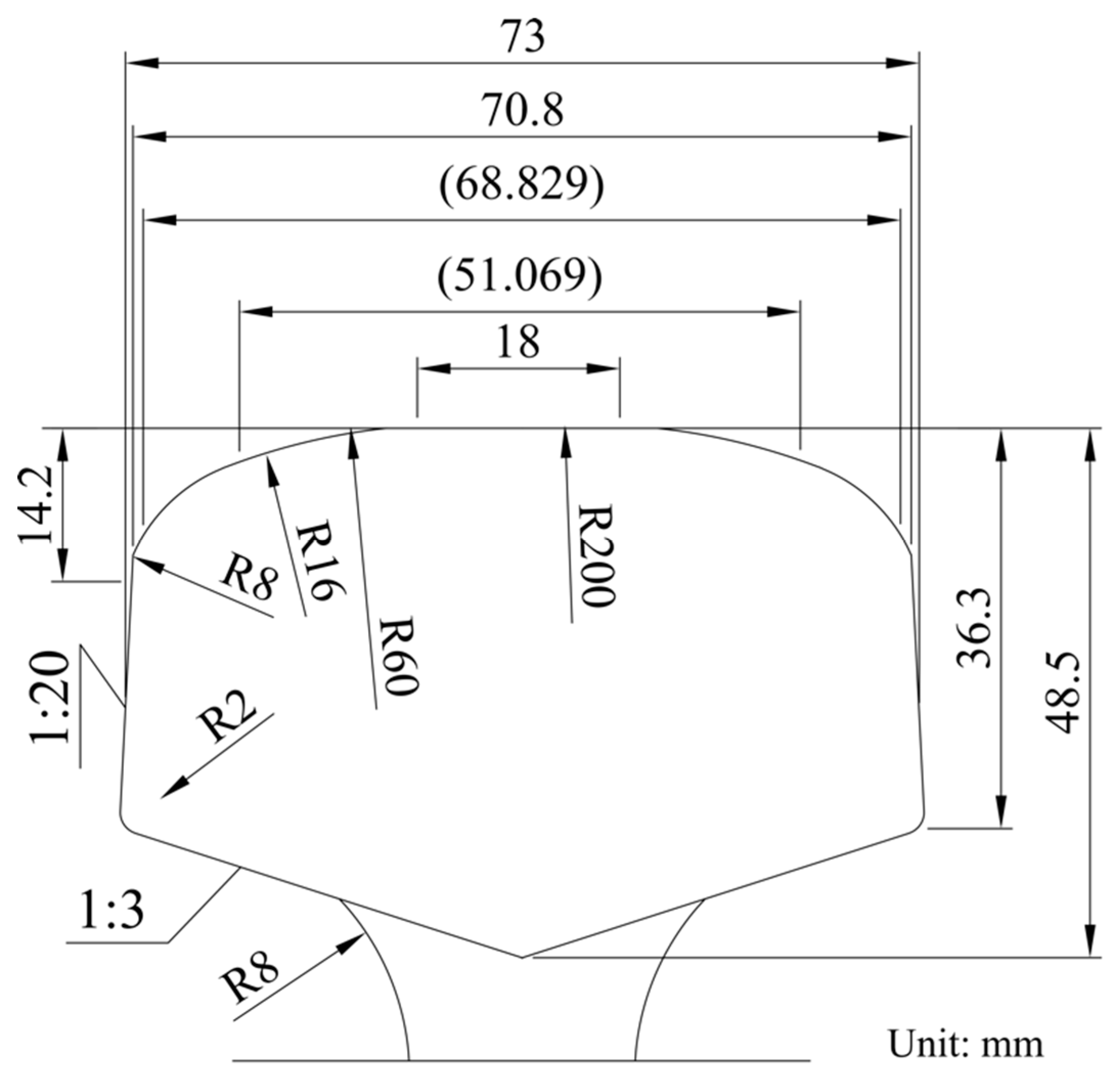
2. Rail Profile Design
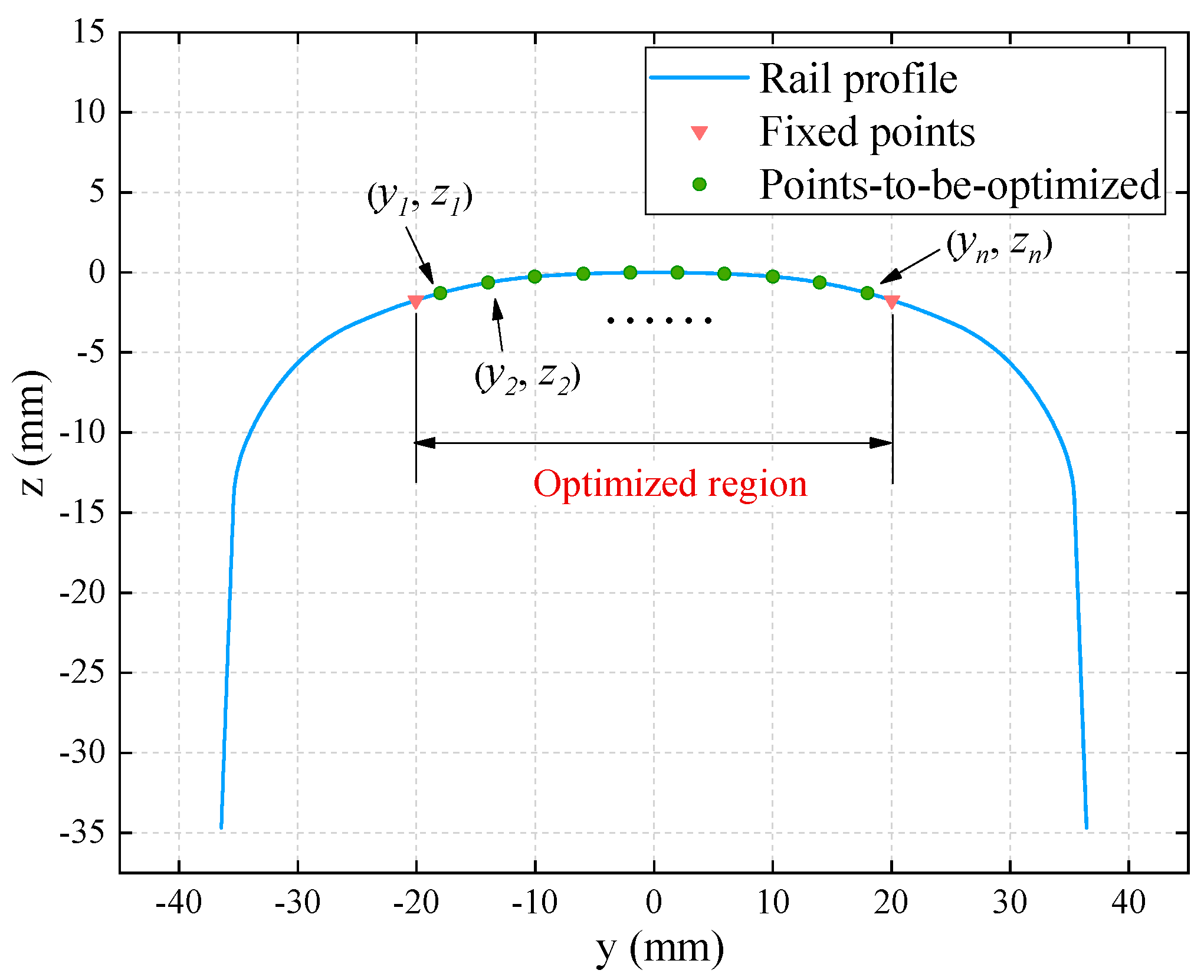
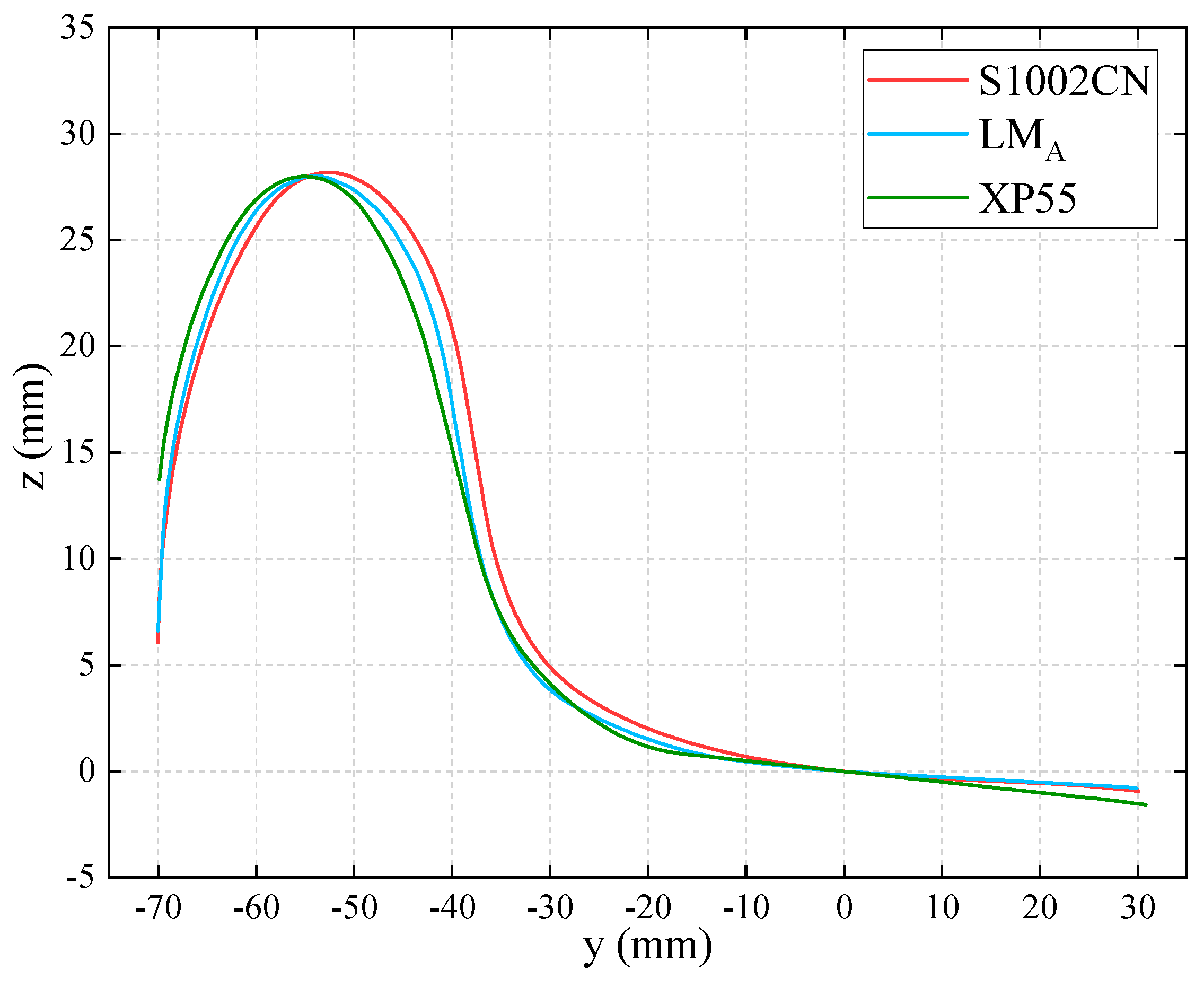
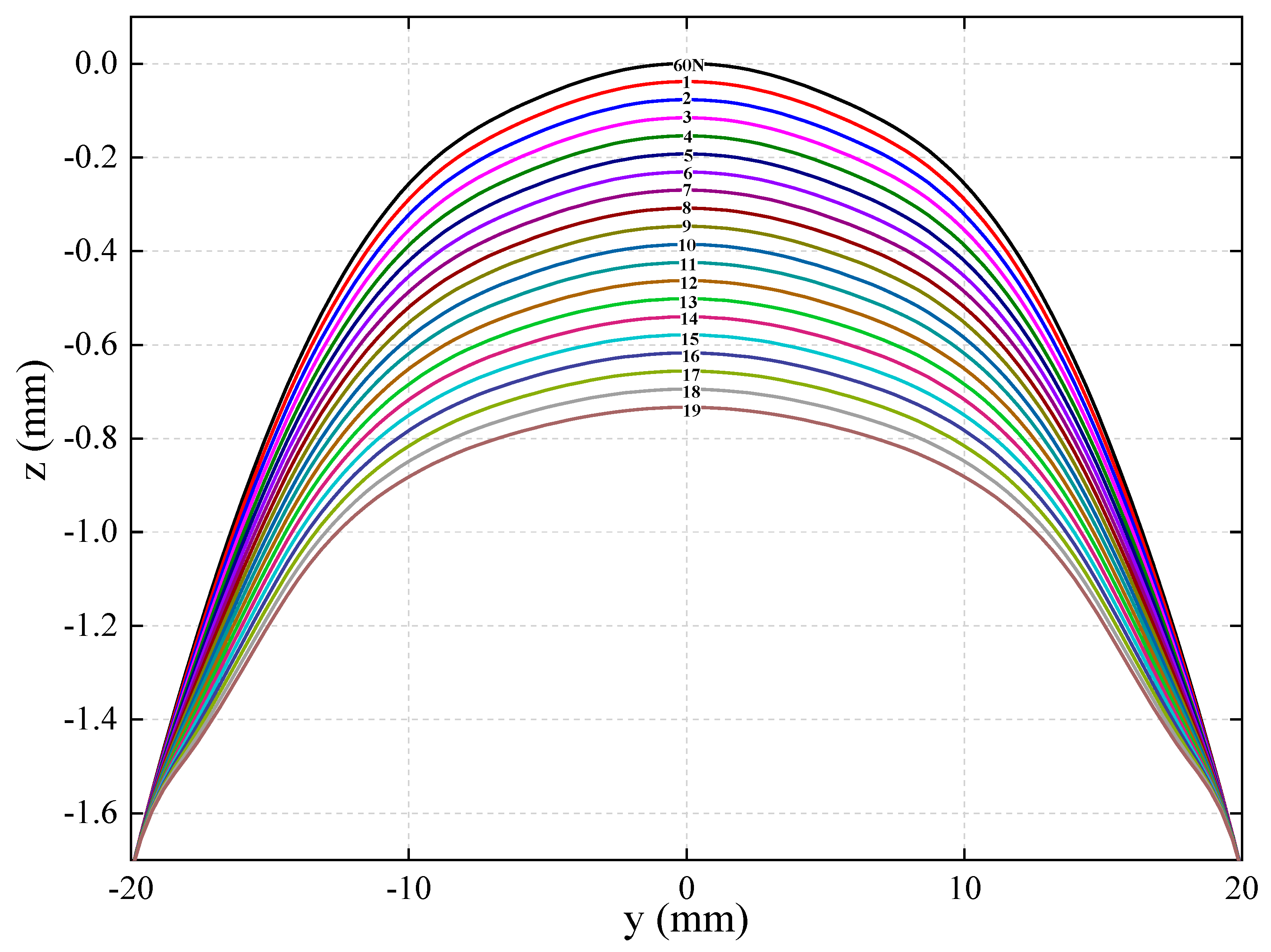
2.1. Variables Design
2.2. Objective Function
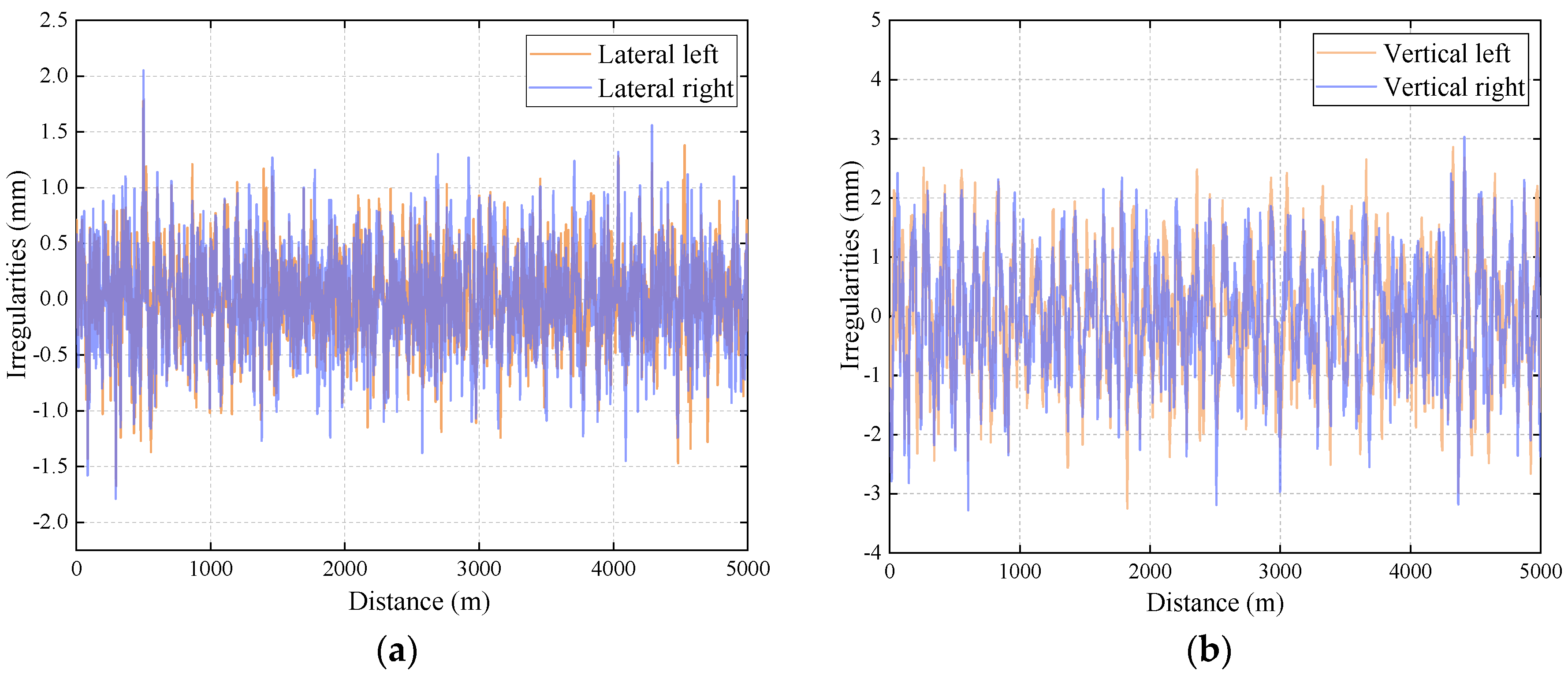
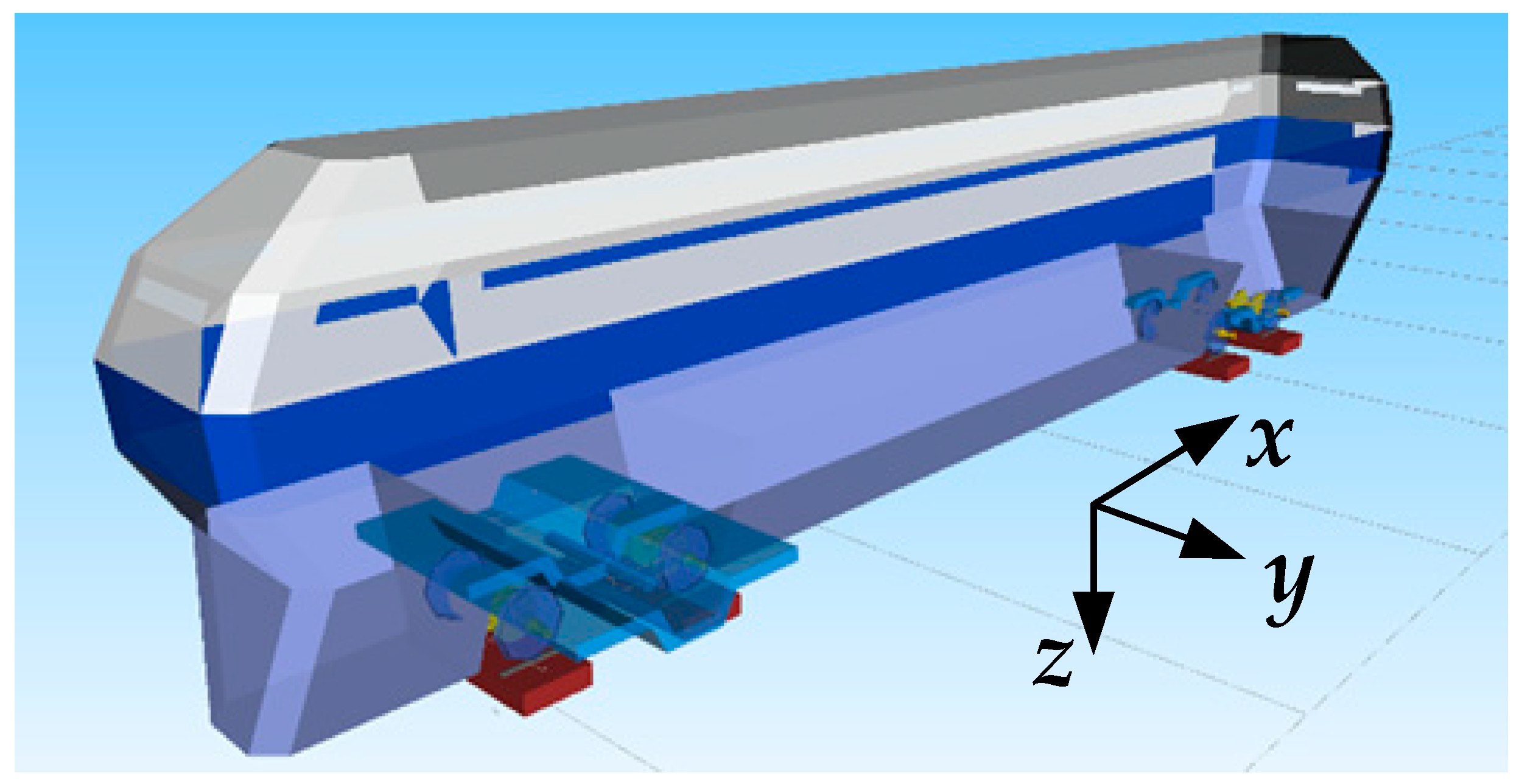
2.2.1. Multibody Dynamics Model
2.2.2. Wear Model
2.2.3. Model Verification
2.3. Constraint Function
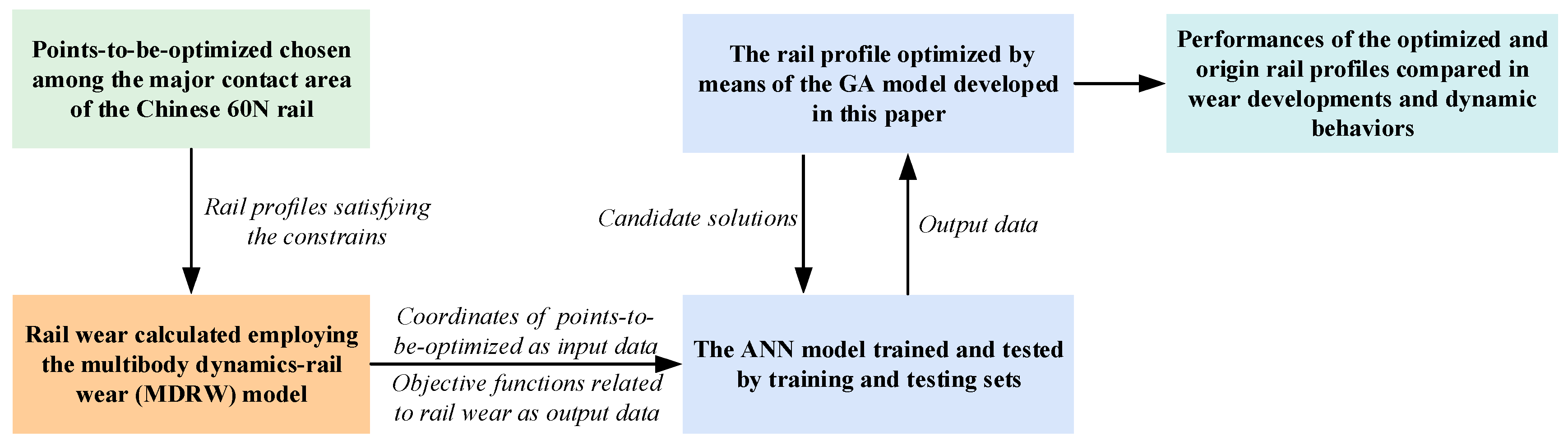
3. Optimization Model
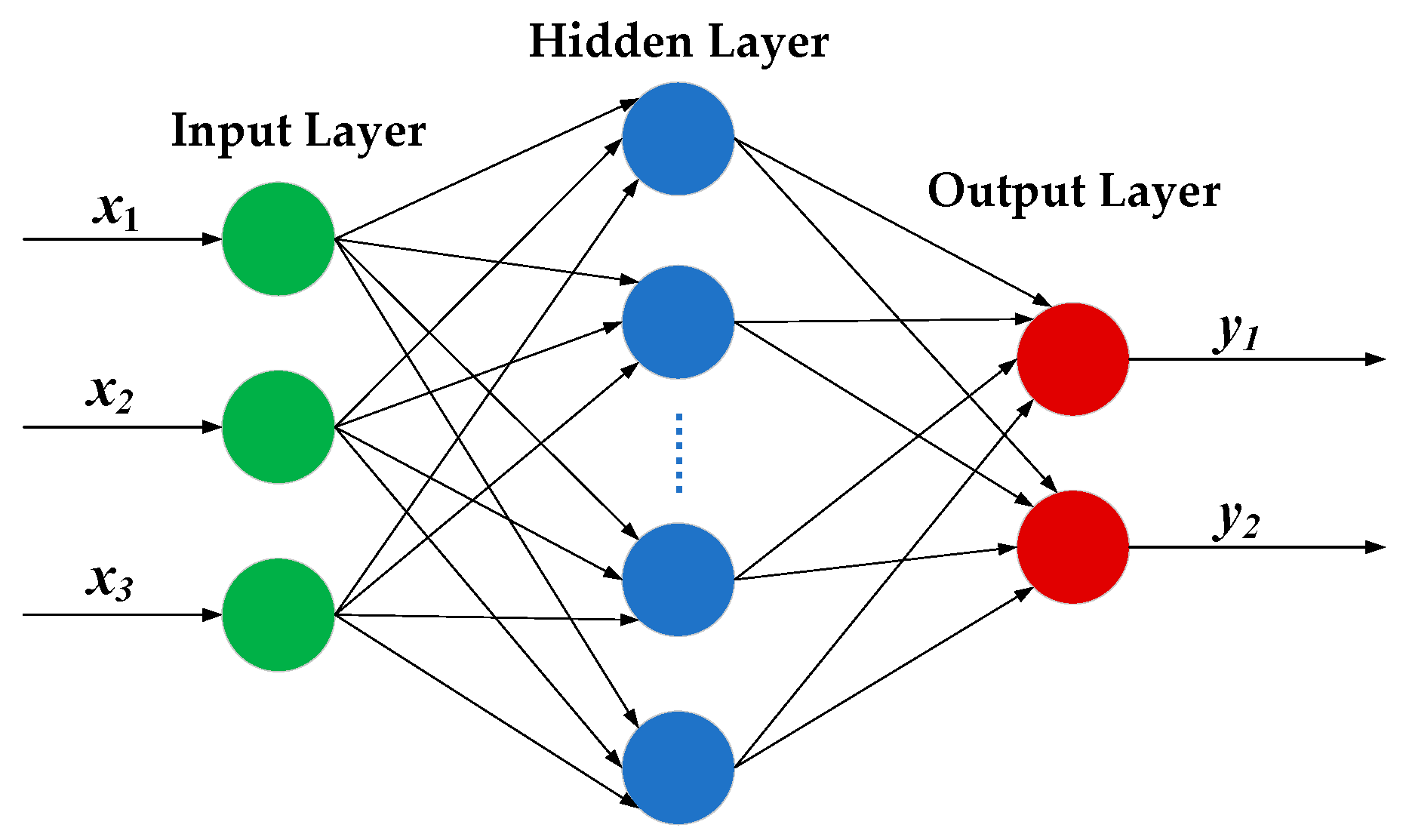
3.1. ANN Model
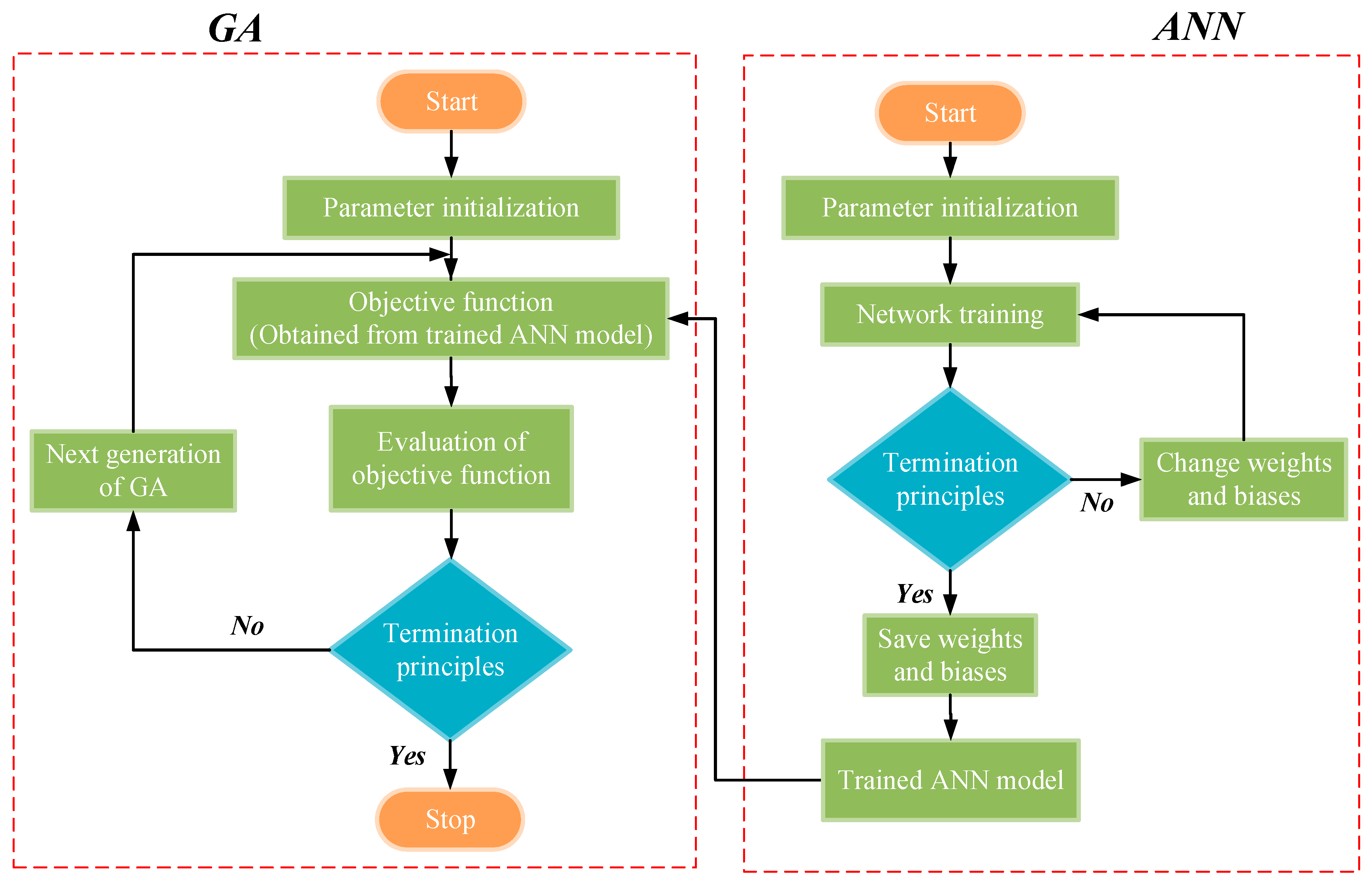
3.2. GA Model
4. Results and Discussion
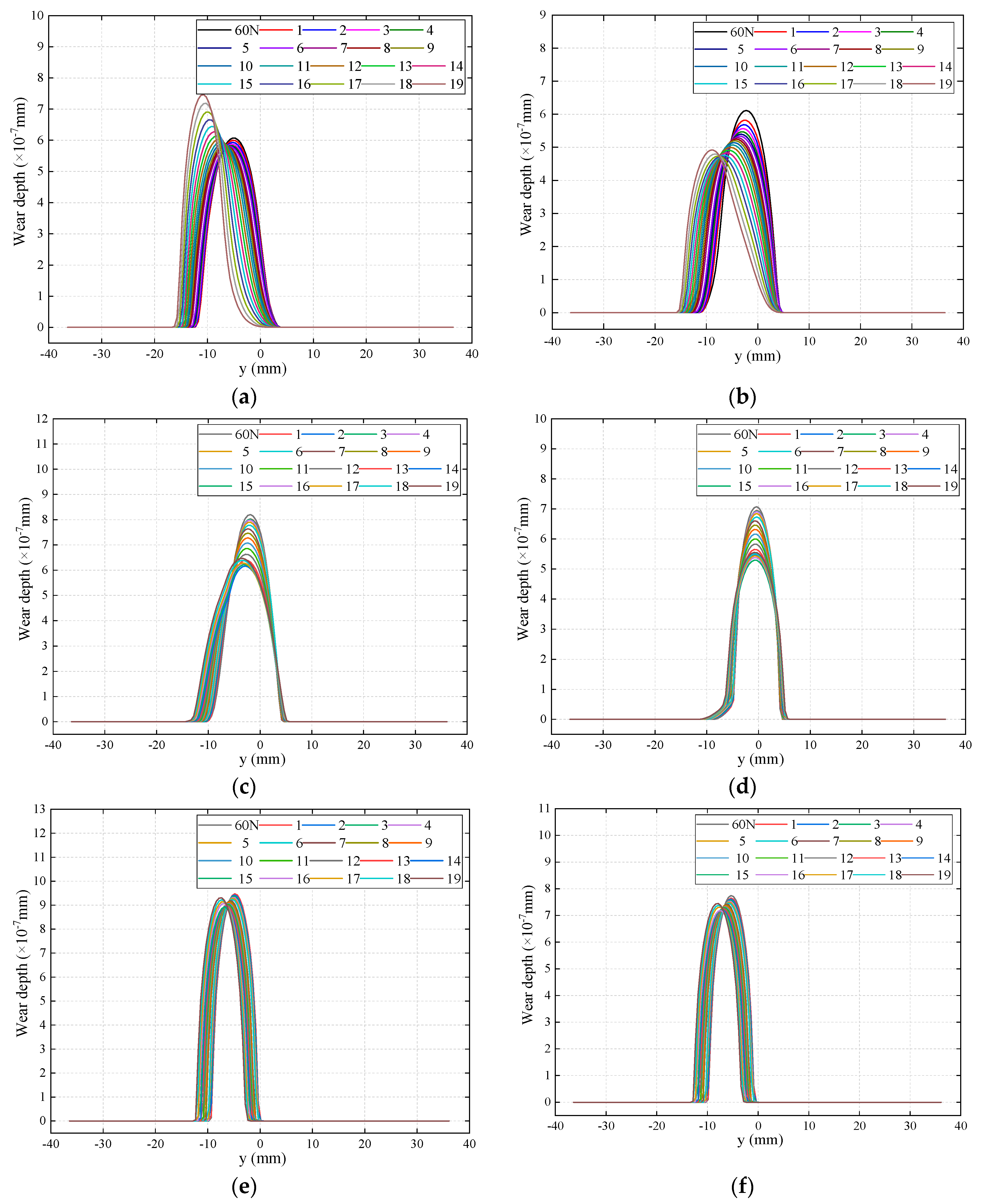
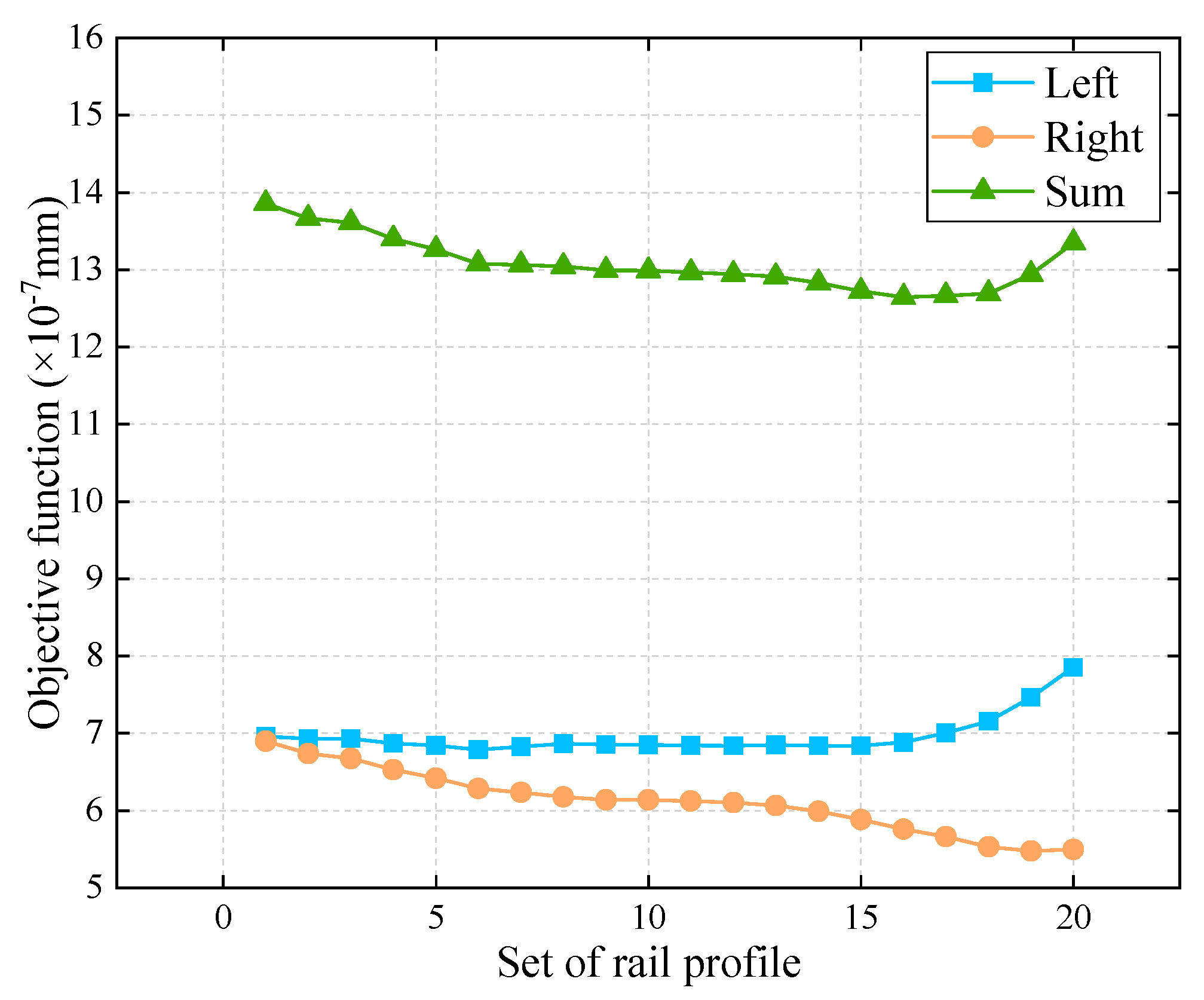
4.1. Simulation Results of MDRW Model
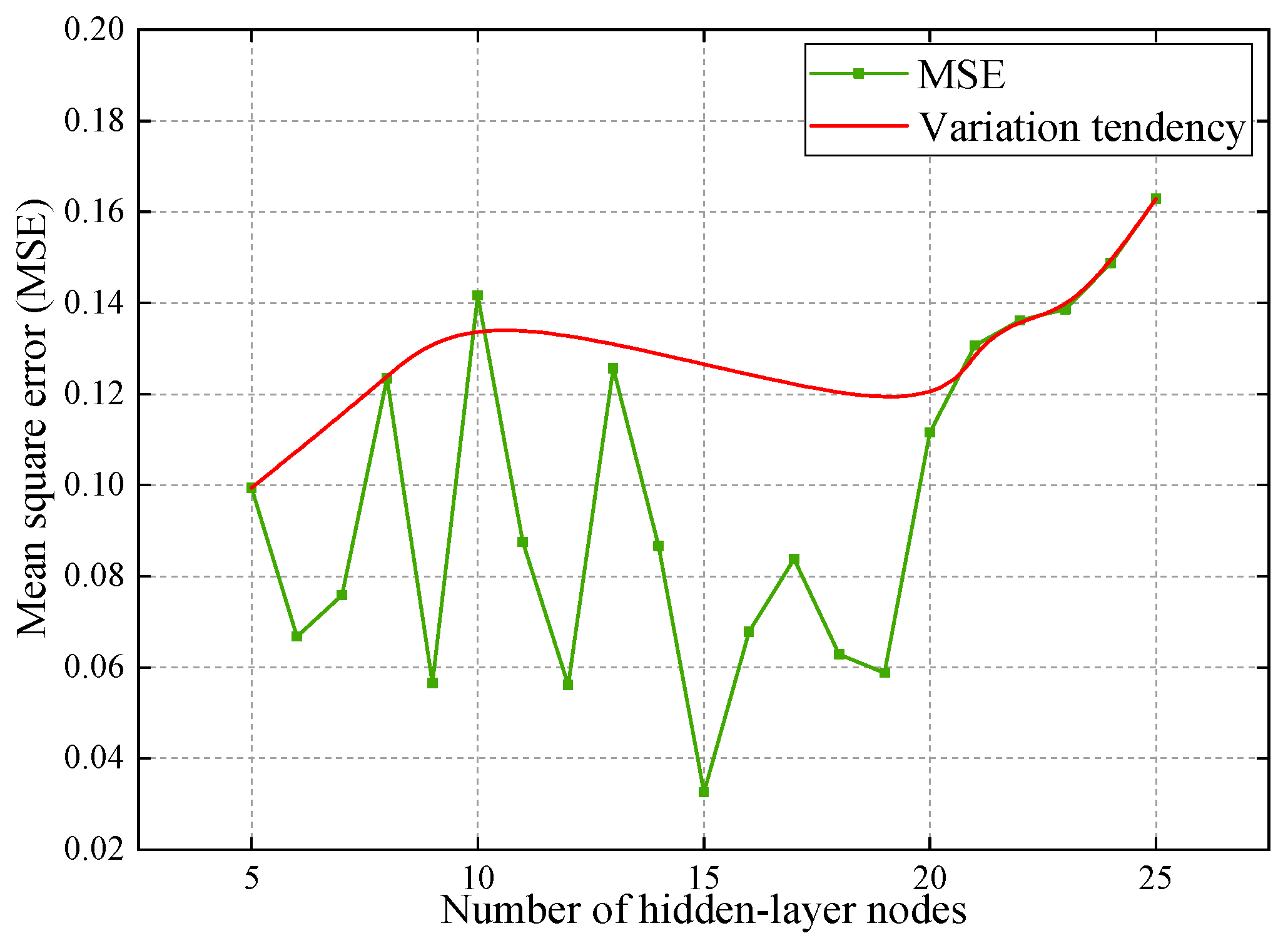
4.2. Prediction Accuracy of the ANN Model
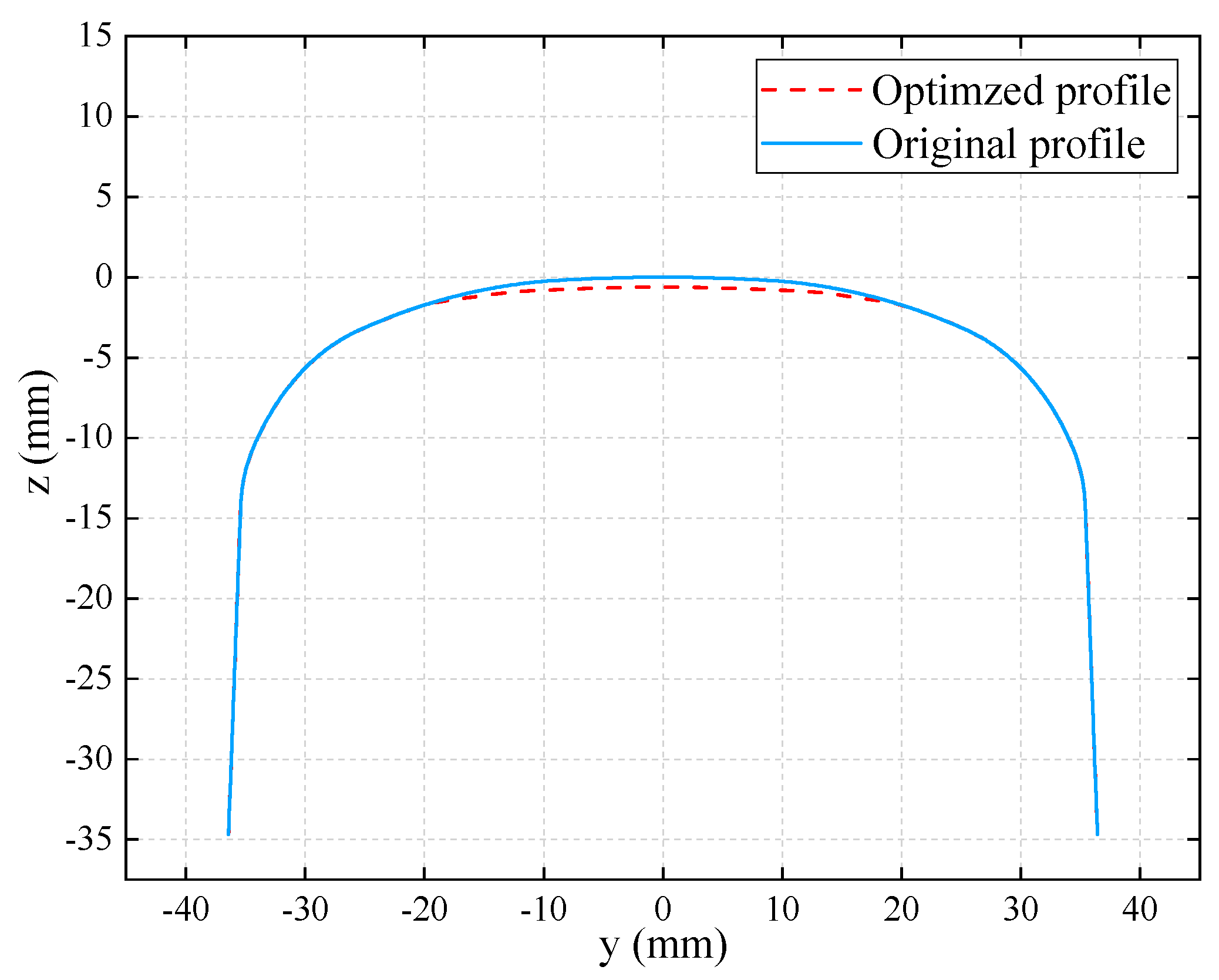
4.3. Optimizaiton Results of the ANN-GA Coupled Model
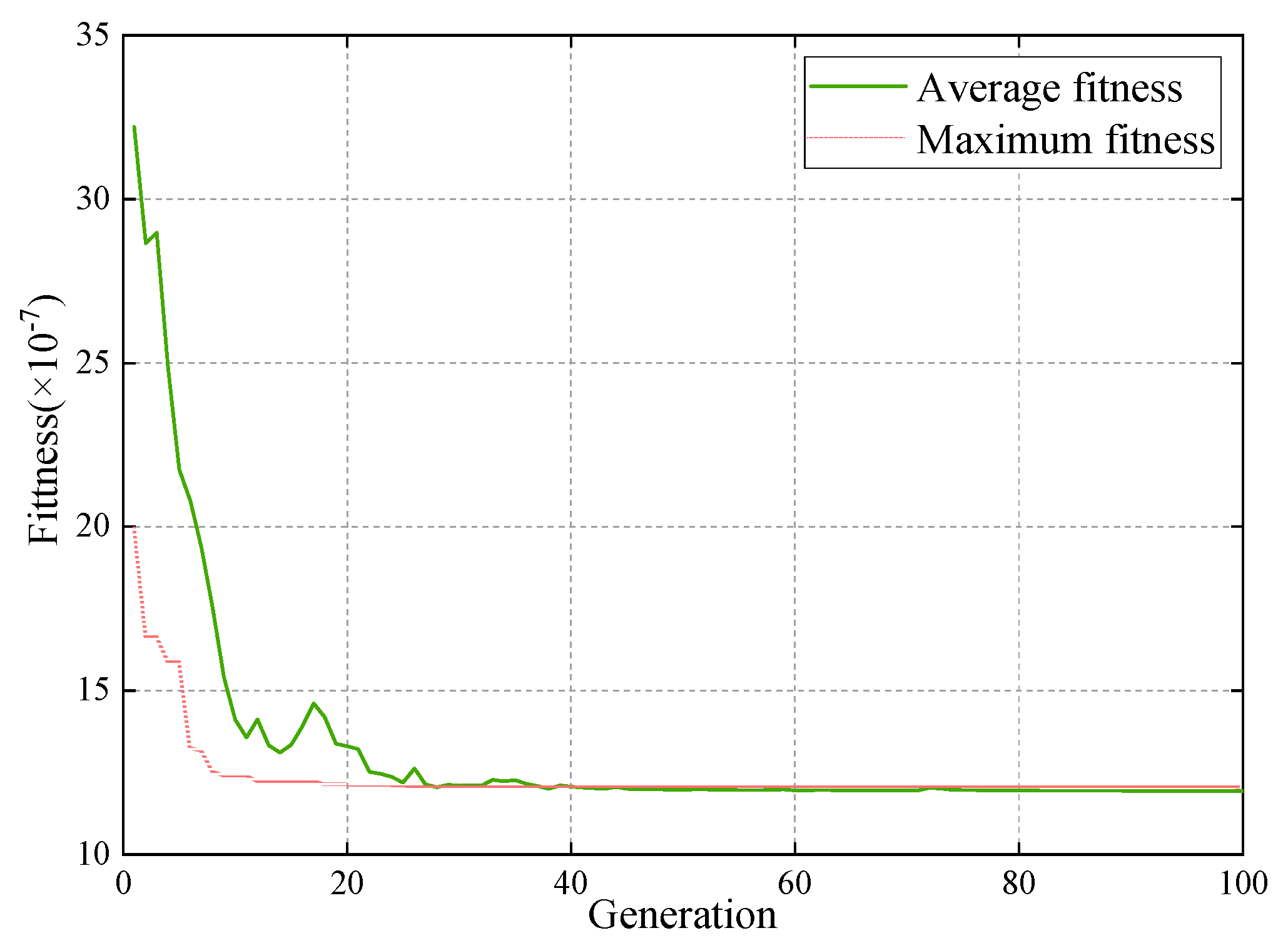
4.3.1. Optimization Process
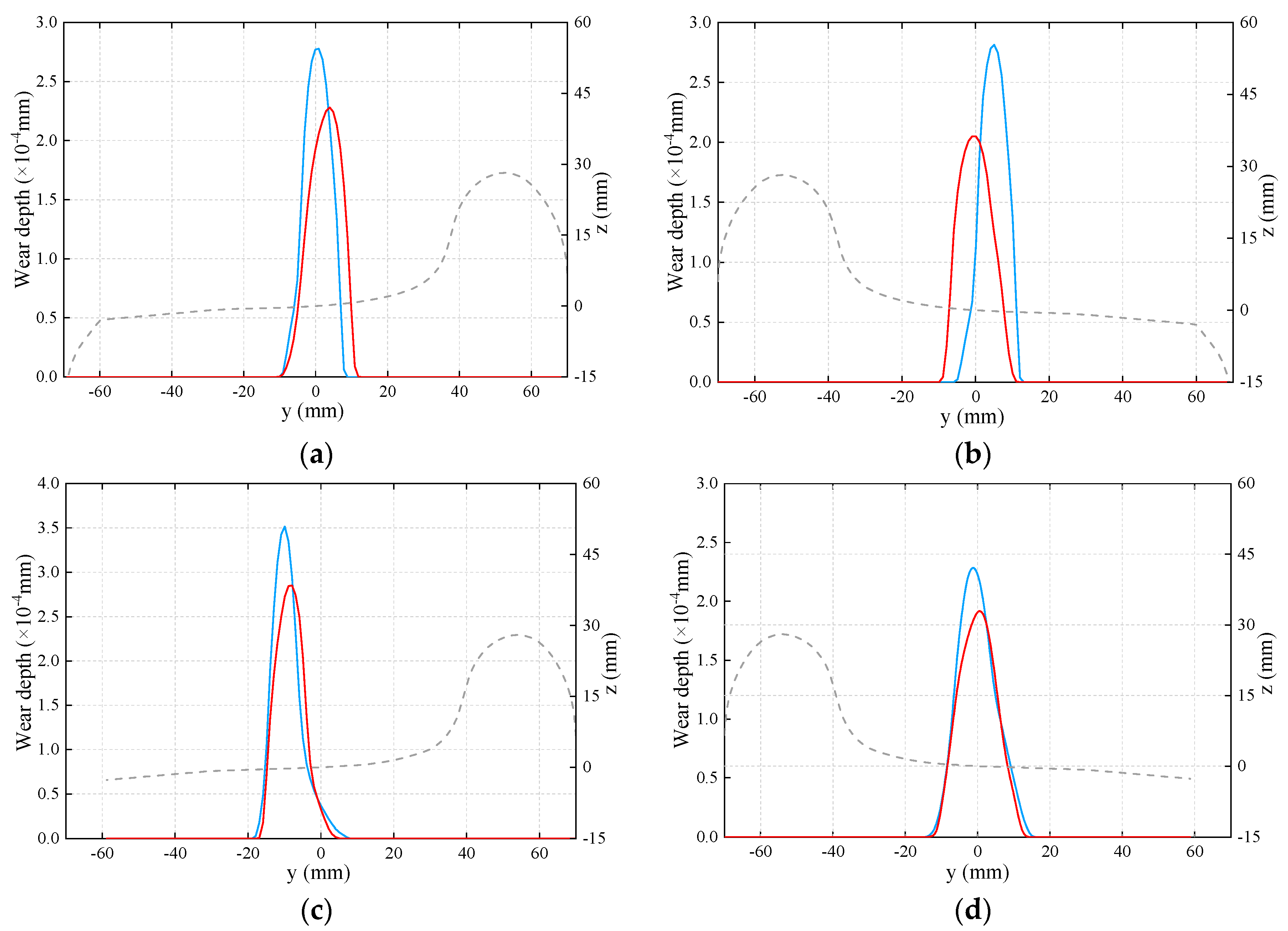
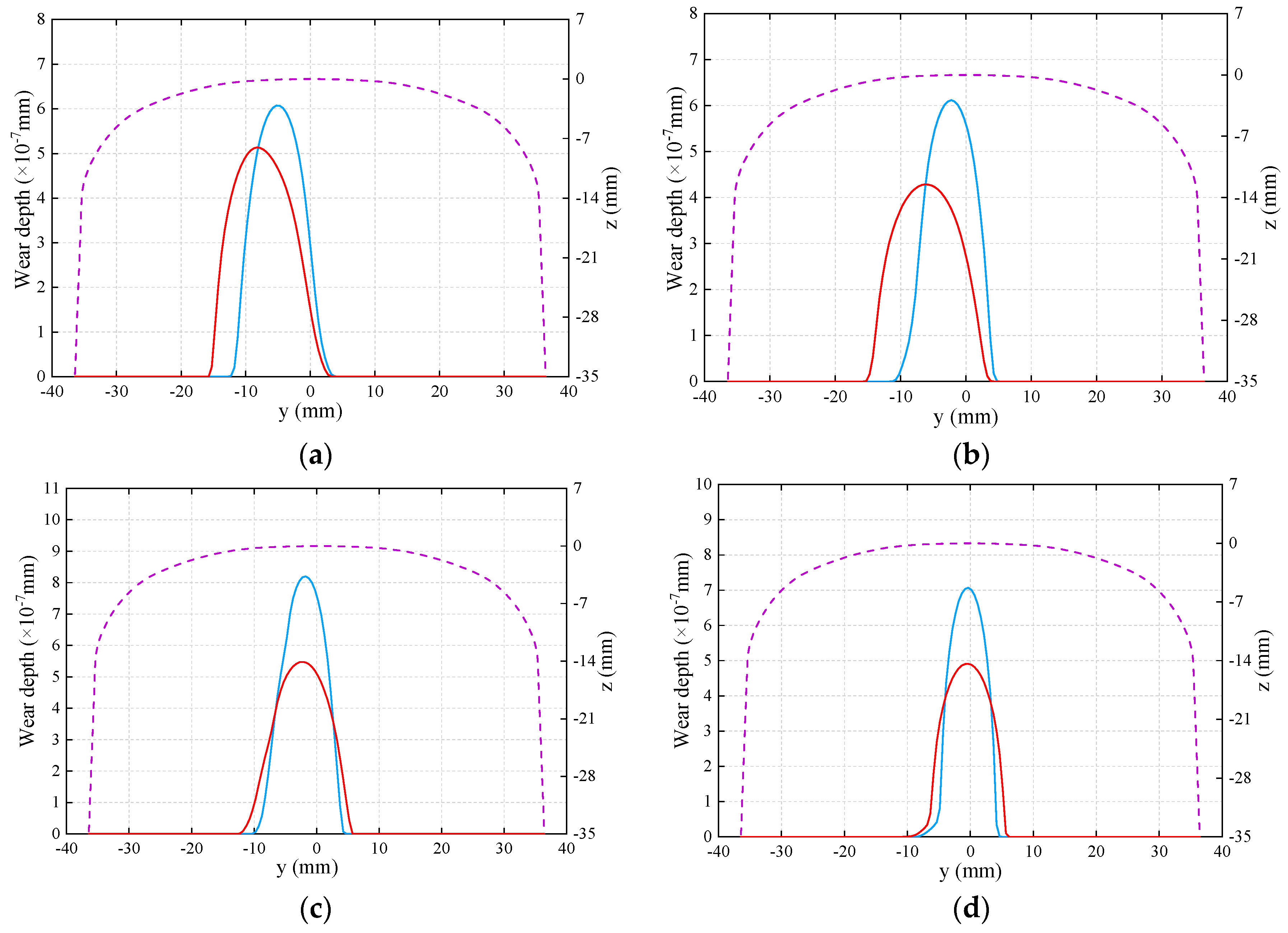
4.3.2. Wear Performances
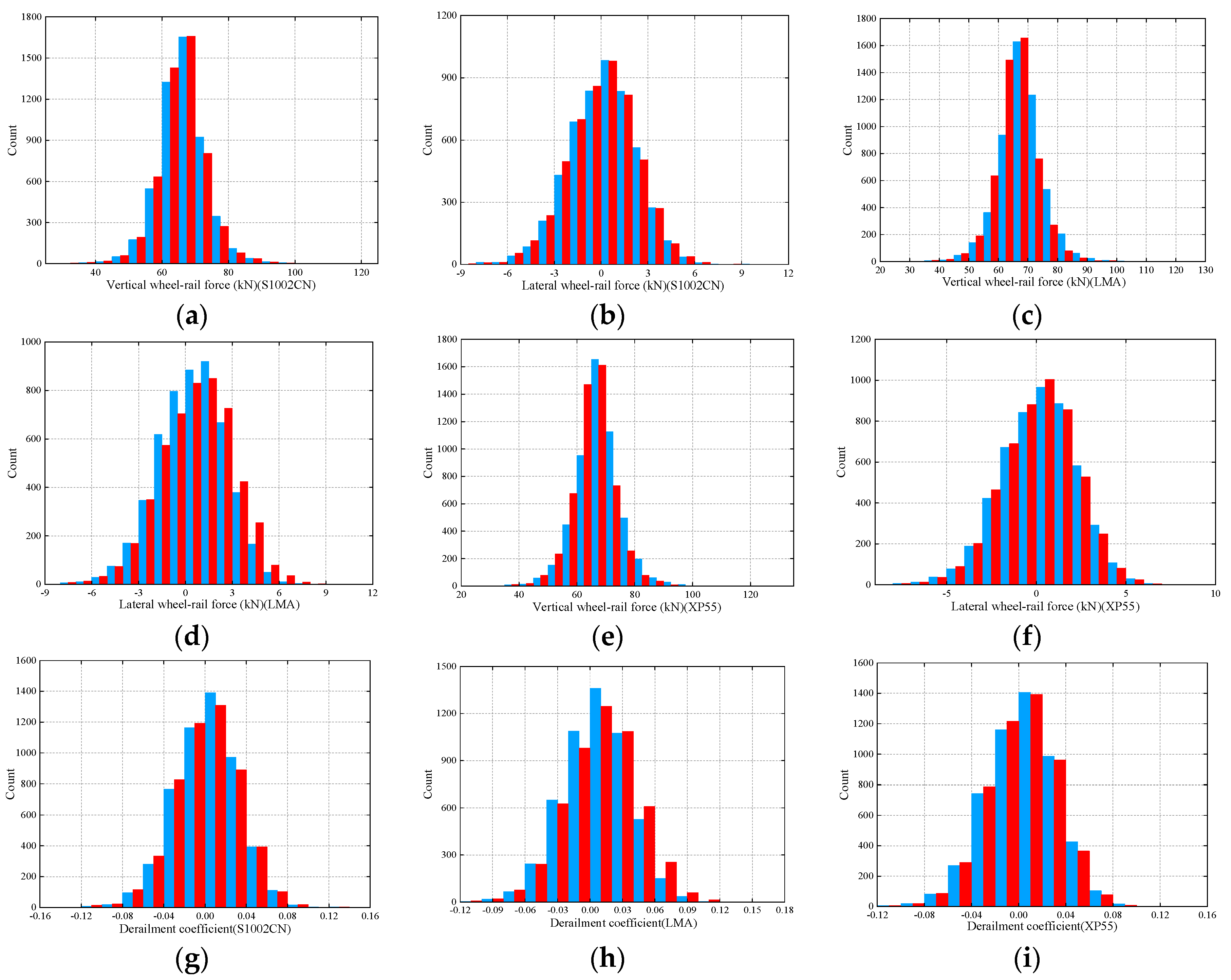
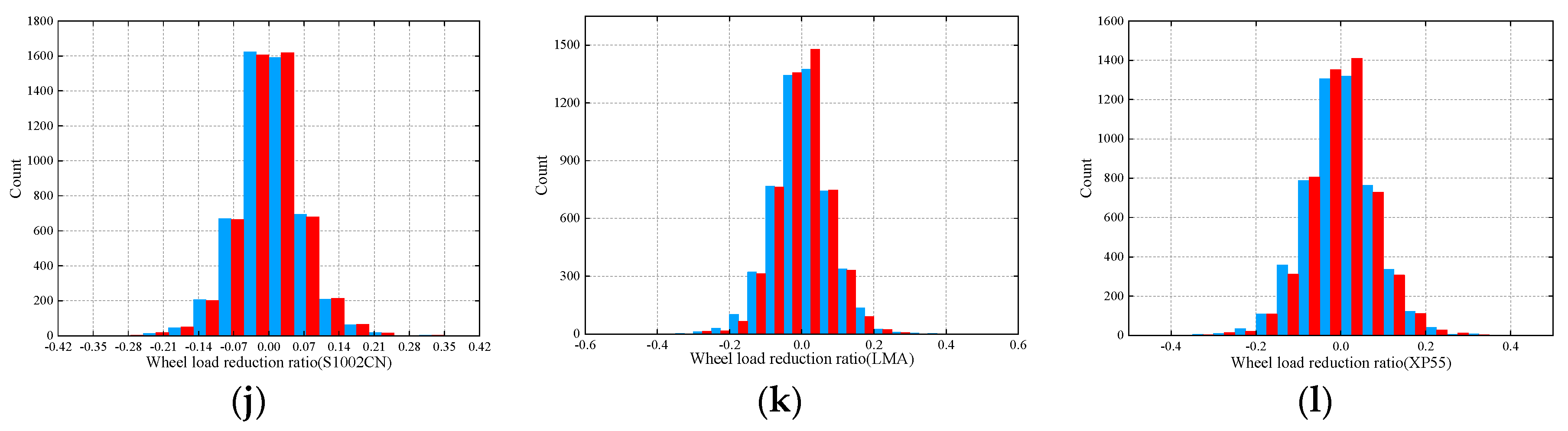
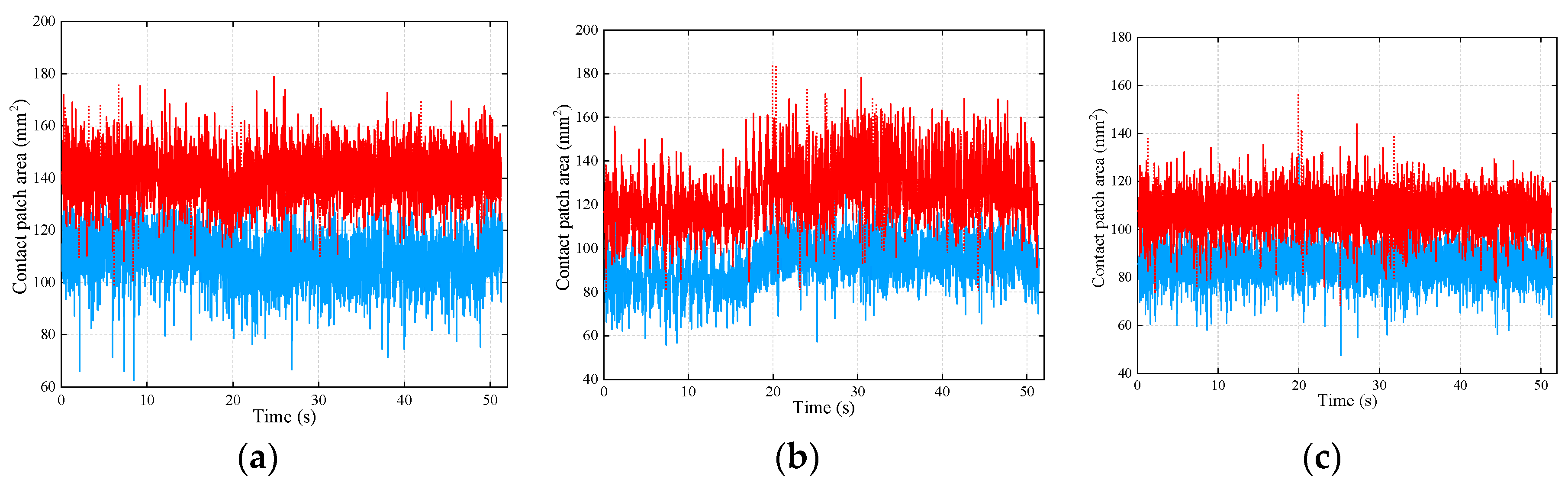
4.3.3. Dynamic Performances
4.3.4. Effectiveness Evaluation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Wang, W.; Liu, Q. Matching Characteristics between Four Kinds of Wheel Steels and U71Mn Hot-Rolled Rail. J. Southwest Jiaotong Univ. 2015, 50, 1130–1136. [Google Scholar]
- Ollivier, G.; Bullock, R.; Jin, Y.; Zhou, N. High-speed railways in China: A look at traffic. China Transp. Top. 2014, 11, 1–12. [Google Scholar]
- Cui, D.; Wang, R.; Allen, P.; An, B.; Li, L.; Wen, Z. Multi-objective optimization of electric multiple unit wheel profile from wheel flange wear viewpoint. Struct. Multidiscip. Optim. 2019, 59, 279–289. [Google Scholar] [CrossRef] [Green Version]
- Zeng, W.; Qiu, W.; Ren, T.; Sun, W.; Yang, Y. Multi-Objective Optimization of Rail Pre-Grinding Profile in Straight Line for High Speed Railway. J. Shanghai Jiaotong Univ. (Science) 2018, 23, 527–537. [Google Scholar] [CrossRef]
- Wang, P.; Gao, L.; Xin, T.; Cai, X.; Xiao, H. Study on the numerical optimization of rail profiles for heavy haul railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 649–665. [Google Scholar] [CrossRef]
- Jahed, H.; Farshi, B.; Eshraghi, M.A.; Nasr, A. A numerical optimization technique for design of wheel profiles. Wear 2008, 264, 1–10. [Google Scholar] [CrossRef]
- Persson, I.; Nilsson, R.; Bik, U.; Lundgren, M.; Iwnicki, S. Use of a genetic algorithm to improve the rail profile on Stockholm underground. Veh. Syst. Dyn. 2010, 48, 89–104. [Google Scholar] [CrossRef]
- Ignesti, M.; Innocenti, A.; Marini, L.; Meli, E.; Rindi, A.; Toni, P. Wheel profile optimization on railway vehicles from the wear viewpoint. Int. J. Non-Linear Mech. 2013, 53, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Shevtsov, I.; Markine, V.; Esveld, C. Optimization of Railway Wheel Profile Using MARS Method. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002; p. 1320. [Google Scholar]
- Shevtsov, I.Y.; Markine, V.L.; Esveld, C. One procedure for optimal design of wheel profile. In Proceedings of the IQPC Conference on Achieving Best Practice in Wheel/Rail Interface Management, Amsterdam, The Netherlands, 31 January–1 February 2002. [Google Scholar]
- Wang, P.; Ma, X.; Wang, J.; Xu, J.; Chen, R. Optimization of rail profiles to improve vehicle running stability in switch panel of high-speed railway turnouts. Math. Probl. Eng. 2017, 2017, 2856030. [Google Scholar] [CrossRef]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. Aiche. J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Singh, A.K.; Panda, S.S.; Chakraborty, D.; Pal, S.K. Predicting drill wear using an artificial neural network. Int. J. Adv. Manuf. Technol. 2006, 28, 456–462. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, D. Artificial neural network-based wear loss prediction for a390 aluminium alloy. J. Theor. Appl. Inf. Technol. 2008, 4, 961–964. [Google Scholar]
- Shebani, A.; Iwnicki, S. Prediction of wheel and rail wear under different contact conditions using artificial neural networks. Wear 2018, 406–407, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Juanjuan, R.; Huawei, Z.; Ming, O. Influence of rail grinding on wheel-rail contact relationship for high-speed railway. J. Huazhong Univ. Sci. Technol. (Natural Science Edition) 2016, 44, 95–100. [Google Scholar]
- Xin, T.; Wang, P.; Ding, Y. Effect of Long-Wavelength Track Irregularities on Vehicle Dynamic Responses. Shock Vib. 2019, 2019, 4178065. [Google Scholar] [CrossRef]
- Zhai, W. Vehicle-Track Coupled Dynamics, 4th ed.; China Science Publishing & Media Ltd.: Beijing, China, 2014. [Google Scholar]
- Archard, J. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Xu, J.; Wang, P.; Wang, J.; An, B.; Chen, R. Numerical analysis of the effect of track parameters on the wear of turnout rails in high-speed railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 709–721. [Google Scholar] [CrossRef]
- Luo, R.; Shi, H.; Teng, W.; Song, C. Prediction of wheel profile wear and vehicle dynamics evolution considering stochastic parameters for high-speed train. Wear 2017, 392, 126–138. [Google Scholar] [CrossRef]
- Bevan, A.; Molyneux-Berry, P.; Eickhoff, B.; Burstow, M. Development and validation of a wheel wear and rolling contact fatigue damage model. Wear 2013, 307, 100–111. [Google Scholar] [CrossRef] [Green Version]
- Iwnicki, S. The effect of profiles on wheel and rail damage. Inte. J. Veh. Struct. Syst. 2009, 1, 99–104. [Google Scholar] [CrossRef]
- Jendel, T. Prediction of wheel profile wear—Comparisons with field measurements. Wear 2002, 253, 89–99. [Google Scholar] [CrossRef]
- Sebaaly, H.; Varma, S.; Maina, J.W. Optimizing asphalt mix design process using artificial neural network and genetic algorithm. Constr. Build. Mater. 2018, 168, 660–670. [Google Scholar] [CrossRef] [Green Version]
- Pappu, S.M.J.; Gummadi, S.N. Artificial neural network and regression coupled genetic algorithm to optimize parameters for enhanced xylitol production by Debaryomyces nepalensis in bioreactor. Biochem. Eng. J. 2017, 120, 136–145. [Google Scholar] [CrossRef]
- Khudhair, A. Neural Network Analysis for Sliding Wear of 13% Cr Steel Coatings by Electric Arc Spraying. Diyal. J. Eng. Sci. 2010, first, 157–169. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Kavzoglu, T.; Mather, P.M. The use of backpropagating artificial neural networks in land cover classification. Int. J. Remote Sens. 2003, 24, 4907–4938. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples; PHI Learning Pvt. Ltd.: New Delhi, India, 2012. [Google Scholar]
- Conn, A.R.; Gould, N.I.; Toint, P. A globally convergent augmented Lagrangian algorithm for optimization with general constraints and simple bounds. Siam. J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef] [Green Version]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Conn, A.; Gould, N.; Toint, P. A globally convergent Lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Math. Comput. Am. Math. Soc. 1997, 66, 261–288. [Google Scholar] [CrossRef]
- China, S.A. Technical regulations for dynamic acceptance for high-speed railways construction. In TB 10761-2013; Standards Press of China: Beijing, China, 2013. [Google Scholar]
- Cui, D.; Li, L.; Jin, X. Study on Rail Goal Profile by Grinding. Eng. Mech. 2011, 28, 178–184. [Google Scholar]
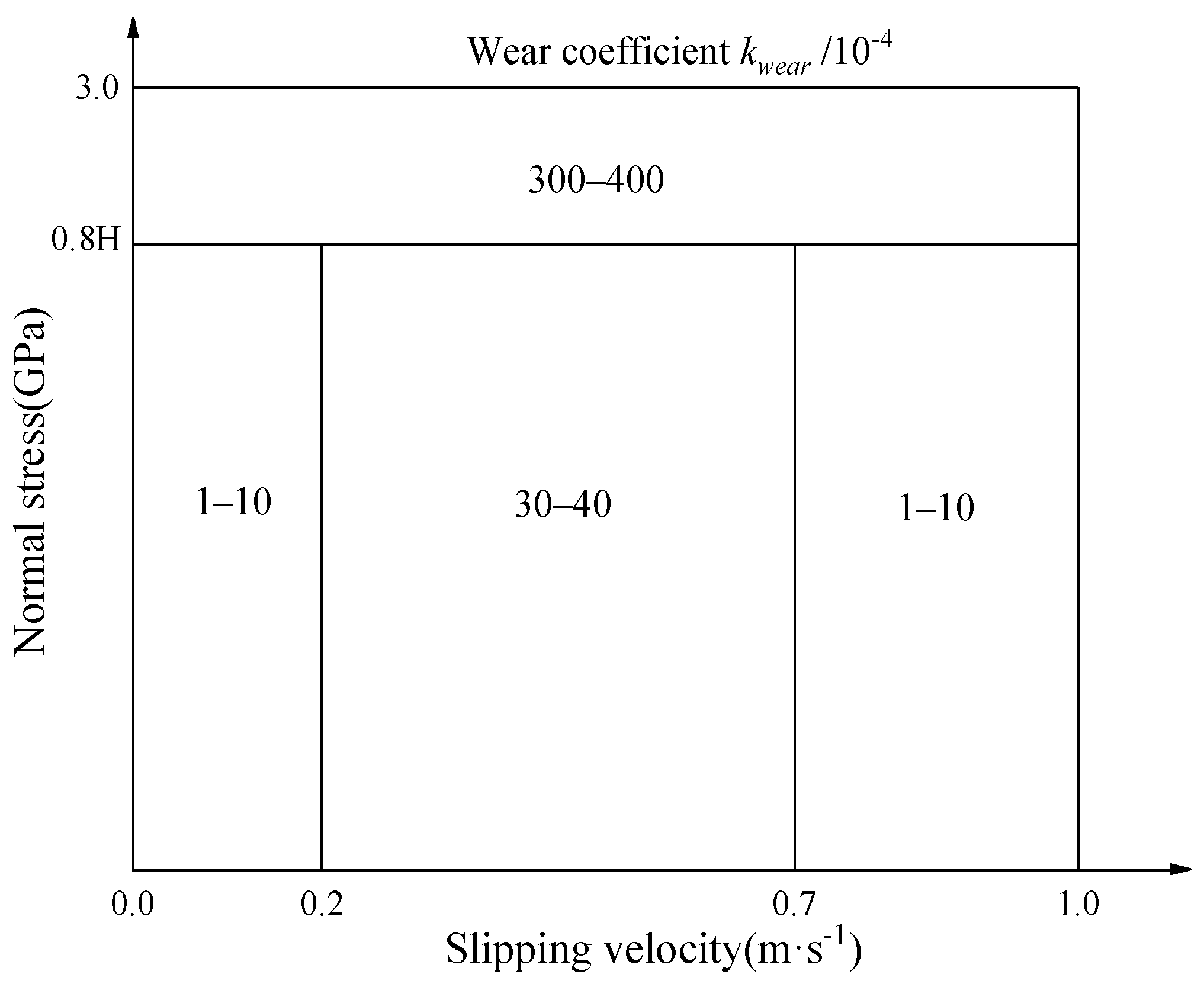
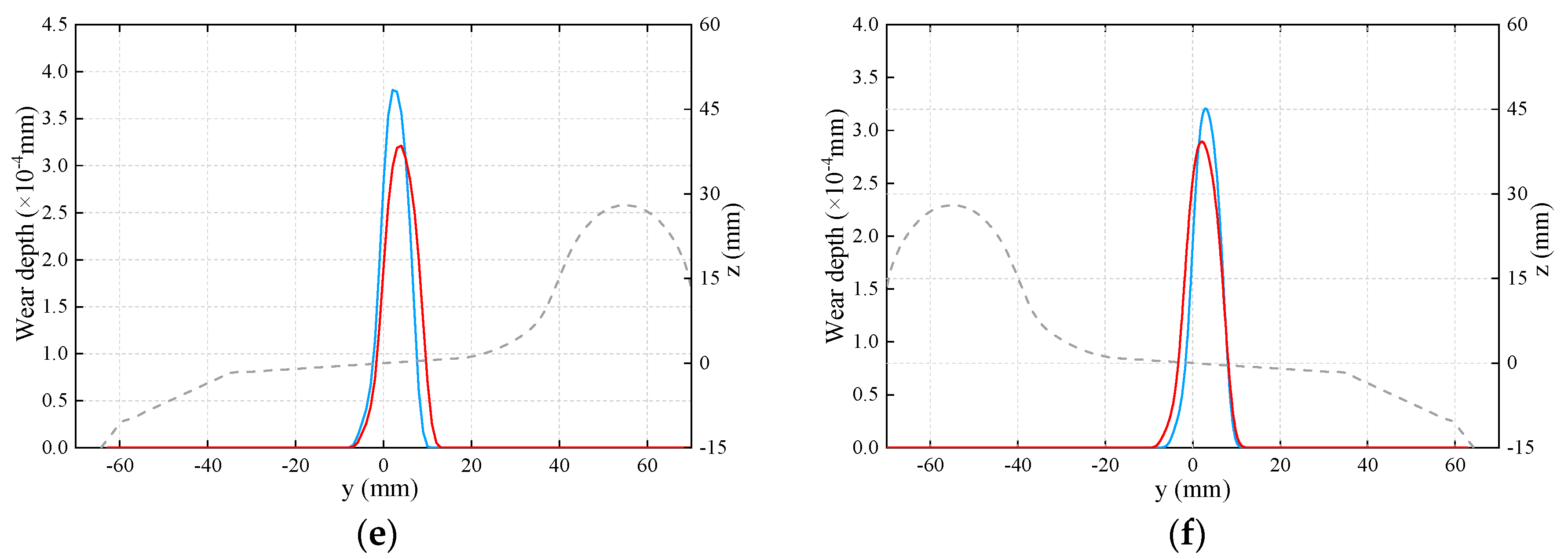


| Rigid Body Name | Longitudinal | Lateral | Vertical | Roll | Pitch | Yaw |
|---|---|---|---|---|---|---|
| Car body | xc | yc | zc | φc | γc | Φc |
| Frame | xfi | yfi | zfi | φfi | γfi | Φfi |
| Axle box | None | None | None | None | γai | None |
| Wheelset | xwi | ywi | zwi | φwi | γwi | Φwi |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rail cant | 1/40 | Rail gauge (mm) | 1435 |
| Radius of curve (m) | 7000 | Superelevation (mm) | 150 |
| Length of transition curve (m) | 670 | Length of circular curve (m) | 2000 |
| Length of tangent section before curved section (m) | 1380 | Length of tangent section after curved section (m) | 280 |
| Running speed (km/h) | 300 |
| Evaluation Index | This Paper | Zhai [18] |
|---|---|---|
| Vertical wheel-rail force (kN) | 132.33 | 140.89 |
| Lateral wheel-rail force (kN) | 19.01 | 24.38 |
| Derailment coefficient | 0.21 | 0.29 |
| Datasets | Input Data (×–1 mm) | Output Data (×10−7 mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.292 | 0.633 | 0.257 | 0.088 | 0.010 | 0.010 | 0.088 | 0.257 | 0.633 | 1.292 | 13.8580 |
| 2 | 1.302 | 0.657 | 0.290 | 0.125 | 0.048 | 0.048 | 0.125 | 0.290 | 0.657 | 1.302 | 13.6690 |
| 3 | 1.312 | 0.682 | 0.323 | 0.162 | 0.087 | 0.087 | 0.162 | 0.323 | 0.682 | 1.312 | 13.6080 |
| 4 | 1.321 | 0.707 | 0.356 | 0.198 | 0.125 | 0.125 | 0.198 | 0.356 | 0.707 | 1.321 | 13.4005 |
| 5 | 1.331 | 0.731 | 0.389 | 0.235 | 0.163 | 0.163 | 0.235 | 0.389 | 0.731 | 1.331 | 13.2630 |
| 6 | 1.341 | 0.756 | 0.422 | 0.271 | 0.202 | 0.202 | 0.271 | 0.422 | 0.756 | 1.341 | 13.0758 |
| 7 | 1.351 | 0.780 | 0.455 | 0.308 | 0.240 | 0.240 | 0.308 | 0.455 | 0.780 | 1.351 | 13.0643 |
| 8 | 1.361 | 0.805 | 0.488 | 0.345 | 0.279 | 0.279 | 0.345 | 0.488 | 0.805 | 1.361 | 13.0418 |
| 9 | 1.371 | 0.829 | 0.520 | 0.381 | 0.317 | 0.317 | 0.381 | 0.520 | 0.829 | 1.371 | 12.9944 |
| 10 | 1.381 | 0.854 | 0.553 | 0.418 | 0.355 | 0.355 | 0.418 | 0.553 | 0.854 | 1.381 | 12.9913 |
| 11 | 1.391 | 0.878 | 0.586 | 0.455 | 0.394 | 0.394 | 0.455 | 0.586 | 0.878 | 1.391 | 12.9652 |
| 12 | 1.401 | 0.903 | 0.619 | 0.491 | 0.432 | 0.432 | 0.491 | 0.619 | 0.903 | 1.401 | 12.9441 |
| 13 | 1.411 | 0.928 | 0.652 | 0.528 | 0.471 | 0.471 | 0.528 | 0.652 | 0.928 | 1.411 | 12.9136 |
| 14 | 1.421 | 0.952 | 0.685 | 0.565 | 0.509 | 0.509 | 0.565 | 0.685 | 0.952 | 1.421 | 12.8299 |
| 15 | 1.431 | 0.977 | 0.718 | 0.601 | 0.547 | 0.547 | 0.601 | 0.718 | 0.977 | 1.431 | 12.7234 |
| 16 | 1.440 | 1.001 | 0.751 | 0.638 | 0.586 | 0.586 | 0.638 | 0.751 | 1.001 | 1.440 | 12.6435 |
| 17 | 1.450 | 1.026 | 0.784 | 0.675 | 0.624 | 0.624 | 0.675 | 0.784 | 1.026 | 1.450 | 12.6669 |
| 18 | 1.460 | 1.050 | 0.817 | 0.711 | 0.663 | 0.663 | 0.711 | 0.817 | 1.050 | 1.460 | 12.6900 |
| 19 | 1.470 | 1.075 | 0.849 | 0.748 | 0.701 | 0.701 | 0.748 | 0.849 | 1.075 | 1.470 | 12.9405 |
| 20 | 1.480 | 1.099 | 0.882 | 0.785 | 0.739 | 0.739 | 0.785 | 0.882 | 1.099 | 1.480 | 13.3525 |
| Number of Rail Profiles | Prediction Result (×10−7 mm) | Target Value (×10−7 mm) | Relative Error ξ (%) |
|---|---|---|---|
| 16 | 12.6435 | 10.5575 | 0.9141 |
| 3 | 13.6080 | 9.7627 | −2.2523 |
| 15 | 12.7234 | 10.3132 | −0.5516 |
| Evaluation Index | S1002CN | LMA | XP55 | Cui et al. [36] |
|---|---|---|---|---|
| Increment of the area of contact | 29.59% | 33.00% | 25.08% | 16.11% |
| Decrease of the maximum contact pressure | 28.06% | 33.65% | 26.21% | 23.50% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Gao, L. Optimizing the Rail Profile for High-Speed Railways Based on Artificial Neural Network and Genetic Algorithm Coupled Method. Sustainability 2020, 12, 658. https://doi.org/10.3390/su12020658
Jiang H, Gao L. Optimizing the Rail Profile for High-Speed Railways Based on Artificial Neural Network and Genetic Algorithm Coupled Method. Sustainability. 2020; 12(2):658. https://doi.org/10.3390/su12020658
Chicago/Turabian StyleJiang, Hanwen, and Liang Gao. 2020. "Optimizing the Rail Profile for High-Speed Railways Based on Artificial Neural Network and Genetic Algorithm Coupled Method" Sustainability 12, no. 2: 658. https://doi.org/10.3390/su12020658
APA StyleJiang, H., & Gao, L. (2020). Optimizing the Rail Profile for High-Speed Railways Based on Artificial Neural Network and Genetic Algorithm Coupled Method. Sustainability, 12(2), 658. https://doi.org/10.3390/su12020658





