Improved Salp–Swarm Optimizer and Accurate Forecasting Model for Dynamic Economic Dispatch in Sustainable Power Systems
Abstract
1. Introduction
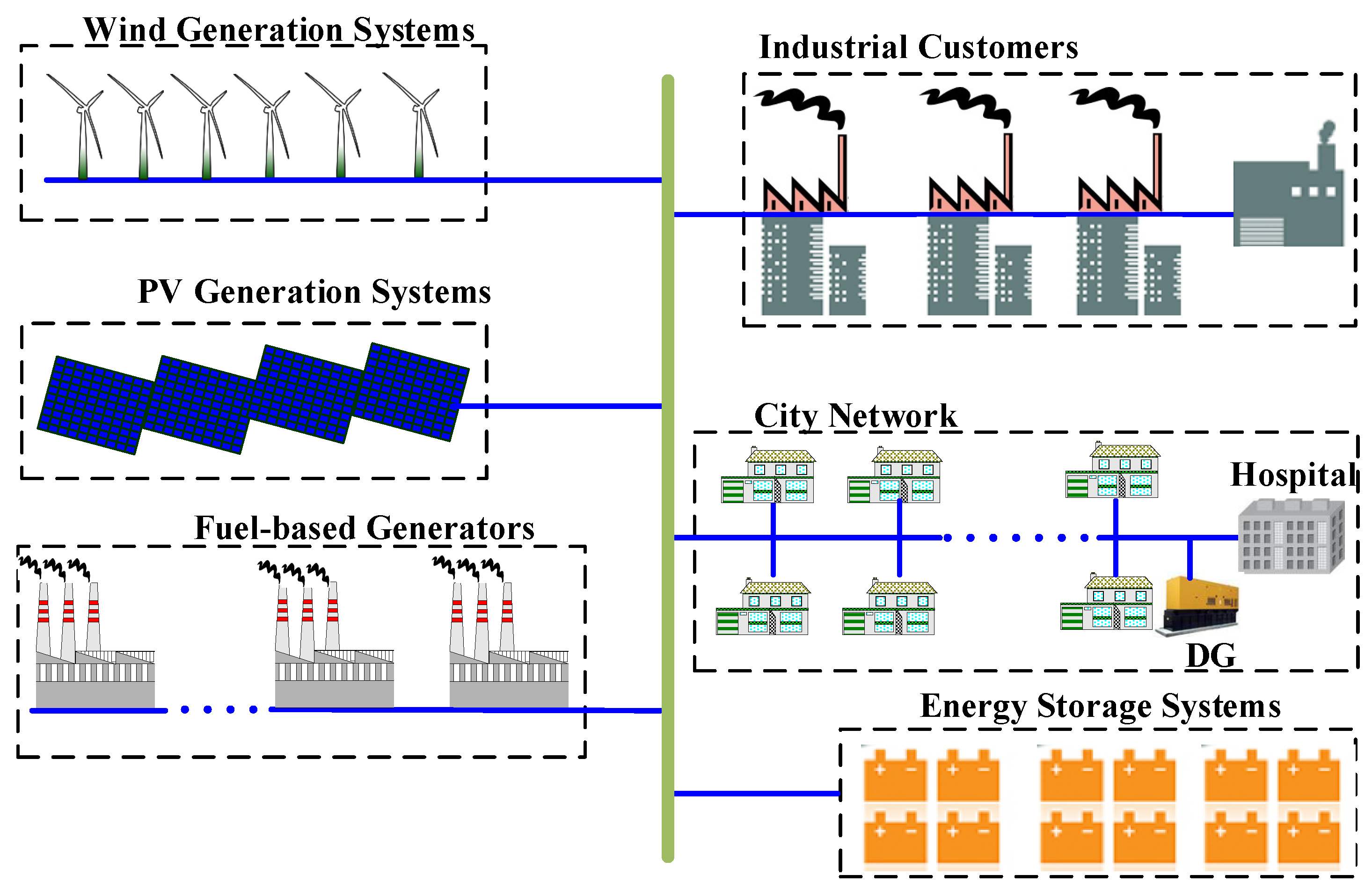
- Comprehensive DED framework: A comprehensive DED framework is formulated that includes fuel-based generators, PV, and storage devices in a sustainable power system, considering clear and cloudy profiles of PV.
- Improved optimizer: We propose an improved salp–swarm optimizer that helps manage the global exploration of the DED algorithm and reach reasonable DED solutions. Specifically, we apply a mutation operator to the salp swarm optimizer to increase the exploitation of the search space for improved solutions. The proposed algorithm is validated with ten benchmark problems and then used to optimize the DED problem for a sustainable power system with PV within the studied period.
- Deep learning-based forecasting models: We propose a DED handling strategy that involves the use of PV power and load forecasting models based on deep learning techniques.
2. Comprehensive DED Framework
- Equality constraints
- Inequality constraints
3. Proposed DED Algorithm
- Step 1: Read system data, including cost coefficients of generation stations, power limits of generation stations, ramp rate limits for each generation station, and B-loss coefficients. Read the historical datasets of load and PV solar radiation, and data of energy storage systems.
- Step 2: Set the population of the improved SSA algorithm, number of agents, and the maximum number of iterations.
- Step 3: Forecast the PV radiation and load for the period in which the system is required to be optimally dispatched.
- Step 4: Run the improved SSA algorithm considering the mutation operator and the handling strategy of the various constraints.
- Step 5: Save and print the calculated results, including the scheduling of the generation stations, and energy storage systems, and the total costs.
3.1. Improved Salp–Swarm Algorithm (ISSA)
3.2. Satisfying Various Constraints
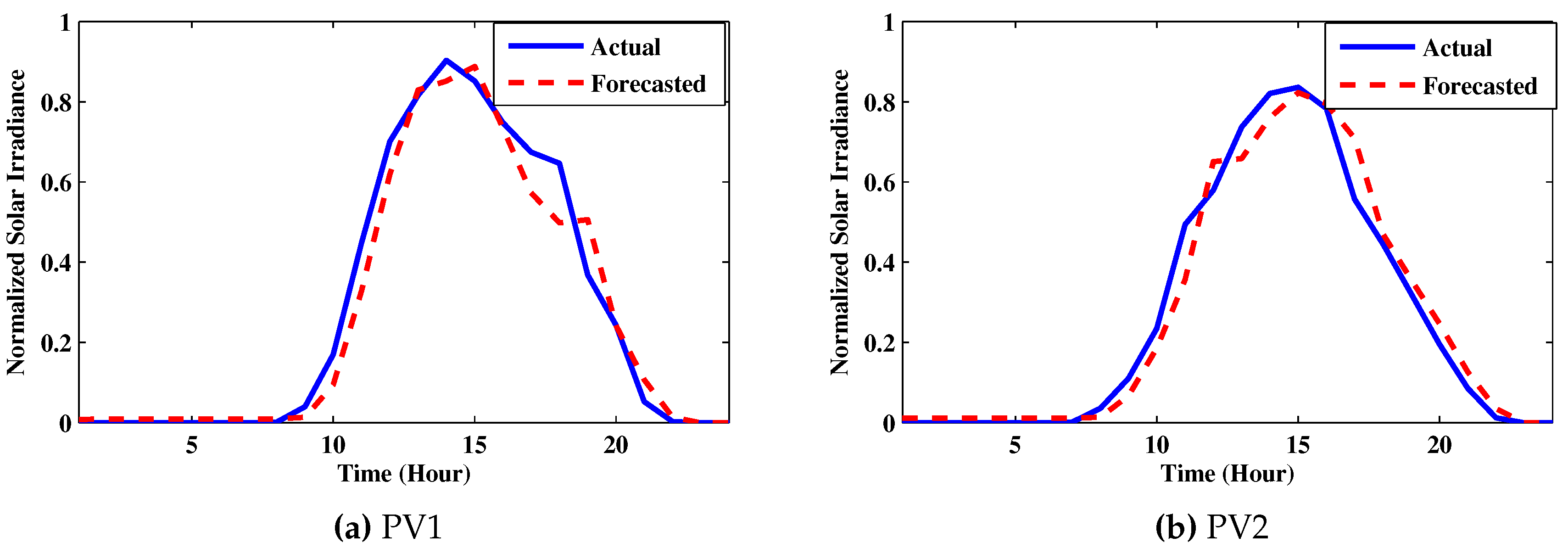
3.3. Forecasting Models
4. Results and Discussion
4.1. Analyzing the Performance of ISSA with Ten Benchmark Problems
4.2. Analyzing the Performance of an LSTM Forecasting Model
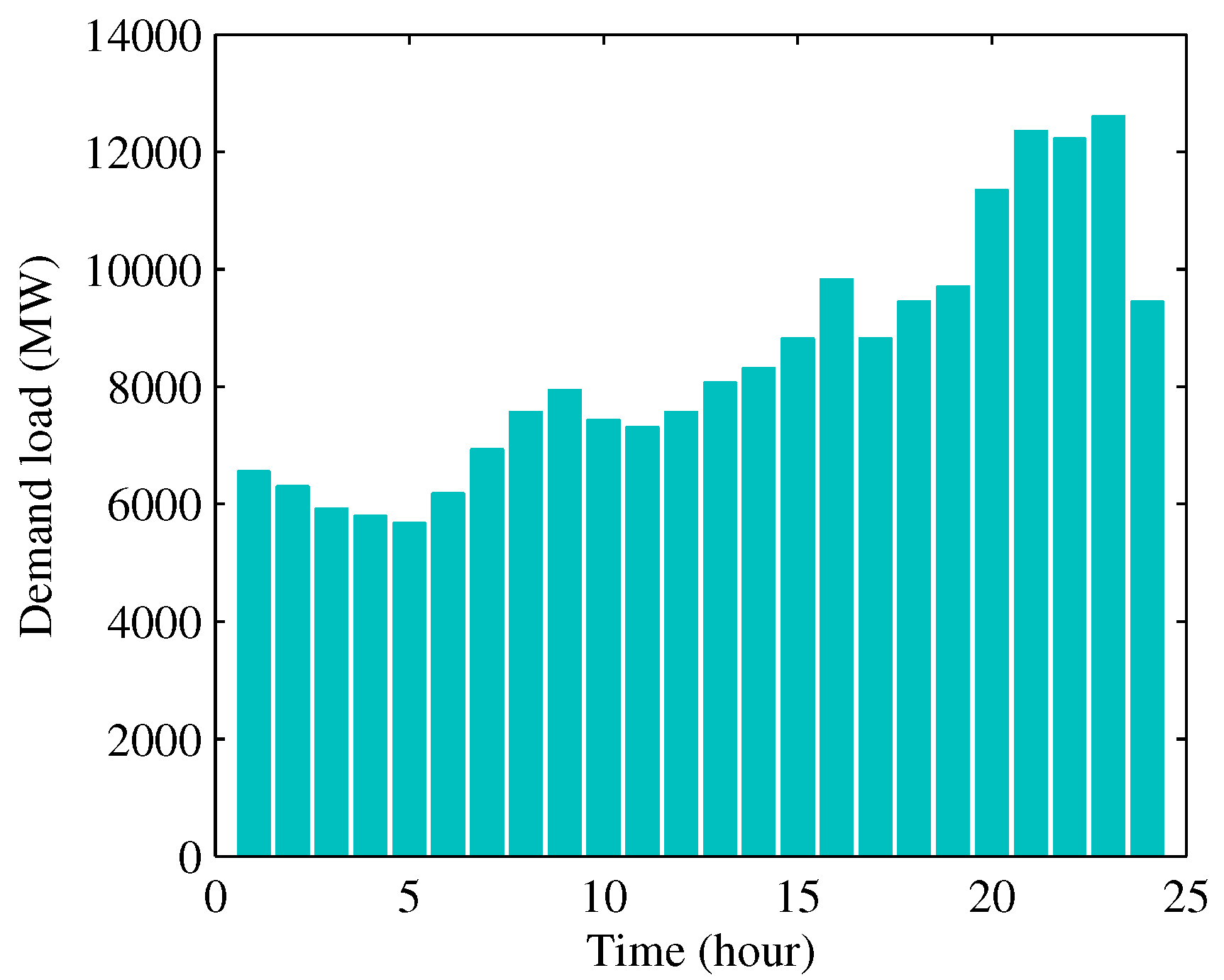
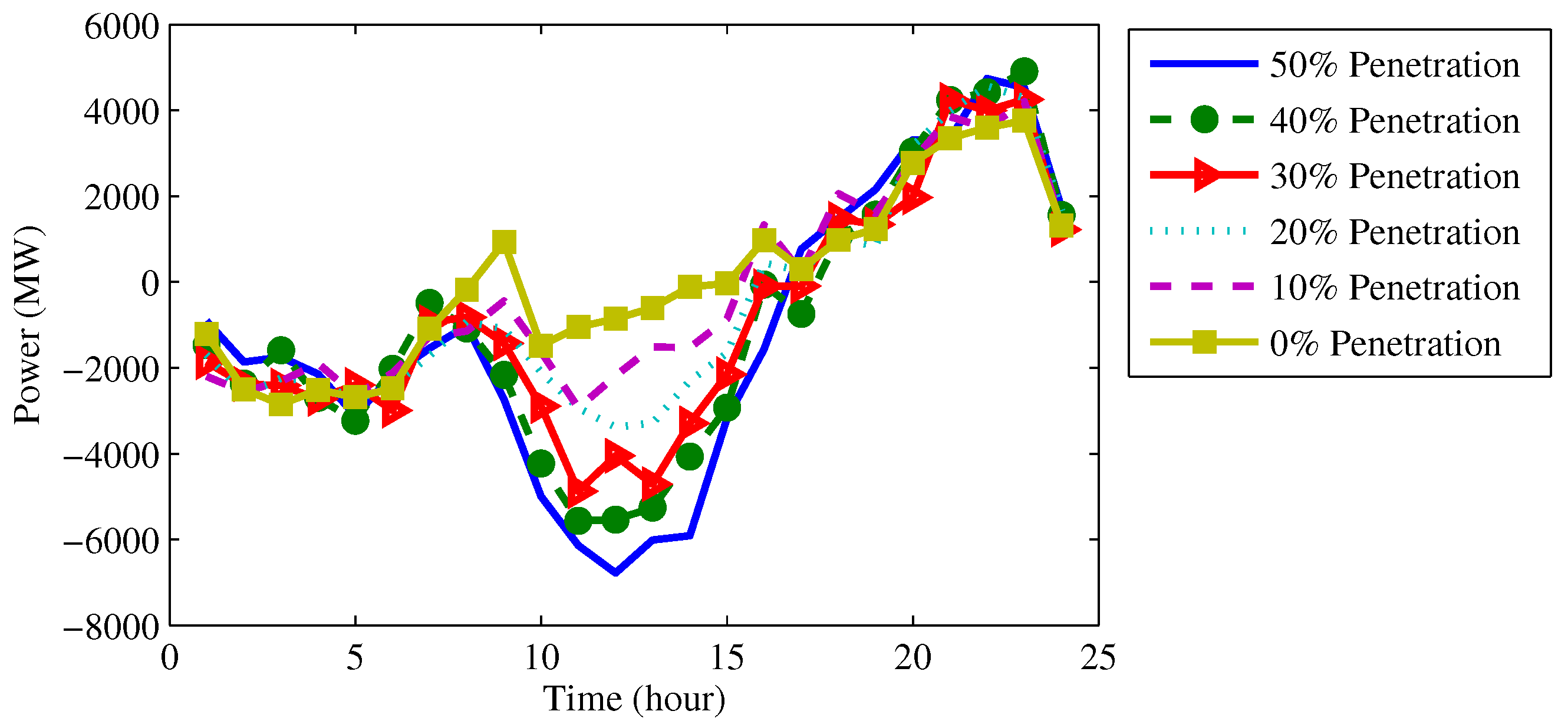
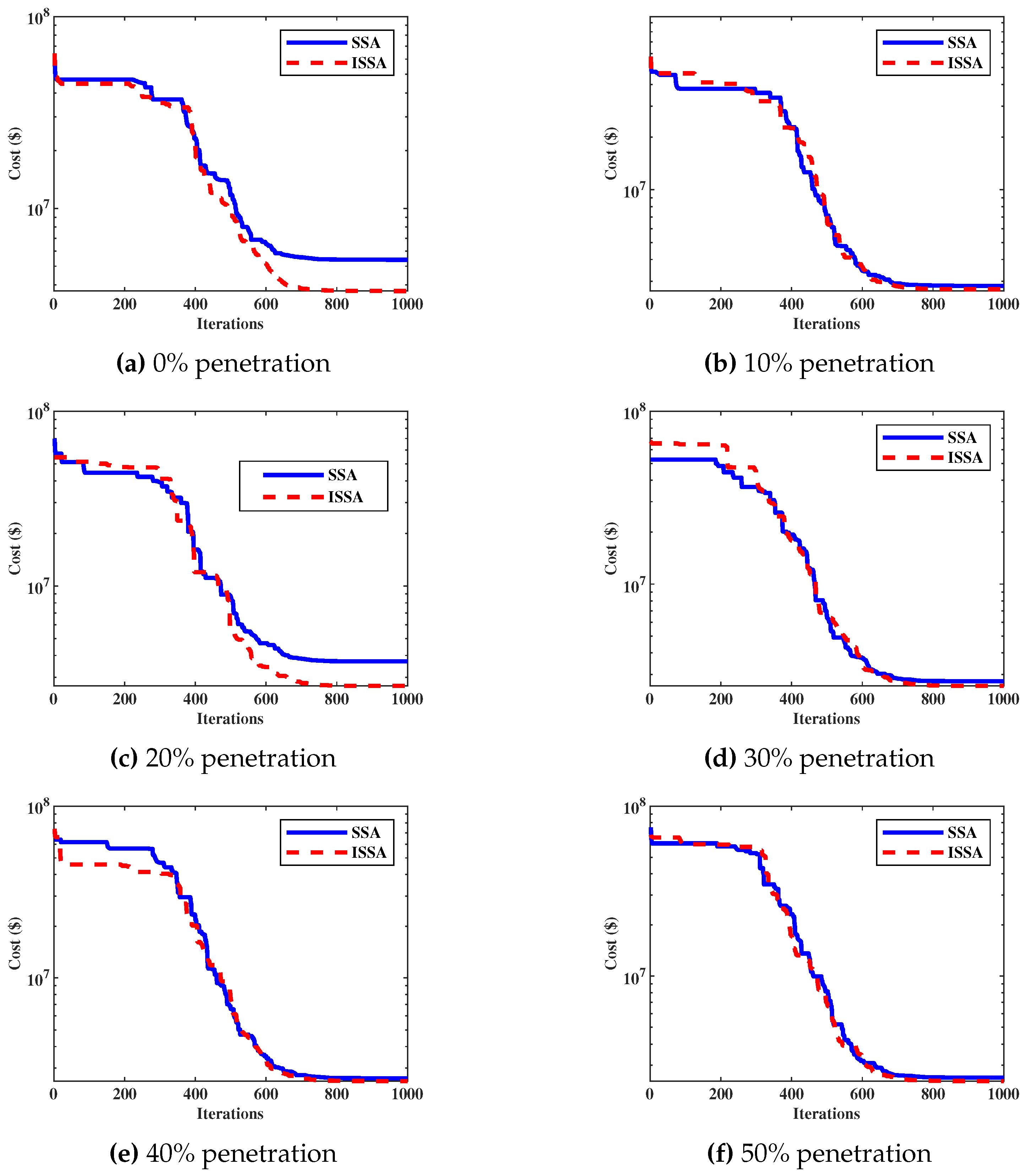
4.3. Analyzing the Performance of ISSA with the DED Problem
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Yang, S.; Tan, S.; Xu, J.X. Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- Abujarad, S.Y.; Mustafa, M.; Jamian, J. Recent approaches of unit commitment in the presence of intermittent renewable energy resources: A review. Renew. Sustain. Energy Rev. 2017, 70, 215–223. [Google Scholar] [CrossRef]
- Lee, F.N.; Breipohl, A.M. Reserve constrained economic dispatch with prohibited operating zones. IEEE Trans. Power Syst. 1993, 8, 246–254. [Google Scholar] [CrossRef]
- Zaman, M.; Elsayed, S.M.; Ray, T.; Sarker, R.A. Evolutionary algorithms for dynamic economic dispatch problems. IEEE Trans. Power Syst. 2015, 31, 1486–1495. [Google Scholar] [CrossRef]
- Rahman, M.M.; Mostafiz, S.B.; Paatero, J.V.; Lahdelma, R. Extension of energy crops on surplus agricultural lands: A potentially viable option in developing countries while fossil fuel reserves are diminishing. Renew. Sustain. Energy Rev. 2014, 29, 108–119. [Google Scholar] [CrossRef]
- Abas, N.; Kalair, A.; Khan, N. Review of fossil fuels and future energy technologies. Futures 2015, 69, 31–49. [Google Scholar] [CrossRef]
- Mohamed, A.A.A.; Ali, S.; Alkhalaf, S.; Senjyu, T.; Hemeida, A.M. Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm. Sustainability 2019, 11, 6550. [Google Scholar] [CrossRef]
- Alkhalaf, S.; Senjyu, T.; Saleh, A.A.; Hemeida, A.M.; Mohamed, A.A.A. A MODA and MODE Comparison for Optimal Allocation of Distributed Generations with Different Load Levels. Sustainability 2019, 11, 5323. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Aly, M.; Elmelegi, A.; Alharbi, A.G.; Ali, Z.M. Multifunctional Distributed MPPT Controller for 3P4W Grid-Connected PV Systems in Distribution Network with Unbalanced Loads. Energies 2019, 12, 4799. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K.; Kashef, H. A Novel Smart Grid State Estimation Method Based on Neural Networks. IJIMAI 2018, 5, 92–100. [Google Scholar] [CrossRef]
- Mahmoud, K.; Hussein, M.M.; Abdel-Nasser, M.; Lehtonen, M. Optimal Voltage Control in Distribution Systems With Intermittent PV Using Multiobjective Grey-Wolf-Lévy Optimizer. IEEE Syst. J. 2019, 1–11. [Google Scholar] [CrossRef]
- Clancy, J.; Gaffney, F.; Deane, J.; Curtis, J.; Gallachóir, B.Ó. Fossil fuel and CO2 emissions savings on a high renewable electricity system–a single year case study for Ireland. Energy Policy 2015, 83, 151–164. [Google Scholar] [CrossRef]
- Mohamed, F.; AbdelNasser, M.; Mahmoud, K.; Kamel, S. Accurate economic dispatch solution using hybrid whale-wolf optimization method. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 922–927. [Google Scholar]
- Mahmoud, K.; Abdel-Nasser, M. Efficient SPF approach based on regression and correction models for active distribution systems. IET Renew. Power Gener. 2017, 11, 1778–1784. [Google Scholar] [CrossRef]
- Novakovic, B.; Nasiri, A. 1-Introduction to electrical energy systems. In Electric Renewable Energy Systems; Rashid, M.H., Ed.; Academic Press: Boston, MA, USA, 2016; pp. 1–20. [Google Scholar] [CrossRef]
- Mahmoud, K.; Abdel-Nasser, M. Fast-yet-Accurate Energy Loss Assessment Approach for Analyzing/Sizing PV in Distribution Systems using Machine Learning. IEEE Trans. Sustain. Energy 2018, 1025–1033. [Google Scholar] [CrossRef]
- Cirocco, L.R.; Belusko, M.; Bruno, F.; Boland, J.; Pudney, P. Maximising revenue via optimal control of a concentrating solar thermal power plant with limited storage capacity. IET Renew. Power Gener. 2016, 10, 729–734. [Google Scholar] [CrossRef]
- Shaahid, S.M. Economic feasibility of decentralized hybrid photovoltaic-diesel technology in saudi arabia. Therm. Sci. 2017, 21, 745–756. [Google Scholar] [CrossRef]
- Mahor, A.; Prasad, V.; Rangnekar, S. Economic dispatch using particle swarm optimization: A review. Renew. Sustain. Energy Rev. 2009, 13, 2134–2141. [Google Scholar] [CrossRef]
- Rastgoufard, S.; Iqbal, S.; Hoque, M.T.; Charalampidis, D. Genetic algorithm variant based effective solutions for economic dispatch problems. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Kamboj, V.K.; Bath, S.; Dhillon, J. Solution of non-convex economic load dispatch problem using Grey Wolf Optimizer. Neural Comput. Appl. 2016, 27, 1301–1316. [Google Scholar] [CrossRef]
- Pothiya, S.; Ngamroo, I.; Kongprawechnon, W. Ant colony optimisation for economic dispatch problem with non-smooth cost functions. Int. J. Electr. Power Energy Syst. 2010, 32, 478–487. [Google Scholar] [CrossRef]
- Jayabarathi, T.; Raghunathan, T.; Adarsh, B.; Suganthan, P.N. Economic dispatch using hybrid grey wolf optimizer. Energy 2016, 111, 630–641. [Google Scholar] [CrossRef]
- Mostafa, E.; Abdel-Nasser, M.; Mahmoud, K. Performance evaluation of metaheuristic optimization methods with mutation operators for combined economic and emission dispatch. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1004–1009. [Google Scholar]
- Duman, S. Symbiotic organisms search algorithm for optimal power flow problem based on valve-point effect and prohibited zones. Neural Comput. Appl. 2017, 28, 3571–3585. [Google Scholar]
- Mellouk, L.; Boulmalf, M.; Aaroud, A.; Zine-Dine, K.; Benhaddou, D. Genetic Algorithm to Solve Demand Side Management and Economic Dispatch Problem. Procedia Comput. Sci. 2018, 130, 611–618. [Google Scholar] [CrossRef]
- Chen, G.; Li, C.; Dong, Z. Parallel and distributed computation for dynamical economic dispatch. IEEE Trans. Smart Grid 2016, 8, 1026–1027. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Geng, N.; Sun, X.Y. Hybrid bare-bones PSO for dynamic economic dispatch with valve-point effects. Appl. Soft Comput. 2014, 18, 248–260. [Google Scholar] [CrossRef]
- Lu, P.; Zhou, J.; Zhang, H.; Zhang, R.; Wang, C. Chaotic differential bee colony optimization algorithm for dynamic economic dispatch problem with valve-point effects. Int. J. Electr. Power Energy Syst. 2014, 62, 130–143. [Google Scholar] [CrossRef]
- Rabiee, A.; Mohammadi-Ivatloo, B.; Moradi-Dalvand, M. Fast dynamic economic power dispatch problems solution via optimality condition decomposition. IEEE Trans. Power Syst. 2013, 29, 982–983. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Z.; You, P.; Fei, M. Multi-objective biogeography-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging. Energy 2017, 135, 101–111. [Google Scholar] [CrossRef]
- Jebaraj, L.; Venkatesan, C.; Soubache, I.; Rajan, C.C.A. Application of differential evolution algorithm in static and dynamic economic or emission dispatch problem: A review. Renew. Sustain. Energy Rev. 2017, 77, 1206–1220. [Google Scholar] [CrossRef]
- Hongfeng, Z. Dynamic economic dispatch based on improved differential evolution algorithm. Clust. Comput. 2018, 1–8. [Google Scholar] [CrossRef]
- Dubey, H.M.; Pandit, M.; Panigrahi, B. Hybrid flower pollination algorithm with time-varying fuzzy selection mechanism for wind integrated multi-objective dynamic economic dispatch. Renew. Energy 2015, 83, 188–202. [Google Scholar] [CrossRef]
- Elattar, E.E. A hybrid genetic algorithm and bacterial foraging approach for dynamic economic dispatch problem. Int. J. Electr. Power Energy Syst. 2015, 69, 18–26. [Google Scholar] [CrossRef]
- Nanjundappan, D. Hybrid weighted probabilistic neural network and biogeography based optimization for dynamic economic dispatch of integrated multiple-fuel and wind power plants. Int. J. Electr. Power Energy Syst. 2016, 77, 385–394. [Google Scholar]
- Xie, M.; Luo, W.; Cheng, P.; Ke, S.; Ji, X.; Liu, M. Multidisciplinary collaborative optimisation-based scenarios decoupling dynamic economic dispatch with wind power. IET Renew. Power Gener. 2018, 12, 727–734. [Google Scholar] [CrossRef]
- Basu, M. Quasi-oppositional group search optimization for multi-area dynamic economic dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 356–367. [Google Scholar] [CrossRef]
- Pattanaik, J.K.; Basu, M.; Dash, D.P. Improved real coded genetic algorithm for dynamic economic dispatch. J. Electr. Syst. Inf. Technol. 2018, 5, 349–362. [Google Scholar] [CrossRef]
- Pan, S.; Jian, J.; Yang, L. A hybrid MILP and IPM approach for dynamic economic dispatch with valve-point effects. Int. J. Electr. Power Energy Syst. 2018, 97, 290–298. [Google Scholar] [CrossRef]
- Somuah, C.; Khunaizi, N. Application of linear programming redispatch technique to dynamic generation allocation. IEEE Trans. Power Syst. 1990, 5, 20–26. [Google Scholar] [CrossRef]
- Lin, C.E.; Viviani, G. Hierarchical economic dispatch for piecewise quadratic cost functions. IEEE Trans. Power Appar. Syst. 1984, 1170–1175. [Google Scholar] [CrossRef]
- Irisarri, G.; Kimball, L.; Clements, K.; Bagchi, A.; Davis, P. Economic dispatch with network and ramping constraints via interior point methods. IEEE Trans. Power Syst. 1998, 13, 236–242. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Naso, D.; Turchiano, B.; Lewis, F.L. A distributed auction-based algorithm for the nonconvex economic dispatch problem. IEEE Trans. Ind. Inform. 2013, 10, 1124–1132. [Google Scholar] [CrossRef]
- Atwa, Y.; El-Saadany, E.; Salama, M.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2009, 25, 360–370. [Google Scholar] [CrossRef]
- Ali, A.; Raisz, D.; Mahmoud, K.; Lehtonen, M. Optimal placement and sizing of uncertain PVs considering stochastic nature of PEVs. IEEE Trans. Sustain. Energy 2019. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 1–14. [Google Scholar] [CrossRef]
- Kim, S.G.; Jung, J.Y.; Sim, M.K. A Two-Step Approach to Solar Power Generation Prediction Based on Weather Data Using Machine Learning. Sustainability 2019, 11, 1501. [Google Scholar] [CrossRef]
- Li, G.; Wang, H.; Zhang, S.; Xin, J.; Liu, H. Recurrent neural networks based photovoltaic power forecasting approach. Energies 2019, 12, 2538. [Google Scholar] [CrossRef]
- Yu, Y.; Cao, J.; Zhu, J. An LSTM Short-Term Solar Irradiance Forecasting Under Complicated Weather Conditions. IEEE Access 2019, 7, 145651–145666. [Google Scholar] [CrossRef]
- Jeon, B.K.; Lee, K.H.; Kim, E.J. Development of a Prediction Model of Solar Irradiances Using LSTM for Use in Building Predictive Control. J. Korean Sol. Energy Soc. 2019, 39, 41–52. [Google Scholar]
- Husein, M.; Chung, I.Y. Day-Ahead Solar Irradiance Forecasting for Microgrids Using a Long Short-Term Memory Recurrent Neural Network: A Deep Learning Approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67. [Google Scholar] [CrossRef]
- Güvenç, U.; Sönmez, Y.; Duman, S.; Yörükeren, N. Combined economic and emission dispatch solution using gravitational search algorithm. Sci. Iran. 2012, 19, 1754–1762. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- You, S.; Rasmussen, C.N. Generic modelling framework for economic analysis of battery systems. In Proceedings of the IET Renewable Power Generation Conference, Edinburgh, UK, 6–8 September 2011. [Google Scholar]







| Function | Dimension | Limits | |
|---|---|---|---|
| 30 | [−100,100] | 0 | |
| 10 | [−10,10] | 0 | |
| 10 | [−100,100] | 0 | |
| 10 | [−100,100] | 0 | |
| 10 | [−30,30] | 0 | |
| 10 | [−100,100] | 0 | |
| 10 | [−1.28,1.28] | 0 | |
| 10 | [−500,500] | 0 | |
| 10 | [−5.12,5.12] | 0 | |
| 100 | [−32,32] | 0 |
| Unit | Cost Coefficients | Power Limits | |||||
|---|---|---|---|---|---|---|---|
| a ($/MW2 h) | b ($/MWh) | c ($/h) | e ($/h) | f (rad/MW) | Pmin (MW) | Pmax (MW) | |
| 1 | 0.00690 | 6.73 | 94.705 | 100 | 0.084 | 36 | 114 |
| 2 | 0.00690 | 6.73 | 94.705 | 100 | 0.084 | 36 | 114 |
| 3 | 0.02028 | 7.07 | 309.540 | 100 | 0.084 | 60 | 120 |
| 4 | 0.00942 | 8.18 | 369.030 | 150 | 0.063 | 80 | 190 |
| 5 | 0.01140 | 5.35 | 148.890 | 120 | 0.077 | 47 | 97 |
| 6 | 0.01142 | 8.05 | 222.330 | 100 | 0.084 | 68 | 140 |
| 7 | 0.00357 | 8.03 | 287.710 | 200 | 0.042 | 110 | 300 |
| 8 | 0.00492 | 6.99 | 391.980 | 200 | 0.042 | 135 | 300 |
| 9 | 0.00573 | 6.60 | 455.760 | 200 | 0.042 | 135 | 300 |
| 10 | 0.00605 | 12.9 | 722.820 | 200 | 0.042 | 130 | 300 |
| 11 | 0.00515 | 12.9 | 635.200 | 200 | 0.042 | 94 | 375 |
| 12 | 0.00569 | 12.8 | 654.690 | 200 | 0.042 | 94 | 375 |
| 13 | 0.00421 | 12.5 | 913.400 | 300 | 0.035 | 125 | 500 |
| 14 | 0.00752 | 8.84 | 1760.400 | 300 | 0.035 | 125 | 500 |
| 15 | 0.00752 | 8.84 | 1760.400 | 300 | 0.035 | 125 | 500 |
| 16 | 0.00752 | 8.84 | 1760.400 | 300 | 0.035 | 125 | 500 |
| 17 | 0.00313 | 7.97 | 647.850 | 300 | 0.035 | 220 | 500 |
| 18 | 0.00313 | 7.95 | 647.850 | 300 | 0.035 | 220 | 500 |
| 19 | 0.00313 | 7.97 | 647.850 | 300 | 0.035 | 242 | 550 |
| 20 | 0.00313 | 7.97 | 647.850 | 300 | 0.035 | 242 | 550 |
| 21 | 0.00298 | 6.63 | 785.960 | 300 | 0.035 | 254 | 550 |
| 22 | 0.00298 | 6.63 | 785.960 | 300 | 0.035 | 254 | 550 |
| 23 | 0.00284 | 6.66 | 794.530 | 300 | 0.035 | 254 | 550 |
| 24 | 0.00284 | 6.66 | 794.530 | 300 | 0.035 | 254 | 550 |
| 25 | 0.00277 | 7.10 | 801.320 | 300 | 0.035 | 254 | 550 |
| 26 | 0.00277 | 7.10 | 801.320 | 300 | 0.035 | 254 | 550 |
| 27 | 0.52124 | 3.33 | 1055.100 | 120 | 0.077 | 10 | 150 |
| 28 | 0.52124 | 3.33 | 1055.100 | 120 | 0.077 | 10 | 150 |
| 29 | 0.52124 | 3.33 | 1055.100 | 120 | 0.077 | 10 | 150 |
| 30 | 0.01140 | 5.35 | 148.890 | 120 | 0.077 | 47 | 97 |
| 31 | 0.00160 | 6.43 | 222.920 | 150 | 0.063 | 60 | 190 |
| 32 | 0.00160 | 6.43 | 222.920 | 150 | 0.063 | 60 | 190 |
| 33 | 0.00160 | 6.43 | 222.920 | 150 | 0.063 | 60 | 190 |
| 34 | 0.00010 | 8.95 | 107.870 | 200 | 0.042 | 90 | 200 |
| 35 | 0.00010 | 8.62 | 116.580 | 200 | 0.042 | 90 | 200 |
| 36 | 0.00010 | 8.62 | 116.580 | 200 | 0.042 | 90 | 200 |
| 37 | 0.01610 | 5.88 | 307.450 | 80 | 0.098 | 25 | 110 |
| 38 | 0.01610 | 5.88 | 307.450 | 80 | 0.098 | 25 | 110 |
| 39 | 0.01610 | 5.88 | 307.450 | 80 | 0.098 | 25 | 110 |
| 40 | 0.00313 | 7.97 | 647.830 | 300 | 0.035 | 242 | 550 |
| Function | Optimization Method | |||||||
|---|---|---|---|---|---|---|---|---|
| ISSA | SSA | MFO | MVO | |||||
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | |
| F1 | 0.00000 | 0.00000 | 0.00001 | 0.00000 | 0.00014 | 0.00017 | 1.1969 | 0.1407 |
| F2 | 0.00001 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.0357 | 0.0128 |
| F3 | 0.00000 | 0.00000 | 0.0000 | 0.0000 | 0.00000 | 0.00001 | 0.1152 | 0.0771 |
| F4 | 0.00002 | 0.00000 | 0.00002 | 0.00000 | 0.6032 | 1.3682 | 0.0927 | 0.035 |
| F5 | 4.16500 | 3.1621 | 7.2112 | 2.4367 | 8.1502 | 7.7184 | 88.0909 | 125.6254 |
| F6 | 0.00000 | 0.00000 | 0.0000 | 0.0000 | 0.00000 | 0.00000 | 0.0156 | 0.0043 |
| F7 | 0.00130 | 0.0014 | 0.0048 | 0.00300 | 0.00490 | 0.00260 | 0.0035 | 0.0018 |
| F8 | −2955.8 | 184.4003 | −2746.9 | 239.6771 | −3305.9 | 243.2327 | −3006 | 337.0665 |
| F9 | 0.29850 | 0.6715 | 14.9244 | 4.5474 | 17.4118 | 6.7359 | 14.6334 | 4.7858 |
| F10 | 6.3844 | 1.3105 | 7.4999 | 1.5513 | 19.8439 | 0.2259 | 7.1737 | 6.7536 |
| Method | MLR | BRT | ANN | LSTM |
|---|---|---|---|---|
| RMSE of dataset1 | 384.8951 | 494.4633 | 377.072 | 82.15 |
| RMSE of dataset2 | 329.11 | 416.212 | 348.931 | 136.87 |
| Recurrent? | × | × | × | √ |
| Can it remember? | × | × | × | √ |
| Penetration | Fuel Cost*106 ($) | |||
|---|---|---|---|---|
| ISSA | SSA | MFO | MVO | |
| 0% | 2.7687 | 2.8451 | 3.0904 | 2.8945 |
| 10% | 2.7017 | 2.8162 | 2.9153 | 2.8945 |
| 20% | 2.6790 | 2.7783 | 2.8518 | 2.8945 |
| 30% | 2.5714 | 2.7385 | 2.7949 | 2.7446 |
| 40% | 2.5155 | 2.6131 | 2.7614 | 2.7446 |
| 50% | 2.4228 | 2.5395 | 2.5892 | 2.7446 |
| Penetration | Fuel Cost*106 ($) | |||
|---|---|---|---|---|
| ISSA | SSA | MFO | MVO | |
| 0% | 2.7687 | 2.8451 | 3.0904 | 2.8945 |
| 10% | 2.7261 | 2.8298 | 2.8824 | 2.8824 |
| 20% | 2.6849 | 2.7861 | 2.7945 | 2.7945 |
| 30% | 2.6710 | 2.7861 | 2.7823 | 2.7823 |
| 40% | 2.5244 | 2.6905 | 2.7171 | 2.7171 |
| 50% | 2.4877 | 2.6495 | 2.6641 | 2.6641 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, K.; Abdel-Nasser, M.; Mustafa, E.; M. Ali, Z. Improved Salp–Swarm Optimizer and Accurate Forecasting Model for Dynamic Economic Dispatch in Sustainable Power Systems. Sustainability 2020, 12, 576. https://doi.org/10.3390/su12020576
Mahmoud K, Abdel-Nasser M, Mustafa E, M. Ali Z. Improved Salp–Swarm Optimizer and Accurate Forecasting Model for Dynamic Economic Dispatch in Sustainable Power Systems. Sustainability. 2020; 12(2):576. https://doi.org/10.3390/su12020576
Chicago/Turabian StyleMahmoud, Karar, Mohamed Abdel-Nasser, Eman Mustafa, and Ziad M. Ali. 2020. "Improved Salp–Swarm Optimizer and Accurate Forecasting Model for Dynamic Economic Dispatch in Sustainable Power Systems" Sustainability 12, no. 2: 576. https://doi.org/10.3390/su12020576
APA StyleMahmoud, K., Abdel-Nasser, M., Mustafa, E., & M. Ali, Z. (2020). Improved Salp–Swarm Optimizer and Accurate Forecasting Model for Dynamic Economic Dispatch in Sustainable Power Systems. Sustainability, 12(2), 576. https://doi.org/10.3390/su12020576








