Influential Factors Regarding Carbon Emission Intensity in China: A Spatial Econometric Analysis from a Provincial Perspective

Abstract

Emission reduction strategies based on provinces are key for China to mitigate its carbon emission intensity (CEI). As such, it is valuable to analyze the driving mechanism of CEI from a provincial view, and to explore a coordinated emission mitigation mechanism. Based on spatial econometrics, this study conducts a spatial-temporal effect analysis on CEI, and constructs a Spatial Durbin Model on the Panel data (SDPM) of CEI and its eight influential factors: GDP, urbanization rate (URB), industrial structure (INS), energy structure (ENS), energy intensity (ENI), technological innovation (TEL), openness level (OPL), and foreign direct investment (FDI). The main findings are as follows: (1) overall, there is a significant and upward trend of the spatial autocorrelation of CEI on 30 provinces in China. (2) The spatial spillover effect of CEI is positive, with a coefficient of 0.083. (3) The direct effects of ENI, ENS and TEL are significantly positive in descending order, while INS and GDP are significantly negative. The indirect effects of URB and ENS are significantly positive, while GDP, ENI, OPL and FDI are significantly negative in descending order. Economic and energy-related emission reduction measures are still crucial to the achievement of CEI reduction targets for provinces in China.

1. Introduction

With worldwide energy consumption in a constant increase, large amounts of Greenhouse Gasses (GHG), especially CO₂, are being emitted directly into the atmosphere. This has triggered a series of global climate change issues—such as the Greenhouse Effect—and is posing a considerable threat to human survival and development. In order to address these challenges, through the United Nations Framework Convention on Climate Change (UNFCCC) in 2010, the United Nations advised all parties to make urgent efforts to significantly reduce their global carbon emissions [1]. Against such a background, countries all over the world are facing huge pressure to reduce emissions, especially developing countries, which need to balance the dual needs of environmental protection and economic growth. As the largest developing country, in the past few decades, China’s rapid economic development has caused steep increases in CO₂ emissions, which mainly stem from fossil fuel combustion [2]. In 2017, CO₂ emissions from fossil fuel combustion in China reached up to 9.26 Gt, accounting for 28.19% of the global total emissions (IEA Statistics, 2018, IEA Energy Atlas, http://energyatlas.iea.org/#!/tellmap/1378539487), which represents an over-fourfold increase from 2.12 Gt in 1990. As the country with the largest CO₂ emissions in the world, China is facing tremendous pressure to reduce its emissions. In its Intended Nationality Determined Contributions (INDC) submitted to the United Nations Framework Convention on Climate Change (UNFCCC) on 30th June 2015, China promised that CO₂ emissions per unit of GDP (CO₂/GDP) will be reduced by 60–65% by 2030, on a 2005 basis [3]. In order to achieve national CEI reduction targets, it is crucial to delve into the influential factors and to clarify the driving mechanisms of CEI.

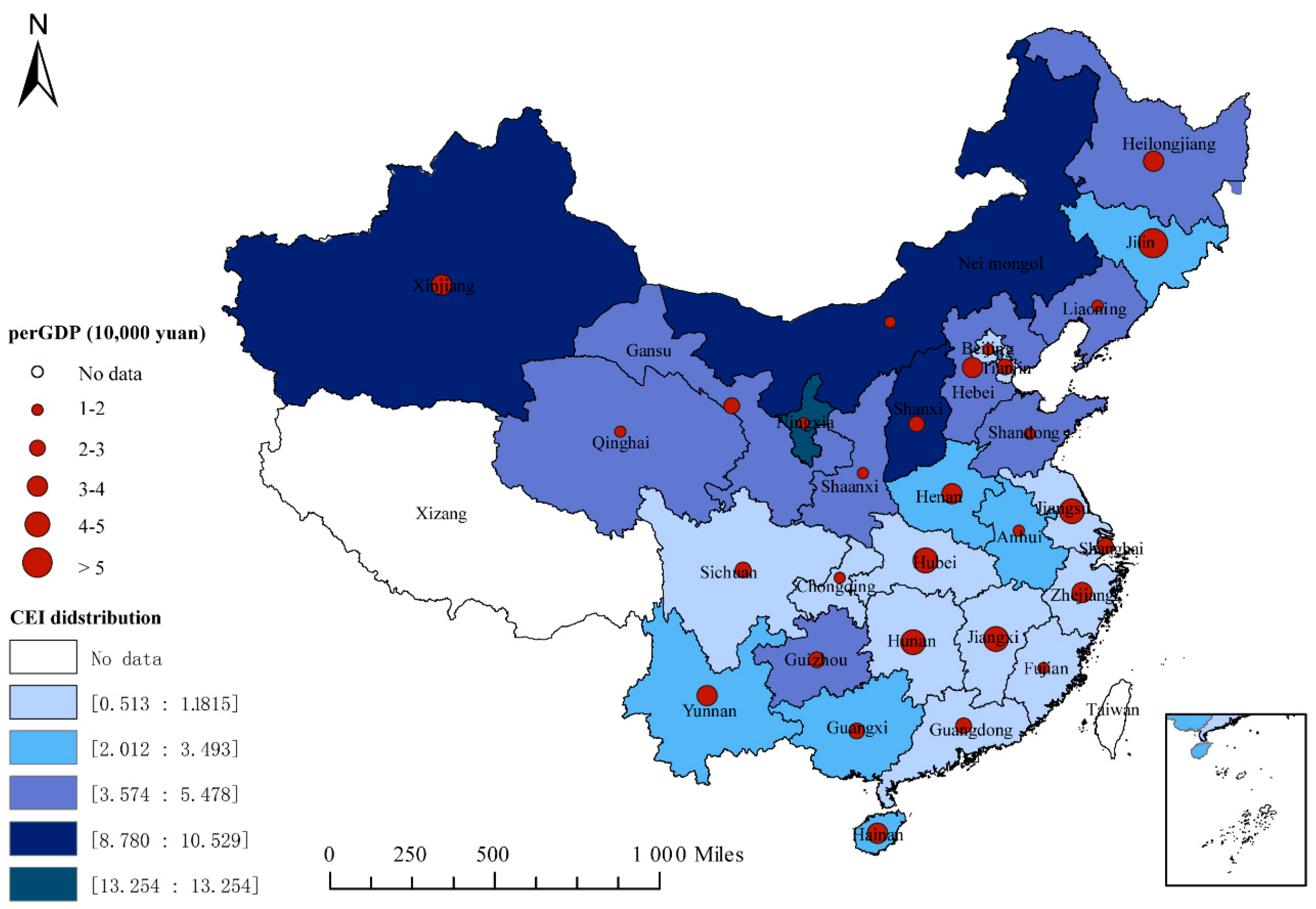
Since 2005, China has been committed to the simultaneous effort of economic development and environmental protection. Carbon intensity was reduced from 2.88 tons/10,000 yuan in 2005 to 1.11 tons/10,000 yuan in 2017. However, uneven regional development remains an urgent development problem. As shown in Figure 1, the level of China’s economic development has been significantly differentiated between regions, and the regional distribution of CEI has been characterized as high in the north and low in the south. The gap between the maximum value of 13.254 tons/10,000 yuan and the minimum value of 0.513 tons/10,000 yuan is quite large. The huge differences urgently need to be improved through the coordinated regional development route in order to achieve overall low-carbon development. In 2019, Chinese President Xi Jinping proposed to further promote the regional coordinated development strategy [4], which provides good strategic guidance and policy support for regionally-coordinated emission reduction. Therefore, studying the temporal and spatial characteristics of carbon intensity in China’s provinces, and the driving mechanism under the spatial effect, is of great significance for regional low-carbon cooperation in China. In addition, research on carbon intensity reduction from a provincial perspective in China can also provide a reference for emission reduction research in other countries or regions, especially in terms of regional cooperation in emission reduction.

China has a vast territory, a large population, complex national conditions, and great differences in its economy, industrial structure, energy consumption, and humanities and social sciences environment around its regions [5]. As a result, the complex CO₂ emission situation leads to the great difficulty of CO₂ mitigation. The difficulty of carbon emission reduction mainly comes from the spatial effects—such as spatial spillover and spatial heterogeneity—around provinces, caused by the negative externalities of CO₂ emissions [6], leading to the complexity of its driving mechanism. In order to clarify the CEI driving mechanism, traditional methods can provide only limited help, because they neglect the spatial interaction, which may lead to inaccurate estimate results. This kind of spatial interaction can be solved by spatial econometrics; that is, by introducing spatial weight variables to handle the spatial effects in regression.

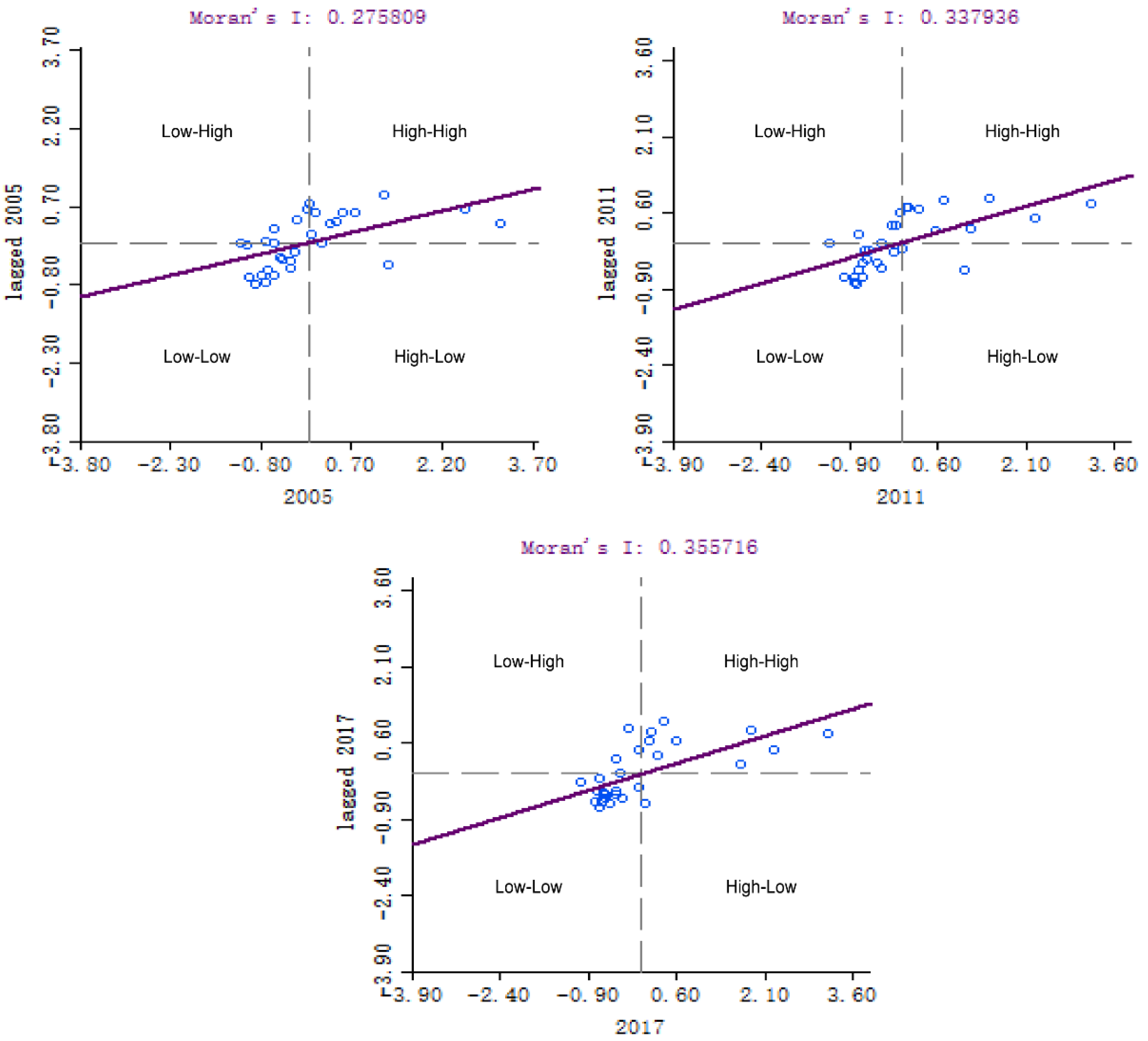
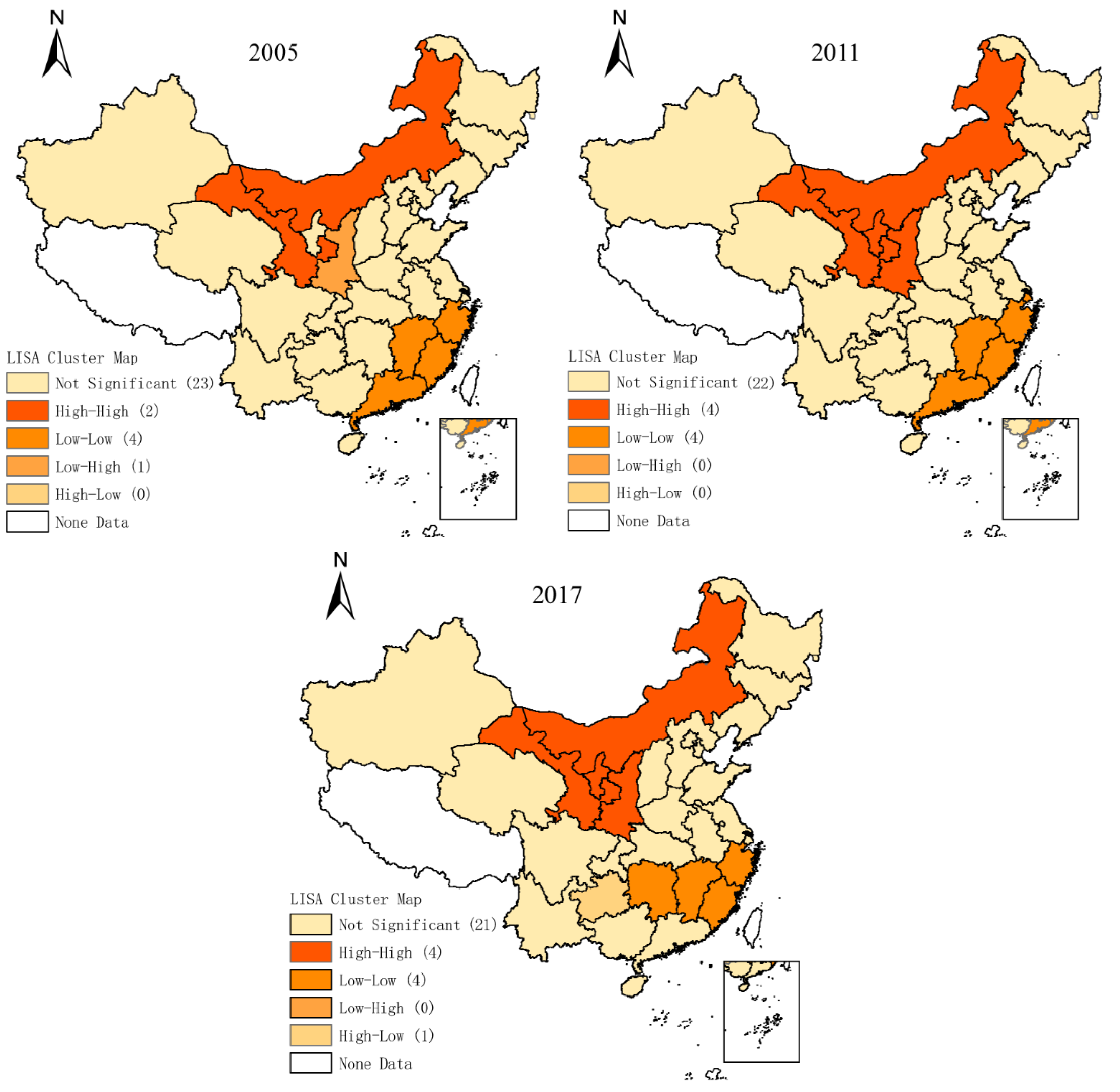
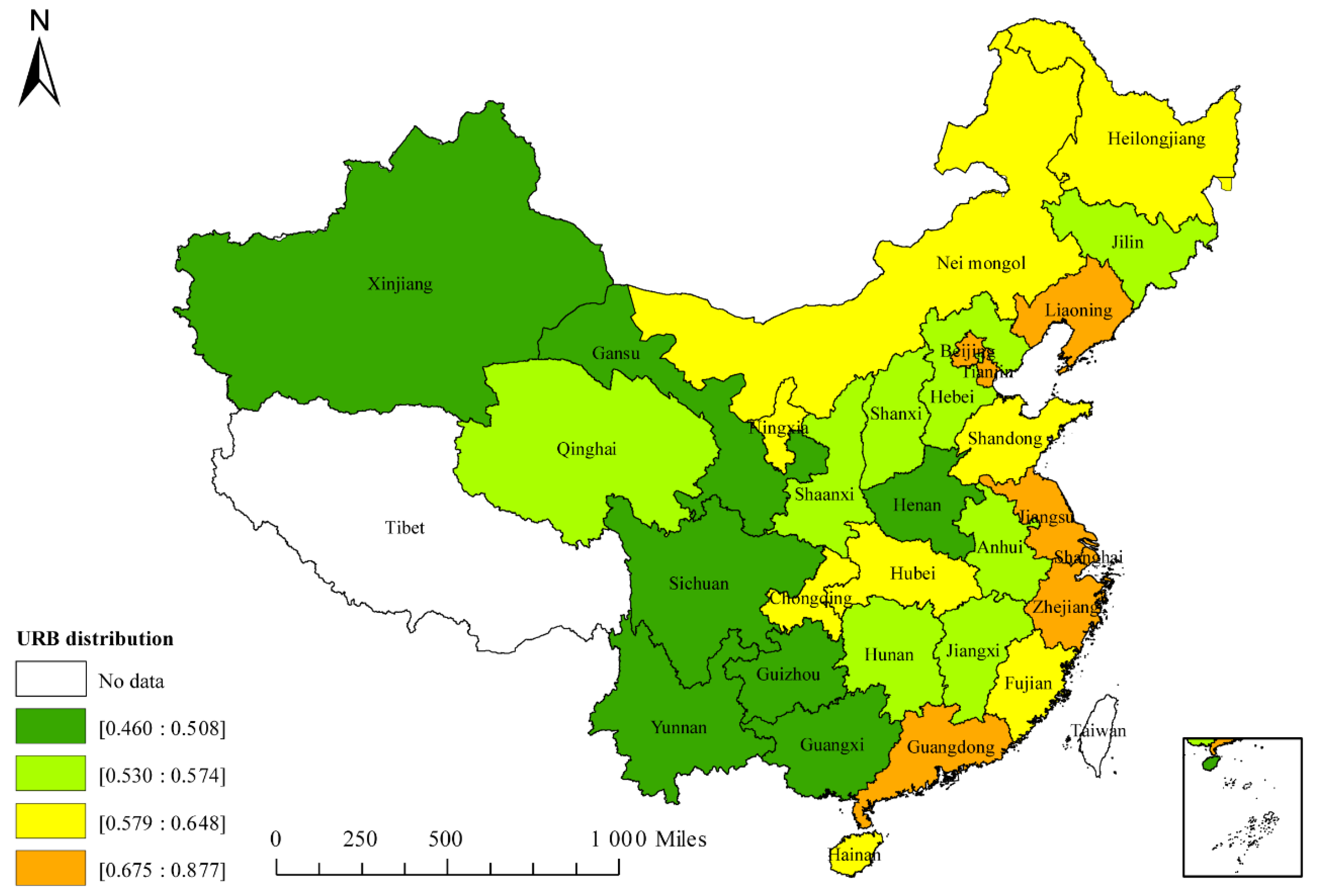
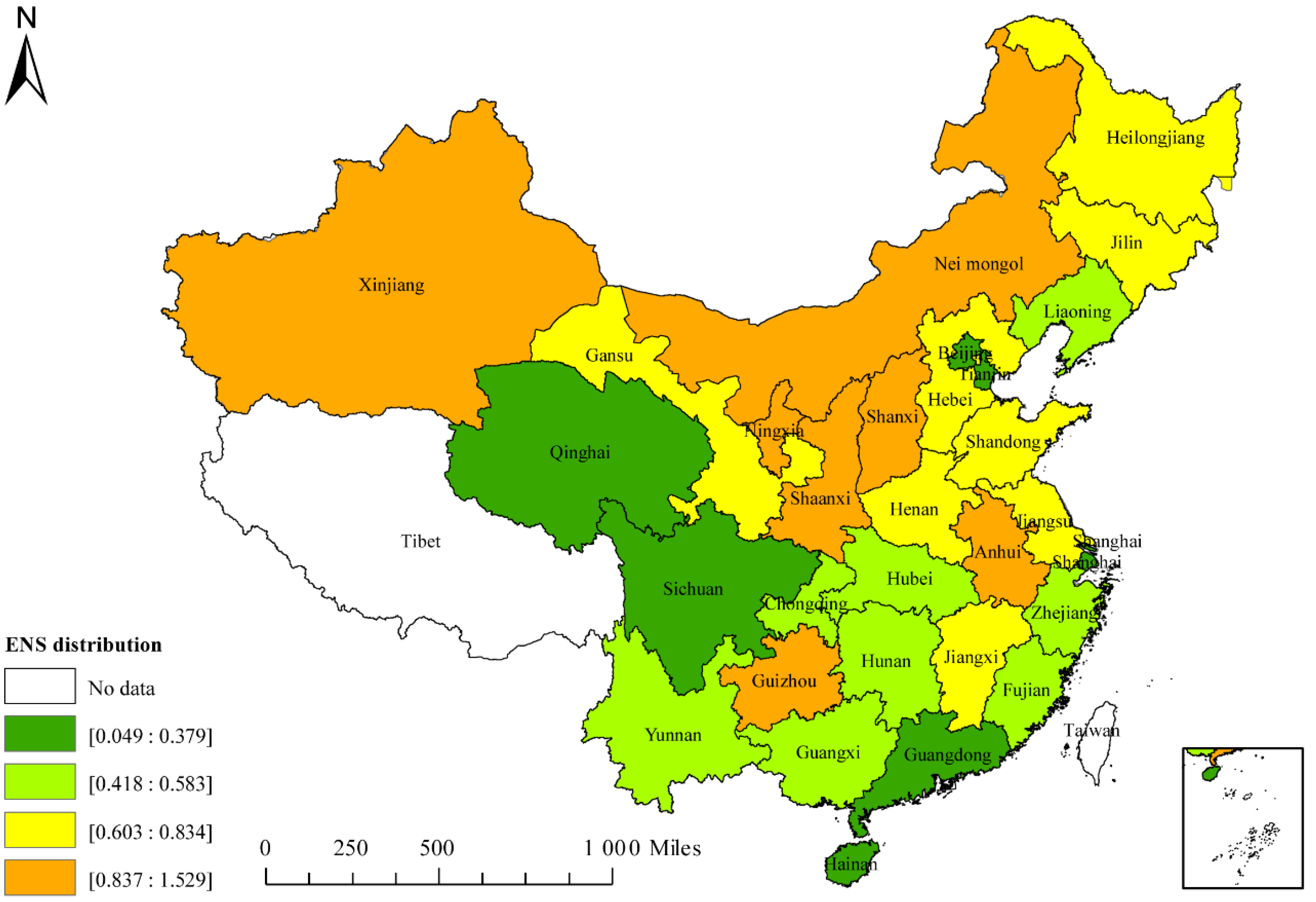
Based on the above description of the background and necessity, this article conducts research on the temporal and spatial effects and influencing factors of CEI in 30 provinces in China, from 2005 to 2017. The global Moran index and the local Moran index of the panel data are measured, providing a detailed analysis of the spatial and temporal characteristics of 30 provinces. Besides this, a spatial panel econometric model including eight independent variables of GDP, URB, INS, ENS, ENI, TEL, OPL, and FDI, and one dependent variable of CEI is established, which supplements the vacancy of the research on the full-factor driving mechanism of carbon intensity. This model is superior in reflecting spatial effects, so it can provide more realistic estimation results. The rest of this article is organized as follows: Section 2 reviews the existing literature and previous research on CEI, and based on this, the main innovations and specific research contents of this research are further clarified. Section 3 describes the research methods and data sources, including the carbon intensity measurement, influential factors selection, spatial econometric analysis, and data sources and processing. Section 4 presents the results in the form of charts and graphs, and conducts a preliminary analysis and discussion based on the results. Section 5 shows the main conclusions and proposes some policy implications according to the results.

2. Literature Review

At present, there is a large amount papers on CEI regarding carbon reduction in different countries, which mainly focus on spatial and temporal characteristics, influencing factors, and prediction research, etc. Specifically, the research on the spatial and temporal characteristics of CEI mainly focuses on spatial difference [6,7], the evolution of spatiotemporal patterns [8,9], and spatiotemporal heterogeneity [10,11], etc. The research on predictions regarding CEI focuses on the construction of predictive models [12,13], the prediction of CEI reduction target achievements [14,15,16], and scenario evolution analysis [17,18]. Based on the researches above, more and more studies have focused on the factors affecting carbon intensity, and have committed to accurately identifying the driving mechanism of carbon intensity, improving emission reduction policies, and realizing low-carbon development.

The research on influencing factors has mostly focused on energy-related (ENR) and economy-related (ECO) factors, as economic growth, energy consumption and carbon emission are causal to each other, and there is a direct and inevitable connection [19]. Fernandoa and Hor [20] analyzed the impact of energy management on carbon emissions in Malaysian manufacturing based on PLS-SEM (Partial Least Squares-Structural Equation Modeling) software, and found that energy audits and energy efficiency are the key factors for the mitigation of carbon emissions. Vujović et al. [21] used the neuro-fuzzy method to explore the relationship between energy, carbon intensity and economic growth. It was found that alternative energy has the greatest impact on carbon emission intensity. Some papers have also conducted research on the impact of urbanization (URB) on carbon emissions, as urbanization has a large demand for infrastructure construction, which has caused a lot of carbon emissions [22]. Liu and Liu [5] researched the spatial spillover effects of urbanization on carbon emissions in China by dividing China into Eastern, Middle and Western regions, in order to find the regional disparity. The results show that, as urbanization improves, its influence on local carbon emissions changes from positive to negative, and then the negative influence becomes weaker. With the development of economic globalization, factors related to international trade (INT), including import and export trade, foreign direct investment, etc., have become more and more important to the carbon emissions of countries and regions [23]. Pan et al. [24] studied the carbon intensity influencing factors of 34 OECD (Organization for Economic Co-operation and Development) countries based on genetic programming (GP) and symbolic regression methods (SRM), creatively using foreign direct investment as an influencing factor. In addition, technological innovation (TEI) is one of the main measures that can be used to reduce carbon emissions without reducing economic growth performance [25]. Nguyen et al. [26] explored the role of information and communication technologies and innovation in driving carbon emissions in 13 selected G-20 countries, based on quantile panel regression (QPR). Besides this, the impact of carbon emission trading (CET) [27,28] and power (POW) factors [29,30] on carbon intensity has been studied in recent years. The list of the research of related papers is shown in

Table 1. The list of research on the influential factors of CO₂ emissions.

Paper	Research Object	Drivers	Dimension	Methods
Liu and Liu [5]	China’s three regions	ENR, URB	Spatial-temporal	STIRPAT-SDM
Azomahou et al. [19]	100 countries.	ECO	Temporal	EKC
Fernandoa and Hor [20]	Malaysian manufacturing firms	ENR	Spatial	PLS-SEM
Vujović et al. [21]	European Union	ECO, ENR	Temporal	Neuro-fuzzy
Abdallh and Abugamos [22]	MENA countries	URB	Temporal	STIRPAT-EKC
Yang and Su [23]	44 world regions	INT	Spatial	LMDI
Pan et al. [24]	34 OECD countries	ECO, INT, TEI, URB	Temporal	GP-SRM
Erdoğan et al. [25]	14 G-20 countries	TEI	Temporal	Panel data analysis
Nguyen et al. [26]	13 G-20 countries	ENR, INT, TEI	Temporal	QPR
Zhou et al. [27]	China’s 7 provinces	CER, ENR	Temporal	LMDI; PSM-DID
Cui et al. [28]	China’s 30 provinces	CER	Spatial	CGE
De Oliveira [29]	Latin America & the Caribbean	POW	Spatial-temporal	IDA-LMDI
Zhang [30]	27 China’s manufacturing sectors	POW	Temporal	STIRPAT
Jeffrey and Perkins [31]	European Union	CER, ENR, ENT	Temporal
Ahmad et al. [32]	India	ECO, ENR	Temporal	EKC
Li et al. [33]	China’s eight regions	ENR	Spatial-temporal	GWR
Zhang et al. [34]	China’s 30 provinces	URB	Spatial	STIRPAT-SDM

. It can be seen that most studies only consider factors of one or two aspects, and few consider all of the aspects of factors as a system. This has led to relatively one-sided conclusions and limited reference for the overall planning and reduction of emissions. With respect to the research dimensions, most studies have only carried out research on the influential factors of CEI from a temporal dimension, and relatively few studies come from a comprehensively spatial-temporal dimension using space panel data.

The methods for the analysis of the driving mechanism of CEI in existing research are mainly based on the following three theories: decomposition analysis, machine learning, and spatial econometrics. Decomposition analysis is one of the classic theories that addresses influencing factors. It has been widely applied to the exploration of the factors that influence CO₂ and other polluting gas emissions since the 1990s, and continues to be examined with respect to influential factors regarding CEI [35]. It can be divided into the two main categories of index decomposition analysis (IDA) [23,27,29,36,37] and structural decomposition analysis (SDA) [38,39,40,41]. The advent of Machine Learning (ML) technology has greatly improved research on influencing factors, it can solve some of the problems which exist in traditional research, such as the selection of indicators and the limitation of large data processing. Therefore, it has been widely used in various research fields, including carbon intensity, in recent years [12,24]. Although the above two mainstream methods have their own advantages in the research of carbon intensity factors, none of them can deal with complex spatial effects in theory, leading to a lack of research on the estimation of the influencing factors considering spatial effects.

Spatial econometric analysis, as a branch of econometrics, can handle spatial effects in regression models of panel data, such as spatial interaction and spatial autocorrelation. Since Anselin [42] systematically structured the spatial econometric method, it has been widely used in economic policy-related research. With greater emphasis being placed on CO₂ emissions-related research over the last few years, spatial econometric analysis has begun to be applied to the research on CEI. However, due to its relatively late appearance, few related studies are currently available. Zhang et al. [34] studied the effect of urbanization on China’s CEI using the spatial Durbin mode, which is based on spatial econometric analysis, and comprehensively estimated the impact of population and land urbanization on carbon emissions, with consideration of the spatial effects. It has been proved that spatial econometric analysis can restore the actual spatial effects well [5,34], but there are few studies on the application of this method to carbon intensity, and there is a lack of the comprehensive consideration of various factors on the driving mechanism of carbon intensity. This article aims to analyze the carbon intensity in China from a spatial-temporal dimension, and to explore the driving mechanism of carbon emission with the consideration of spatial effects. The complexity of the driving mechanism requires the consideration of various factors as comprehensively as possible, and the analysis of the temporal and spatial characteristics of carbon intensity can provide policy makers with a multi-angle reference. Spatial econometric analysis can provide a theoretical basis for spatial regression estimation, and has been applied in this article.

The main contributions and innovations of this article are as follows. (1) In order to supplement the vacancy of the research on the full-factor driving mechanism of carbon intensity, this paper selected the influencing factors of carbon intensity from five aspects: economy, energy, urbanization, international trade, and technology. (2) Spatial-temporal analysis was carried out based on the space penal data of China’s 30 provinces from 2005 to 2017; 2005 was selected as the starting point for the study period (the base year), as it is the year that China put forward carbon emission reduction commitments, and from then on China attached importance to emission reduction and strengthened emission reduction efforts. Although there have been some studies on China’s carbon intensity from spatial-temporal dimensions [5,33], most of them focus on the analysis of three regions [5], eight regions [33] or others, and there is a lack of detailed analysis of the spatial and temporal characteristics of the 30 provinces. (3) Spatial econometric theory provides a theory for the spatial regression estimation of the influencing factors in this article, which can accurately describe the spatial interaction and spatial spillover effects that exist between the regions; this advantage is irreplaceable by other influencing factor research methods. Regression estimation which includes spatial variables can provide policymakers with more practical and effective emission reduction suggestions, and can provide an important reference for regional coordinated emission reduction. Besides this, the application of spatial econometrics to CEI influencing factors and the emission reduction strategies under regional coordination in China will provide a valuable reference to other countries facing similar problems.

In conclusion, in order to complete the research on the influential factors with respect to CEI in China from a provincial perspective, spatial econometrics is used as the theoretical support. First, we will perform global and local spatial autocorrelation tests on the CEI of 30 provinces in China (except Tibet, Hong Kong, Macao and Taiwan) between 2005 and 2017 in order to analyze the spatial effects. Then, a spatial Durbin panel model (SDPM) will be constructed, and the effect of the factors will be analyzed based on the estimation results. Finally, according to the analysis above, the provincial CEI driving mechanism will be discussed in depth, and realistic recommendations will be suggested for China’s regional cooperation emission reduction strategy in the context of regional coordinated development.

3. Methodology and Data

3.1. Energy-Related CEI in Provinces

The definition of carbon emission intensity according to the INDCs is “the amount of carbon dioxide emissions per unit of GDP”. Accordingly, the calculation of the carbon intensity of each province is shown in Equation (1).

$$CE{I}_{i,t}=C{E}_{i,t}/GD{P}_{i,t}$$

(1)

where $CE{I}_{i,t}$ is the carbon emission intensity, $GD{P}_{i,t}$ is the gross regional product (at a constant price of 2000), $C{E}_{i,t}$ is the CO₂ emissions from fossil fuel combustion, i indicates the province, and t indicates the year. Equation (2) shows the calculation for CO₂ emissions:

$$C{E}_{i,t}={\displaystyle \sum _{r}C{E}_{i,r,t}}={\displaystyle \sum _r{E}_{i,r,t}\times {\delta }_r\times {\tau }_r\times {\sigma }_r\times {\eta }_r\times \frac{44}{12}}$$

(2)

where r indicates the energy type, and $E_{i,r,t}$ is energy consumption of province i in year t. ${\delta }_r$ is the carbon content per unit of calorific value, ${\tau }_r$ is the average low calorific value, ${\sigma }_r$ is the average carbon oxidation rate, and ${\eta }_r$ is the coefficient converted to standard coal. The specific index values are shown in

Table 2. Values of the parameters and CO₂ emission factors of various energy sources.

Parameters	Coal	Coke	Crude Oil	Gasoline	Kerosene	Diesel Oil	Fuel Oil	LPG
${\delta }_i$	26.37	29.5	20.1	18.9	19.5	20.2	21.1	15.3
${\tau }_r$	20,908	28,435	41,816	43,070	43,070	42,652	41,816	38,931
${\delta }_r$	0.94	0.93	0.98	0.98	0.98	0.98	0.98	0.99
${\eta }_r$	0.7143	0.9714	1.4286	1.4714	1.4714	1.4571	1.4286	1.33

.

3.2. Influential Factors

The factors that affect carbon emission intensity can be roughly summarized into three aspects—scale effects, structural effects, and technical effects [43]—and can be specifically divided into economic, energy, foreign trade, technological innovation, and urbanization, etc. from Section 2. This paper has further integrated the relevant research of domestic and foreign scholars on the influential factors of CEI in

Table 3. Literature review of the influential factors of CEI.

Literature	Period	Object	Influential Factors
Song et.al [5]	2000–2015	China’s 30 provinces	Carbon coefficient effect, INS, ENS, ENI
Pan et.al [24]	1995–2014	34 OECD’s countries	GDP, TP, IND, FDI, URB, TEL
Zhang et.al [34]	2005–2014	China’s 30 provinces	GDP, TP, IND, ENI, OPL
Sapkota et.al [44]	1980–2010	14 LA’s countries	PGDP, PEN, PD, FDI
Lin et.al [45]	1978–2008	China as a whole	PGDP, URB, ENI, Cement output
Zhao [46]	1980–2010	China as a whole	INS, ENS, TEL, URB
Yang et.al [47]	1995–2009	China’s regions	PGDP, INS, ENI, ENS

. According to the literatures listed and unlisted, it can be found that the influential factors selected by domestic and foreign scholars have a great overlap, and are basically involved in the three aspects mentioned above. For example, GDP, TP, and OPL reflect the scale effects; INS, URB, and ENS reflect the structural effects; and TEL and IND reflect the technical effects.

The abbreviations of the influential factors in Table 3 are laid out as follows: TP is total population, PD is population density, PGDP is GDP per capita, and PEN is energy consumption per capita. IND represents the industrialization rate, URB represents the urbanization rate, ENI means the energy intensity, ENS means the energy structure (reflecting the proportion of coal consumption), and INS means the industrial structure (reflecting the proportion of tertiary industry). FDI represents foreign direct investment, TEL indicates the level of technology, and OPL is the abbreviation of the openness level, meaning the degree of foreign trade.

Among the influential factors listed in Table 3, the effects of GDP, INS, ENS and ENI are relatively strong, and the effects of URB, FDI, TEL and OPL are controversial. For instance, the effect of GDP on CEI reflects the economic–environmental interaction relationship, and its direction depends largely on the degree of economic development according to the Kuznets curve. INS reflects the proportion of the contribution of the primary, secondary, and tertiary industries to economic growth, and its effect on CEI recognized by most of the literature is that the larger the proportion of the tertiary industry, the smaller the proportion of the secondary industry, and the more beneficial for carbon intensity reduction. The effects of FDI on CEI reflect the environmental impact of the injection of capital from other countries on the host country, and there are hypotheses of a ‘pollution heaven’ and ‘pollution halo’ [48], which respectively believe that FDI will aggravate and slow down the environmental pollution problems. Hence, eight influential factors, including GDP, URB, INS, ENS, EDI, FDI, TEL, and OPL, were selected for the stability tests, in order to avoid the pseudo-regression of the panel data using an ADF-Fisher unit root test. The description of the indicators in detail is shown in Appendix A

Table A1. Description of the influential factors of CEI.

Indicator	Abbreviation	Description
Gross regional product	GDP	Gross regional product (2000 constant price)
Urbanization rate	URB	Proportion of urban population in total population
Industrial structure	INS	Proportion of value added of tertiary industry to regional GDP
Energy structure	ENS	Proportion of coal consumption in total energy consumption
Energy intensity	ENI	Energy consumption per unit of GDP
Technology level	TEL	Number of patent applications granted
Open level	OPL	Total regional import and export trade
Foreign direct investment	FDI	Actual utilization of foreign direct investment

.

3.3. Spatial Econometric Analysis

Spatial econometric analysis is a branch of econometrics that refers to a series of methods for the study of various characteristics caused by space in the statistical analysis of regional scientific models [41]. Spatial econometric analysis focuses on the problem of spatial effects, and is of great significance to the research objects with spatial spillover effects. According to Section 1, it has been elaborated and discussed that the CEI of China’s 30 provinces is likely to have spatial spillover due to the negative externalities of carbon emissions, so the use of spatial econometrics for this study is necessary and meaningful. On the one hand, the spatial agglomeration and spatial heterogeneity of CEI could be clarified and analyzed based on Moran’s I test. On the other hand again, the complex driving mechanism of CEI under spatial effects could be figured out by constructing a spatial panel econometric model of the influencing factors of CEI based on the model established by Elhorst [49]. In this paper, a pooled panel dataset containing 30 regions and 13 years was analyzed; in order to avoid the spurious regression, it was necessary to test the stability of the panel data. This paper used an ADF-Fisher unit root test to verify the stability of the panel data, and the results show that all of the variables passed the stationarity test.

3.3.1. Spatial Weight Matrix

In the study of spatial effect, Tobler’s First Law of Geography shows that everything is related to everything else, but closer things are more related to each other [50]. As such, a spatial weight matrix was introduced in this research in order to elaborate upon this relation. In order to construct the spatial weight matrix, Geoda is regarded as the preferred software, as it has the advantages of processing spatial data and easy operation. First, a shape file with panel data and geospatial information needed to be created. Then, it was imported into the Geoda software in order to construct the spatial weight matrix. There are generally two types of connection methods: ‘Queen’, which means that the spots of the analysis unit are adjacent to each other (usually planar); and ‘Rook’, which means that the analyzed spots are not adjacent to each other (dots). The analyzed units of this paper are China’s 30 provinces, which are adjacent to each other in a planar shape. Therefore, this paper used ArcGIS 10.5 to create the shape file, and Geoda 1.10.0.8 to construct the spatial weight matrix with the connection method ‘Queen’. The matrix elements are composed of 0 and 1, and reflect whether the regions are adjacent or not.

3.3.2. Moran’s I Test

Moran’s I is a common indicator used to test spatial autocorrelation, and is divided into Global Moran’s I and Local Moran’s I. Global Moran’s I is also called the narrow Moran’s I, and is used to test overall spatial autocorrelation. Anselin [51] proposed Local Moran’s I based on Global Moran’s I, which is used to reflect the local spatial association and agglomeration characteristics. We first used Global Moran’s I in order to test whether CEI has spatial autocorrelation at the country level, and then utilized Local Moran’s I in order to test the local spatial autocorrelation characteristics of the provinces. The formulae of Global Moran’s I and Local Moran’s I are shown as Equation (3) and Equation (4), respectively:

$$\begin{array}{c}Moran’sI=\frac{n{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne i}^n{w}_{i,j}\left(y_i-\overline{y}\right)\left(y_j-\overline{y}\right)}}}{S^2{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne i}^n{w}_{i,j}}}},\\ \overline{y}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{y}_i},S^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}\end{array}$$

(3)

where $y_i$ represents the CEI in province i, and n = 30 is the number of space units. $w_{i,j}$ is the spatial weight of province i and j, which reflects adjacency features among the regions using values of 0 and 1. When $w_{i,j}$= 0, it indicates that province i and j not adjacent, and vice versa.

$$I_i=y_i{\displaystyle \sum _{i\ne j}^n{w}_{i,j}{y}_j}$$

(4)

where $I_i$ represents the Local Moran’s I in province i.

3.3.3. Spatial Panel Econometric Model

The spatial panel econometric model was used to describe the temporal effects and the spatial effects of the spatial panel data. It can be divided into three basic models according to the characteristics of the model variables. As pointed out by Elhorst [52], if there is a spatial lag dependent variable, it is called a spatial lag model (SLM), which is also known as a spatial autocorrelation model (SAR). If a spatial autoregressive process exists in the error term, it is called a spatial error model (SEM). The third model is named the Space Durbin Model (SDM), and was originally proposed by LeSage and Pace [53]; the SDM is an improvement on the bases of the SLM, adding a spatial lag independent variable into the model.

The basic form of the SLM is shown as Equation (5):

$$y_{i,t}=\rho {\displaystyle \sum _{j=1}^n{w}_{i,j}{y}_{i,t}}+\alpha +x_{i,t}\beta +{\mu }_i+{\lambda }_t+{\epsilon }_{i,t}$$

(5)

where $y_{i,t}$ and $x_{i,t}$ are dependent and independent variables of province i in year t respectively. ${\displaystyle \sum _{j=1}^n{w}_{i,j}{y}_{i,t}}$ describes the spatial adjacency interaction of the dependent variables $y_{i,t}$ and $y_{j,t}$. $\rho$ is the spatial autocorrelation coefficient, $\alpha$ is a constant parameter, $\beta$ is a fixed unknown coefficient parameter of the independent variable $x_{i,t}$, ${\epsilon }_{i,t}$ is an independent and uniformly distributed error term, ${\mu }_i$ and ${\lambda }_t$ are used to describe space-specific effects and time-specific effects, respectively.

The basic form of SEM is shown as Equation (6):

$$y_{i,t}=\alpha +x_{i,t}\beta +{\mu }_i+{\lambda }_t+{\epsilon }_{i,t}+{\varphi }_{i,t},{\varphi }_{i,t}=\theta {\displaystyle \sum _{j=1}^n{w}_{i,j}{\varphi }_{i,t}+{\epsilon }_{i,t}}$$

(6)

where ${\varphi }_{i,t}$ reflects spatial error autocorrelation, and $\theta$ is the spatial autocorrelation coefficient of the error term.

The basic form of SDM is shown as Equation (7):

$$y_{i,t}=\rho {\displaystyle \sum _{j=1}^n{w}_{i,j}{y}_{i,t}}+\alpha +x_{i,t}\beta +{\displaystyle \sum _{j=1}^n{w}_{i,j}{x}_{i,j,t}\phi }+{\mu }_i+{\lambda }_t+{\epsilon }_{i,t}$$

(7)

where $\phi$ is a fixed unknown parameter.

Then, the selected eight factors are added to the model for the construction of the spatial panel econometric model of the CEI. The most suitable model can be determined through a series of statistical tests.

(1)

Spatial Lag Panel data Model (SLPM)

The basic form of the SLPM established in this paper is shown in Equation (8):

$$\begin{array}{l}lnCE{I}_{i,t}=\rho {\displaystyle \sum _{j=1}^n{w}_{i,j}lnCE{I}_{i,t}}+\alpha +{\beta }_1\left(lnGD{P}_{i,t}\right)+{\beta }_2\left(lnUR{B}_{i,t}\right)+{\beta }_3\left(lnIN{S}_{i,t}\right)+\\ {\beta }_4\left(lnEN{S}_{i,t}\right)+{\beta }_5\left(lnEN{I}_{i,t}\right)+{\beta }_6\left(lnTE{L}_{i,t}\right)+{\beta }_7\left(lnOP{L}_{i,t}\right)+{\beta }_8\left(lnFD{I}_{i,t}\right)+{\mu }_i+{\lambda }_t+{\epsilon }_{i,t}\end{array}$$

(8)

where CEI is the dependent variable, and GDP, URB, INS, ENS, ENI, TEL, OPL and FDI are the independent variables, which were introduced in Section 3.2; all of the variables are logarithmic, in order to ensure the same order of magnitude and eliminate the heteroscedasticity problem of the data.

(2)

Spatial Error Panel data Model (SEPM)

The basic form of the SEPM established in this paper is shown in Equation (9):

$$\begin{array}{l}lnCE{I}_{i,t}=\alpha +{\beta }_1\left(lnGD{P}_{i,t}\right)+{\beta }_2\left(lnUR{B}_{i,t}\right)+{\beta }_3\left(lnIN{S}_{i,t}\right)+{\beta }_4\left(lnEN{S}_{i,t}\right)+{\beta }_5\left(lnEN{I}_{i,t}\right)+\\ {\beta }_6\left(lnTE{L}_{i,t}\right)+{\beta }_7\left(lnOP{L}_{i,t}\right)+{\beta }_8\left(lnFD{I}_{i,t}\right)+{\mu }_i+{\lambda }_t+{\epsilon }_{i,t}+{\varphi }_{i,t},{\varphi }_{i,t}=\theta {\displaystyle \sum _{j=1}^n{w}_{i,j}{\varphi }_{i,t}+{\epsilon }_{i,t}}\end{array}$$

(9)

(3)

Spatial Durbin Panel data Model (SDPM)

The basic form of the SDPM established in this paper is shown in Equation (10):

$$\begin{array}{l}lnCE{I}_{i,t}=\rho {\displaystyle \sum _{j=1}^n{w}_{i,j}lnCE{I}_{i,t}}+\alpha +{\beta }_1\left(lnGD{P}_{i,t}\right)+{\beta }_2\left(lnUR{B}_{i,t}\right)+{\beta }_3\left(lnIN{S}_{i,t}\right)+{\beta }_4\left(lnEN{S}_{i,t}\right)+{\beta }_5\left(lnEN{I}_{i,t}\right)+\\ {\beta }_6\left(lnTE{L}_{i,t}\right)+{\beta }_7\left(lnOP{L}_{i,t}\right)+{\beta }_8\left(lnFD{I}_{i,t}\right)+{\phi }_1{\displaystyle \sum _{j=1}^n{w}_{i,j}lnGD{P}_{i,j,t}}+{\phi }_2{\displaystyle \sum _{j=1}^n{w}_{i,j}lnUR{B}_{i,j,t}}+{\phi }_3{\displaystyle \sum _{j=1}^n{w}_{i,j}lnIN{S}_{i,j,t}}+\\ {\phi }_4{\displaystyle \sum _{j=1}^n{w}_{i,j}lnEN{S}_{i,j,t}}+{\phi }_5{\displaystyle \sum _{j=1}^n{w}_{i,j}lnEN{I}_{i,j,t}+{\phi }_6{\displaystyle \sum _{j=1}^n{w}_{i,j}lnTE{L}_{i,j,t}}}+{\phi }_7{\displaystyle \sum _{j=1}^n{w}_{i,j}lnOP{L}_{i,j,t}}+{\phi }_8{\displaystyle \sum _{j=1}^n{w}_{i,j}lnFD{I}_{i,j,t}}+{\mu }_i+{\lambda }_t+{\epsilon }_{i,t}\end{array}$$

(10)

3.4. Data Sources

The parameters involved in the calculation of the energy-related CEI mainly refer to the ‘2006 IPCC National Greenhouse Gas Inventory Guide’ (Volume 2), in which the average carbon oxidation rate is adjusted according to the ‘Provincial Greenhouse Gas Inventory Guidelines’ (NDRC Climate [2011] 1041), and the average low calorific value of each energy type comes from the ‘General Rules for the Calculation of Comprehensive Energy Consumption’ (GB/T 2589-2008).

The data sources of the indicators involved in the influencing factors are as follows: the FDI data were obtained from the provincial statistical yearbooks, and some missing data were filled in with data from the Wind and iFinD databases; the energy-related data are from the ‘China Energy Statistical Yearbook’; the rest of the data come from the ‘China Statistical Yearbook’.

In addition, in order to ensure the longitudinal comparability of the data, the economically relevant data involved in the calculation of carbon intensity and the influencing factors were adjusted to a constant price in 2000.

4. Results and Discussions

4.1. Spatial Autocorrelation Analysis of the Provincial CEI in China

4.1.1. Global Space Autocorrelation Test

In order to verify the spatial autocorrelation of the CEI among the provinces, a global spatial autocorrelation (GSA) test was performed using the Global Moran’s I. The results are shown in

Table 4. Results of the Global Moran’s I test.

Year	Moran’I	Year	Moran’I	Year	Moran’I
2005	0.2758 *** (2.8989)	2010	0.3335 *** (3.3896)	2014	0.3269 *** (3.1652)
2006	0.3307 *** (3.3227)	2011	0.3379 *** (3.5004)	2015	0.3287 *** (3.2544)
2007	0.2997 ** (2.8704)	2012	0.3386 *** (3.4396)	2016	0.3501 *** (3.4675)
2008	0.3422 *** (3.2573)	2013	0.3236 *** (3.2126)	2017	0.3557 *** (3.6891)
2009	0.3160 *** (3.0303)

Note: the standardized Moran’s I value is in parentheses. *, **, and *** respectively denote the significance at different levels (10%, 5% and 1%).

. In total, the values of the Moran’s I from 2005 to 2017 are all positive and greater than 0.25, and all of the, passed the significance test at the 1% level or more, except for 2007, in which the Moran’s I was significant at the level of 5%. This indicates that the CEI among provinces in China had obvious positive spatial autocorrelation characteristics; that is, when the CEI is higher than average in a province, it is often higher than average in the regions around it, and vice versa. In addition, during the research period, the Moran’s I values showed an overall upward trend, meaning that the spatial autocorrelation of CEI became stronger and stronger.

4.1.2. Local Space Autocorrelation Test

The GSA test can only prove that there is a spatial autocorrelation in the CEI among the provinces. The specific spatial autocorrelation of each province needs to be further tested using the local space autocorrelation (LSA) test. In order to express the result more clearly, the spatial distribution characteristics of the CEI in the provinces are divided into four categories: High–High, High–Low, Low–High, and Low–Low. The specific meanings are as follows: High–High indicates that the CEI of a province, as well as its neighboring provinces, are higher than the average level, Low–Low is the opposite; High–Low indicates that the CEI of a province is higher than the average level, while its neighboring provinces are lower than average, and Low–High is the opposite. High–High and Low–Low reflect the spatial aggregation effect; High–Low and Low–High reflect the spatial heterogeneity effect. The results of the LSA test are revealed by the Moran Scatter Plot (MSP) and the Local Indication of the Spatial Association (LISA) cluster map, respectively.

Figure 2 shows the MSP in 2005, 2011 and 2017, which intuitively indicates the local spatial autocorrelation and the dynamic trends of the provincial CEI in China. The other years within the research period are omitted here, as they show small fluctuations but not affect the overall change trend.

From the distribution of the points, most of the points are distributed in the first and third quadrants, while there are just a few in the second and fourth quadrants for all of the years under consideration. This indicates that the CEI of most of the provinces shows a positive spatial correlation, which is consistent with the result of the GSA test. The provinces located in Low–Low often form a good low-carbon development model with their neighboring provinces through mutual benefits and win–win arrangements, which can provide reference for regional emission reduction for other provinces. The provinces located in High–High have a high potential for emission reduction, and it is necessary to carry out the key analysis and use national power to promote the CEI reduction of these provinces. While the provinces located in High–Low and Low–High show obvious spatial heterogeneity, more attention should be paid to the rational allocation of resources and CEI reduction responsibilities among the provinces from the perspective of regional coordination. Furthermore, the emission reduction of the provinces in High–Low and Low–High is the key to regional cooperation, as well as a breakthrough point in achieving the low-CEI development of the whole region.

From the dynamic change over time, the number of points in the third quadrant is increasing, and the number of points in the second quadrant is decreasing, if we compare the MSP in different years. This indicates that the spatial clustering effect of CEI is gradually increasing, and this is especially obvious in the Low–Low provinces. The successful transformation of provinces from Low–High to Low–Low has considerable guiding significance for regional cooperation in reducing emissions, and will be further analyzed in the following part.

In order to show the local spatial correlation of specific provinces more intuitively, Local Indication of Spatial Association (LISA) agglomeration maps of China’s provincial CEI in different years at a 5% significance level were drawn (Figure 3). According to the maps, High–High provinces are mainly distributed in northern inland areas, such as Inner Mongolia and Gansu, while Low–Low provinces are mainly distributed in southeastern coastal areas, such as Zhejiang and Fujian. This distribution is mainly caused by the uneven distribution of various resources. The inland areas of northern China are rich in mineral resources, but are relatively undeveloped in their technology and economy. Their industrial structure is dominated by secondary industry, and their tertiary industry is mainly driven by transportation, so there is a strong dependence on fossil energy—such as mineral resources—in these provinces. The provinces located in the southeast coastal area are relatively developed in their economies, and their industrial structure is dominated by tertiary industry, which is mainly driven by the financial industry, the service industry, and high-tech industries, so these areas are less dependent on energy.

By comparing the LISA clustering maps in different years, we find that both of the High–High and Low–Low clusters show a dynamic trend of gradually spreading to the central region. This indicates that the uneven distribution of resources in China has gradually improved. Specifically, Ningxia and Shaanxi have respectively transferred from insignificant spatial agglomeration and Low–High clusters to significant High–High clusters. This is because Ningxia and Shaanxi are adjacent to the two large resource-rich provinces of Inner Mongolia and Shanxi; on the one hand, the spatial overflow of CO₂ emissions from Inner Mongolia and Shanxi increased the CO₂ emissions of Ningxia and Shaanxi. On the other hand, the low cost of energy resource acquisition lead to higher profits for the local industries that rely on these resources, forming a high-carbon industrial structure and development model. Hunan Province has transferred from an insignificant spatial agglomeration to a significant Low–Low cluster. This was caused by the depletion of the mineral resources in Hunan Province in recent years, which lead to the transformation of its industrial structure and energy consumption structure. In addition, the adjacency to regions with relatively developed economies (such as Guangdong and Fujian) has also promoted the transformation of Hunan’s development concept and development model to a certain extent, which was achieved through the sharing and diffusion of human resources; high-tech and other resources can also promote the rapid development of tertiary industry. The transformation of Hunan Province can provide a reference for the low carbon transformation of similar provinces, such as Hebei Province, which is adjacent to economically developed provinces such as Beijing and Tianjin.

In this part, the results of the global and local spatial autocorrelation test proved that there is a significant spatial autocorrelation in China’s provincial carbon emission intensity (CEI), and the degree of the spatial correlation shows an upward trend with time, which puts forward an urgent need for the exploration on the driving mechanism of CEI under the space effect, and for the formulation of emission reduction measures from the perspective of regional coordination.

4.2. Spatial Econometric Model Regression Results

4.2.1. Construction of the Spatial Econometric Model

This paper referenced Elhorst [54] in order to a construct spatial panel econometric model in Matlab software. First, we established a general spatial econometric model for CEI and its influential factors, and tested the spatial effects of the panel data using Lagrange multipliers (LM) and robust Lagrange multipliers (R-LM). Then, a joint LR test was performed in order to confirm which type of fixed effect is optimal in the model: space fixed effects, time fixed effects or space–time fixed effects. The statistical test results are shown in

Table 5. Results of the LM and joint LR tests.

Variable	Panel OLS	Space Fixed	Time Fixed	Space-Time Fixed
Intercept	2.126 *** (16.118)	-	-	-
lnGDP	−0.126 *** (−6.619)	−0.018 (−0.541)	−0.164 *** (−6.875)	−0.055 (−0.865)
lnURB	0.099 * (1.912)	−0.110 * (−1.304)	0.015 (0.246)	−0.100 * (−1.153)
lnINS	0.098 * (1.601)	−0.057 * (−1.392)	0.060 (0.898)	−0.078 * (−1.125)
lnENS	0.647 *** (25.232)	0.469 *** (19.327)	0.645 *** (25.274)	0.474 *** (18.914)
lnENI	0.905 *** (27.814)	0.926 *** (19.141)	0.929 *** (27.349)	0.906 *** (16.854)
lnTEL	0.000 (0.012)	0.014 ** (2.391)	−0.004 (−0.742)	0.014 ** (2.244)
lnOPL	0.060 ** (4.939)	0.003 (0.187)	0.088 *** (5.418)	0.003 (0.193)
lnFDI	−0.002 (−0.163)	−0.007 * (−1.126)	0.009 (0.777)	−0.009 * (−1.407)
R2	0.940	0.920	0.936	0.787
Corrected R2	0.938	0.918	0.935	0.783
σ2	0.022	0.004	0.022	0.004
Durbin-Watson	1.750	2.002	1.777	2.030
LM panel lag	4.707 (0.030)	0.438 (0.508)	62.772 (0.000)	0.022 (0.883)
R-LM panel lag	9.451 (0.002)	4.487 (0.034)	56.400 (0.000)	1.609 (0.205)
LM panel error	4.959 (0.026)	2.992 (0.084)	6.937 (0.008)	2.752 (0.097)
R-LM panel error	9.703 (0.002)	7.041 (0.008)	0.565 (0.452)	4.339 (0.037)
LR ratio of joint test	Fixed effects	Statistics	DOF	p-value
	Space fixed	698.31	30	0.000
	Time fixed	5.26	13	0.969

Note: the t statistics are shown in parentheses. For the LM tests, we show the p-values in brackets. DOF refers to the degree of freedom. *, **, and *** respectively denote significance at different levels (10%, 5% and 1%).

, which indicate that the spatial variables can effectively improve the accuracy of the estimation results of the influencing factor regression of the CEI, and that the spatial fixed effect is optimal for this panel dataset among all of the sets of fixed effects.

Next, the SDPM model (as shown in Equation (10)) of the spatial fixed effect was constructed, and the Wald test and the LR test were used to judge whether it could be simplified to an SEPM or SLPM model. The test results are shown in the last four rows of

Table 6. Results of the SDPM under a space fixed effect.

Variables	Coefficient	Variables	Coefficient
W*lnCEI	0.083 (1.214)
lnGDP	−0.142 *** (−3.106)	W*lnGDP	−0.563 *** (−6.454)
lnURB	0.040 (0.396)	W*lnURB	0.553 *** (2.738)
lnINS	−0.258 *** (−4.820)	W*lnINS	0.100 (1.202)
lnENS	0.402 *** (14.111)	W*lnENS	0.065 (1.095)
lnENI	0.945 *** (14.465)	W*lnENI	−0.518 *** (−4.423)
lnTEL	0.017 ** (2.564)	W*lnTEL	0.002 (0.221)
lnOPL	−0.008 (−0.502)	W*lnOPL	−0.053 * (−1.879)
lnFDI	0.005 (0.734)	W*lnFDI	−0.035 ** (−2.335)
R2	0.9921
Corrected squared	0.9687
σ2	0.0036
log-likelihood	557.1403
Wald spatial lag	110.509 (0.000)
LR spatial lag	104.772 (0.000)
Wald spatial error	98.064 (0.000)
LR spatial error	127.566 (0.000)

Note: the t statistics are in parentheses. As for the Wald tests and the LR tests, we show the p-values in brackets. *, **, and *** respectively denote significance at different levels (10%, 5% and 1%).

, and it can be seen that the Wald spatial lag, LR spatial lag, Wald spatial error, and LR spatial error all reject the null hypothesis at a significance level of 1%, which means that the SDPM model cannot be simplified to the SLPM model or SEPM model, and proves that the SDPM model is optimal for the spatial regression estimation of the CEI. Therefore, this paper finally constructed the SDPM model with a spatial fixed effect in order to calculate and analyze the influencing factors of CEI.

4.2.2. Spatial Panel Data Regression Analysis

Having calculated the spatial fixed effect SDPM model constructed above, the spatial autocorrelation coefficient of CEI and the spatial regression estimation result of the influential factors of CEI are shown in Table 6.

The variable W*lnCEI, valued at 0.083 in Table 5, reflects the spatial autocorrelation effect of CEI, indicating that, for every 1% reduction in the CEI in the surrounding regions, there will be a 0.083% reduction in the local region. This proves that it is more efficient to explore CEI mitigation routes from the spatial proximity between regions. Besides this, the variables lnGDP to lnFDI reflect the direct effects of the eight influencing factors on the local CEI, and the variables W*lnGDP to W*lnFDI reflect the spatial lag effects of the eight influencing factors.

On the one hand, the direct effects of GDP and INS are significantly negative at the level of 1%, with coefficients of −0.142 and −0.258, indicating that the two factors can inhibit the growth of the CEI in the local are; for every 1% increase in GDP and INS in a region, the CEI will decrease by an average of 0.142% and 0.258%, respectively. While the direct effects of ENS, ENI, and TEL are all significantly positive at levels above 5%, with coefficients of 0.402, 0.945 and 0.017, these factors can promote the growth of CEI. In addition, the effects of energy-related factors on CEI are relatively strong, so reducing the energy intensity and improving the energy structure are always important measures to reduce CEI in the local area. On the other hand, there are significant spatial lag effects with GDP, URB, ENI, OPL and FDI on CEI in the surrounding areas, reflecting the existence of the spatial effects of these factors on CEI. Among them, the spatial lag effect of URB is significantly positive, reflecting the positive correlation of URB to the CEI of the surrounding areas. The spatial lag effects of GDP, ENI, OPL, and FDI are all significantly negative, thus inhibiting the growth of the CEI in surrounding areas. Besides this, GDP and ENI have stronger negative space correlation effects on CEI compared with the other factors, indicating that the improvement of the economic development level and the reduction of energy intensity are effective ways to reduce the CEI in the surrounding areas.

4.3. Regional Coordinated Emission Mitigation Mechanism

In order to explore regionally-cooperated emission mitigation mechanisms, it is necessary to clarify the spatial spillover effects of the factors that influence CEI, which is reflected by the indirect effect of changes in the local influencing factors on the CEI of the adjacent areas. Figure 4 shows the direct, indirect and total effects of various influential factors on the CEI obtained from the SDPM based on spatial fixed effects (the values and significance levels of each effect of the influential factors are shown in Appendix A

Table A2. The direct, indirect and total effects of SDPM under a space fixed effect.

Variable	Direct Effects	Indirect Effects	Total Effects
lnGDP	−0.154 *** (−3.442)	−0.613 *** (−7.429)	−0.767 *** (−10.865)
lnURB	0.055 (0.545)	0.589 ** (2.713)	0.644 *** (3.127)
lnINS	−0.257 *** (−4.713)	0.011 (0.952)	−0.173 ** (−2.042)
lnENS	0.405 *** (14.244)	0.105 * (1.901)	0.510 *** (9.278)
lnENI	0.935 *** (15.116)	−0.468 *** (−4.194)	0.468 *** (4.954)
lnTEL	0.017 ** (2.691)	0.004 (0.355)	0.021 (1.667)
lnOPL	−0.009 (−0.582)	−0.059 * (−1.964)	−0.067 ** (−2.108)
lnFDI	0.004 (0.677)	−0.037 ** (−2.185)	−0.032 * (−1.724)

Note: the t statistics are given in parentheses. *, **, and *** respectively denote significance at different levels (10%, 5% and 1%).

).

It can be seen from Figure 4 that the direct and indirect effects of GDP, URB, ENS, and TEL are in the same direction, while the direct and indirect effects of INS, ENI, OPL, and FDI are reversed. Among them, the total effects of GDP, INS, OPL, and FDI on CEI are negative in descending order of the coefficient, while the total effects of URB, ENS, ENI and TEL are positive in descending order of the coefficient. Besides this, according to the significance test results of the regression coefficients (shown in Appendix A Table A2), with the exception of INS and TEL, there are significant indirect effects with respect to the other six influencing factors, reflecting the spatial spillover effects. To sum up, GDP, URB, ENS and ENI have relatively stronger effects on CEI, with a significant space spillover effect. Therefore, further analysis of these four influencing factors should be carried out.

4.3.1. Provincial and Regional Analysis of the Effect of GDP on CEI

The direct and indirect effects of GDP are both significant and negative at the 1% level (Figure 4), indicating that GDP has a significant inhibitory effect on the CEI in the local and surrounding areas. Furthermore, the direct and indirect effect coefficients are −0.154 and −0.613; that is, each 1% increase in provincial GDP can reduce the CEI of the local and surrounding regions by 0.154% and 0.613%, respectively. From the perspective of the environmental Kuznets curve (EKC), taking CEI as an environmental quality index, the spatial regression results show that the average level of China’s economic development has reached the right side of the inflection point of the EKC, indicating that China has found a feasible economically- and environmentally-friendly development model. In addition, the indirect effect of GDP on CEI is significantly stronger than the direct effect, indicating that the contribution of economic growth to regional CEI reduction is considerable. According to China’s provincial GDP distribution (Figure 5), the GDP levels of Beijing, Shanghai, Guangdong, Zhejiang, and Jiangsu are relatively high; these provinces have a remarkable ‘low-carbon economy’ development model, which mainly depends on tertiary industry in order to achieve economic growth. Provinces such as Xinjiang, Qinghai, Guizhou, and Jilin are relatively undeveloped in economy, and are facing the dual pressures of economic development and environmental governance. For these provinces, it is necessary to abandon the existing development model and inject new impetus into their economic growth.

From the perspective of regional cooperated emission reduction, more economically developed provinces should fan out from point to area, and should use their own experiences and development advantages to drive the transformation of the model of the economic development of their surrounding areas, thereby reducing the degree of the dependence of regional economic growth on energy consumption and achieving regionally coordinated emission mitigation. Taking the Beijing–Tianjin–Hebei region as an example, Beijing and Tianjin can lead Hebei to achieve industrial restructuring and economically-driven transformation by providing technical innovation support and talent introduction strategies. By pushing Hebei into the beneficial development trend of a ‘low-carbon economy’, the overall carbon intensity of the region will be reduced effectively.

4.3.2. Provincial and Regional Analysis of the Effect of URB on CEI

The direct and indirect effects of URB on carbon intensity are both significant and positive (Figure 4), indicating that URB has a positive effect on CEI in China, which is consistent with the findings of Zhang et al. [34]. The process of urbanization involves the transformation of production and lifestyle from agriculture to industrial manufacturing, and its demand for energy increases consistently, leading to an increase in fossil fuel combustion and CO₂ emissions in the local and adjacent areas. Besides this, urbanization could form a more standardized and collective model of production and life, which helps to control the CO₂ emissions in the local area; for example, the central heating in urban areas is significantly conducive to saving energy and reducing CO₂ emissions compared to decentralized direct burning coal and other heating methods in rural areas. Therefore, the indirect effect of URB on CEI is much stronger than the direct effect, as shown in Figure 4. According to the distribution of URB in China’s provinces (Figure 6), provinces like Beijing, Tianjin, Zhejiang and Jiangsu are so highly urbanized that it is difficult to make the energy consumption in these areas self-sufficient, which has caused a great demand for energy supply from other areas, leading a positive effect on the spatial spillover of CEI from near to far. The provinces Xinjiang, Yunnan, Guizhou and Henan are not relatively urbanized. On the one hand, these areas must speed up the urbanization process; on the other hand, the government of these areas must regulate the activities that generate CO₂ emissions in rural production and life.

From the perspective of regional cooperated emission reduction, the provinces with higher urbanization rates are generally economically developed and low-CEI. The urbanization in these regions requires a large amount of infrastructure, which promotes the development of the housing, real estate, construction, automotive, household appliances and other industries, and stimulates the growth of CEI in local urban construction. Meanwhile, it will also encourage a high demand for high-carbon products in the surrounding underdeveloped areas, which will in turn lead to an increase in the CEI in the surrounding regions. In such a scenario, it is necessary for a high-URB province to provide compensation to the surrounding high-CEI areas, so as to achieve regional CEI reductions.

4.3.3. Provincial and Regional Analysis of the Effect of ENS on CEI

The direct and indirect effects of ENS on CEI are both significant and positive (Figure 4), indicating that the proportion of coal consumption in energy consumption in China is positively related to carbon intensity. The coefficients of the direct and indirect effects are 0.405 and 0.105, respectively. As such, by developing clean energy and promoting the transition to green production, the proportion of coal consumption per 1% decline will realize a 0.405% and 0.105% CEI reduction in the local and surrounding areas. This is because CO₂ emissions are primarily from the combustion fossil fuels, especially coal; the high proportion of coal consumption will directly lead to high CEI. According to the distribution of ENS in China’s provinces (Figure 7), the ENS value in Xinjiang, Shanxi, and Inner Mongolia, etc., is quite high, and there are cases where the value is greater than 1. This is due to the existence of energy conversion projects; a large amount of coal consumption is used to generate electricity, which is transmitted to other areas as a kind of energy supply. Although clean energy sources—such as wind energy and nuclear energy—are being developed, the technical and policy issues are difficult to resolve over the short term. The big coal resources share of the whole energy will not change in a long run. The relatively high degree of ENS in Hebei, Henan, and Jilin, etc., is caused by their location adjacent to large resource-rich provinces; if the cost of fossil energy such as coal is relatively low, it is easier to form a high-energy consumption development model, which leads to the positive spatial spillover effect of ENS.

From the perspective of regional cooperated emission reduction, for regions that are rich in coal resources, the consumption costs of coal are relatively low, which makes it easier to form a high-energy consumption development model in the local and surrounding areas. Hence, for the regions adjacent to the provinces with higher resource levels, the awareness regarding energy conservation and emission reduction should be increased. Furthermore, policies that require transformations in production methods should be put in place in order to reduce the demands for coal supplies in the provinces with large coal resources, thereby achieving reductions in the intensity of carbon emissions.

4.3.4. Provincial and Regional Analysis of the Effect of ENI on CEI

The direct effect, indirect effect, and total effect of ENI are all significant at the 1% level (Figure 4), where the direct effects and total effects are positive, and the indirect effects are negative. This indicates that ENI has positive effects on CEI both in the local and total regions, with suppressive effects in the surrounding areas. Furthermore, from the perspective of the effect coefficients, each 1% reduction in ENI reduces the local CEI by 0.935% and increases the CEI of the surrounding area by 0.468%. Because of the adjustments in the structures of production and consumption in the region, there has been a reduction in the dependence of economic growth on energy consumption. However, this adjustment is likely to result in compensation in the surrounding areas. Lower demands for energy in this area will be compensated for by the surrounding areas, thus increasing the burden on the surrounding areas. One example of this is the manner in which the Beijing–Tianjin–Hebei region developed. According to the distribution of ENI in China’s provinces (Figure 8), the ENI of Beijing and Tianjin are both relatively lower in the country, while the ENI in Hebei is higher than the national average. Here, the high-energy-consuming and high-polluting enterprises in Beijing and Tianjin either have been shut down or transferred to the Hebei region. This resulted in the higher emissions of CO₂ in Hebei Province as compensation for the development of Beijing and Tianjin. From a national perspective, the ENI level shows a gradual upward trend from the northwest inland to the southeast coast. The distribution of ENI is directly related to resource endowment. Therefore, the ENI of the inland provinces should be reduced due to the reduction of the energy consumption demand and effective energy utilization.

From the perspective of regional cooperated emission reduction, provinces with higher ENI have compensated energy consumption and carbon emissions for the developed regions around them. As such, the developed regions have a responsibility to compensate these high ENI regions through reductions in CEI. Taking Beijing–Tianjin–Hebei as an example; Beijing and Tianjin should provide technical and economic support for the reduction of ENI in Hebei Province, so that Hebei Province can reduce its energy intensity through technological progress, thereby achieving the goal of the reduction of the regional carbon emission intensity.

Besides this, the INS indicator reflects the proportion of tertiary industry; the direct effect of INS is significantly negative and the indirect effect not obvious, indicating that the development of tertiary industry has a significant inhibitory effect on the local carbon intensity, but this does not hold true for the surrounding areas. The direct effect coefficient of INS is −0.257, which means that every 1% increase in INS reduces the local CEI by 0.257%. From the perspective of regional coordination, strategies such as strengthening regional technical support, knowledge sharing, and talent introduction are needed to increase the proportion of high-tech and financial service industries, and to optimize the internal structure of the tertiary industry in the region as a whole. The direct effect of TEL on CEI is significantly positive, the indirect and total effects are not significant, and the influence coefficients are all relatively small, indicating that TEL has little positive effect on CEI. Grossman and Krueger [43], suggest that the impact of technological effects on environmental quality can be divided into two types: ‘technical progress–carbon emissions’ and ‘technical progress–economic growth–carbon emissions’. The former manifests the direct suppression of carbon emissions through technology, and the latter manifests the indirect promotion of carbon emissions by promoting economic growth. The two effects are offset by the final impact of technical effects on carbon emissions. The effect of the first model in China is smaller than the second model; that is, the development of clean technology needs to be further improved. OPL and FDI reflect China’s level of opening-up and internationalization. The direct effects of these two indicators are not significant, but the indirect effects are significant and negative, indicating that the improvement of the opening-up level can inhibit the carbon intensity to some extent. From the perspective of regional cooperation, the higher the level of the openness of a region, the more likely it is to be able to stimulate the surrounding areas and industries to reduce environmental costs through market competition mechanisms, and through the transition to green and clean production. At the same time, foreign direct investment can provide international technical support and concept guidance for the transformation of production modes, thereby playing a positive role in promoting regionally coordinated CEI reductions. This result also confirms the establishment of the ‘pollution halo hypothesis’ in China; that is, FDI is conducive to host country emission reductions, which is consistent with the findings of Shao et al. [55].

5. Conclusions and Policy Implications

Based on the theory of spatial econometrics, this paper has established panel data on the intensity of the carbon emissions and its influential factors of 30 provinces (municipalities and autonomous regions) in China between 2005 and 2017. The spatial effects, driving mechanisms, and regionally-coordinated emission reduction measures of the provincial carbon emission intensity were explored through the calculation of the Moran’s I and the construction of the SDPM model. The main conclusions are as follows: (a) China’s provincial carbon emission intensity has significant spatial autocorrelation characteristics, and it shows an increasing trend with time; (b) economic development has a negative correlation with carbon intensity, and the space spillover effect is significant, which is a great driving force for regional carbon intensity reduction; (c) energy intensity has a positive correlation with local carbon intensity, but the spatial spillover effect is negative. When reducing carbon intensity by adjusting energy intensity, the impact on surrounding areas should be fully considered. (d) The energy structure and urbanization have a relatively important effect on the intensity of carbon emissions, and have significant space spillover effects. Based on the analysis and discussion of the results, the following policy recommendations are proposed for regional collaborative carbon intensity emission reduction.

First, Low-CEI regions, such as Beijing, Tianjin and Zhejiang, can use their advantages with respect to economic development in order to drive the industrial transition of the surrounding regions and the other regions of the nation with high-CEI. They could fully mobilize their own technology and talent advantages to provide technical support for the development of clean energy and waste gas treatment in large resource-rich provinces, such as Xinjiang, Inner Mongolia, and Heilongjiang. Furthermore, with the state’s strategy of encouraging regional cooperation, regional resources can be shared, such as educational, cultural, tourism, and transportation resources.

Next, the CO₂ emission quotas and emission reduction responsibilities allocated from a whole region would be more sensible for Low–High agglomeration regions, such as the Beijing–Tianjin–Hebei region. The responsibilities and quotas of the provinces should be distributed in the region as a whole, and should jointly shoulder the carbon intensity target assigned by the country. For regions that lie close to provinces with large resource reserves, their high CEI levels are often the result of the ease and convenience of procurement, and low transportation costs. These regions, such as Shaanxi and Hebei, bordering Shanxi; Qinghai and Gansu, bordering Xinjiang; and regions bordering Inner Mongolia, should focus on reducing their own demands for energy consumption by adjusting their industrial structures and transforming their underdeveloped production capacity. Simultaneously, other low-CEI regions that are not adjacent to high-carbon provinces with large resource reserves should assume more carbon emission reduction responsibilities as compensation, and should provide some support for the high emissions in high-carbon regions caused by their energy supply. In addition, high-CEI regions should work hard to advance the process of urbanization in a scientific and reasonable way, increase their talent introduction and research funding in order to promote the development of tertiary industry, and attract foreign direct investment, especially in energy production-related industries, which can bring advanced technologies, management models and cleaner production models from developed countries into the region.

Finally, for energy-dependent high-CEI regions—such as Shanxi, Shaanxi, Inner Mongolia, Ningxia, Xinjiang, Heilongjiang and Jilin—the energy intensity and coal consumption ratio are much higher, and the development of the whole nation depends on the resource endowment and energy industry in these regions. Based on these conditions, it is important to replace traditional fossil energy sources, such as coal, with clean energy sources, such as wind and nuclear energy. It is very important to develop solutions for the practical technical problems and policy issues that stand in the way of acceptance, such as the problem of grid connection and electricity pricing in wind power generation technology.