Evolution of Clustering Quantified by a Stochastic Method—Case Studies on Natural and Human Social Structures
Abstract
1. Introduction
2. Methodology
2.1. Stochastic Analysis of Clustering in 2D Space: The 2D-C Tool
2.2. Temporal Evolution of 2D Clustering
3. Case Studies
3.1. Evolution of Clustering in Nature
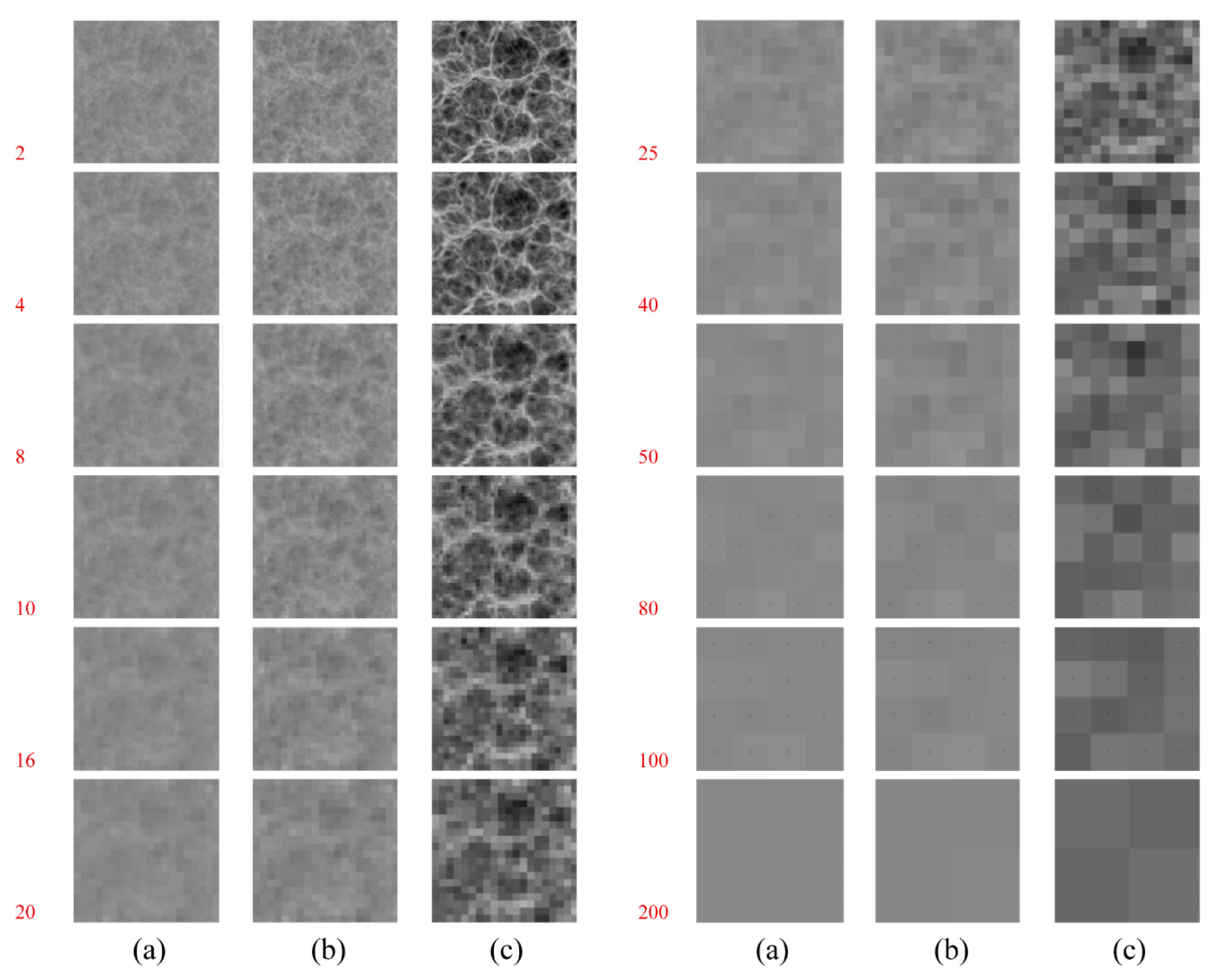
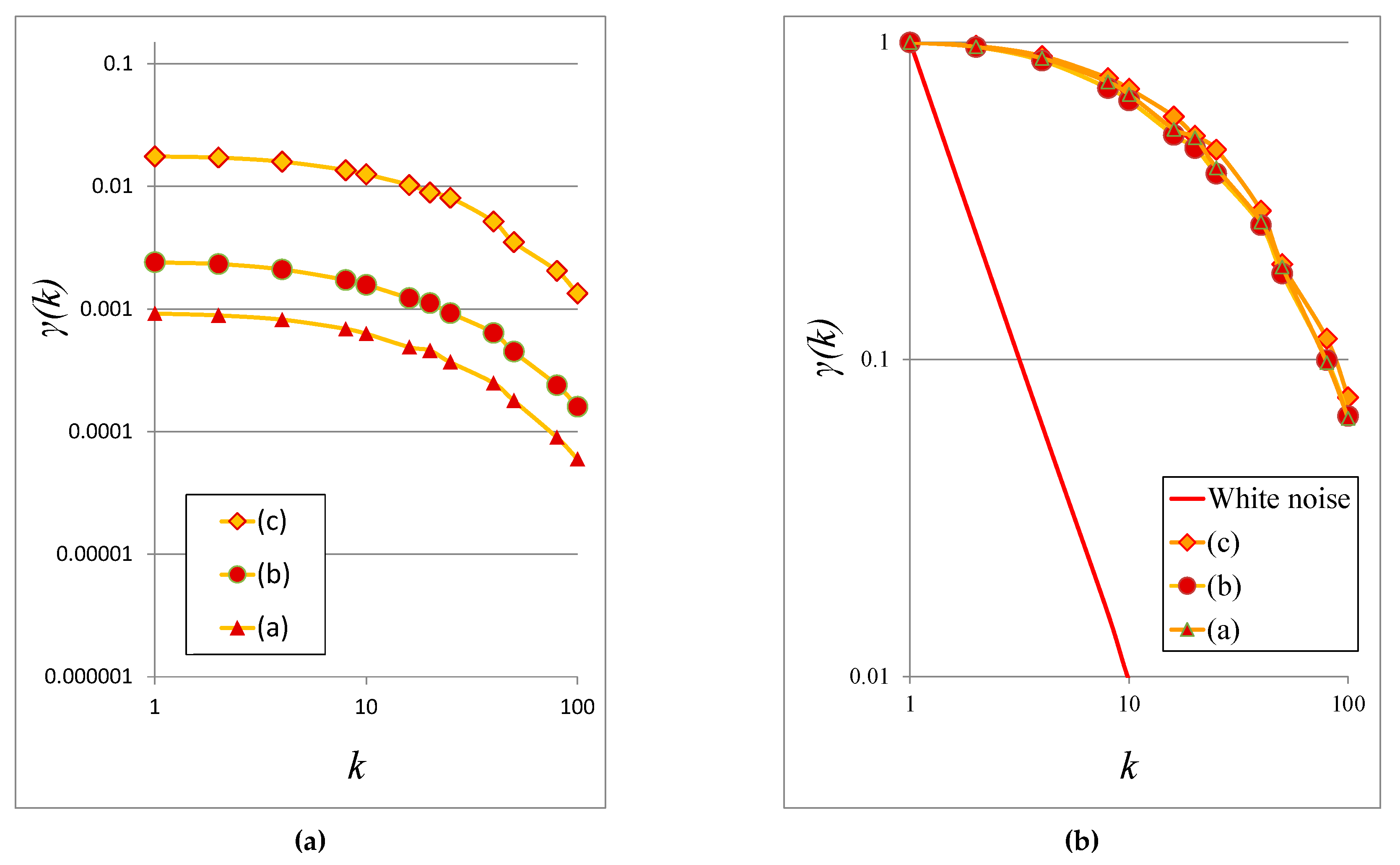
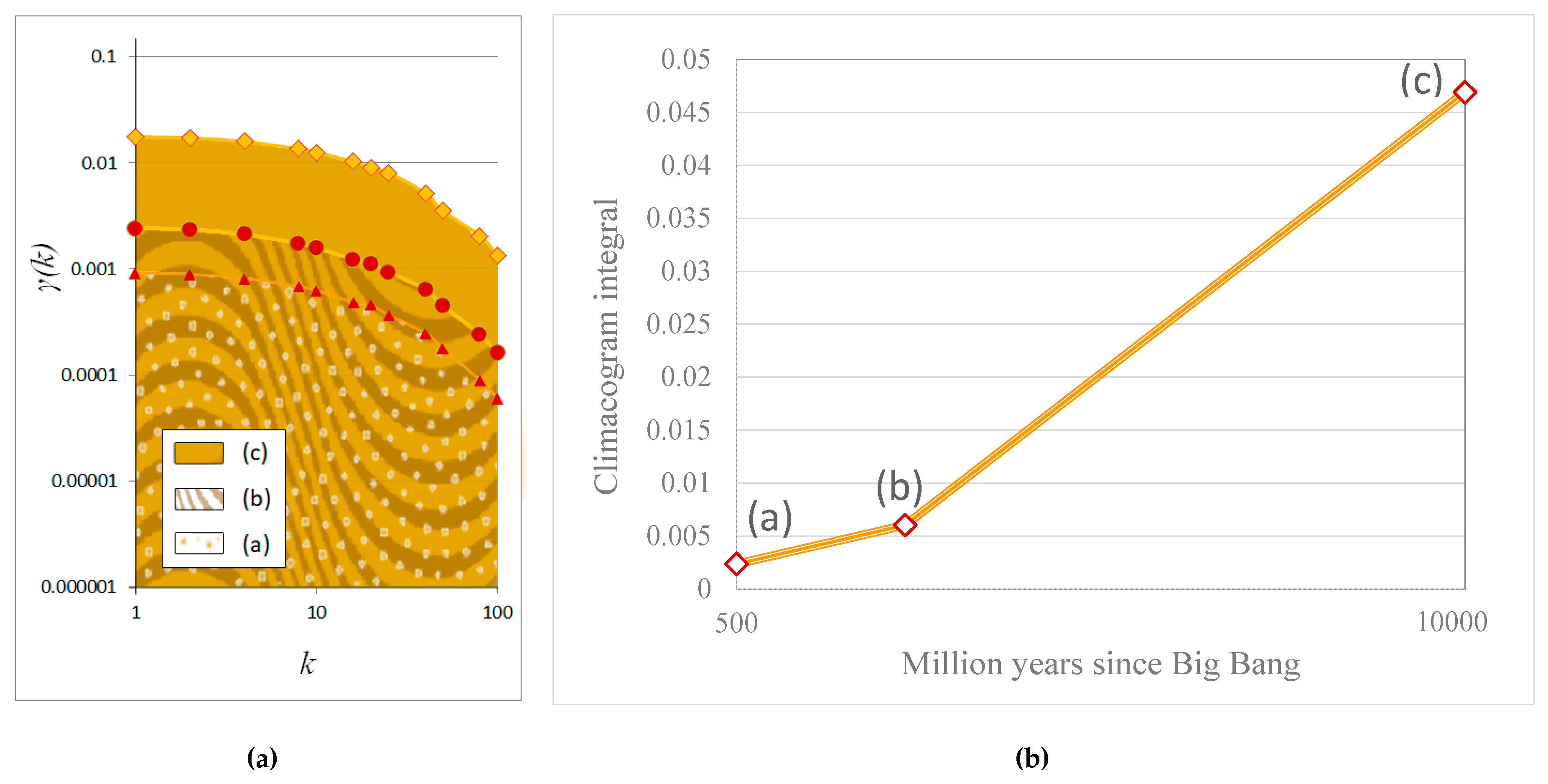
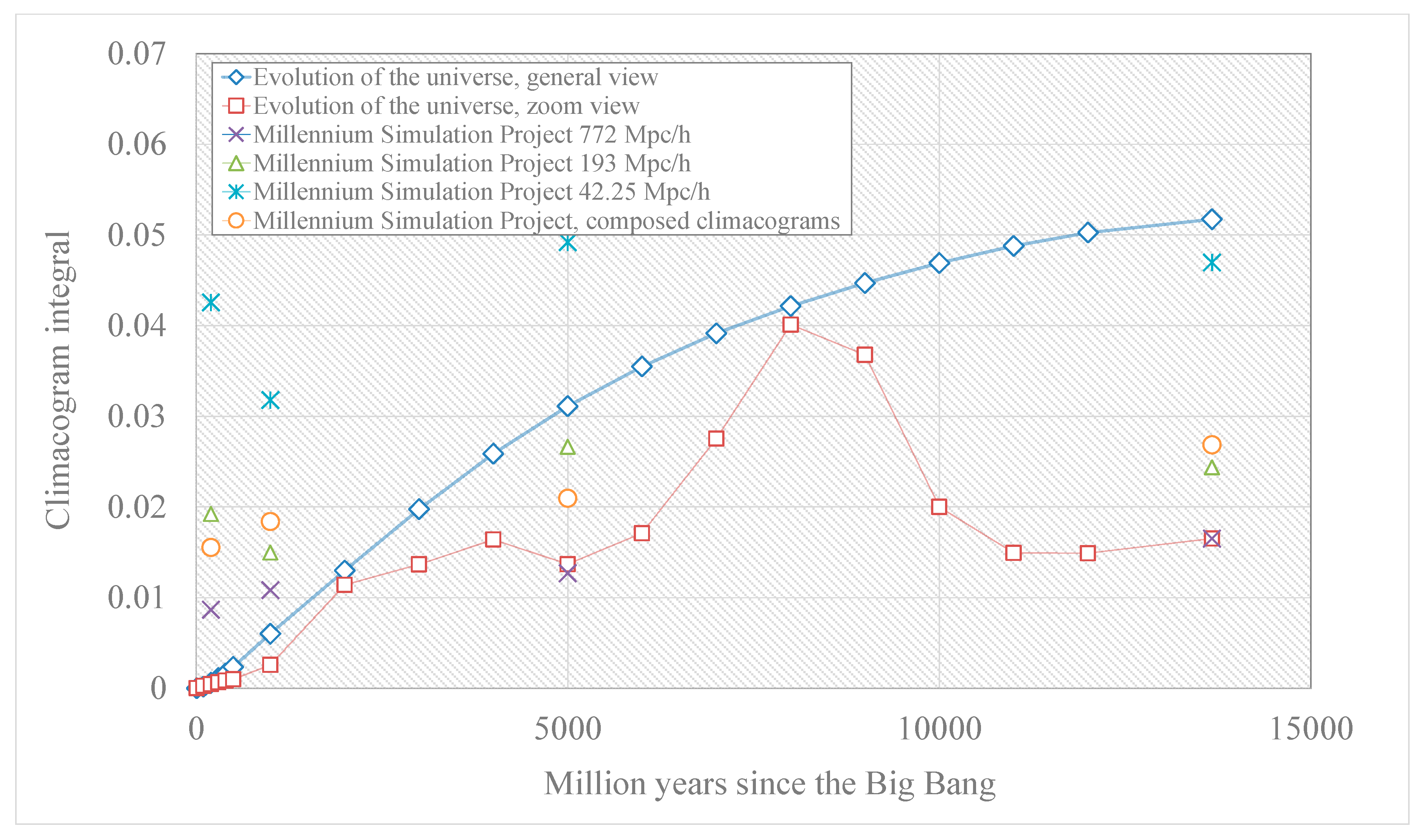
3.1.1. Cosmological Simulations
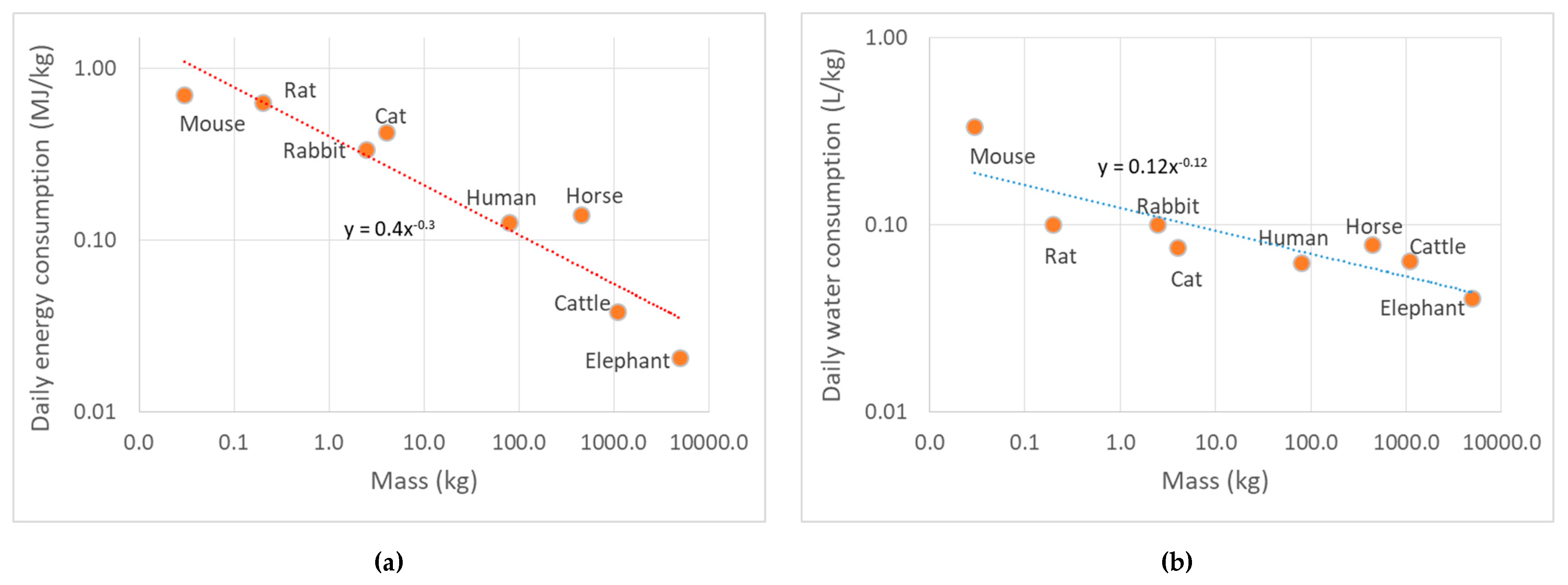
3.1.2. Ecosystems
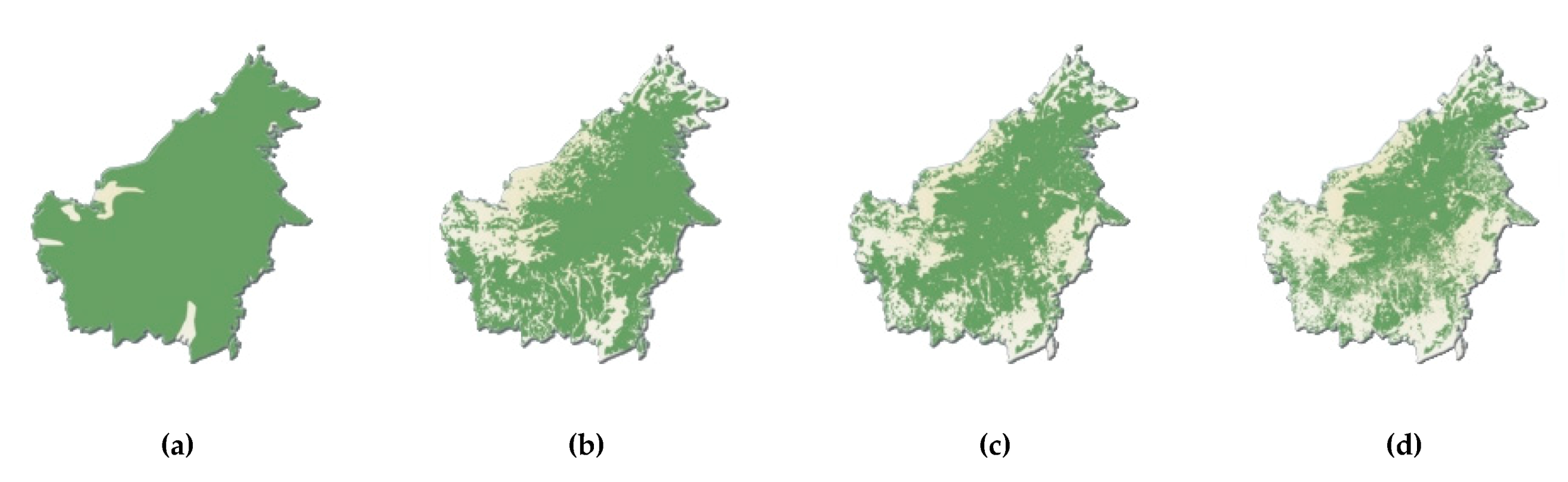
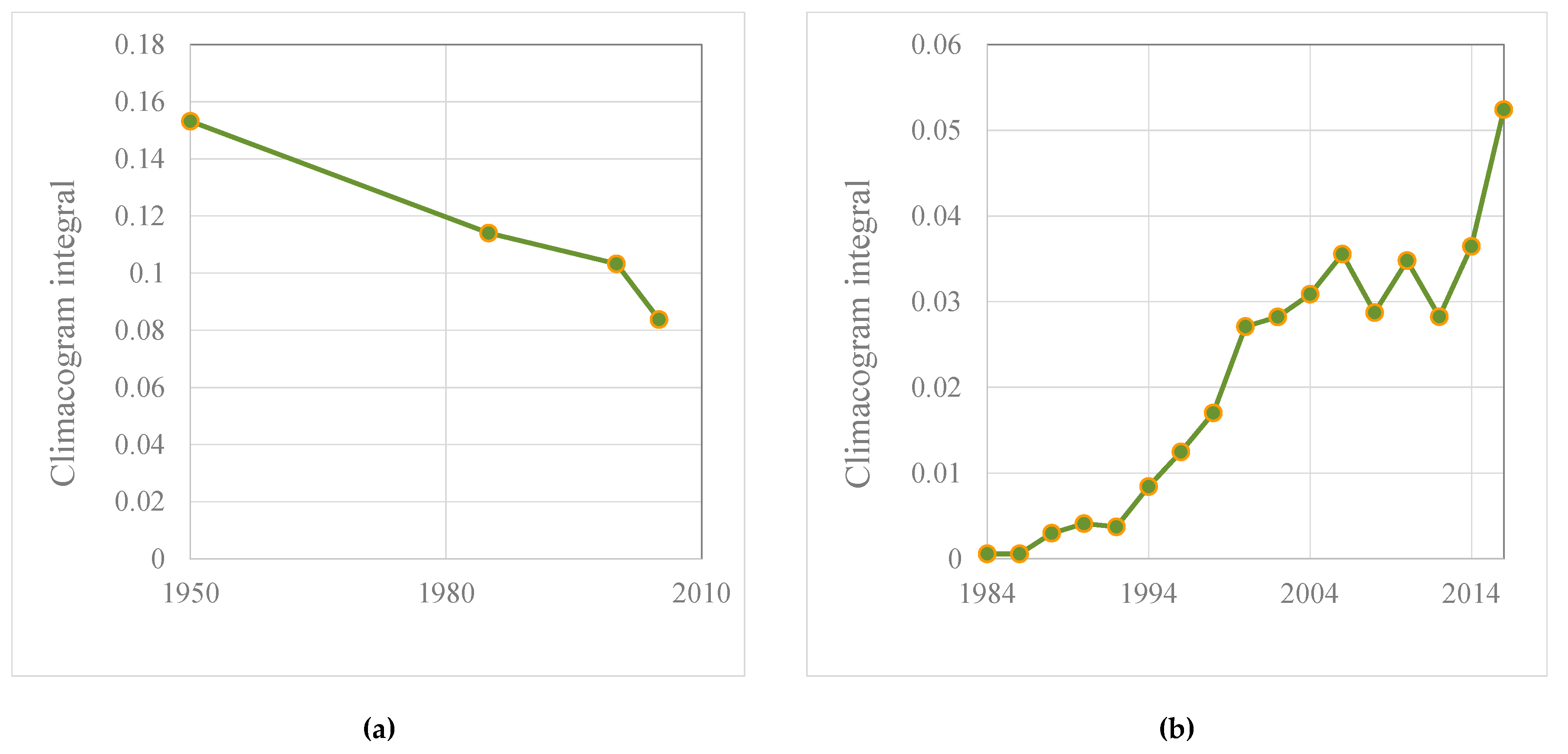
- the deforestation of Borneo, Figure 7, Figure 9a, Figure S8: Deforestation in Borneo 1950–2005 (a) 1950; (b) 1985; (c) 2000 (d) 2005 [54], Figure S9: Climacograms of the deforestation in Borneo, Figure S10: Evaluation of climacograms and rhythm of clustering in demolition of fosters’ clustering in Borneo,
- the deforestation of the Amazon, Figure 8, Figure 9b, Figure S11: Deforestation of Amazon, creation of clustering of dry land and urban areas inside forest [55], Figure S12: Climacograms of the deforestation in Amazon, Figure S13: Evaluation of climacograms and rhythm of clustering evolution of dry-lands’ clustering in Amazon
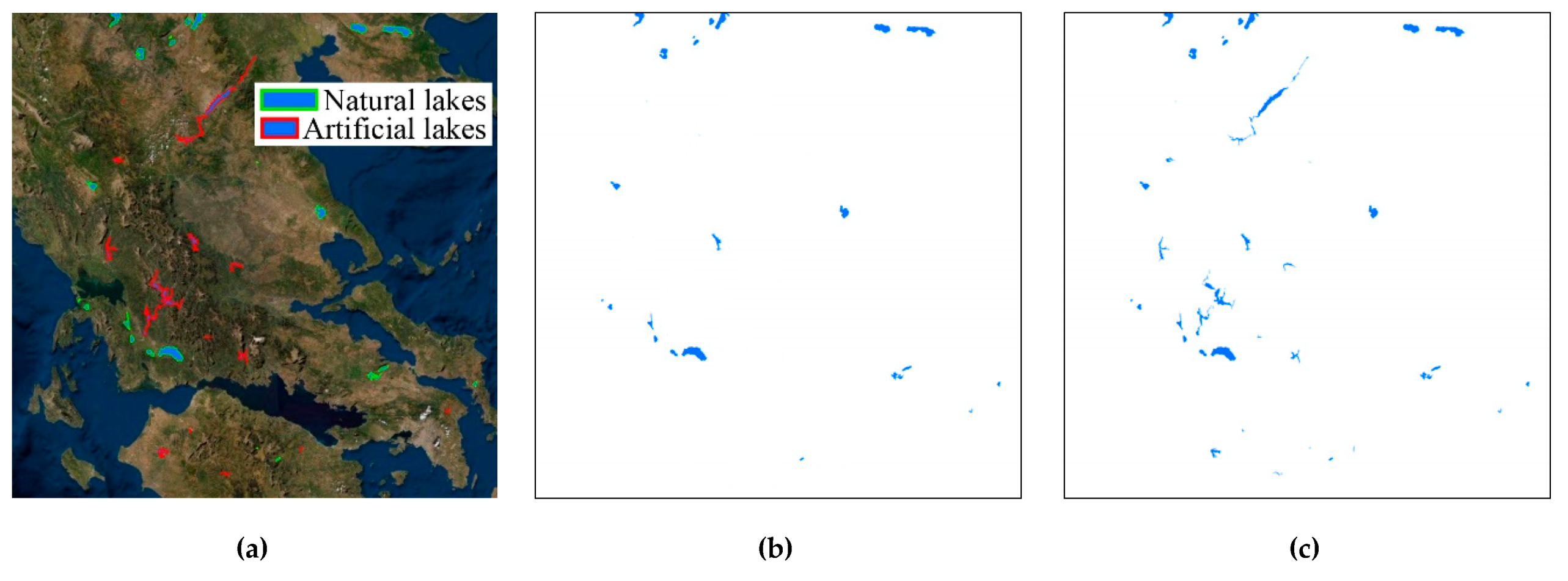
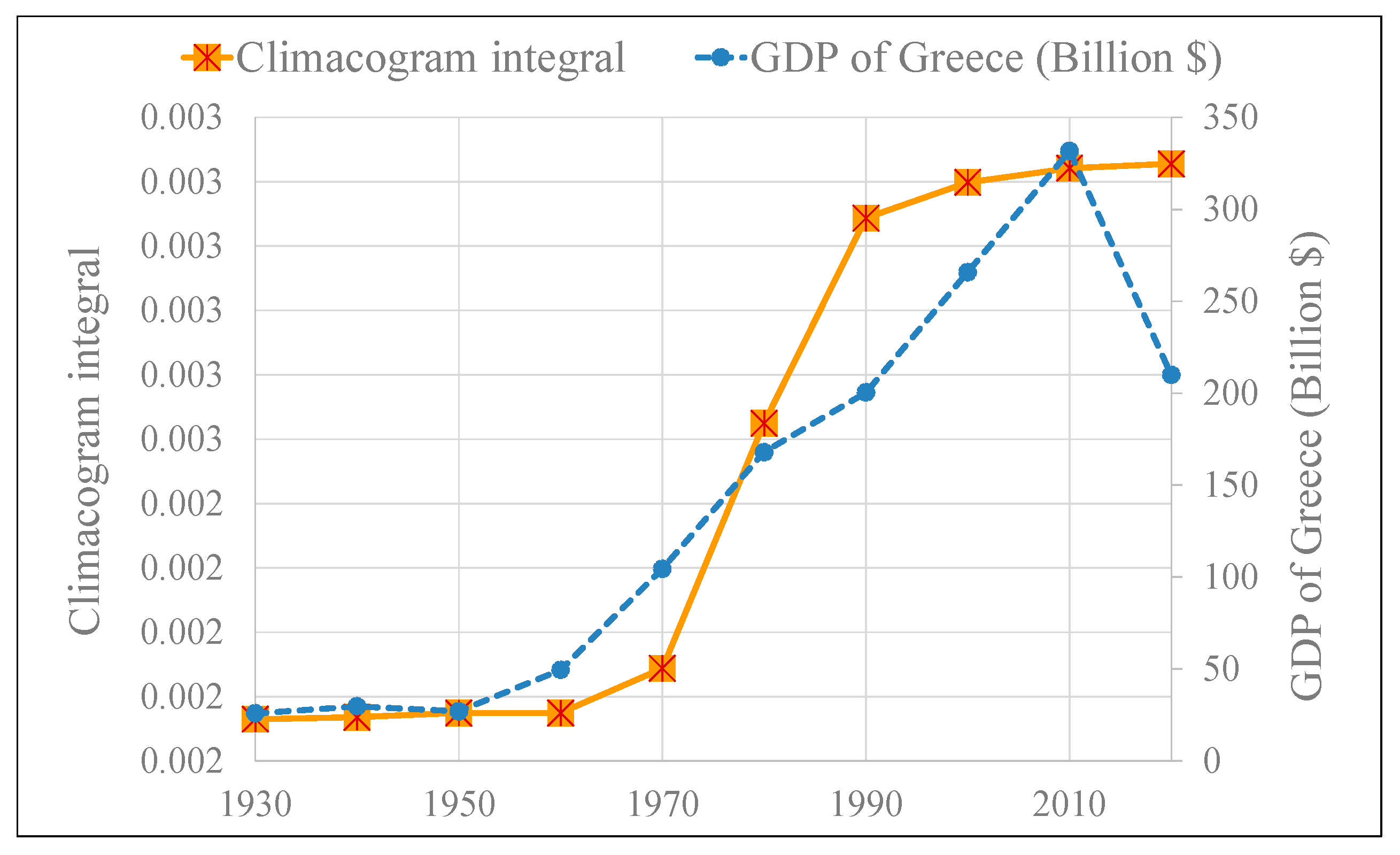
- the evolution of water bodies in Greece, Figure 10, Figure 11, Figure S14: Greece, natural and artificial lakes (a) overview map of the area with natural and artificial lakes in 2020; (b) layer of the map; natural and artificial lakes 2020; (c) layer of the map; lakes 2020, Figure S15: Evolution of water bodies in Greece as new big dams are constructed and new artificial lakes are created, Figure S16: Climacograms of the evolution of water bodies in Greece.
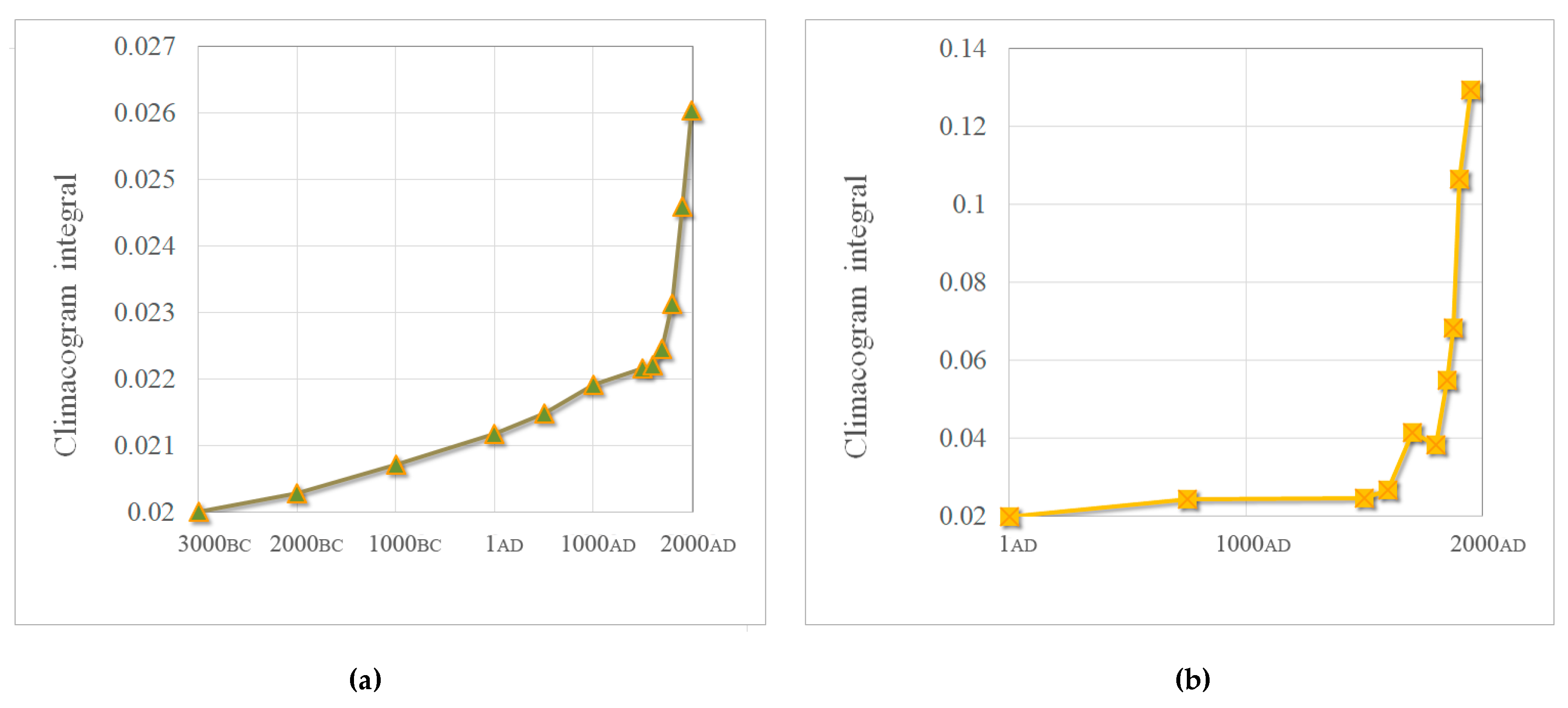
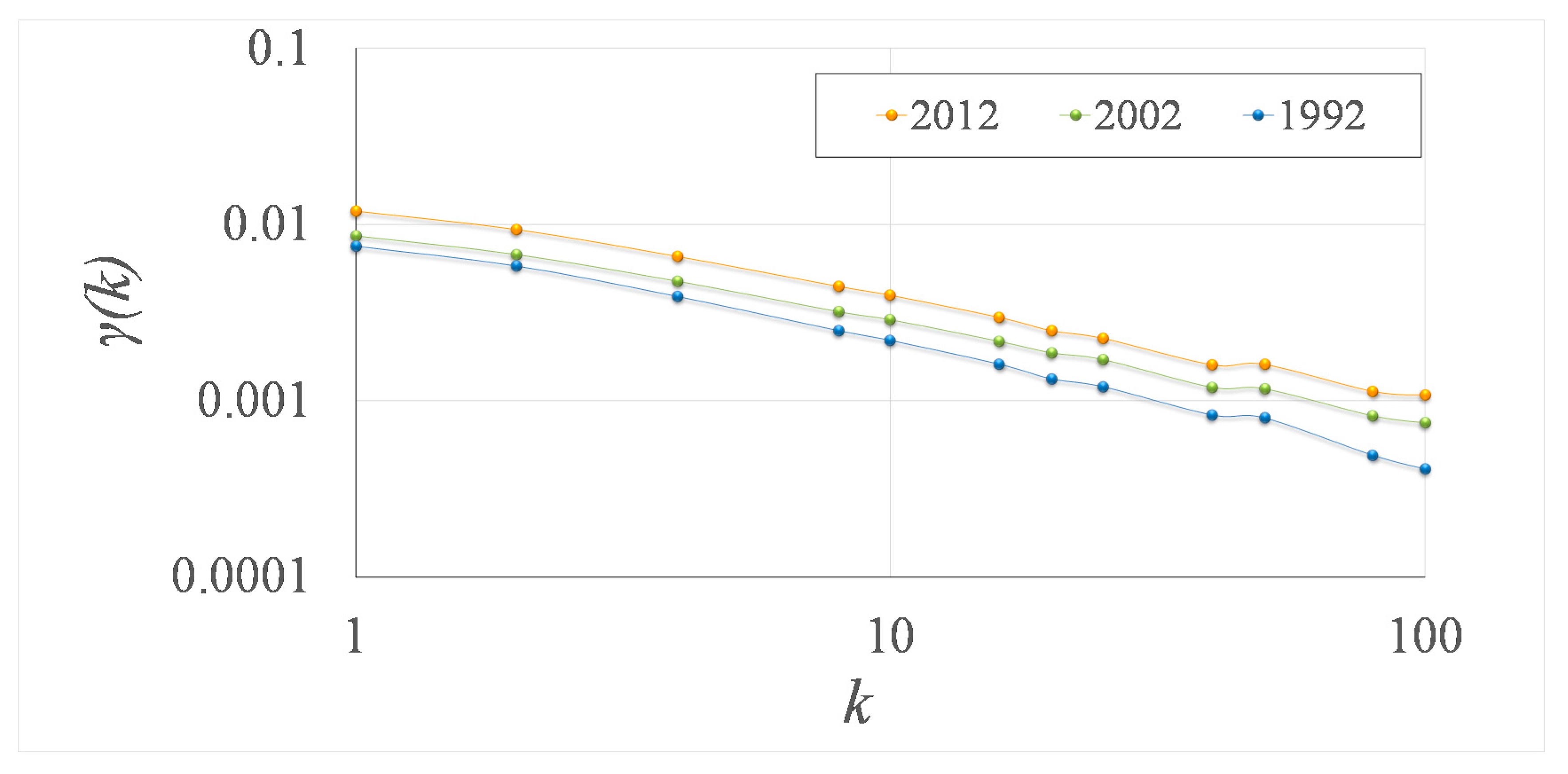
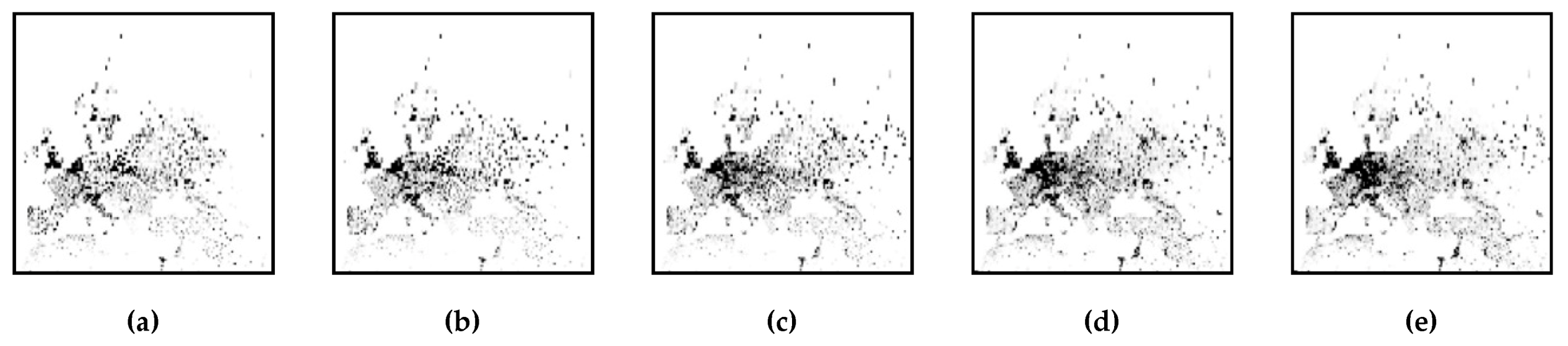
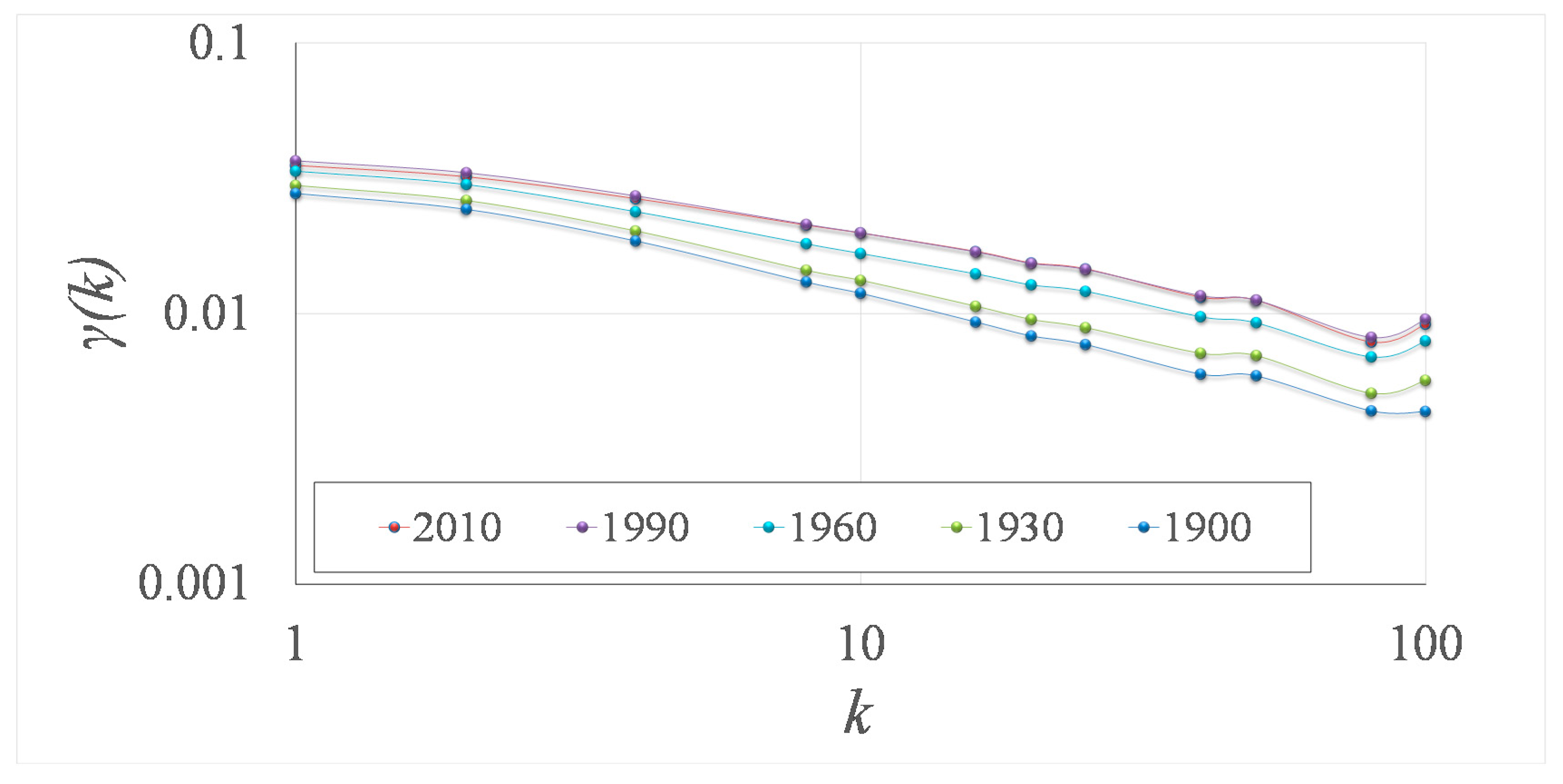
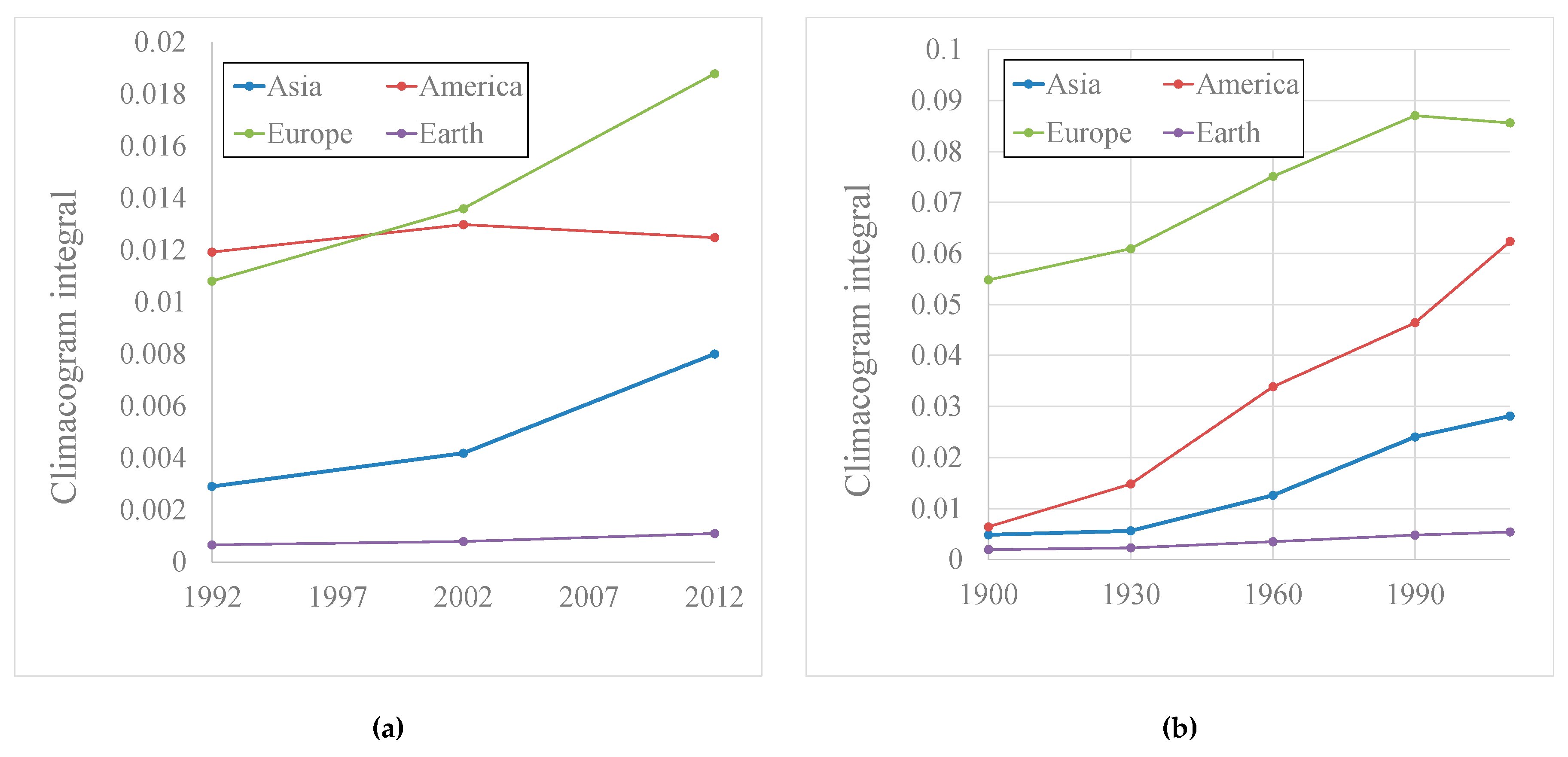
3.2. Evolution of Human Social Clustering
4. Discussion
4.1. Human Social Clustering as a Means for Development and Progress
4.2. Risks From Large-Scale Clustering
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Homer, Odyssey. Available online: http://users.uoa.gr/~nektar/arts/tributes/omhros/od17.htm (accessed on 15 September 2020).
- A Brief History of Dinosaurs. Available online: https://www.livescience.com/3945-history-dinosaurs (accessed on 3 February 2020).
- Mammal. Available online: https://en.wikipedia.org/wiki/Mammal (accessed on 3 February 2020).
- Upham, N.S.; Esselstyn, J.A.; Jetz, W. Mammals Inferring the mammal tree: Species-level sets of phylogenies for questions in ecology, evolution and conservation. PLoS Biol. 2019, 17. [Google Scholar] [CrossRef] [PubMed]
- Urushihara, H. Developmental biology of the social amoeba: History, current knowledge and prospects. Dev. Growth Differ. 2008, 50. [Google Scholar] [CrossRef] [PubMed]
- Kleiber’s Law. Available online: https://en.wikipedia.org/wiki/Kleiber%27s_law (accessed on 17 January 2020).
- Of Mice and Elephants: A Matter of Scale. Available online: http://courses.missouristate.edu/chrisbarnhart/bio121/lab/respiration/of_mice_and_elephants.htm (accessed on 12 January 2020).
- Sargentis, G.-F.; Ioannidis, R.; Karakatsanis, G.; Sigourou, S.; Lagaros, N.D.; Koutsoyiannis, D. The Development of the Athens Water Supply System and Inferences for Optimizing the Scale of Water Infrastructures. Sustainability 2019, 11, 2657. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Ioannidis, R.; Iliopoulou, T.; Frangedaki, E.; Koutsoyiannis, D. Optimal utilization of water resources for local communities in mainland Greece (case study of Karyes, Peloponnese). Procedia Manuf. 2020, 44, 253–260. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Scale of water resources development and sustainability: Small is beautiful, large is great. Hydrol. Sci. J. 2011, 56, 553–575. [Google Scholar] [CrossRef]
- Koutsoyiannis, A. Modern Microeconomics, 2nd ed.; Springer: London, UK, 1979. [Google Scholar]
- Asian Elephant Nutrition. Available online: https://asianelephantnutrition.wordpress.com/2015/02/25/big-body-lots-of-energy-maintenance/ (accessed on 18 January 2020).
- Energy Requirements of Adult Cats. Available online: https://www.cambridge.org/core/journals/british-journal-of-nutrition/article/energy-requirements-of-adult-cats/225A91E97C8B94CAB4A5BF0646EFA2A2/core-reader (accessed on 18 January 2020).
- Nutrient Requirements of Laboratory Animals. Available online: https://www.ncbi.nlm.nih.gov/books/NBK231925/ (accessed on 18 January 2020).
- How to Survive Mass Extinction. Available online: https://www.theguardian.com/science/lost-worlds/2012/sep/20/dinosaurs-fossils (accessed on 15 January 2020).
- McGarvey, R.; Feenstra, J.E.; Mayfield, S.; Erin, V.; Sautter, B. A diver survey method to quantify the clustering of sedentary invertebrates by the scale of spatial autocorrelation. Mar. Freshw. Res. 2010, 61, 153–162. [Google Scholar] [CrossRef]
- Tachmazidou, I.; Verzilli, C.J.; Iorio, M.D. Genetic Association Mapping via Evolution-Based Clustering of Haplotypes. PLoS Genet. 2007, 3, e111. [Google Scholar] [CrossRef]
- Hütt, M.-T.; Neff, R. Quantification of spatiotemporal phenomena by means of cellular automata techniques. Phys. A Stat. Mech. Appl. 2001, 289, 498–516. [Google Scholar] [CrossRef]
- Khater, I.M.; Nabi, I.R.; Hamarneh, G. A Review of Super-Resolution Single-Molecule Localization Microscopy Cluster Analysis and Quantification Methods. Patterns 2020, 1, 100038. [Google Scholar] [CrossRef]
- Murase, K.; Kikuchi, K.; Miki, H.; Shimizu, T.; Ikezoe, J. Determination of arterial input function using fuzzy clustering for quantification of cerebral blood flow with dynamic susceptibility contrast-enhanced MR imaging. J. Magn. Reson. Imaging 2001, 13, 797–806. [Google Scholar] [CrossRef]
- Mier, P.; Andrade-Navarro, M.A. FastaHerder2: Four Ways to Research Protein Function and Evolution with Clustering and Clustered Databases. J. Comput. Biol. 2016, 23, 270–278. [Google Scholar] [CrossRef] [PubMed]
- McDermott, P.L.; Wikle, C.K. Bayesian Recurrent Neural Network Models for Forecasting and Quantifying Uncertainty in Spatial-Temporal Data. Entropy 2019, 21, 184. [Google Scholar] [CrossRef]
- Beck, R.; Dickmann, F.; Lovas, R.G. Quantification of the clustering properties of nuclear states. Ann. Phys. 1987, 173, 1–29. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Dynamical evolution of clustering in complex network of earthquakes. Eur. Phys. J. B 2007, 59, 93–97. [Google Scholar] [CrossRef]
- Ellam, L.; Girolami, M.; Pavliotis, G.A.; Wilson, A. Stochastic modelling of urban structure. Proc. R. Soc. A 2018, 474, 20170700. [Google Scholar] [CrossRef] [PubMed]
- Levine, N. Spatial Statistics and GIS: Software Tools to Quantify Spatial Patterns. J. Am. Plan. Assoc. 1996, 62, 381–391. [Google Scholar] [CrossRef]
- Lee, J.; Gangnon, R.E.; Zhu, J.; Liang, J. Uncertainty of a detected spatial cluster in 1D: Quantification and visualization. Stat 2017, 6, 345–359. [Google Scholar] [CrossRef]
- Watch the strange growth of Los Angeles, from 1877 to 2000. Available online: https://la.curbed.com/2014/4/3/10121264/los-angeles-sprawl-history-map-animation (accessed on 15 September 2020).
- How African Cities Have Grown over 200 Years. Available online: https://www.smartcitiesdive.com/ex/sustainablecitiescollective/watch-how-african-cities-have-grown-over-200-years/246636/ (accessed on 15 September 2020).
- Norberg, P.; Gaztañaga, E.; Baugh, C.M.; Croton, D.J.; Statistical analysis of galaxy surveys–IV. An objective way to quantify the impact of superstructures on galaxy clustering statistics. Mon. Not. R. Astron. Soc. 2011, 418, 2435–2450. [Google Scholar] [CrossRef]
- Baugh, C.M.; Benson, A.J.; Cole, S.; Frenk, C.S.; Lacey, C.G. Modelling the evolution of galaxy clustering. Mon. Not. R. Astron. Soc. 1999, 305, L21–L25. [Google Scholar] [CrossRef][Green Version]
- Koutsoyiannis, D. Hydrology and Change. Hydrol. Sci. J. 2013, 58, 1177–1197. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, N. Evolution and clustering of rich clusters. Mon. Not. R. Astron. Soc. 1986, 222, 323–345. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. HESS Opinions A random walk on water. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Dimitriadis, P. Hurst-Kolmogorov Dynamics in Hydrometeorological Processes and in the Microscale of Turbulence. Ph.D. Thesis, Department of Water Resources and Environmental Engineering, National Technical University of Athens, Athens, Greece, 2017. [Google Scholar]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Ioannidis, R.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works. Energies 2019, 12, 2817. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Koutsoyiannis, D. Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage 2020, 3, 283–305. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. An entropy-based objective evaluation method for image segmentation, Proc. SPIE 5307. Storage Retr. Methods Appl. Multimed. 2004, 5307, 8–49. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J.A. Database of human segmented natural images and its application to evaluating algorithms and measuring ecological statistics. ICCV 2001, 2, 16–423. [Google Scholar]
- Koutsoyiannis, D. Encolpion of Stochastics: Fundamentals of Stochastic Processes; Department of Water Resources and Environmental Engineering, National Technical University of Athens: Athens, Greece, 2013; Volume 12. [Google Scholar]
- Koutsoyiannis, D. Climacogram-based pseudospectrum: A simple tool to assess scaling properties, European Geosciences Union General Assembly 2013. In Geophysical Research Abstracts; EGU2013-4209; European Geosciences Union: Vienna, Austria, 2013; Volume 5, p. 700. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus autocovariance and power spectrum in stochastic modelling for Markovian and Hurst–Kolmogorov processes. Stoch. Environ. Res. Risk Assess. 2015, 29, 1649–1669. [Google Scholar] [CrossRef]
- O’Connell, P.E.; Koutsoyiannis, D.; Lins, H.F.; Markonis, Y.; Montanari, A.; Cohn, T. The scientific legacy of Harold Edwin Hurst (1880–1978). Hydrol. Sci. J. 2016, 61, 1571–1590. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Iliopoulou, T.; Ioannidis, R.; Koutsoyiannis, D. Stochastic investigation of the Hurst-Kolmogorov behaviour in arts, European Geosciences Union General Assembly 2018. In Geophysical Research Abstracts; EGU2018-17082; European Geosciences Union: Vienna, Austria, 2018; Volume 20. [Google Scholar]
- Dimitriadis, P.; Tzouka, K.; Koutsoyiannis, D.; Tyralis, H.; Kalamioti, A.; Lerias, E.; Voudouris, P. Stochastic investigation of long-term persistence in two-dimensional images of rocks. Spat. Stat. 2019, 29, 177–191. [Google Scholar] [CrossRef]
- Evolution of the Universe. Available online: http://timemachine.cmucreatelab.org/wiki/Early_Universe (accessed on 24 August 2020).
- Di Matteo, T.; Colberg, J.; Springel, V.; Hernquist, L.; Sijacki, D. Direct cosmological simulations of the growth of black holes and galaxies. Astrophys. J. 2008, 676, 33–53. [Google Scholar] [CrossRef]
- The Millennium Simulation Project. Available online: https://wwwmpa.mpa-garching.mpg.de/galform/virgo/millennium/ (accessed on 16 September 2020).
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Smith, S. Solving sparse nonlinear programs using GRG. ORSA J. Comput. 1992, 4, 2–15. [Google Scholar]
- Markonis, Y.; Koutsoyiannis, D. Climatic variability over time scales spanning nine orders of magnitude: Connecting Milankovitch cycles with Hurst–Kolmogorov dynamics. Surv. Geophys. 2013, 34, 181–207. [Google Scholar] [CrossRef]
- Creator Credit Hugo Ahlenius. Available online: https://www.grida.no/resources/8324 (accessed on 15 September 2020).
- The Human Impact on the World’s Forest. Available online: https://www.visualcapitalist.com/human-impact-on-forests/ (accessed on 15 September 2020).
- Ioannidis, R.; Koutsoyiannis, D. A review of land use, visibility and public perception of renewable energy in the context of landscape impact. Appl. Energy 2020, 276, 115367. [Google Scholar] [CrossRef]
- Klein Goldewijk, K.; Beusen, A.; van Drecht, G.; de Vos, M. The HYDE 3.1 spatially explicit database of human-induced global land-use change over the past 12,000 years. Glob. Ecol. Biogeogr. 2011, 20, 73–86. [Google Scholar] [CrossRef]
- The Evolution of London: The City’s near-2000 Year History Mapped. Available online: https://www.theguardian.com/cities/2014/may/15/the-evolution-of-london-the-citys-near-2000-year-history-mapped (accessed on 15 September 2020).
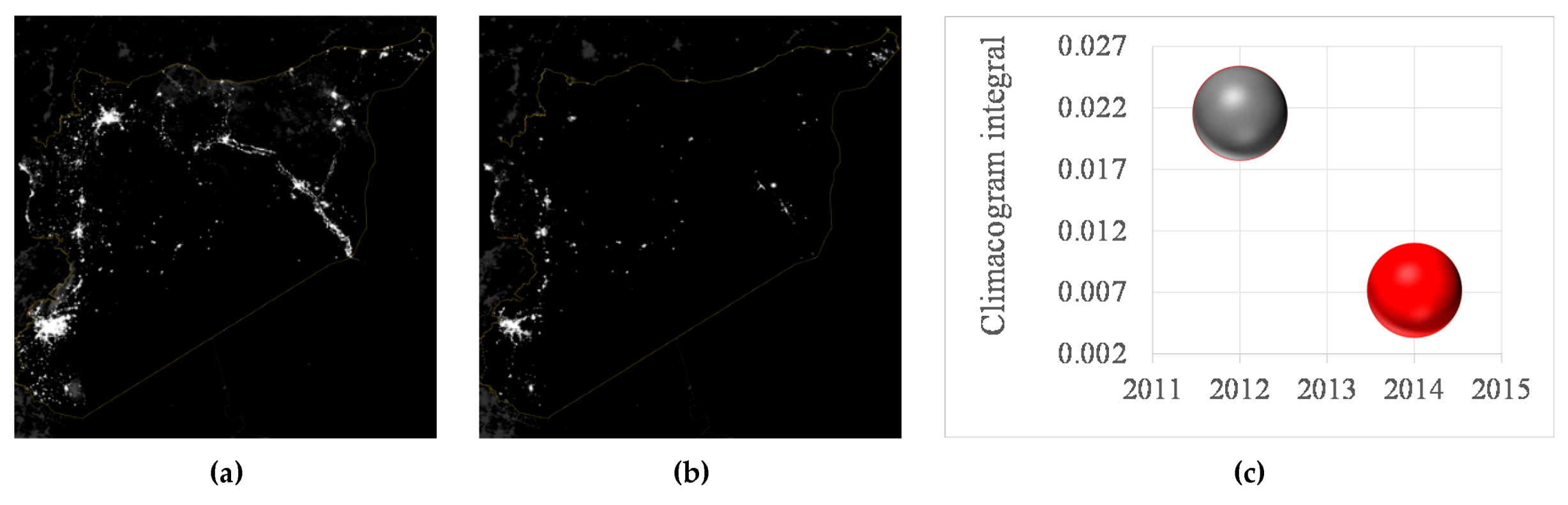
- Syria after Four Years of Mayhem. Available online: https://www.nytimes.com/interactive/2015/03/12/world/middleeast/syria-civil-war-after-four-years-map.html?mc_cid=bbef5eadb7&mc_eid=236cd449ae&_r=0 (accessed on 15 September 2020).
- Elvidge, C.; Baugh, K.; Kihn, E.; Kroehl, H.; Davis, E. Mapping city lights with nighttime data from the DMSP operational linescan system. Photogramm. Eng. Remote Sens. 1997, 63, 727–734. [Google Scholar]
- Chen, X.; Nordhaus, W. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef]
- Chand, T.; Badarinath, K.; Elvidge, C.; Tuttle, B. Spatial characterization of electrical power consumption patterns over India using temporal DMSP-OLS night-time satellite data. Int. J. Remote Sens. 2009, 30, 647–661. [Google Scholar] [CrossRef]
- Elvidge, C.; Sutton, P.; Ghosh, T.; Tuttle, B.; Baugh, K.; Bhaduri, B.; Bright, E. A global poverty map derived from satellite data. Comput. Geosci. 2009, 35, 1652–1660. [Google Scholar] [CrossRef]
- Ceola, S.; Laio, F.; Montanari, A. Satellite nighttime lights reveal increasing human exposure to floods worldwide. Geophys. Res. Lett. 2014, 41, 7184–7190. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations FAO, Land Use. Available online: http://faostat.fao.org/site/377/default.aspx#ancor (accessed on 15 September 2020).
- O’Sullivan, A.; Sheffrin, S.M. Economics: Principles in Action; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2013; p. 157. ISBN 978-0-13-063085-8. [Google Scholar]
- Manta, E.; Ioannidis, R.; Sargentis, G.-F.; Efstratiadis, A. Aesthetic evaluation of wind turbines in stochastic setting: Case study of Tinos island, Greece, Aesthetic evaluation of wind turbines in stochastic setting: Case study of Tinos island, Greece, European Geosciences Union General Assembly 2020. Geophys. Res. Abstr. 2020, 22. [Google Scholar] [CrossRef]
- Vickerman, R. Cost–Benefit Analysis and Large-Scale Infrastructure Projects: State of the Art and Challenges. Environ. Plan. B Plan. Des. 2007, 34, 598–610. [Google Scholar] [CrossRef]
- Jadhav, S.R.; Desai, D.B. A Review on Impact of Large Infrastructure Project on Local Economy. Int. Res. J. Eng. Technol. (IRJET) 2019, 6. Available online: https://www.irjet.net/archives/V6/i11/IRJET-V6I1183.pdf (accessed on 15 September 2020).
- Tribe, M.A.; Alpine, R.L.W. Scale Economies and the “0.6 RULE”, Engineering Costs and Production Economics; Elsevier Science Publisher: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Haldi, J.H. Economies of Scale in Economic Development. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1961. [Google Scholar]
- Wenban-Smith, H.B. Economies of Scale, Distribution Costs and Density Effects in Urban Water Supply: A Spatial Analysis of the Role of Infrastructure in Urban Agglomeration. PhD Thesis, The London School of Economics and Political Science (LSE), London, UK, 2009. [Google Scholar]
- North American Water and Power Alliance. Available online: https://en.wikipedia.org/wiki/North_American_Water_and_Power_Alliance (accessed on 15 September 2020).
- Nuclear Nawapa XXI Gateway to the Fusion Economy, 21st Century Science & Technology, Special Report. 2013. Available online: https://21sci-tech.com/Nuclear_NAWAPA_XXI/Nuclear_NAWAPA_sm.pdf (accessed on 15 September 2020).
- Tehri Dam. Available online: https://en.wikipedia.org/wiki/Tehri_Dam (accessed on 15 September 2020).
- Three Gorges Dam. Available online: https://en.wikipedia.org/wiki/Three_Gorges_Dam (accessed on 15 September 2020).
- Mohammed, G.S.; Toropov, V.V.; Gandomi, A.H. A Review on Traditional and Modern Structural Optimization: Problems and Techniques. In Special Issue: Metaheuristic Applications in Structures and Infrastructures; Elsevier: Amsterdam, The Netherlands, 2012; Available online: https://books.google.gr/books?id=fKKcI4uVTvcC&lpg=PP1&ots=2JHjMkQNdi&dq=optimum%20scale%20civil%20infrastructure&lr&pg=PR7#v=onepage&q=optimum%20scale%20civil%20infrastructure&f=false (accessed on 15 September 2020).
- Great Pyramid of Giza. Available online: https://en.wikipedia.org/wiki/Great_Pyramid_of_Giza (accessed on 15 September 2020).
- Notre-Dame de Paris. Available online: https://en.wikipedia.org/wiki/Notre-Dame_de_Paris (accessed on 15 September 2020).
- Eiffel Tower. Available online: https://en.wikipedia.org/wiki/Eiffel_Tower (accessed on 15 September 2020).
- Hobbes, T. Leviathan 1588–1679; Penguin Books: Baltimore, MD, USA, 1968. [Google Scholar]
- Aristoteles. Politica; Oxford Clarendon Press: Oxford, UK, 1957; Available online: https://books.google.gr/books/about/Aristotelis_Politica_recognovit_brevique.html?id=--LdnQEACAAJ&redir_esc=y (accessed on 15 September 2020).
- Aristotle, Politics, English Translation. Available online: https://www.loebclassics.com/view/aristotle-politics/1932/pb_LCL264.461.xml (accessed on 1 August 2020).
- India Environment Portal Knowledge for Change, Natural Disasters: Saving Lives Today, Building Resilience for Tomorrow. Available online: http://www.indiaenvironmentportal.org.in/content/383261/natural-disasters-saving-lives-today-building-resilience-for-tomorrow/ (accessed on 20 August 2020).
- India Environment Portal Knowledge for Change, Mind the Risk: A Global Ranking of Cities under Threat from Natural Disasters. Available online: http://www.indiaenvironmentportal.org.in/content/389862/mind-the-risk-a-global-ranking-of-cities-under-threat-from-natural-disasters/ (accessed on 20 August 2020).
- Hill, D. The City as Destructive System: Wildfires, Dresden and the Case against Urban Sprawl. Available online: https://www.cityofsound.com/blog/2007/10/the-city-as-des.html (accessed on 15 September 2020).
- At our Current Pace it’ll take 80 years to Repair all the Structurally Deficient Bridges in the US, A Report Finds. Available online: https://edition.cnn.com/2019/04/02/us/deficient-bridge-report-2019-trnd/index.html (accessed on 15 September 2020).
- Large Dams: Learning from the Past Looking at the Future, Part 166. Available online: https://books.google.gr/books?id=Ug2YrzNl8EUC&pg=PA33&lpg=PA33&dq=icald+big+dams&source=bl&ots=MeSqBoHIUU&sig=ACfU3U0L57Q-yhtNvFS78CXu5An_yuovIw&hl=en&sa=X&ved=2ahUKEwilr5PO6KPpAhVynVwKHdc9BGIQ6AEwAHoECAYQAQ#v=onepage&q=icald%20big%20dams&f=false (accessed on 15 September 2020).
- Genova, Crollo del Ponte Morandi sull’A10: Cosa è Successo. Available online: https://www.corriere.it/cronache/18_agosto_14/genova-crollo-ponte-morandi-sull-a10-cosa-sappiamo-finora-46d3d094-9fb5-11e8-9437-bcf7bbd7366b.shtml (accessed on 15 September 2020).
- Holy Bible, Old Testament, Genesis 11. Available online: http://www.apostoliki-diakonia.gr/bible/bible.asp?contents=old_testament/contents.asp&main=OldTes (accessed on 15 September 2020).
- Holy Bible, New Testament, 8:20-22. Available online: http://www.apostoliki-diakonia.gr/bible/bible.asp?contents=new_testament/contents.asp&main= (accessed on 15 September 2020).
- 21 Godina od NATO Agresije- „Nemilosrdnog anđela “nema Zaborava. Available online: https://pvportal.me/2020/03/15-godina-od-nato-agresije-nemilosrdnog-andela-nema-zaborava/ (accessed on 15 September 2020).
- September_11_Attacks. Available online: https://en.wikipedia.org/wiki/September_11_attacks (accessed on 15 September 2020).
- Nearly 3 Billion People around the Globe under COVID-19 Lockdowns-Today’s Coronavirus Updates. Available online: https://www.weforum.org/agenda/2020/03/todays-coronavirus-updates/ (accessed on 15 September 2020).
- Smith, M.F. Lucretius: On the Nature of Thing, Hackett Publishing Company, Inc. 2001. Available online: https://books.google.gr/books?id=iKdij3ErDnMC&printsec=frontcover&dq=lucretius+on+the+nature+of+things&hl=en&sa=X&ved=2ahUKEwjjhpiQ5uvrAhUqlIsKHQeUD5MQ6AEwAHoECAMQAg#v=onepage&q=lucretius%20on%20the%20nature%20of%20things&f=false (accessed on 15 September 2020).
- Why a Roman Philosopher’s Views on the Fear of Death Matter as Coronavirus Spreads. Available online: https://theconversation.com/why-a-roman-philosophers-views-on-the-fear-of-death-matter-as-coronavirus-spreads-132951 (accessed on 15 September 2020).
- Holbrook, C.; Sousa, P.; Hahn-Holbrook, J. Unconscious vigilance: Worldview defense without adaptations for terror, coalition, or uncertainty management. J. Personal. Soc. Psychol. 2011, 101, 451–466. [Google Scholar] [CrossRef]
- Xanthopoulos, T. Requiem with Crescendo, Homo Sapiens the Ultimate Genus of Human; National Technical University of Athens: Athens, Greece, 2020; Volume 1–3. [Google Scholar]
- A Thing Called Civilization. Available online: https://isi.org/intercollegiate-review/a-thing-called-civilization/ (accessed on 15 September 2020).
- Banuri, T. Editorial: The Future of Development. Development 2013, 56, 1–9. [Google Scholar] [CrossRef][Green Version]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sargentis, G.-F.; Iliopoulou, T.; Sigourou, S.; Dimitriadis, P.; Koutsoyiannis, D. Evolution of Clustering Quantified by a Stochastic Method—Case Studies on Natural and Human Social Structures. Sustainability 2020, 12, 7972. https://doi.org/10.3390/su12197972
Sargentis G-F, Iliopoulou T, Sigourou S, Dimitriadis P, Koutsoyiannis D. Evolution of Clustering Quantified by a Stochastic Method—Case Studies on Natural and Human Social Structures. Sustainability. 2020; 12(19):7972. https://doi.org/10.3390/su12197972
Chicago/Turabian StyleSargentis, G.-Fivos, Theano Iliopoulou, Stavroula Sigourou, Panayiotis Dimitriadis, and Demetris Koutsoyiannis. 2020. "Evolution of Clustering Quantified by a Stochastic Method—Case Studies on Natural and Human Social Structures" Sustainability 12, no. 19: 7972. https://doi.org/10.3390/su12197972
APA StyleSargentis, G.-F., Iliopoulou, T., Sigourou, S., Dimitriadis, P., & Koutsoyiannis, D. (2020). Evolution of Clustering Quantified by a Stochastic Method—Case Studies on Natural and Human Social Structures. Sustainability, 12(19), 7972. https://doi.org/10.3390/su12197972









