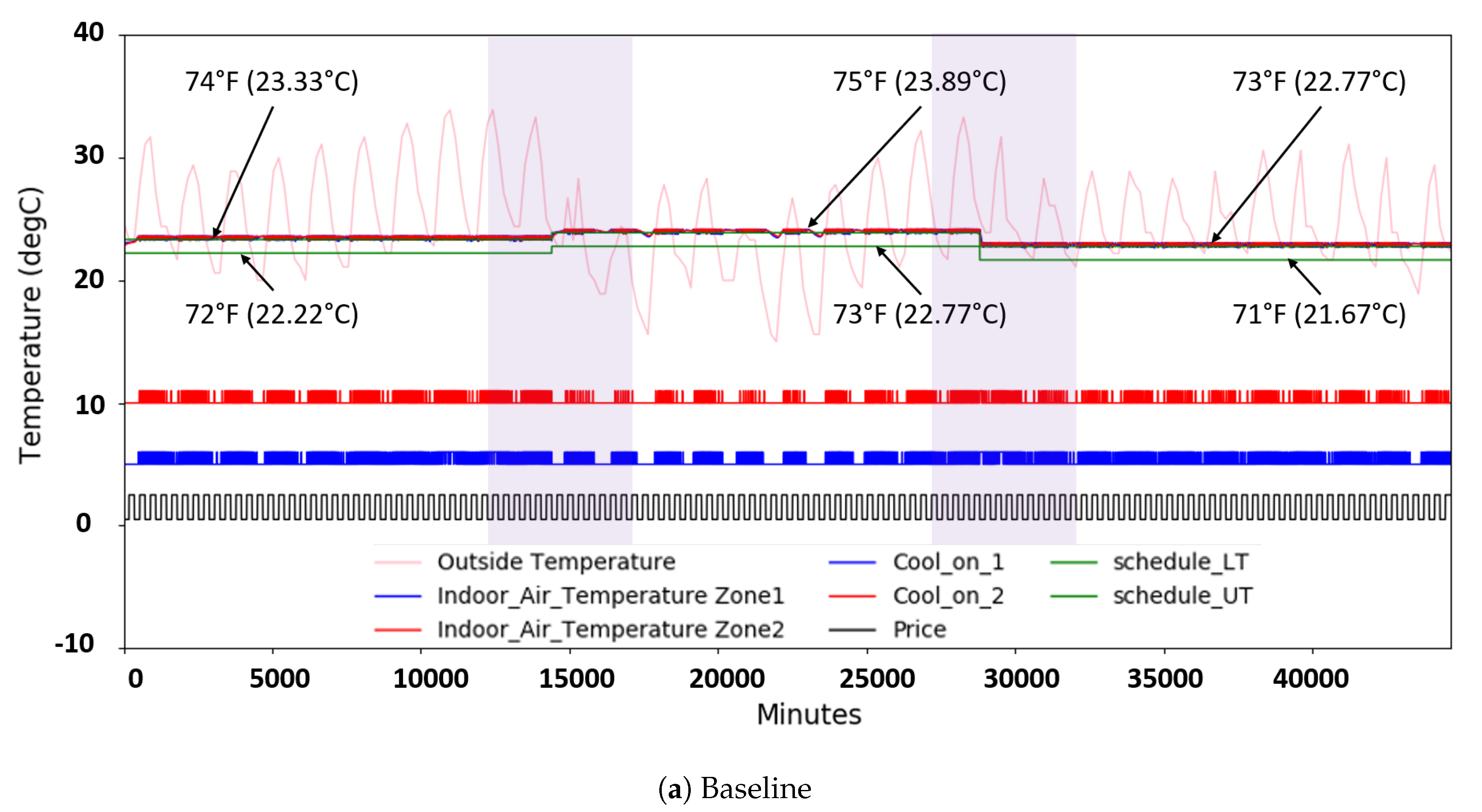
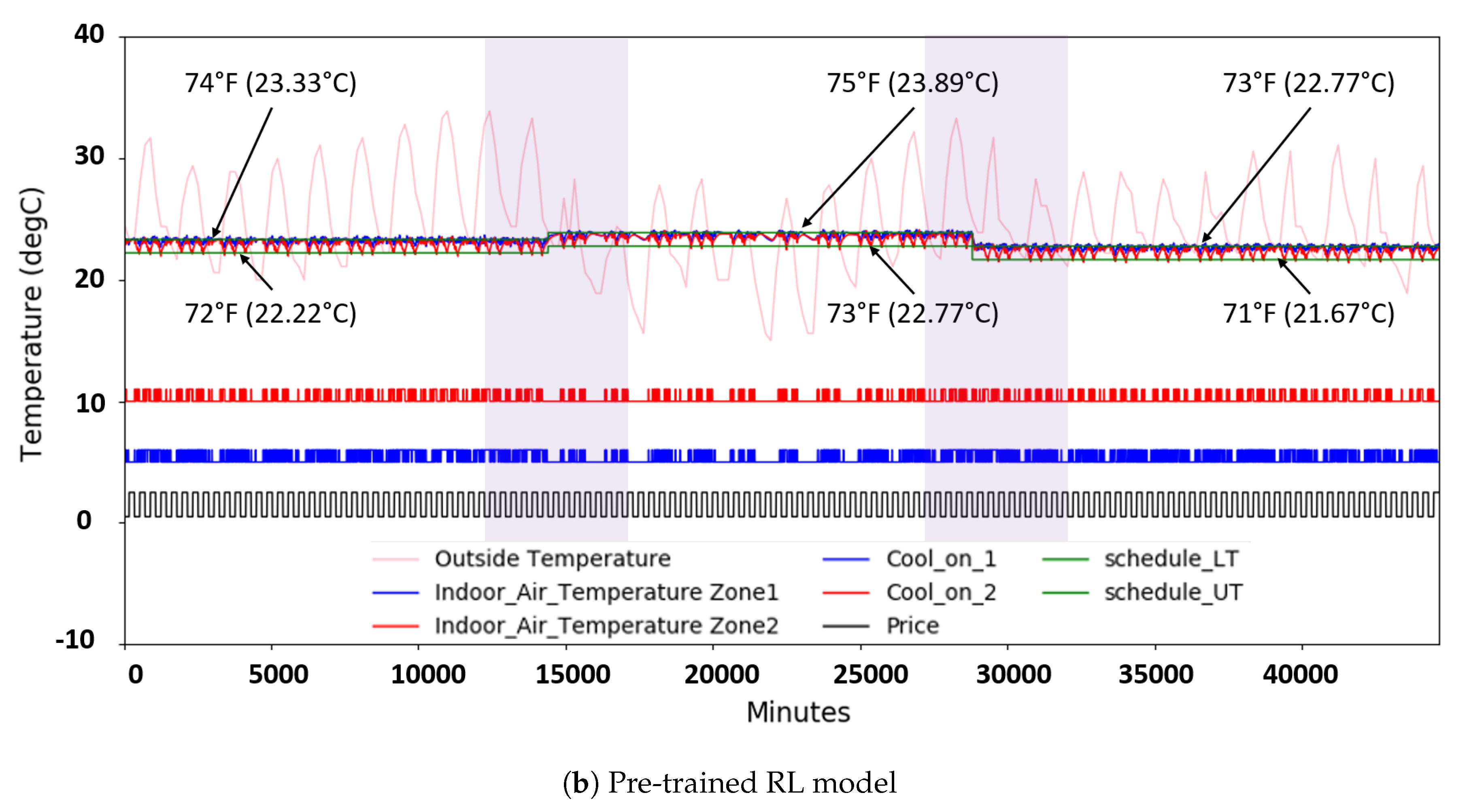
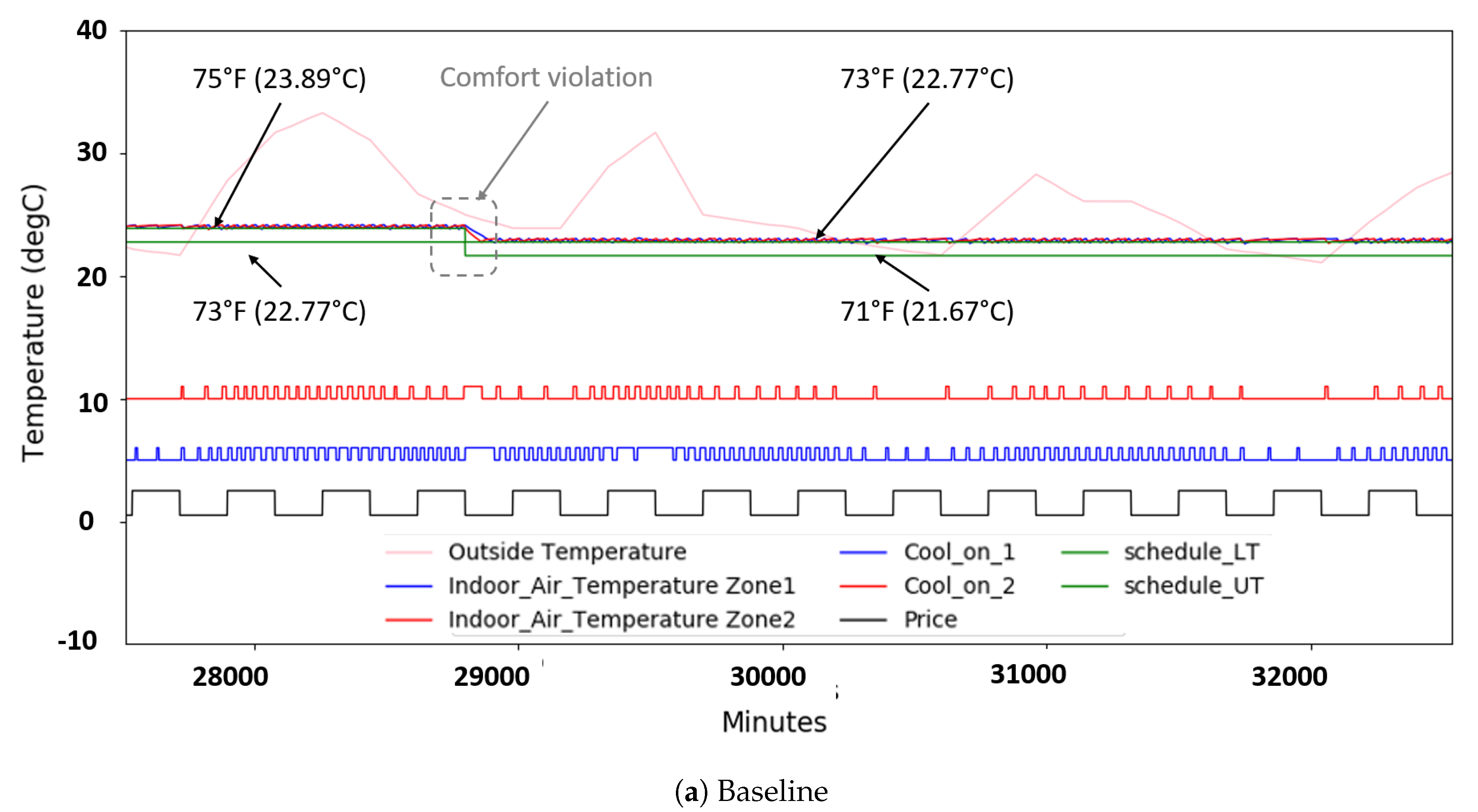
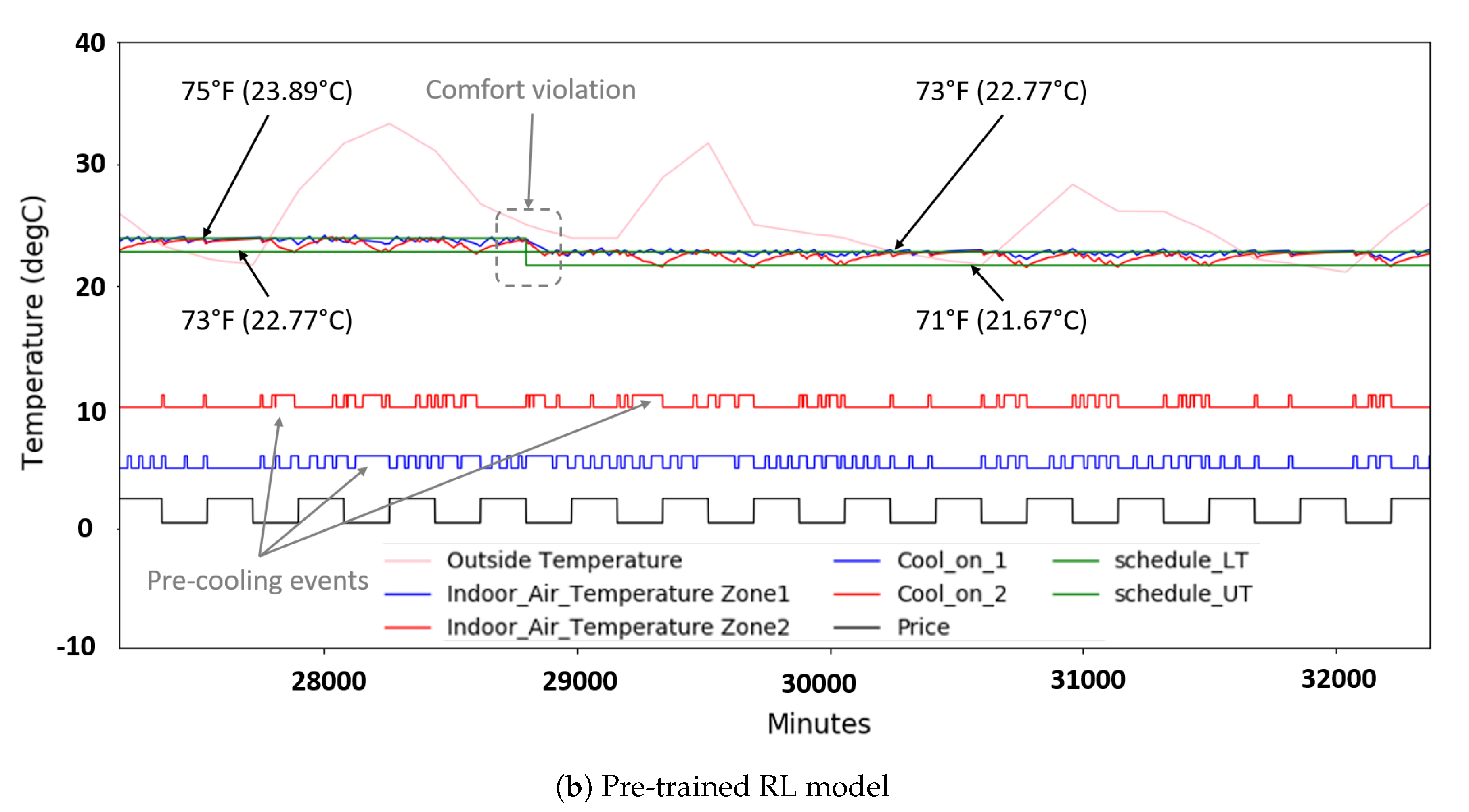
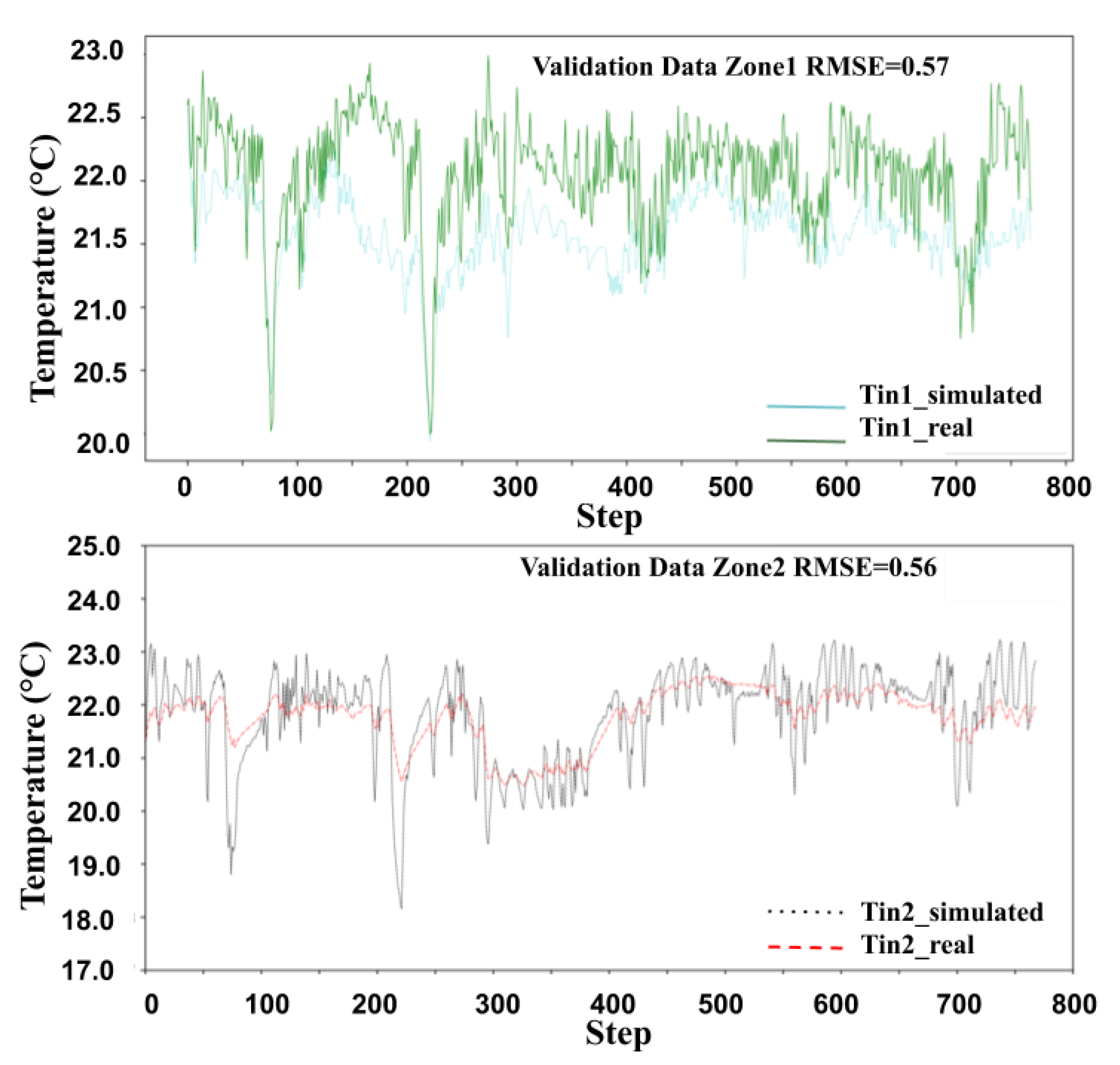
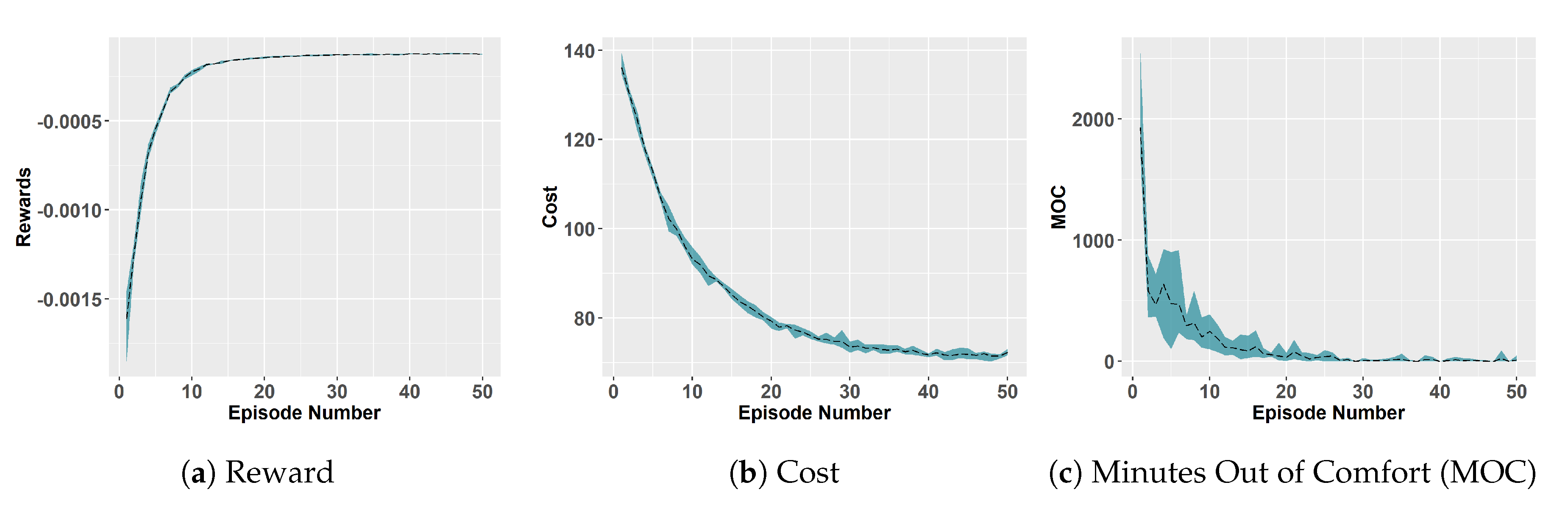
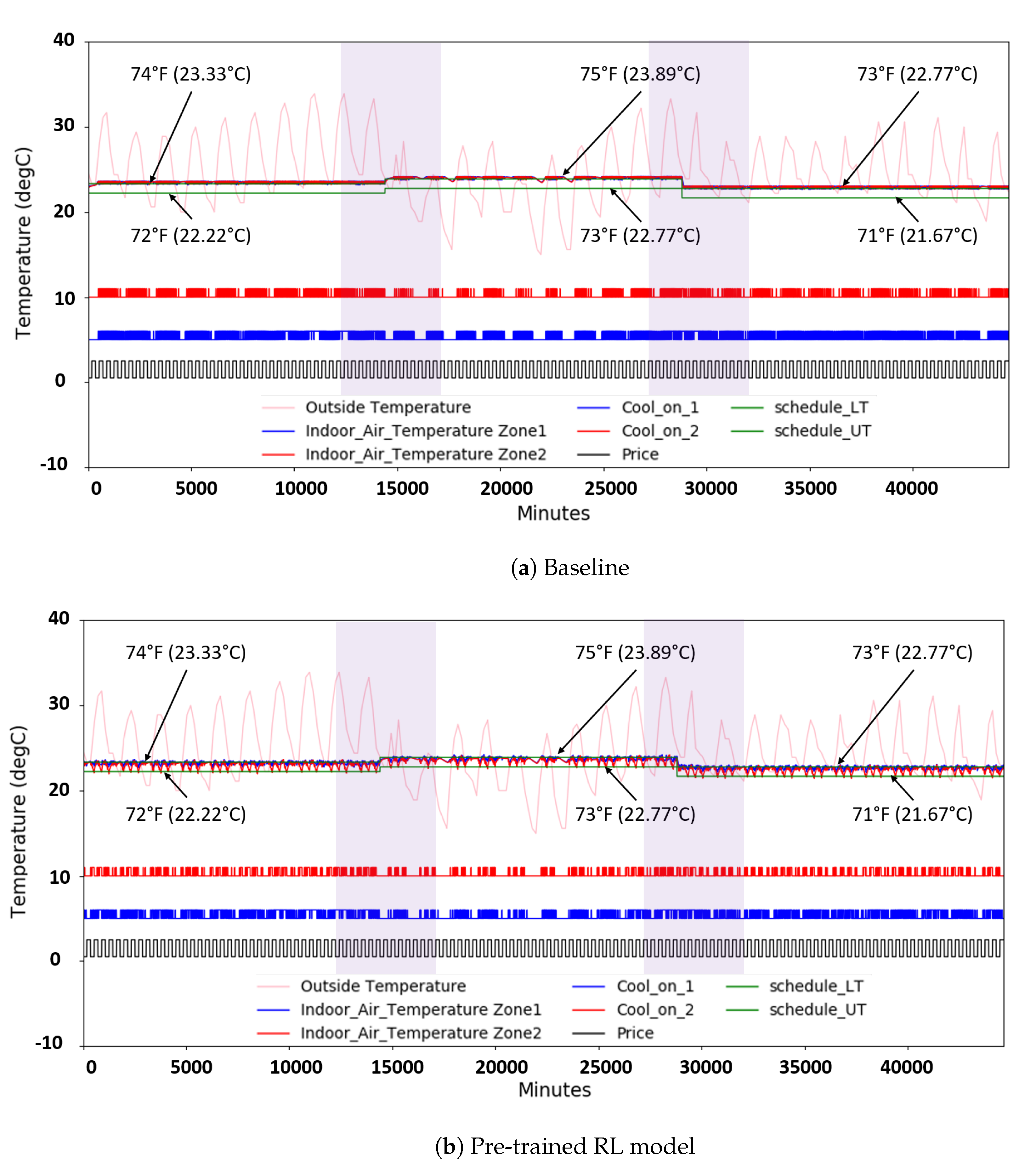
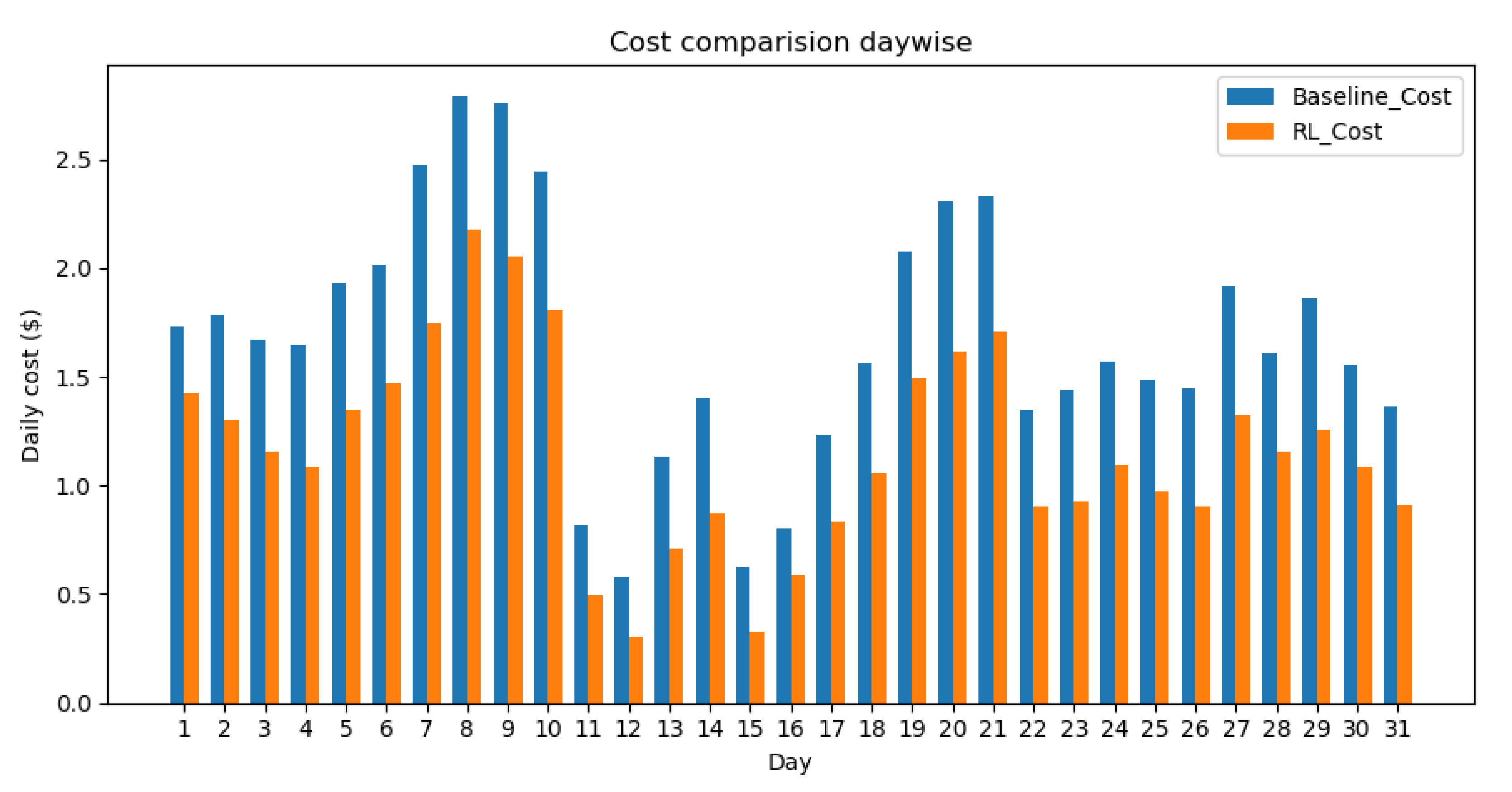
3.3. RL Model Development Based on DQN
In this work, we plan to deploy the DRL model for HVAC control during the summer 2020 season, i.e., HVAC will be in cooling mode only. The objective of the RL-based HVAC control is to learn optimal cooling policy (policy ) for HVAC to control the variations in the indoor temperature while maintaining the homeowner’s comfort and lower operational cost. We assume that the indoor temperature () at any time instant t is dependent on the indoor temperature (), outdoor temperature (), and the action taken () (i.e., set point in this case) at the time instant and formulate the HVAC control problem as a Markov Decision Process (MDP).
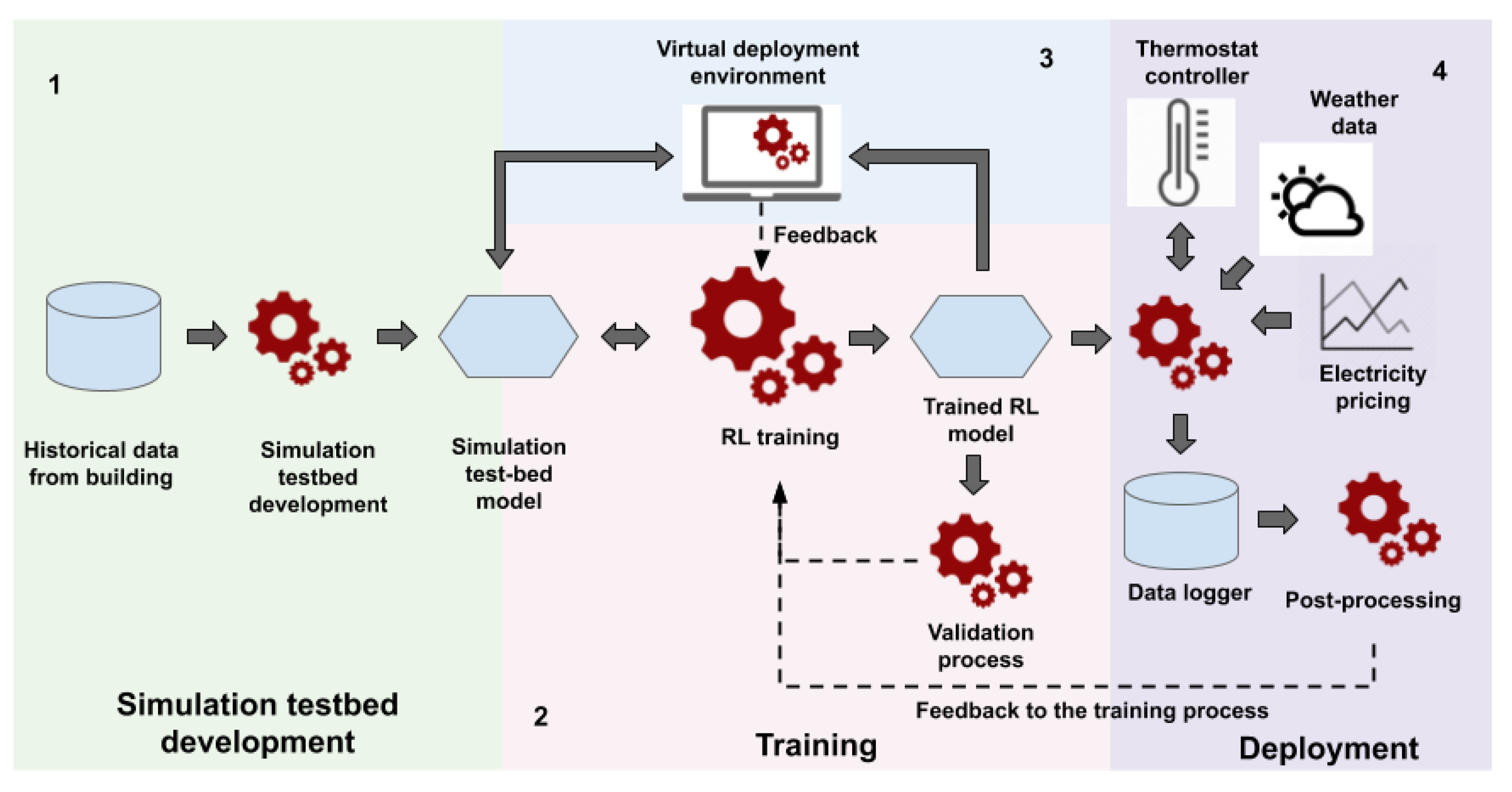
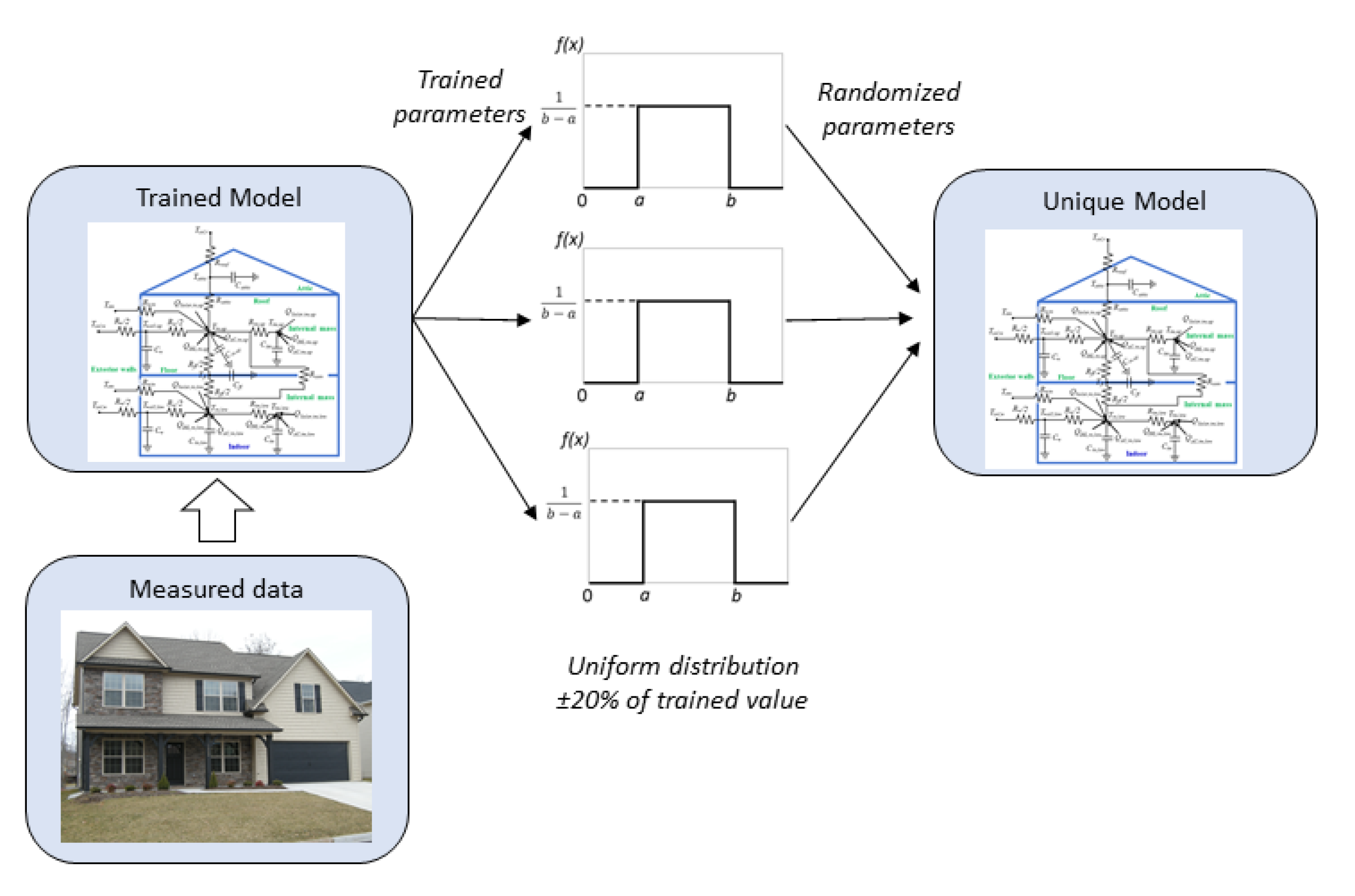
During offline training, i.e., in phase 2 (refer to
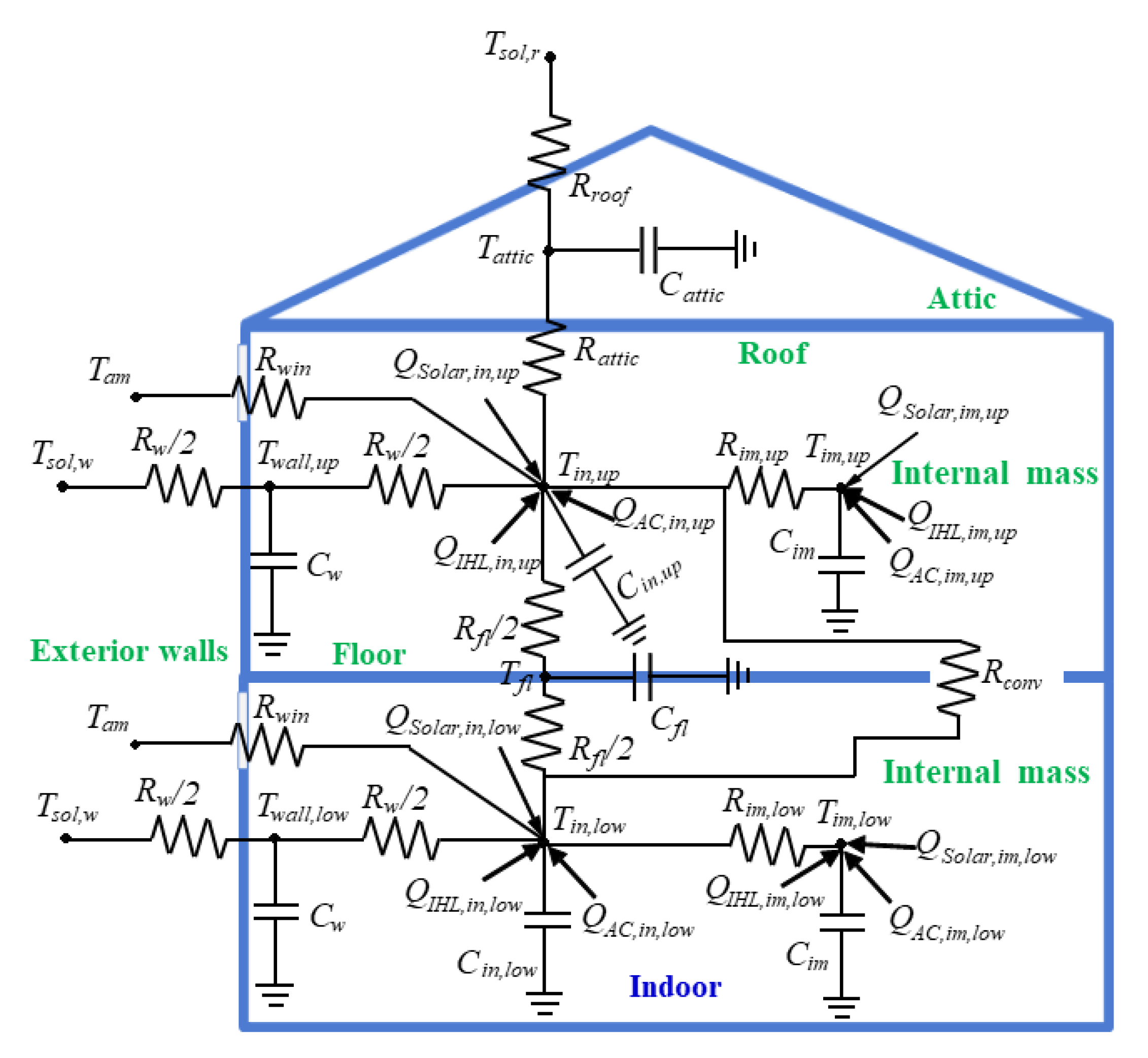
Figure 1), RL agent interacts with a building simulation model. We described the development of the building simulation model in
Section 3.1. We define two control steps (also described in the [
18]): (1) simulation step (
) and (2) control step (
). The building simulation model simulates building’s thermal behavior for every minute, i.e.,
min. The RL agent interacts with the building simulation at every
time steps (
), observes the indoor environment, and takes appropriate action. The observations about the building’s indoor environment are modeled as a state (
S) in the MDP formulation. For instance, a set of observations on the building’s indoor environment at a time instant
t such as indoor temperatures and other factors such as electricity prices forms the current state of the building’s environment, i.e.,
. In our case, it includes time of the day information (
t), indoor temperature (
), outdoor temperature (
), and a look-ahead of electricity pricing (
). Thus, the current state
is defined as
. Similarly, the state at the previous control step is defined as
.
In this work, we used a deep Q-learning approach mentioned in [
18,
24] and utilized a deep Q-network (DQN), a neural network, as a function approximator. We built upon our previous work on DQN-based HVAC control for a single-zone house [
30] and developed a DQN architecture for a two-zone house. There are two thermostats in the house, one for each zone, and capable of taking set point values through APIs. Since Q-learning works well for finite and discrete action space, we train DQN for ON = 1/OFF = 0 actions for both the zones and further translate the ON/OFF actions to the appropriate set point values using Equation (
1), where
is the small decrement factor (in case the action is ON) and increment factor (in case the action is OFF). The action = ON (‘1’) signifies the status ON for the AC, which will reduce the indoor temperature. To achieve this, we decrease the setpoint by a factor of
than the current indoor temperature. In the similar fashion, the action = OFF (‘0’) signifies the RL’s intention on increasing the indoor temperature by a small amount (i.e.,
) by turning OFF the AC. As there are two zones and two possible AC states (ON/OFF), there are total four possible actions
, where
indicates OFF status for AC in both the zones which will be translated further by setting the higher set point than the current indoor temperature. The other actions can be explained in the same way as shown in
Table 1.
As discussed in the earlier paragraph, during offline training, RL agent interacts with the building simulation at every
control interval, observes the indoor environment, and receives reward (
) as an incentive for taking the previous action, i.e.,
. This reward is designed as a function consisting of two parts, (1) cost of performing action, i.e.,
and (2) comfort penalty. Equation (
2) shows the reward function used in this work; it is inspired from the reward function used in the work by Wei et al. [
18]. This is a negative reward function in which the reward value close to zero signifies better performance, i.e., less penalty and more negative values signifies poor action, i.e., more penalty. The first term in Equation (
2) is the cost incurred due to the action taken by RL agent at time
. This cost is calculated as an average over the time duration
. The second term of the equation represents the average comfort violation over the time duration
. Here,
represents the cooling set point and
is some lower temperature value such that
represents a flexibility range of temperature below the cooling set point. The RL agent would make use of this flexible temperature band to save on some costs by taking optimal actions such that the indoor temperature will always remain below the cooling set point, i.e., the homeowner’s comfort. We can provide similar arguments while the RL agent operates in the heating mode. In that case, the heating set point is used to define the
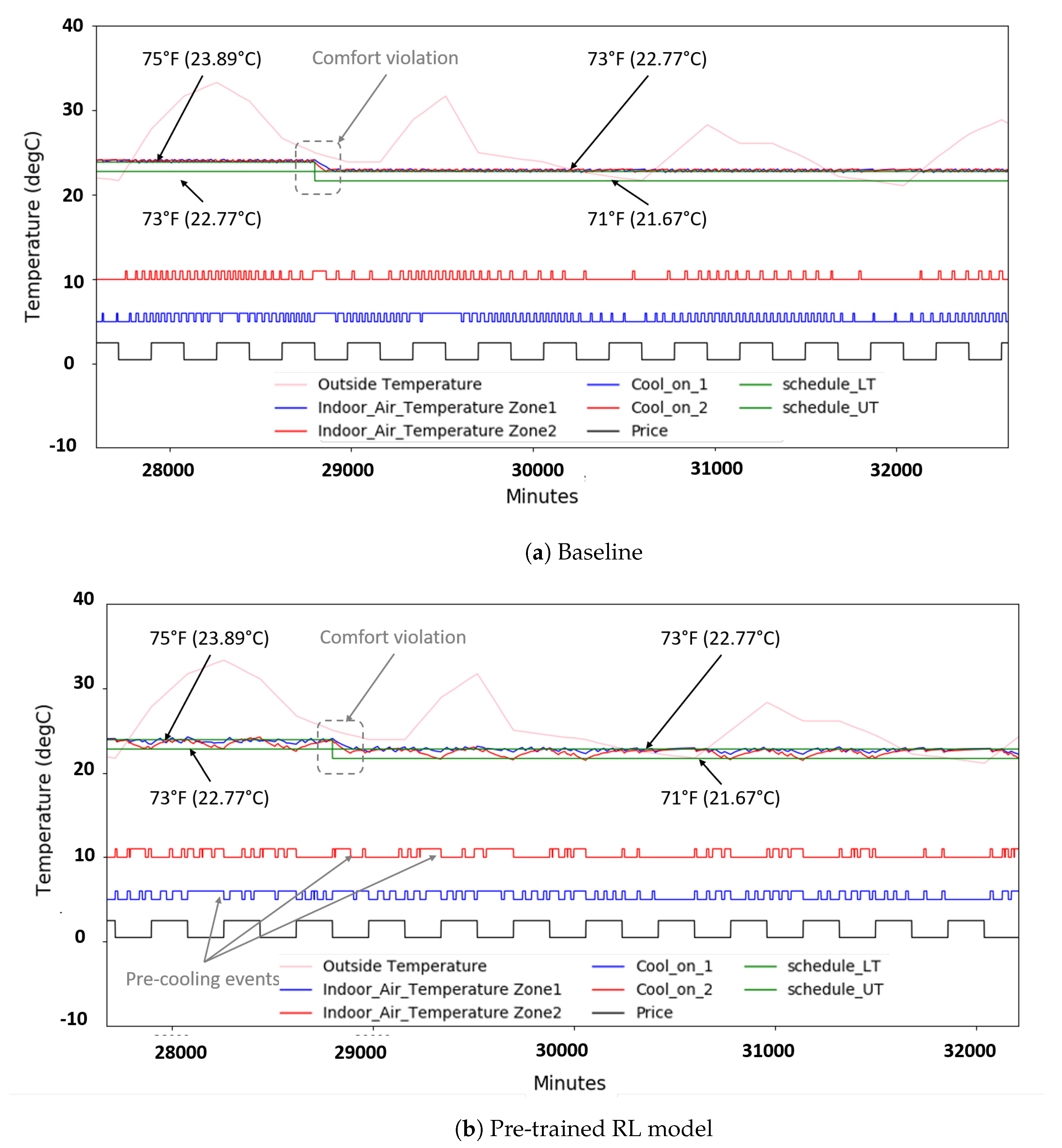
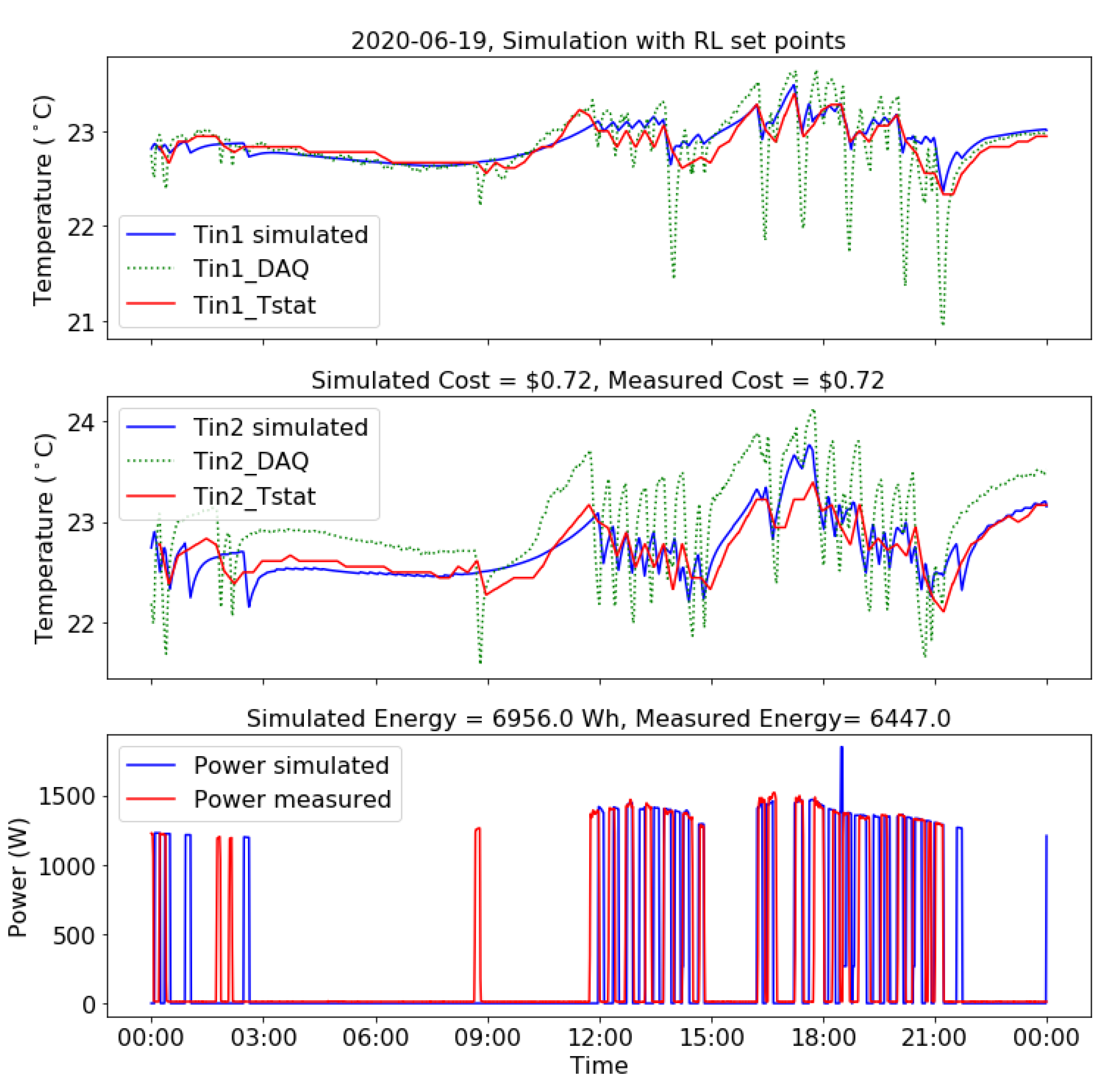
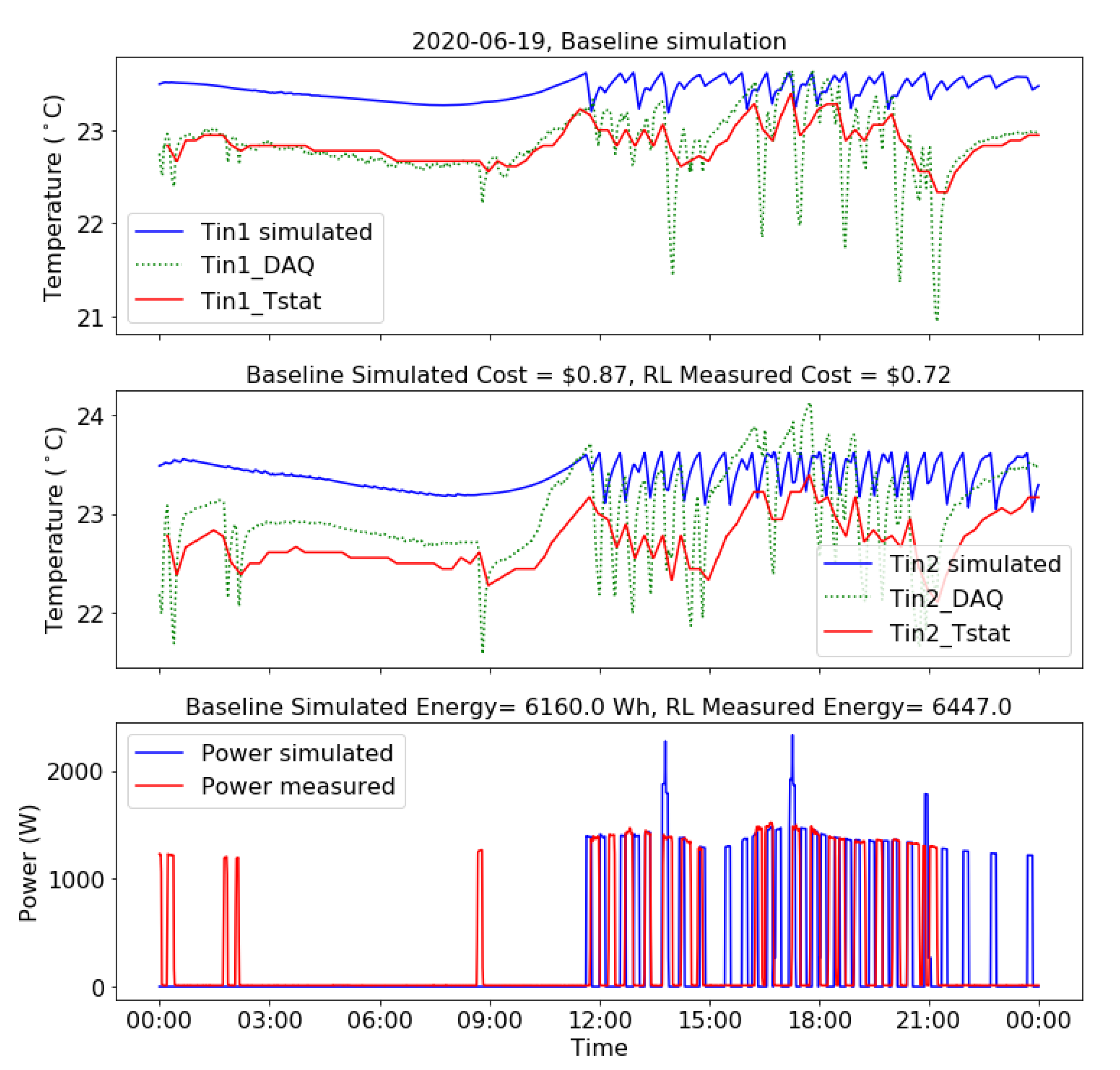
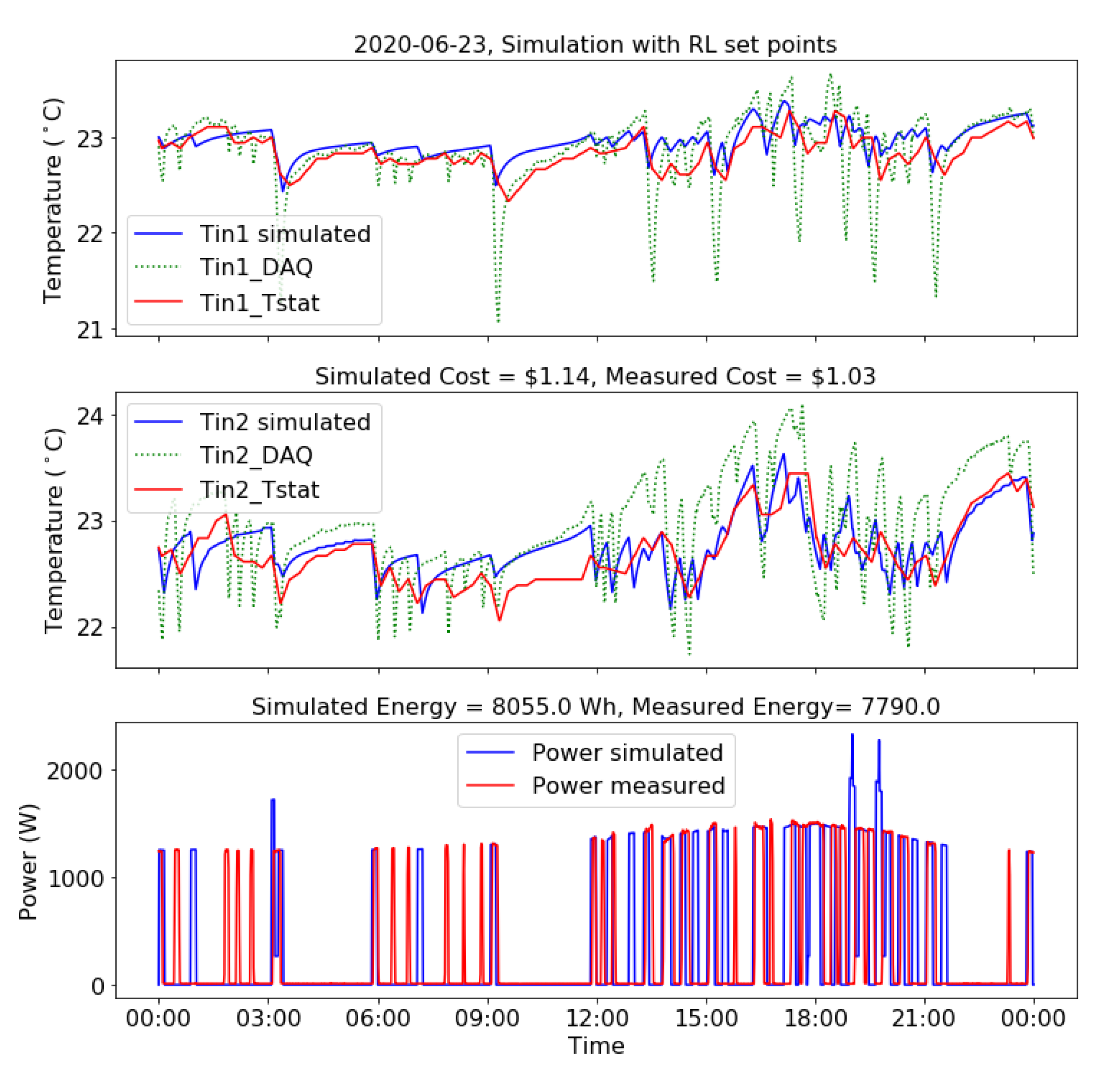
flexibility band of temperature. In this work, we used 68 °F and 74 °F as heating and cooling set points, respectively:
The goal of our RL agent is to learn a policy which will minimize the cost of operation and incur less or no comfort violation. More specifically, under MDP formulation, the RL agent should learn the policy (i.e., action) which will maximize not only the current reward, but also future rewards. This is represented as the total discounted accumulated reward in Equation (
3) [
24]. The
is a discount factor whose value ranges from
that controls the weights of the future rewards, and
T represents the time step when episode ends. The
considers only the current reward and does not take the future rewards into account. This is characterized as an RL agent being “short-sighted” by not accounting for the future benefits (rewards) and may not achieve the optimum solution. The rationale behind using future rewards is that sometimes the current low rewarded state could lead the RL agent to the high rewarded states in the future. In this work, we chose
, which exponentially decreases the weights of the future rewards. In other words, the current reward would still get higher weight and the exponentially discounted futures rewards are taken into account as well. The higher the
value, the better the RL’s ability to account for the future rewards and obtain the optimal solution. The lower
value reduces RL’s ability to look into the future rewards which may not lead to the optimal solution.
In case of Q-learning, RL tries to learn an optimal action-value function
which maximizes the expected future rewards (represented by Equation (
3)) for action taken
in the state
by following policy
i.e.,
[
24]. This can be defined as a recursive function using Bellman’s equation as shown in Equation (4) [
18]. The Q-learning RL algorithm estimates this optimal action-value function via iterative updates for a large number of iterations using Equation (5), where
represents a learning rate with the range of
. For a large number of iterations and under an MDP environment, Equation (5) converges to the optimal
over time [
18,
24]:
The iterative Q-learning strategy of Equation (5) uses a tabular method to store state-action Q values. This method works well with the discrete state-action space and quickly becomes intractable for a large state-action space. For instance, in our case, the indoor temperature and outdoor temperature are the continuous quantities that make infinite state-action space. This is where DQN is useful that uses a neural network as a functional approximator to approximate the state-action value
. Algorithm 1 represents the deep Q-learning procedure used in this work, which is inspired from Wei et al. [
18] and Mnih et al. [
24]. This approach uses the DQN neural network structure as shown in
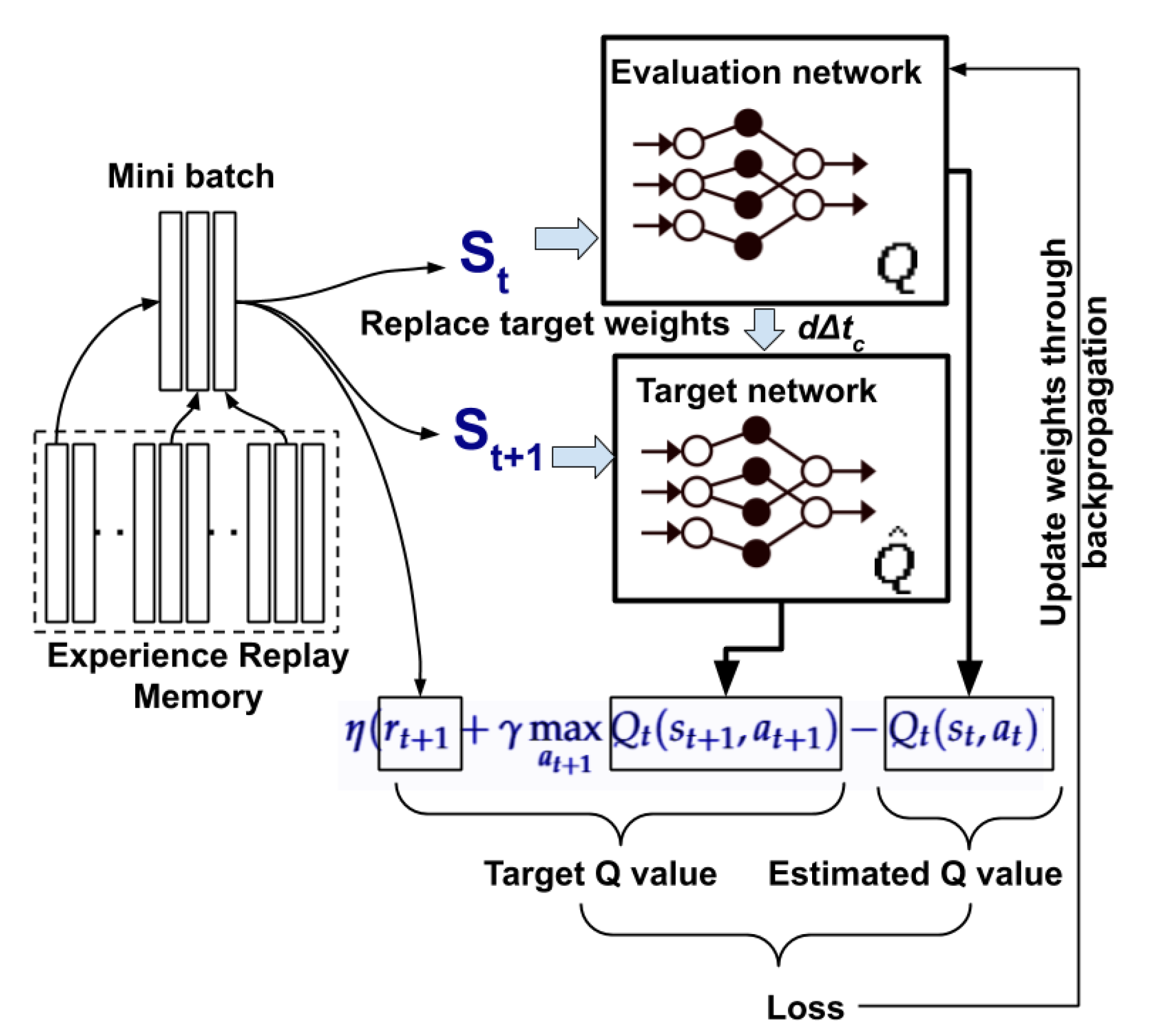
Figure 5. Mnih et al. [
24] implemented a Q-learning strategy using deep Q-networks (DQN), that uses two neural networks and experience replay. The first network
Q is called the “evaluation network”, and the second network
is called a “target network” (refer to
Figure 5). Equation (5) needs two
Q values to be computed. The first is
: the Q-value of the action
in the current state
, and the second is
: to calculate the maximum of the Q-values of the next state
. The evaluation network (
Q) is used to evaluate
using one forward pass with
as an input. The term “(
” represents a “target” Q-value that RL-agent should learn. If we use the same network to compute both Q-values i.e.,
and
makes the target unstable due the frequent updates made in the evaluation network. To avoid this, Mnih et al. suggested using two separate neural networks such that the evaluation network performs frequent updates in the network and copies updated weights to the target network after certain updates. Thus, the target network updates itself slowly compared to the evaluation network, which improves the stability of the learning process.
The training starts by initializing weights of both the networks (i.e.,
Q and
) randomly, reserving the experience replay buffer (
) and initializing other necessary variables (lines 1–12 in Algorithm 1). We train the RL agent for multiple episodes where each episode consists of multiple training days (e.g., two months of summer). In the beginning of each episode, we reset the building environment of the simulator, get the initial observation (
) from the building environment, and randomly choose some initial action (refer to lines 15–18 in Algorithm 1). The lines 19–38 of the algorithm represent a loop where the building simulation model simulates the thermal behavior of the building at each
time step. If the current time step
is a control step, i.e.,
, then we fetch the current state of the building’s indoor environment (
) and calculate the reward (
r) as a response of the action taken at the previous control step (refer to lines 21–22 in Algorithm 1). Furthermore, we store the tuple
to the experience replay memory (
) (refer line 23). Next, a mini-batch of tuples is randomly chosen from this replay memory and used for the mini-batch update (described on lines 24–25 of Algorithm 1), and if it’s time to update the target network, then copy the weights of the evaluation network to the target network (refer to line 26). Lines 26–32 choose action using a decaying
-greedy strategy. In the beginning, the RL agent explores random actions with high probability (line 28), whereas, as training progresses, the probability of exploitation increases, and the RL-agent uses the learned actions more than choosing random actions (line 30). Line 36 continues executing the earlier action if the current time step is not a control step.
| Algorithm 1 Neural network-based Q-learning. |
- 1:
Env ← Setup simulated building environment - 2:
MB ← Experience Replay Buffer - 3:
Δts ← Simulation time step (here, 1 min) - 4:
Δtc ← k × Δts RL’s control step interval (here, k = 15) - 5:
NDays ← Number of operating days for training - 6:
Nepisodes ← Number of training episodes - 7:
TSmax ← NDays × 24 × (60/Δts) - 8:
nbatch ← minibatchsize - 9:
ϵ ← initial exploration rate - 10:
Δϵ ← exploration rate decay - 11:
Q(s, a; θ)←Initialize(Q, θ) - 12:
← Initialize() - 13:
- 14:
forepisode = 1 to Nepisodes do - 15:
Env← ResetBuildingSimulation(Env) - 16:
Spre ← ObserveBuildingState(Env, 0)
- 17:
a ← GetInitialAction(Env) - 18:
Set points ← ConvertActionToSetpoints(Spre, a) - 19:
for ts = 1 to TSmax do - 20:
if ts mod Δtc = 0 then - 21:
Scurr ← ObserveBuildingState(Env, ts)
- 22:
r ← CalReward(Env, Spre, a, Scurr)
- 23:
AppendTransition(MB, 〈Spre, a, r, Scurr〉) - 24:
[T] ← DrawRandomMiniBatch(MB, nbatch) - 25:
TrainQNetwork(Q(·;θ),[T]) - 26:
if time to update target: - 27:
if GenerateRandomNumber([0, 1]) < ϵ then - 28:
a ← ChooseRandomAction([a0, a1, a2, a3]) - 29:
else - 30:
- 31:
end if - 32:
- 33:
Setpoints ← ConvertActionToSetpoints(Scurr, a) - 34:
Spre ← Scurr - 35:
end if - 36:
SimulateBuilding(Env, ts, Setpoints) - 37:
end for - 38:
end for
|