Study on Evolutionary Characteristics of Toppling Deformation of Anti-Dip Bank Slope Based on Energy Field
Abstract
1. Introduction
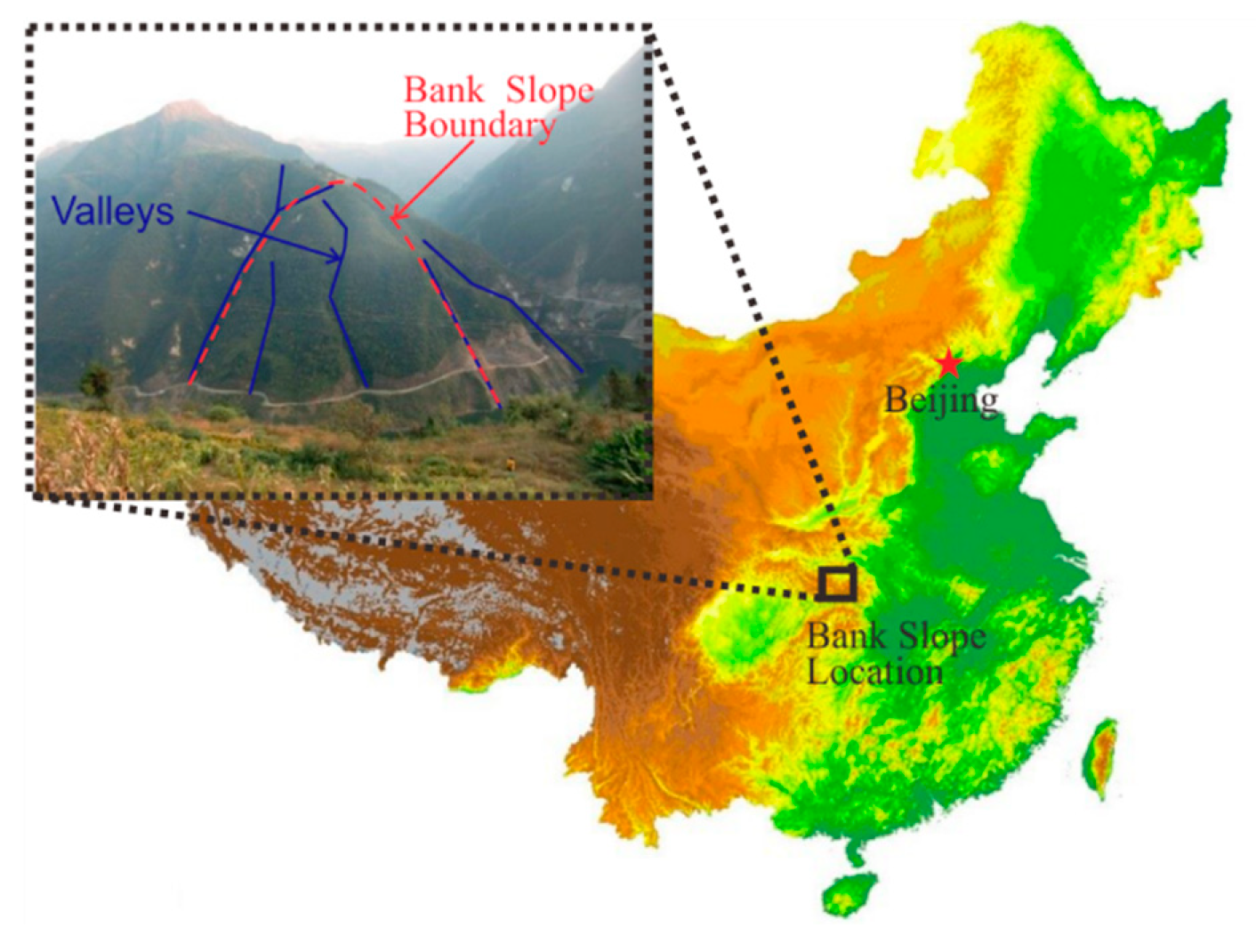
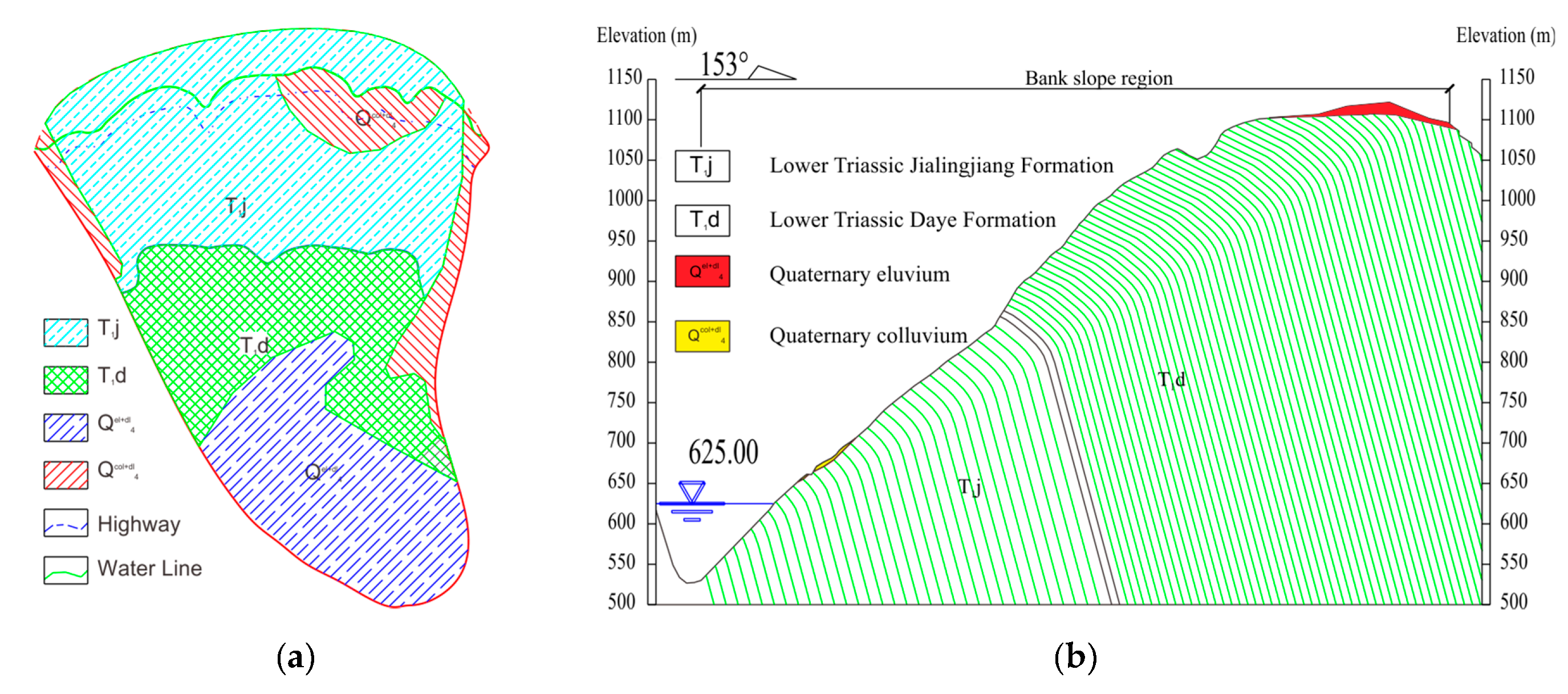
2. Geological Background of the Bank Slope
2.1. Engineering Overview
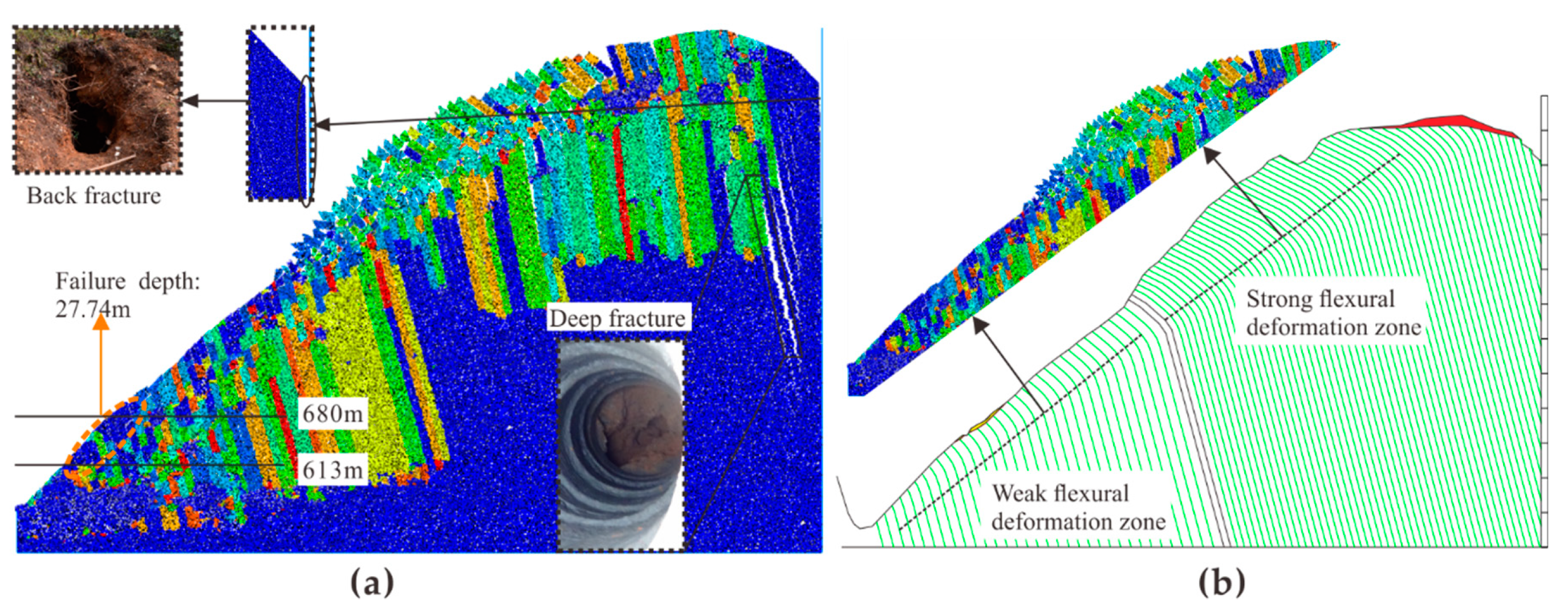
2.2. Regionalization of Surface Deformation of the Bank Slope
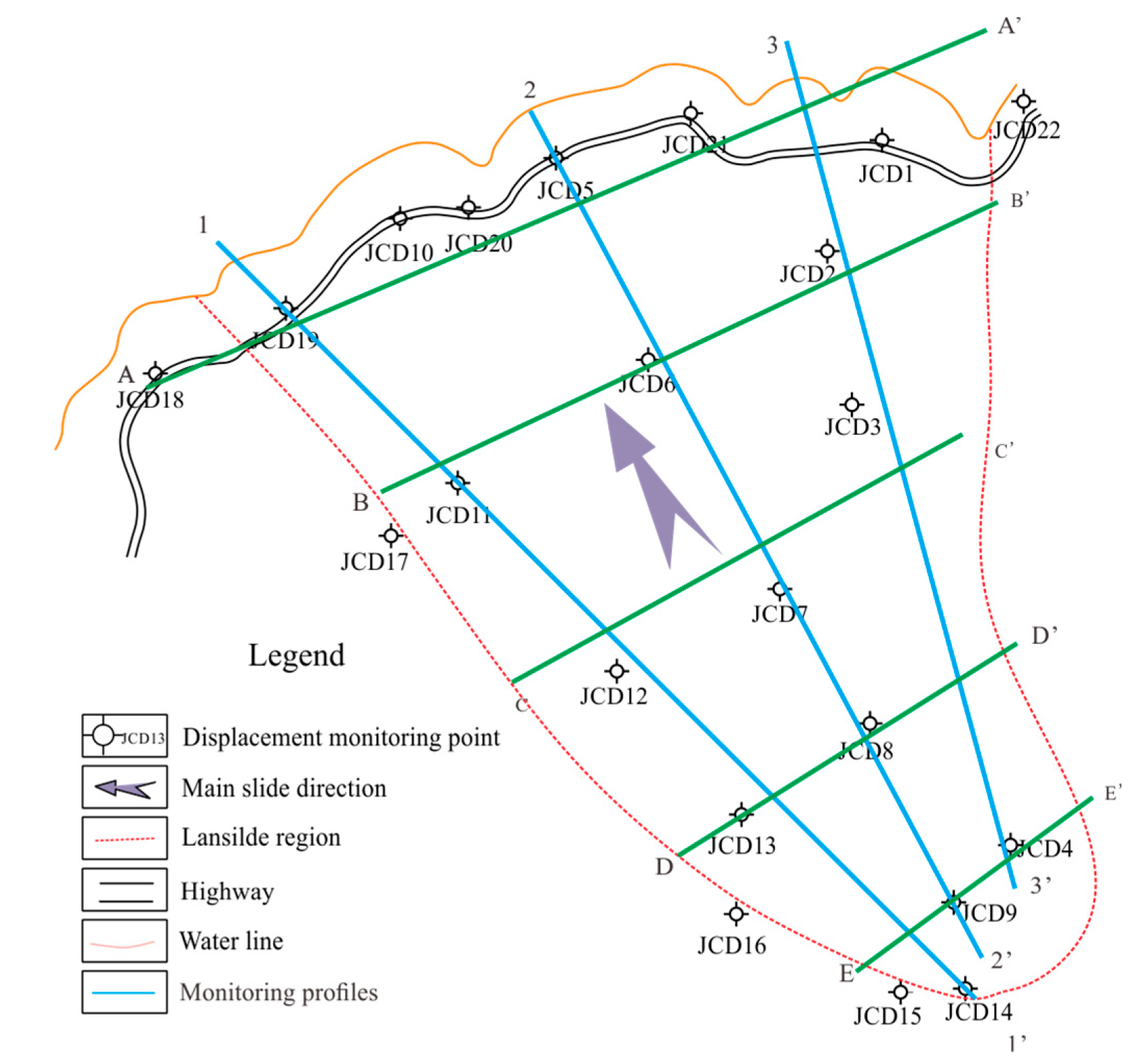
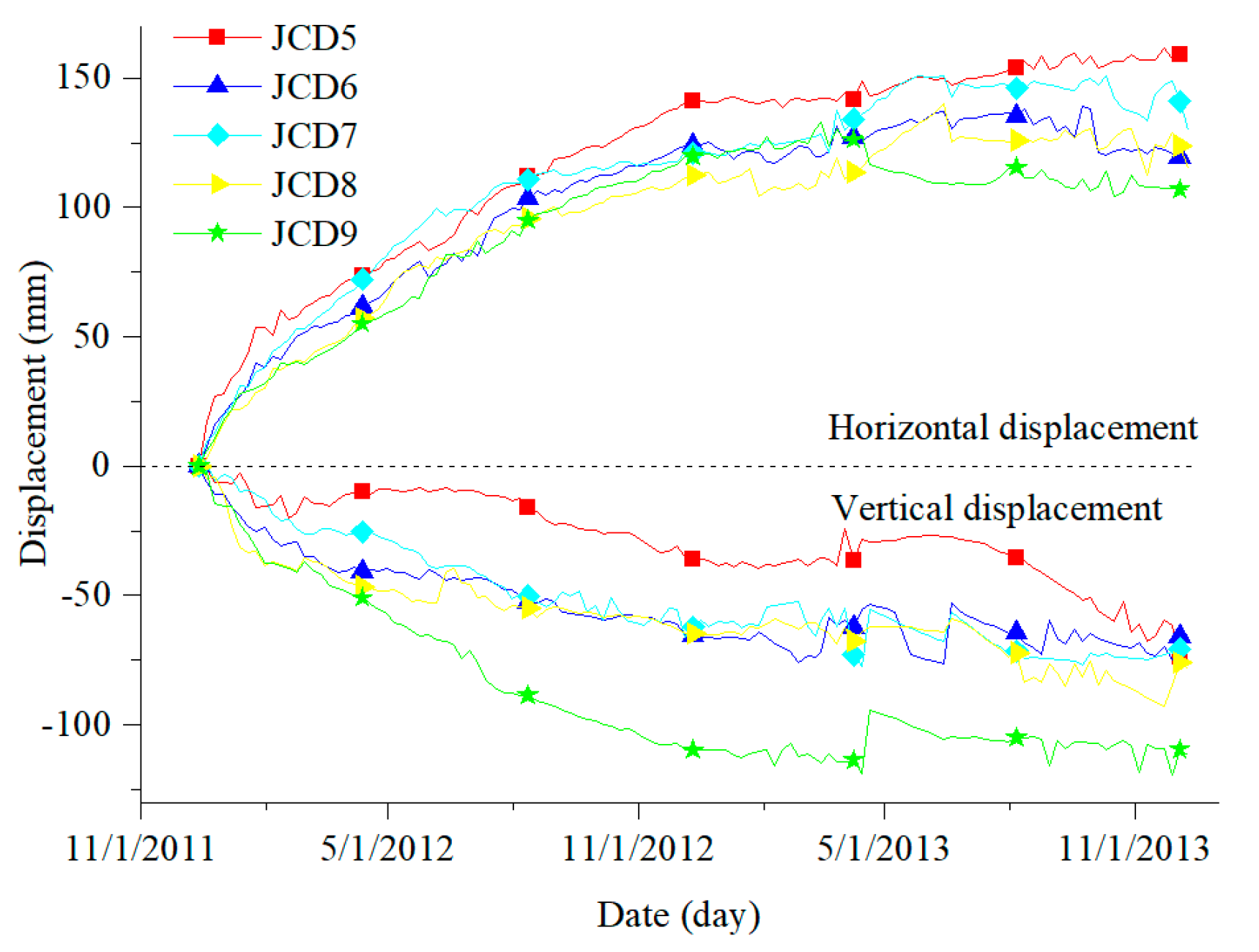
2.3. Monitoring System
3. Establishing Engineering Geological Model for Bank Slope
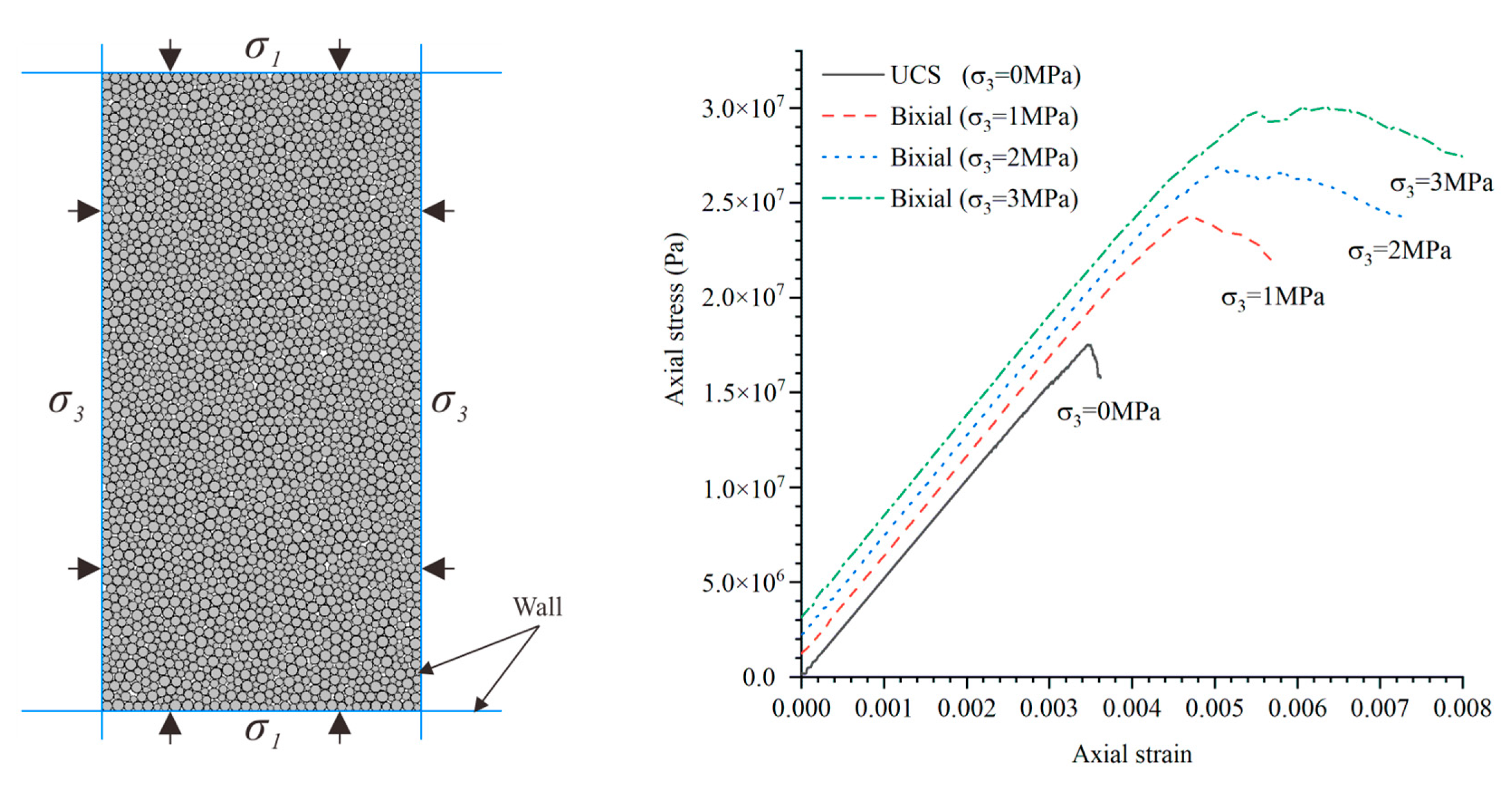
3.1. Parameter Calibration
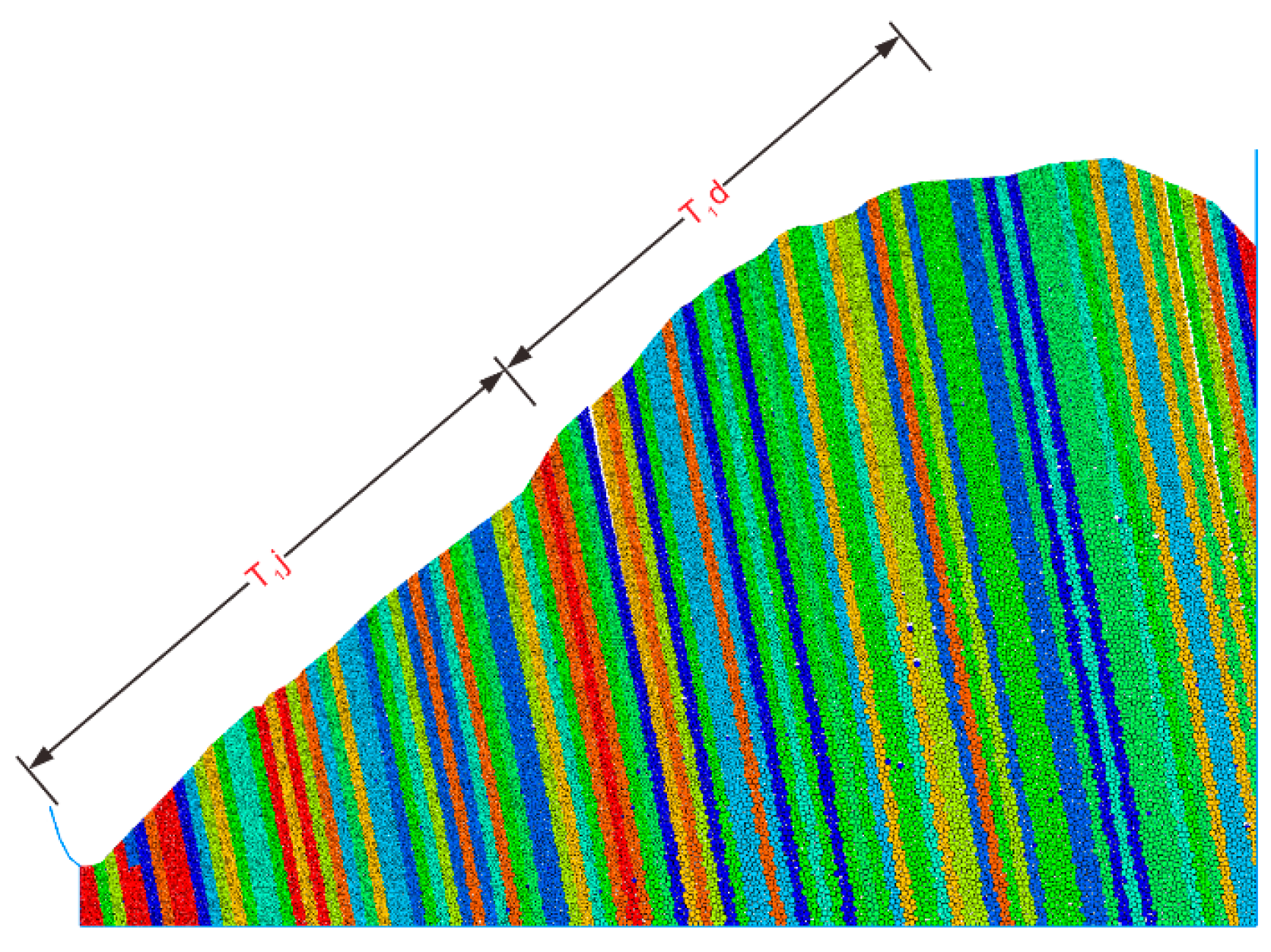
3.2. Model Introduction and Arrangement of Monitoring Points
3.3. Model Verification
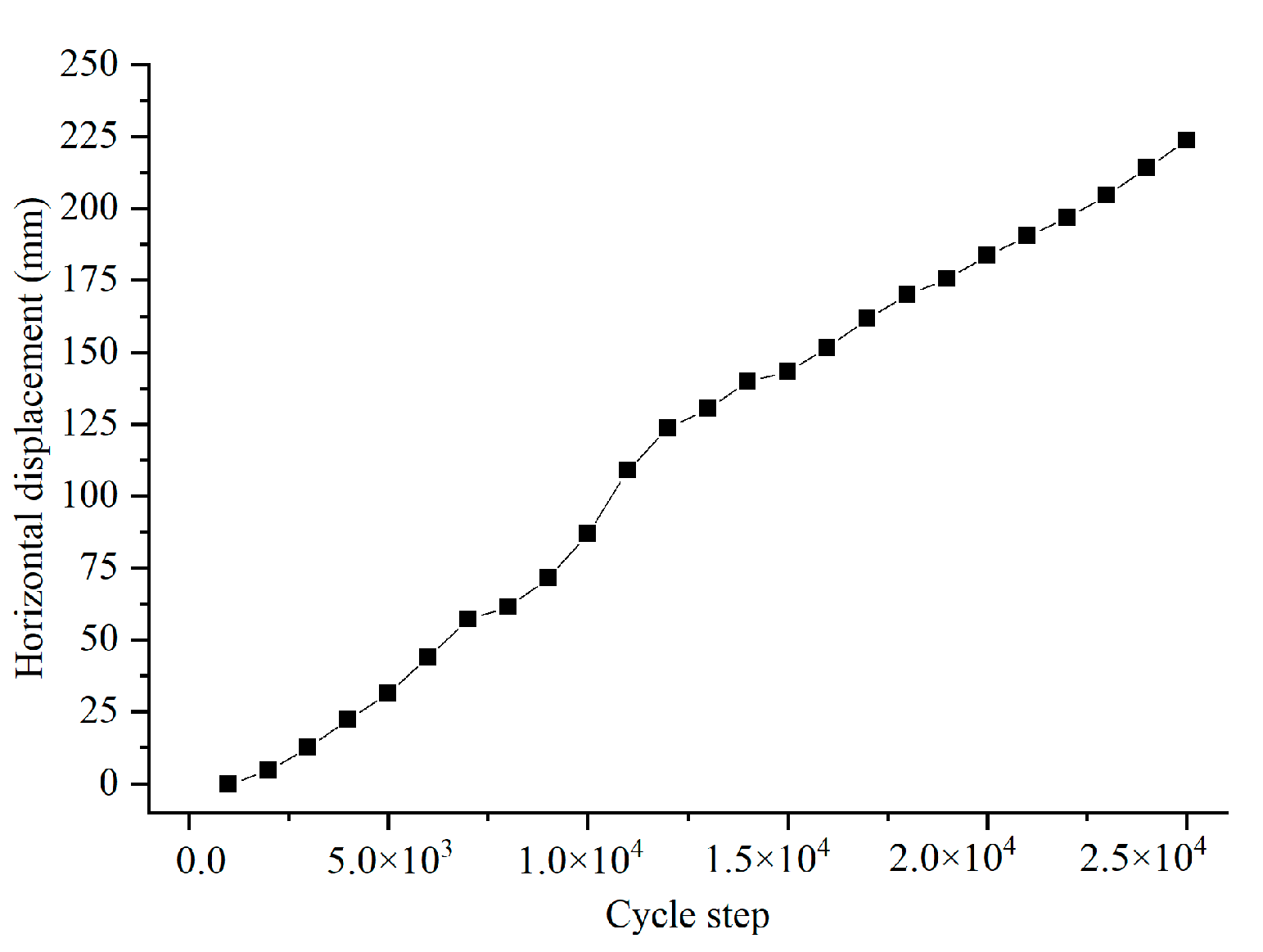
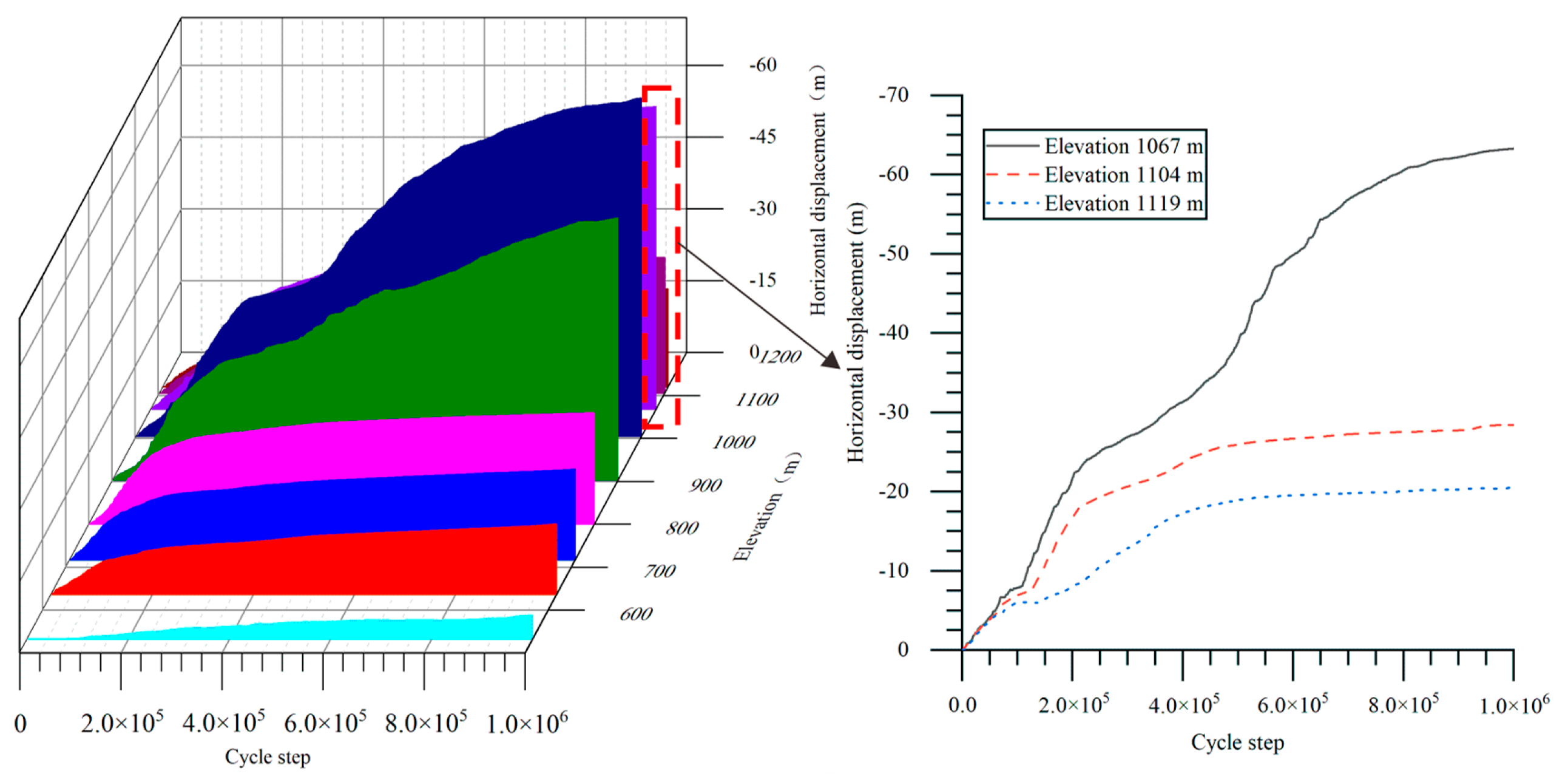
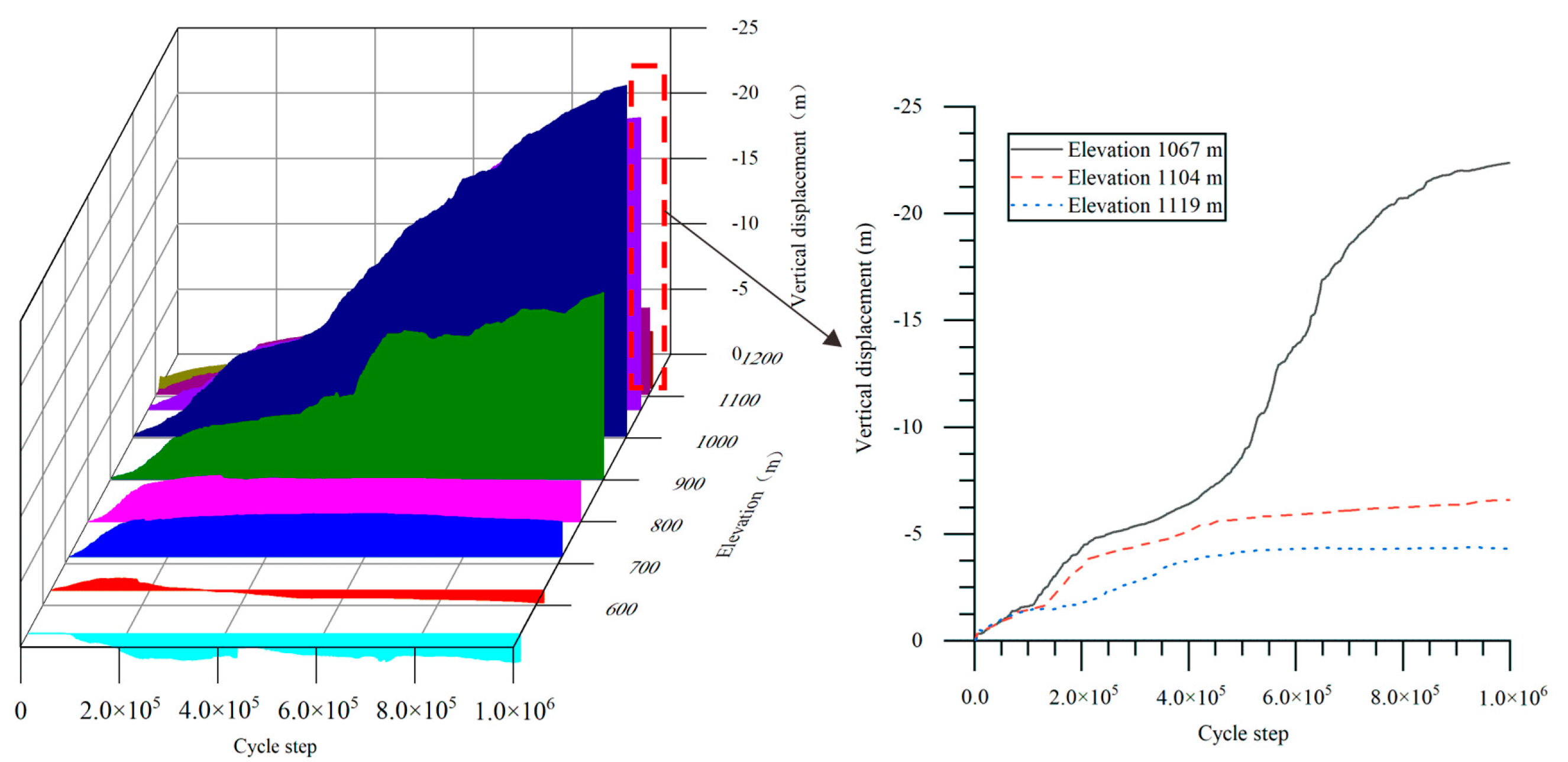
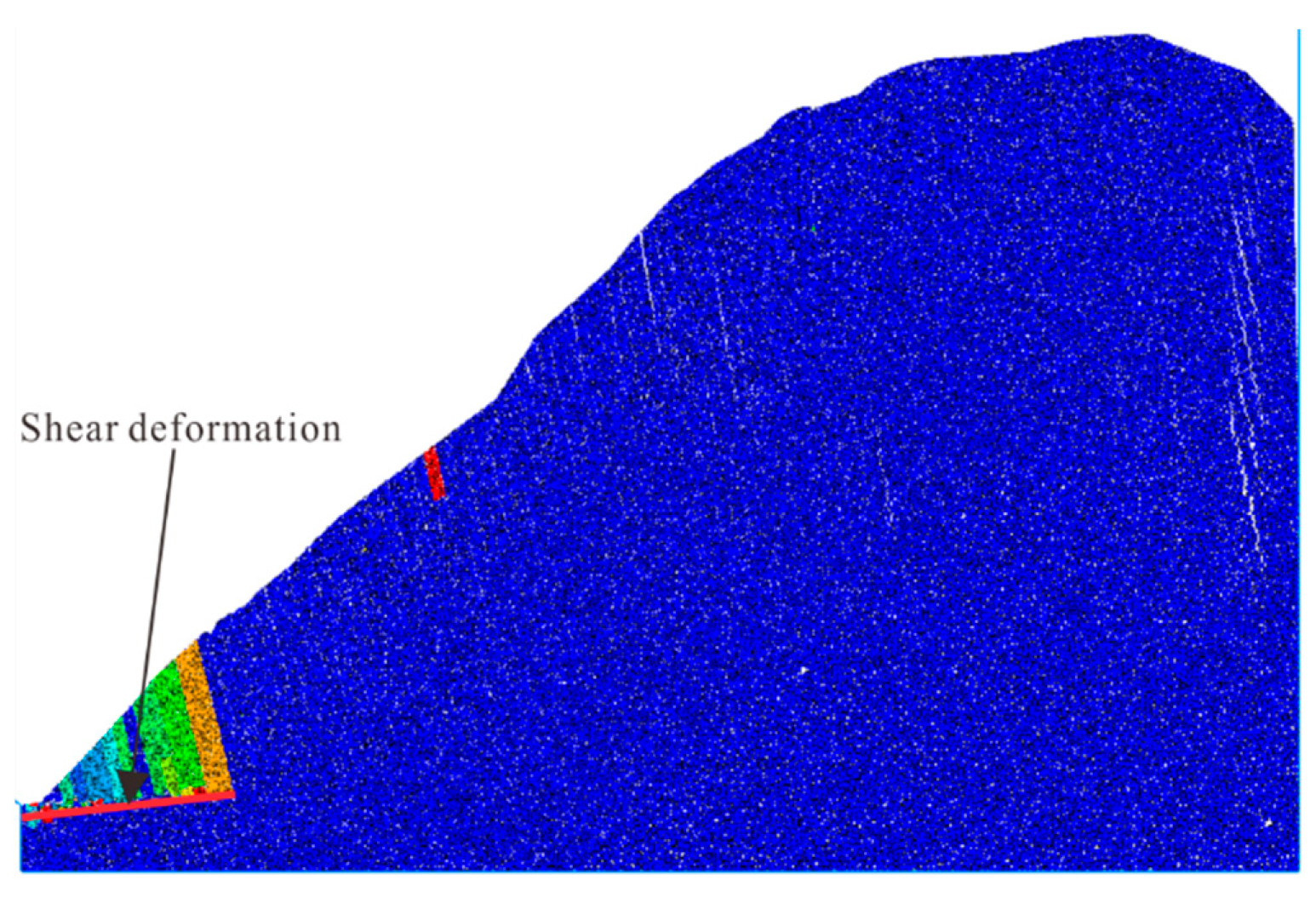
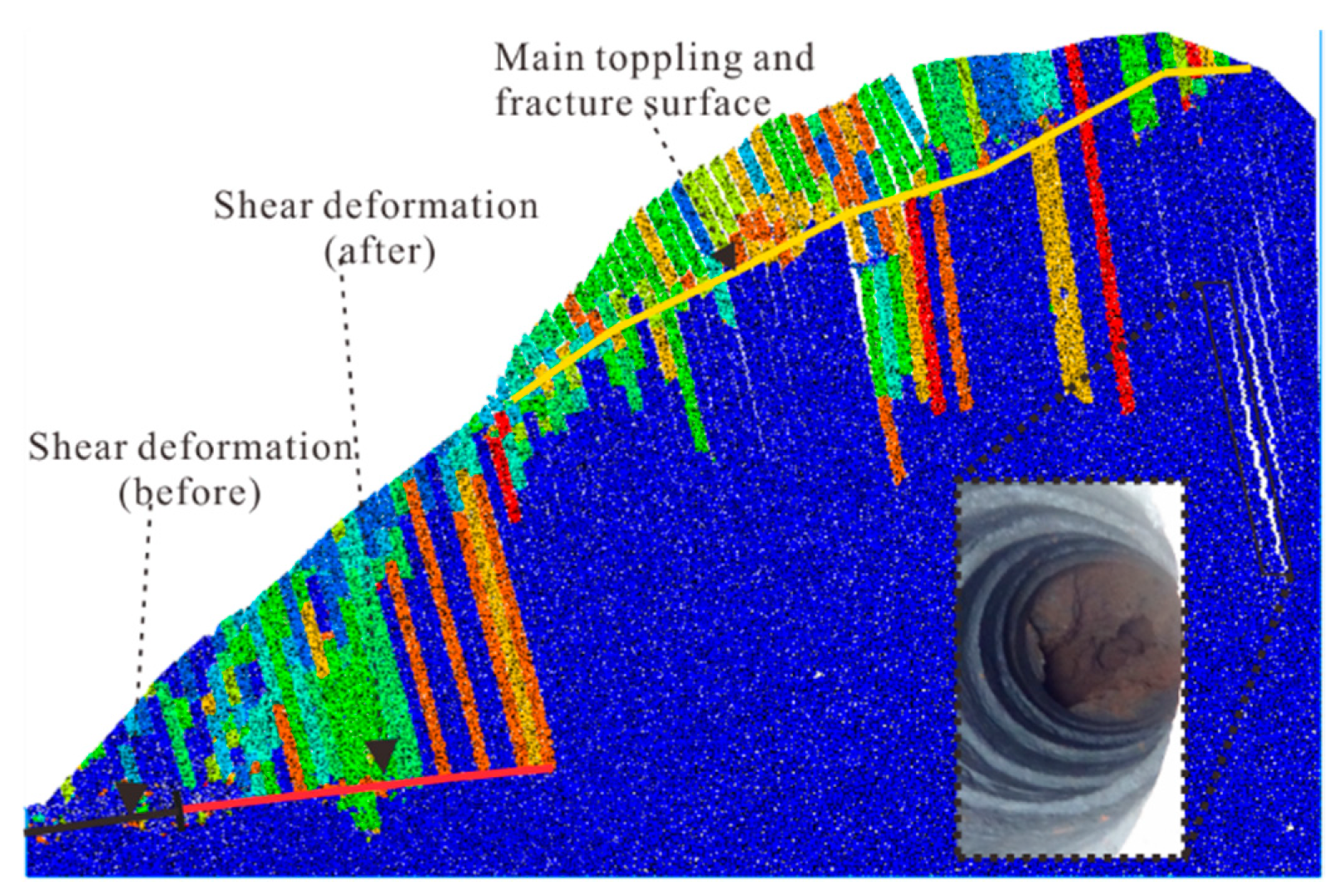
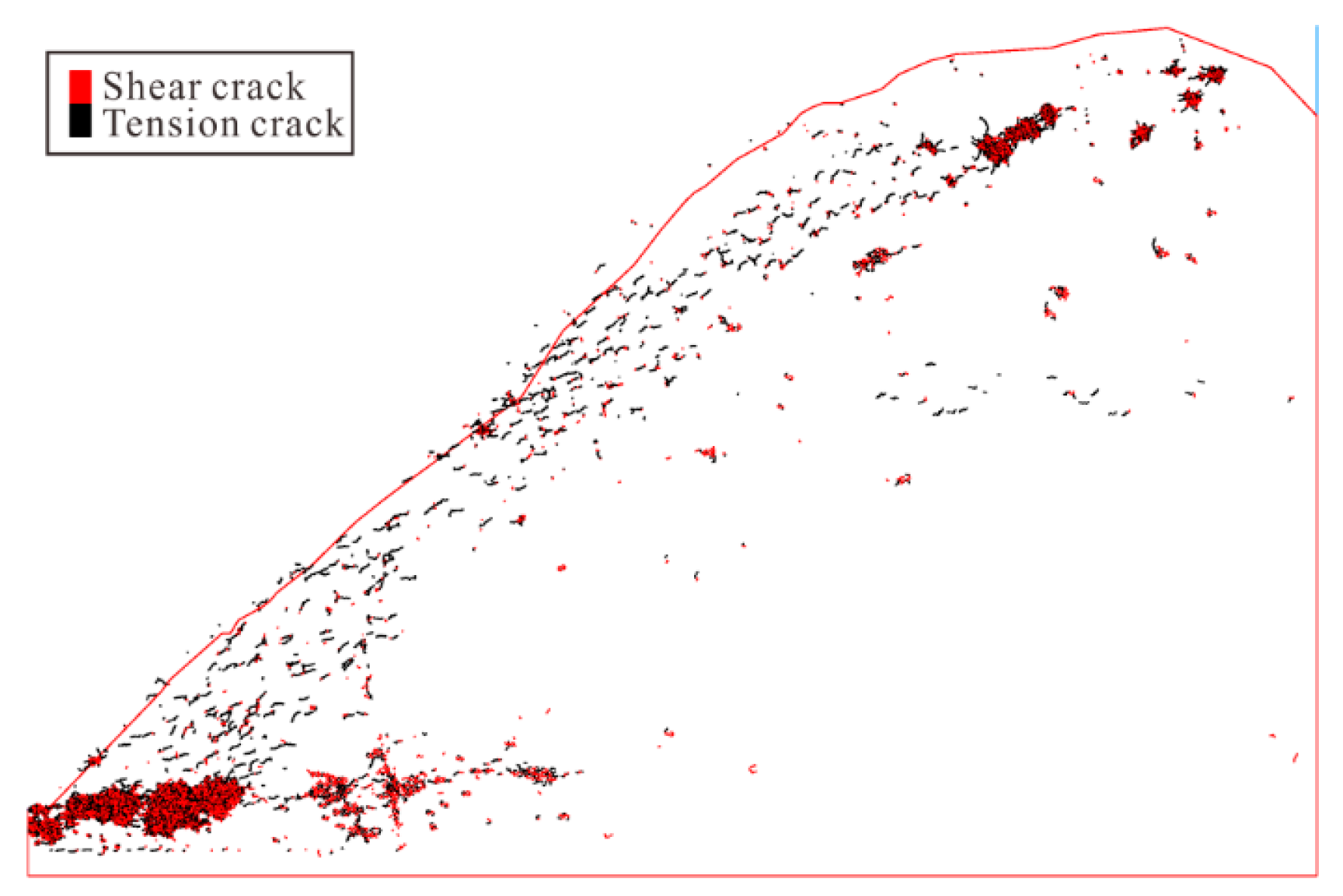
4. Evolutionary Characteristics of Displacement Field
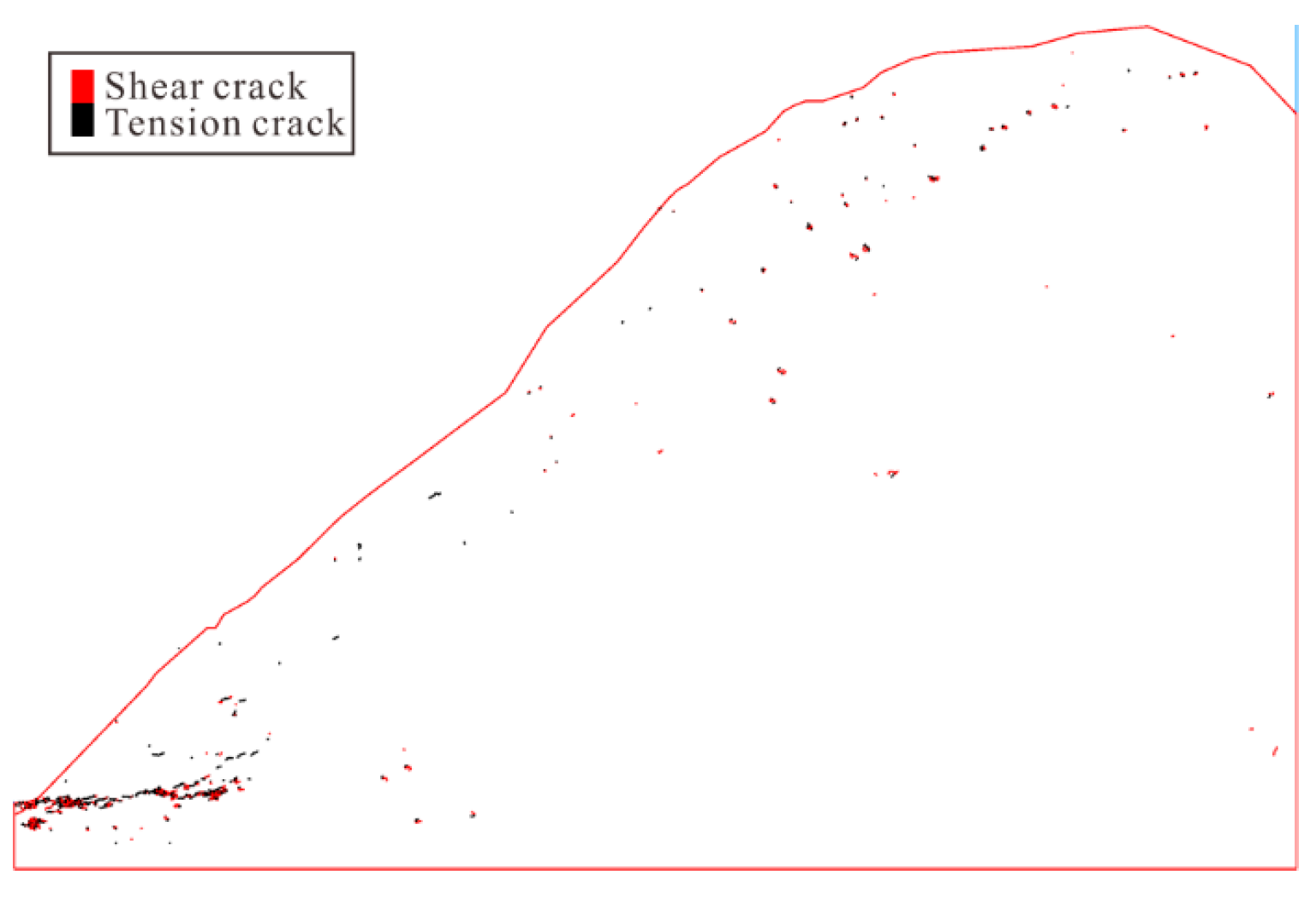
5. Evolutionary Characteristics of Energy Field
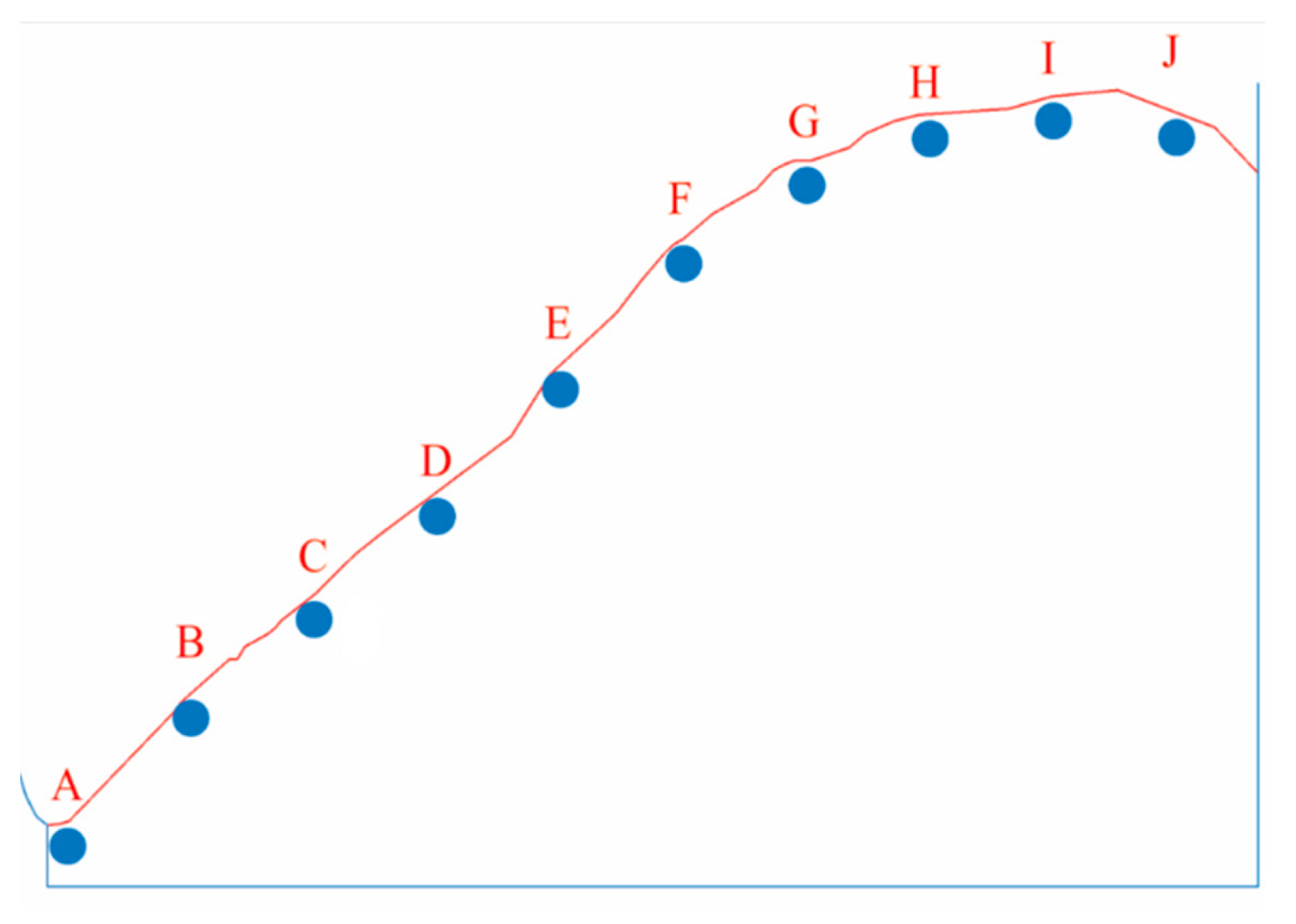
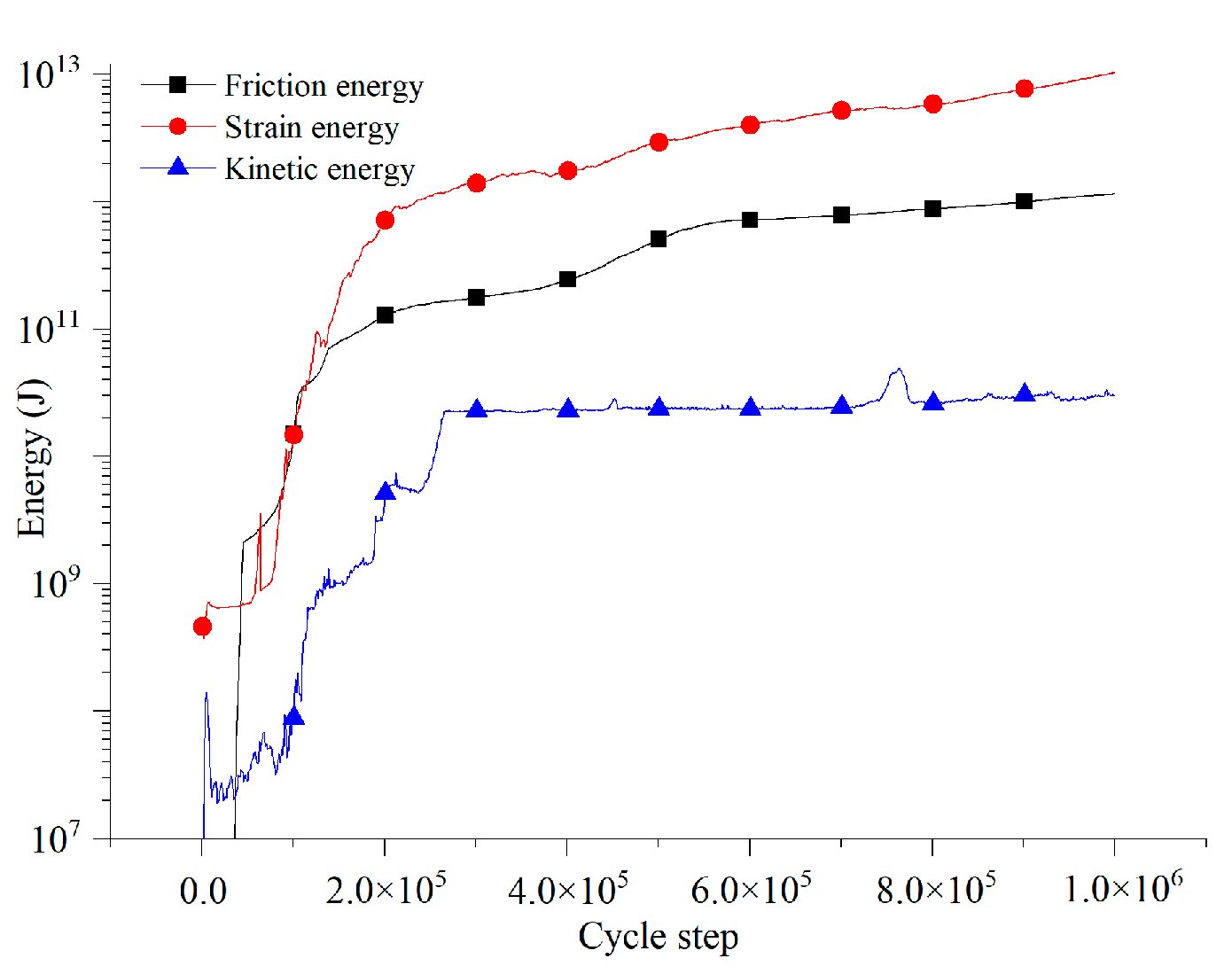
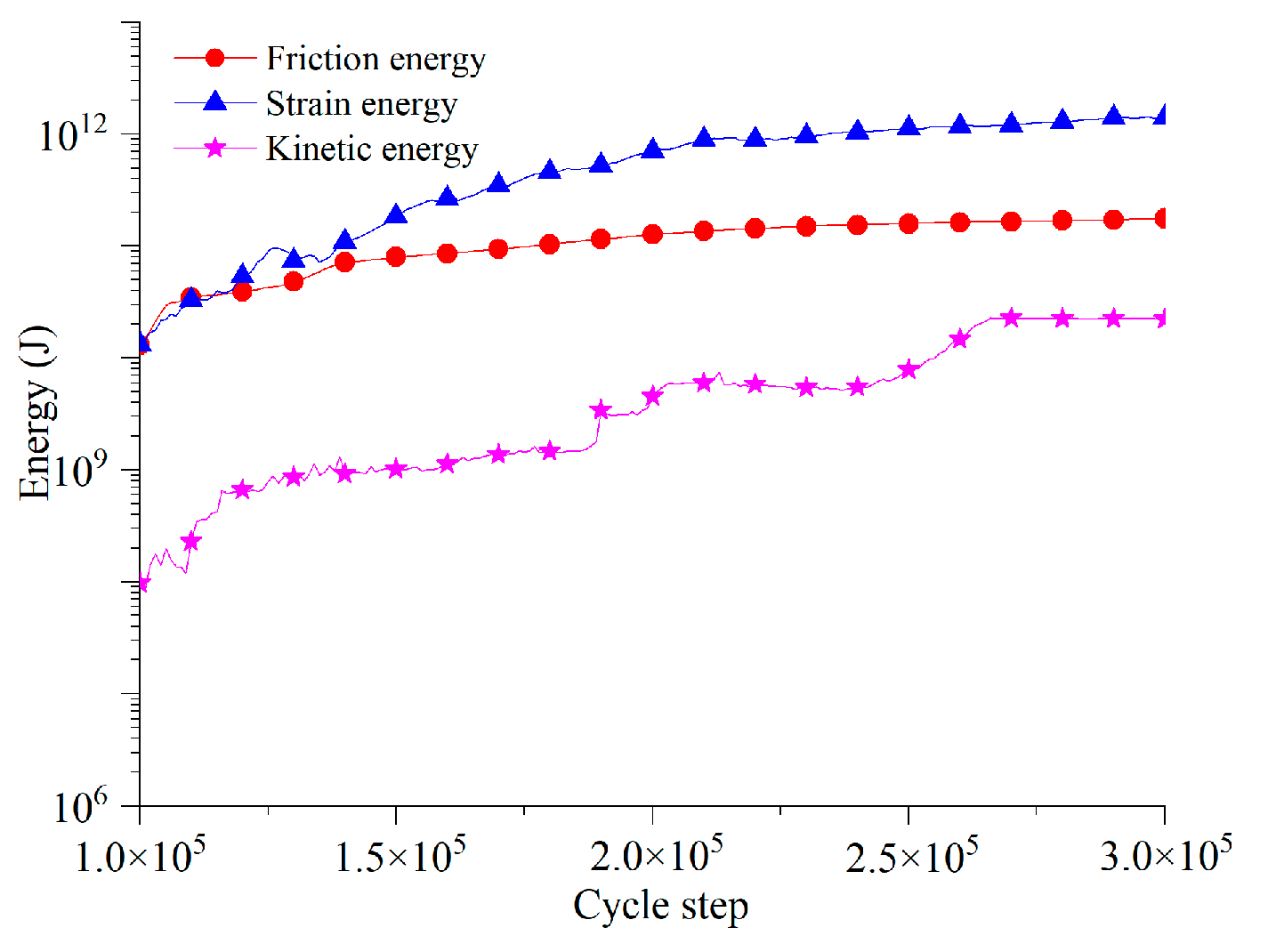
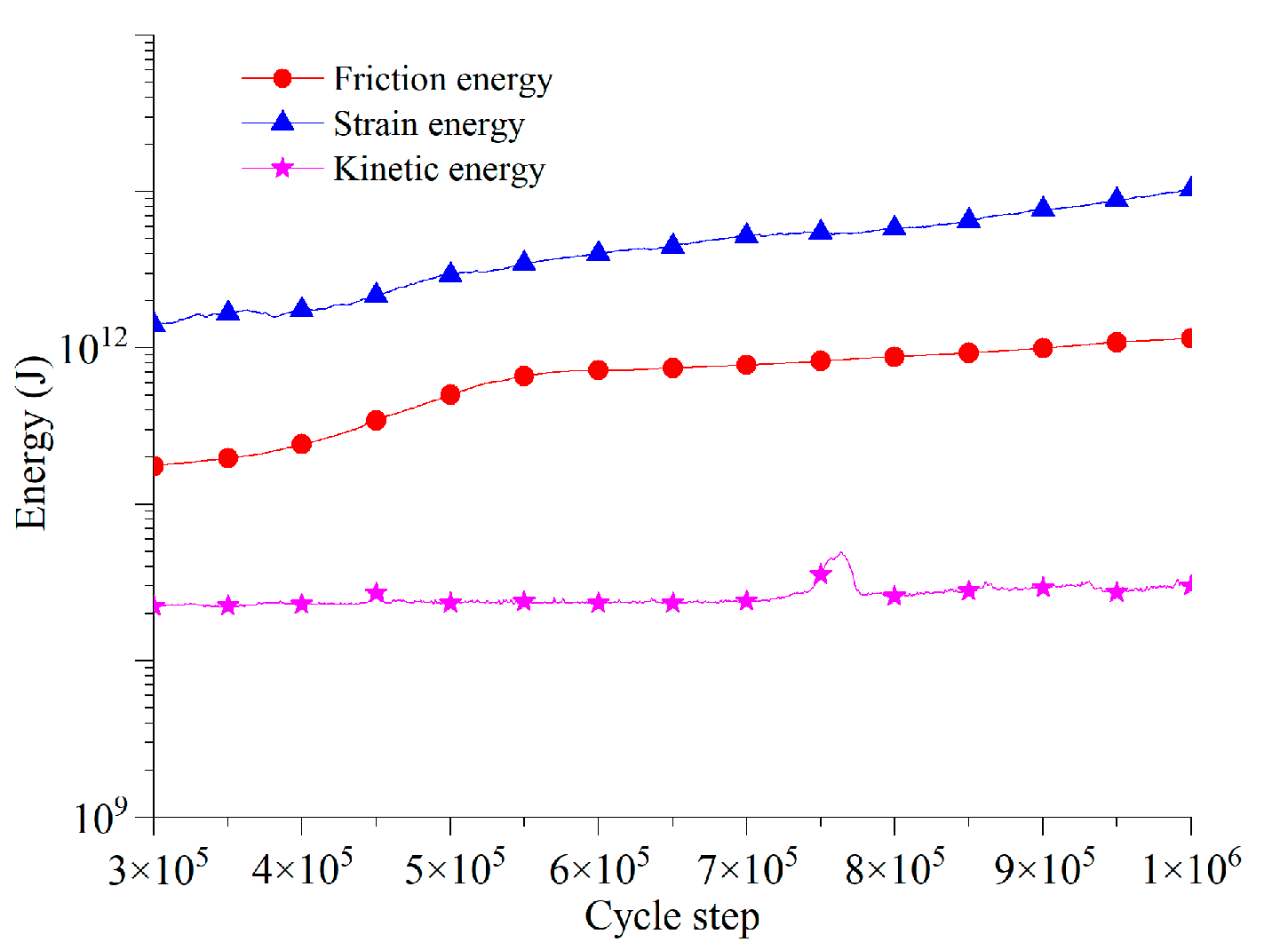
5.1. Energy Evolution Characteristics in Whole Toppling Process
- : Particle velocity
- : Particle mass
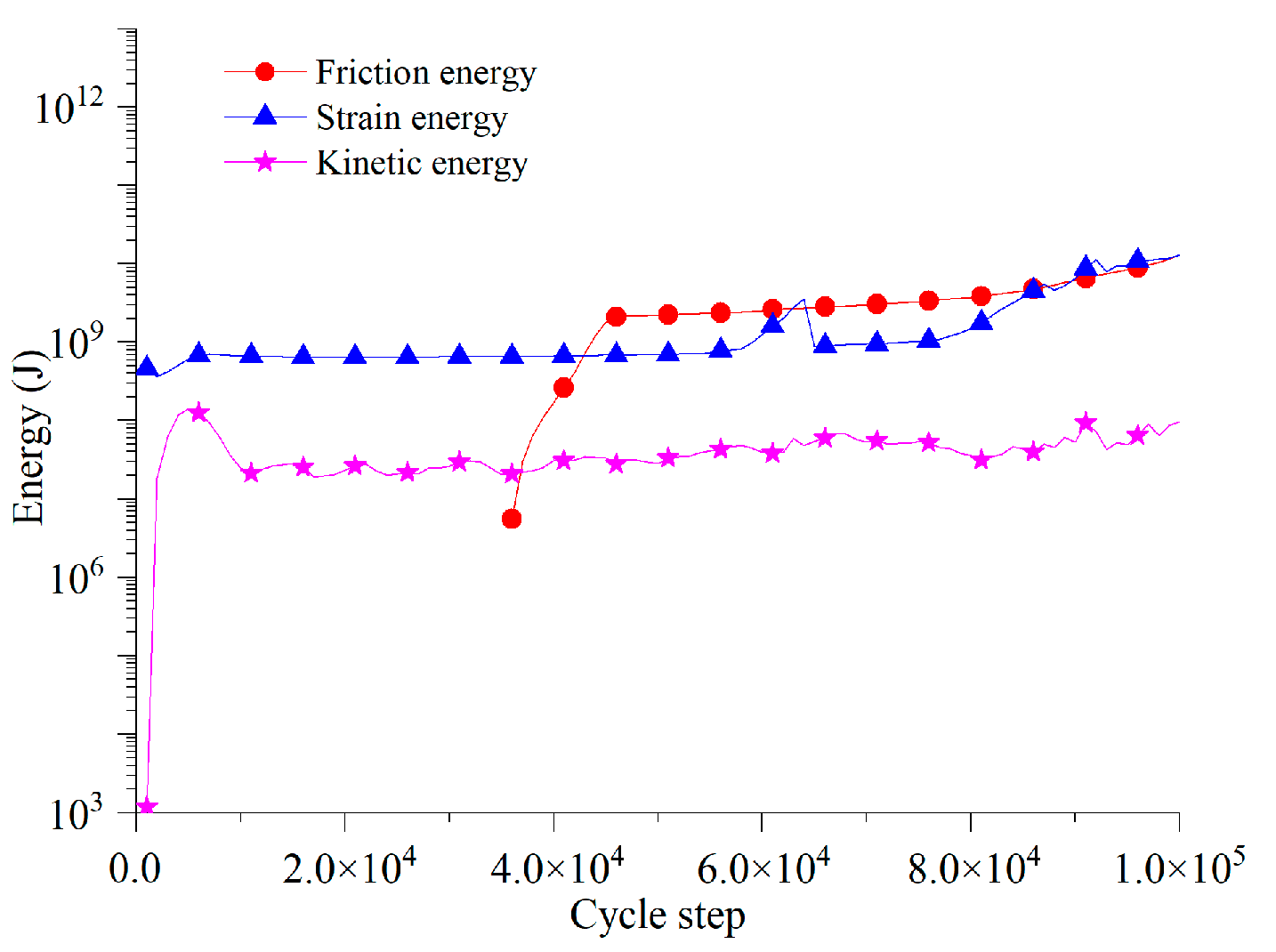
5.2. Dividing Evolution Stage of Toppling Deformation Based on Characteristics of Energy Field
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, R. Large-scale landslides and their sliding mechanisms in China since the 20th century. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2007, 26, 433–454. [Google Scholar]
- Mathis, J.I. Toppling failure—A proposed analytic solution. CIM Bull. 2004, 97, 60–61. [Google Scholar]
- Tu, X.; Dai, F.; Lu, X.; Zhong, H. Toppling and stabilization of the intake slope for the Fengtan Hydropower Station enlargement project, Mid-South China. Eng. Geol. 2007, 91, 152–167. [Google Scholar] [CrossRef]
- Alejano, L.R.; Gómez-Márquez, I.; Martínez-Alegría, R. Analysis of a complex toppling-circular slope failure. Eng. Geol. 2010, 114, 93–104. [Google Scholar] [CrossRef]
- Liu, C.H.; Jaksa, M.B.; Meyers, A.G. Toppling mechanisms of rock slopes considering stabilization from the underlying rock mass. Int. J. Rock Mech. Min. Sci. 2010, 47, 348–354. [Google Scholar] [CrossRef]
- Cruden, D.; Hu, X.-Q.; Lu, Z. Rock topples in the highway cut west of Clairvaux Creek, Jasper, Alberta. Can. Geotech. J. 2011, 30, 1016–1023. [Google Scholar] [CrossRef]
- Bi, J.; Luo, X.; Zhang, H.; Shen, H. Stability analysis of complex rock slopes reinforced with prestressed anchor cables and anti-shear cavities. Bull. Eng. Geol. Environ. 2019, 78, 2027–2039. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, Y.; Peng, X. Simulation of Toppling Failure of Rock Slope by Numerical Manifold Method. Int. J. Comput. Methods 2010, 7, 167–189. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Zhang, H.; Xia, K.; Liu, F. Study on the mechanisms of flexural toppling failure in anti-inclined rock slopes using numerical and limit equilibrium models. Eng. Geol. 2018, 237, 116–128. [Google Scholar] [CrossRef]
- Cai, J.-C.; Ju, N.-P.; Huang, R.-Q.; Zheng, D.; Zhao, W.-H.; Li, L.-Q.; Huang, J. Mechanism of toppling and deformation in hard rock slope: A case of bank slope of Hydropower Station, Qinghai Province, China. J. Mt. Sci. 2019, 16, 924–934. [Google Scholar] [CrossRef]
- Tao, Z.; Geng, Q.; Zhu, C.; He, M.; Cai, H.; Pang, S.; Meng, X. The mechanical mechanisms of large-scale toppling failure for counter-inclined rock slopes. J. Geophys. Eng. 2019, 16, 541–558. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, J. Extended finite element simulation of step-path brittle failure in rock slopes with non-persistent en-echelon joints. Eng. Geol. 2019, 250, 65–88. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Xia, K.; Liu, X. Stability analysis of rock slopes against sliding or flexural-toppling failure. Bull. Eng. Geol. Environ. 2018, 77, 1383–1403. [Google Scholar] [CrossRef]
- Eberhardt, E. Twenty-ninth Canadian Geotechnical Colloquium: The role of advanced numerical methods and geotechnical field measurements in understanding complex deep-seated rock slope failure mechanisms. Can. Geotech. J. 2008, 45, 484–510. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Dyskin, A.V.; Jewell, R.J.; Stewart, D.P.J.R.M.; Engineering, R. A study of the mechanism of flexural toppling failure of rock slopes. Rock Mech. Rock Eng. 1997, 30, 75–93. [Google Scholar] [CrossRef]
- Brideau, M.-A.; Stead, D. Controls on Block Toppling Using a Three-Dimensional Distinct Element Approach. Rock Mech. Rock Eng. 2010, 43, 241–260. [Google Scholar] [CrossRef]
- Wu, J.; Ohnishi, Y.; Shi, G.; Nishiyama, S. Three dimensional discontinuous deformation analysis (3d dda) and its application to the rock slope toppling. Chin. J. Rock Mech. Eng. 2003, 22, 937–942. [Google Scholar]
- Gschwind, S.; Loew, S.; Wolter, A. Multi-stage structural and kinematic analysis of a retrogressive rock slope instability complex (Preonzo, Switzerland). Eng. Geol. 2019, 252, 27–42. [Google Scholar] [CrossRef]
- Alejano, L.R.; Veiga, M.; Pérez-Rey, I.; Castro-Filgueira, U.; Arzúa, J.; Castro-Caicedo, Á.J. Analysis of a complex slope failure in a granodiorite quarry bench. Bull. Eng. Geol. Environ. 2017, 78, 1209–1224. [Google Scholar] [CrossRef]
- Xu, N.; Wu, J.; Dai, F.; Fan, Y.; Li, T.; Li, B. Comprehensive evaluation of the stability of the left-bank slope at the Baihetan hydropower station in southwest China. Bull. Eng. Geol. Environ. 2017, 77, 1567–1588. [Google Scholar] [CrossRef]
- Wu, C.S.; Feng, Z.Y.; Yang, H.; Zhang, D.M.; Wang, Y. Evolution Mechanism of Rock Slope Slide Based on Fiber Optic Sensors. J. Nanoelectron. Optoelectron. 2017, 12, 913–919. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, G.; Wu, S.; Tang, H.; Wang, T.; Li, G.; Liang, C. Rock slope deformation mechanism in the Cihaxia Hydropower Station, Northwest China. Bull. Eng. Geol. Environ. 2015, 74, 943–958. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.A.; Li, L.; Wang, L.; Liang, R.Y. A case study integrating numerical simulation and GB-InSAR monitoring to analyze flexural toppling of an anti-dip slope in Fushun open pit. Eng. Geol. 2015, 197, 20–32. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Corkum, B.; Hoek, E.; Carranza-Torres, C. Hoek-Brown Failure Criterion—2002. Proc. NARMS-Tac. 2002, 1, 267–273. [Google Scholar]
- Cai, J.-S.; Yan, E.C.; Wang, Z.-Q.; Yang, J.-G.; Tang, R.-X. Study of cantilever beam limit equilibrium model of anti-dip layered rock slopes. Yantu Lixue/Rock Soil Mech. 2014, 35, 15–28. [Google Scholar]
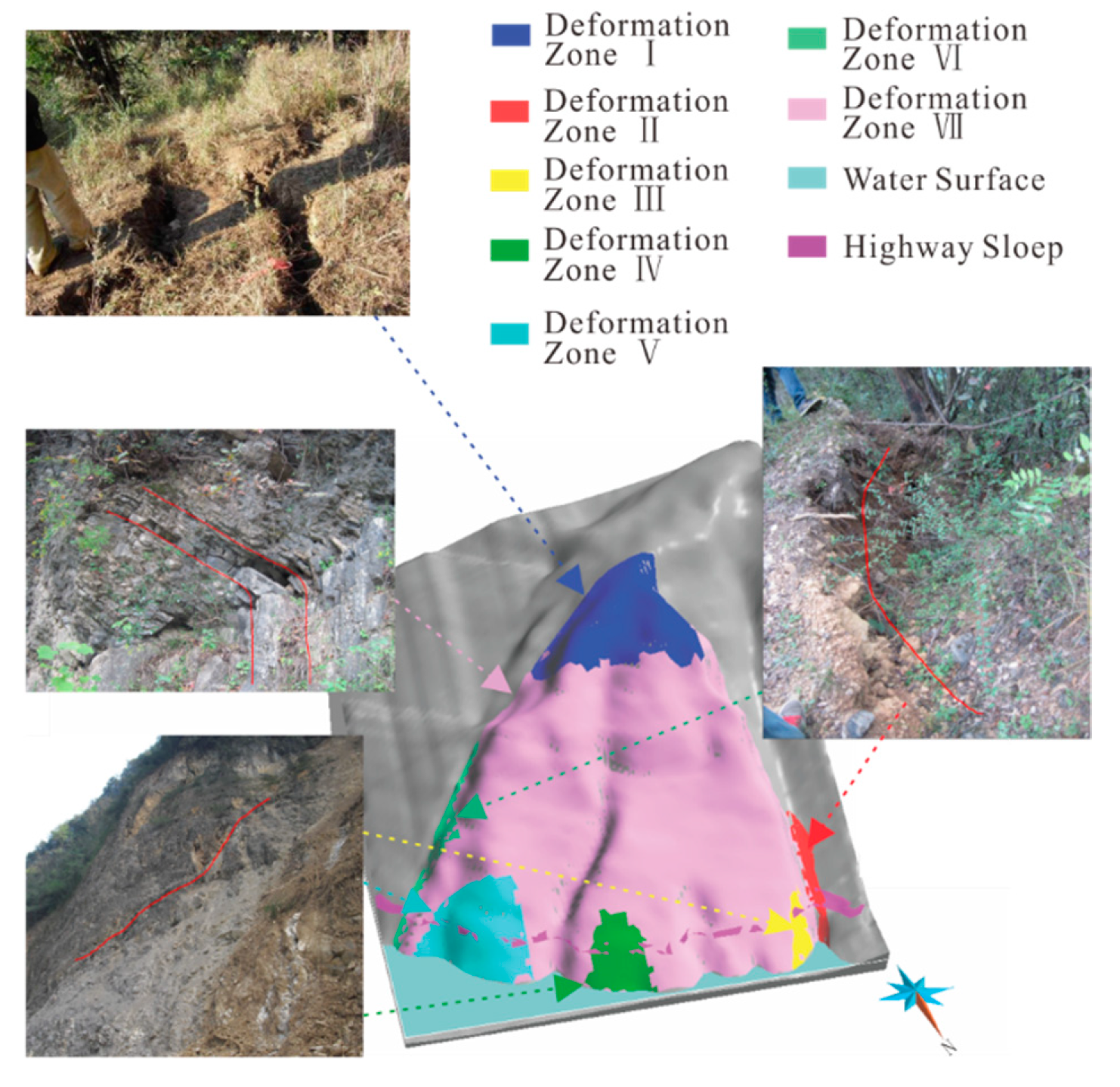
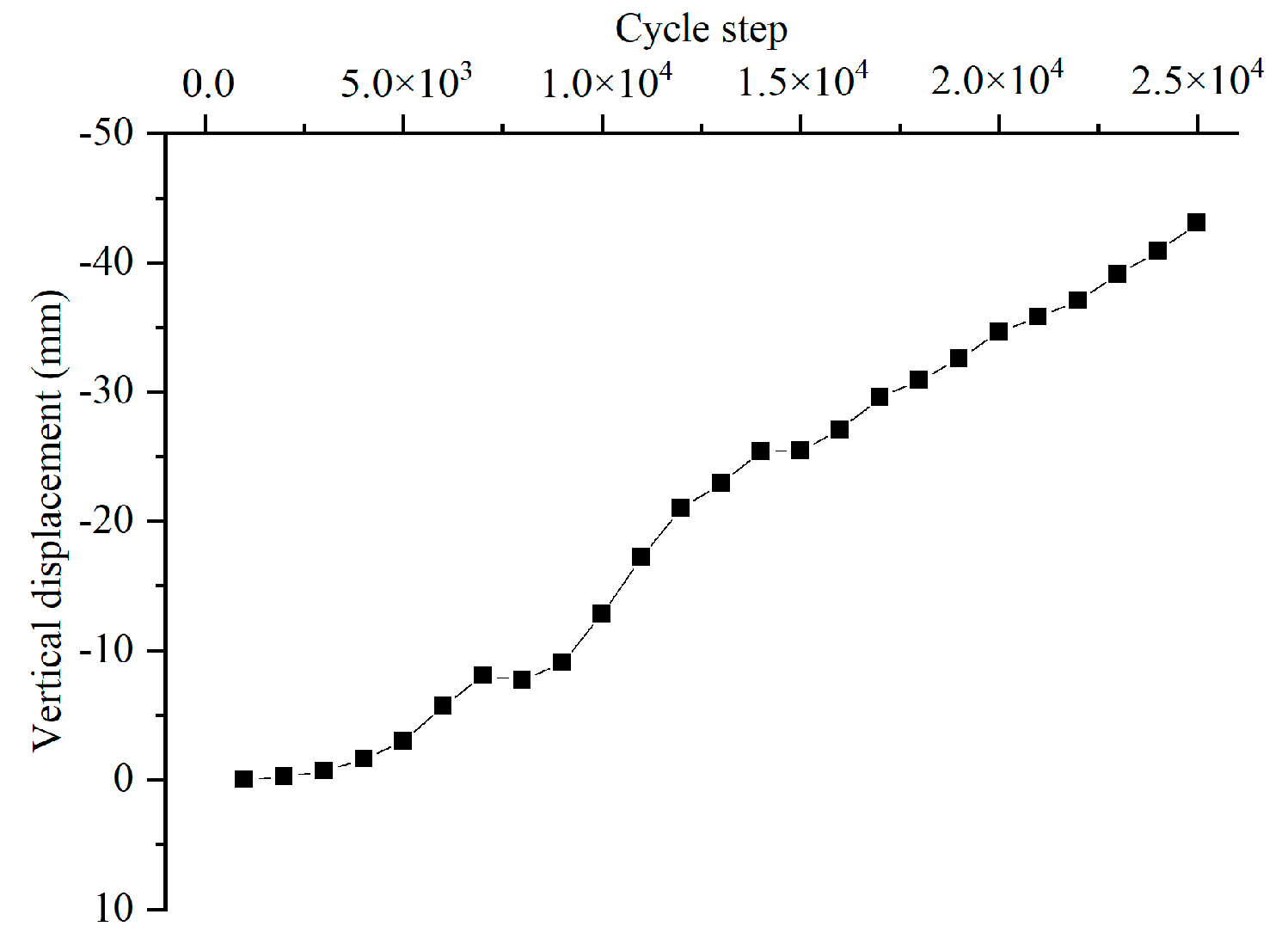



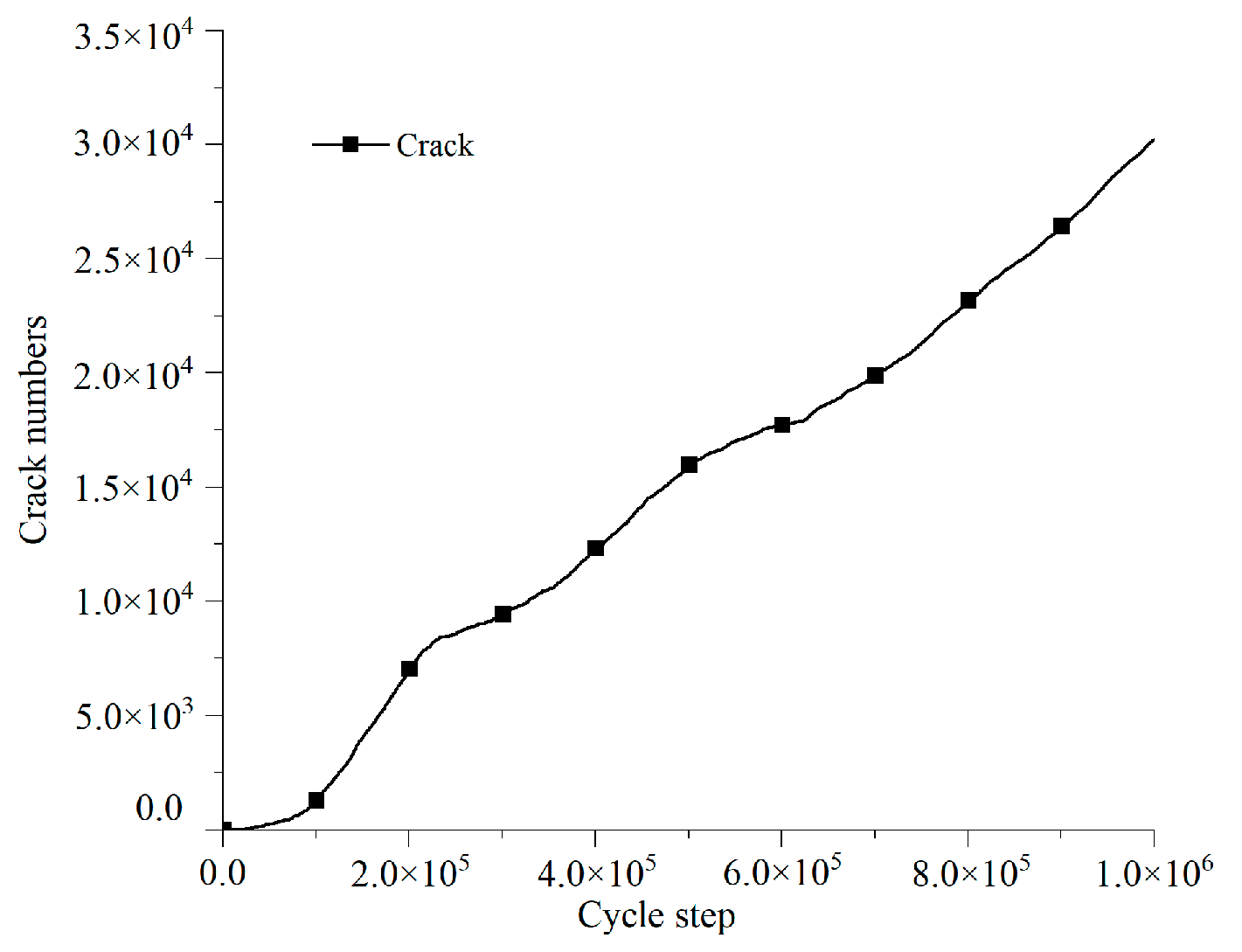


| Zone Number | Deformation Extent | Position | Distribution Height (m) | Area (104 m2) | Material Structure | Deformation Characteristics |
|---|---|---|---|---|---|---|
| I | Failure | Trailing edge | 1070–1180 | 4.9 | Residual slope, mainly silty clay | Cracks, house deformation |
| II | Weak deformation Local failure | Ditch four | 610–880 | 0.2 | Landslide layer, block stone | Rock mass collapse |
| III | Failure | Right side of ditch four | 610–755 | 1.2 | Strongly weathered rock mass | Rock and soil slide |
| IV | Weak deformation | Left side of ditch two | 650–720 | 0.5 | Landslide layer, gravelly soil | Rock and soil slide |
| V | Failure | Right side of ditch four | 610–755 | 2.4 | Landslide layer, gravelly soil | Rock and soil slide |
| VI | Failure | Ditch one | 610–1160 | 1.1 | Landslide layer, block stone | Rock mass collapse |
| VII | Weak deformation | The whole bank slope | 526–1180 | 62.8 | Dolomite limestone, mud limestone | Flexural toppling |
| Formation Lithology | Young′ s Modulus | Poisson’s Ratio | Uniaxial Compressive Strength | Tension Strength | Cohesion | Internal Friction Angle |
|---|---|---|---|---|---|---|
| E/GPa | ν | c/MPa | φ/° | |||
| T1j | 5.540 | 0.245 | 18.15 | −0.186 | 1.843 | 29.74 |
| T1d | 2.254 | 0.297 | 10.16 | −0.037 | 1.003 | 20.33 |
| Items | Values | |
|---|---|---|
| Formation Lithology | T1j | T1d |
| Minimum particle size (m) | 0.5 | 0.5 |
| Maximum particle size (m) | 1.0 | 1.0 |
| Particle contact module (GPa) | 2.5 | 1.2 |
| Ratio of contact module | 1.8 | 2.2 |
| Particle friction coefficient | 0.2 | 0.1 |
| Parallel bond module (GPa) | 2.5 | 1.2 |
| Ratio of parallel bond module | 1.8 | 2.2 |
| Normal strength (MPa) | 10.0 | 6.0 |
| Tangential strength (MPa) | 5.0 | 3.0 |
| Friction angle (°) | 10.0 | 5.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Zhu, Q.; Qin, Y.; Wang, J.; Qian, J. Study on Evolutionary Characteristics of Toppling Deformation of Anti-Dip Bank Slope Based on Energy Field. Sustainability 2020, 12, 7544. https://doi.org/10.3390/su12187544
Xie L, Zhu Q, Qin Y, Wang J, Qian J. Study on Evolutionary Characteristics of Toppling Deformation of Anti-Dip Bank Slope Based on Energy Field. Sustainability. 2020; 12(18):7544. https://doi.org/10.3390/su12187544
Chicago/Turabian StyleXie, Liangfu, Qingyang Zhu, Yongjun Qin, Jianhu Wang, and Jiangu Qian. 2020. "Study on Evolutionary Characteristics of Toppling Deformation of Anti-Dip Bank Slope Based on Energy Field" Sustainability 12, no. 18: 7544. https://doi.org/10.3390/su12187544
APA StyleXie, L., Zhu, Q., Qin, Y., Wang, J., & Qian, J. (2020). Study on Evolutionary Characteristics of Toppling Deformation of Anti-Dip Bank Slope Based on Energy Field. Sustainability, 12(18), 7544. https://doi.org/10.3390/su12187544





