Assessing the Impact of Public Rental Housing on the Housing Prices in Proximity: Based on the Regional and Local Level of Price Prediction Models Using Long Short-Term Memory (LSTM)
Abstract
1. Introduction
- Do proximity measures direct toward PRH increase the predictive power of regional housing prices?
- Are there any differences in trends between the regional housing prices and the ones in proximity to PRH?
- For the apartments that are located in proximity to PRH, are there any differences in trends if they are located in the neighborhood with a more “favorable” local housing market?
- Does LSTM produce improved predictive power than the traditional multivariate time series model?
2. Background
2.1. Public Rental Housing (PRH) Provisions in Korea
2.2. The Effect of PRH on Real Estate
Case Studies: The Effect of PRH on Real Estate
2.3. Application of Advanced Valuation Methods
2.3.1. Application of Machine Learning
2.3.2. Case Studies: Application of Advanced Valuation Method
3. Experiment
3.1. Research Design and Data
- Construct 1:
- The most basic price prediction model constructed with the sequence of housing prices.
- Construct 2:
- The apartment characteristics are added to Construct 1. Considering that apartment characteristics are known to be strong determinants of the price, it is likely that the predictive power will increase as they are added in the model. Thus, the change in predictive power will be able to determine the relative importance of apartment characteristics on housing prices.
- Construct 3:
- Two of the proximity measures to the nearest PRH are added to Construct 2. If the addition of those variables increases the predictive power from Construct 2, then it suggests that the distance and size of the nearest PRH have a meaningful effect on housing prices.
- Construct 4:
- The comprehensive measure of exposure to PRH within 1 km is added to Construct 3. If the addition of the variable increases the predictive power from the best performing model in the previous stage, then it suggests that the exposure to closer and larger PRH has a meaningful effect on housing prices.
- Model 1.
- This model is subjected to the entire region of Busan. Herein, the housing price prediction model at the city level can be referred to as the regional model, which represents the regional housing market.
- Model 2.
- This model is subjected to the neighborhoods (or areas within 1 km) of PRH. The housing price prediction model at the neighborhood level can be referred to as the local model, which represents the local housing market.
- Model 3.
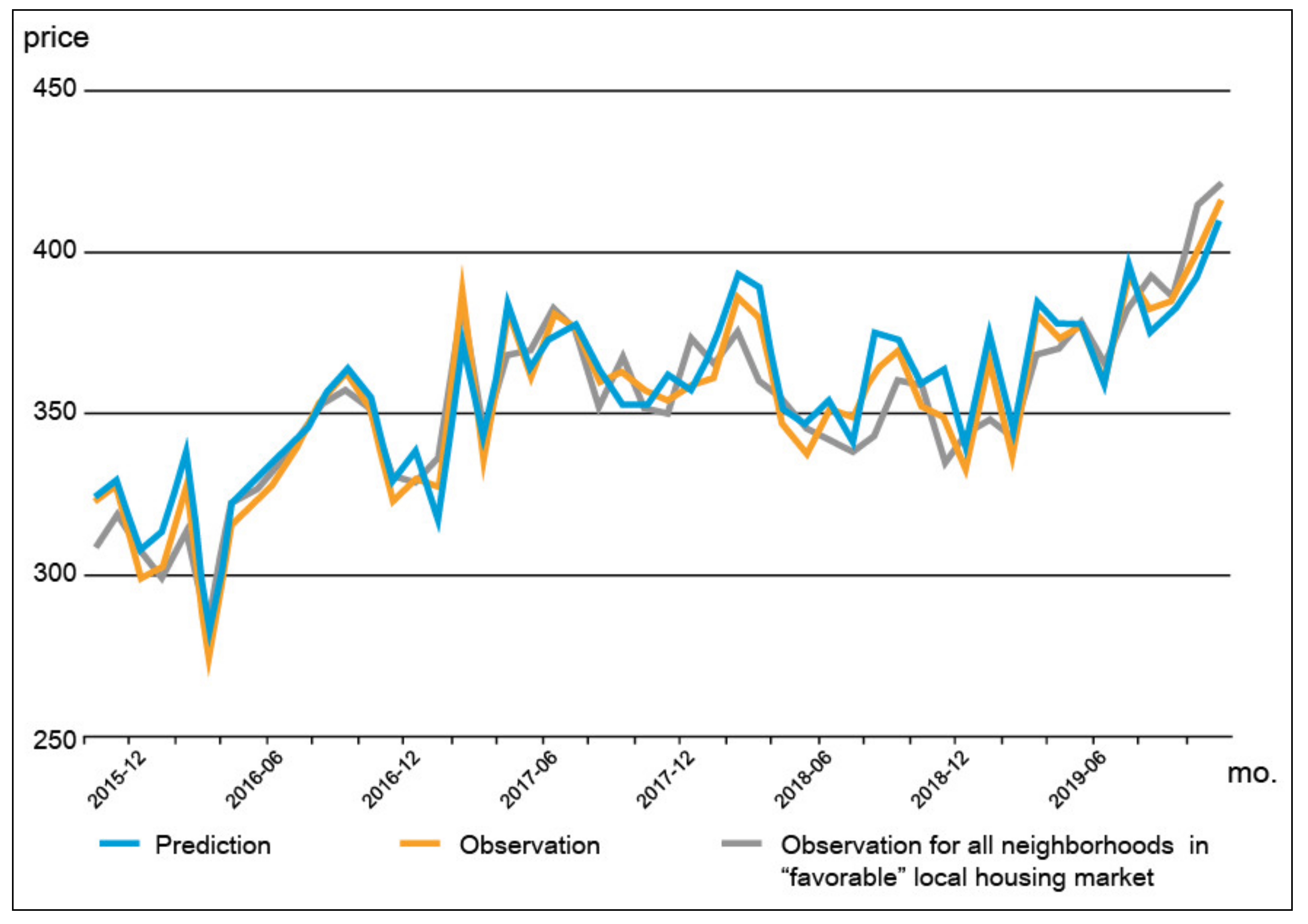
- This model is subjected to the neighborhoods of PRH units that are located in the “favorable” local housing markets, where the average change in housing price is above that of Busan, which is based on the transaction data used in this study. The observed price trends of the neighborhoods in Busan that have “favorable” local housing markets are also included for comparison.
- Model 4.
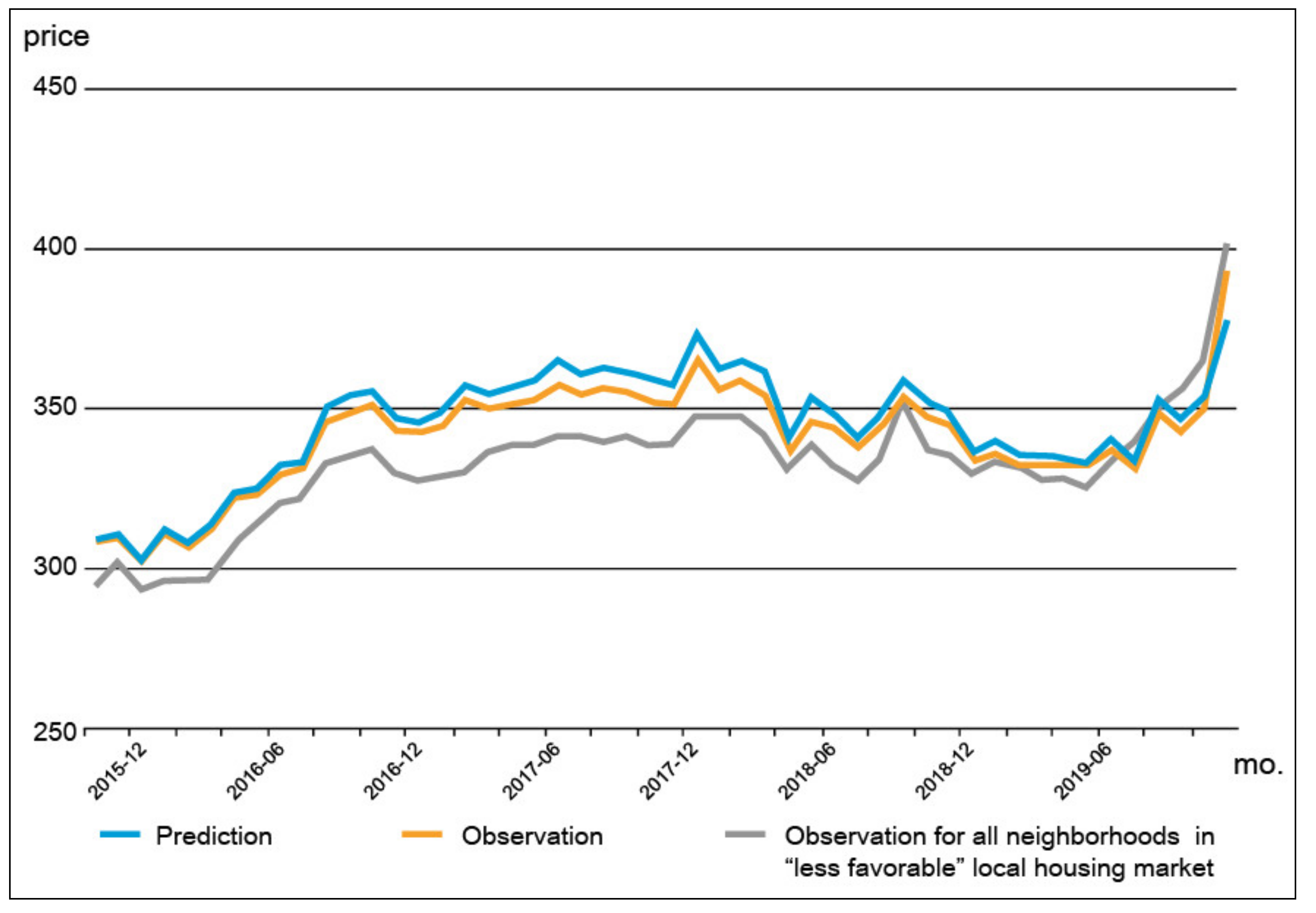
- This model is subjected to the neighborhoods of PRH units that are located in the less favorable local housing markets, where the average change in housing price is below that of Busan, based on the transaction data used in this study. The observed price trend of all neighborhoods in Busan that have “less favorable” local housing markets is also included for comparison.
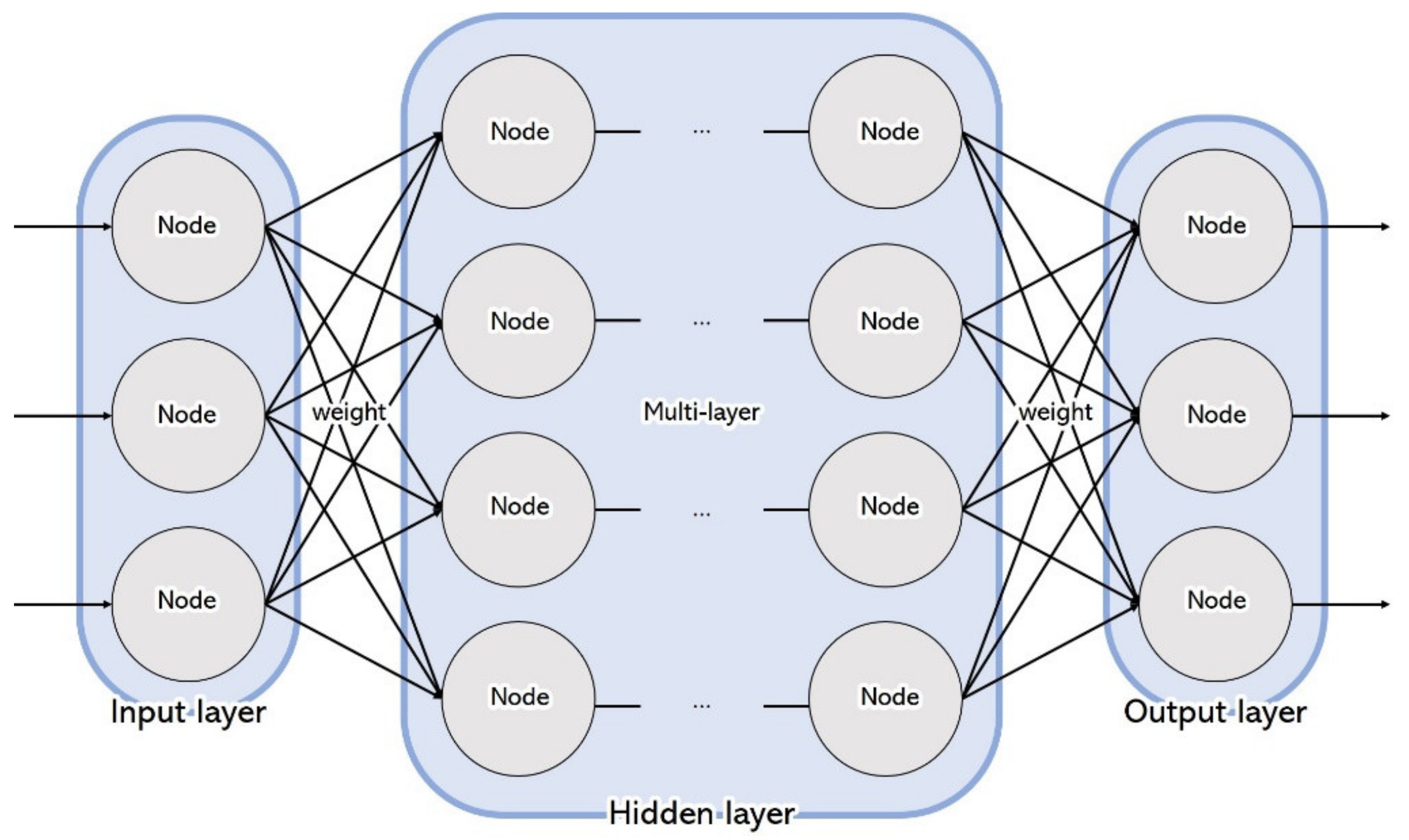
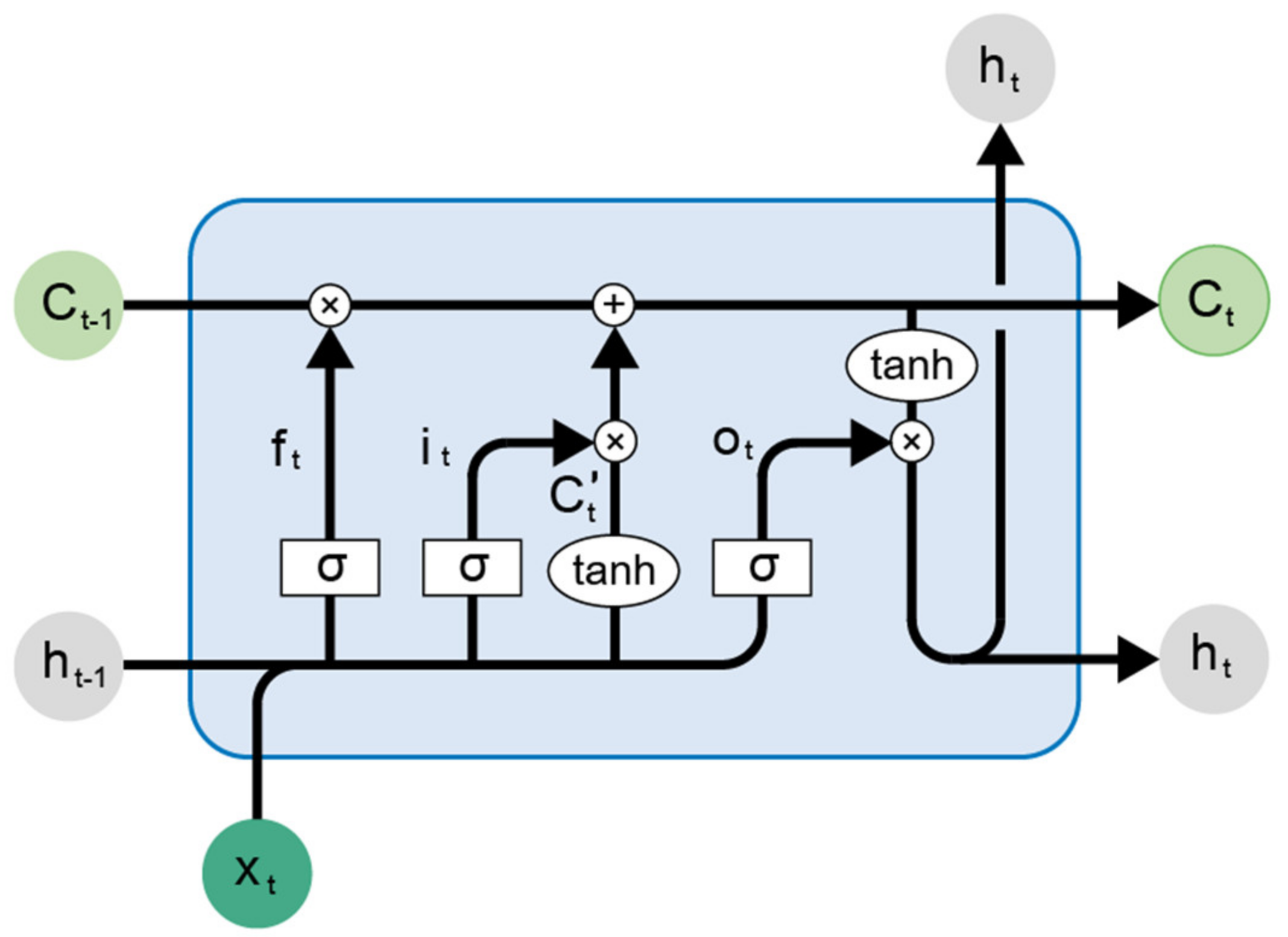
3.2. Specification of Long Short-Term Memory (LSTM)
4. Results and Discussion
4.1. Analysis of the Data
4.2. Model Production
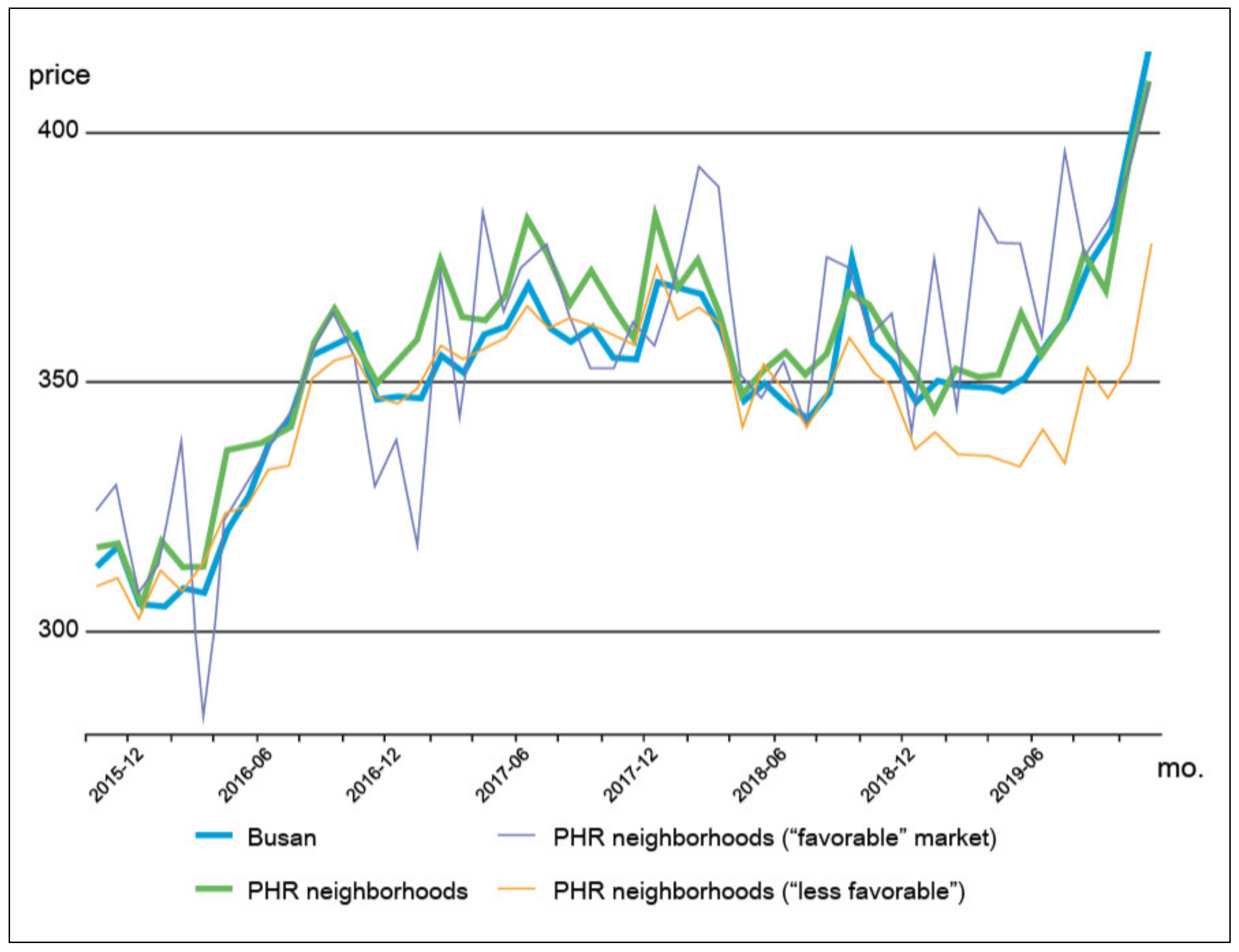
4.3. Analysis Results of the Proximity Effect of PRH
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monroy, A.M.; Gars, J.; Matsumoto, T.; Crook, J.; Ahrend, R.; Schumann, A. Housing Policies for Sustainable and Inclusive Cities; OECD Regional Development Working Papers 2020; OECD Publishing: Paris, France, 2020. [Google Scholar] [CrossRef]
- World Bank Systems of Cities: Harnessing Urbanization for Growth & Poverty Alleviation. The World Bank Urban & Local Government Strategy. 2010. Available online: http://documents1.worldbank.org (accessed on 1 September 2020).
- Tusell, M.S. Affordable Housing in Europe: Innovative Public Policies that Can Effectively Address the Housing Crisis. Barcelona Centre for International Affairs. 2017. Available online: https://cidob.org (accessed on 1 September 2020).
- Dawkins, C. Realizing housing justice through comprehensive housing policy reform. Int. J. Urban. Sci. 2020. [Google Scholar] [CrossRef]
- Galster, G.; Lee, K.O. Housing affordability: A framing, synthesis of research and policy, and future directions. Int. J. Urban Sci. 2020. [Google Scholar] [CrossRef]
- Galdini, R.; Lucciarini, S. Social Innovation and Environmental Sustainability in Social Housing Policies: Learning from Two Experimental Case Studies in Italy. In Different Strategies of Housing Design; IntechOpen Limited: London, UK, 2019. [Google Scholar] [CrossRef]
- Li, D.; Chen, Y.; Chen, H.; Guo, K.; Hui, C.M.; Yang, J. Assessing the integrated sustainability of a public rental housing project from the perspective of complex eco-system. Habitat Int. 2016, 53, 546–555. [Google Scholar] [CrossRef]
- Wu, G.; Duan, K.; Zuo, J.; Zhao, X.; Tang, D. Integrated sustainability assessment of public rental housing community based on a hybrid method of AHP-Entropy weigh and cloud model. Sustainability 2017, 9, 603. [Google Scholar] [CrossRef]
- OECD Better Life Index. Available online: http://www.oecdbetterlifeindex.org/topics/housing/ (accessed on 3 January 2020).
- Park, J.H.; Yu, J.; Geem, Z.W. Optimal project planning for public rental housing in South Korea. Sustainability 2020, 12, 600. [Google Scholar] [CrossRef]
- Currie, J.; Yelowitz, A. Are public housing projects good for kids? J. Public Econ. 2000, 75, 99–124. [Google Scholar] [CrossRef]
- Finkel, M.; Climaco, C.; Elwood, P.; Feins, J.; Locke, G.; Popkin, S. Learning from Each Other: New Ideas for Managing the Section 8 Certificate and Voucher Programs; Department of Housing and Urban Development: Washington, DC, USA, 1996.
- Kean, T.; Ashley, T. “Not in My Back Yard” Removing Barriers to Affordable Housing; Department of Housing and Urban Development: Washington, DC, USA, 1991.
- Scally, C.P.; Koenig, R. Beyond NIMBY and poverty deconcentration: Reframing the outcomes of affordable rental housing development. Hous. Policy Debate 2012, 22, 435–461. [Google Scholar] [CrossRef]
- Read, D.; Tsvetkova, A. Housing and social issues: A cross disciplinary review of the existing literature. J. Real Estate Lit. 2012, 20, 3–35. [Google Scholar] [CrossRef]
- Woo, A. Analysis research trends examining the impacts of subsidized housing developments on nearby property values in the U.S.: A critical review on empirical methodologies. J. Korea Real Estate Anal. Assoc. 2015, 26, 71–82. [Google Scholar]
- Selim, H. Determinants of house prices in Turkey: Hedonic regression versus artificial neural network. Expert Syst. Appl. 2009, 36, 2843–2852. [Google Scholar] [CrossRef]
- Park, S.; Bae, Y. Predicting the real estate price index using machine learning methods and time series analysis model. Hous. Stud. Rev. 2015, 26, 107–133. [Google Scholar] [CrossRef]
- Koschinsky, J. Spatial heterogeneity in spillover effects of assisted and unassisted rental housing. J. Urban Aff. 2009, 31, 319–347. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. A deep learning approach to forecasting monthly demand for residential–sector electricity. Sustainability 2020, 12, 3103. [Google Scholar] [CrossRef]
- Hung, C.; Hung, C.; Lin, S. Predicting time series using integration of moving average and support vector regression. Int. J. Mach. Learn. Comput. 2014, 4, 491–495. [Google Scholar] [CrossRef][Green Version]
- Hu, L.; He, S.; Han, Z.; Xiao, H.; Su, S.; Weng, M.; Cai, Z. Monitoring housing rental prices based on social media: An integrated approach of machine-learning algorithms and hedonic modeling to inform equitable housing policies. Land Use Policy 2019, 82, 657–673. [Google Scholar] [CrossRef]
- Temür, A.S.; Melek, A.; Günay, T. Predicting housing sales in Turkey using ARIMA, LSTM and hybrid models. J. Bus. Econ. Manag. 2019, 20, 920–938. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Li, X.; Liu, Y.; Xu, X. Mapping the fine-scale spatial pattern of housing rent in the metropolitan area by using online rental listings and ensemble learning. Appl. Geogr. 2016, 75, 200–212. [Google Scholar] [CrossRef]
- Ministry of Land. Infrastructure and Transport. Rental Housing Statistics 2018. Available online: https://stat.molit.go.kr/ (accessed on 20 August 2020).
- Cheon, H.S. Assessment of public rental housing policy and assignment. Real Estate Focus 2017, 105, 22–31. [Google Scholar]
- Statistics Korea. Population and Housing Census. 2018. Available online: https://kostat.go.kr/ (accessed on 20 August 2020).
- Lee, Y.M.; Seong, J.W. A Comprehensive Report on the Characteristics and Quality of Life of Public Rental Housing Tenants. Seoul Housing and Communities Corporation. 2017. Available online: https://i-sh.co.kr/ (accessed on 20 August 2020).
- Hwang, Y.W. Evaluation of Public Rental Housing Policy and Improvement Plan in Busan Metropolitan Area; Policy Report 2019-04-860; Busan Development Institute: Busan, Korea, 2019. [Google Scholar]
- Nguyen, M.T. Does affordable housing detrimentally affect property values? A review of the literature. J. Plan. Lit. 2005, 20, 15–26. [Google Scholar] [CrossRef]
- Cummings, M.; Landis, J. Relationships between Affordable Housing Developments and neighboring Property Values: An Analysis of BRIDGE Housing Corporation Developments in the San Francisco Bay Area; IURD Working paper 599; Institute of Urban and Regional Development, University of California: Berkeley, CA, USA, 1993. [Google Scholar]
- Briggs, S.; Darden, X.; Joe, T.; Aidala, A. In the wake of desegregation: Early impacts of scattered-site public housing on neighborhoods in Yonkers, New York. J. Am. Plan. Assoc. 1999, 65, 27–49. [Google Scholar] [CrossRef]
- Kim, J. Analysis on the effect of public housing complex’s location conditions on the neighborhood apartment prices in Daegu. Korea Spat. Plan. Rev. 2013, 79, 23–32. [Google Scholar]
- Johnson, J.; Bednarz, B. Neighborhood Effects of the Low Income Housing Tax Credit Program: Final Report; Department of Housing and Urban Development: Washington, DC, USA, 2002.
- Woo, A.; Joh, K.; Van Zandt, S. Unpacking the impacts of the Low-Income Housing Tax Credit program on nearby property values. Urban Stud. 2016, 53, 2488–2510. [Google Scholar] [CrossRef]
- Baum-Snow, N.; Marion, J. The Effects of Low Income Housing Tax Credit Developments on Neighborhoods. J. Public Econ. 2009, 93, 654–666. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, A.; Ellen, I.; Voicu, I.; Schill, M. The external effects of place-based subsidized housing. Reg. Sci. Urban Econ. 2006, 36, 679–707. [Google Scholar] [CrossRef]
- Diamond, R.; McQuade, T. Who wants affordable housing in their backyard? An equilibrium analysis of low-income property development. J. Political Econ. 2019, 127, 1063–1117. [Google Scholar] [CrossRef]
- Lyons, R.F.; Loveridge, S. An Hedonic Estimation of the Effect of Federally Subsidized Housing on Nearby Residential Property Values; Department of Applied Economics, University fo Minnesota: St Paul, MN, USA, 1993. [Google Scholar] [CrossRef]
- Davison, G.; Han, H.; Liu, E. The impacts of affordable housing development on host neighbourhoods: Two Australian case studies. J. Hous. Built Environ. 2017, 32, 733–753. [Google Scholar] [CrossRef]
- Zahirovich-Herbert, V.; Gibler, K.M. The effect of new residential construction on housing prices. J. Hous. Econ. 2014, 26, 1–18. [Google Scholar] [CrossRef]
- Kim, H.; Lee, G.; Lee, J.; Choi, Y. Understanding the local impact of urban park plans and park typology on housing price: A case study of the Busan metropolitan region, Korea. Landsc. Urban Plan. 2019, 184, 1–11. [Google Scholar] [CrossRef]
- Rossi-Hansberg, E.; Pierre-Daniel, S.; Raymond, O., III. Housing externalities. J. Political Econ. 2010, 118, 485–535. [Google Scholar] [CrossRef]
- Santiago, A.; Galster, G.C.; Tatian, P. Assessing the property value impacts of the dispersed subsidy housing program in Denver. J. Assoc. Public Policy Anal. Manag. 2001, 20, 65–88. [Google Scholar] [CrossRef]
- Galster, G.C.; Tatian, P.; Smith, R. The impact of neighbors who use Section 8 certificates on property values. Hous. Policy Debate 1999, 10, 879–917. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Melichar, J.; Kaprova, K. Revealing preferences of Prague’s homebuyers toward greenery amenities: The empirical evidence of distance-size effect. Landsc. Urban Plan. 2013, 109, 56–66. [Google Scholar] [CrossRef]
- Hickman, E.P.; Gaines, J.P.; Ingram, F.J. The influence of neighbourhood quality on residential values. Real Estate Apprais. Anal. 1984, 50, 36–42. [Google Scholar]
- Herath, S.; Maier, G. The Hedonic Price Method in Real Estate and Housing Market research: A Review of the Literature; SRE-Discussion Papers 2010; WU Vienna University of Economics and Business: Vienna, Austria, 2010. [Google Scholar]
- Fan, G.; Ong, S.E.; Koh, H.C. Determinants of house price: A decision tree approach. Urban Stud. 2006, 43, 2301–2315. [Google Scholar] [CrossRef]
- Locurcio, M.; Morano, P.; Tajani, F.; Liddo, F.D. An innovative GIS-based territorial information tool for the evaluation of corporate properties: An application to the Italian context. Sustainability 2020, 12, 5836. [Google Scholar] [CrossRef]
- Chen, S.; Zhuang, D.; Zhang, H. GIS-based spatial autocorrelation analysis of housing prices oriented towards a view of spatiotemporal homogeneity and nonstationarity: A case study of Guangzhou, China. Complexity 2020, 2020, 1079024. [Google Scholar] [CrossRef]
- Chica-Olmo, J.; Canp-Guervos, R.; Chica-Revas, M. Estimation of housing price variations using spatio-temporal data. Sustainability 2019, 11, 1551. [Google Scholar] [CrossRef]
- Zhang, G.P. Times series forecasting using a hybrid ARIMA and neural network model. Nuerocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Sims, C. Macroeconomics and reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Morano, P.; Rosato, P.; Tajani, F.; Manganelli, B. Contextualized property market models vs. generalized mass appraisals: An innovative approach. Sustainability 2019, 11, 4896. [Google Scholar] [CrossRef]
- Wong, Y.; Solomon, P.L. Community integration of persons with psychiatric disabilities in supportive independent housing: A conceptual model and methodological considerations. Ment. Health Serv. Res. 2002, 4, 13–28. [Google Scholar] [CrossRef] [PubMed]
- Allan, D.; Hoesli, M.; Bender, A. Environmental variables and real estate prices. Urban Stud. 2001, 38, 1989–2000. [Google Scholar] [CrossRef]
- Worzala, E.; Lenk, M.; Silva, A. An exploration of neural networks and its application to real estate valuation. J. Real Estate Res. 1995, 10, 185–201. [Google Scholar]
- Werbos, P.J. Generalization of backpropagation with application to a recurrent gas market model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; California University San Diego La Jolla Inst for Cognitive Science, Institute for Cognitive Science, University of California: San Diego, CA, USA, 1985. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Hermans, M.; Schrauwen, B. Training and analysing deep recurrent neural networks. In Advances in Neural Information Processing Systems 26, Proceedings of the Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 190–198. [Google Scholar]
- Hoiem, D.; Chodpathumwan, Y.; Dai, Q. Diagnosing error in object detectors. Comput. Vis. 2012, 7574, 340–353. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 1735–1780. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.H.; Jun, M.-J. Prediction of Seoul House Price Index using deep learning algorithms withmultivariate time series data. SH Urban. Res. Insight 2018, 8, 39–56. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, H.J.; Kim, S.J. An Analysis on the Determinants of Mountainous and Coastal Area’s Housing Value Caused by the Characteristics of the Natural Environment. J. Korean Soc. Civ. Eng. 2013, 33, 811–819. [Google Scholar] [CrossRef]
- Reimers, N.; Gurevych, I. Optimal Hyperparameters for Deep LSTM-Networks for Sequence Labeling Tasks. arXiv 2017, arXiv:1707.06799. [Google Scholar]
- Qiumei, Z.; Dan, T.; Fenghua, W. Improved convolutional neural network based on fast exponentially linear unit activation function. IEEE Access 2019, 7, 151359–151367. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef]
- Zhang, Z. Improved Adam Optimizer for Deep Neural Networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, C.; Xin, H.; Wang, Y.; Wang, K. Prediction on housing price based on deep learning. Int. J. Comput. Inf. Eng. 2018, 12, 90–99. [Google Scholar]
- Enders, W. Applied Econometric Time Series, 3rd ed.; Wiley Series in Probability and Statistics: Hoboken, NJ, USA, 2010. [Google Scholar]
- Li, C.W.; Wong, S.K.; Chau, K.W. An analysis of spatial autocorrelation in Hong Kong’s housing market. Pac. Rim Prop. Res. J. 2011, 17, 443–462. [Google Scholar]

| Type * | Tenant | Income Quintile ** | Rent *** | Unit Size | Total Supply | |
|---|---|---|---|---|---|---|
| Build-to-rent | Permanent rental (permanent or 50-year contract) | Extremely low-income household, social/medical security recipients, disabled | 1st (less than 50%) | ~30% | less than 40 m2 | 307,115 |
| Citizens’ rental (30-year contract) | Low-income household | 2nd to 4th (70–100%) | 60%–80% | less than 85m2 (mostly less than 60 m2) | 509,248 | |
| Rent-to-own (5/10-year contract) | Low-income household, newlywed, multiple children, senior dependent | 3rd to 5th (100–120%) | ~90% | less than 85 m2 | 223,412 | |
| ‘Haengbok’ rental | Low-income household, college student, newlywed, young adults | 2nd to 5th (80–100%) | 60%–80% | less than 45 m2 | 2041 | |
| Buy-to-rent | Low-income household |
1st to 2nd (below 50%) | ~30% | less than 85 m2 | 92,004 | |
| Rent-to-rent | Low-income household |
1st to 2nd (below 50%) | ~30% | less than 85 m2 | 165,764 | |
| Variable | Description | Source |
|---|---|---|
| Apartment Price | Monthly average transaction price per m2 for each APT complex | MOLIT (Ministry of Land, Infrastructure, and Transport) Apartment real transaction price open system |
| Transaction volume | Total number of transactions made for each APT complex per month | MOLIT (Ministry of Land, Infrastructure and Transport) Apartment real transaction price open system |
| Total area | Total lot area for each APT complex | MOLIT (Ministry of Land, Infrastructure and Transport) Building Administration System |
| Floor | Maximum number of floors | MOLIT (Ministry of Land, Infrastructure and Transport) Building Administration System |
| Age | Building age of APT complex at the time of transaction | MOLIT (Ministry of Land, Infrastructure and Transport) Apartment real transaction price open system |
| Household | Total number of households | MOLIT (Ministry of Land, Infrastructure and Transport) Building Administration System |
| Brand | 1: Top 10 APT brands determined by the performance of constructor | MOLIT (Ministry of Land, Infrastructure and Transport) Building Administration System |
| Distance to PRH | Distance to the nearest PRH | Produced in GIS software (ArcGIS 10.3.1) |
| Household in PRH | Total number of households in the nearest PRH | Produced in GIS software (ArcGIS 10.3.1) |
| Exposure to PRH | comprehensive exposure to PRH(s) within 1 km | Produced in GIS software with Python (ArcGIS 10.3.1) |
| Construct 1 | Construct 2 | Construct 3 | Construct 4 | |
|---|---|---|---|---|
| Apartment Price | O | O | O | O |
| Apartment Characteristics Transaction volume Total area Floor Age Household Brand | O O O O O O | O O O O O O | O O O O O O | |
| Proximity to PRH(s) Distance to PRH Household in PRH Exposure to PRH | O O | O O O |
| Hyper-Parameters | ||
|---|---|---|
| #Cell Unit | #Hidden Layer | Sequence Length |
| 3/5/7 | 3/5 | 1/3/6/12 |
| Model 1 | Model 2 | Model 3 | Model 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Unit | Mean (Std. dev.) | Mean (Std. dev.) | Mean (Std. dev.) | Mean (Std. dev.) | ||||
| Apt. Price | 10,000 KRW/m2 | 263.27 | (73.18) | 266.87 | (73.76) | 292.47 | (89.29) | 259.31 | (69.25) |
| Trans. vol. | sales/mo. | 76.05 | (7.97) | 68.16 | (7.18) | 61.58 | (19.74) | 69.76 | (6.07) |
| Total area | 1,000m2 | 118.41 | (11.89) | 98.81 | (10.51) | 114.99 | (35.86) | 94.27 | (6.84) |
| Floor | #of floors | 21.00 | (0.79) | 21.40 | (0.91) | 21.25 | (2.67) | 21.38 | (0.75) |
| Age | years | 14.74 | (2.77) | 14.38 | (2.66) | 14.13 | (2.32) | 14.50 | (2.87) |
| Household | # of households | 950.99 | (67.51) | 885.16 | (82.25) | 783.75 | (162.86) | 911.71 | (89.91) |
| Brand | dummy | 0.10 | (0.03) | 0.11 | (0.03) | 0.18 | (0.07) | 0.09 | (0.02) |
| Dist. to PRH | m | 1571.36 | (78.1) | 571.30 | (17.75) | 595.05 | (40.78) | 565.21 | (17.77) |
| Household in PRH | #of households | 633.87 | (37.59) | 789.52 | (58.35) | 454.16 | (96.02) | 878.20 | (59.90) |
| Exposure to PRH | number | 0.29 | (0.22) | 0.64 | (0.44) | 0.25 | (0.07) | 0.74 | (0.56) |
| Variable | Apt. Price | Trans. Vol. | Total Area | Floor | Age | Household | Brand | Distance to PRH | Scale of PRH |
|---|---|---|---|---|---|---|---|---|---|
| Moran’s I * | 0.892 | 0.117 | 0.115 | 0.162 | 0.246 | 0.139 | 0.589 | 0.761 | 0.704 |
| Construct 1 | Construct 2 | Construct 3 | Construct 4 | ||
|---|---|---|---|---|---|
| Hyper-parameters | Fixed | Learning / Validation = 70/30 Activation function = ELU Initialization = He Optimizer = Adam Batch size = 1 Learning rate = 0.001 Dropout rate = 0.5 # of epochs = 5000 | |||
| # of cell unit | 3 | 7 | 7 | 7 | |
| # of hidden layer | 3 | 3 | 5 | 3 | |
| Sequence length | 1 | 1 | 1 | 1 | |
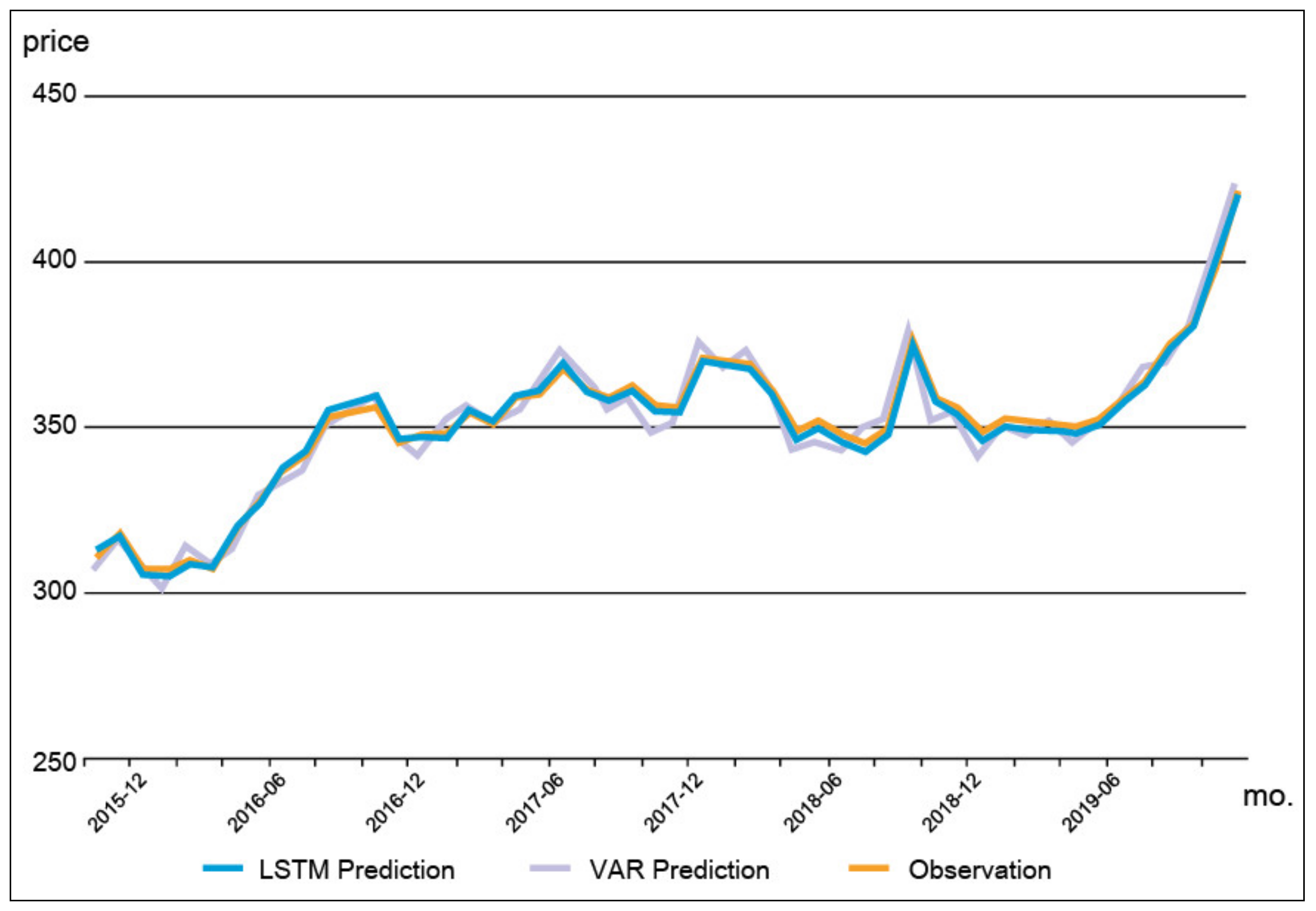
| RMSE | LSTM | 0.0563 | 0.0328 | 0.0317 | 0.0338 |
| VAR | 0.0849 | 0.0703 | 0.0548 | 0.0658 | |
| Construct 1 | Construct 2 | Construct 3 | Construct 4 | ||
|---|---|---|---|---|---|
| Hyper-parameters | Fixed | Learning / Validation = 70/30 Activation function = ELU Initialization = He Optimizer = Adam Batch size = 1 Learning rate = 0.001 Dropout rate = 0.5 # of epochs = 5000 | |||
| # of cell unit | 3 | 5 | 7 | 5 | |
| # of hidden layer | 3 | 3 | 5 | 5 | |
| Sequence length | 1 | 1 | 1 | 1 | |
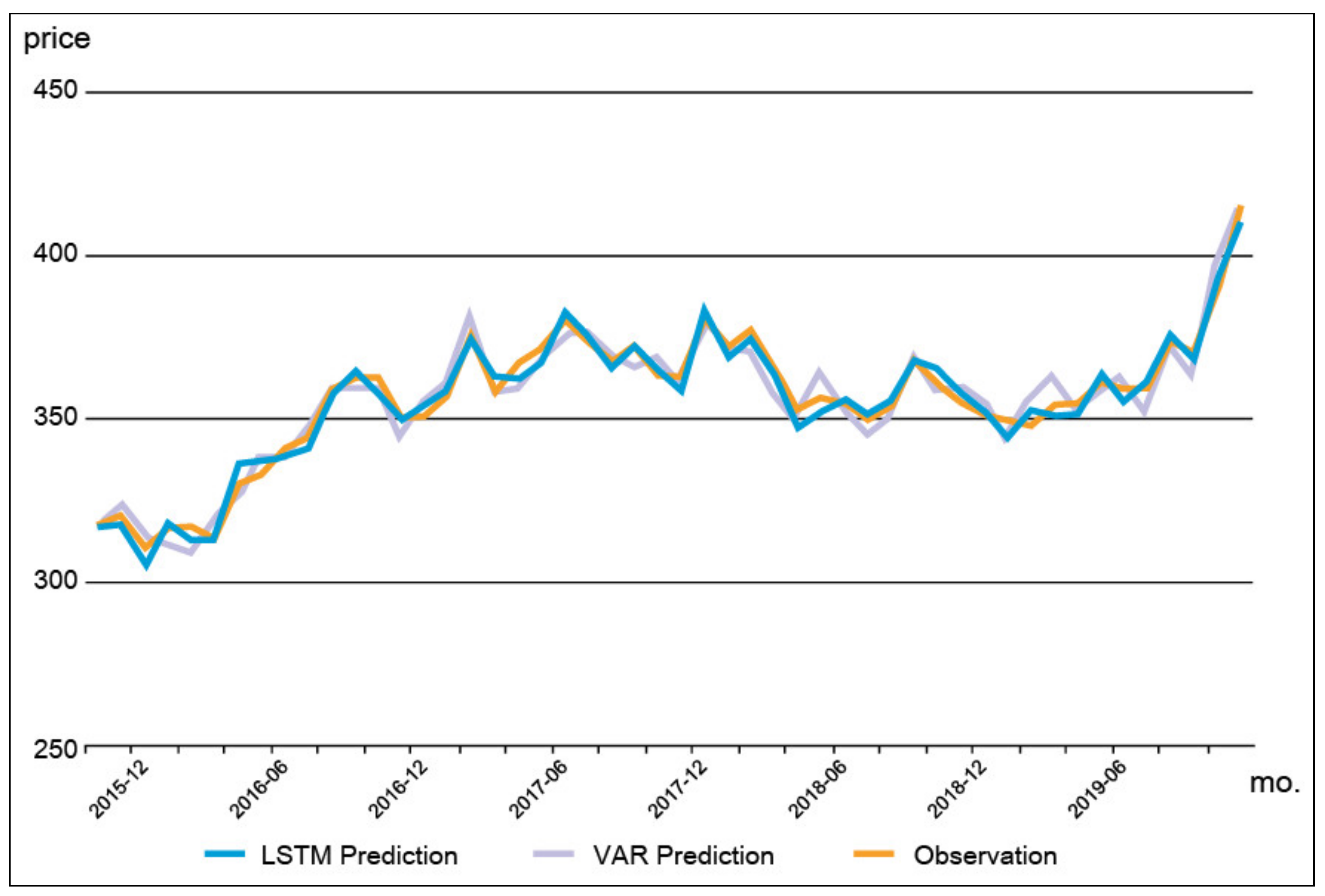
| RMSE | LSTM | 0.0670 | 0.0594 | 0.0573 | 0.0407 |
| VAR | 0.0796 | 0.0815 | 0.0626 | 0.0494 | |
| Subject | RMSE | |
|---|---|---|
| Model 1 (construct 3) | APT prices for the entire city | 0.0317 (0.0548) * |
| Model 2 (construct 4) | APT prices for the neighborhoods of PRH | 0.0407 (0.0494) * |
| Model 3 (construct 4) | APT prices for the neighborhoods of PRH located in “favorable” local housing market | 0.0490 |
| Model 4 (construct 4) | APT prices for the neighborhoods of PRH located in “less favorable” local housing market | 0.0489 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kwon, Y.; Choi, Y. Assessing the Impact of Public Rental Housing on the Housing Prices in Proximity: Based on the Regional and Local Level of Price Prediction Models Using Long Short-Term Memory (LSTM). Sustainability 2020, 12, 7520. https://doi.org/10.3390/su12187520
Kim H, Kwon Y, Choi Y. Assessing the Impact of Public Rental Housing on the Housing Prices in Proximity: Based on the Regional and Local Level of Price Prediction Models Using Long Short-Term Memory (LSTM). Sustainability. 2020; 12(18):7520. https://doi.org/10.3390/su12187520
Chicago/Turabian StyleKim, Hyunsoo, Youngwoo Kwon, and Yeol Choi. 2020. "Assessing the Impact of Public Rental Housing on the Housing Prices in Proximity: Based on the Regional and Local Level of Price Prediction Models Using Long Short-Term Memory (LSTM)" Sustainability 12, no. 18: 7520. https://doi.org/10.3390/su12187520
APA StyleKim, H., Kwon, Y., & Choi, Y. (2020). Assessing the Impact of Public Rental Housing on the Housing Prices in Proximity: Based on the Regional and Local Level of Price Prediction Models Using Long Short-Term Memory (LSTM). Sustainability, 12(18), 7520. https://doi.org/10.3390/su12187520





