Classification of Inter-Urban Highway Drivers’ Resting Behavior for Advanced Driver-Assistance System Technologies using Vehicle Trajectory Data from Car Navigation Systems

Abstract

Fatigue-related crashes, which are mainly caused by drowsy or distracted driving, account for a significant portion of fatal accidents on highways. Smart vehicle technologies can address this issue of road safety to improve the sustainability of transportation systems. Advanced driver-assistance system (ADAS) can aid drowsy drivers by recommending and guiding them to rest locations. Past research shows a significant correlation between driving distance and driver fatigue, which has been actively studied in the analysis of resting behavior. Previous research efforts have mainly relied on survey methods at specific locations, such as rest areas or toll booths. However, such traditional methods, like field surveys, are expensive and often produce biased results, based on sample location and time. This research develops methods to better estimate travel resting behavior by utilizing a large-scale dataset obtained from car navigation systems, which contain 591,103 vehicle trajectories collected over a period of four months in 2014. We propose an algorithm to statistically categorize drivers according to driving distances and their number of rests. The main algorithm combines a statistical hypothesis test and a random sampling method based on the renowned Monte-Carlo simulation technique. We were able to verify that cumulative travel distance shares a significant relationship with one’s resting decisions. Furthermore, this research identifies the resting behavior pattern of drivers based upon their travel distances. Our methodology can be used by sustainable traffic safety operators to their driver guiding strategies criterion using their own data. Not only will our methodology be able to aid sustainable traffic safety operators in constructing their driver guidance strategies criterion using their own data, but it could also be implemented in actual car navigation systems as a mid-term solution. We expect that ADAS combined with the proposed algorithm will contribute to improving traffic safety and to assisting the sustainability of road systems.

1. Introduction

Fatigue-related crashes, which are mainly caused by drowsy or distracted driving, account for a significant portion of fatal accidents on highways [1]. Increased fatigue during driving is a consequence of repetitive and monotonous tasks, which result in a deterioration of driving performance [2]. Prolonged driving time without sufficient rest induces fatigue, which is a critical factor in careless driving. To reduce fatigue-related traffic accidents, it is crucial for drivers to get sufficient rest and avoid long periods of continuous driving. Highway associations such as Korea Expressway Corporation manage rest areas on the interurban highways by following the highway design guidelines. The standard distance between two rest areas in Korea is 15 km, and the maximum recommended distance is 25 km [3].

Lapses in driving tasks are highly associated with traffic accidents [4,5,6,7,8]. The authors of [4] identify behavioral factors that affect road safety by employing Analytic Hierarchy Process techniques. Their results indicate that lapses and error are the most significant factors. One’s driving time on roads stretched across a monotonous landscape also has an effect on driving performance, which causes drowsiness and errors in maneuvering [2]. The authors of [9] measure drivers’ blink duration on the wheel in a driving simulator and found that the blink duration of a drowsy driver is substantially affected by time-on-task. Those drivers have a higher risk of lane departure. The authors of [10] add performance impairment in driving by driving distance.

Highway operators and safety managers are interested in guidance systems that can encourage potentially drowsy drivers to stop at the nearest rest area. Variable message signs (VMSs) on the roadside have little influence on compliance. Noting the location of a message sign increases the driver’s attitudes about VMSs [11]. Previous studies report that over 2 hours of driving without rest induces a driver to be close to falling asleep [12]. This fact supports the need for effective countermeasures to discourage drivers from driving for extended periods of time by guiding them to take a rest in a designated rest area. VMSs can be more effective if their design integrates the knowledge of drivers’ fatigue or resting behavior. However, the fixed location of VMSs limits the incorporation of details regarding the driving distances of each driver.

Motivation and Contribution of the Study

We were motivated by recent vehicle technologies such as informatics from car navigation and driver-assistance systems (ADAS) to improve sustainable traffic safety by appropriately alerting drivers to take a break. A short-term feasible countermeasure can be a recommendation alert through a car navigation system when a driver is likely to feel sleepy. Another solution can be to enforce regulatory policies on drivers, specifically commercial truck drivers, to not drive more than certain driving distances or hours. The Hours of Services Regulation enacted by the USA Federal Motor Carrier Safety Administration is an example [13].

Possible mid- and long- term solutions can include the use of ADAS. This technology benefits drivers through vehicle control features, such as lane-keeping assistance, adaptive cruise control, and data collection [14]. This research focuses on data collection and an adaptive alert system. We envision an ADAS equipped vehicle that collects information about drivers’ behavior and surrounding road conditions and using that information to issue an appropriate warning message to drivers to rest. We expect that drivers would comply at higher rates knowing that the message was customized for them by their car, as opposed to the usual scenario where safety message signs are displayed on highways for every driver to see.

For these solutions, understanding the proper distance criteria for guiding drivers to stop driving is of critical importance, but the criteria’s reliability depends on the method of data collection. The most common method is a field survey. Traditional survey methods have been widely conducted to gather information about drivers’ behavior. However, surveys are dependent on limited budgets and locations, which implies that the accumulated data is not comprehensive, both qualitatively and quantitatively. Therefore, if one requires an abundant number of samples to establish relevant policies, conducting a field survey naturally entails exorbitant costs. Therefore, the survey cannot be conducted continuously over time and space, which cannot meet the expectations of sustainable transportation data management and policy on highway safety. Also, a field survey cannot be free from bias for other reasons. For instance, it will only generate responses from those who use rest areas at certain times.

This study aims to analyze resting behavior based on highway drivers’ travel distance data collected from a large-scale real navigation dataset, and to provide a rest criterion for drivers based on their travel distance using the Monte-Carlo simulation method. The criterion we suggest could be utilized as a guideline for policymakers and/or highway operators.

If actual datasets are available, the overall analysis and conclusion of drivers’ resting behavior will be less biased and more reliable. Additionally, if datasets can be obtained on a regular basis, transportation policies can be sustainably updated to consider future drivers’ behavior affected by new mobility technologies. Using a large-scale dataset from car navigation systems, which are less biased samples than datasets obtained from spot-based field surveys, this study analyzes drivers’ resting behavior. Results from statistical analyses confirm that drivers on turnpikes in Korea tend to have a correlation between travel distances and the number of rests, which motivates the authors to categorize groups of drivers based on these two variables. Previous research and details about the methodologies will be addressed in the rest of the paper. The rest of the paper is structured as follows: In Section 2, we review relevant research in this area; in Section 3, we describe the characteristics of datasets acquired from car navigation systems and the methodology to cluster highway driver behaviors; in Section 4, we present the clustering results, including a discussion about said results. Finally, Section 5 concludes this study.

2. Literature Review

Rest stations in highways are pivotal facilities for drivers because these stations provide a place to reduce driver fatigue and offer various services. The Federal-Aid Highway Act of 1956, which led to the creation of a national interstate system in the United States, declared the purpose of a rest area as being for safety and convenience [15]. A 1958 policy by the American Association of State Highway Officials [16] initiated the half-hour rule of thumb (i.e., that drivers can access a place to break every 30 min driving) and set detailed design regulations for rest areas. This 30-min rule has been an unofficial standard considered during highway construction from the following year. Besides the Federal rules, some states have since issued their own guidelines. In 2007, the Minnesota Department of Transportation [17] suggested a distance of 30 m between rest areas as an appropriate standard.

The enhancement of service quality based on an understanding of driving behavior is essential. Various survey methods have been proposed in the literature. The most common method is a personal interview survey [4,5,6,8,18,19,20,21,22,23]. The second approach is to utilize a driving simulator [2,10,24,25]. In addition, a retrospective case-control study based on actual traffic accident data is conducted [20,26]. Last but not least, recent researchers employ the actual driving dataset [7].

Regardless of the type of survey applied, research indicates that prolonged driving time is a major factor in traffic accidents. In other words, long travel distances and driving times distract drivers excessively and increase fatigue levels. The authors of [19,20] imply that the usages of a rest area highly correlated to not only the use of restrooms, but also to stretch/take a break from driving. Research [20] identifies that driver-at-fault crashes related to sleepiness strongly correlate to instances where rest havens/truck stops are located over 20 m apart. Research [24] also finds that overextended driving time in a driving simulator decreases the driver’s maneuver performance. Considering experiments with driving simulators, Ref. [27] reveal that drivers tend to increase their safety margins when their fatigue has accumulated over long period trips. Focusing on the speed drop at a sag section on an expressway utilizing probe cars, Ref. [28] divides driver fatigue level into three stages: (1) Stage 1 being in a healthy or normal state; (2) Stage 2 being in a transitional state between normal and fatigued; (3) Stage 3 being in-fully fatigued state. In their study, the researchers discovered that drivers’ fatigue status transitioned from one stage to the next approximately every 80 min. From the results of simulator-based experiments, Ref. [29] concludes that long-period driving is a vital factor in driving fatigue and might cause fatigue-related accidents. They also suggest that 80 min is the safe driving limit for the driver on the highway without resting. The authors of [18] indicate that rest areas within 20 m from each other contribute to the decline of fatigue-related accidents.

The large body of literature regarding drivers’ fatigue shows driving time and distance are significantly correlated to driver-fatigue, which causes traffic accidents on highways; previous research relies on survey methods to compile information about drivers’ resting behavior or their satisfaction levels on the distribution of rest areas on highways. As previously discussed, survey methods for highway drivers are not desirable in that the survey is restricted to only places where the survey is conducted. A simulation-based approach is preferable when tackling geographical limitations. However, a driving simulator approach is expensive, and results will fluctuate depending on the participants involved, due to the issue of participant bias. For instance, Ref. [2] states that the dominant group in such experiments tends to be young and more aggressive, which skews the collected data. Another example is [25], where the samples predominantly consisted of male drivers. Therefore, it is necessary to analyze highway drivers’ rest behavior based on real vehicle trajectory data and build an analysis methodology accordingly. In the next section, we describe a new method to demonstrate the relationship between highway drivers’ resting behavior by their usual travel distance by harnessing data from car navigation systems.

3. Methodologies

3.1. Car Navigation Database for this Study

This research utilizes the car navigation database (CNDB) of the entire Korea region that comes from the Korea Transportation DB (KTDB) center at the Korea Transportation Institute (KOTI). CNDB had collected data from August 2013 to December 2015 for research purposes from Car Navigation Systems (CNS) under a memorandum of understanding with MN-soft, which is a child company of Hyundai Motors.

By limiting the target analysis period to March, April, October, and November in 2014, this research minimizes the consequences of seasonal variances and traditional Korean holidays such as Lunar New Year (February) and Chuseok (September). In the same manner, the data for Tuesday, Wednesday, and Thursday are used to eliminate weekly inconsistencies of Monday and Friday. The dataset contains vehicles’ trajectory and their identification numbers.

One of the main advantages of data from CNS is that it provides aggregate-level data of a link-level trajectory and link accessing/egressing time, which reduces the data size compared to the total data set from Global Positioning Systems. Being able to match link IDs to link type and their geometry enables us to analyze specific travel behaviors of drivers accurately. Due to the existence of data security measures and privacy requirements, vehicle type information cannot be obtained. The size of the total dataset is 279 GB, and it contains 14,614,137 vehicle trips. For the purpose of analyzing the behavior of turnpike drivers, we filtered drivers to only include those who traveled on highways with limited road geometry. As a result, total vehicle trajectories were reduced to 591,103. Figure 1 indicates the paths of all vehicles using highways. These paths not only contain highway links, but also surface streets as drivers’ stress depends on total travel distances accumulated from their origin.

We make the following assumptions to capture drivers’ rest behavior. Since vehicle trajectory data do not provide specific information on where/when drivers take a break, this research firstly defines the scope of rest areas to the spots that the highway operation company officially designates and operates. There are two types of rest areas: (1) On-route service centers that are a place to purchase refreshments, refuel gas, and use restrooms, and (2) a rest stop where a driver pulls over to take a short nap. We could identify rest areas from digital map data and link information on the trajectory. Each link has an associated link type information, which is used to check whether it is an entrance or exit link of a rest area. Once a vehicle passed an entrance link and took a break for a certain duration, we regarded the driver rests upon a rest area. We also set the time duration as 5 min, meaning that only some drivers were regarded to be at rest when the vehicle had stopped for over 5 min on the link with the rest area attribute.

3.2. Travel Distance and the Number of Rests in Highway Driving

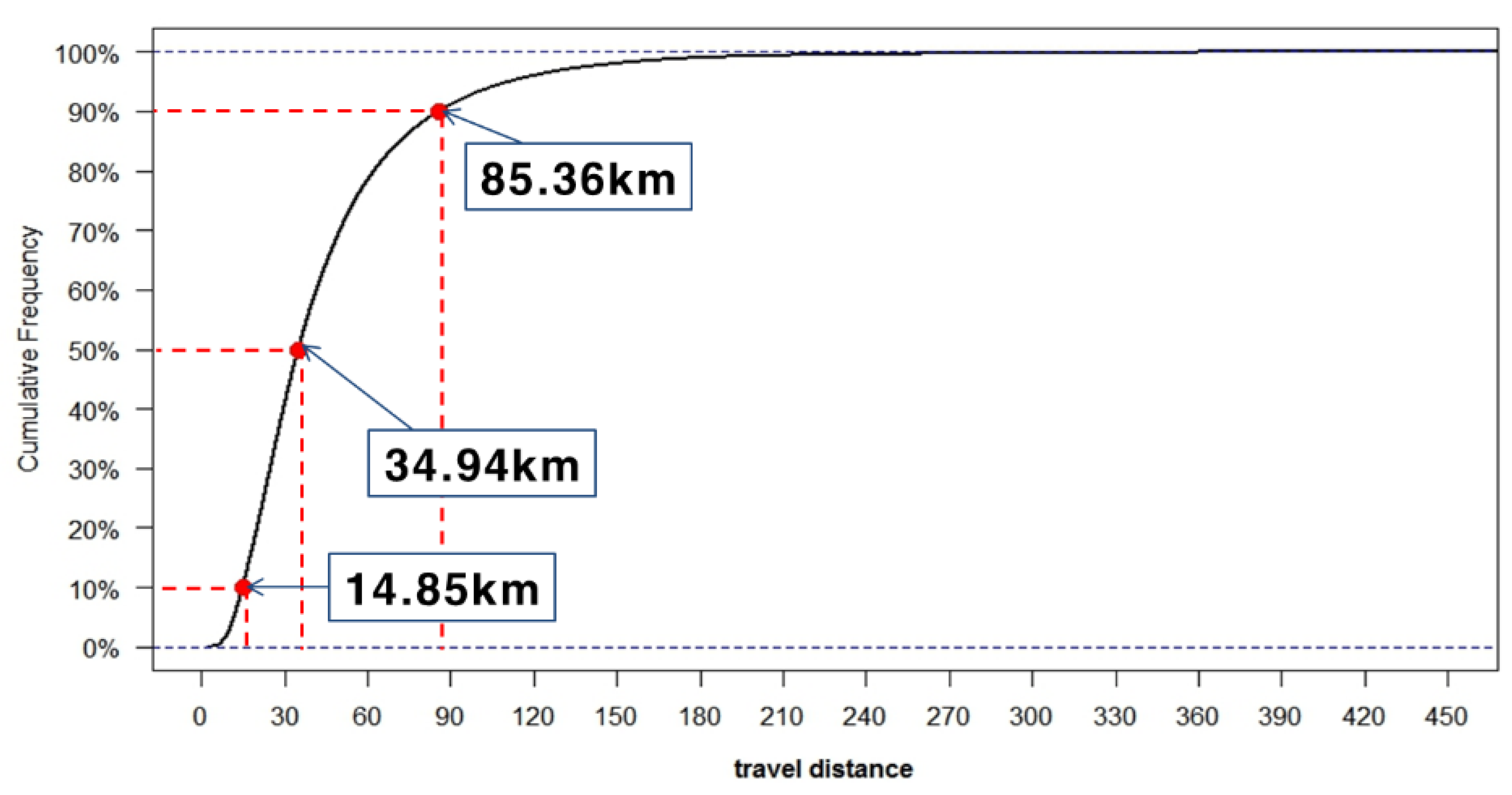
Based on the CNS data, it is possible to analyze drivers’ rest behavior in relation to their trip distance. Before analyzing resting behavior, we first generate the trip distance distribution for analysis. As demonstrated in Figure 2, which is the cumulative curve of travel distances by the CNS data, the medium travel distance is 34.94 km. Its 10 and 90 percentiles are 14.85 km and 85.36 km, respectively. These statistics imply that most trips coming from CNS on the highway were inter-urban trips.

To identify patterns of rest stop frequencies according to the distance traveled, we analyze the rest ratio of drivers by each driving distance range. In our preliminary analysis, we divide the driving distance into 50 km-distance intervals to experimentally find the rest ratio.

Table 1. The comparison of the number of rest and travel distance.

Rest Behavior	Travel Distance (km)
	0–50	50–100	100–150	150–200	200–250	250–300	300–350	350 over
Zero rest	410,195	128,594	21,637	4207	773	271	154	49
One-time rest	3247	8954	5476	2563	826	413	322	139
Two-times rest	80	709	781	576	423	237	189	132
Three-times rest	0	14	22	36	30	16	23	15
Total numbers of samples	413,522	138,271	27,916	7382	2052	937	688	335
Rest numbers of samples	3327	9677	6279	3175	1279	666	534	286
Average resting rate (%)	0.80%	7.00%	22.49%	43.01%	62.33%	71.08%	77.62%	85.37%

shows the comparison of the number of rests and the travel distance at every 50-km interval range. The general pattern indicates that the number of rests is proportional to a driving distance. For short distances of less than 50 km, only 0.08% of drivers take a rest. The average resting rate of drivers in the 150–200 km travel distance interval is 43.01%—approximately 85% of drivers who drive more than 350 km stop at least once at rest areas.

From Table 1, we could also infer that a large proportion of drivers make trips less than 50 km on highways. About 70% (413,552) of those trips are within 50 km. These trips are unlikely to require a period of rest. Only 0.8% of drivers stopped by rest areas, whereas only a small portion of trajectory data are captured in the CNS data. The travel range from 300 to 350 km trips has only 688 trips, which represent 0.1% of the total, but 77.62% of them stopped by rest areas. In this regard, the number of long-distance trips was excessively low compared to the number of short-distance trips. Even though there is a difference between the sample proportions in terms of each trip distance interval, CNS data are enough to impute drivers’ resting behavior depending on their trip distance because there are distinct resting behaviors in relation to each trip distance interval. In addition, the least number of samples that were collected at an ‘above 350-km’ travel distance interval is 286. The statistics discussed here indicate that drivers’ resting behavior is related to driving distance.

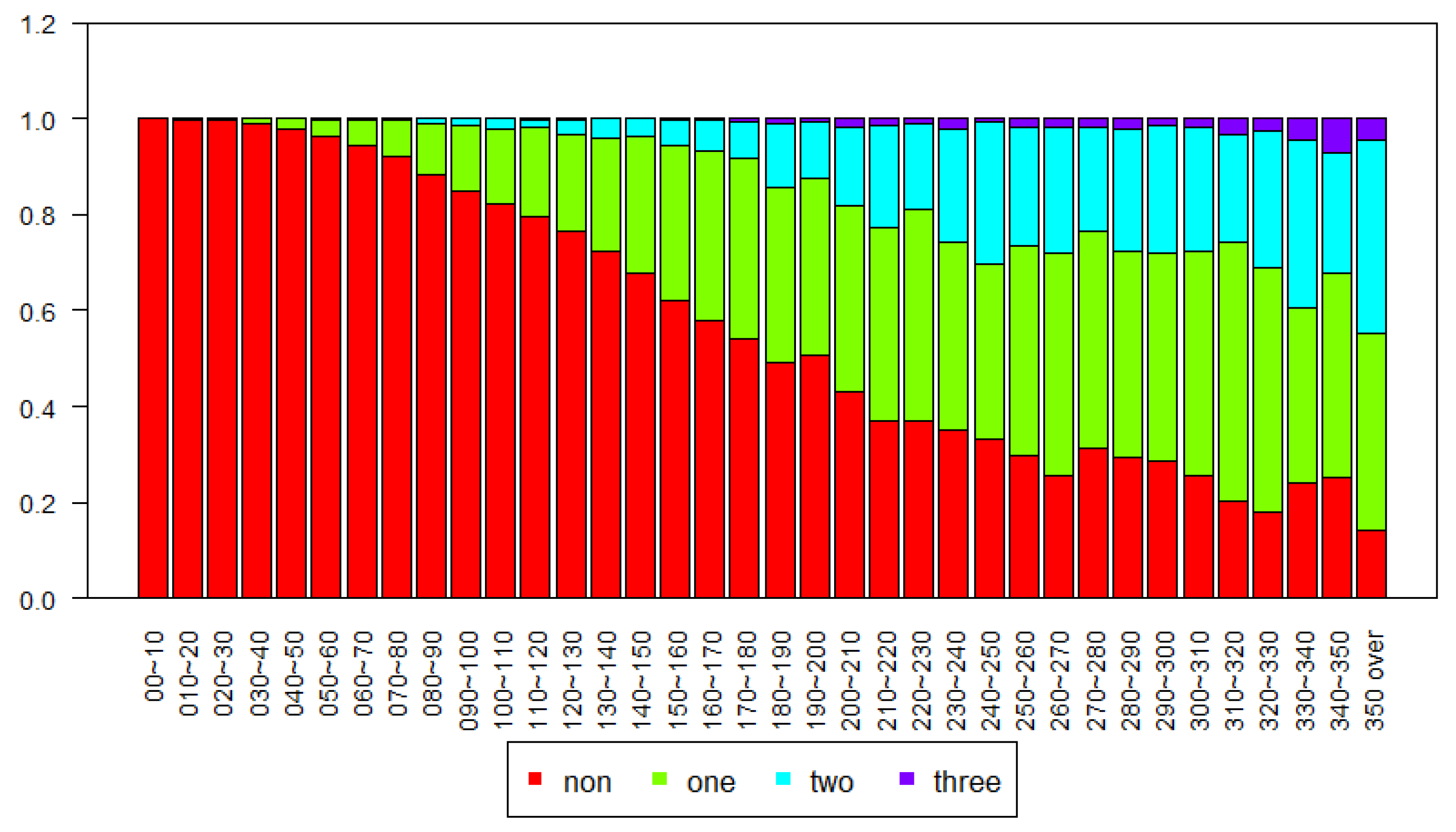
For more detailed investigations, we conduct a random sampling analysis to calculate the proportion of the number of rests associated with driving distances. Here, we further discretize the driving distance into 10 km intervals to examine detailed behavior, and then we apply a random sampling method, which is useful not only to explain a characteristic feature of a large-scale population data, but also to balance the number of sample data, which would be selected from the data at each interval. Note that only 88 individual trips were collected in the 340–350 km interval, as shown in Figure 3. In this research, by considering this number as the minimum base criterion, we select 80 sample trips in a range and averaged those samples. We reiterate this process ten times. By averaging the 10-averaged data at each range, we could also reduce the impact of outliers.

Very few drivers took a rest within a 30-km drive. However, the proportion of drivers who rested at least once increased as the travel distances rose accordingly. In the travel distance interval of 50–60 km, 3.5% of drivers took a rest once, while at the travel distance of 80–90 km, 10% of drivers took a rest at least once. The longer the travel distance, the more people took rests once or more. As a matter of fact, when drivers’ trip distance was over 180 km, about half of drivers chose to rest at least once.

In Figure 3, drivers’ resting behavior is distinctly different according to their travel distance. Drivers who drive less than 100 km rarely take rests twice. However, the proportion of drivers who take rests twice increases when drivers travel more than 200 km. For instance, about 16.7% of drivers stop at rest areas two times. From these patterns, we classify drivers’ resting behavior into two groups: (a) First group drivers—who may or may not take any rests; (b) second group—drivers who may or may not take rests twice. From one’s resting behavior patterns, we could identify that the rate of drivers who take rests is proportional to their trip distance.

3.3. A Clustering Approach for Highway Drivers’ Behavior Analysis

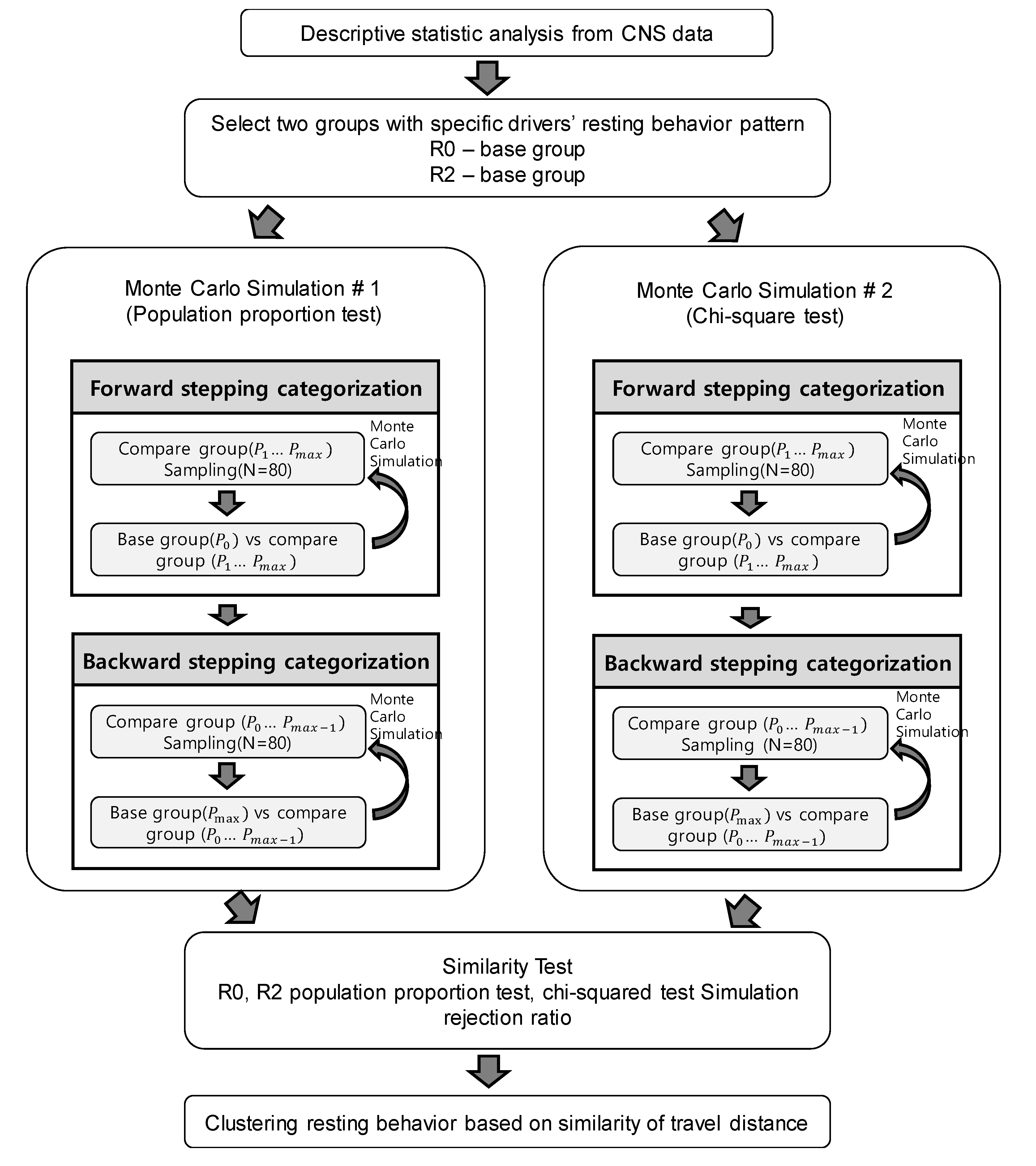
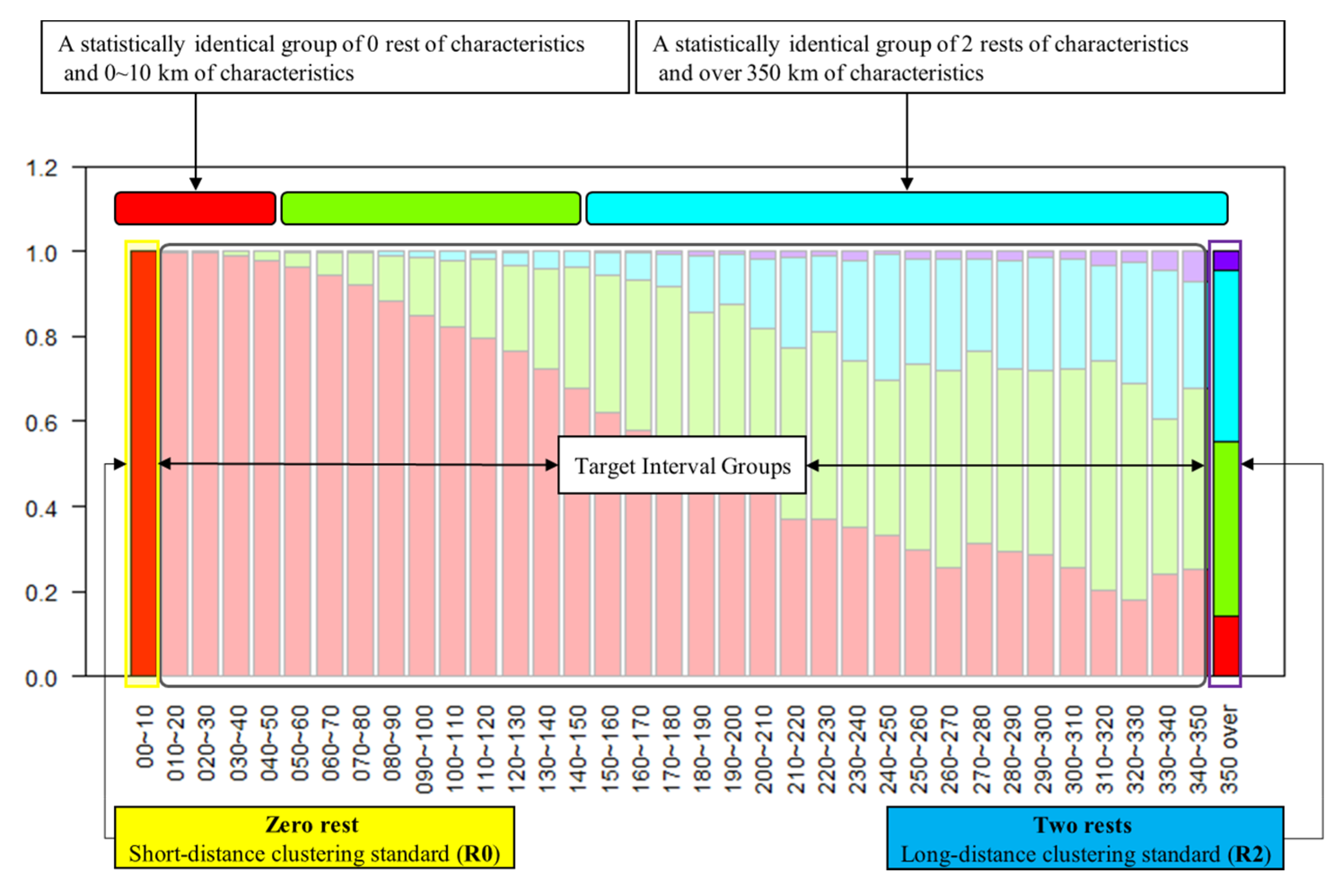
Figure 4 shows an overview of the proposed method for clustering resting behavior. The preceding section expands the possibility of categorizing drivers’ resting behaviors according to travel distances. From an operational point of view, we divide drivers into three categories based on their distance traveled: (1) Short distance (R0); (2) mid-range distance (R1); and (3) long-distance (R3). As analyzed in the previous section, there are distinctive rest patterns according to the travel distance. Having an appropriate criterion can help policymakers or highway operators when they design guidelines for specific drivers to take a rest. For instance, a driver traveling a long distance and taking fewer rests than drivers in his driving group is more likely to be drowsy. Therefore, if a highway operator can recognize drivers who are traveling longer distances, they will be able to guide drivers to the nearest rest area.

However, setting a clustering criterion without a sound mathematical basis is bound to be subjective, which is why we propose a statistical clustering approach. Once we identify the base groups, we start to categorize from a statistical comparison between a base group and an experimental group. Here, the experimental group is a subsequent group that is the next base group based on distance traveled. If a rest pattern of the experimental group is significantly different, we categorize it as the other group. This process can be regarded as semi-supervised learning since the categorization is computed by comparing a labeled base group and an unlabeled experimental group.

In this regard, this research categorizes highway drivers by travel distance and the number of rests, utilizing data from CNS. Intuitively, the descriptive statistics confirm that the pattern of the number of breaks for the shortest travel distance group (within 10 km) is significantly different from the pattern of longest distance trips (over 350 km). This distinctive pattern difference inspires us to identify whether the rest driver groups belong to a group of the shortest distance or longest distance, and this categorization is conducted by a statistical test. The pre-defined two base groups have their statistics (mean and variance), which are used to decide the rest drivers’ group identity. The statistical test plays a role in identifying their status, but if a driver could not be placed in any group, he/she is assigned to the middle group. In other words, a trip group not belonging to the short or the long-distance group belongs to the mid-distance group. The details about this test will be addressed in the next section.

With the two defined base groups, we derive a ratio of the number of drivers who took a rest to the number of drivers at each travel group. None of the drivers took a rest in the first base group (i.e., the shortest travel distance group). For the second base group (i.e., the most extended travel distance group), 43.88% of drivers took a rest at least twice. With these results, we are able to define patterns of highway drivers. We claim that a feature of the short distance travelers would have a similar drive behavior derived from the first base group (i.e., approximately zero percent of rest behavior based on drivers’ travel distance), and b) a feature of the long-distance travelers would have a similar drive behavior derived from the second base group (i.e., roughly 43.88% of at least two-times rest behavior based on drivers’ travel distance). We simply categorize these independent resting-behaviors in R0 and R2, respectively. Otherwise, drivers would fall into the mid-distance group, and this group of people would fall under the category, R1 (

Table 2. Resting behavior category.

Driving Behavior Group	Description
R0	Drivers who have approximately a zero probability of taking a rest which is a similar proportion as the first base group drivers who do not take a rest
R2	Drivers who have approximately a 43.88 percentage of probability of taking at least two rests which is similar to ‘two-times resting behavior’ proportion of the second base group drivers
R1	Drivers who do not belong to both R0 and R1 groups

). For example, if a percentage of non-rest drivers in the target group is similar to the ratio of the first base group, then this group will be categorized as a short-distance traveler, and therefore belong to ‘R0 category’.

Figure 5 visually illustrates the details of the proposed methodology. All trip distance groups with the exception of the last group are defined by 10 km trip distances. This means that drivers in each interval have similar travel distances, but resting behaviors in each range are heterogeneous. The second to last interval, where trip distance is between 340 km and 350 km, has the lowest observation number at 88. We heuristically define the previous range that travels more than 350 km, since the sample rate is insignificant, and its drivers tend to take a rest at least two times in their journey.

3.4. A Statistical Approach for Resting Behavior Analysis

Basically, we applied a semi-supervised analytical categorization method, which categorizes the sample data by comparing the target group to a pre-defined comparison group. Once the target group violates a null hypothesis that the target group is statistically identical with the pre-defined group, the model generates the target group. Otherwise, the target group belongs to the pre-defined group.

The null hypothesis of our study is that there is no difference in proportion between the two groups. The alternative hypothesis is that there are significant proportional differences between the two groups; thus, these tests are of a two-tailed test, as the null hypothesis would be rejected when the test statistic does not fall into the range within the value of a significant level.

$${\mathrm{H}}_0:{\mathrm{P}}_1-{\mathrm{P}}_2=0$$

(1)

$${\mathrm{H}}_1:{\mathrm{P}}_1-{\mathrm{P}}_2\ne 0$$

(2)

Algorithm 1 displays the overall process. The bi-directional comparison method plays a vital role in categorizing driving groups. In summary, the statistical comparisons are conducted from both directions: (1) Short-distance group to long-distance group (Steps 1 and 2), and (2) long-distance group to short-distance group (Steps 3 and 4). Finally, the path groups not allocated to the base groups are regarded as a mid-distance group. The main advantage of statistical comparison is that it is consistent and mathematically sound. However, a notable disadvantage is that it is likely to be unsuitable for a large-scale dataset. The characteristic of a large sample size deters clustering performances since statistical comparison tests tend to be stricter as the size of samples is larger. A significantly narrow confidence interval from the large dataset results in a very low p-value that is most likely to reject the hypothesis [30].

Algorithm 1. Classification Algorithm

01  Step 0. Initialization

02  Divide vehicle trips according to trip distance by 10 km

03  path_group = [P0, P1, …, , Pmax ]

04  nofgroups = len(path_group) # the number of path groups

05  Gshort = [P0]

06  Glong = [Pmax]

07  Gmid = [∅]

08  Step 1. Forward stepping categorization (Multiple Simulations approach)

09  base_group = P0 # the shortest travel path group (0–10 km driving)

10  compare_groups = [P1, …, , Pmax ]

11  N_S = Simulation-based Statistical test(base_group, compare_groups)

12  Step 2. Categorizing a short driving distance path group

13  for n ∈ N_s:

14    If n < Criteria: # number of accepted hypothesis in each path group (Gj) <Criteria

15      Gshort = [Gshort ∪ Gj]

16    End if

17   End for

18  Step 3. Backward stepping categorization (Multiple Simulations approach)

19  base_group = Pmax # the shortest travel path group (>350 km driving)

20  compare_groups = [Pmax-1 , …, , P0 ]

21  N_L = Simulation-based Statistical test (base_group, compare_groups)

22  Step 4. Define a long driving distance group

23  for n ∈ N_L:

24    If n < Criteria: # number of accepted hypothesis in each path group (Gj) <Criteria

25      Glong = [Glong ∪ Gj]

26    End if

27   End for

28  Step 5. Define a mid-range driving distance group

29  Gmid = path_group – [Gshort ∪ Glong]

30  End

To the authors’ best knowledge, however, the most practical solution to this problem has not been identified. Hence, we propose a potential solution that utilizes the Monte-Carlo simulation technique. Instead of testing the entire large-sample data, this heuristic approach uses repeated random sampling methods and conducts multiple hypothetical tests, as shown in Algorithm 2, which we call multiple simulations based statistical test.

Algorithm 2. Simulation-based Statistical test

Input: base_group, compare_groups (k intervals)

significance level (alpha = 0.05), number of samples = 80

Output: Number of accepted for the hypothesis (N = [N0, N1, …, Nk]) of k intervals

00  Step A. Initialization

01  N = zeros(compare_groups) # for all Ni = 0, N will be used to decide the group is in

the group or not

02  Step B. Hypothetical tests with Multiple simulations

03  For i: I ∈ (0,100): # 100 trials

04    sample1 = Random Sampling(base_group, nofsamples)

05    for pj ∈ compare_groups:

06      sample2 = Random Sampling(pj, nofsamples)

07      Accepted = Hypothetical Test(sample1, sample2, alpha)

08      if Accepted:

09        N[pj] + = 1

10      End if

11    End for

12  End for

13  End

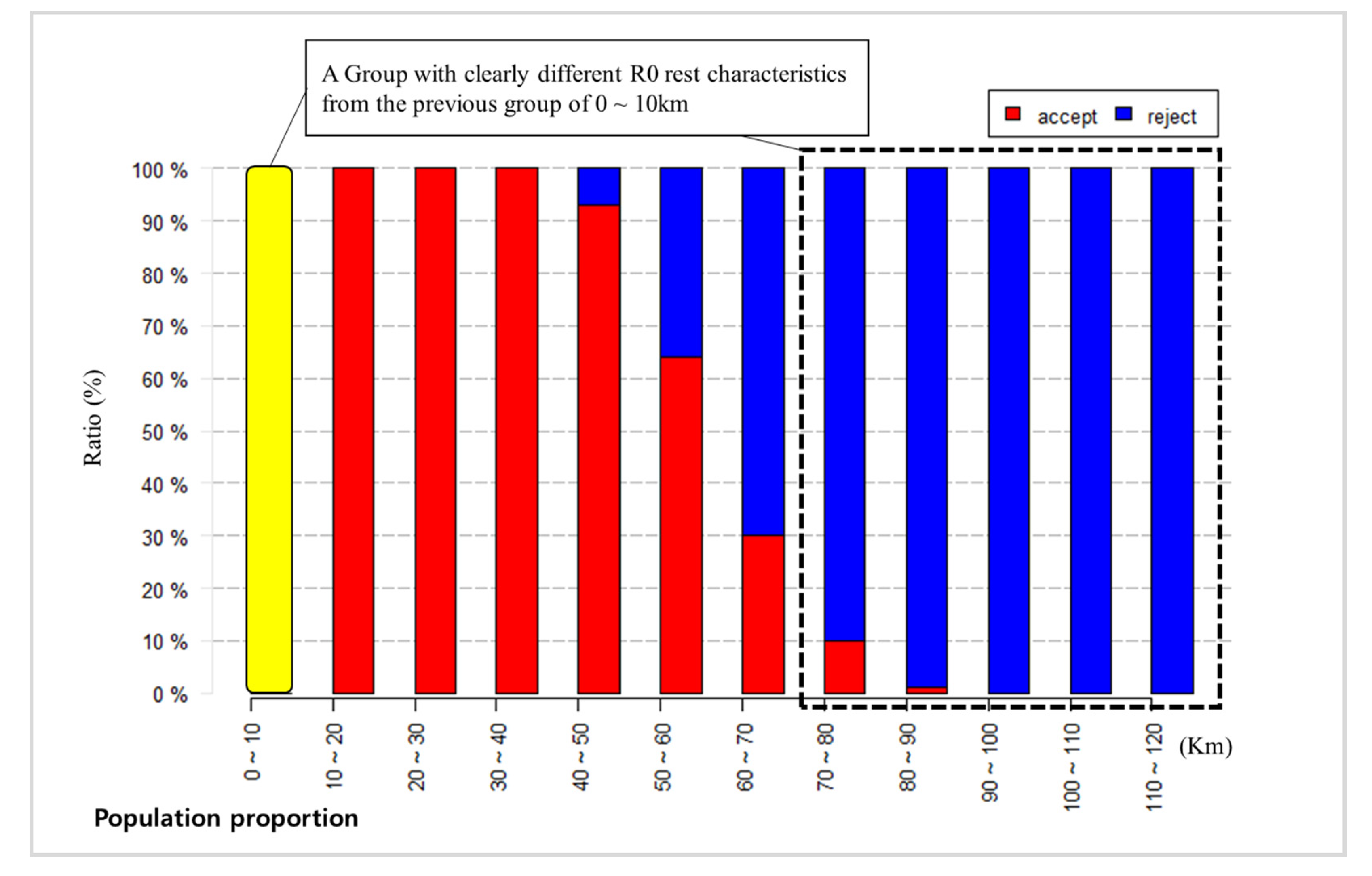
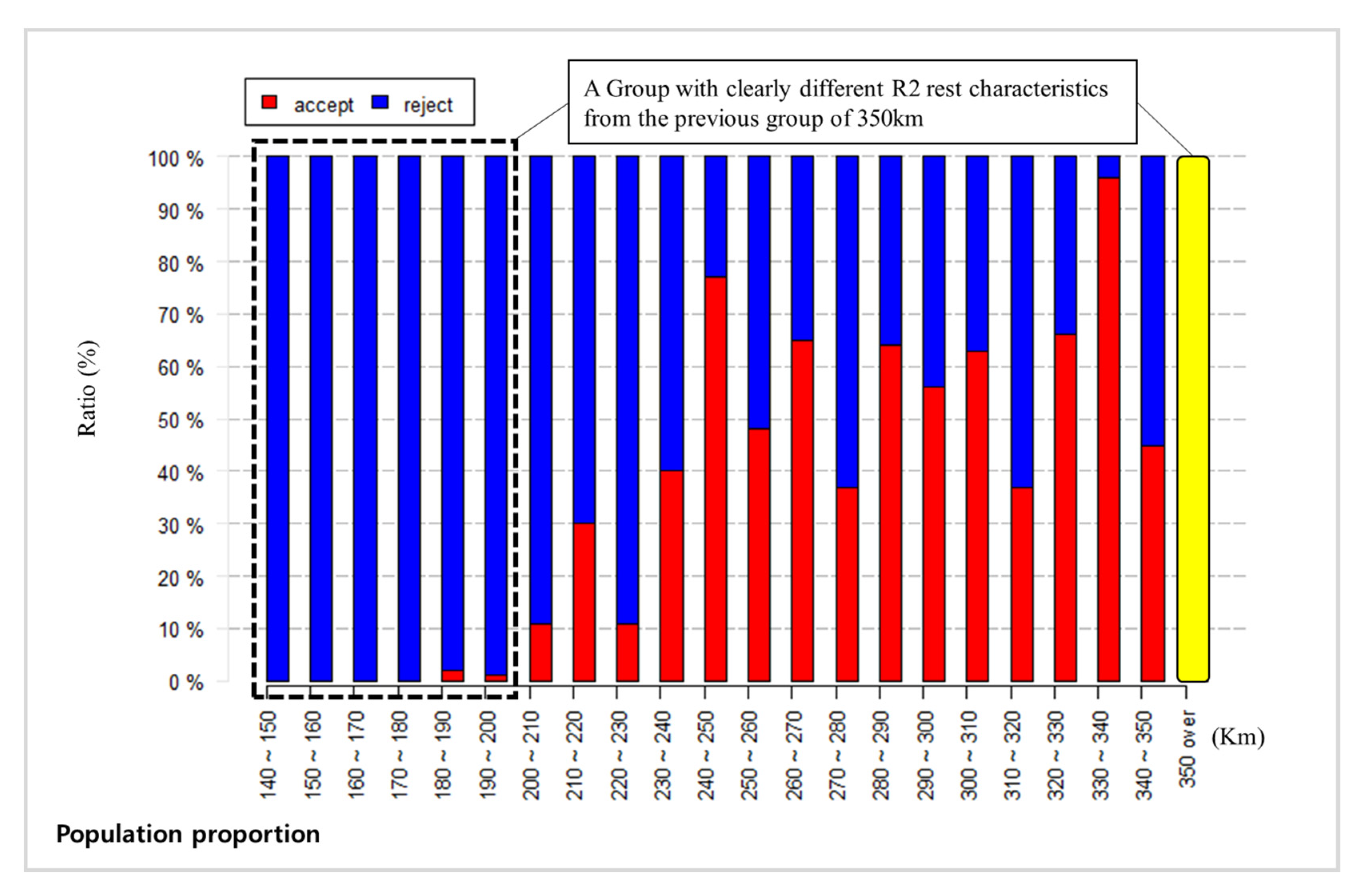
Eighty travel paths are randomly selected from each group, and 100 statistical comparisons are created. This algorithm generates the group decision array, including the number of accepted instances of the null hypothesis in Steps 1 and 3 of Algorithm 1. From multiple trials, our method determines whether two groups have similar characteristics or not by comparing the number of accepted hypotheses. Step 2 and Step 4 determine whether the target group is in the shortest group or the longest group. The path group sets that have not been assigned to one of two groups are allocated to the mid-distance group in Step 5.

The presented algorithm requires a statistical test in Step 1 and 3. Step B in Algorithm 2 in both steps applies both a two-sample z-test for the difference between proportions (Equation (1)) and a chi-square test (Equation (2)) as criteria to classify the samples. The chi-square test, one of the nonparametric methods, is also used to compare two groups, to ascertain whether the proportion of some characteristic is equal in several populations. Theoretically, chi-square statistics is equivalent to a z-test’s. The chi-square test of proportions is derived from z-statistics. Note that the test value of the chi-square test for one degree of freedom is equivalent to the z-test’s value squared. Details about the two tests can be found in [31]. The main difference between the two statistic tests is the assumption of distribution. Z-statistics is based upon the normal approximation of binomial distribution, which can be used for a parametric study where the number of samples is large enough (over 30) and proportional values approximate to 0.5. However, the chi-square test does not require these strict assumptions and is based on the chi-square distribution.

$$\mathrm{Z}=\frac{\left({\widehat{p}}_1-{\widehat{p}}_2\right)-0}{\sqrt{\widehat{p}\left(1-\widehat{p}\right)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$$

(3)

$${\mathrm{X}}^2=\frac{{\left({\widehat{p}}_1-{\widehat{p}}_2\right)}^2}{\widehat{p}\left(1-\widehat{p}\right)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}$$

(4)

sample proportion for sample 1:

$${\widehat{p}}_1=\frac{x_1}{n_1}$$

(5)

sample proportion for sample 2:

$${\widehat{p}}_2=\frac{x_2}{n_2}$$

(6)

combined proportion in both samples:

$$\widehat{p}=\frac{x_1+x_2}{n_1+n_2}$$

(7)

4. Results

Highway Driver Classification Based on the Resting Behavior

Figure 6 and Figure 7 show the results of the z-test simulation in terms of R0. Each simulation is run 100 times for reliability. The test results establish the point that it is possible to classify groups which have different R0 resting behaviors from the standard group (0–10 km). Notably, the groups that have a travel distance more than 70 km with the Population proportion method, and the groups that traveled more than 80 km with the Chi-squared method, show completely different results than those of the standard group.

From the overall z-test simulation results between the standard group and each sample group, a criterion is established whereby if there are 90 rejects out of 100 tests, then the sample group has a completely disparate effect compared to that of the standard group (

Table 3. Population proportion test and chi-square test simulation results in terms of R0.

R0 Test
Km	Population Proportion		Chi-Square
	Accept	Reject	Accept	Reject
0–10	0	0	0	0
010–20	100	0	100	0
020–30	100	0	100	0
030–40	100	0	99	1
040–50	93	7	91	9
050–60	64	36	84	16
060–70	30	70	52	48
070–80	10	90	25	75
080–90	1	99	5	95
090–100	0	100	0	100
100–110	0	100	0	100
110–120	0	100	0	100
120–130	0	100	0	100
130–140	0	100	0	100

). According to results from different methodologies, despite there being a 10 km gap in clustering reference distances, the proportion of acceptance and rejection for each result is not substantially changed. When the clustering reference distance is more than 90 km for each R0 test, no acceptance result is shown. Considering the arbitrary nature of the simulation method, it can be assumed that if the proportion of rejection is more than 90% of total simulation tests, then it has the status of “completely different result.”

Figure 8 and Figure 9 show the z-test simulation results in terms of R2 for the clustering reference distance. In this case, the travel distance of the standard group for the z-test is above 350 km. The population proportion method and chi-square method are applied, and as for the results, the R2 value of drivers who drive less than 200 km produces an entirely different outcome to the R2 value of standard group drivers with both methods (

Table 4. Population proportion test and chi-square test simulation results in terms of R2.

R2 Test
Km	Population Proportion		Chi-Square
	Accept	Reject	Accept	Reject
140–150	0	100	0	100
150–160	0	100	0	100
160–170	0	100	0	100
170–180	0	100	1	99
180–190	2	98	10	90
190–200	1	99	4	96
200–210	11	89	17	83
210–220	30	70	45	55
220–230	11	89	20	80
230–240	40	60	50	50
240–250	77	23	88	12
250–260	48	52	72	28
260–270	65	35	71	29
270–280	37	63	49	51
280–290	64	36	68	32
290–300	56	44	72	28
300–310	63	37	80	20
310–320	37	63	58	42
320–330	66	34	74	26
330–340	96	4	96	4
340–350	45	55	66	34
350 over	0	0	0	0

). The “completely different result” for R2 z-test has the same meaning as the one for R0 z-test.

It is evident in Figure 6 and Figure 7 that the rejection ratio increases consistently as the travel distance increases. However, Figure 8 and Figure 9 support the point that the rejection ratio decreases as the travel distance decrease and that there is fluctuation while the rejection ratio is dropping. This might occur because the sample number of long-distance trips is also low, making it difficult to extrapolate these results to the entire population. More general observations can be made for long-distance trips once more data become available.

From the clustering results in terms of the sample proportion and travel distance, highway drivers could be divided into three groups (

Table 5. The clustering results in terms of travel distance.

Clustering Method	Travel Distance(km)
	Short-Distance Group	Middle-Distance Group	Long-Distance Group
Population proportion method	0–70	70–200	200 ~
Chi-square method	0–80	80–200	200 ~

). Even though there are some differences due to the two clustering methods, drivers who travel 0–70 km or 80 km are clustered as a short-distance trip group based on their resting behavior, whereas drivers who travel more than 200 km are clustered as a long-distance trip group with two-times rest behavior. A middle-distance trip group is defined for the drivers who stand between the two groups.

5. Discussion

As aforementioned, fatigue-related crashes, which are mainly caused by drowsy or distracted driving, account for a significant portion of fatal accidents on highways. The most traditional way to analyze drivers’ travel and rest behavior is by conducting surveys at rest areas on highways. The benefit of such surveys is that interviewers can directly gather accurate travel information (i.e., trip purpose, origin and destination, average travel time, travel experience, the number of resting before the current rest area, etc.) from the survey respondents. However, collected survey data are mostly based on respondents’ memory and approximation. Moreover, it is challenging to amass travel information from people who are not taking the survey, which leads to researchers having to estimate or ignore that information. This means that the survey sampling will be inevitably biased, not to mention that survey results can also be affected by the design, sentence structure, and vocabulary of the survey questionnaire. The budget for the survey is another limitation. Thus, this study used real sample data, car navigation data, which are big enough and comfortable to collect, to analyze the resting behavior of drivers according to their travel distance.

Many studies in the literature mentioned have revealed that the level of fatigue is related to travel distance. Moreover, continuous driving (i.e., especially more than two hours traveling) without rest can increase the probability of drowsy driving occurrences on highways. Putting this into consideration, we hypothesize that resting behaviors vary by the number of rests and driving distances. Then, this study applies the Monte-Carlo Simulation method to classify drivers based on statistical tests with respect to an average travel distance and the number of resting behavior and then indicates a unique rest behavior of drivers in each group. Instead of the more traditional method of conducting surveys at rest areas on highways, we incorporate CNS data to impute highway drivers’ travel patterns and reduce sampling bias, which could happen with missing data. Our method identifies that drivers are highly likely to take a rest after over 80 km (50 m) of driving. The average distance between rest sites in Korea is 15 km [3]. ADAS can give a soft alert to a driver to stop at a rest site after 80 km driving and increase the intensity of the recommendation by each rest site. A smart highway management association can also devise a platform to increase highway safety and rest area usage for sustainable transportation systems. A mobility platform attracts a driver who has prolonged driving by providing store coupons in the nearest rest area through the ADAS system.

However, the limitation of using CNS data instead of survey data is that it is hard to define trip purposes for each trip. Kim and Bae surveyed to analyze the purpose of stopping at a rest area on highways in Korea [32]. In their study, 92.9% of survey respondents said that they visit rest areas to use the highway restrooms, and 72.0% of them responded that they visited rest areas to purchase food. Only 58.3% of respondents stopped at rest areas for a brief excursion. From these survey results, we could assume that some people merely stopped at rest areas for a while without taking appropriate rest. With CNS data, it is possible to estimate the purposes of rest area users from the driver’s destination searching log. In addition, CNS data have the potential to include exogenous variables such as gender, age, departure time for further analysis, but we did not have access to such private information. In further research, this study will conduct a survey that targets CNS users and combine them with CNS data to analyze highway drivers’ rest behavior in detail and provide a more accurate resting criterion. The uncertainty of collected data also remains an issue, so our future research may also be extended to include time-space dynamics of traffic conditions.

6. Conclusions

The effectiveness of sustainable traffic safety systems can be enhanced by the proper analysis of driving behavior by providing decisionmakers with a drivers’ behavior criterion [4]. This study utilizes data obtained from CNS to confirm that the highway drivers’ resting behavior is dependent on the length of their travel distance. To efficiently utilize the large-scale data that contain 591,103 vehicle trajectories, we suggest new criteria to classify the driver traveled distance groups according to the drivers’ rest behaviors on highways. We initially categorize two base groups, which represent a short-distance travel behavior (R0) and long-distance travel behavior (R2), respectively. To identify whether the rest drivers belong to base groups or not, we adopt a random sampling method based on Monte-Carlo simulation for each target group and conduct z-test and chi-square test. As a result, we find that people who drive less than 70–80 km share a similar rest pattern of short-distance travelers. Also, drivers who travel more than 200 km have a similar rest pattern of long-distance travelers. Therefore, we conclude that (a) the length for the short distance traveler group is a range between 0 km to 70–80 km, and (b) the length for the long-distance traveler group is over 200 km.

We expect this proposed method to contribute to the construction of a proper resting strategy or a drowsy-driving avoidance strategy, resulting in fewer traffic accidents related to drowsy-driving or loss of concentration while driving. For instance, it is possible to build some wake-up facilities to attract short-trip drivers’ attention and provide information to long-trip drivers to let them take a rest, as necessary. Furthermore, the study can provide policy implications and a highway-safety investment basis by verifying the behavioral patterns through the simulation-based approach.

This research applied a statistical method to identify the relationship between driver’s resting behavior and categorical resting behavior patterns. To apply a statistical model to large-scale data, the authors introduce the Monte-Carlo simulation approach. Future research will extend the statistic approach to a nonparametric method such as Neural network, Random Forest classification tree, and K-nearest clustering. The authors of [33] identify influential factors on traffic accidents by injury severity using the Random Forest classification tree. Our data also include the categorical relationship between driving distance and the number of rests. We expect that machine learning approaches could also help identify the proper distance criteria. However, future research should consider the limitation of nonparametric methods, which are not able to explicitly identify the factors that significantly affect the classification of resting behavior.