Application of Bipartite Networks to the Study of Water Quality
Abstract
1. Introduction
2. Topological Analysis to Assess Water Quality
- is the dominant (most abundant) taxon.
- is the rare (least abundant) taxon.
- is the maximal frequency of the tolerance value .
- is the minimum frequency of the tolerance value .
- If the macroinvertebrate families’ abundance in the system is uniform (), then .
- The topological index is a function of the maximal abundance of one or more families, that is, it is in close relation to the load capacity of the system and the present dominant families; therefore, it provides a more objective measure than the index (where the presence or absence of a single family can significantly modify the water quality evaluation) and states the functional relation between the uniformity and diversity of macroinvertebrate families.
2.1. Water Quality Classification
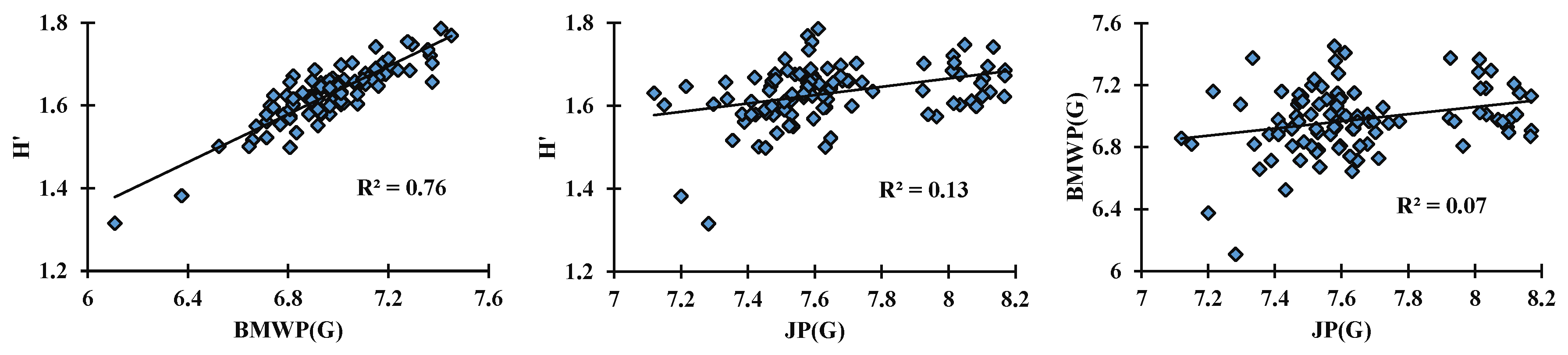
2.2. Comparison between Indices to Study Water Quality
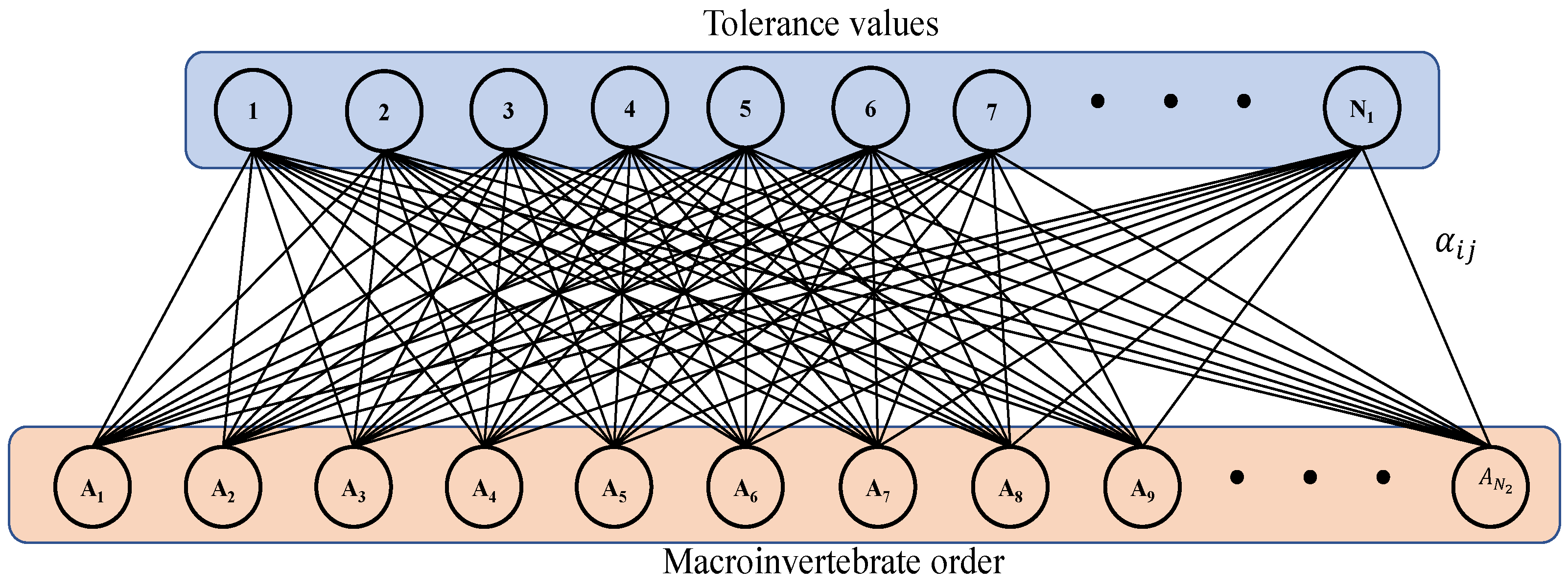
3. Spectral Analysis of the Bipartite Network Associated with the Guájaro Reservoir
4. Result Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Graph Theory
How to Compute the Jp(G) Index

Appendix B
| Tolerance Value | Abundance |
|---|---|
| 1 | 10,749 |
| 2 | 892 |
| 3 | 946 |
| 4 | 142 |
| 5 | 722 |
| 6 | 497 |
| 7 | 296 |
| 8 | 1 |
References
- United Nations. Transforming our world: The 2030 agenda for sustainable development. In Proceedings of the General Assembley 70 Session, New York, NY, USA, 15 September 2015–13 September 2016. [Google Scholar]
- Cantoni, J.; Kalantari, Z.; Destouni, G. Watershed-Based Evaluation of Automatic Sensor Data: Water Quality and Hydroclimatic Relationships. Sustainability 2020, 12, 396. [Google Scholar] [CrossRef]
- Kumari, P.; Maiti, S.K. Bioassessment in the aquatic ecosystems of highly urbanized agglomeration in India: An application of physicochemical and macroinvertebrate-based indices. Ecol. Indic. 2020, 111, 106053. [Google Scholar] [CrossRef]
- Dalu, T.; Chauke, R. Assessing macroinvertebrate communities in relation to environmental variables: The case of Sambandou wetlands, Vhembe Biosphere Reserve. Appl. Water Sci. 2020, 10, 16. [Google Scholar] [CrossRef]
- Fan, J.; Wu, J.; Kong, W.; Zhang, Y.; Li, M.; Zhang, Y.; Meng, W. Predicting Bio-indicators of Aquatic Ecosystems Using the Support Vector Machine Model in the Taizi River, China. Sustainability 2017, 9, 892. [Google Scholar] [CrossRef]
- Kattel, G.; Cai, Y.; Yang, X.; Zhang, K.; Hao, X.; Wang, R.; Dong, X. Potential Indicator Value of Subfossil Gastropods in Assessing the Ecological Health of the Middle and Lower Reaches of the Yangtze River Floodplain System (China). Geosciences 2018, 8, 222. [Google Scholar] [CrossRef]
- Carvalho, R.L.; Andersen, A.N.; Anjos, D.V.; Pacheco, R.; Chagas, L.; Vasconcelos, H.L. Understanding what bioindicators are actually indicating: Linking disturbance responses to ecological traits of dung beetles and ants. Ecol. Indic. 2020, 108, 105764. [Google Scholar] [CrossRef]
- Parmar, T.K.; Rawtani, D.; Agrawal, Y.K. Bioindicators: The natural indicator of environmental pollution. Front. Life Sci. 2016, 9, 110–118. [Google Scholar] [CrossRef]
- Duran, M. Monitoring Water Quality Using Benthic Macroinvertebrates and Physicochemical Parameters of Behzat Stream in Turkey. Pol. J. Environ. Stud. 2006, 15, 5. [Google Scholar]
- Forio, M.A.E.; Lock, K.; Radam, E.D.; Bande, M.; Asio, V.; Goethals, P.L. Assessment and analysis of ecological quality, macroinvertebrate communities and diversity in rivers of a multifunctional tropical island. Ecol. Indic. 2017, 77, 228–238. [Google Scholar] [CrossRef]
- Czerniawska-Kusza, I. Comparing modified biological monitoring working party score system and several biological indices based on macroinvertebrates for water-quality assessment. Limnol.-Ecol. Manag. Inland Waters 2005, 35, 169–176. [Google Scholar] [CrossRef]
- Alba-Tercedor, J.; Sanchez-Ortega, A. Un método rápido y simple para evaluar la calidad biológica de las aguas corrientes basado en el de Hellawell (1978). Limnetica 1988, 4, 1–56. [Google Scholar]
- Hellawell, J.M. Biological Surveillance of Rivers: A Biological Monitoring Handbook; Water Research Centre: Stevenage, UK, 1978. [Google Scholar]
- Hawkes, H.A. Origin and development of the biological monitoring working party score system. Water Res. 1998, 22, 964–968. [Google Scholar] [CrossRef]
- Bieger, L.; Carvalho, A.; Strieder, M.; Maltchik, L.; Stenert, C. Are the streams of the Sinos River basin of good water quality? Aquatic macroinvertebrates may answer the question. Braz. J. Biol. 2010, 70, 1207–1215. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gutiérrez-Fonseca, P.E.; Ramírez, A. Evaluación de la calidad ecológica de los ríos en Puerto Rico: Principales amenazas y herramientas de evaluación. Hidrobiológica 2016, 26, 433–441. [Google Scholar]
- Sharifinia, M.; Mahmoudifard, A.; Namin, J.I.; Ramezanpour, Z.; Yap, C.K. Pollution evaluation in the Shahrood River: Do physico-chemical and macroinvertebrate-based indices indicate same responses to anthropogenic activities? Chemosphere 2016, 159, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Armitage, P.; Moss, D.; Wright, J.; Furse, M. The performance of a new biological water quality score system based on macroinvertebrates over a wide range of unpolluted running-water sites. Water Res. 1983, 17, 333–347. [Google Scholar] [CrossRef]
- Chang, F.-H.; Lawrence, J.E.; Rios-Touma, B.; Resh, V.H. Tolerance values of benthic macroinvertebrates for stream biomonitoring: Assessment of assumptions underlying scoring systems worldwide. Environ. Monit. Assess. 2014, 186, 2135–2149. [Google Scholar] [CrossRef]
- Edegbene, A.O.; Elakhame, L.A.; Arimoro, F.O.; Osimen, E.C.; Odume, O.N. Development of macroinvertebrate multimetric index for ecological evaluation of a river in North Central Nigeria. Environ. Monit. Assess. 2019, 191, 274. [Google Scholar] [CrossRef]
- Arslan, N.; Salur, A.; Kalyoncu, H.; Mercan, D.; Barişik, B.; Odabaşi, D.A. The use of BMWP and ASPT indices for evaluation of water quality according to macroinvertebrates in Küçük Menderes River (Turkey). Biologia 2016, 71, 49–57. [Google Scholar] [CrossRef]
- Wondmagegn, T.; Mengistou, S. Effects of anthropogenic activities on macroinvertebrate assemblages in the littoral zone of Lake Hawassa, a tropical Rift Valley Lake in Ethiopia. Lakes Reserv. Res. Manag. 2020, 25, 61–71. [Google Scholar] [CrossRef]
- Luo, K.; Hu, X.; He, Q.; Wu, Z.; Cheng, H.; Hu, Z.; Mazumder, A. Impacts of rapid urbanization on the water quality and macroinvertebrate communities of streams: A case study in Liangjiang New Area, China. Sci. Total. Environ. 2018, 621, 1601–1614. [Google Scholar] [CrossRef] [PubMed]
- Patang, F.; Soegianto, A.; Hariyanto, S. Benthic macroinvertebrates diversity as bioindicator of water quality of some rivers in East Kalimantan, Indonesia. Int. J. Ecol. 2018, 2018, 5129421. [Google Scholar] [CrossRef]
- Zand, S.M. Indexes associated with information theory in water quality. J. Water Pollut. Control. Fed. 1976, 48, 2026–2031. [Google Scholar]
- Gualdoni, C.M.; Oberto, A.M. Estructura de la comunidad de macroinvertebrados del arroyo Achiras (Córdoba, Argentina): Análisis previo a la construcción de una presa. Iheringia SéRie Zool. 2012, 102, 177–186. [Google Scholar] [CrossRef][Green Version]
- Delmas, E.; Besson, M.; Brice, M.-H.; Burkle, L.A.; Dalla Riva, G.V.; Fortin, M.-J.; Gravel, D.; Guimarães, P.R., Jr.; Hembry, D.H.; Newman, E.A.; et al. Analysing ecological networks of species interactions. Biol. Rev. 2019, 94, 16–36. [Google Scholar] [CrossRef]
- Koutrouli, M.; Karatzas, E.; Paez-Espino, D.; Pavlopoulos, G.A. A Guide to Conquer the Biological Network Era Using Graph Theory. Front. Bioeng. Biotechnol. 2020, 8, 34. [Google Scholar] [CrossRef]
- Hernandez-Gomez, J.C.; Romero-Valencia, J.; Carreto, R.R. Mathematical Aspects on the Harmonic Index. Int. J. Math. Anal. 2017, 11, 85–95. [Google Scholar] [CrossRef]
- Ramirez, A.; Reyna, G.; Rosario, O. Spectral study of the inverse index. Adv. Appl. Discret. Math. 2018, 19, 195–211. [Google Scholar] [CrossRef]
- Sigarreta, J.M. Bounds for The Geometric-Arithmetic Index of a Graph. Miskolc Math. Notes 2015, 16, 1199–1212. [Google Scholar] [CrossRef]
- Jordan, F.; Scheuring, I. Network ecology: Topological constraints on ecosystem dynamics. Phys. Life Rev. 2004, 1, 139–172. [Google Scholar] [CrossRef]
- Navia, A.F.; Cortes, E.; Mejia-Falla, P.A. Topological analysis of the ecological importance of elasmobranch fishes: A food web study on the Gulf of Tortugas, Colombia. Ecol. Model. 2010, 221, 2918–2926. [Google Scholar] [CrossRef]
- Rodriguez, A.; Infante, D. Network models in the study of metabolism. Electron. J. Biotechnol. 2009, 12, 11–12. [Google Scholar]
- Aguilar-Becerra, C.D.; Frausto-Martínez, O.; Avilés-Pineda, H.; Pineda-Pineda, J.J.; Caroline Soares, J.; Reyes- Umaña, M. Path Dependence and Social Network Analysis on Evolutionary Dynamics of Tourism in Coastal Rural Communities. Sustainability 2019, 11, 4854. [Google Scholar] [CrossRef]
- Dormann, C.F.; Fründ, J.; Blüthgen, N.; Gruber, B. Indices, graphs and null models: Analyzing bipartite ecological networks. Open Ecol. J. 2009, 2, 7–24. [Google Scholar] [CrossRef]
- Holme, P.; Liljeros, F.; Edling, C.R.; Kim, B.J. Network bipartivity. Phys. Rev. E 2003, 68, 056107. [Google Scholar] [CrossRef] [PubMed]
- Pasquaretta, C.; Jeanson, R. Division of labor as a bipartite network. Behav. Ecol. 2017, 29, 342–352. [Google Scholar] [CrossRef]
- Hellawell, J.M. Biological Indicators of Freshwater Pollution and Environmental Management; Elsevier Science Publishers Ltd.: New York, NY, USA, 2012. [Google Scholar]
- Pineda-Pineda, J.J.; Rosas-Acevedo, J.L.; Hernandez-Gomez, J.C.; Rosario, O.; Sigarreta, J.M. Approximation to the Study of Water Quality. Appl. Math. Sci. 2018, 12, 421–430. [Google Scholar] [CrossRef]
- Martínez-Martínez, C.T.; Méndez-Bermúdez, J.A.; Moreno, Y.; Pineda-Pineda, J.J.; Sigarreta, J.M. Spectral and localization properties of random bipartite graphs. Chaos Solitons Fractals X 2019, 3, 100021. [Google Scholar] [CrossRef]
- Barbour, M.T.; Gerritsen, J.; Snyder, B.D.; Stribling, J.B. Rapid Bioassessment Protocols for Use in Streams and Wadeable Rivers: Periphyton, Benthic Macroinvertebrates and Fish; US Environmental Protection Agency, Office of Water: Washington, DC, USA, 1999; Volume 339.
- Carayon, D.; Eulin-Garrigue, A.; Vigouroux, R.; Delmas, F. A new multimetric index for the evaluation of water ecological quality of French Guiana streams based on benthic diatoms. Ecol. Indic. 2020, 113, 106248. [Google Scholar] [CrossRef]
- Romero, K.C.; Del Rio, J.P.; Villarreal, K.C.; Anillo, J.C.C.; Zarate, Z.P.; Gutierrez, L.C.; Franco, O.L.; Valencia, J.W.A. Lentic water quality characterization using macroinvertebrates as bioindicators: An adapted BMWP index. Ecol. Indic. 2017, 72, 53–66. [Google Scholar] [CrossRef]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. ICWSM 2009, 8, 361–362. [Google Scholar]
- Ministerio del Ambiente y Energia; Ministra de Salud. Reglamento para la Evaluación y Clasificación de la Calidad de Cuerpos de Agua Superficiales No. 33903-MINAE-S. Available online: http://www.digeca.go.cr/sites/default/files/de-33903reglamento_evaluacion_clasificacion_cuerpos_de_agua_0.pdf (accessed on 8 June 2020).
- Pineda-Pineda, J.J.; Rosas-Acevedo, J.L.; Sigarreta, J.M.; Hernández-Gómez, J.C.; Reyes-Umaña, M. Biotic Indices to Evaluate Water Quality: BMWP. Int. J. Environ. Ecol. Fam. Urban Stud. (IJEEFUS) 2018, 8, 23–36. [Google Scholar]
- Everaert, G.; De Neve, J.; Boets, P.; Dominguez-Granda, L.; Mereta, S.T.; Ambelu, A.; Thas, O. Comparison of the abiotic preferences of macroinvertebrates in tropical river basins. PLoS ONE 2014, 9, e108898. [Google Scholar] [CrossRef] [PubMed]
- Yazdian, H.; Jaafarzadeh, N.; Zahraie, B. Relationship between benthic macroinvertebrate bio-indices and physicochemical parameters of water: A tool for water resources managers. J. Environ. Health Sci. Eng. 2014, 12, 30. [Google Scholar] [CrossRef]
- Kaller, M.D.; Kelso, W.E. Association of macroinvertebrate assemblages with dissolved oxygen concentration and wood surface area in selected subtropical streams of the southeastern USA. Aquat. Ecol. 2007, 41, 95–110. [Google Scholar] [CrossRef]
- Wilson, P.C. Water Quality Notes: Dissolved Oxygen. Sea 2010, 1000, 5000. [Google Scholar]
- Hooda, P.S.; Moynagh, M.; Svoboda, I.F.; Miller, A. Macroinvertebrates as bioindicators of water pollution in streams draining dairy farming catchments. Chem. Ecol. 2000, 17, 17–30. [Google Scholar] [CrossRef]
- Hynes, H.B.N. The Ecology of Running Waters; Liverpool University Press: Liverpool, UK, 1970; p. 555. [Google Scholar]
- Schreier, H.; Erlebach, W.; Albright, L. Variations in water quality during winter in two Yukon rivers with emphasis on dissolved oxygen concentration. Water Res. 1980, 14, 1345–1351. [Google Scholar] [CrossRef]
- Tixier, G.; Felten, V.; Guérold, F. Life cycle strategies of Baetis species (Ephemeroptera, Baetidae) in acidified streams and implications for recovery. Fundam. Appl. Limnol. Hydrobiol. 2009, 174, 227–243. [Google Scholar] [CrossRef]
- Connolly, N.M.; Crossland, M.R.; Pearson, R.G. Effect of low dissolved oxygen on survival, emergence, and drift of tropical stream macroinvertebrates. J. N. Am. Benthol. Soc. 2004, 23, 251–270. [Google Scholar] [CrossRef]
- Koçer, M.A.T.; Sevgili, H. Parameters selection for water quality index in the assessment of the environmental impacts of land-based trout farms. Ecol. Indic. 2014, 36, 672–681. [Google Scholar] [CrossRef]
- Zamora-Muñoz, C.; Sáinz-Cantero, C.E.; Sánchez-Ortega, A.; Alba-Tercedor, J. Are biological indices BMPW’and ASPT’and their significance regarding water quality seasonally dependent? Factors explaining their variations. Water Res. 1995, 29, 285–290. [Google Scholar] [CrossRef]
- Zhao, C.; Pan, T.; Dou, T.; Liu, J.; Liu, C.; Ge, Y.; Zhang, Y.; Yu, X.; Mitrovic, S.; Lim, R. Making global river ecosystem health assessments objective, quantitative and comparable. Sci. Total. Environ. 2019, 667, 500–510. [Google Scholar] [CrossRef] [PubMed]
- Clairmont, L.K.; Slawson, R.M. Contrasting water quality treatments result in structural and functional changes to wetland plant-associated microbial communities in lab-scale mesocosms. Microb. Ecol. 2020, 79, 50–63. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication 1949; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Magnussen, S.; Boyle, T. Estimating sample size for inference about the Shannon-Weaver and the Simpson indices of species diversity. For. Ecol. Manag. 1995, 78, 71–84. [Google Scholar] [CrossRef]
- Pla, L. Biodiversidad: Inferencia basada en el índice de Shannon y la riqueza. Interciencia 2006, 31, 583–590. [Google Scholar]
- Jørgensen, S.E.; Xu, F.L.; Salas, F.; Marques, J.C. Handbook of Ecological Indicators for Assessment of Ecosystem Health; CRC Press: Boca Raton, FL, USA, 2016; pp. 9–64. [Google Scholar]







| Family | Family | ||||||
|---|---|---|---|---|---|---|---|
| 8 | Trichoptera1 | Xiphocentronidae | 0 | 5 | Hemiptera2 | Notonectidae | 55 |
| 8 | Trichoptera2 | Cantharidae | 1 | 5 | Hemiptera3 | Naucoridae | 13 |
| 8 | Ephemeroptera1 | Tricorythidae | 0 | 5 | Hemiptera4 | Mesoveliidae | 9 |
| 8 | Odonata1 | Gomphydae | 0 | 5 | Coleoptera5 | Noteridae | 288 |
| 8 | Amphipoda | Gammaridae | 0 | 5 | Odonata1 | Aeshnidae | 2 |
| 7 | Trichoptera1 | Leptoceridae | 39 | 4 | Hemiptera1 | Belostomatidae | 109 |
| 7 | Diptera1 | Stratiomyidae | 3 | 4 | Diptera1 | Tabanidae | 33 |
| 7 | Hemiptera1 | Pleidae | 71 | 4 | Diptera2 | Dolichopodidae | 0 |
| 7 | Acari | Hydrachnidae | 127 | 4 | Unionoida | Hyriidae | 0 |
| 7 | Hemiptera2 | Corixidae | 7 | 3 | Coleoptera1 | Chrysomelidae | 0 |
| 7 | Coleoptera1 | Lampyridae | 48 | 3 | Diptera1 | Tipulidae | 2 |
| 7 | Gastropoda1 | Chilinnidae | 1 | 3 | Diptera2 | Muscidae | 1 |
| 6 | Trichoptera | Polycentropodidae | 53 | 3 | Diptera3 | Ceratopogonidae | 167 |
| 6 | Ephemeroptera1 | Baetidae | 12 | 3 | Gastropoda1 | Ampullaridae | 345 |
| 6 | Lepidoptera | Pyralidae | 13 | 3 | Gastropoda2 | Lymnaeidae | 48 |
| 6 | Odonata1 | Coenagrionidae | 128 | 3 | Gastropoda3 | Planorbidae | 383 |
| 6 | Coleoptera1 | Staphylinidae | 3 | 3 | Cyclostheriidae | Cyclostheriidae | 0 |
| 6 | Odonata2 | Libellulidae | 96 | 2 | Diptera1 | Culicidae | 17 |
| 6 | Hemiptera1 | Saldidae | 0 | 2 | Hirudinidae1 | Glossiphoniidae | 165 |
| 6 | Coleoptera2 | Scirtidae | 52 | 2 | Hirudinidae2 | Hirudinidae | 155 |
| 6 | Ephemeroptera2 | Caenidae | 28 | 2 | Oligochaeta | Tubificidae | 469 |
| 6 | Gastropoda1 | Ancylidae | 112 | 2 | Gastropoda1 | Physidae | 86 |
| 5 | Hemiptera1 | Hydrometridae | 2 | 1 | Ephemeroptera1 | Polymitarcyidae | 996 |
| 5 | Hemiptera2 | Nepidae | 2 | 1 | Gastropoda1 | Hydrobiidae | 6127 |
| 5 | Coleoptera1 | Hydrophilidae | 226 | 1 | Gastropoda2 | Thiaridae | 1751 |
| 5 | Coleoptera2 | Curculionidae | 78 | 1 | Diptera1 | Chironomidae | 1861 |
| 5 | Coleoptera3 | Dytiscidae | 15 | 1 | Diptera2 | Syrphidae | 14 |
| 5 | Coleoptera4 | Elmidae | 32 |
| Class | Water Quality | (mg/L) | Stress | |||
|---|---|---|---|---|---|---|
| I | excellent | >9.2 | >231.8 | very high | 0.81–1.00 | |
| II | very good | 161–231 | 6.9–9.1 | 173.1–230.7 | high | 0.61–0.80 |
| III | good | 102–160 | 4.6–6.8 | 115.4–173.0 | regular | 0.41–0.60 |
| IV | regular | 46–101 | 2.3–4.5 | 57.70–115.3 | low | 0.21–0.40 |
| V | low | <45 | <2.2 | <57.6 | very low | 0.00–0.20 |
| Class | Water Quality | |||
|---|---|---|---|---|
| I | excellent | |||
| II | very good | |||
| III | good | |||
| IV | regular | |||
| V | low |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pineda-Pineda, J.J.; Martínez-Martínez, C.T.; Méndez-Bermúdez, J.A.; Muñoz-Rojas, J.; Sigarreta, J.M. Application of Bipartite Networks to the Study of Water Quality. Sustainability 2020, 12, 5143. https://doi.org/10.3390/su12125143
Pineda-Pineda JJ, Martínez-Martínez CT, Méndez-Bermúdez JA, Muñoz-Rojas J, Sigarreta JM. Application of Bipartite Networks to the Study of Water Quality. Sustainability. 2020; 12(12):5143. https://doi.org/10.3390/su12125143
Chicago/Turabian StylePineda-Pineda, Jair J., C. T. Martínez-Martínez, J. A. Méndez-Bermúdez, Jesús Muñoz-Rojas, and José M. Sigarreta. 2020. "Application of Bipartite Networks to the Study of Water Quality" Sustainability 12, no. 12: 5143. https://doi.org/10.3390/su12125143
APA StylePineda-Pineda, J. J., Martínez-Martínez, C. T., Méndez-Bermúdez, J. A., Muñoz-Rojas, J., & Sigarreta, J. M. (2020). Application of Bipartite Networks to the Study of Water Quality. Sustainability, 12(12), 5143. https://doi.org/10.3390/su12125143







