Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Study Area
Study Area
2.2. Methods
2.2.1. Mann–Kendall Test
2.2.2. Correlation
2.2.3. Application of the Copula Theory
- sector 1—LHFA–LHFB/LMFA–LMFB (X ≤ A62.5%, Y ≤ B62.5%)
- sector 5—MHFA–MHFB/MMFA–MMFB (A62.5%< X ≤ A37.5%, B62.5% < Y ≤ B37.5%)
- sector 9—HHFA–HHFB/HMFA–HMFB (X > A37.5%, Y > B37.5%)
- sector 2—LHFA–MHFB/LMFA–MMFB (X ≤ A62.5%, B62.5% < Y ≤ B37.5%)
- sector 3—LHFA–HHFB/LMFA–HMFB (X ≤ A62.5%, Y > B37.5%)
- sector 4—MHFA–LHFB/MMFA–LMFB (A62.5%< X ≤ A37.5%, Y ≤ B62.5%)
- sector 6—MHFA–HHFB/MMFA–HMFB (A62.5%< X ≤ A37.5%, Y > B37.5%)
- sector 7—HHFA–LHFB/HMFA–LMFB (X > A37.5%, Y ≤ B62.5%)
- sector 8—HHFA–MHFB/HMFA–MMFB (X > A37.5%, B62.5% < Y ≤ B37.5%)
- X—values of x-coordinates of generated points;
- Y—values of y-coordinates of generated points;
- A62.5%—value of AMAXF/MAF with probability of exceedance of 62.5%;
- A37.5%—value of AMAXF/MAF with probability of exceedance of 37.5%;
- B62.5%—value of AMAXF/MAF with probability of exceedance of 62.5%;
- B37.5%—value of AMAXF/MAF with probability of exceedance of 37.5%;
- F—flow;
- H—high (maximum);
- M—mean.
- Probable AMAXF and MAF with probability of occurrence of <62.5% were designated as LHF/LMF,
- Probable AMAXF and MAF with probability of occurrence in a range of >62.5% and <37.5% were designated as MHF/MMF,
- Probable AMAXF and MAF with probability of occurrence of >37.5% were designated as HHF/HMF.
3. Results
3.1. Mann–Kendall Test
3.2. Correlation
3.2.1. Annual Maximum Flows (AMAXF)
3.2.2. Mean Annual Flows (MAF)
3.3. Synchronous–Asynchronous Encounter Probability
3.3.1. Annual Maximum Flows (AMAXF)
3.3.2. Mean Annual Flows (MAF)
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Archer, D.R.; Forsythe, N.; Fowler, H.J.; Shah, S.M. Sustainability of water resources management in the Indus Basin under changing climatic and socio-economic conditions. Hydrol. Earth Syst. Sci. 2010, 14, 1669–1680. [Google Scholar] [CrossRef] [Green Version]
- Young, W.J.; Anwar, A.; Bhatti, T.; Borgomeo, E.; Davies, S.; Garthwaite, W.R., III.; Gilmont, E.M.; Leb, C.; Lytton, L.; Makin, I.; et al. Pakistan: Getting More from Water; World Bank Group: Washington, DC, USA, 2019. [Google Scholar]
- Piracha, A.; Majeed, Z. Water Use in Pakistan’s Agricultural Sector: Water Conservation under the Changed Climatic Conditions. Intl. J. Water Resour. Arid Environ. 2011, 1, 170–179. [Google Scholar]
- Rao, M.P.; Cook, E.R.; Cook, B.I.; Palmer, J.G.; Uriarte, M.; Devineni, N.; Lall, U.; D’Arrigo, R.D.; Woodhouse, C.A.; Ahmed, M.; et al. Six Centuries of Upper Indus Basin Streamflow Variability and Its Climatic Drivers. Water Resour. Res. 2018, 54, 5687–5701. [Google Scholar] [CrossRef] [PubMed]
- Liniger, H.; Weingartner, R.; Grosjean, M. Mountains of the World: Water Towers for the 21st Century; Mountain agenda for the comparison on sustainable development (CSD), BO12; University of Bern: Bern, Switzerland, 1998. [Google Scholar]
- Hasson, S.; Pascale, S.; Lucarini, V.; Böhner, J. Seasonal cycle of Precipitation over Major River Basins in South and Southeast Asia: A Review of the CMIP5 climate models data for present climate and future climate projections. J. Atmos. Res. 2016, 180, 42–63. [Google Scholar] [CrossRef] [Green Version]
- Mukhopadhyay, B.; Khan, A. A quantitative assessment of the genetic sources of the hydrologic flow regimes in Upper Indus Basin and its significance in a changing climate. J. Hydrol. 2014, 509, 549–572. [Google Scholar] [CrossRef]
- Khan, A.; Richards, K.S.; Parker, G.T.; McRobie, A.; Mukhopadhyay, B. How large is the Upper Indus Basin? The pitfalls of auto-delineation using DEMs. J. Hydrol. 2014, 509, 442–453. [Google Scholar] [CrossRef]
- Commission on Science and Technology for Sustainable Development in the South. In Water Resources in the South: Present Scenario and Future Prospects; COMSATS’ Series of Publications on Science and Technology: Islamabad, Pakistan, 2003.
- Archer, D.R. Contrasting hydrological regimes in the Upper Indus Basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
- Khan, A.R. Searching Evidence for Climatic Change: Analysis of Hydro-meteorological Time Series in the Upper Indus Basin; IWMI working paper 23; Pakistan Country Series Number 7; International Water Management Institute: Lahore, Pakistan, 2001. [Google Scholar]
- Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the Upper Indus Basin: Global Teleconnections and Hydrological Implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Immerzeel, W.W.; Droogers, P.; de Jong, S.M.; Bierkens, M.F.P. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Fowler, H.J.; Archer, D.R. Hydro-climatological variability in the Upper Indus Basin and implications for water resources. In Regional Hydrological Impacts of Climatic Change-Impact Assessment and Decision Making; IAHS Publication: Wallingford, UK, 2005; Volume 295, pp. 131–138. [Google Scholar]
- Akhtar, M.; Ahmad, N.; Booij, M.J. The impact of climate change on the water resources of Hindukush–Karakorum–Himalaya region under different glacier coverage scenarios. J. Hydrol. 2008, 355, 148–163. [Google Scholar] [CrossRef]
- Bhutiyani, M.R.; Vishwas, S.K.; Pawar, N.J. Changing streamflow patterns in the rivers of northwestern Himalaya: Implications of global warming in the 20th century. Curr. Sci. 2008, 95, 618–626. [Google Scholar]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Ahmad, B. Snow cover dynamics and hydrological regime of the Hunza River basin, Karakoram Range, Northern Pakistan. Hydrol. Earth Syst. Sci. 2011, 15, 2821–2860. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Archer, D.R.; Fowler, H.J.; Forsythe, N. Trends in timing and magnitude of flow in the Upper Indus Basin. Hydrol. Earth Syst. Sci. 2012, 9, 9931–9966. [Google Scholar] [CrossRef] [Green Version]
- Hasson, S.; Lucarini, V.; Khan, M.R.; Petitta, M.; Bolch, T.; Gioli, G. Early 21st century snow cover state over the western river basins of the Indus River system. Hydrol. Earth Syst. Sci. 2014, 18, 4077–4100. [Google Scholar] [CrossRef] [Green Version]
- Hussain, M.S.; Lee, S. Long-term variability and changes of the precipitation regime in Pakistan. Asia-Pac. J. Atmos. Sci. 2014, 50, 271–282. [Google Scholar] [CrossRef]
- Mukhopadhyaya, B.; Khan, A. Rising river flows and glacial mass balance in central Karakoram. J. Hydrol. 2014, 513, 192–203. [Google Scholar] [CrossRef]
- Mukhopadhyaya, B.; Khan, A.; Gautam, R. Rising and falling river flows: Contrasting signals of climate change and glacier mass balance from the eastern and western Karakoram. Hydrol. Sci. J. 2014, 7, 2062–2085. [Google Scholar] [CrossRef]
- Khan, K.; Yaseen, M.; Latif, Y.; Nabi, G. Detection of river flow trends and variability analysis of Upper Indus Basin, Pakistan. Sci. Int. (Lahore) 2015, 27, 1261–1270. [Google Scholar]
- Yaseen, M.; Khan, K.; Nabi, G.; Bhatti, H.A.; Afzal, M. Hydrological trends and variability in the Mangla watershed, Pakistan. Sci. Int. (Lahore) 2015, 27, 1327–1335. [Google Scholar]
- Hasson, S.; Böhner, J.; Lucarini, V. Prevailing climatic trends and runoff response from Hindukush–Karakoram–Himalaya, upper Indus Basin. Earth Syst. Dynam. 2017, 8, 337–355. [Google Scholar] [CrossRef] [Green Version]
- Shamshad, J.; Ahmad, S.R.; Ahmad, I.; Azim, F. Footprints of climate change on hydrological behaviour of Jhelum, Upper Indus and Hunza river basins, Pakistan. Transylv. Rev. 2018, 1, 32. [Google Scholar]
- Faiz, M.A.; Liu, D.; Fu, Q.; Wrzesiński, D.; Muneer, S.; Khan, M.I.; Li, T.X.; Cui, S. Assessment of precipitation variability and uncertainty of stream flow in the Hindu Kush Himalayan and Karakoram River basins of Pakistan. Meteorol. Atmos. Phys. 2019, 131, 127–136. [Google Scholar] [CrossRef]
- Waseem, M.; Ahmad, I.; Mujtaba, A.; Tayyab, M.; Si, C.; Lü, H.S.; Dong, X.H. Spatiotemporal Dynamics of Precipitation in Southwest Arid-Agriculture Zones of Pakistan. Sustainability 2020, 12, 2305. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Gu, S.X.; Zhang, T. Synchronous-Asynchronous Encounter Probability Analysis of High-Low Runoff for Jinsha River, China, using Copulas. MATEC Web Conf. 2018, 246, 01094. [Google Scholar] [CrossRef]
- Akhtar, A. Indus Basin Floods: Mechanisms, Impacts, and Management; Asian Development Bank: Mandaluyong, Philippines, 2013; ISBN 978-92-9254-284-9. [Google Scholar]
- Khan, F.; Moench, M.; Rehman, A.; Saadi, F.A.; Malik, S.; Sabbag, L.; MacClune, K. Desk Study: Indus Floods Research Project. In Result Sharing Session: Climate Change Resilience; International Development Research Centre, Department for International Development: Islamabad, Pakistan, 30 January 2013. [Google Scholar]
- Gaurav, K.; Sinha, R.; Panda, P.K. The Indus flood of 2010 in Pakistan: A perspective analysis using remote sensing data Nat. Hazards 2011, 52, 1. [Google Scholar] [CrossRef]
- Ahmad, Z.; Hafeez, M.; Zhmad, I. Hydrology of mountainous areas in the upper Indus Basin, Northern Pakistan with the perspective of climate change. Environ. Monit. Assess 2012, 184, 5255–5274. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Fu, Q.; Khan, M.I.; Li, T.X.; Cui, S. Assessment of characteristics and distinguished hydrological periods of a river regime. Environ. Earth Sci. 2018, 77, 729. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin & Co.: London, UK, 1975; ISBN 0-85264-199-0. [Google Scholar]
- Önöz, B.; Bayazit, M. The power of statistical tests for trend detection. Turk. J. Eng. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Partal, T.; Küçük, M. Long-term trend analysis using discrete wavelet components of annual precipitations measurements in Marmara region (Turkey). Phy. Chem. Earth Parts A/B/C 2006, 31, 1189–1200. [Google Scholar] [CrossRef]
- Salmi, T.; Määttä, A.; Anttila, P.; Ruoho-Airola, T.; Amnell, T. Detecting Trends of Annual Values of Atmospheric Pollutants by the Mann-Kendall Test and Sen’s Slope Estimates–The Excel Template Application MAKESENS; Publications on Air Quality 31; Finnish Meteorological Institute: Helsinki, Finland, 2002. [Google Scholar]
- Sklar, A. Fonction de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Fan, L.L.; Wang, H.R.; Wang, C.; Lai, W.L.; Zhao, Y. Exploration of Use of Copulas in Analysing the Relationship between Precipitation and Meteorological Drought in Beijing, China. Adv. Meteorol. 2017, 43, 1–11. [Google Scholar] [CrossRef]
- Gurgul, P.; Syrek, R. Application of a mixture of copulas to model dependences between selected sectors of the economy. Ekon. Menedżerska 2009, 6, 129–139. (In Polish) [Google Scholar]
- De Michele, C.; Salvadori, G. A Generalized Pareto intensity duration model of storm rainfall exploiting 2-Copulas. J. Geophys. Res. 2003, 108, 4067. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef] [Green Version]
- Bárdossy, A.; Li, J. Geostatistical interpolation using copulas. Water Resour. Res. 2008, 44, W07412. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Sobkowiak, L.; Wang, Z.; Guo, F. Spatial Pattern Characterization and Multivariate Hydrological Frequency Analysis of Extreme Precipitation in the Pearl River Basin, China. Water Resour. Manag. 2012, 26, 3619–3637. [Google Scholar] [CrossRef]
- Kuchment, L.S.; Demidov, V.N. On the application of copula theory for determination of probabilistic characteristics of springflood. Russ. Meteorol. Hydrol. 2013, 38. [Google Scholar] [CrossRef]
- Rizwan, M.; Guo, S.L.; Yin, J.B.; Xoing, F. Deriving Design Flood Hydrographs Based on Copula Function: A Case Study in Pakistan. Water 2019, 11, 1531. [Google Scholar] [CrossRef] [Green Version]
- Sugimoto, T.; Bárdossy, A.; Pegram, G.G.S.; Cullmann, J. Investigation of hydrological time series using copulas for detecting catchment characteristics and anthropogenic impacts. Hydrol. Earth Syst. Sci. 2016, 20, 2705–2720. [Google Scholar] [CrossRef] [Green Version]
- Zhou, N.Q.; Zhao, L.; Shen, X.P. Copula-based Probability Evaluation of Rich-Poor Runoff and Sediment Encounter in Dongting Lake Basin. Sci. Geogr. Sin. 2014, 34, 242–248. (In Chinese) [Google Scholar] [CrossRef]
- You, Q.; Jiang, H.; Liu, Y.; Liu, Z.; Guan, Z. Probability Analysis and Control of River Runoff–sediment Characteristics based on Pair-Copula Functions: The Case of the Weihe River and Jinghe River. Water 2019, 11, 510. [Google Scholar] [CrossRef] [Green Version]
- Bacova, M.V.; Halmova, D. Joint modeling of flood peak discharges, volume and duration: A case study of the Danube River in Bratislava. J. Hydrol. Hydromech. 2014, 62. [Google Scholar] [CrossRef] [Green Version]
- Plewa, K.; Perz, A.; Wrzesiński, D.; Sobkowiak, L. Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water 2019, 11, 1292. [Google Scholar] [CrossRef] [Green Version]
- Perz, A.; Plewa, K. Synchronous Occurrence of Mean Water Levels of Coastal Lakes and the Baltic Sea. Bad. Fizjogr. Ser. A–Geogr. Fiz. 2019, A70, 65–82. (In Polish) [Google Scholar]
- Chen, L.; Guo, S.L. Copulas and Its Application in Hydrology and Water Resources; Springer Water: Berlin/Heidelberg, Germany, 2019; ISBN 978-981-13-0573-3. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–722. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C. Everything you always wanted to know about copula Modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.-P. Statistical inference procedure for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; You, J. The joint probability distribution of runoff and sediment and its change characteristics with multi-time scales. J. Hydrol. Hydromech. 2014, 62, 218–225. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Yu, Z.; Li, G.; Ju, Q. Nonstationary Multivariate Hydrological Frequency Analysis in the Upper Zhanghe River Basin, China. Water 2018, 10, 772. [Google Scholar] [CrossRef] [Green Version]
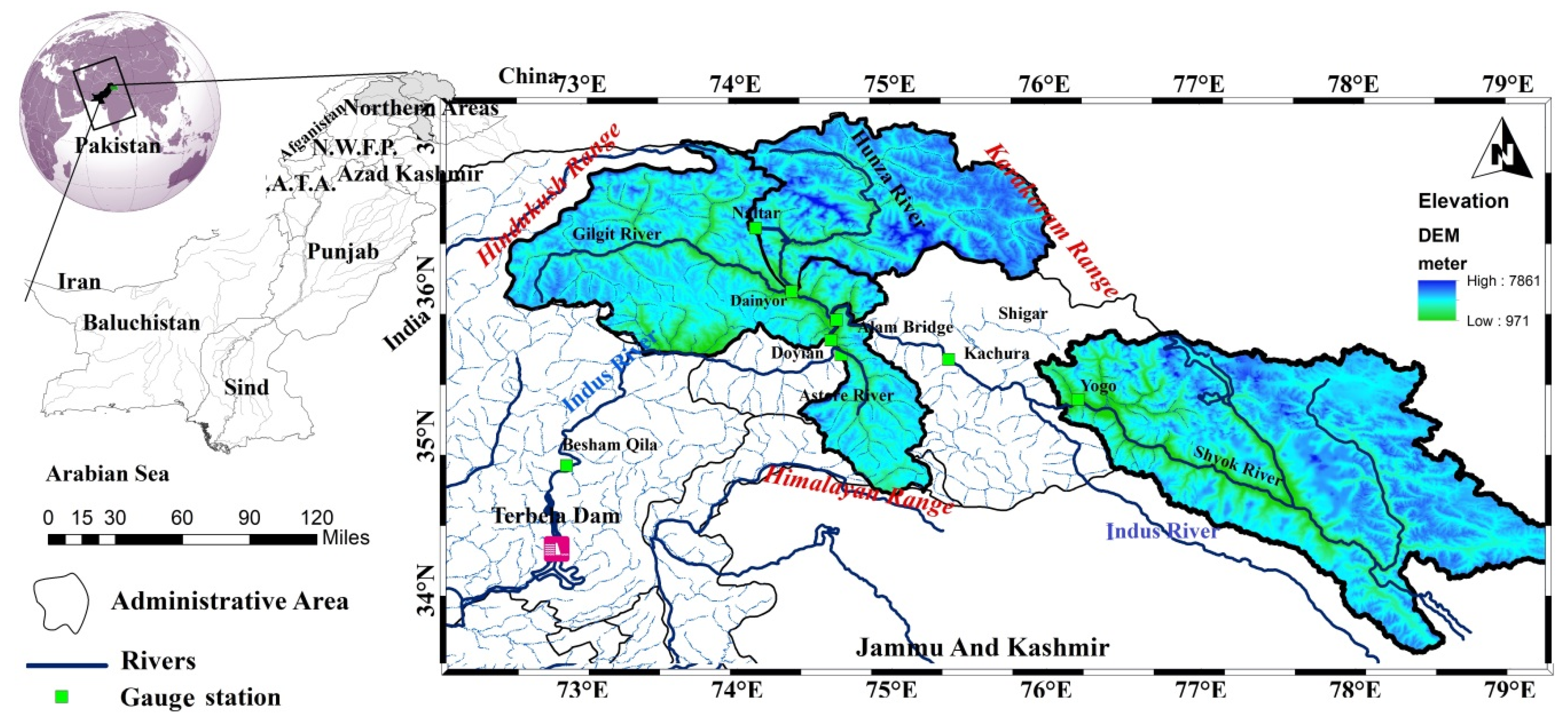

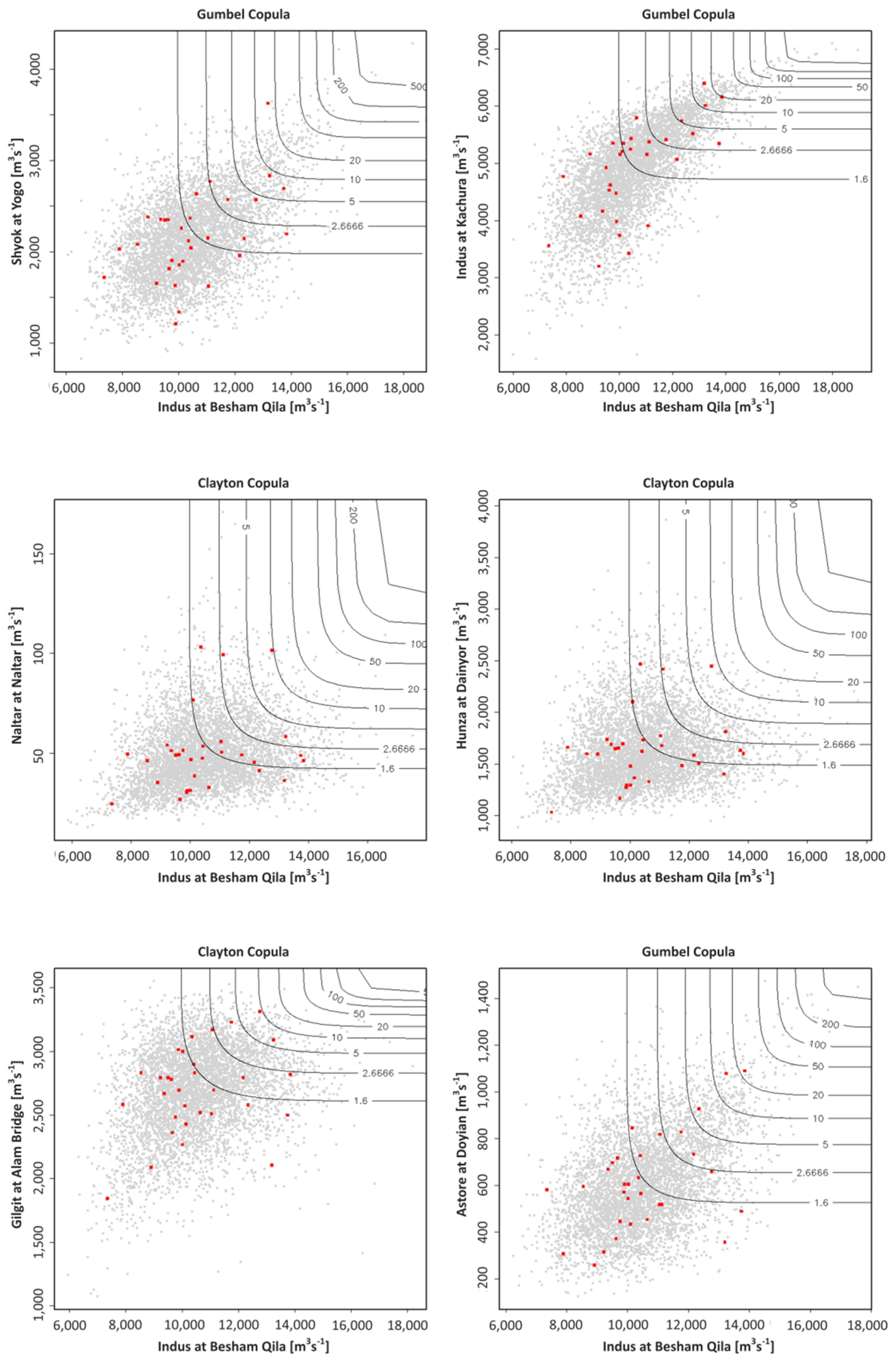
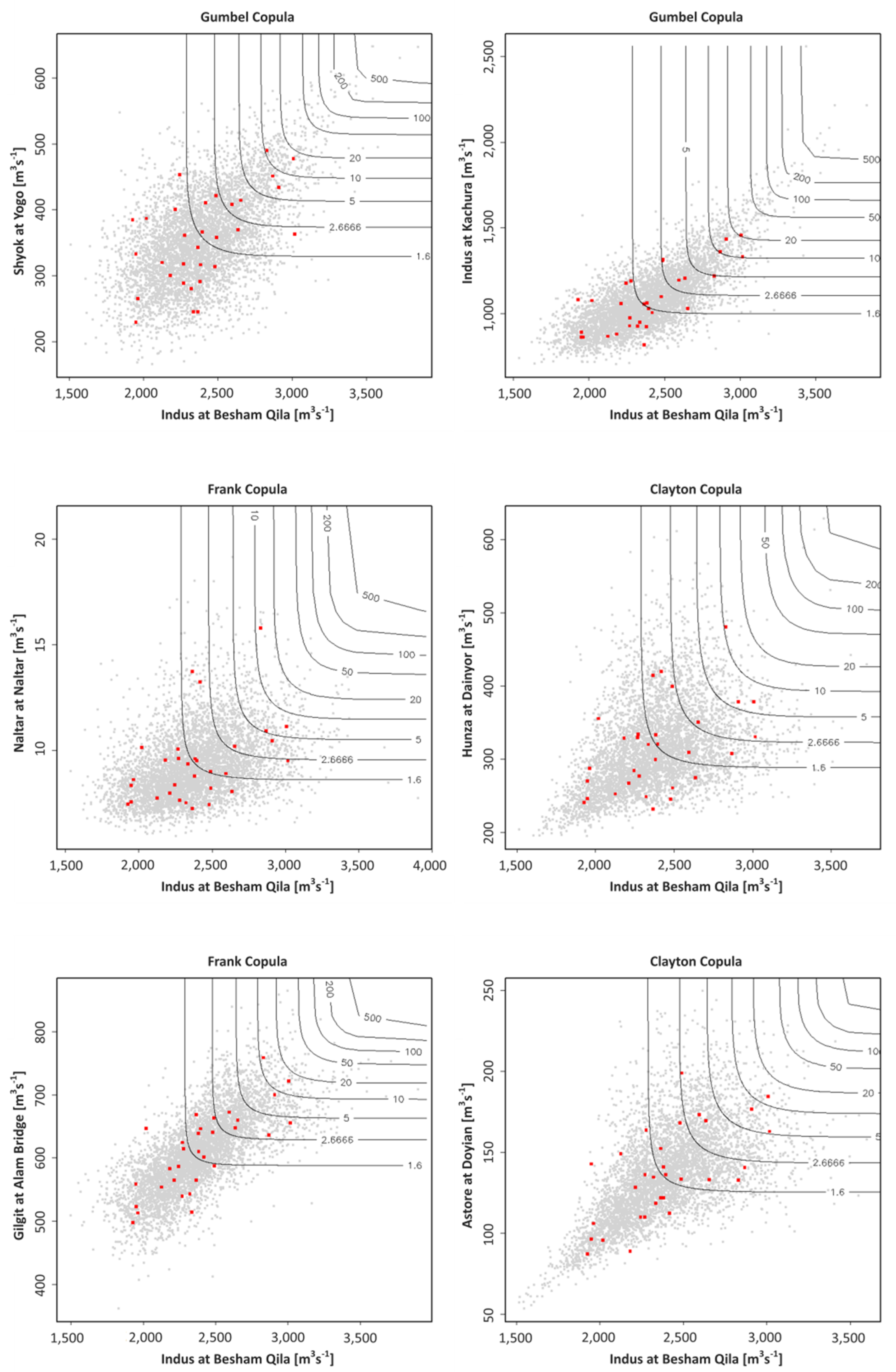
| No. | River | Gauge | Catchment Area (km2) | Elevation (m a.s.l.) | Mean Annual Flow (m3·s−1) | Standard Deviation | Skewness |
|---|---|---|---|---|---|---|---|
| 1 | Shyok | Yogo | 33,041 | 2469 | 356 | 70.2 | 0.04 |
| 2 | Indus | Kachura | 113,035 | 2341 | 1081 | 181.2 | 0.49 |
| 3 | Naltar | Naltar | N/A | 2858 | 9.4 | 2.0 | 1.63 |
| 4 | Hunza | Dainyor | 13,734 | 1370 | 315 | 60.7 | 0.81 |
| 5 | Gilgit | Alam Bridge | 27,035 | 1280 | 611 | 64.4 | 0.14 |
| 6 | Astore | Doyian | 3,903 | 1583 | 136 | 28.9 | 0.21 |
| 7 | Indus | Besham Qila | 163,528 | 580 | 2399 | 305.5 | 0.44 |
| Copula Family | ||||
|---|---|---|---|---|
| Clayton | ||||
| Gumbel–Hougaard | ||||
| Frank |
| River | Gauge | Period | Annual Maximum Flow | Mean Annual Flow |
|---|---|---|---|---|
| Shyok | Yogo | 1974–2004 | −0.642 | −0.234 |
| Indus | Kachura | 1974–2004 | 3.403 *** | 2.005 * |
| Naltar | Naltar | 1974–2004 | 3.032 ** | 2.937 ** |
| Hunza | Dainyor | 1974–2004 | −0.082 | 0.233 |
| Gilgit | Alam Bridge | 1974–2004 | −0.944 | −0.723 |
| Astore | Doyian | 1974–2004 | 0.612 | −0.724 |
| Indus | Besham Qila | 1974–2004 | 1.006 | 1.017 |
| No. | Gauges | Period | Annual Maximum Flow | ||
|---|---|---|---|---|---|
| Correlation Coefficient | Synchronicity [%] | Asynchronicity [%] | |||
| 1 | Besham Qila–Yogo | 1974–2004 | 0.52 *** | 50.66 | 49.34 |
| 2 | Besham Qila–Kachura | 1974–2004 | 0.66 *** | 61.26 | 38.74 |
| 3 | Besham Qila–Naltar | 1974–2004 | 0.24 | 42.06 | 57.94 |
| 4 | Besham Qila–Dainyor | 1974–2004 | 0.25 | 43.22 | 56.78 |
| 5 | Besham Qila–Alam Bridge | 1974–2004 | 0.31 | 42.86 | 57.14 |
| 6 | Besham Qila–Doyian | 1974–2004 | 0.48 *** | 49.04 | 50.96 |
| No. | Gauges | Period | Mean Annual Flow | ||
|---|---|---|---|---|---|
| Correlation Coefficient | Synchronicity [%] | Asynchronicity [%] | |||
| 1 | Besham Qila–Yogo | 1974–2004 | 0.57 *** | 52.62 | 47.38 |
| 2 | Besham Qila–Kachura | 1974–2004 | 0.76 *** | 61.82 | 38.18 |
| 3 | Besham Qila–Naltar | 1974–2004 | 0.44 *** | 49.00 | 51.00 |
| 4 | Besham Qila–Dainyor | 1974–2004 | 0.47 *** | 49.04 | 50.96 |
| 5 | Besham Qila–Alam Bridge | 1974–2004 | 0.76 *** | 66.96 | 33.04 |
| 6 | Besham Qila–Doyian | 1974–2004 | 0.64 *** | 59.70 | 40.30 |
| Sector | Besham—Yogo | Besham Qila—Kachura | Besham Qila—Naltar | Besham Qila—Dainyor | Besham Qila—Alam Bridge | Besham Qila—Doyian |
|---|---|---|---|---|---|---|
| 1 | 20.54 | 25.28 | 17.82 | 19.10 | 18.52 | 19.78 |
| 5 | 7.14 | 8.66 | 6.78 | 6.60 | 6.60 | 7.16 |
| 9 | 22.98 | 27.32 | 17.46 | 17.52 | 17.74 | 22.10 |
| 2 | 9.46 | 8.54 | 8.54 | 8.18 | 8.70 | 9.28 |
| 4 | 9.94 | 9.20 | 7.96 | 8.48 | 8.58 | 9.68 |
| 8 | 7.94 | 7.26 | 9.94 | 10.06 | 10.80 | 8.22 |
| 6 | 7.96 | 6.94 | 10.04 | 9.22 | 9.86 | 8.42 |
| 3 | 7.14 | 3.28 | 10.72 | 10.54 | 9.48 | 7.66 |
| 7 | 6.90 | 3.52 | 10.74 | 10.30 | 9.72 | 7.70 |
| Syn. | 50.66 | 61.26 | 42.06 | 43.22 | 42.86 | 49.04 |
| Asyn. | 49.34 | 38.74 | 57.94 | 56.78 | 57.14 | 50.96 |
| Sector | Besham Qila—Yogo | Besham Qila—Kachura | Besham Qila—Naltar | Besham Qila—Dainyor | Besham Qila—Alam Bridge | Besham Qila—Doyian |
|---|---|---|---|---|---|---|
| 1 | 21.50 | 25.04 | 22.12 | 22.50 | 28.56 | 26.44 |
| 5 | 8.12 | 9.72 | 6.84 | 7.22 | 11.00 | 8.78 |
| 9 | 23.00 | 27.06 | 20.04 | 19.32 | 27.40 | 24.48 |
| 2 | 9.20 | 9.00 | 9.08 | 7.72 | 7.08 | 6.82 |
| 4 | 9.30 | 8.32 | 9.04 | 7.64 | 7.56 | 6.30 |
| 8 | 8.80 | 7.22 | 8.68 | 10.28 | 7.26 | 10.02 |
| 6 | 7.62 | 7.04 | 9.46 | 10.64 | 7.40 | 8.88 |
| 3 | 6.52 | 3.36 | 7.18 | 7.48 | 1.80 | 4.36 |
| 7 | 5.94 | 3.24 | 7.56 | 7.20 | 1.94 | 3.92 |
| Syn. | 52.62 | 61.82 | 49.00 | 49.04 | 66.96 | 59.70 |
| Asyn. | 47.38 | 38.18 | 51.00 | 50.96 | 33.04 | 40.30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobkowiak, L.; Perz, A.; Wrzesiński, D.; Faiz, M.A. Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions. Sustainability 2020, 12, 5122. https://doi.org/10.3390/su12125122
Sobkowiak L, Perz A, Wrzesiński D, Faiz MA. Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions. Sustainability. 2020; 12(12):5122. https://doi.org/10.3390/su12125122
Chicago/Turabian StyleSobkowiak, Leszek, Adam Perz, Dariusz Wrzesiński, and Muhammad Abrar Faiz. 2020. "Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions" Sustainability 12, no. 12: 5122. https://doi.org/10.3390/su12125122
APA StyleSobkowiak, L., Perz, A., Wrzesiński, D., & Faiz, M. A. (2020). Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions. Sustainability, 12(12), 5122. https://doi.org/10.3390/su12125122





