Selection of Winter Season Crop Pattern for Environmental-Friendly Agricultural Practices in India
Abstract
:1. Introduction
- (a)
- To formulate a comprehensive framework that covers all the major criteria involved in the selection of ideal crop patterns for Rabi season crops in terms of sustainable agricultural practices, and
- (b)
- to provide rough set modeling for the selection of Rabi season crops based on sustainable farming practices.
2. Literature Review
3. Methodology
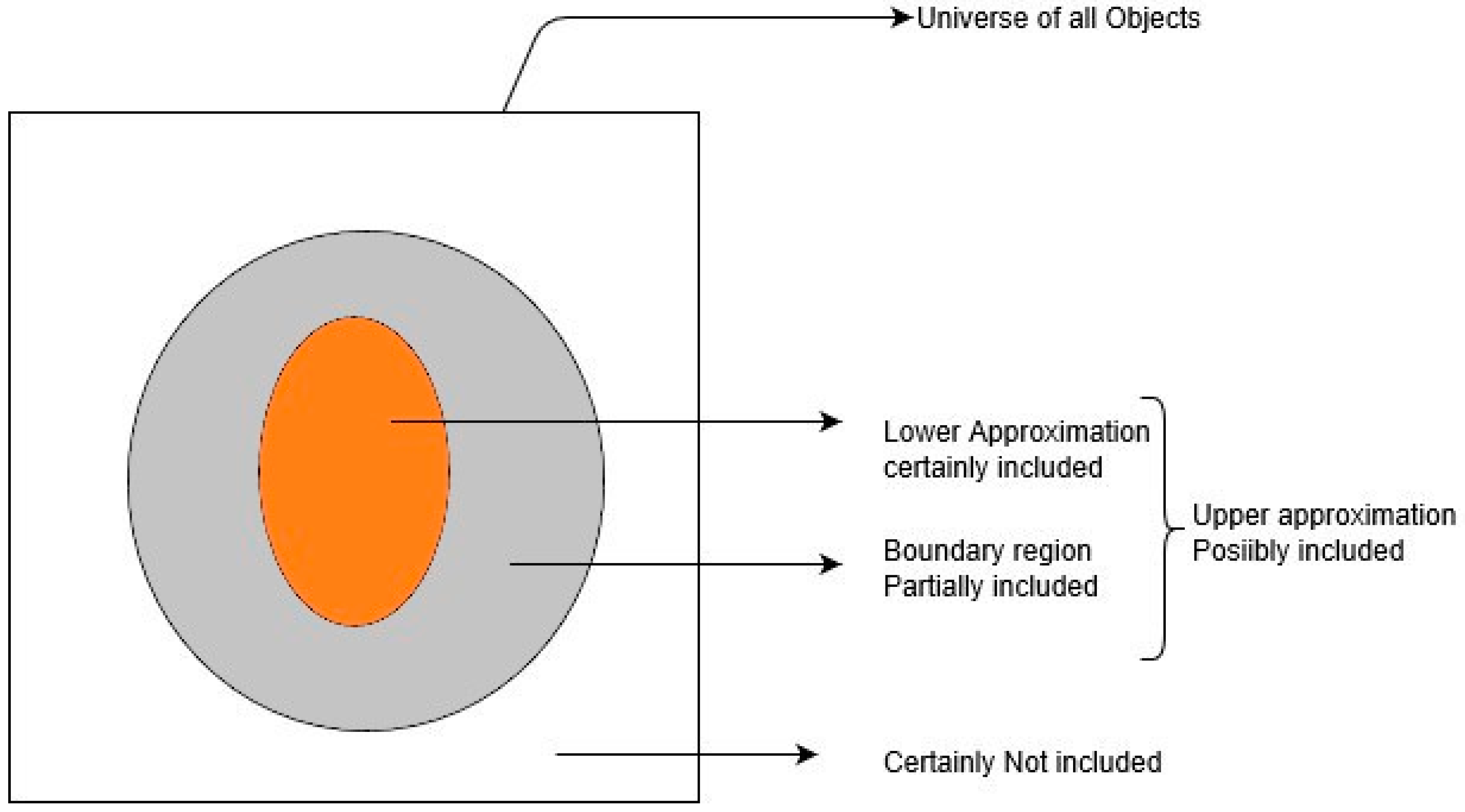
3.1. Rough Set Theory
3.2. Rough Analytical Hierarchy Process
3.3. Rough TOPSIS Method
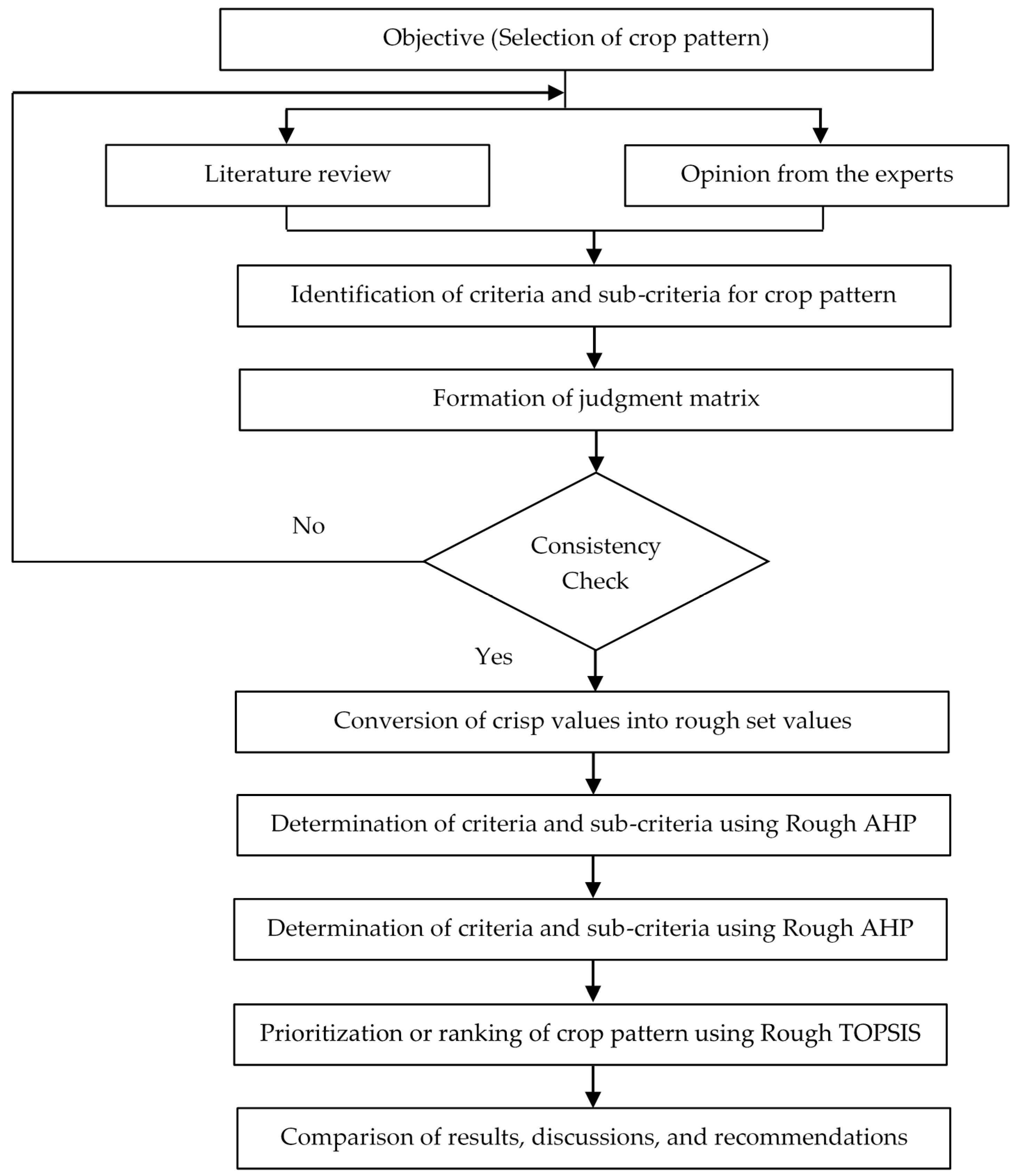
4. Implementation of Developed Framework
Implementation of Rough AHP-TOPSIS Methods
5. Results and Discussions
- Due to the fluctuating socioeconomic conditions and limited resources over the states and regions of India, the selection of appropriate Rabi crop patterns is incredibly challenging. The majority of farmers in India depend on state or government-sponsored subsidies for managing basic crop production resources like water, seeds, fertilizers, labor, and electricity [8]. Proper government support is needed to control the crop value and minimum support price (MSP) so that farmers can grow Rabi crops economically and are not affected by the overflowing stock of granaries [8].
- To ensure proper utilization of existing arable lands between Kharif and Rabi seasons, intercropping of pulses and growing short-duration varieties can be performed. The Department of Agriculture and Cooperation (DAC) of New Delhi, India, has also proposed some strategies to introduce summer pulses (for example, green gram, black gram, and cowpea) in irrigated areas after the harvest of Rabi crops. Replacement of upland paddy with Rabi pulses can be another potential option to ensure more profits to farmers [43].
- For sustainable production, appropriate strategies are required to reduce post-harvest losses, which can cause an immense economic deficit. It is important to identify the crucial causal factors of post-harvest losses in the Rabi crops supply chain. The reduction of post-harvest losses can support to achieve sustainability balancing social, economic, and environmental dimensions [44].
- Lack of proper knowledge and information regarding the demand of pulses and their market price fluctuations may cause overproduction or underproduction, which leads to the unfortunate realization of costs, complicates transportation issues, and leads to substantial losses [45].
- Proper communication and knowledge about the quality of seeds are also essential, as Negi and Anand [46] highlighted that many Indian farmers are unaware of the fact that crops grown from high-quality seeds can actively fight diseases and pests.
- Effective integration and exchange of information between the government, public and private institutions, industries, and farmers are vital for sustainable agricultural practices [47]. The consideration of effective policies for farming, processing, distribution, and sufficient knowledge and training for handling crops can reduce the harvest losses significantly and improve productivity.
- Effective backward–forward integration from farmers to consumers can reduce the dependencies and risks in agricultural supply chains. Effective backward–forward integration can also provide proper control over critical resources and competencies, which can increase the effectiveness and competitiveness of a supply chain [48].
- In India, during Rabi season, most of the crops (i.e., Rabi pulses, Rabi cereals, wheat, barley, gram) are used for annual food consumption in addition to cash crops (i.e., vegetables, sugarcane, spices) [8]. These help farmers to meet their annual food requirements and to generate additional income for future agricultural practices. Thus, for the sustainable consumption, availability of the resources, government support, climatic factors, and economic support are critical to the Rabi season [8].
- For low-income countries, pulse protein is a relatively large share of the overall protein consumption. India is one of the largest producers, consumers, and importers of pulses in the world. Therefore, enhancing Rabi pulse productivity and diversifying cropping systems are key challenges to policymakers, government, scientists, and farming communities for the reduction of the demand–supply gap and to meet the national and local consumptions [40].
- While sustainable agricultural policies are important for India, dedicated efforts also need to be put in practice from all stakeholders in agricultural supply chains for improving health and nutrition through pulse consumption. To develop sustainable water-use and consumption policies, changes in crops and an increased level of intercropping of pulses would be an important strategic consideration [49].
6. Conclusions, Limitations, and Future Research Direction
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Availability | Agricultural Management Practices | Economic Factor | Environmental Impact | |
|---|---|---|---|---|
| Availability | 1 | 3 | 5 | 6 |
| Agricultural management practices | 1 | 3 | 3 | |
| Economic factor | 1 | 2 | ||
| Environmental impact | 1 |
| Crop Demand | Crop Value | Water Tariff | Crop Inventory | |
|---|---|---|---|---|
| Crop demand | 1 | 1 | 4 | 6 |
| Crop value | 1 | 5 | 7 | |
| Water tariff | 1 | 4 | ||
| Crop inventory | 1 |
| Irrigation Methods | Cultivation Methods | |
|---|---|---|
| Irrigation methods | 1 | |
| Cultivation methods | 3 | 1 |
| Water Availability | Soil Quality | Water Quality | |
|---|---|---|---|
| Water availability | 1 | 1 | 2 |
| Soil quality | 1 | 3 | |
| Water quality | 1 |
| Climatic Condition | Rain Fall | |
|---|---|---|
| Climatic condition | 1 | 8 |
| Rainfall | 1 |
| Wheat | Gram | Barley | Rabi Spices | Rabi Cereals | Rabi Vegetables | Rabi Pulses | Rabi Fruits | |
|---|---|---|---|---|---|---|---|---|
| Crop demand | 4 | 4 | 1 | 3 | 5 | 5 | 4 | 3 |
| Crop value | 3 | 3 | 1 | 4 | 3 | 3 | 2 | 1 |
| Crop inventory | 3 | 2 | 2 | 2 | 2 | 1 | 2 | 2 |
| Water tariff | 5 | 4 | 1 | 3 | 4 | 4 | 3 | 2 |
| Irrigation method | 4 | 1 | 4 | 1 | 4 | 1 | 2 | 2 |
| Cultivation method | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 2 |
| Water availability | 2 | 1 | 2 | 2 | 1 | 2 | 3 | 3 |
| Soil quality | 2 | 3 | 2 | 3 | 2 | 1 | 3 | 4 |
| Water quality | 2 | 3 | 2 | 4 | 2 | 2 | 4 | 4 |
| Climatic condition | 1 | 2 | 1 | 3 | 3 | 2 | 3 | 3 |
| Rainfall | 2 | 2 | 1 | 4 | 2 | 3 | 3 | 2 |
Appendix B
| Availability | Agr Mgt Prc | Economic | Environmental | |||||
|---|---|---|---|---|---|---|---|---|
| Limits | L | U | L | U | L | U | L | U |
| Availability | 1.00 | 1.00 | 2.58 | 3.42 | 4.56 | 4.94 | 6.25 | 6.75 |
| Agr mgt prc | 0.30 | 0.41 | 1.00 | 1.00 | 2.58 | 3.42 | 3.27 | 4.25 |
| Economic | 0.20 | 0.22 | 0.30 | 0.41 | 1.00 | 1.00 | 2.33 | 3.75 |
| Environmental | 0.15 | 0.16 | 0.26 | 0.49 | 0.31 | 0.46 | 1.00 | 1.00 |
| Irrigation Methods | Cultivation Methods | |||
|---|---|---|---|---|
| Limits | L | U | L | U |
| Irrigation | 1.00 | 1.00 | 0.58 | 1.41 |
| Cultivation | 1.01 | 2.28 | 1.00 | 1.00 |
| Water Availability | Soil Quality | Water Quality | ||||
|---|---|---|---|---|---|---|
| Limits | L | U | L | U | L | U |
| Water availability | 1.00 | 1.00 | 0.92 | 1.75 | 2.27 | 3.25 |
| Woil quality | 0.73 | 1.88 | 1.00 | 1.00 | 3.27 | 4.25 |
| Water quality | 0.33 | 0.46 | 0.25 | 0.31 | 1.00 | 1.00 |
| Climatic Conditions | Rainfall | |||
|---|---|---|---|---|
| Limits | L | U | L | U |
| Climatic conditions | 1.00 | 1.00 | 6.58 | 7.42 |
| Rainfall | 0.14 | 0.15 | 1.00 | 1.00 |
| Crop Demand | Crop Value | Crop Inventory | Water Tariff | |||||
|---|---|---|---|---|---|---|---|---|
| Limits | L | U | L | U | L | U | L | U |
| Crop demand | 1.00 | 1.00 | 1.00 | 1.76 | 2.75 | 4.60 | 5.75 | 6.73 |
| Crop value | 0.66 | 1.37 | 1.00 | 1.00 | 3.58 | 4.42 | 6.25 | 6.75 |
| Crop inventory | 0.25 | 0.55 | 0.26 | 0.29 | 1.00 | 1.00 | 4.25 | 4.75 |
| Water tariff | 0.15 | 0.17 | 0.15 | 0.16 | 0.21 | 0.24 | 1.00 | 1.00 |
Appendix C
| Limits | Wheat | Gram | Barley | Rabi Spices | Rabi Cereals | Rabi Vegetables | Rabi Pulses | Rabi Fruits | |
|---|---|---|---|---|---|---|---|---|---|
| Crop demand | L | 2.68 | 3.06 | 1.18 | 2.58 | 4.56 | 4.56 | 4.25 | 3.58 |
| U | 3.81 | 3.43 | 2.31 | 3.41 | 4.93 | 4.93 | 4.75 | 4.41 | |
| Crop value | L | 2.12 | 3.56 | 1.12 | 4.00 | 3.06 | 3.27 | 2.75 | 2.12 |
| U | 2.87 | 3.93 | 1.87 | 4.00 | 3.43 | 4.25 | 3.72 | 2.87 | |
| Crop inventory | L | 1.75 | 2.27 | 2.25 | 2.27 | 2.25 | 2.00 | 2.56 | 2.062 |
| U | 3.25 | 3.25 | 2.75 | 3.25 | 2.75 | 3.52 | 2.93 | 2.43 | |
| Water tariff | L | 1.95 | 3.56 | 1.18 | 3.06 | 3.56 | 3.56 | 3.56 | 2.58 |
| U | 4.04 | 3.93 | 2.31 | 3.43 | 3.93 | 3.93 | 3.93 | 3.41 | |
| Irrigation method | L | 3.12 | 1.33 | 2.68 | 1.06 | 3.12 | 1.25 | 2.06 | 2.00 |
| U | 3.87 | 2.75 | 3.81 | 1.43 | 3.87 | 1.75 | 2.43 | 2.00 | |
| Cultivation method | L | 1.50 | 1.75 | 1.12 | 2.12 | 1.58 | 1.64 | 2.06 | 2.12 |
| U | 2.50 | 2.72 | 1.87 | 2.87 | 2.41 | 2.89 | 2.43 | 2.87 | |
| Water availability | L | 2.50 | 1.71 | 2.06 | 2.58 | 2.68 | 2.58 | 3.25 | 3.06 |
| U | 3.50 | 3.37 | 2.43 | 3.41 | 3.81 | 3.41 | 3.75 | 3.43 | |
| Soil quality | L | 2.27 | 3.06 | 1.64 | 3.25 | 3.10 | 2.22 | 3.27 | 4.00 |
| U | 3.25 | 3.43 | 2.89 | 3.75 | 4.35 | 4.18 | 4.25 | 4.00 | |
| Water quality | L | 1.75 | 3.06 | 1.58 | 3.25 | 2.75 | 2.58 | 3.25 | 3.25 |
| U | 3.25 | 3.43 | 2.41 | 3.75 | 3.72 | 3.41 | 3.75 | 3.75 | |
| Climatic condition | L | 1.50 | 2.75 | 1.50 | 3.25 | 3.25 | 2.58 | 3.25 | 3.25 |
| U | 2.50 | 3.73 | 2.50 | 3.75 | 3.75 | 3.41 | 3.75 | 3.75 | |
| Rainfall | L | 1.75 | 2.58 | 1.75 | 3.56 | 3.12 | 3.06 | 3.06 | 2.25 |
| U | 2.72 | 3.41 | 3.25 | 3.93 | 3.87 | 3.43 | 3.43 | 2.75 |
| Limits | Wheat | Gram | Barley | Rabi Spices | Rabi Cereals | Rabi Vegetables | Rabi Pulses | Rabi Fruits | |
|---|---|---|---|---|---|---|---|---|---|
| Crop demand | L | 0.54 | 0.62 | 0.24 | 0.52 | 0.92 | 0.92 | 0.86 | 0.72 |
| U | 0.77 | 0.69 | 0.46 | 0.69 | 1.00 | 1.00 | 0.96 | 0.89 | |
| Crop value | L | 0.50 | 0.83 | 0.26 | 0.94 | 0.72 | 0.76 | 0.64 | 0.50 |
| U | 0.67 | 0.92 | 0.44 | 0.94 | 0.80 | 1.00 | 0.87 | 0.67 | |
| Crop inventory | L | 0.49 | 0.64 | 0.63 | 0.64 | 0.63 | 0.56 | 0.72 | 0.58 |
| U | 0.92 | 0.92 | 0.78 | 0.92 | 0.78 | 1.00 | 0.83 | 0.69 | |
| Water tariff | L | 0.48 | 0.88 | 0.29 | 0.75 | 0.88 | 0.88 | 0.88 | 0.63 |
| U | 1.00 | 0.97 | 0.57 | 0.85 | 0.97 | 0.97 | 0.97 | 0.84 | |
| Irrigation method | L | 0.80 | 0.34 | 0.69 | 0.27 | 0.80 | 0.32 | 0.53 | 0.51 |
| U | 1.00 | 0.70 | 0.98 | 0.37 | 1.00 | 0.45 | 0.62 | 0.51 | |
| Cultivation method | L | 0.51 | 0.60 | 0.38 | 0.73 | 0.54 | 0.56 | 0.71 | 0.73 |
| U | 0.86 | 0.94 | 0.64 | 0.99 | 0.83 | 1.00 | 0.84 | 0.99 | |
| Water availability | L | 0.65 | 0.44 | 0.54 | 0.67 | 0.70 | 0.67 | 0.85 | 0.80 |
| U | 0.91 | 0.88 | 0.63 | 0.89 | 1.00 | 0.89 | 0.98 | 0.90 | |
| Soil quality | L | 0.52 | 0.70 | 0.37 | 0.74 | 0.71 | 0.51 | 0.75 | 0.91 |
| U | 0.74 | 0.78 | 0.66 | 0.86 | 1.00 | 0.96 | 0.97 | 0.91 | |
| Water quality | L | 0.46 | 0.81 | 0.42 | 0.86 | 0.73 | 0.68 | 0.86 | 0.86 |
| U | 0.86 | 0.91 | 0.64 | 1.00 | 0.99 | 0.91 | 1.00 | 1.00 | |
| Climatic condition | L | 0.40 | 0.73 | 0.40 | 0.86 | 0.86 | 0.68 | 0.86 | 0.86 |
| U | 0.66 | 0.99 | 0.66 | 1.00 | 1.00 | 0.91 | 1.00 | 1.00 | |
| Rainfall | L | 0.44 | 0.65 | 0.44 | 0.90 | 0.79 | 0.77 | 0.77 | 0.57 |
| U | 0.69 | 0.86 | 0.82 | 1.00 | 0.98 | 0.87 | 0.87 | 0.69 |
| Limits | Wheat | Gram | Barley | Rabi Spices | Rabi Cereals | Rabi Vegetables | Rabi Pulses | Rabi Fruits | |
|---|---|---|---|---|---|---|---|---|---|
| Crop demand | L | 0.07 | 0.08 | 0.03 | 0.07 | 0.13 | 0.12 | 0.12 | 0.10 |
| U | 0.18 | 0.16 | 0.11 | 0.16 | 0.23 | 0.23 | 0.22 | 0.21 | |
| Crop value | L | 0.06 | 0.11 | 0.04 | 0.12 | 0.09 | 0.10 | 0.09 | 0.07 |
| U | 0.14 | 0.20 | 0.09 | 0.20 | 0.17 | 0.22 | 0.19 | 0.15 | |
| Crop inventory | L | 0.02 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.04 | 0.03 |
| U | 0.07 | 0.07 | 0.06 | 0.07 | 0.06 | 0.08 | 0.07 | 0.06 | |
| Water tariff | L | 0.01 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.01 |
| U | 0.02 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| Irrigation method | L | 0.15 | 0.06 | 0.13 | 0.05 | 0.15 | 0.06 | 0.10 | 0.10 |
| U | 0.37 | 0.26 | 0.36 | 0.14 | 0.37 | 0.17 | 0.24 | 0.19 | |
| Cultivation method | L | 0.13 | 0.15 | 0.10 | 0.19 | 0.14 | 0.15 | 0.18 | 0.19 |
| U | 0.41 | 0.45 | 0.30 | 0.47 | 0.39 | 0.48 | 0.40 | 0.47 | |
| Water availability | L | 0.37 | 0.25 | 0.31 | 0.39 | 0.40 | 0.39 | 0.49 | 0.46 |
| U | 0.82 | 0.79 | 0.57 | 0.80 | 0.89 | 0.80 | 0.88 | 0.81 | |
| Soil quality | L | 0.31 | 0.42 | 0.22 | 0.45 | 0.42 | 0.31 | 0.45 | 0.55 |
| U | 0.74 | 0.78 | 0.66 | 0.86 | 1.00 | 0.96 | 0.97 | 0.92 | |
| Water quality | L | 0.09 | 0.15 | 0.08 | 0.17 | 0.14 | 0.13 | 0.17 | 0.17 |
| U | 0.22 | 0.24 | 0.17 | 0.26 | 0.26 | 0.24 | 0.26 | 0.26 | |
| Climatic condition | L | 0.03 | 0.07 | 0.03 | 0.08 | 0.08 | 0.07 | 0.08 | 0.08 |
| U | 0.08 | 0.13 | 0.08 | 0.13 | 0.13 | 0.12 | 0.13 | 0.13 | |
| Rainfall | L | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| U | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 |
References
- Walle, D. Population growth and poverty: Another look at the Indian time series data. J. Dev. Stud. 2007, 21, 429–439. [Google Scholar] [CrossRef]
- Mahajan, K. Rainfall shocks and the gender wage gap: Evidence from indian agriculture. World Dev. 2017, 91, 156–172. [Google Scholar] [CrossRef]
- Goel, R.; Morhan, D. Investigating the association between population density and travel patterns in Indian cities—An analysis of 2011 census data. Cities 2020, 100. [Google Scholar] [CrossRef] [PubMed]
- NCRB. 2019. Available online: http://ncrb.gov.in/ (accessed on 27 June 2019).
- Mariappan, K.; Zhou, D. A Threat of Farmers’ Suicide and the Opportunity in Organic Farming for Sustainable Agricultural Development in India. Sustainability 2019, 11, 2400. [Google Scholar] [CrossRef] [Green Version]
- Tzouramani, I.; Mantziaris, S.; Karanikolas, P. Assessing Sustainability Performance at the Farm Level: Examples from Greek Agricultural Systems. Sustainability 2020, 12, 2929. [Google Scholar] [CrossRef] [Green Version]
- Nageswararao, M.M.; Dhekale, B.S.; Mohanty, U.C. Impact of climate variability on various Rabi crops over Northwest India. Theor. Appl. Climatol. 2018, 131, 503–521. [Google Scholar] [CrossRef]
- Qureshi MR, N.; Singh, R.K.; Hasan, M.A. Decision support model to select crop pattern for sustainable agricultural practices using fuzzy MCDM. Environ. Dev. Sustain. 2018, 20, 641–659. [Google Scholar] [CrossRef]
- Adewale Johnson Alonge, R.A.M. Assessment of the Adoption Of Sustainable Agriculture Practices: Implications For Agricultural Education. J. Agric. Educ. 1995, 36, 34–42. [Google Scholar] [CrossRef] [Green Version]
- Chandre Gowda, M.J.; Jayaramaiah, K.M. Comparative evaluation of rice production systems for their sustainability. Agric. Ecosyst. Environ. 1998, 69, 1–9. [Google Scholar] [CrossRef]
- Nambiar KK, M.; Gupta, A.P.; Fu, Q.; Li, S. Biophysical, chemical and socio-economic indicators for assessing agricultural sustainability in the Chinese coastal zone. Agric. Ecosyst. Environ. 2001, 87, 209–214. [Google Scholar] [CrossRef]
- Zhen, L.; Routray, J.K.; Zoebisch, M.A.; Chen, G.; Xie, G.; Cheng, S. Three dimensions of sustainability of farming practices in the North China Plain: A case study from Ningjin County of Shandong Province, PR China. Agric. Ecosyst. Environ. 2005, 105, 507–522. [Google Scholar] [CrossRef]
- Sydorovych, O.; Wossink, A. The meaning of agricultural sustainability: Evidence from a conjoint choice survey. Agric. Syst. 2008, 98, 10–20. [Google Scholar] [CrossRef]
- An Integrative Approach for Introducing Conservation Agriculture Practices to Tribal Societies in India. Available online: https://vtechworks.lib.vt.edu/bitstream/handle/10919/70446/5149_Cambodia_poster_2011.pdf?sequence=1&isAllowed=y (accessed on 27 May 2020).
- Yadav, S.K.; Babu, S.; Yadav, M.K.; Singh, K.; Yadav, G.S.; Pal, S. A Review of Organic Farming for Sustainable Agriculture in Northern India. Int. J. Agron. 2013, 2013, 718145. [Google Scholar] [CrossRef] [Green Version]
- Demartini, E.; Gaviglio, A.; Bertoni, D. Environmental Science & Policy Integrating agricultural sustainability into policy planning: A geo-referenced framework based on Rough Set theory. Environ. Sci. Policy 2015, 54, 226–239. [Google Scholar]
- Zdzislaw, P. Rough Sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments. Qual. Reliab. Eng. Int. 2014, 30, 473–486. [Google Scholar] [CrossRef]
- Shankarnarayan, V.K.; Ramakrishna, H. Paradigm change in Indian agricultural practices using big data: Challenges and Opportunities from field to plate. Inf. Process. Agric. 2020. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Mishra, S. Regulatory reform and market efficiency: The case of Indian agricultural commodity futures markets. Res. Int. Bus. Financ. 2020, 52, 101145. [Google Scholar] [CrossRef]
- Barry, P.J.; Fraser, D.R. Risk Management in Primary Agricultural Production: Methods, Distribution, Rewards, and Structural Implications. Am. J. Agric. Econ. 2006, 58, 286. [Google Scholar] [CrossRef]
- Dadhwal, V.K.; Singh, R.P.; Dutta, S.; Parihar, J.S. Remote sensing based crop inventory: A review of Indian experience. Trop. Ecol. 2002, 43, 107–122. [Google Scholar]
- Pathak, H.; Pramanik, P.; Khanna, M.; Kumar, A. Climate change and water availability in Indian agriculture: Impacts and adaptation. Indian J. Agric. Sci. 2014, 84, 671–679. [Google Scholar]
- German, R.N.; Thompson, C.E.; Benton, T.G. Relationships among multiple aspects of agriculture’s environmental impact and productivity: A meta-analysis to guide sustainable agriculture. Biol. Rev. 2017, 92, 716–738. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M.; Lewandowski, I. Relevance of environmental impact categories for perennial biomass production. Bioenergy 2016, 9, 215–228. [Google Scholar] [CrossRef] [Green Version]
- Krishna Kumar, K.; Rupa Kumar, K.; Ashrit, R.G.; Deshpande, N.R.; Hansen, J.W. Climate impacts on Indian agriculture. Int. J. Climatol. 2004, 24, 1375–1393. [Google Scholar] [CrossRef]
- ENVIS Centre. Environmental Information System. State of Environment and Related Issues. 2019. Available online: http://www.envis.nic.in/ (accessed on 25 June 2019).
- Zhang, Q.; Xie, Q.; Wang, G. A survey on rough set theory and its applications. CAAI Trans. Intell. Technol. 2016, 1, 323–333. [Google Scholar] [CrossRef]
- Skowron, A.; Dutta, S. Rough sets: Past, present, and future. Nat. Comput. 2018, 17, 855–876. [Google Scholar] [CrossRef] [Green Version]
- Vluymans, S.; D’eer, L.; Saeys, Y.; Cornelis, C. Applications of fuzzy rough set theory in machine learning: A survey. Fundam. Inform. 2015, 142, 53–86. [Google Scholar] [CrossRef] [Green Version]
- Skowron, A.; Jankowski, A. Rough sets and interactive granular computing. Fundam. Inform. 2016, 147, 371–385. [Google Scholar]
- Pawlak, Z.; Skowron, A. Rudiments of rough sets. Inf. Sci. 2007, 177, 3–27. [Google Scholar] [CrossRef]
- Skowron, A.; Suraj, Z. (Eds.) Rough Sets and Intelligent Systems-Professor Zdzisław Pawlak in Memoriam; Series Intelligent Systems Reference Library; Springer: Heidelberg, Germany, 2013; Volume 42–43. [Google Scholar]
- Li, Y.; Sun, M.; Yuan, G.; Zhou, Q.; Liu, J. Study on Development Sustainability of Atmospheric Environment in Northeast China by Rough Set and Entropy Weight Method. Sustainability 2019, 11, 3793. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.-W.; Lo, H.-W.; Chen, K.-Y.; Liou, J.J.H. A novel FMEA model based on rough BWM and Rough TOPSIS-AL for Risk Assessment. Mathematics 2019, 7, 874. [Google Scholar] [CrossRef] [Green Version]
- He, Y.H.; Wang, L.B.; He, Z.Z.; Xie, M. A fuzzy TOPSIS and rough set based approach for mechanism analysis of product infant failure. Eng. Appl. Artif. Intel. 2016, 47, 25–37. [Google Scholar] [CrossRef]
- Berchoux, T.; Watmough, G.R.; Hutton, C.W.; Atkinson, P.M. Agricultural shocks and drivers of livelihood precariousness across Indian rural communities. Landsc. Urban Plan. 2019, 189, 307–319. [Google Scholar] [CrossRef]
- Vetter, S.H.; Sapkota, T.B.; Hillier, J.; Stirling, C.M.; Macdiarmid, J.I.; Aleksandrowicz, L.; Green, R.; Joy, E.J.M.; Dangour, A.D.; Smith, P. Greenhouse gas emission from agricultural food production to supply Indian diets: Implications for climate change mitigation. Agric. Ecosyst. Environ. 2017, 237, 234–241. [Google Scholar] [CrossRef] [Green Version]
- Sapkota, T.B.; Vetter, S.H.; Jat, M.L.; Sirohi, S.; Shirsath, P.B.; Singh, R.; Jat, H.S.; Smith, P.; Hillier, J.; Stirling, C.M. Cost-effective opportunities for climate change mitigation in Indian agriculture. Sci. Total Environ. 2019, 655, 1342–1354. [Google Scholar] [CrossRef]
- Choudhary, A.K. Technological and extension yield gaps in pulse crops in Mandi district of Himachal Pradesh, India. Indian J. Soil Conserv. 2013, 41, 88–98. [Google Scholar]
- Yadav, A.; Suri, V.K.; Kumar, A.; Choudhary, A.K.; Meena, A.L. Enhancing plant water relations, quality, and productivity of pea (Pisum sativum L.) through arbuscular mycorrhizal fungi, inorganic phosphorus, and irrigation regimes in an Himalayan acid Alfisol. Commun. Soil Sci. Plant Anal. 2015, 46, 80–93. [Google Scholar] [CrossRef]
- Sharma, D.P.; Singh, M.P.; Gupta, S.K.; Sharma, N.L. Response of pigeonpea to short-term water stagnation in a moderately sodic soil under field conditions. J. Indian Soc. Soil Sci. 2005, 53, 243–248. [Google Scholar]
- Pooniya, V.; Choudhary, A.K.; Dass, A.; Bana, R.S.; Rana, K.S.; Rana, D.S.; Tyagi, V.K.; Puniya, M.M. Improved crop management practices for sustainable pulse production: An Indian perspective. Indian J. Agric. Sci. 2015, 85, 747–758. [Google Scholar]
- Raut, R.D.; Gardas, B.B.; Kharat, M.; Narkhede, B. Modeling the drivers of post-harvest losses–MCDM approach. Comput. Electron. Agric. 2018, 154, 426–433. [Google Scholar] [CrossRef]
- Modi, P.; Mishra, D.; Gulati, H.; Murugesan, K. Uttarakhand state cooperative federation: Can it help the horticulture farmers? Vision 2009, 13, 53–61. [Google Scholar] [CrossRef]
- Negi, S.; Anand, N. Supply chain of fruits & vegetables’ agribusiness in Uttarakhand (India): Major issues and challenges. J. Supply Chain Manag. Syst. 2015, 4, 43–57. [Google Scholar]
- Van Roekel, J.; Willems, S.; Boselie, D.M. Agri-supply chain management: To stimulate cross-border trade in developing countries and emerging economies. World Bank Pap. Cross Bord. Agri Supply Chain Manag. 2002, 1–28. [Google Scholar]
- Singh, S.P.; Sikka, B.K.; Singh, A. Supply chain management and Indian fresh produce supply chain: Opportunities and challenges. In Proceedings of the International Food & Agribusiness Management Association, 19th Annual World Symposium, Budapest, Hungary, 20–23 June 2009. [Google Scholar]
- McDermott, J.; Wyatt, A.J. The role of pulses in sustainable and healthy food systems. Ann. N. Y. Acad. Sci. 2017, 1392, 30–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| No | Criteria | Brief Description | Literature |
|---|---|---|---|
| 1 | Economic factor | The economic factor is one of three major factors of sustainable agriculture. It accounts for all the economic aspects that are involved in agricultural practices. | Shankarnarayan & Ramakrishna [19]; Mohanty & Mishra [20] |
| 2 | Water tariff | It’s one of the sub-criteria of the economic factor. Water tariff is the cost of water that is assigned by the Government. | Qureshi et al. [8] |
| 3 | Crop value | Crop value is a part of the economic factor, which tells the value of a crop in the local and global market at one time. | Sydorovych & Wossink [13] |
| 4 | Crop demand | It measures the requirement of a particular crop in the local and global markets. | Qureshi et al. [8] |
| 5 | Crop inventory | Price variability risks are more associated with the crop inventory. The fluctuations in the agricultural market challenge the forecast of crop inventory. | Barry&Fraser, [21]; Dadhwal et al. [22] |
| 6 | Agricultural management practices | This factor accounts for all the processes from sowing seeds until the harvesting. | Nambiar et al. [11] |
| 7 | Irrigation methods | This is a part of agricultural management practice which illustrates the type of irrigation method (surface, sub-surface, drip, sprinkler) that will be suitable for a particular crop. | Qureshi et al. [8] |
| 8 | Cultivation methods | It is a sub-criteria of agricultural management practices. It covers all the processes other than irrigation. | Nambiar et al. [11] |
| 9 | Availability | This factor indicates the availability of all the factors that are necessary for sustainable agricultural practices. | Sydorovych & Wossink [13] |
| 10 | Water availability | The quantity of water for agriculture in India shows a progressive increase over the years as more and more areas are brought under irrigation. | H Pathak et al. [23] |
| 11 | Soil quality | Initial practice to improve soil quality is very costly for a farmer for the first year, but a continuous following of organic farming over a period of time can contribute to high yielding, and also preserves the soil for further cultivation. Vermicompost generated by earthworms gives us plenty of opportunities to utilize the soil for sustainable farming for the crops. | Yadav et al. [15] |
| 12 | Water quality | Water quality is one of the most important ecological components for measuring agricultural sustainability. | Sydorovych & Wossink [13] |
| 13 | Environmental impact | Soil erosion; acidification potential; abiotic depletion potential; terrestrial ecotoxicity; freshwater ecotoxicity; marine water ecotoxicity; and polluted water. | German et al. [24]; Wagner & Lewandowski [25] |
| 14 | Climatic conditions | Global warming potential; photochemical ozone creation potential; ozone depletion potential; and heavy rainfall | Krishna et al. [26]; Wagner & Lewandowski [25]; Qureshi et al. [8] |
| References | Method | Application |
|---|---|---|
| Adewale Johnson Alonge [9] | Population sample, data collection, and data analysis | To assess how much the farmers in Iowa adopt sustainable agriculture practices. |
| Chandre et al. [10] | Normalized rank approach | To find the Agriculture Sustainability Index (ASI). |
| Nambiar et al. [11] | Indicator and rating system | To find the Agriculture Sustainability Index (ASI). |
| Krishna Kumar et al. [26] | Statistics of crop data and climate data were used to analyze. | To find out the relationship between the crops of both Kharif and Rabi season with respect to climate change. |
| Zhen et al. [12] | Setting up the threshold values of site-specific indicators. | To assess the socio-institutional and environmental aspects of major cropping systems. |
| Sydorovych & Wossink [13] | Method of conjoint analysis | Aggregation on sustainable agriculture. |
| Yadav et al. [15] | Systematic literature review | How Organic farming helps to improvise the crop yield, soil fertility. |
| German et al. [24] | Used meta-analysis to assess the relationships between multiple measures of sustainability | Provide strong evidence of the relationship between yield and negative externalities created by farming |
| Nageswararao et al. [7] | Calculating the correlation coefficient. | To measure the impact of climate variability in the growth of Rabi season crops. |
| Qureshi et al. [8] | AHP-TOPSIS method | To find the crop pattern of sustainable agriculture. |
| Intensity of Importance | Explanation |
|---|---|
| 1 | Equal importance |
| 2 | Weak or slight |
| 3 | Moderate importance |
| 4 | Moderate plus |
| 5 | Strong importance |
| 6 | Strong plus |
| 7 | Very strong importance |
| 8 | Very, very strong importance |
| 9 | Extreme importance |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.52 | 0.89 | 1.11 | 1.25 | 1.35 | 1.40 | 1.45 | 1.49 |
| Goal | Criteria | Sub-Criteria | Alternatives |
|---|---|---|---|
| Selection of Crop Pattern | Economic Factor | Crop Demand | Barley |
| Crop Value | Gram | ||
| Crop Inventory | Rabi Cereals | ||
| Water Tariff | Rabi Fruits | ||
| Agriculture Management Practices | Irrigation Methods | Rabi Pulses | |
| Cultivation Methods | Rabi Spices | ||
| Availability | Water Availability | Rabi Vegetables | |
| Water Quality | Wheat | ||
| Soil Quality | |||
| Environmental Factor | Climatic Condition | ||
| Rainfall |
| Criteria | Score Values | Definition |
|---|---|---|
| Crop demand, crop value, water tariff, crop inventory, water requirement, soil quality, water quality, climatic conditions, rainfall | 1 | Very low |
| 2 | Low | |
| 3 | Moderate | |
| 4 | High | |
| 5 | Very high | |
| Irrigation methods | 1 | Sprinkle irrigation |
| 2 | Drip irrigation | |
| 3 | Sub-surface irrigation | |
| 4 | Surface irrigation | |
| Cultivation methods | 1 | Low care |
| 2 | Medium care | |
| 3 | High care |
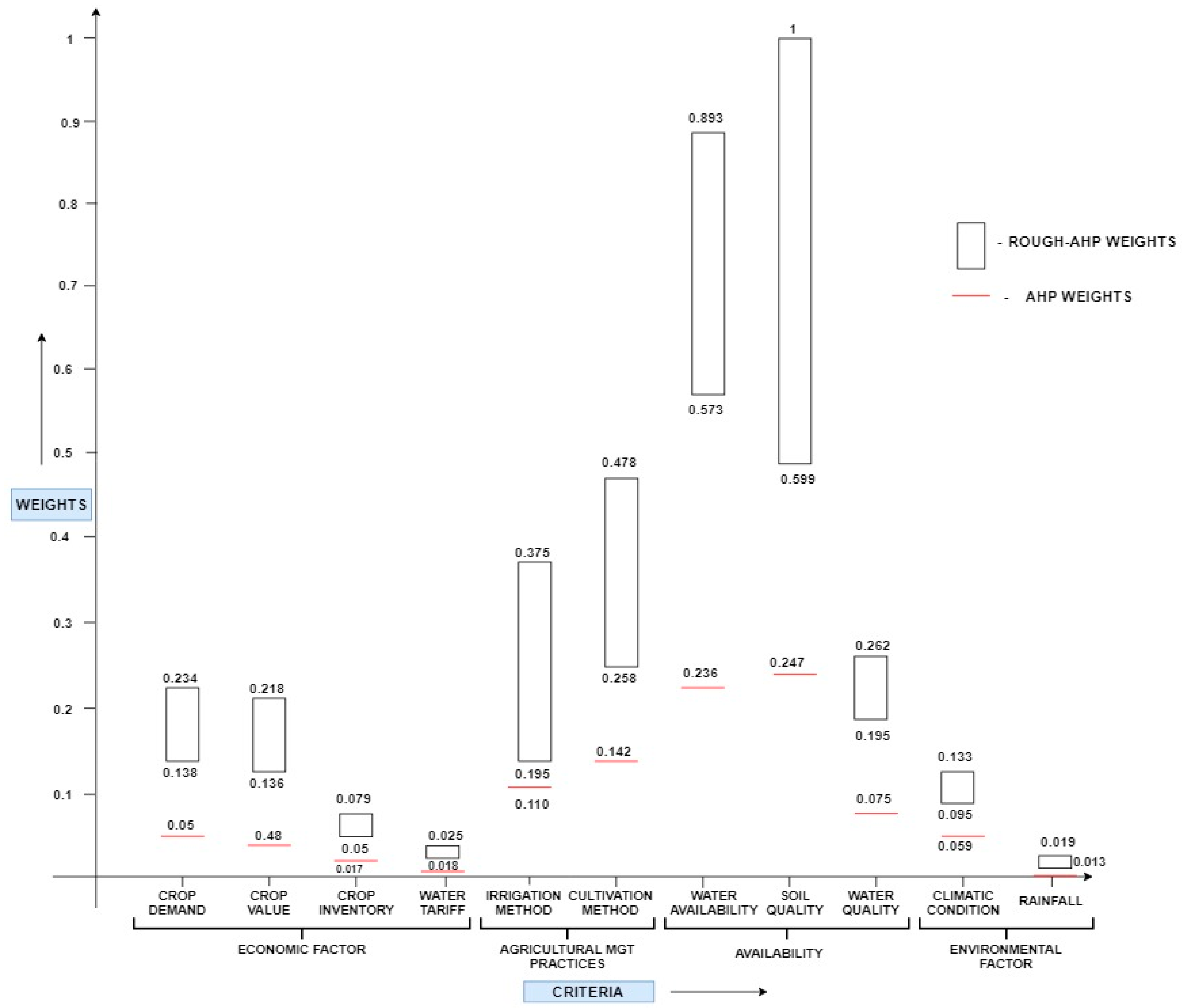
| Criteria | Criteria Weight | Sub-Criteria | Sub-Criteria Weight | Global Weight | |||
|---|---|---|---|---|---|---|---|
| Limits | L | U | L | U | L | U | |
| Crop Demand | 0.73 | 1.00 | 0.14 | 0.23 | |||
| Economic | 0.19 | 0.23 | Crop Value | 0.72 | 0.93 | 0.13 | 0.22 |
| Crop Inventory | 0.27 | 0.34 | 0.05 | 0.08 | |||
| Water Tariff | 0.09 | 0.11 | 0.02 | 0.02 | |||
| Agr mgt Prac | 0.39 | 0.48 | Irrigation | 0.50 | 0.79 | 0.19 | 0.37 |
| Cultivation | 0.66 | 1.00 | 0.25 | 0.48 | |||
| Water Availability | 0.63 | 0.89 | 0.57 | 0.89 | |||
| Availability | 0.89 | 1.00 | Soil Quality | 0.67 | 1.00 | 0.59 | 1.00 |
| Water Quality | 0.22 | 0.26 | 0.19 | 0.26 | |||
| Environmental | 0.10 | 0.13 | Climatic Condition | 0.94 | 1.00 | 0.09 | 0.13 |
| Rainfall | 0.14 | 0.14 | 0.01 | 0.02 | |||
| Distance | d+ | D− |
|---|---|---|
| Wheat | 0.99 | 0.92 |
| Gram | 0.99 | 0.92 |
| Barley | 1.12 | 0.67 |
| Rabi Spices | 0.89 | 0.97 |
| Rabi Cereals | 0.87 | 1.14 |
| Rabi Vegetables | 0.99 | 1.05 |
| Rabi Pulses | 0.81 | 1.08 |
| Rabi Fruits | 0.77 | 1.01 |
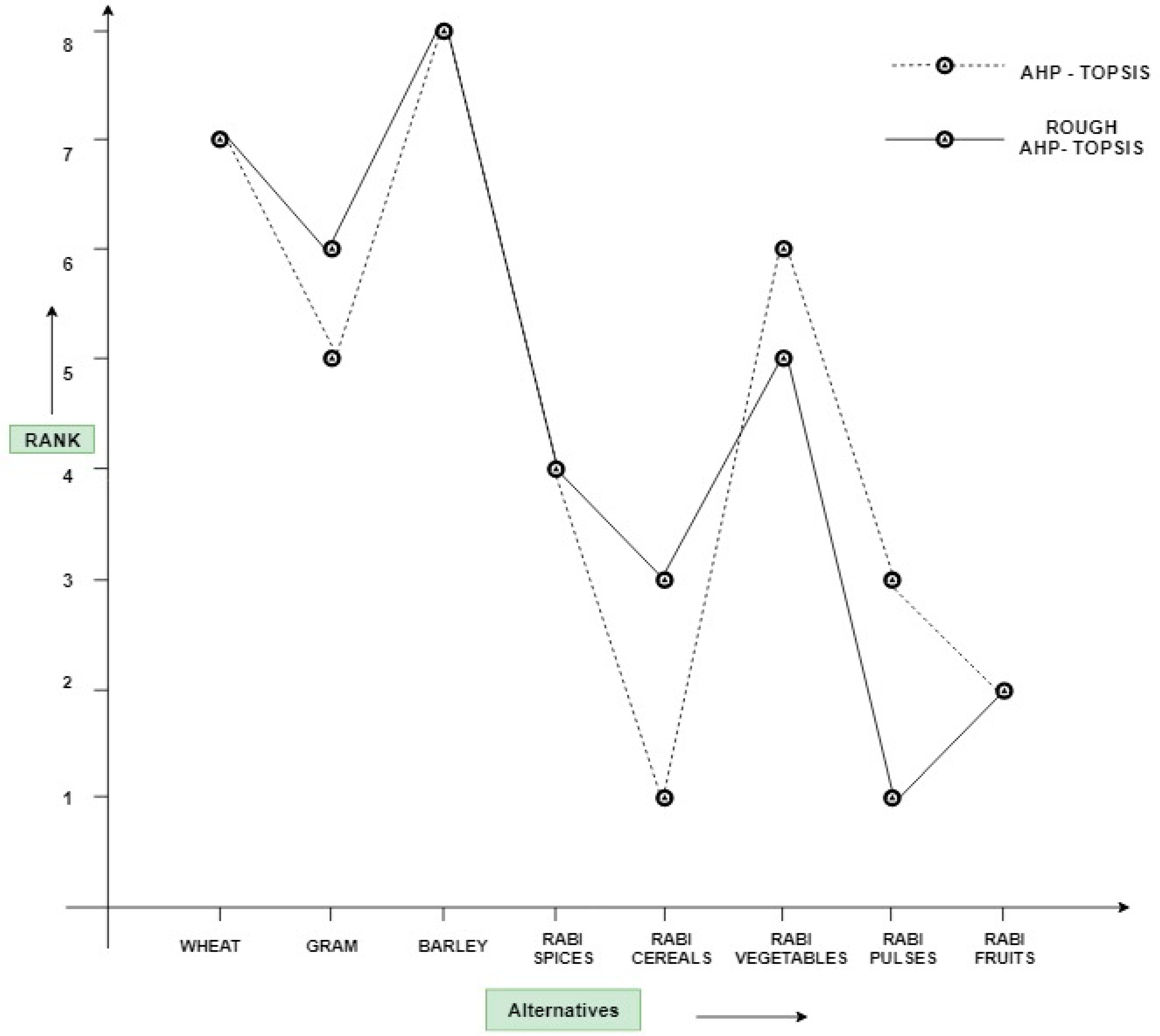
| Distance | Closeness Coefficient (Ci) | Rank |
|---|---|---|
| Wheat | 0.48 | 7 |
| Gram | 0.48 | 6 |
| Barley | 0.38 | 8 |
| Rabi Spices | 0.52 | 4 |
| Rabi Cereals | 0.56 | 3 |
| Rabi Vegetables | 0.51 | 5 |
| Rabi Pulses | 0.57 | 1 |
| Rabi Fruits | 0.56 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sambasivam, V.P.; Thiyagarajan, G.; Kabir, G.; Ali, S.M.; Khan, S.A.R.; Yu, Z. Selection of Winter Season Crop Pattern for Environmental-Friendly Agricultural Practices in India. Sustainability 2020, 12, 4562. https://doi.org/10.3390/su12114562
Sambasivam VP, Thiyagarajan G, Kabir G, Ali SM, Khan SAR, Yu Z. Selection of Winter Season Crop Pattern for Environmental-Friendly Agricultural Practices in India. Sustainability. 2020; 12(11):4562. https://doi.org/10.3390/su12114562
Chicago/Turabian StyleSambasivam, Veerasekar Palaniappan, Gowtham Thiyagarajan, Golam Kabir, Syed Mithun Ali, Syed Abdul Rehman Khan, and Zhang Yu. 2020. "Selection of Winter Season Crop Pattern for Environmental-Friendly Agricultural Practices in India" Sustainability 12, no. 11: 4562. https://doi.org/10.3390/su12114562
APA StyleSambasivam, V. P., Thiyagarajan, G., Kabir, G., Ali, S. M., Khan, S. A. R., & Yu, Z. (2020). Selection of Winter Season Crop Pattern for Environmental-Friendly Agricultural Practices in India. Sustainability, 12(11), 4562. https://doi.org/10.3390/su12114562








