Shear-Torque Fatigue Performance of Geogrid-Reinforced Asphalt Interlayers
Abstract
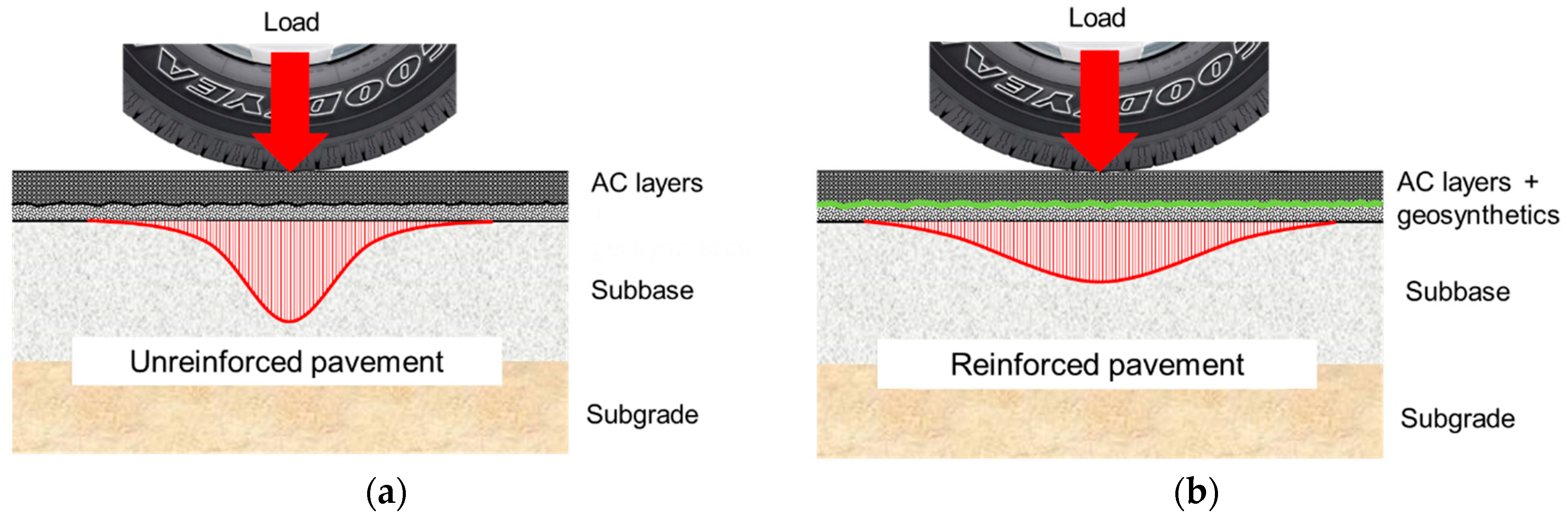
1. Introduction
Objective and Scope
2. Experimental Program
2.1. Reinforcing Materials
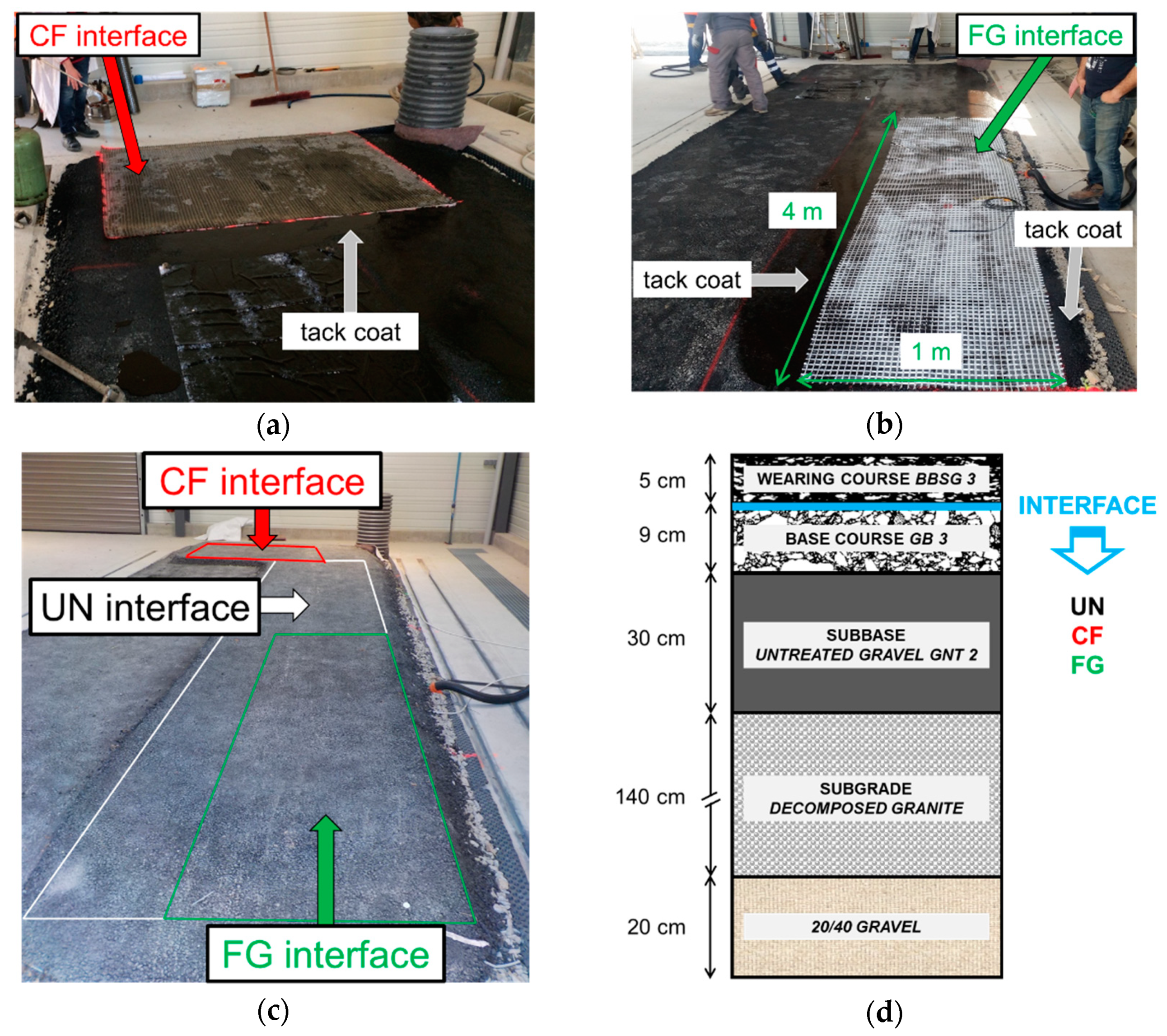
2.2. Trial Section and Specimen Preparation
- unreinforced with a tack coat interface used as a reference for comparison purposes (coded as UN);
- tack coat and carbon fiber geogrid (coded as CF);
- tack coat and glass fiber geogrid (coded as FG).
- 20/40 gravel with a thickness of 20 cm on the bottom of the pit;
- subgrade course, having a thickness of 140 cm, prepared with decomposed granite;
- subbase course, having a thickness of 30 cm, prepared with untreated gravel GNT 2 (GNT stands for “Grave Non-Traitée” in French) [46] of maximum diameter 31.5 mm;
- base course, having a thickness of 9 cm, prepared with asphalt concrete GB 3 0/14 (GB stands for “Grave Bitume” in French) [47];
- accurate cleaning and preparation of the upper base course surface and application of the tack coat (bituminous emulsion of pure bitumen) with a residual dosage of 0.5 kg/m2;
- application of the geogrids directly on the fresh emulsion right after spreading (except for the unreinforced section);
- application of the tack coat with a residual dosage of 0.5 kg/m2 only above the FG geogrid;
- wearing course, having a thickness of 5 cm, with asphalt concrete BBSG 3 0/10 (BBSG stands for “Béton Bitumineux Semi Grenu” in French) [47], once the tack coat emulsion was fully cured.
2.3. Testing Methods
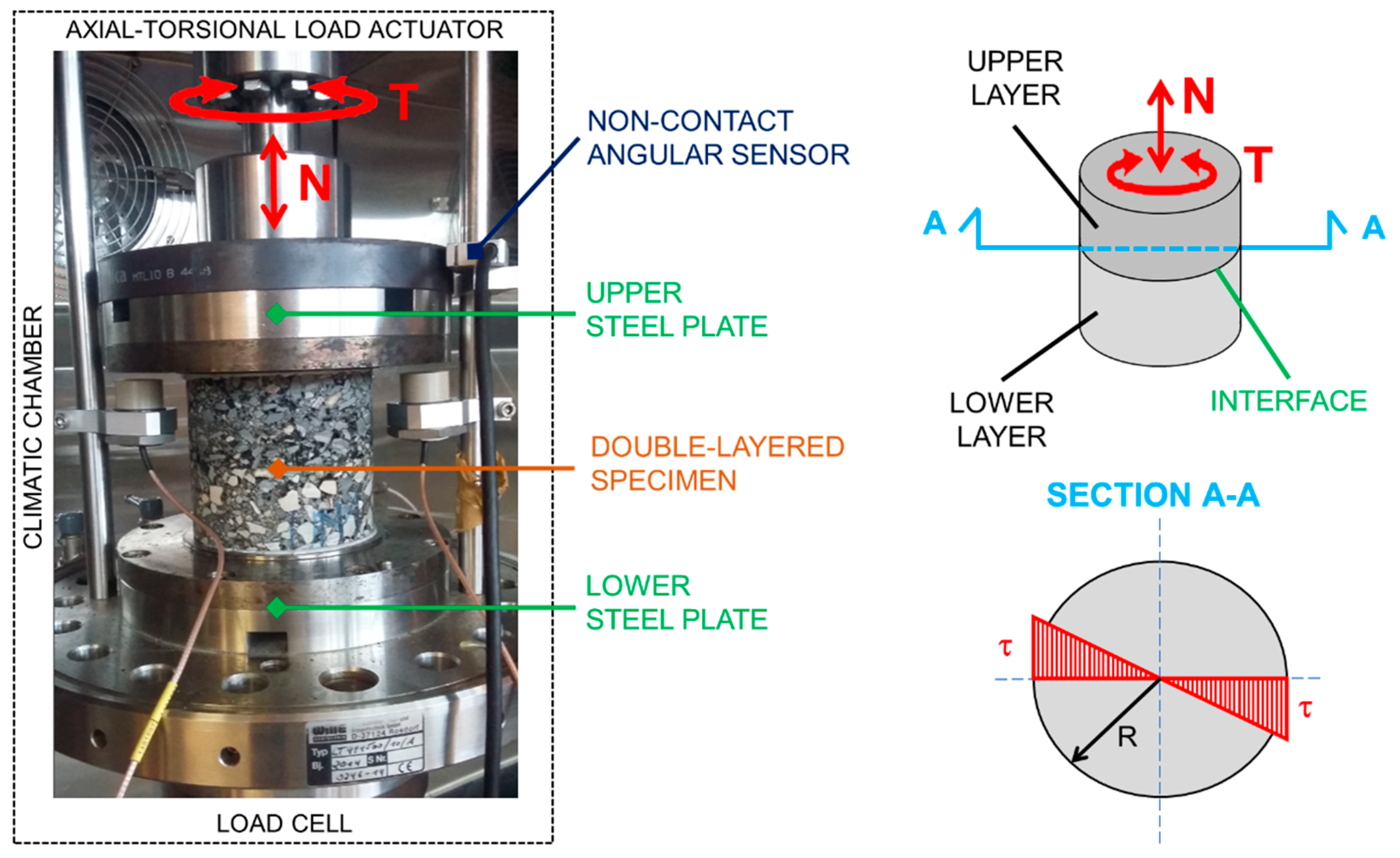
2.3.1. Shear-Torque Fatigue Test
2.3.2. Leutner Test
2.4. Testing Program
3. Results
3.1. Shear-Torque Fatigue Test Results
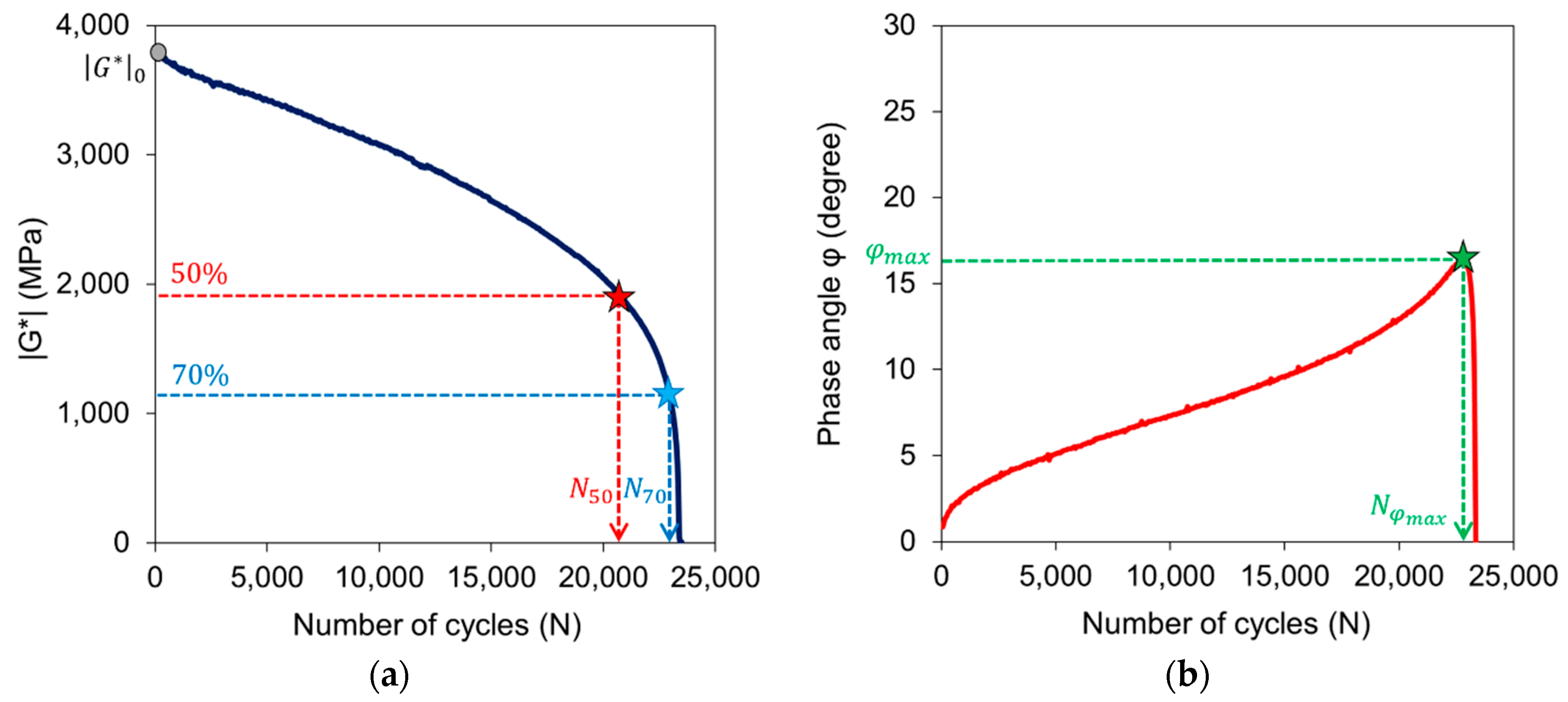
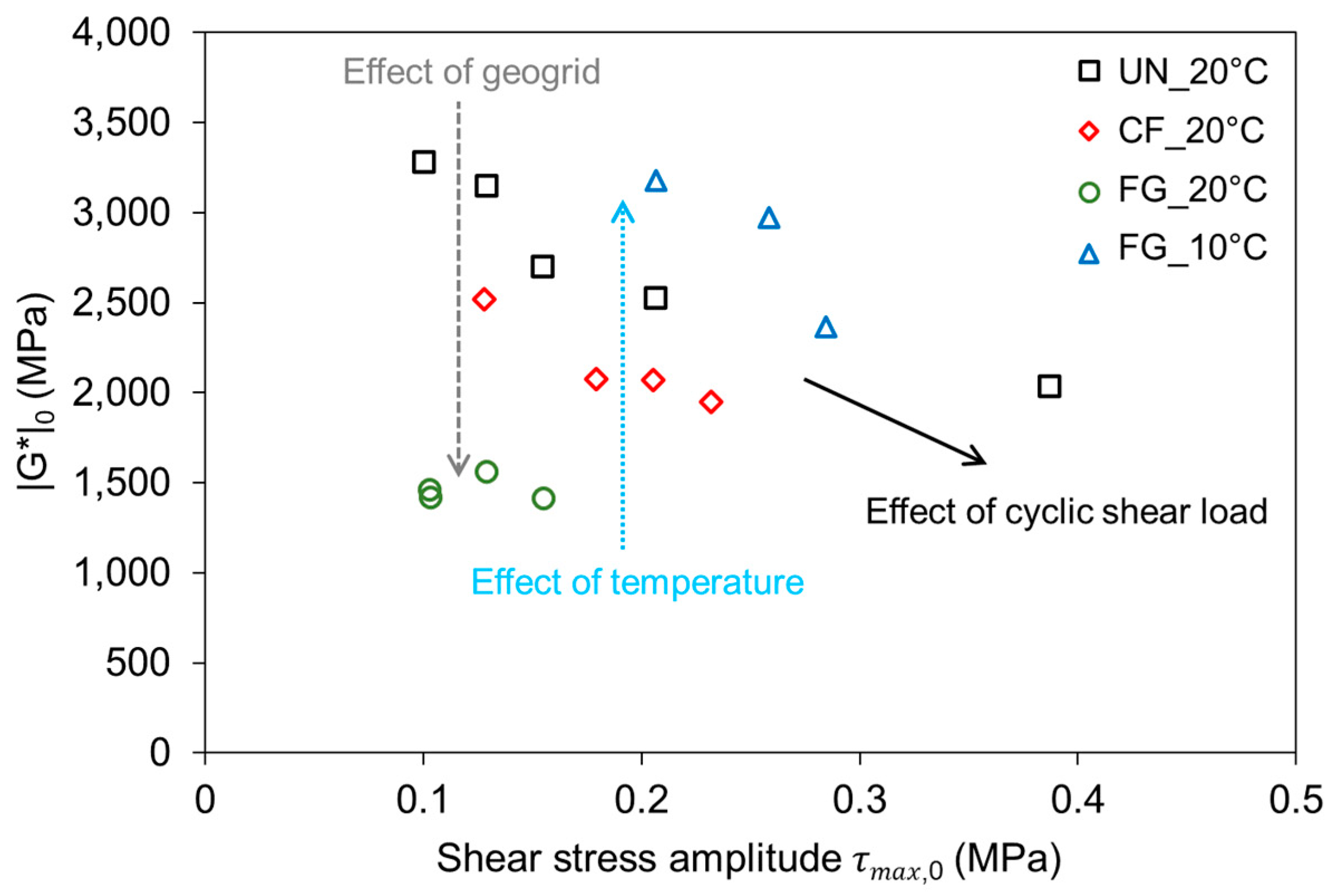
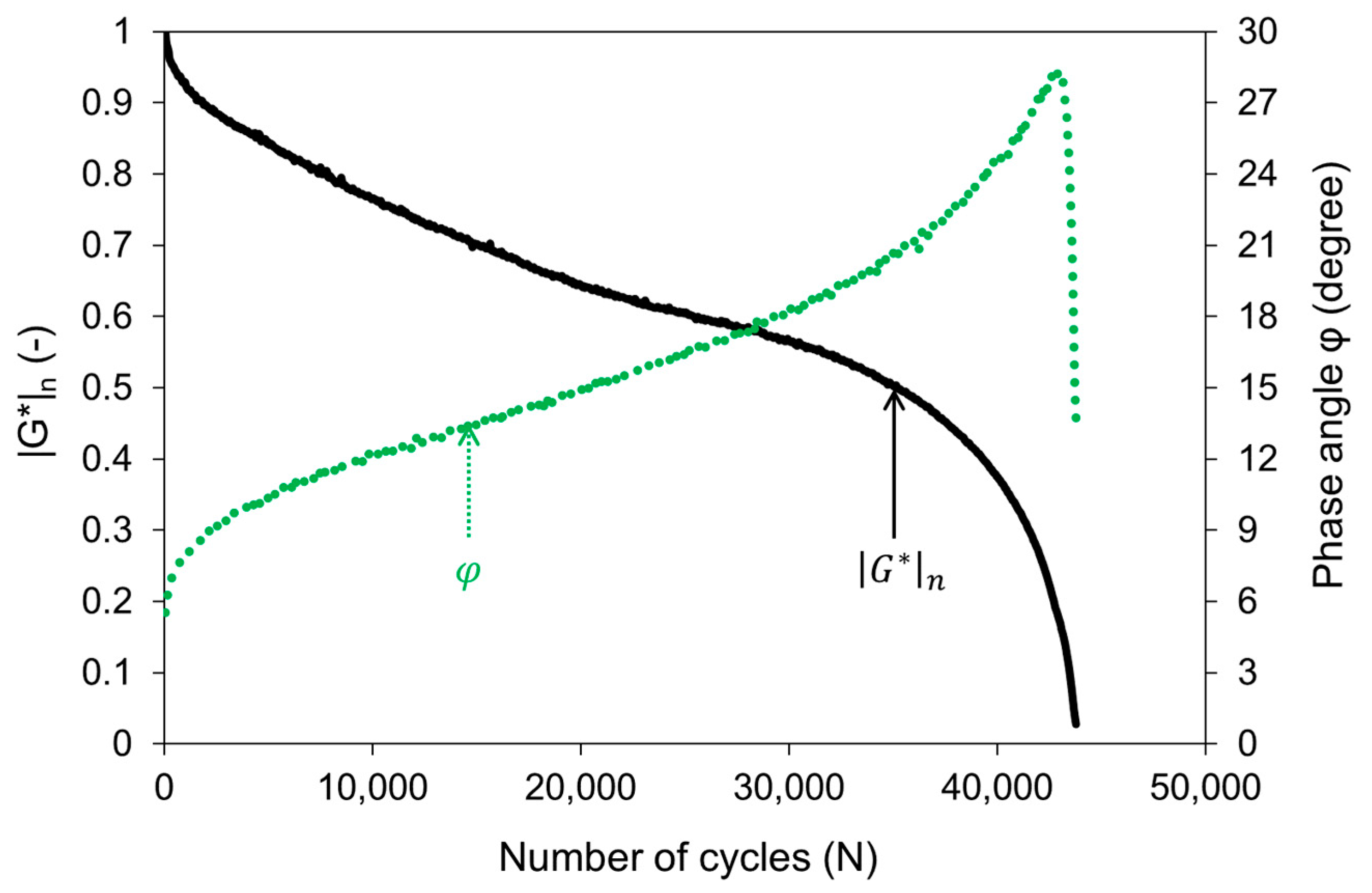
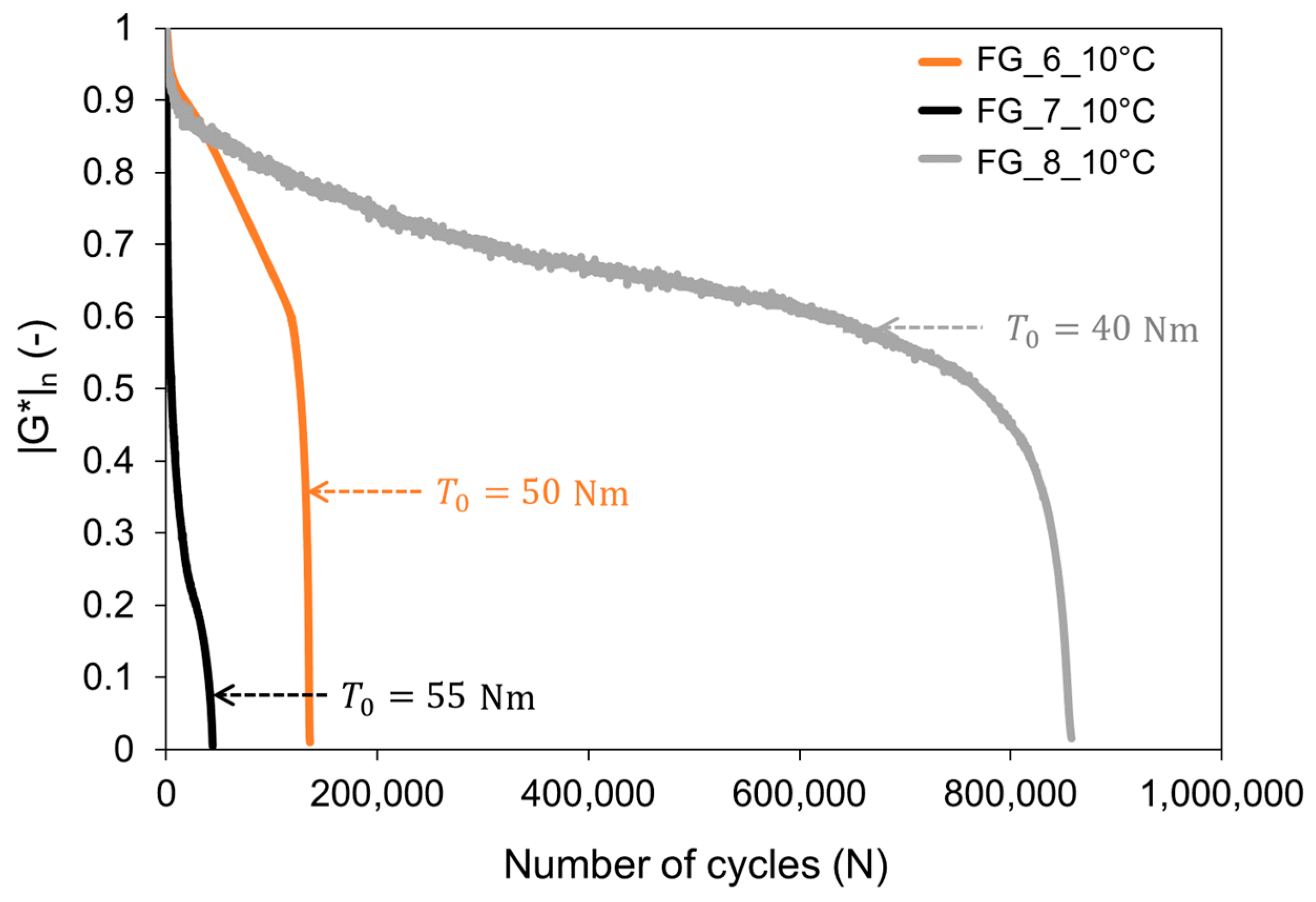
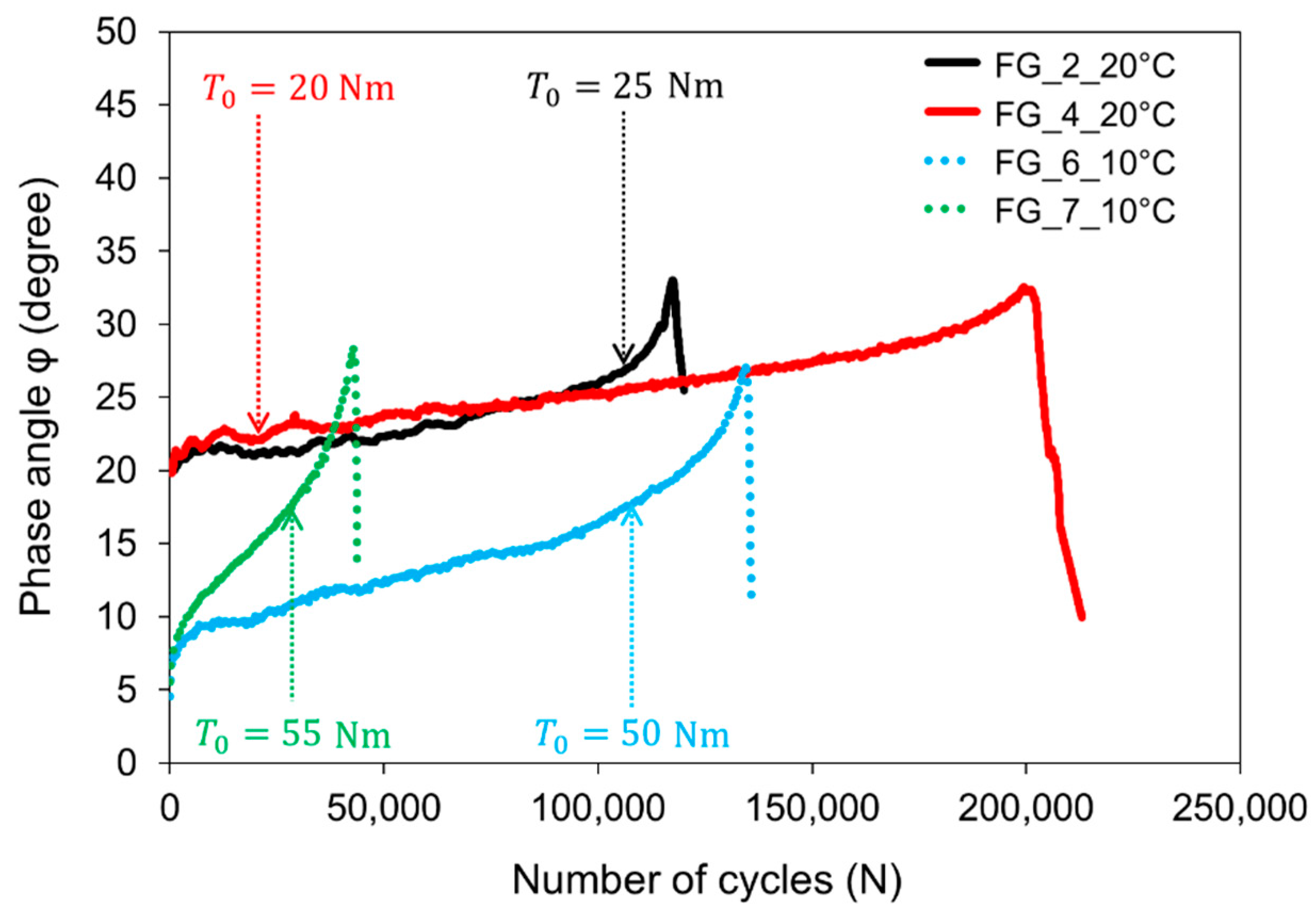
3.1.1. Viscoelastic Properties
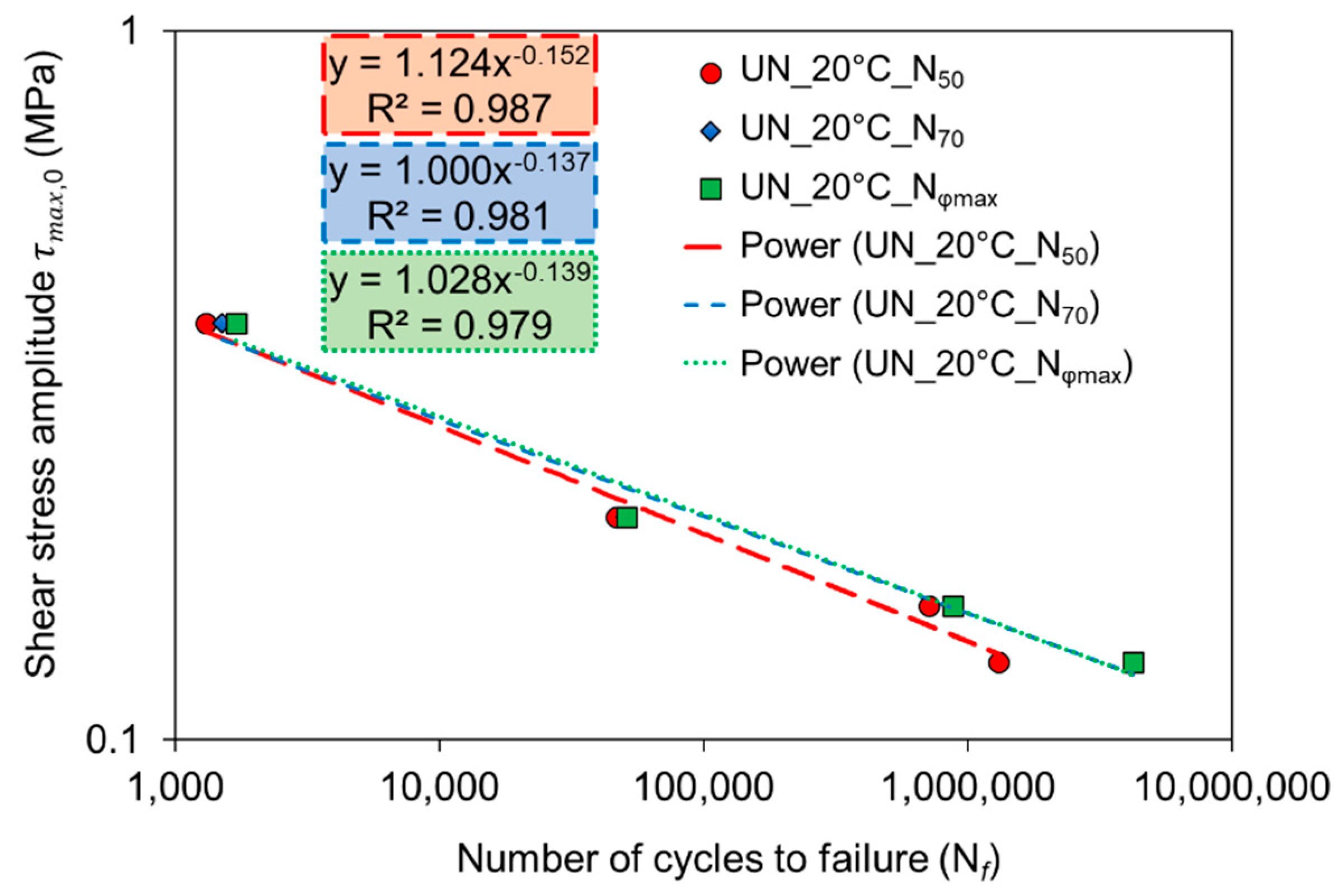
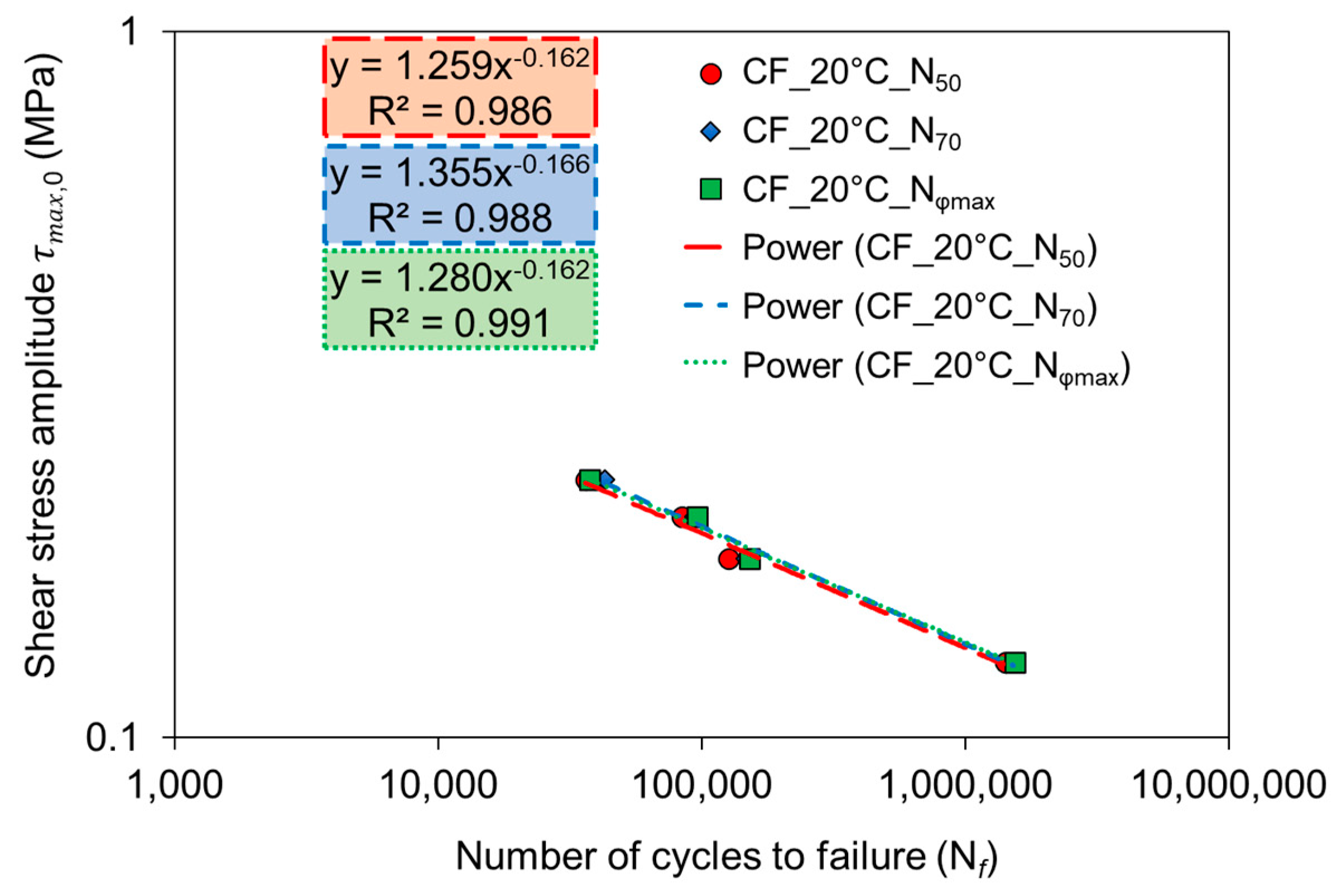
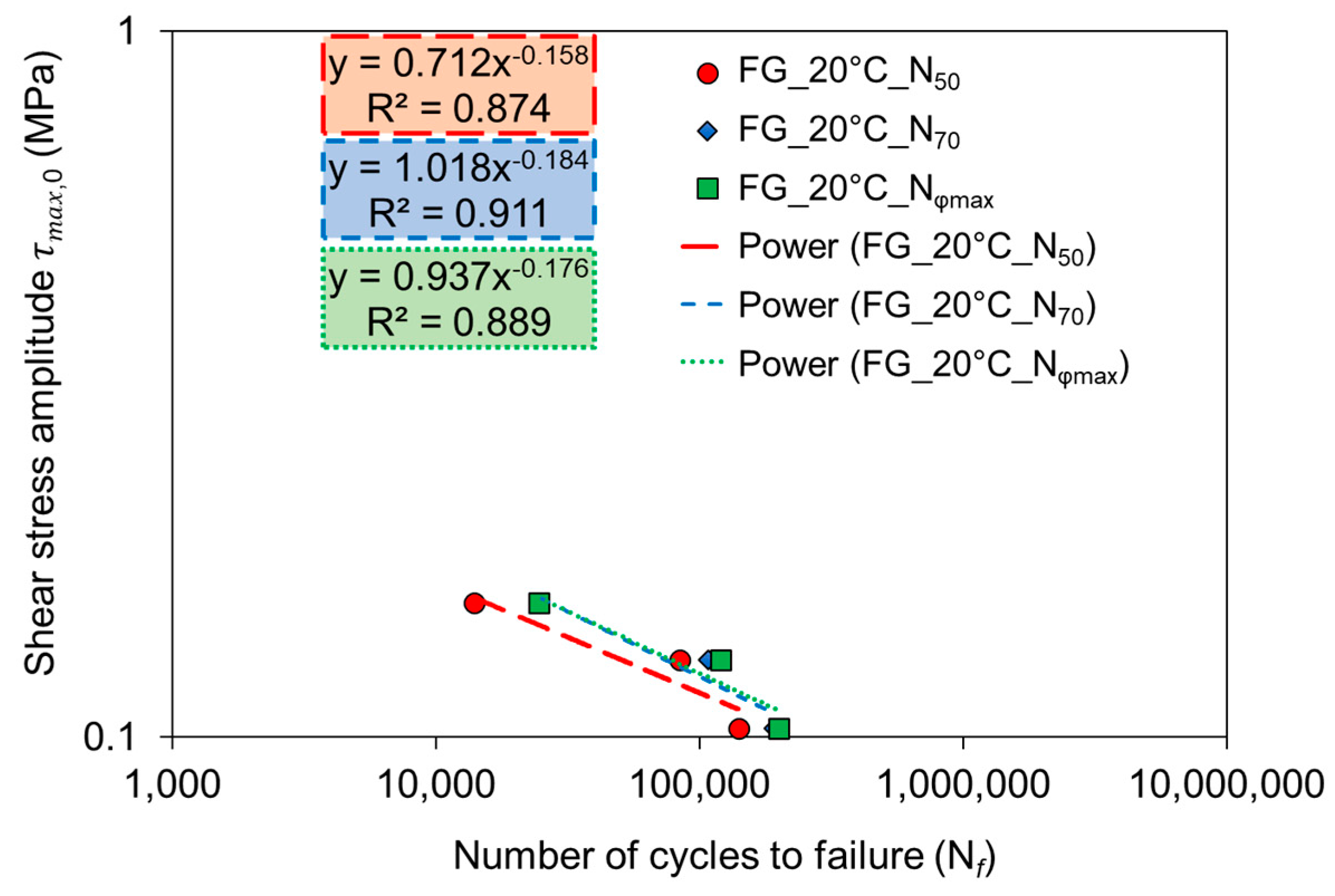
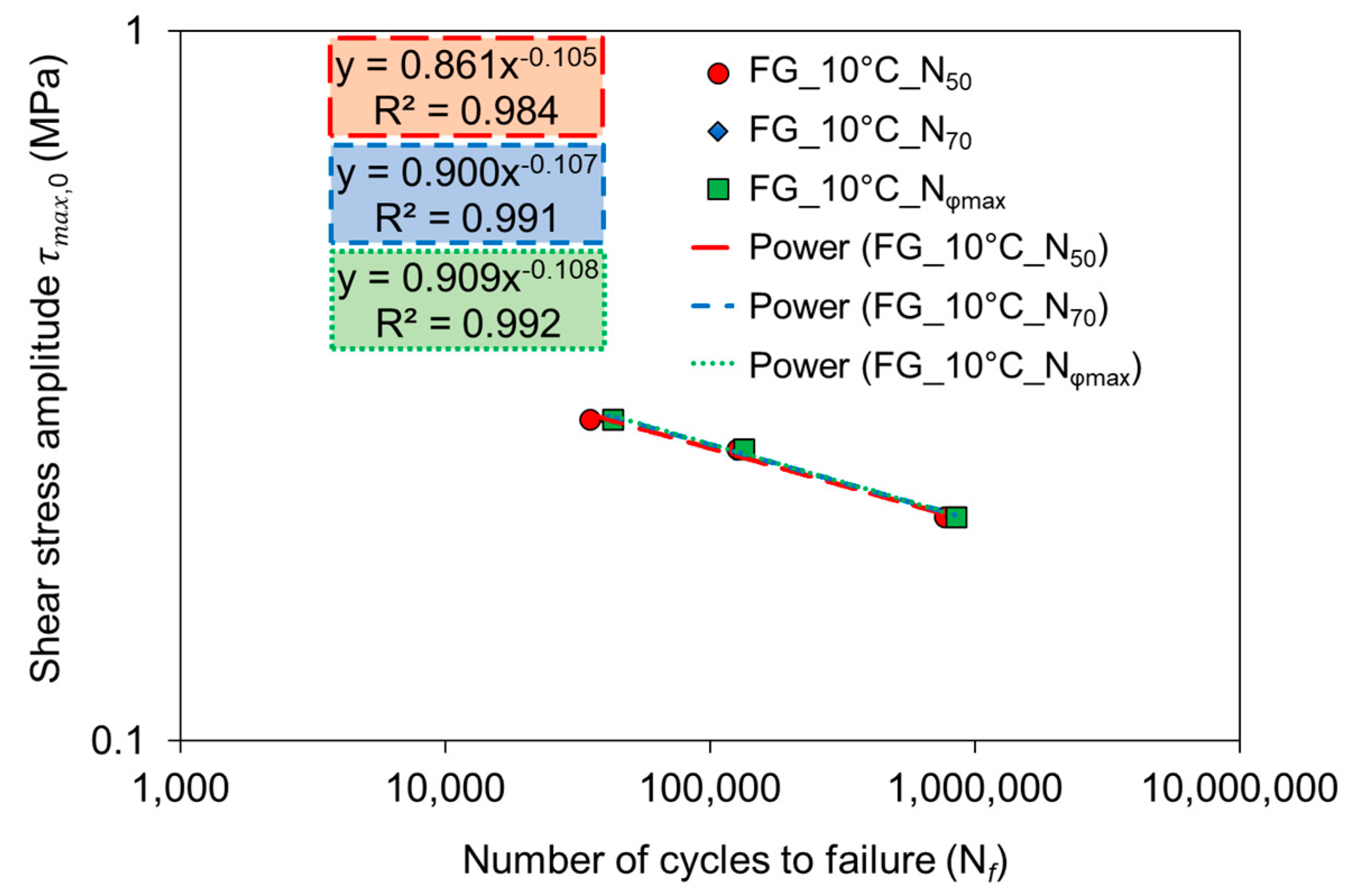
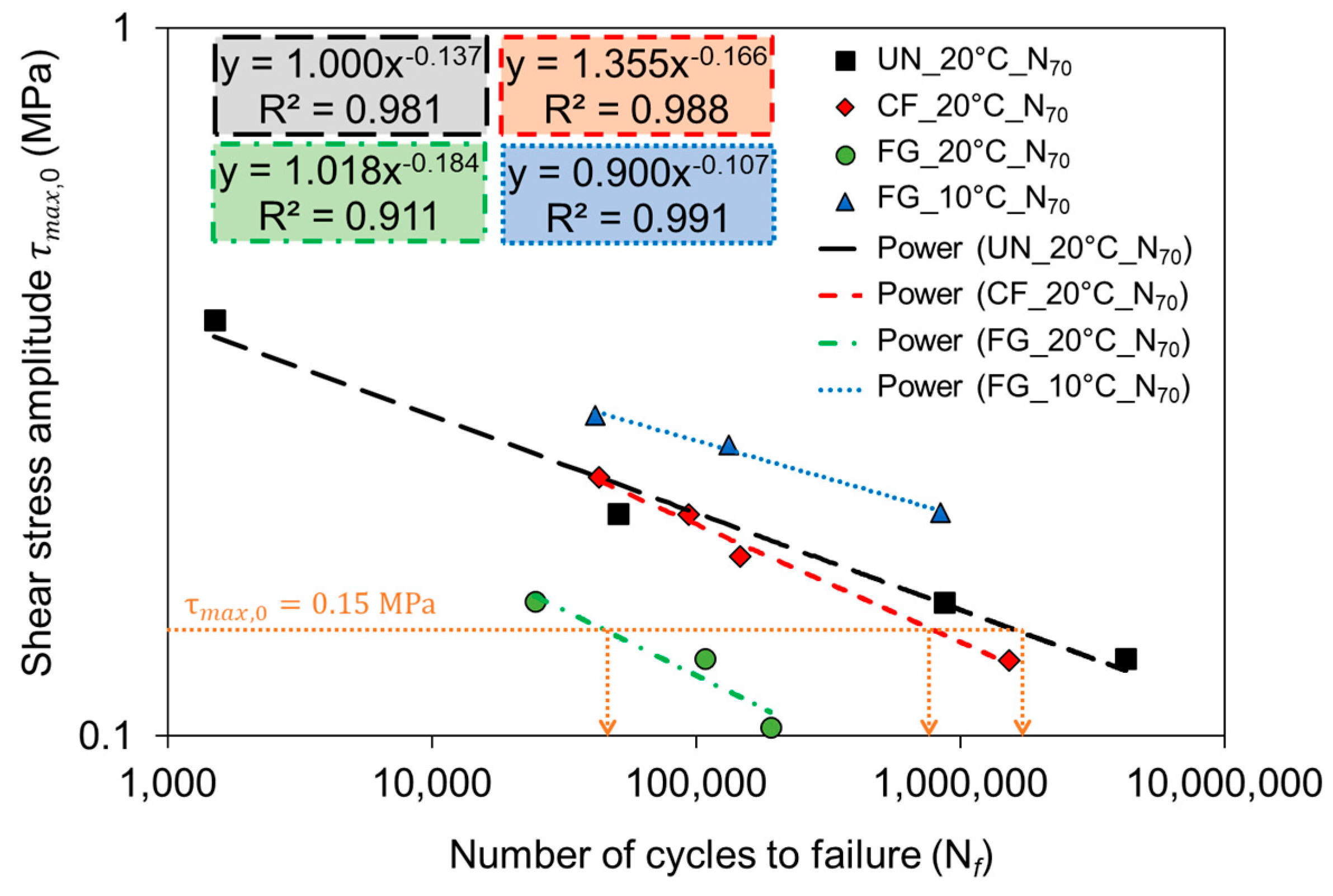
3.1.2. Interlayer Shear Fatigue Curve
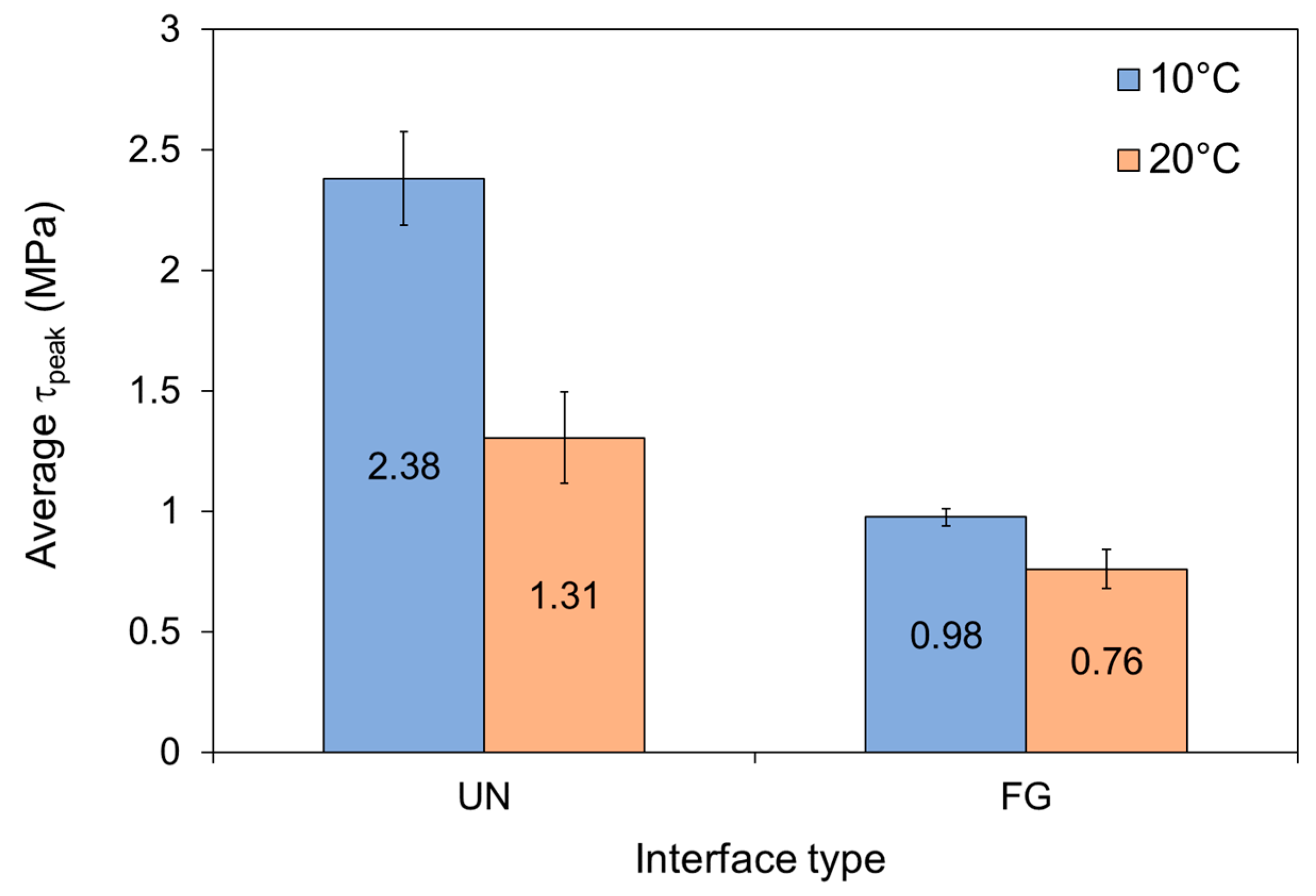
3.2. Static Leutner Test Results
3.3. Comparison between Cyclic and Static Shear Tests
4. Conclusions
- Shear-torque fatigue test results clearly ranked the studied materials, showing that the carbon fiber geogrid (CF) reinforced interface provides similar shear fatigue behavior to the unreinforced interface (UN). In contrast, a significant reduction in shear fatigue behavior is evident with the glass fiber geogrid (FG) reinforced interface.
- As far as the temperature effect is concerned, it was observed that shear fatigue resistance significantly increases with decreasing temperature for the FG interface. Further research is needed to investigate the influence of temperature also for the CF interface.
- Good correlations were found between maximum phase angle and 70% stiffness modulus value reduction failure criteria. The results indicate that even though these fatigue failure criteria were not originally developed to be used with double-layered reinforced specimens, they may still be useful in ranking the different reinforced interfaces and appear to be able to predict the actual interlayer shear fatigue life.
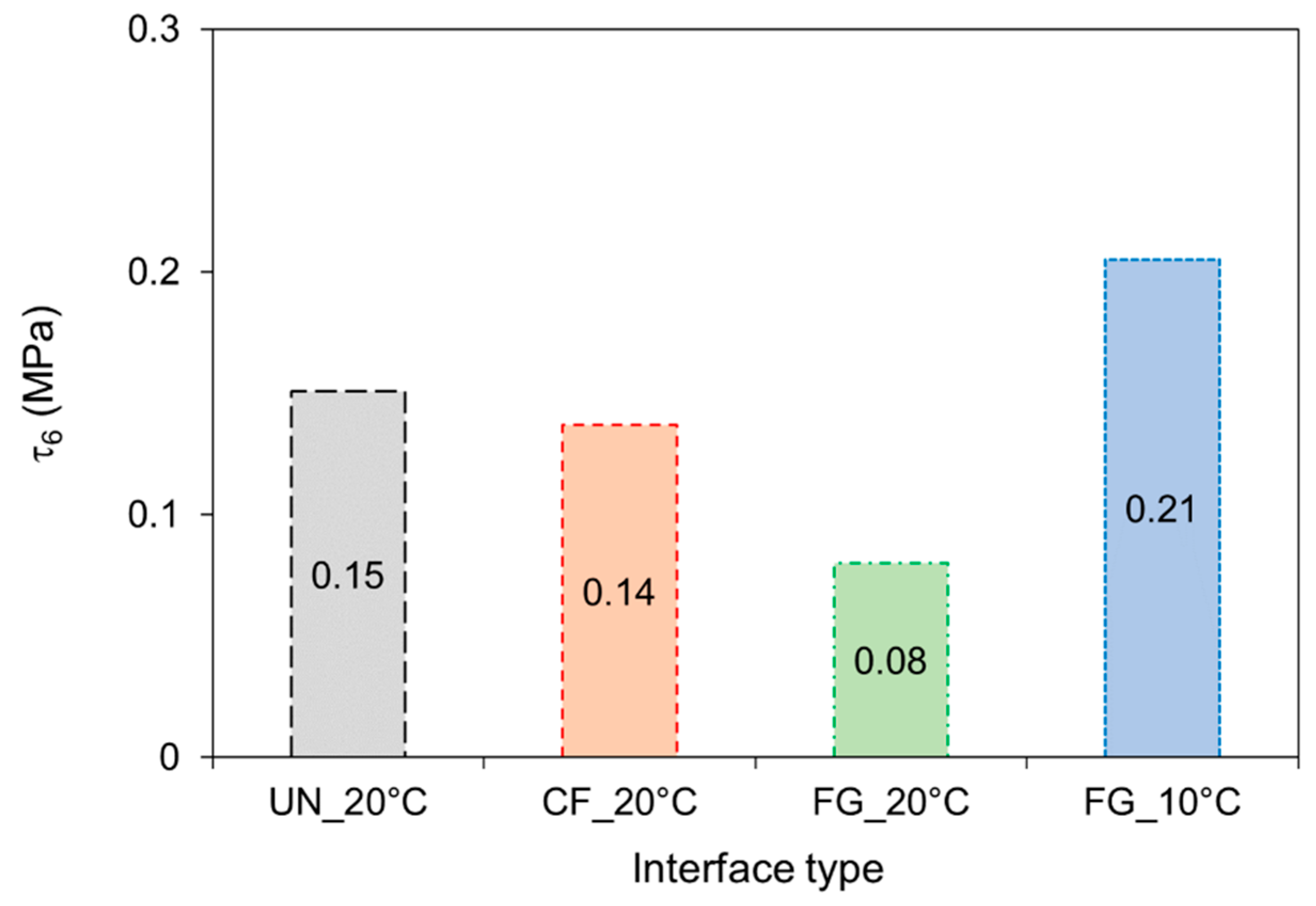
- Static Leutner test results showed that the interlayer shear strength () decreases with increasing temperature and with the presence of the FG geogrid.
- A promising correlation was found between the shear-torque fatigue test and the static Leutner test results. Such an approach is worthy of further investigation but needs to be validated through extensive research activity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gudipudi, P.; Underwood, B.S.; Zalghout, A. Impact of climate change on pavement structural performance in the United States. Transp. Res. D Trans. Environ. 2017, 57, 172–184. [Google Scholar] [CrossRef]
- Underwood, B.S.; Guido, Z.; Gudipudi, P.; Feinburg, Y. Increased costs to US pavement infrastructure from future temperature rise. Nat. Clim. Change 2017, 7, 704–707. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Elseifi, M.A. Field installation and design considerations of steel reinforcing netting to reduce reflection of cracks. In Proceedings of the 5th International RILEM Conference on Reflective Cracking in Pavements, Limoges, France, 5–8 May 2004; pp. 97–104. [Google Scholar]
- Button, J.W.; Lytton, R.L. Guidelines for using geosynthetics with hot-mix asphalt overlays to reduce reflective cracking. Transp. Res. Rec. J. Transp. Res. Board 2007, 2004, 111–119. [Google Scholar] [CrossRef]
- Zornberg, J.G. Functions and applications of geosynthetics in roadways. Procedia Eng. 2017, 189, 298–306. [Google Scholar] [CrossRef]
- Ferrotti, G.; Canestrari, F.; Virgili, A.; Grilli, A. A strategic laboratory approach for the performance investigation of geogrids in flexible pavements. Constr. Build. Mater. 2011, 25, 2343–2348. [Google Scholar] [CrossRef]
- Bocci, M.; Grilli, A.; Santagata, F.A.; Virgili, A. Influence of reinforcement geosynthetics on flexion behaviour of double-layer bituminous systems. In Proceedings of the International Conference on Advanced Characterisation of Pavement and Soil Engineering Materials, Athens, Greece, 20–22 June 2007; pp. 1415–1424. [Google Scholar]
- Francken, L. Prevention of cracks in pavements: Achievements and open questions. Road Mater. Pavement Des. 2005, 6, 407–425. [Google Scholar] [CrossRef]
- Shukla, S.K.; Yin, J.-H. Functions and installation of paving geosynthetics. In Proceedings of the 3rd Asian Regional Conference on Geosynthetics, Seoul, Korea, 21–23 June 2004. [Google Scholar]
- Uijting, B.G.J.; Jenner, C.G.; Gilchrist, A.J.T. Evaluation of 20 years experience with asphalt reinforcement using geogrids. In Proceedings of the 3rd International Conference Bituminous Mixtures and Pavements, Thessaloniki, Greece, 21–22 November 2002; pp. 869–877. [Google Scholar]
- Vanelstraete, A.; De Visscher, J. Long term performance on site of interface systems. In Proceedings of the 5th International RILEM Conference on Reflective Cracking in Pavements, Limoges, France, 5–8 May 2004; pp. 699–706. [Google Scholar]
- Brown, S.F.; Thom, N.H.; Sanders, P.J. A study of grid reinforced asphalt to combat reflection cracking. J. Assoc. Asphalt Paving Technol. 2001, 70, 543–569. [Google Scholar]
- Canestrari, F.; Belogi, L.; Ferrotti, G.; Graziani, A. Shear and flexural characterization of grid-reinforced asphalt pavements and relation with field distress evolution. Mater. Struct. 2015, 48, 959–975. [Google Scholar] [CrossRef]
- Correia, N.S.; Zornberg, J.G. Strain distribution along geogrid-reinforced asphalt overlays under traffic loading. Geotex. Geomembr. 2018, 46, 111–120. [Google Scholar] [CrossRef]
- Ferrotti, G.; Canestrari, F.; Pasquini, E.; Virgili, A. Experimental evaluation of the influence of surface coating on fiberglass geogrid performance in asphalt pavements. Geotex. Geomembr. 2012, 34, 11–18. [Google Scholar] [CrossRef]
- Ingrassia, L.P.; Virgili, A.; Canestrari, F. Investigating the effect of geocomposite reinforcement on the performance of thin asphalt pavements through accelerated pavement testing and laboratory analysis. Case Stud. Constr. Mater. 2020, 12, e00342. [Google Scholar] [CrossRef]
- Nejad, F.M.; Asadi, S.; Fallah, S.; Vadood, M. Statistical-experimental study of geosynthetics performance on reflection cracking phenomenon. Geotex. Geomembr. 2016, 44, 178–187. [Google Scholar] [CrossRef]
- Ragni, D.; Montillo, T.; Marradi, A.; Canestrari, F. Fast falling weight accelerated pavement testing and laboratory analysis of asphalt pavements reinforced with geocomposites. Lect. Notes Civil Eng. 2020, 48, 417–430. [Google Scholar] [CrossRef]
- Saride, S.; Kumar, V.V. Influence of geosynthetic-interlayers on the performance of asphalt overlays on pre-cracked pavements. Geotex. Geomembr. 2017, 45, 184–196. [Google Scholar] [CrossRef]
- Sobhan, K.; Tandon, V. Mitigating reflection cracking in asphalt overlay using geosynthetic reinforcements. Road Mater. Pavement Des. 2008, 9, 367–387. [Google Scholar] [CrossRef]
- Zofka, A.; Maliszewski, M.; Maliszewska, D. Glass and carbon geogrid reinforcement of asphalt mixtures. Road Mater. Pavement Des. 2017, 18, 471–490. [Google Scholar] [CrossRef]
- Caltabiano, M.A.; Brunton, J.M. Reflection cracking in asphalt overlays. J. Assoc. Asphalt Paving Technol. 1991, 60, 310–330. [Google Scholar]
- Canestrari, F.; Grilli, A.; Santagata, F.A.; Virgili, A. Interlayer shear effect of geosynthetic reinforcements. In Proceedings of the 10th International Conference on Asphalt Pavements, Québec City, QC, Canada, 12–17 August 2006. [Google Scholar]
- Canestrari, F.; Pasquini, E.; Belogi, L. Optimization of geocomposite for double layer bituminous system. In 7th RILEM International Conference on Cracking in Pavements; Scarpas, A., Kringos, N., Al-Qadi, I.A.L., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 1229–1239. [Google Scholar] [CrossRef]
- Pasquini, E.; Bocci, M.; Ferrotti, G.; Canestrari, F. Laboratory characterisation and field validation of geogrid-reinforced asphalt pavements. Road Mater. Pavement Des. 2013, 14, 17–35. [Google Scholar] [CrossRef]
- Pasquini, E.; Bocci, M.; Canestrari, F. Laboratory characterisation of optimised geocomposites for asphalt pavement reinforcement. Geosynth. Int. 2014, 21, 24–36. [Google Scholar] [CrossRef]
- Raab, C.; Partl, M.N. Interlayer shear performance: Experience with different pavement structures. In Proceedings of the 3rd Eurasphalt and Eurobitume Congress, Vienna, Austria, 12–14 May 2004; pp. 535–545. [Google Scholar]
- Zamora-Barraza, D.; Calzada-Peréz, M.; Castro-Fresno, D.; Vega-Zamanillo, A. New procedure for measuring adherence between a geosynthetic material and a bituminous mixture. Geotex. Geomembr. 2010, 28, 483–489. [Google Scholar] [CrossRef]
- Canestrari, F.; Santagata, E. Temperature effects on the shear behaviour of tack coat emulsions used in flexible pavements. Int. J. Pavement Eng. 2005, 6, 39–46. [Google Scholar] [CrossRef]
- Jaskula, P.; Rys, D. Effect of interlayer bonding quality of asphalt layers on pavement performance. IOP Conf. Ser. Mater. Sci. Eng. 2017, 236, 012005. [Google Scholar] [CrossRef]
- Graziani, A.; Pasquini, E.; Ferrotti, G.; Virgili, A.; Canestrari, F. Structural response of grid-reinforced bituminous pavements. Mater. Struct. 2014, 47, 1391–1408. [Google Scholar] [CrossRef]
- Canestrari, F.; Ferrotti, G.; Lu, X.; Millien, A.; Partl, M.N.; Petit, C.; Phelipot-Mardelé, A.; Piber, H.; Raab, C. Mechanical testing of interlayer bonding in asphalt pavements. In Advances in Interlaboratory Testing and Evaluation of Bituminous Materials, RILEM State-of-the-Art Reports; Partl, M., Bahia, H.U., Canestrari, F., De la Roche, C., Di Benedetto, H., Piber, H., Sybilski, D., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 9, pp. 303–360. [Google Scholar] [CrossRef]
- Petit, C.; Chabot, A.; Destrée, A.; Raab, C. Interface debonding behavior. In Mechanisms of Cracking and Debonding in Asphalt and Composite Pavements: State-of-the-Art of the RILEM TC241-MCD, RILEM State-of-the-Art Reports; Buttlar, W.G., Chabot, A., Dave, E.V., Petit, C., Tebaldi, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 103–153. [Google Scholar] [CrossRef]
- Petit, C.; Diakhaté, M.; Millien, A.; Phelipot-Mardelé, A.; Pouteau, B. Pavement design for curved road sections: Fatigue performance of interfaces and longitudinal top-down cracking in multilayered pavements. Road Mater. Pavement Des. 2009, 10, 609–624. [Google Scholar] [CrossRef]
- Ktari, R.; Millien, A.; Fouchal, F.; Pop, I.-O.; Petit, C. Pavement interface damage behavior in tension monotonic loading. Constr. Build. Mater. 2016, 106, 430–442. [Google Scholar] [CrossRef]
- Ragni, D.; Graziani, A.; Canestrari, F. Cyclic interlayer testing in bituminous pavements. In Proceedings of the 7th International Conference Bituminous Mixtures and Pavements, Thessaloniki, Greece, 12–14 June 2019; pp. 207–212. [Google Scholar] [CrossRef]
- Canestrari, F.; Attia, T.; Di Benedetto, H.; Graziani, A.; Jaskula, P.; Kim, Y.R.; Maliszewski, M.; Pais, J.; Petit, C.; Raab, C.; et al. Interlaboratory test to characterize the cyclic behavior of bituminous interlayers: An overview of testing equipment and protocols. In Proceedings of the RILEM International Symposium on Bituminous Materials, Lyon, France, 14–16 December 2020. [Google Scholar]
- Romanoschi, S.A.; Metcalf, J.B. Characterization of asphalt concrete layer interfaces. Transp. Res. Rec. J. Transp. Res. Board 2001, 1778, 132–139. [Google Scholar] [CrossRef]
- Diakhaté, M.; Phelipot, A.; Millien, A.; Petit, C. Shear fatigue behaviour of tack coats in pavements. Road Mater. Pavement Des. 2006, 7, 201–222. [Google Scholar] [CrossRef]
- Donovan, E.P.; Al-Qadi, I.L.; Loulizi, A. Optimization of tack coat application rate for geocomposite membrane on bridge decks. Transp. Res. Rec. J. Transp. Res. Board 2000, 1740, 143–150. [Google Scholar] [CrossRef]
- Cho, S.H.; Safavizadeh, S.A.; Kim, Y.R. Verification of the applicability of the time–temperature superposition principle to interface shear stiffness and strength of GlasGrid-reinforced asphalt mixtures. Road Mater. Pavement Des. 2017, 18, 766–784. [Google Scholar] [CrossRef]
- Safavizadeh, S.A.; Kim, Y.R. DIC technique to investigate crack propagation in grid-reinforced asphalt specimens. J. Mater. Civil Eng. 2017, 29. [Google Scholar] [CrossRef]
- Raab, C.; Arraigada, M.; Partl, M.N.; Schiffmann, F. Cracking and interlayer bonding performance of reinforced asphalt pavements. Eur. J. Environ. Civ. Eng. 2017, 21, 14–26. [Google Scholar] [CrossRef]
- Arraigada, M.; Perrotta, F.; Raab, C.; Tebaldi, G.; Partl, M.N. Use of APT for validating the efficiency of reinforcement grids in asphalt pavements. In The Roles of Accelerated Pavement Testing in Pavement Sustainability; Aguiar-Moya, J., Vargas-Nordcbeck, A., Leiva-Villacorta, F., Loría-Salazar, L., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 509–521. [Google Scholar] [CrossRef]
- Canestrari, F.; D’Andrea, A.; Ferrotti, G.; Graziani, A.; Partl, M.N.; Petit, C.; Raab, C.; Sangiorgi, C. Advanced interface testing of grids in asphalt pavements. In Testing and Characterization of Sustainable Innovative Bituminous Materials and Systems, RILEM State-of-the-Art Reports; Partl, M., Porot, L., Di Benedetto, H., Canestrari, F., Marsac, P., Tebaldi, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 127–202. [Google Scholar] [CrossRef]
- NF EN 13285. French Standards for Unbound Mixtures–Material Specifications.
- NF EN 13108-1. French Standards for Bituminous Mixtures–Material Specifications–Part 1: Asphalt Concrete.
- Petit, C.; Lesueur, D.; Millien, A.; Leguernevel, G.; Dopeux, J.; Picoux, B.; Allou, F.; Terhani, F. Smart geosynthetics for strain measurements in asphalt pavements. In Proceedings of the 13th International Conference on Asphalt Pavements, Fortaleza, Brazil, 19–21 June 2018. [Google Scholar]
- Petit, C.; Lesueur, D.; Millien, A.; Leguernevel, G.; Dopeux, J.; Picoux, B.; Allou, F.; Terhani, F. Des géosynthétiques intelligents pour renforcer et suivre les déformations de chaussées bitumineuses. In Proceedings of the 12th Rencontres Géosynthétiques, Nancy, France, 11–13 March 2019. [Google Scholar]
- EN 12697-6. European Standards for Bituminous Mixtures–Test Methods for Hot Mix Asphalt–Part 6: Determination of Bulk Density of Bituminous Specimens.
- Ragni, D.; Takarli, M.; Petit, C.; Graziani, A.; Canestrari, F. Use of acoustic techniques to analyse interlayer shear-torque fatigue test in asphalt mixtures. Int. J. Fatigue 2020, 131, 105356. [Google Scholar] [CrossRef]
- Ragni, D.; Ferrotti, G.; Petit, C.; Canestrari, F. Analysis of shear-torque fatigue test for bituminous pavement interlayers. Constr. Build. Mater. 2020, 254, 119309. [Google Scholar] [CrossRef]
- Shen, S.; Lu, Z. Energy based laboratory fatigue failure criteria for asphalt materials. J. Test. Eval. 2011, 39, 313–320. [Google Scholar] [CrossRef]
- Reese, R. Properties of aged asphalt binder related to asphalt concrete fatigue life. J. Assoc. Asphalt Paving Technol. 1997, 66, 604–632. [Google Scholar]
- Leutner, R. Untersuchung des schichtenverbundes beim bituminosen oberbau. Bitumen 1979, 41, 84–91. [Google Scholar]
- prEN 12697-48. European Pre-Standard for Bituminous Mixtures–Test Methods for Hot Mix Asphalt–Part 48: Interlayer Bonding.
- Boudabbous, M.; Millien, A.; Petit, C.; Neji, J. Energy approach for the fatigue of thermoviscoelastic materials: Application to asphalt materials in pavement surface layers. Int. J. Fatigue 2013, 47, 308–318. [Google Scholar] [CrossRef]
- Di Benedetto, H.; De la Roche, C.; Baaj, H.; Pronk, A.; Lundström, R. Fatigue of bituminous mixtures. Mater. Struct. 2004, 37, 202–216. [Google Scholar] [CrossRef]
- Pérez-Jiménez, F.; Botella, R.; López-Montero, T.; Miró, R.; Martínez, A.H. Complexity of the behaviour of asphalt materials in cyclic testing. Int. J. Fatigue 2017, 98, 111–120. [Google Scholar] [CrossRef]
- Diakhaté, M.; Millien, A.; Petit, C.; Phelipot-Mardelé, A.; Pouteau, B. Experimental investigation of tack coat fatigue performance: Towards an improved lifetime assessment of pavement structure interfaces. Constr. Build. Mater. 2011, 25, 1123–1133. [Google Scholar] [CrossRef]
- Collop, A.C.; Sutanto, M.H.; Airey, G.D.; Elliott, R.C. Development of an automatic torque test to measure the shear bond strength between asphalt. Constr. Build. Mater. 2011, 25, 623–629. [Google Scholar] [CrossRef]
- Corte, J.-F.; Goux, M.-T. Design of pavement structures: The French technical guide. Transp. Res. Rec. J. Transp. Res. Board 1996, 1539, 116–124. [Google Scholar] [CrossRef]



| Interface Type | Diameter (mm) | Shear-Torque Fatigue Test Replicates (#) | Static Leutner Test Replicates (#) | ||
|---|---|---|---|---|---|
| 20 °C; 10 Hz | 10 °C; 10 Hz | 20 °C; 50.8 mm/min | 10 °C; 50.8 mm/min | ||
| UN | 100 | 5 | - | - | - |
| 150 | - | - | 3 | 3 | |
| CF | 100 | 4 | - | - | - |
| FG | 100 | 5 | 3 | - | - |
| 150 | - | - | 3 | 3 | |
| Total | 14 | 3 | 6 | 6 | |
| Interface Type | Temperature (°C) | Failure Criterion | a | b | R2 |
|---|---|---|---|---|---|
| UN | 20 | 1.124 | −0.152 | 0.987 | |
| 1.000 | −0.137 | 0.981 | |||
| 1.028 | −0.139 | 0.979 | |||
| CF | 20 | 1.259 | −0.162 | 0.986 | |
| 1.355 | −0.166 | 0.988 | |||
| 1.280 | −0.162 | 0.991 | |||
| FG | 20 | 0.712 | −0.158 | 0.874 | |
| 1.018 | −0.184 | 0.911 | |||
| 0.937 | −0.176 | 0.889 | |||
| FG | 10 | 0.861 | −0.105 | 0.984 | |
| 0.900 | −0.107 | 0.991 | |||
| 0.909 | −0.108 | 0.992 |
| Interface Type | Temperature (°C) | C2S2R (-) | ||
|---|---|---|---|---|
| UN | 20 | 0.15 | 1.31 | 0.12 |
| FG | 20 | 0.08 | 0.76 | 0.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ragni, D.; Canestrari, F.; Allou, F.; Petit, C.; Millien, A. Shear-Torque Fatigue Performance of Geogrid-Reinforced Asphalt Interlayers. Sustainability 2020, 12, 4381. https://doi.org/10.3390/su12114381
Ragni D, Canestrari F, Allou F, Petit C, Millien A. Shear-Torque Fatigue Performance of Geogrid-Reinforced Asphalt Interlayers. Sustainability. 2020; 12(11):4381. https://doi.org/10.3390/su12114381
Chicago/Turabian StyleRagni, Davide, Francesco Canestrari, Fatima Allou, Christophe Petit, and Anne Millien. 2020. "Shear-Torque Fatigue Performance of Geogrid-Reinforced Asphalt Interlayers" Sustainability 12, no. 11: 4381. https://doi.org/10.3390/su12114381
APA StyleRagni, D., Canestrari, F., Allou, F., Petit, C., & Millien, A. (2020). Shear-Torque Fatigue Performance of Geogrid-Reinforced Asphalt Interlayers. Sustainability, 12(11), 4381. https://doi.org/10.3390/su12114381







