Estimation of Housing Price Variations Using Spatio-Temporal Data
Abstract
1. Introduction
2. Material and Methods
2.1. Regression-Cokriging Predictor
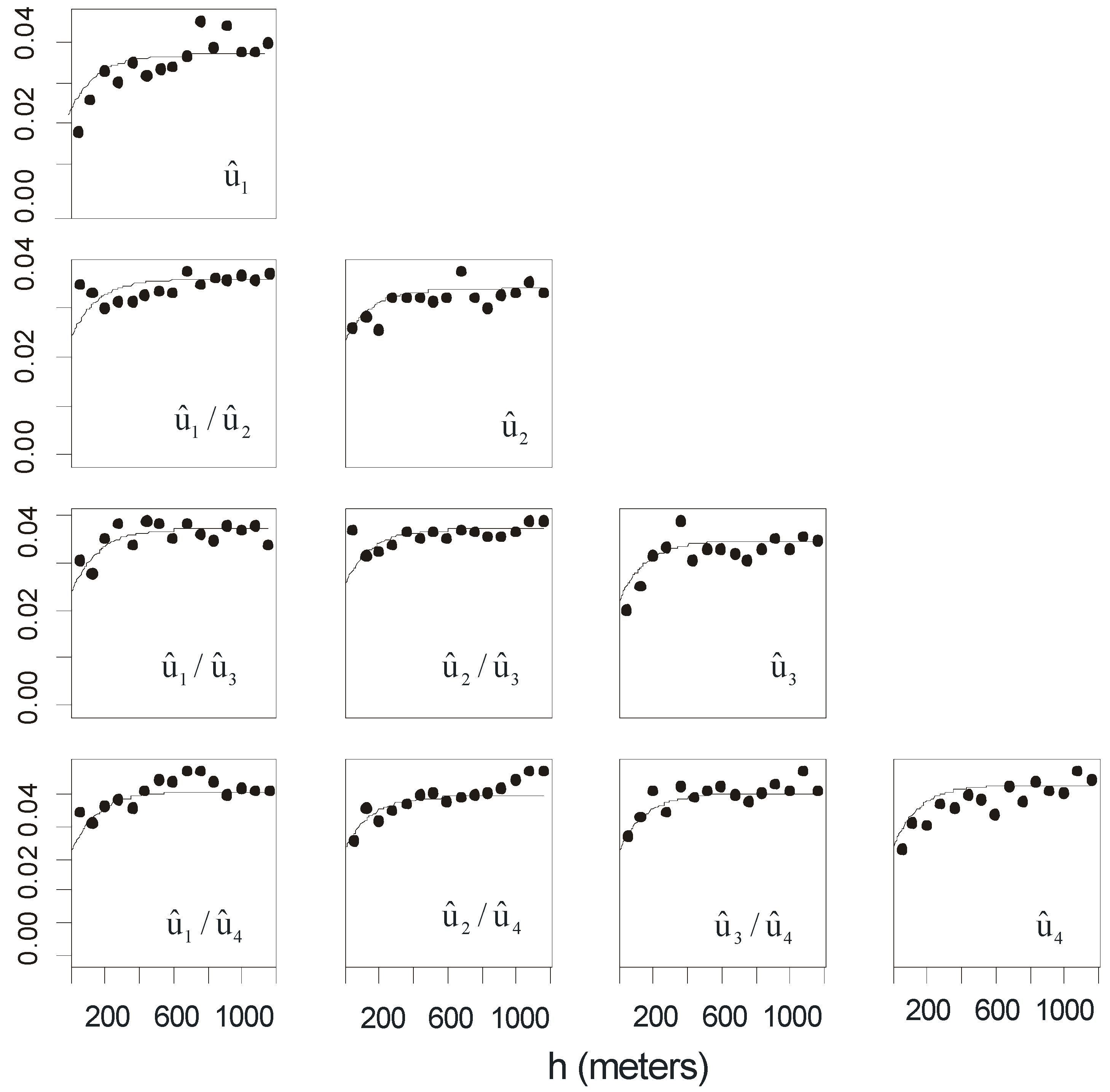
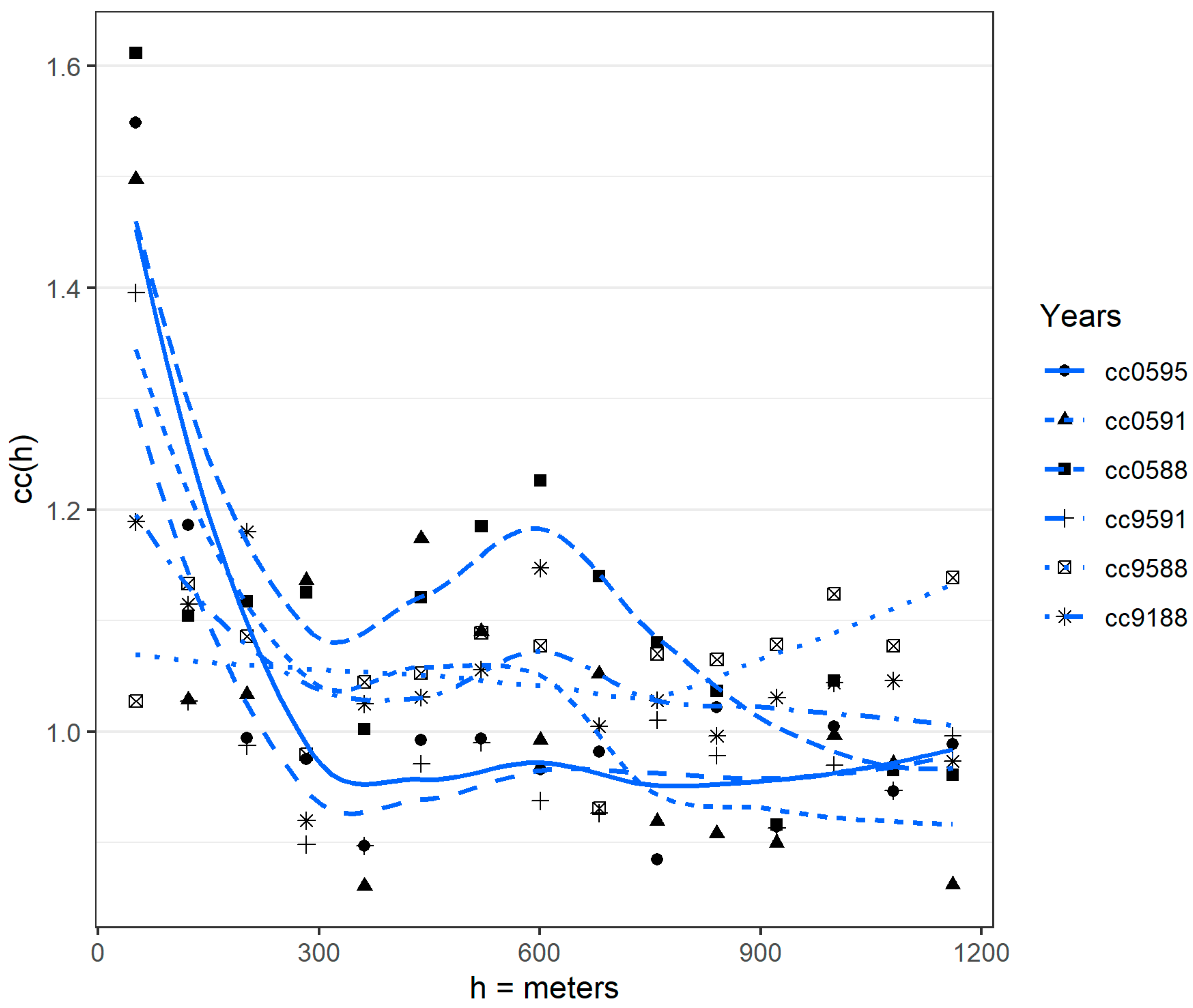
2.2. Direct and Cross-Correlation of Residuals
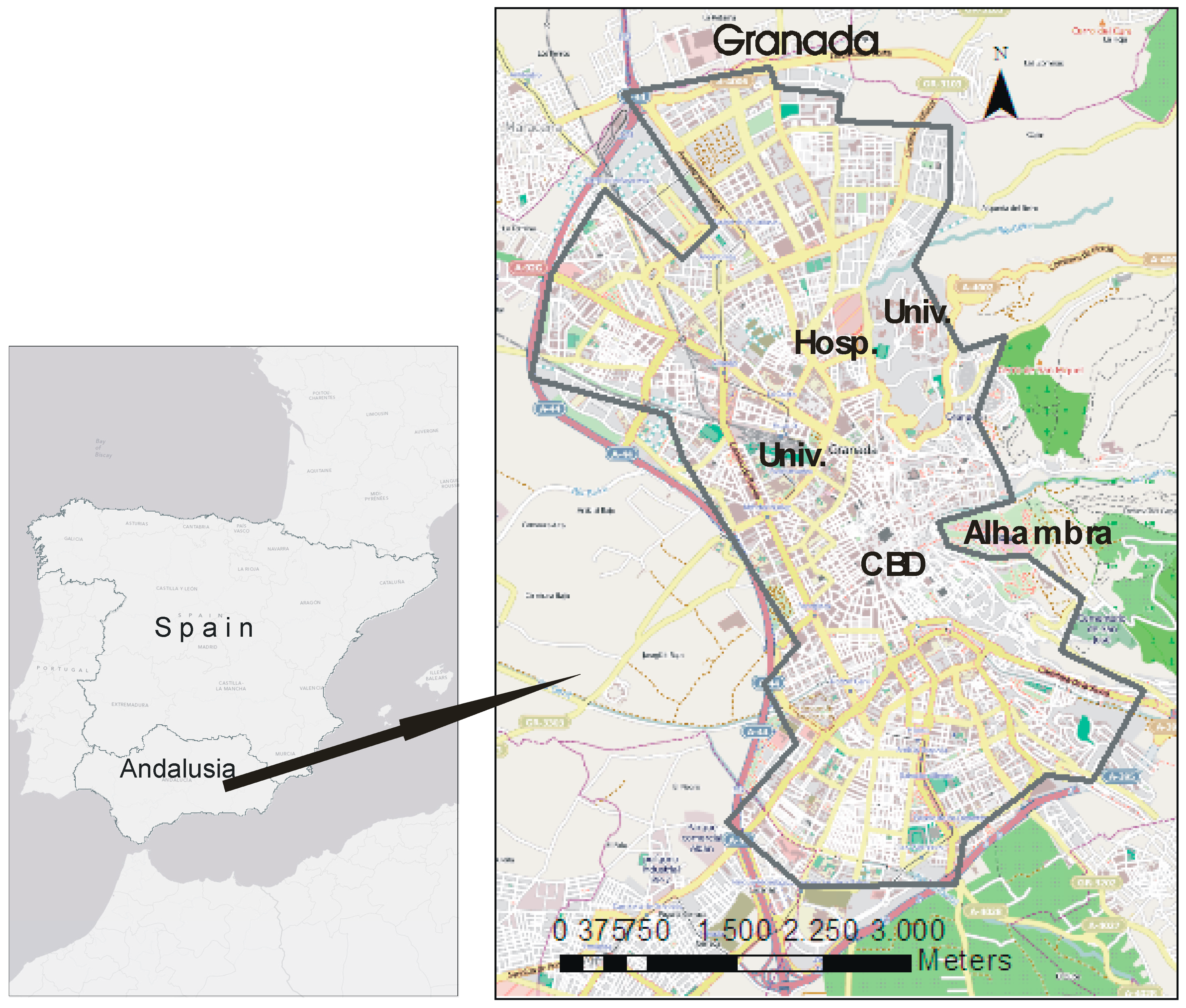
3. Data and Case Study
3.1. Database
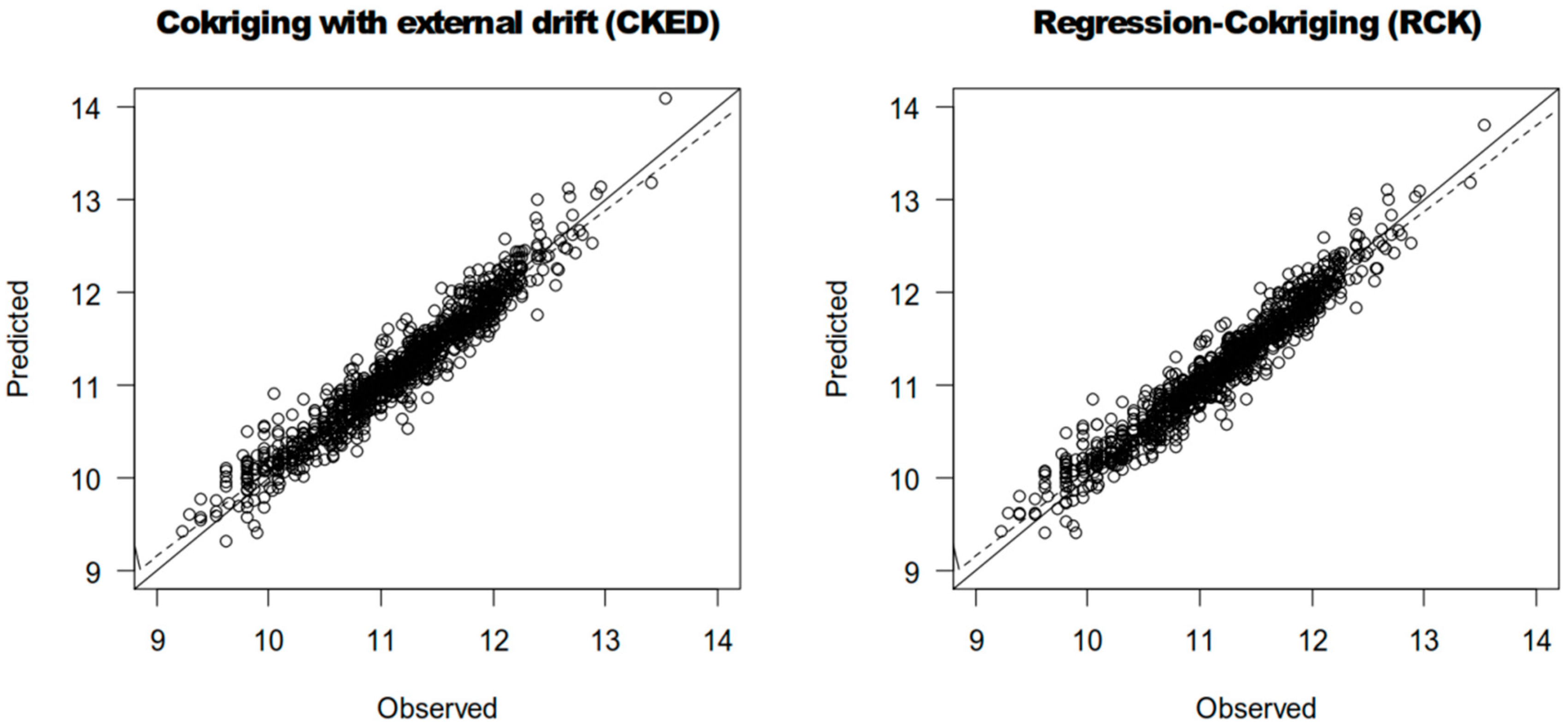
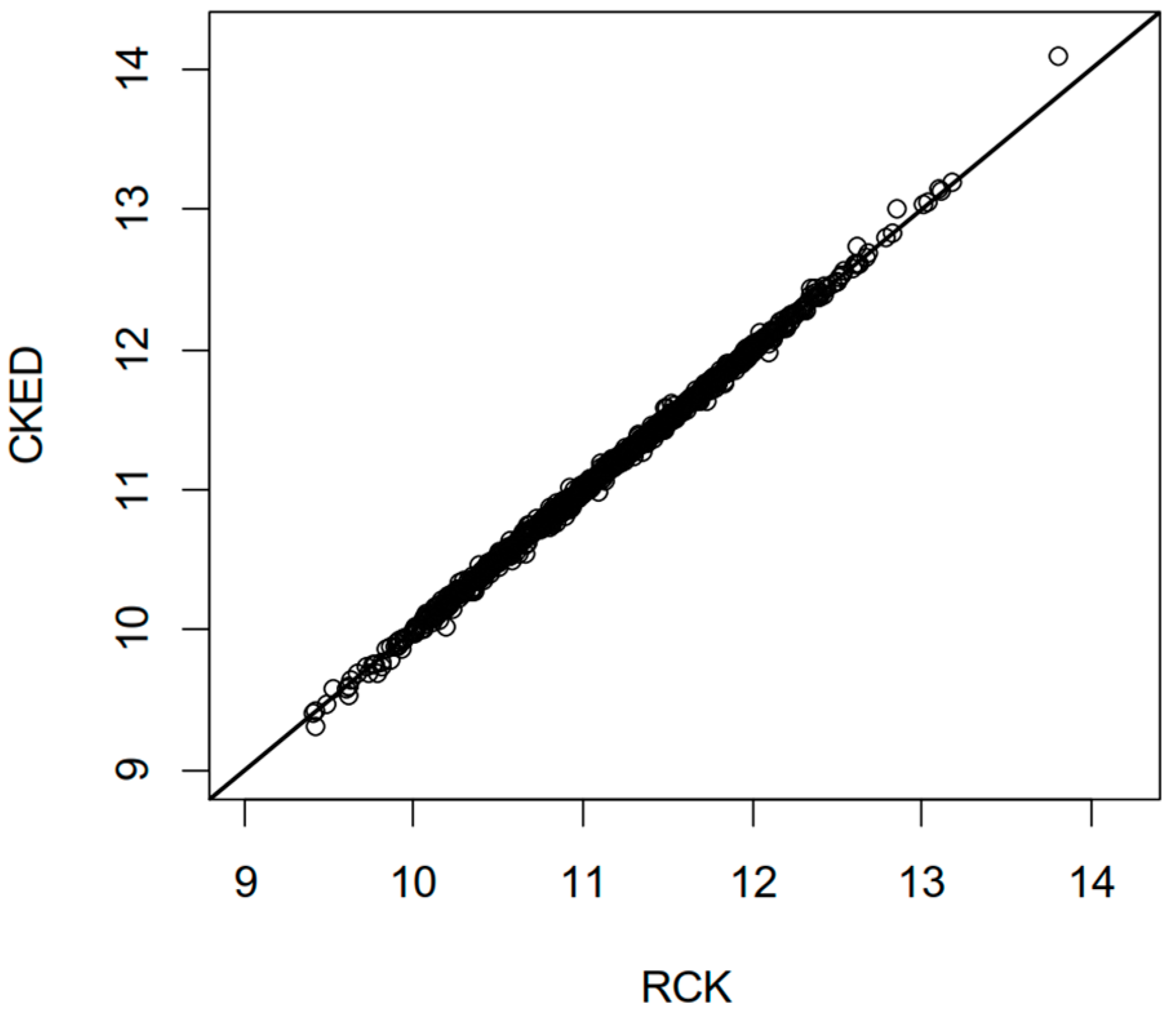
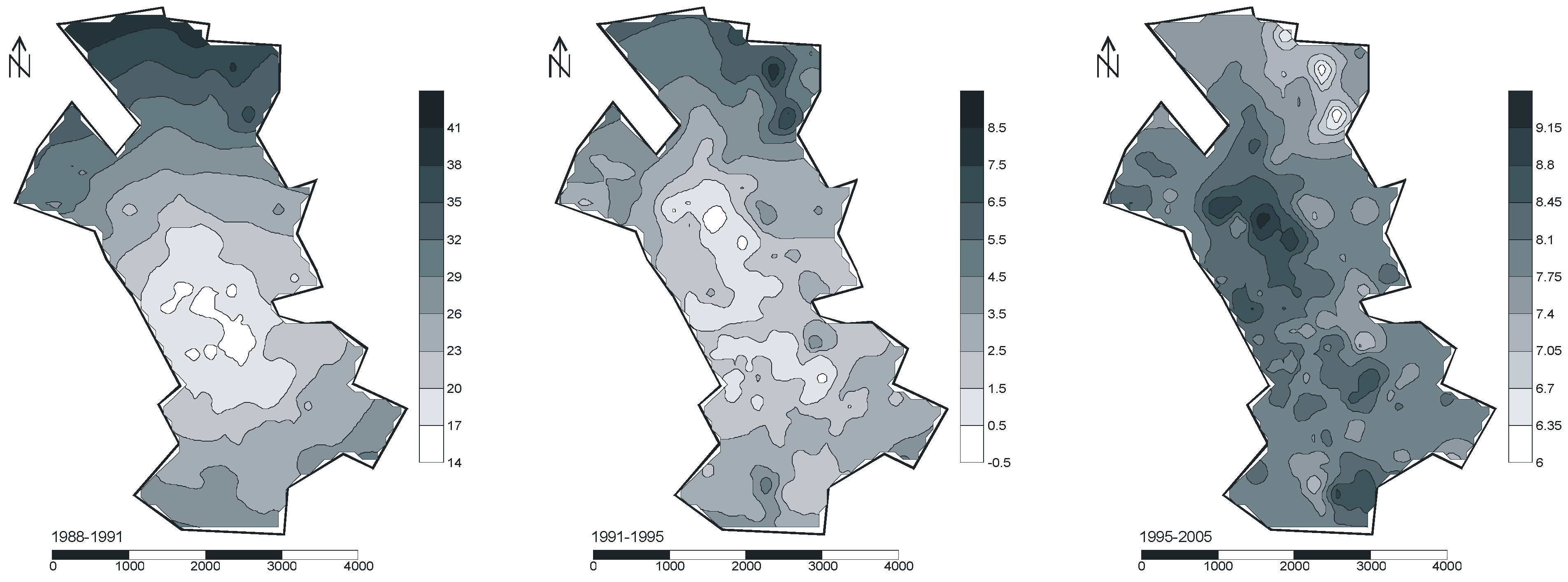
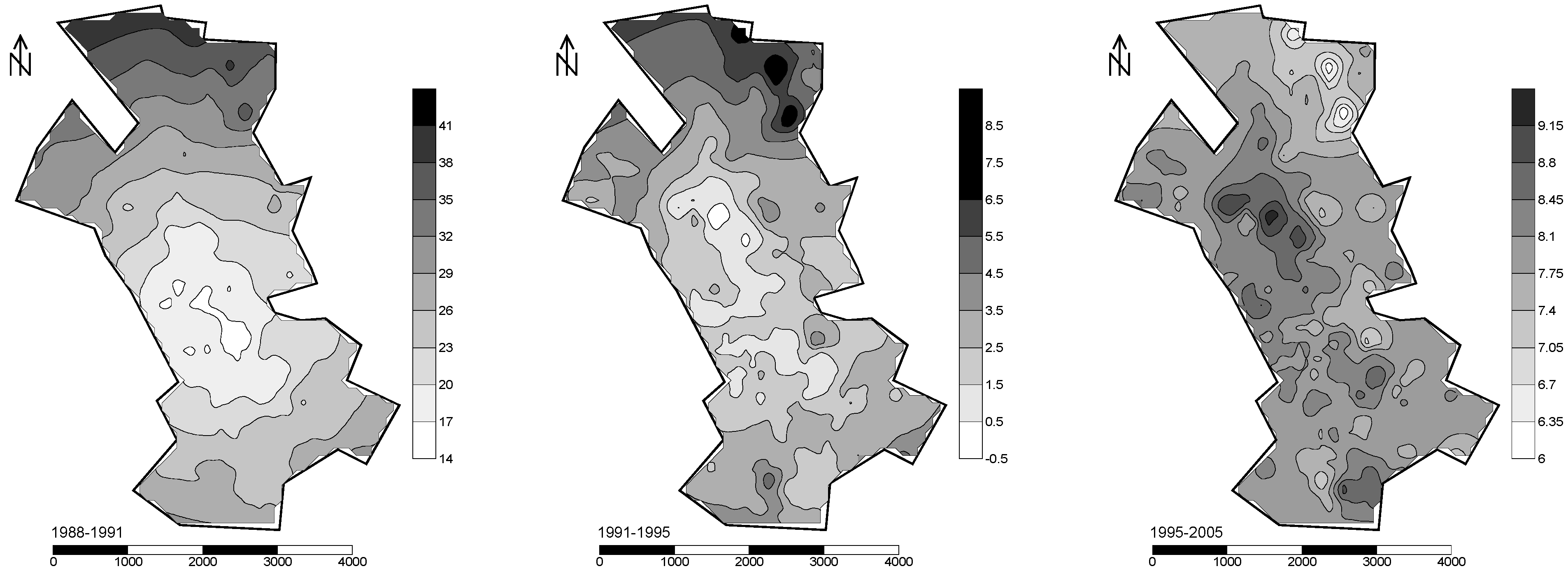
3.2. Results and Discussion
3.3. Estimation of Spatial Price Variation in Multi-Years
4. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anselin, L. Thirty years of spatial econometrics. Reg. Sci. 2010, 89, 3–25. [Google Scholar] [CrossRef]
- Bourassa, S.C.; Cantoni, E.; Hoesli, M. Predicting House Prices with Spatial Dependence: A Comparison of Alternative Methods. J. Hous. Res. 2010, 32, 139–159. [Google Scholar]
- Páez, A. Recent research in spatial real estate hedonic analysis. J. Geogr. Syst. 2009, 11, 311–316. [Google Scholar] [CrossRef]
- Krause, A.; Bitter, C. Spatial econometrics, land values and sustainability: Trends in real estate valuation research. Cities 2012, 29, S19–S25. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Forte, F.; Manganelli, B. Real Estate Appraisals with Bayesian Approach and Markov Chain Hybrid Monte Carlo Method: An Application to a Central Urban Area of Naples. Sustainability 2017, 9, 2138. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Com-petition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Can, A. Specification and estimation of hedonic housing price models. Reg. Sci. Urban Econ. 1992, 22, 453–474. [Google Scholar] [CrossRef]
- Dubin, R.A. Spatial autocorrelation and neighborhood quality. Reg. Sci. Urban Econ. 1992, 22, 433–452. [Google Scholar] [CrossRef]
- Militino, A.F.; Ugarte, M.D.; Garcia-Reinaldos, L. Alternative models for describing spatial dependence among dwelling selling prices. J. Real Estate Financ. Econ. 2004, 29, 193–209. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Tsutsumi, M.; Seya, H. Measuring the impact of large-scale transportation projects on land price using spatial statistical models. Pap. Reg. Sci. 2008, 87, 385–401. [Google Scholar] [CrossRef]
- de Koning, K.; Filatova, T.; Bin, O. Improved Methods for Predicting Property Prices in Hazard Prone Dynamic Markets. Environ. Resour. Econ. 2018, 69, 247–263. [Google Scholar] [CrossRef]
- Hoshino, T.; Kuriyama, K. Measuring the benefits of neighbourhood park amenities: Application and comparison of spatial hedonic approaches. Environ. Resour. Econ. 2010, 45, 429–444. [Google Scholar] [CrossRef]
- Osland, L.; Thorsen, I. Effects on housing prices of urban attraction and labor-market accessibility. Environ. Plan. A 2008, 40, 2490. [Google Scholar] [CrossRef]
- Trojanek, R.; Gluszak, M. Spatial and time effect of subway on property prices. J. Hous. Built Environ. 2018, 33, 359–384. [Google Scholar] [CrossRef]
- Pace, R.K.; Barry, R.; Clapp, J.M.; Rodriquez, M. Spatiotemporal autoregressive models of neighborhood effects. J. Real Estate Financ. Econ. 1998, 17, 15–33. [Google Scholar] [CrossRef]
- Clapp, J.M. A Semiparametric Method for Estimating Local House Price Indices. Real Estate Econ. 2004, 32, 127–160. [Google Scholar] [CrossRef]
- Sun, H.; Tu, Y.; Yu, S.-M. A Spatio-Temporal Autoregressive Model for Multi-Unit Residential Market Analysis. J. Real Estate Financ. Econ. 2005, 31, 155–187. [Google Scholar] [CrossRef]
- Pace, R.; Barry, R.; Gilley, O.W.; Sirmans, C.F. A method for spatial-temporal forecasting with an application to real estate prices. Int. J. Forecast. 2000, 16, 229–246. [Google Scholar] [CrossRef]
- Dubin, R.A.; Pace, J.K.; Thibodeau, T.G. Spatial Autoregression Techniques for Real Estate Data. J. Real Estate Lit. 1999, 7, 79–95. [Google Scholar] [CrossRef]
- McGreal, S.; Taltavull de La Paz, P. Implicit House Prices: Variation over Time and Space in Spain. Urban Stud. 2013, 50, 2024–2043. [Google Scholar] [CrossRef]
- Beamonte San Agustín, A.; Gargallo Valero, P.; Figueras Salvador, M. Evolución espacio-temporal del mercado inmobiliario en Zaragoza mediante el uso de efectos de vecindad. Estadística Española 2008, 50, 5–24. [Google Scholar]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Wu, B.; Li, R.; Huang, B. A geographically and temporally weighted autoregressive model with application to housing prices. Int. J. Geogr. Inf. Sci. 2014, 28, 1186–1204. [Google Scholar] [CrossRef]
- Yao, J.; Stewart Fotheringham, A. Local Spatiotemporal Modeling of House Prices: A Mixed Model Approach. Prof. Geogr. 2016, 68, 189–201. [Google Scholar] [CrossRef]
- Helbich, M.; Griffith, D.A. Spatially varying coefficient models in real estate: Eigenvector spatial filtering and alternative approaches. Comput. Environ. Urban Syst. 2016, 57, 1–11. [Google Scholar] [CrossRef]
- Montero-Lorenzo, J.; Larraz-Iribas, B. Space-time approach to commercial property prices valuation. Appl. Econ. 2012, 44, 3705–3715. [Google Scholar] [CrossRef]
- Chica-Olmo, J. Prediction of Housing Location Price by a Multivariate Spatial Method: Cokriging. J. Real Estate Res. 2007, 29, 91–114. [Google Scholar]
- Chica-Olmo, J.; Cano-Guervos, R.; Chica-Olmo, M. A Coregionalized Model to Predict Housing Prices. Urban Geogr. 2013, 34, 395–412. [Google Scholar] [CrossRef]
- Kuntz, M.; Helbich, M. Geostatistical mapping of real estate prices: An empirical comparison of kriging and cokriging. Int. J. Geogr. Inf. Sci. 2014, 28, 1904–1921. [Google Scholar] [CrossRef]
- D’Agostino, V.; Greene, E.A.; Passarella, G.; Vurro, M. Spatial and temporal study of nitrate concentration in groundwater by means of coregionalization. Environ. Geol. 1998, 36, 285–295. [Google Scholar] [CrossRef]
- Fassò, A.; Finazzi, F. Maximum likelihood estimation of the dynamic coregionalization model with heterotopic data. Environmetrics 2011, 22, 735–748. [Google Scholar] [CrossRef]
- Joyner, T.A.; Friedland, C.J.; Rohli, R.V.; Treviño, A.M.; Massarra, C.; Paulus, G. Cross-correlation modeling of European windstorms: A cokriging approach for optimizing surface wind estimates. Spat. Stat. 2015, 13, 62–75. [Google Scholar] [CrossRef]
- Lark, R. Robust estimation of the pseudo cross-variogram for cokriging soil properties. Eur. J. Soil Sci. 2002, 53, 253–270. [Google Scholar] [CrossRef]
- Gallois, D.; de Fouquet, C.; Le Loc’h, G.; Malherbe, L.; Cardenas, G. Mapping Annual Nitrogen Dioxide Concentrations in Urban Areas. In Geostatistics Banff 2004; Springer: Berlin, Germany, 2005; pp. 1087–1096. [Google Scholar]
- Kyriakidis, P.C.; Journel, A.G. Geostatistical Space Time Models: A Review. Math. Geol. 1999, 31, 651–684. [Google Scholar] [CrossRef]
- De Iaco, S.; Myers, D.E.; Posa, D. Space-time variograms and a functional form for total 3 air pollution measurements. Comput. Stat. Data Anal. 2002, 41, 311–328. [Google Scholar] [CrossRef]
- Schabenberger, O.; Gotway, C.A. Statistical Methods for Spatial Data Analysis; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Montero, J.-M.; Fernández-Avilés, G.; Mateu, J. Spatial and Spatio-Temporal Geostatistical Modeling and Kriging; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Li, L.; Revesz, P. Interpolation methods for spatio-temporal geographic data. Comput. Environ. Urban Syst. 2004, 28, 201–227. [Google Scholar] [CrossRef]
- Papritz, A.; Flühler, H. Temporal change of spatially autocorrelated soil properties: Optimal estimation by cokriging. Geoderma 1994, 62, 29–43. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Ecker, M.D.; Knight, J.R.; Sirmans, C.F. The Dynamics of Location in Home Price. J. Real Estate Financ. Econ. 2004, 29, 149–166. [Google Scholar] [CrossRef]
- Myers, D.E. Matrix Formulation of Cokriging. Math. Geol. 1982, 14, 249–257. [Google Scholar] [CrossRef]
- Ver Hoef, J.M.; Cressie, N. Multivariable Spatial Prediction. Math. Geol. 1993, 25, 219–240. [Google Scholar] [CrossRef]
- Neuman, S.P.; Jacobson, E.A. Analysis of non-intrinsic spatial variability by residual kriging with application to regional groundwater levels. Math. Geol. 1984, 16, 499–521. [Google Scholar] [CrossRef]
- Militino, A.; Palacios, M.; Ugarte, M. Robust predictions of rainfall in Navarre, Spain. In geoENV III—Geostatistics for Environmental Applications; Springer: Berlin, Germany, 2001; pp. 79–90. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.; Stein, A. Comparison of Kriging with External Drift and Regression-Kriging; Technical Note; ITC: Enschede, The Netherlands, 2003.
- McBratney, A.B.; Odeh, I.O.; Bishop, T.F.; Dunbar, M.S.; Shatar, T.M. An overview of pedometric techniques for use in soil survey. Geoderma 2000, 97, 293–327. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Matheron, G. Les Variables Regionalisées et Leur Estimation; Masson y Cie: Paris, France, 1965. [Google Scholar]
- Myers, D.E. Pseudo-Cross Variograms, Positive-Definiteness, and Cokriging. Math. Geol. 1991, 23, 805–816. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Goulard, M.; Voltz, M. Linear coregionalization model: Tools for estimation and choice of cross-variogram matrix. Math. Geol. 1992, 24, 269–286. [Google Scholar] [CrossRef]
- Goetzmann, W.N.; Spiegel, M. A spatial model of housing returns and neighborhood substitutability. J. Real Estate Financ. Econ. 1997, 14, 11–31. [Google Scholar] [CrossRef]
- Hwang, M.; Quigley, J.M. Economic fundamentals in local housing markets: Evidence from US metropolitan regions. J. Reg. Sci. 2006, 46, 425–453. [Google Scholar] [CrossRef]
- Quercia, R.G.; McCarthy, G.W.; Ryznar, R.M.; Can Talen, A. Spatio-Temporal Measurement of House Price Appreciation in Underserved Areas. J. Hous. Res. 2000, 11, 1–28. [Google Scholar]
- Kuethe, T.H.; Pede, V.O. Regional housing price cycles: A spatio-temporal analysis using US state-level data. Reg. Stud. 2011, 45, 563–574. [Google Scholar] [CrossRef]
- Arribas, I.; García, F.; Guijarro, F.; Oliver, J.; Tamošiūnienė, R. Mass appraisal of residential real estate using multilevel modelling. Int. J. Strateg. Prop. Manag. 2016, 20, 77–87. [Google Scholar] [CrossRef]
- Derycke, P.-H. Economie et Planification Urbaines: L’espace Urbain; Presses Universitaires de France: Paris, France, 1979; Volume 1. [Google Scholar]
- Yoo, E.-H.; Kyriakidis, P.C. Area-to-point Kriging in spatial hedonic pricing models. J. Geogr. Syst. 2009, 11, 381–406. [Google Scholar] [CrossRef]
- Brasington, D.M.; Haining, R. Parents, peers, or school inputs: Which components of school outcomes are capitalized into house value? Reg. Sci. Urban Econ. 2009, 39, 523–529. [Google Scholar] [CrossRef]
- Lacombe, D.J.; LeSage, J.P. Using Bayesian posterior model probabilities to identify omitted variables in spatial regression models. Pap. Reg. Sci. 2015, 94, 365–383. [Google Scholar] [CrossRef]
- Mueller, J.M.; Loomis, J.B. Spatial dependence in hedonic property models: Do different corrections for spatial dependence result in economically significant differences in estimated implicit prices? J. Agric. Resour. Econ. 2008, 33, 212–231. [Google Scholar]
- Chica-Olmo, J. Spatial Estimation of Housing Prices and Locational Rents. Urban Stud. 1995, 32, 1331–1344. [Google Scholar] [CrossRef]
- Brunauer, W.; Lang, S.; Umlauf, N. Modelling house prices using multilevel structured additive regression. Stat. Model. 2013, 13, 95–123. [Google Scholar] [CrossRef]
- Seo, D.; Chung, Y.; Kwon, Y. Price determinants of affordable apartments in Vietnam: Toward the public–private partnerships for sustainable housing development. Sustainability 2018, 10, 197. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics; Springer: Berlin, Germany, 1995. [Google Scholar]
- Pardo-Igúzquiza, E.; Dowd, P.A. FACTOR2D: A computer program for factorial cokriging. Comput. Geosci. 2002, 28, 857–875. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.-K.; Schilling, K.; Skopec, M. Cokriging estimation of daily suspended sediment loads. J. Hydrol. 2006, 327, 389–398. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. A cokriging method for estimating population density in urban areas. Comput. Environ. Urban Syst. 2005, 29, 558–579. [Google Scholar] [CrossRef]
- Dubin, R.A. Spatial Autocorrelation: A Primer. J. Hous. Econ. 1998, 7, 304–327. [Google Scholar] [CrossRef]
- Liu, X. Spatial and temporal dependence in house price prediction. J. Real Estate Financ. Econ. 2013, 47, 341–369. [Google Scholar] [CrossRef]
- Bourennane, H.; Nicoullaud, B.; Couturier, A.; Mary, B.; Richard, G.; King, D.; Stafford, J. A Potential Role of Permanent Soil Variables and Field Topography to Reveal Scale Dependence and the Temporal Persistence of Soil Water Content Spatial Patterns. In Proceedings of the Precision Agriculture’05, 5th European Conference on Precision Agriculture, Uppsala, Sweden, 2005; Wageningen Academic Publishers: Wageningen, The Netherlands, 2005; pp. 769–777. [Google Scholar]
- Le Goix, R.; Vesselinov, E. Gated communities and house prices: Suburban change in southern California, 1980–2008. Int. J. Urban Reg. Res. 2013, 37, 2129–2151. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Y.; Fan, P. Polycentric urban development: The case of Hangzhou. Environ. Plan. A 2010, 42, 563. [Google Scholar] [CrossRef]
- Kiel, K.A.; Zabel, J.E. Location, location, location: The 3L Approach to house price determination. J. Hous. Econ. 2008, 17, 175–190. [Google Scholar] [CrossRef]
- Cheshire, P.; Sheppard, S. On the price of land and the value of amenities. Economica 1995, 62, 247–267. [Google Scholar] [CrossRef]


| Minimum | Maximum | Mean | Standard Deviation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 1991 | 1995 | 2005 | 1988 | 1991 | 1995 | 2005 | 1988 | 1991 | 1995 | 2005 | 1988 | 1991 | 1995 | 2005 | |
| PRICE | 10.22 | 15.03 | 15.03 | 22.83 | 240.407 | 300.51 | 330.55 | 751.26 | 45.89 | 75.56 | 90.51 | 162.40 | 30.60 | 36.65 | 50.03 | 85.55 |
| AGE | 1 | 1 | 1 | 2 | 40 | 81 | 84 | 40 | 13.58 | 11.51 | 16.96 | 23.44 | 7.56 | 9.72 | 11.69 | 8.93 |
| BATH | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 4 | 1.23 | 1.51 | 1.60 | 1.45 | 0.44 | 0.56 | 0.54 | 0.58 |
| DIST | 166.30 | 294.98 | 76.39 | 81.27 | 3511.29 | 3723.63 | 3695.92 | 3940.96 | 1492.94 | 1577.95 | 1326.28 | 1557.46 | 851.91 | 963.64 | 812.76 | 823.68 |
| AREA | 65.00 | 49.00 | 40.00 | 40.00 | 340.00 | 320.00 | 325.00 | 390.00 | 109.86 | 112.85 | 118.13 | 108.80 | 33.00 | 35.27 | 42.48 | 38.64 |
| FLOOR | - | - | - | 0 | - | - | - | 1 | - | - | - | 0.039 | - | - | - | 0.19 |
| ELEV | - | - | 0 | 0 | - | - | 1 | 1 | - | - | 0.88 | 0.78 | - | - | 0.31 | 0.41 |
| HEAT | - | - | 0 | 0 | - | - | 1 | 1 | - | - | 0.55 | 0.54 | - | - | 0.50 | 0.50 |
| SPORT | - | - | - | 0 | - | - | - | 1 | - | - | - | 0.06 | - | - | - | 0.24 |
| REHAB | - | - | - | 0 | - | - | - | 1 | - | - | - | 0.35 | - | - | - | 0.48 |
| Nearest | 8.10 | 10.34 | 6.00 | 4.20 | 390.77 | 385.38 | 666.40 | 646.87 | 74.67 | 55.75 | 86.81 | 98.22 | 55.45 | 63.06 | 88.60 | 100.24 |
| Residuals | Nugget | Partial Sill | Practical Range |
|---|---|---|---|
| (2005) | 0.023 | 0.015 | 465.00 |
| (1995) | 0.025 | 0.011 | 465.00 |
| (1991) | 0.026 | 0.014 | 465.00 |
| (1988) | 0.044 | 0.024 | 465.00 |
| 0.024 | 0.012 | 465.00 | |
| 0.024 | 0.014 | 465.00 | |
| 0.032 | 0.019 | 465.00 | |
| 0.025 | 0.011 | 465.00 | |
| 0.034 | 0.016 | 465.00 | |
| 0.033 | 0.018 | 465.00 |
| R2cv | MAE | MSE | |
|---|---|---|---|
| 1988 | |||
| Spherical | 0.8349 | 0.1862 | 0.0557 |
| Gaussian | 0.8461 | 0.1806 | 0.0519 |
| Exponential | 0.8507 | 0.1793 | 0.0503 |
| 1991 | |||
| Spherical | 0.8639 | 0.1406 | 0.0340 |
| Gaussian | 0.8719 | 0.1356 | 0.0320 |
| Exponential | 0.8727 | 0.1371 | 0.0318 |
| 1995 | |||
| Spherical | 0.9285 | 0.1424 | 0.0359 |
| Gaussian | 0.9296 | 0.1396 | 0.0353 |
| Exponential | 0.9332 | 0.1362 | 0.0335 |
| 2005 | |||
| Spherical | 0.7946 | 0.1564 | 0.0428 |
| Gaussian | 0.8075 | 0.1497 | 0.0401 |
| Exponential | 0.8001 | 0.1545 | 0.0416 |
| 1988 | 1991 | 1995 | 2005 | |
|---|---|---|---|---|
| Intercept | 1.042 × 101 | 1.084 × 101 | 1.041 × 101 | 1.148 × 101 |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| AGE | −2.119 × 10−2 | −7.828 × 10−3 | −8.497 × 10−3 | −6.176 × 10−3 |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| BATH | 8.929 × 10−2 | 1.176 × 10−1 | 6.929 × 10−2 | 9.256 × 10−2 |
| (0.020) | (0.000) | (0.000) | (0.000) | |
| AREA | 7.949 × 10−3 | 5.782 × 10−3 | 8.361 × 10−3 | 5.951 × 10−3 |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| DIST | −3.853 × 10−4 | −2.532 × 10−4 | −2.111 × 10−4 | −2.257 × 10−4 |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| REHAB | -- | −1.517 × 10−1 | -- | −6.733 × 10−2 |
| (0.000) | (0.008) | |||
| ELEV | -- | -- | 1.552 × 10−1 | 1.187 × 10−1 |
| (0.000) | (0.000) | |||
| HEAT | -- | -- | 7.528 × 10−2 | 4.679 × 10−2 |
| (0.000) | (0.060) | |||
| FLOOR | -- | -- | -- | −1.056 × 10−1 |
| (0.059) | ||||
| SPORT | -- | -- | -- | 1.278 × 10−1 |
| (0.011) | ||||
| 0.8507 | 0.8727 | 0.9332 | 0.8001 | |
| MAE | 0.1793 | 0.1371 | 0.1362 | 0.1545 |
| MSE | 0.0503 | 0.0318 | 0.0335 | 0.0416 |
| n | 260 | 247 | 293 | 207 |
| CKED | RCK | |
|---|---|---|
| 0.9277 | 0.9331 | |
| MAE | 0.1400 | 0.1355 |
| MSE | 0.0343 | 0.0317 |
| n | 1007 | 1007 |
| 1988 | 1991 | 1995 | 2005 | |
|---|---|---|---|---|
| Intercept | 1.027 × 101 e+01 (0.000) | 1.074 × 101 (0.000) | 1.446 × 101 (0.000) | 1.650 × 101 (0.000) |
| AGE | −2.033 × 10−2 (0.000) | −6.484 × 10−3 (0.000) | −1.035 × 10−2 (0.000) | −6.583 × 10−3 (0.001) |
| BATH | 1.269 × 10−1 (0.004) | 1.788 × 10−1 (0.000) | 9.536 × 10−2 (0.002) | 1.107 × 10−1 (0.002) |
| AREA | 8.506 × 10−3 (0.000) | 5.766 × 10−3 (0.000) | 1.188 × 10−2 (0.000) | 6.125 × 10−3 (0.000) |
| DIST | −3.521 × 10−4 (0.000) | −2.510 × 10−4 (0.000) | −2.685 × 10−4 (0.000) | −2.139 × 10−4 (0.000) |
| REHAB | -- | −1.981 × 10−1 (0.000) | -- | −6.925 × 10−2 (0.048) |
| ELEV | -- | -- | 2.540 × 10−1 (0.000) | 1.875 × 10−1 (0.000) |
| HEAT | -- | -- | 1.550 × 10−1 (0.000) | 7.201 × 10−2 (0.053) |
| FLOOR | -- | -- | -- | −1.482 × 10−1 (0.079) |
| SPORT | -- | -- | -- | 1.376 × 10−1 (0.041) |
| R-squared | 0.8176 | 0.8278 | 0.9234 | 0.7745 |
| 0.8060 | 0.8173 | 0.9180 | 0.7442 | |
| MAE | 0.2056 | 0.1664 | 0.1567 | 0.1767 |
| MSE | 0.0655 | 0.0457 | 0.0411 | 0.0556 |
| n | 260 | 247 | 293 | 207 |
| 1988 | 1991 | 1995 | 2005 | |
|---|---|---|---|---|
| 5.5459 | 6.7784 | 1.6557 | 7.5114 | |
| MAE | 12.7918 | 17.6082 | 13.0823 | 12.5637 |
| MSE | 23.2061 | 30.4157 | 18.4915 | 25.1798 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chica-Olmo, J.; Cano-Guervos, R.; Chica-Rivas, M. Estimation of Housing Price Variations Using Spatio-Temporal Data. Sustainability 2019, 11, 1551. https://doi.org/10.3390/su11061551
Chica-Olmo J, Cano-Guervos R, Chica-Rivas M. Estimation of Housing Price Variations Using Spatio-Temporal Data. Sustainability. 2019; 11(6):1551. https://doi.org/10.3390/su11061551
Chicago/Turabian StyleChica-Olmo, Jorge, Rafael Cano-Guervos, and Mario Chica-Rivas. 2019. "Estimation of Housing Price Variations Using Spatio-Temporal Data" Sustainability 11, no. 6: 1551. https://doi.org/10.3390/su11061551
APA StyleChica-Olmo, J., Cano-Guervos, R., & Chica-Rivas, M. (2019). Estimation of Housing Price Variations Using Spatio-Temporal Data. Sustainability, 11(6), 1551. https://doi.org/10.3390/su11061551







