Use of Life Cycle Cost Analysis and Multiple Criteria Decision Aid Tools for Designing Road Vertical Profiles
Abstract
:1. Introduction
- In 2016, there were 113 million cars and 133 million light trucks;
- In 2016, light vehicles accounted for 90% of the 3.2 trillion driven vehicle miles;
- In 2016, there were 11,499,000 heavy trucks;
- In 2016, heavy trucks and buses accounted for 10% of the 3.2 trillion driven vehicle miles;
- In 2017, transportation petroleum use was 70% of total petroleum use;
- In 2017, petroleum comprised 92% of transportation energy use;
- In 2016, cars and light trucks accounted for 63% of transportation petroleum use;
- In 2016, medium trucks accounted for 4% of transportation petroleum use;
- In 2016, heavy trucks and buses accounted for 19% of transportation petroleum use;
- In 2017, transportation energy use accounted for about 29% of total energy use;
- In 2016, cars and light trucks accounted for 59% of transportation energy use;
- In 2016, medium trucks accounted for 5% of transportation energy use;
- In 2016, heavy trucks and buses accounted for 19% of transportation energy use.
2. Methods
2.1. Life Cycle Cost Analysis
2.2. Multiple Criteria Decision Aid
2.3. Rakha–Pasumarthy–Adjerid (RPA) Car-Following Model
2.3.1. First Order Steady-State Car-Following Model
2.3.2. Collision Avoidance Model
2.3.3. Vehicle Dynamics Model
2.4. Virginia Tech Comprehensive Power-Based Fuel Consumption Model (VT-CPFM)
3. Proposed Evaluation Procedure
4. Case Study: Description, Results, and Discussion
4.1. LCCA Results
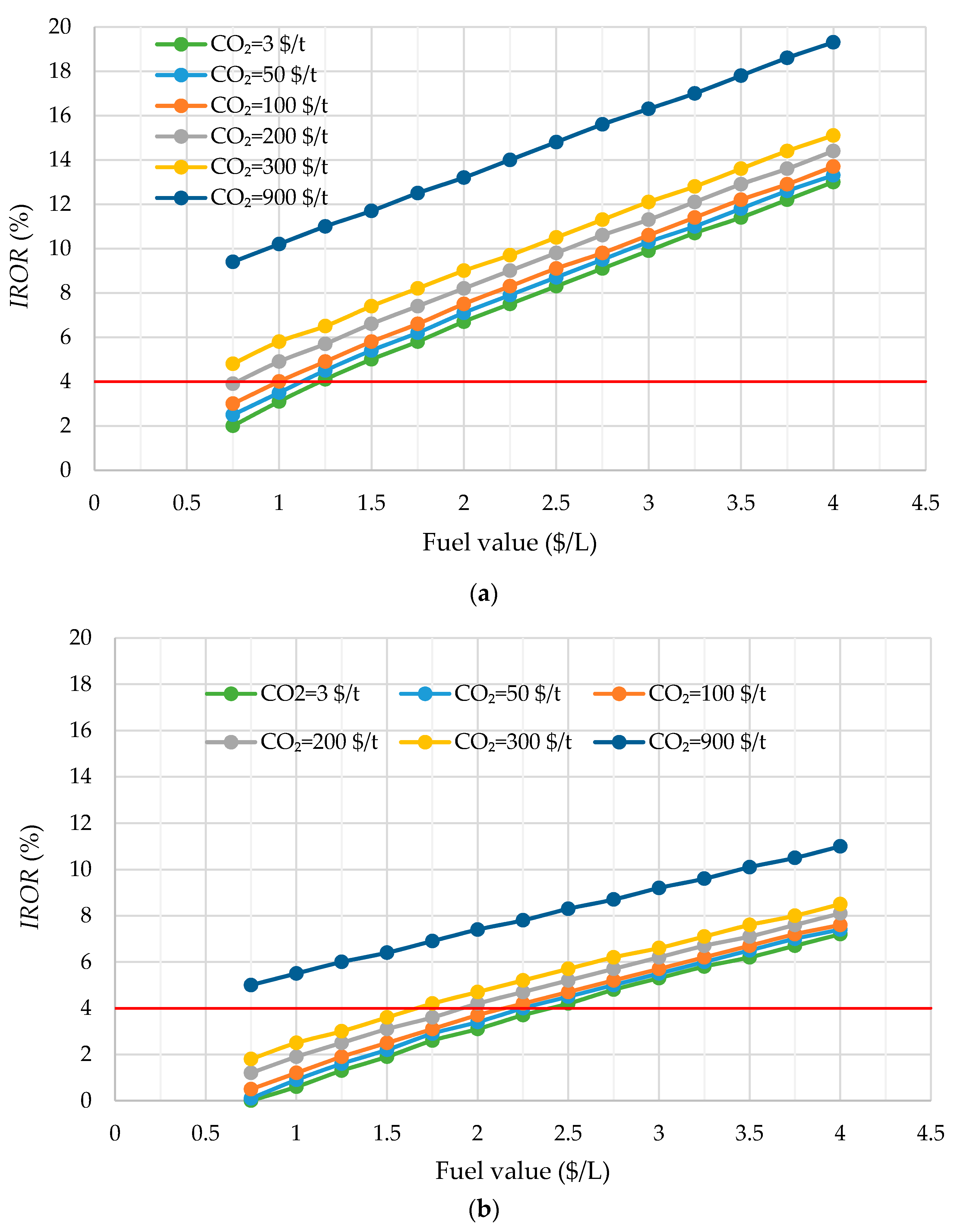
4.2. MCDA Tool Results
5. Conclusions
- The least cost alternative with the lowest required earthwork may not be the “optimal” design.
- As compared to a leveled road (0% grade), the rate of car and truck fuel consumption and CO2 emissions is much higher when going uphill than when going downhill. Therefore, the idea that excess fuel consumed uphill is compensated by lesser fuel consumed downhill is inaccurate.
- Currently, vertical profiles of roads are the role of a geometric designer who is an expert on surveying and geometric road properties. This study recommends that transportation engineers consider a project from all perspectives (planning, design, management, etc.) and understand concepts related to traffic engineering and management.
- A design software could be developed to help the analysis described in this paper. The input to such a software is the associated costs for all alternatives (excavation, filling, transportation, materials, extra lane construction, etc.) as well as the measures of performances predicted for each alternative. The software output would be the LCCA indicators and/or the ranking of the different alternatives using any MCDA tool. Different types of uncertainties could be added to the software analysis tool.
Author Contributions
Funding
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2015; p. 151. [Google Scholar]
- United States Environmental Protection Agency. Inventory of U.S. Greenhouse Gas Emissions and Sinks: 1990–2017; EPA Report No. EPA 430-P-19-001; United States Environmental Protection Agency: Washington, DC, USA, 2019; p. 669.
- Davis, S.C.; Boundy, R.G. Transportation Energy Data Book, 37th ed. Available online: https://info.ornl.gov/sites/publications/Files/Pub116893.pdf (accessed on 12 December 2019).
- Zaniewski, J.P.; Butler, B.C.; Cunningham, G.; Elkins, G.E.; Paggi, M.S.; Machemehl, R. Vehicle Operating Costs, Fuel Consumption, and Pavement Type Condition Factors; FHWA/PL/82/00; FHWA, U.S. Department of Transportation: Washington, DC, USA, 1982.
- Klaubert, E.C. Highway Effects on Vehicle Performance; FHWA-RD-00-164; FHWA, U.S. Department of Transportation: Washington, DC, USA, 2001.
- Park, S.; Rakha, H. Energy and environmental impacts of roadway grades. Transp. Res. Rec. J. Transp. Res. Board 2006, 1987, 148–160. [Google Scholar] [CrossRef]
- Chatti, K.; Zaabar, I. Estimating the Effects of Pavement Condition on Vehicle Operating Costs; NCHRP Report 720; Transportation Research Board: Washington, DC, USA, 2012. [Google Scholar]
- Kang, M.W.; Shariat, S.; Jha, M.K. New highway geometric design methods for minimizing vehicular fuel consumption and improving safety. Transp. Res. C 2013, 31, 99–111. [Google Scholar] [CrossRef]
- Loulizi, A.; Rakha, H.; Bichiou, Y. Quantifying grade effects on vehicle fuel consumption for use in sustainable highway design. Int. J. Sustain. Transp. 2018, 12, 441–451. [Google Scholar] [CrossRef]
- Boriboonsomsin, K.; Barth, M. Impacts of road grade on fuel consumption and carbon dioxide emissions evidenced by use of advanced navigation systems. Transp. Res. Rec. J. Transp. Res. Board 2009, 2139, 21–30. [Google Scholar] [CrossRef]
- Nocera, S.; Galati, O.I.; Cavallaro, F. On the Uncertainty in the Economic Valuation of Carbon Emissions from Transport. J. Transp. Econ. Policy 2018, 52, 68–94. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill International Book Co.: New York, NY, USA, 1980. [Google Scholar]
- Roy, B. Classement et choix en présence de points de vue multiples (la méthode ELECTRE). La Rev. D’Inform. Rech. Opérationelle (RIRO) 1968, 2, 57–75. [Google Scholar]
- Brans, J.P.; Mareschal, P. Promethee Methods, Multiple Criteria Decision Analysis: State of the Art Surveys; Springer Sciences: Boston, MA, USA, 2005; Chapter 5; pp. 163–195. [Google Scholar]
- Brans, J.P. L’Ingénierie de la Décision—Elaboration D’instruments D’aide à La Décision—Méthode PROMETHEE; Université Laval, Colloque d’aide à la décision: Quebec, QC, Canada, 1982; pp. 183–213. [Google Scholar]
- Brans, J.P.; Mareschal, B. The Promcalc and Gaia decision-support system for multicriteria decision aid. Decis. Support Syst. 1994, 12, 297–310. [Google Scholar] [CrossRef]
- Van Aerde, M.; Yagar, S. Dynamic Integrated Freeway/Traffic Signal Networks: A Routeing-Based Modelling Approach. Transp. Res. 1988, 22, 445–453. [Google Scholar] [CrossRef]
- Van Aerde, M.; Rakha, H. INTEGRATION © Release 2.40 for Windows: User’s Guide—Volume I: Fundamental Model Features; M. Van Aerde & Assoc., Ltd.: Blacksburg, VA, USA, 2013. [Google Scholar]
- Rakha, H.; Pasumarthy, P.; Adjerid, S. A Simplified Behavioral Vehicle Longitudinal Motion Model. Transp. Lett. Int. J. Transp. Res. 2009, 1, 95–110. [Google Scholar] [CrossRef]
- Van Aerde, M.; Rakha, H. Multivariate calibration of single regime speed-flow-density relationships [road traffic management]. In Proceedings of the Vehicle Navigation and Information Systems Conference, in conjunction with the Pacific Rim TransTech Conference: 6th International VNIS: A Ride into the Future, Seattle, WA, USA, 30 July–2 August 1995. [Google Scholar]
- Rakha, H.; Ahn, K.; Moran, K.; Saerens, B.; Van Den Bulck, E. Virginia Tech comprehensive power-based fuel consumption model: Model development and testing. Transp. Res. D 2011, 16, 492–503. [Google Scholar] [CrossRef]
- Guo, J.X.; Tan, X.; Gu, B.; Qu, X. The impacts of uncertainties on the carbon mitigation design: Perspective from abatement cost and emission rate. J. Clean. Prod. 2019, 232, 213–223. [Google Scholar] [CrossRef]
- Xu, Z.; Elomri, A.; Pokharel, S.; Zhang, Q.; Ming, X.G.; Liu, W. Global reverse supply chain design for solid waste recycling under uncertainties and carbon emission constraint. Waste Manag. 2017, 64, 358–370. [Google Scholar] [CrossRef]
- Prassas, E.S.; Roess, R.P. Engineering Economics and Finance for Transportation Infrastructure; Springer: Berlin, Germany, 2013. [Google Scholar]

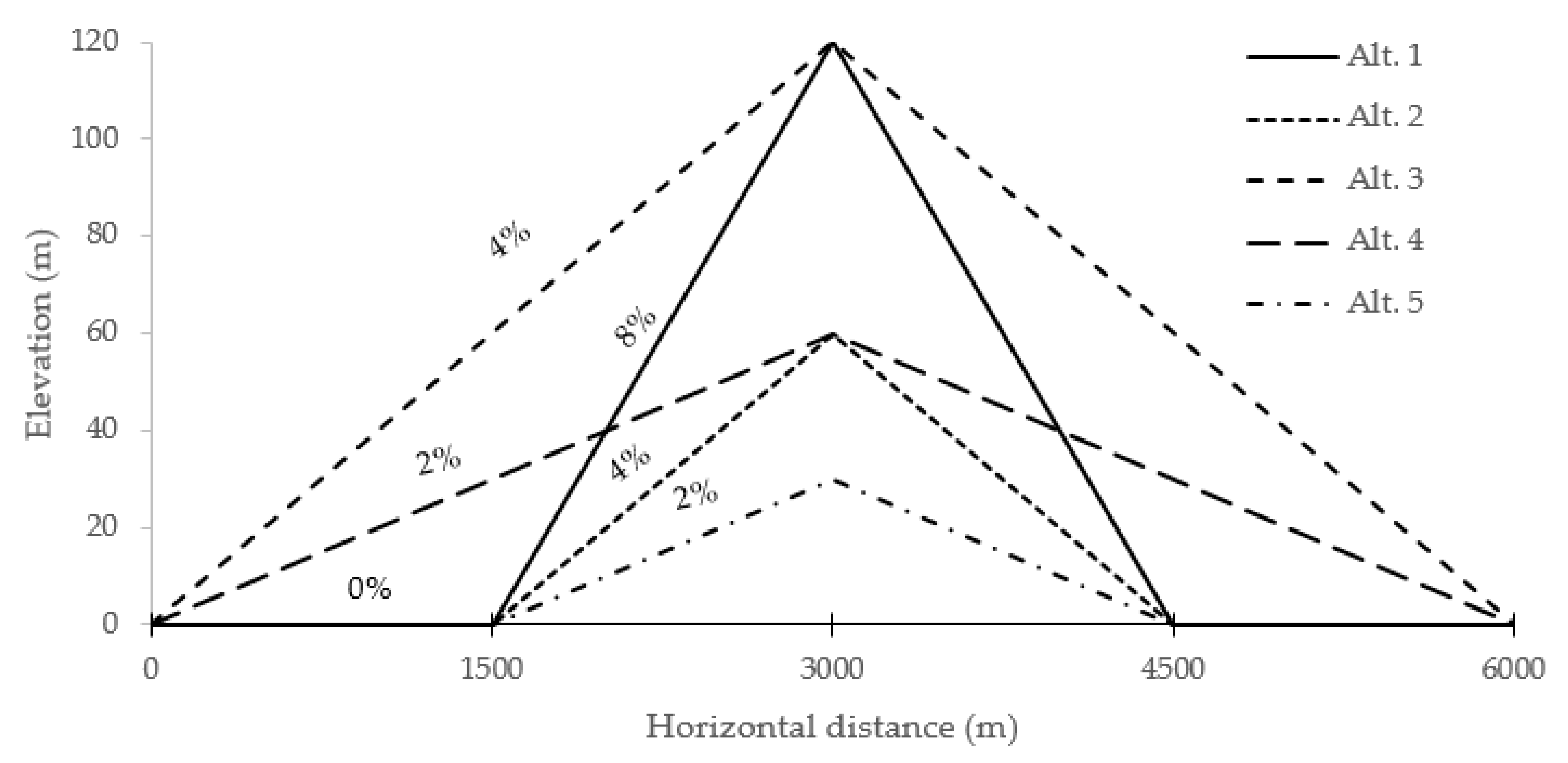



| Characteristics | Value |
|---|---|
| Average annual daily traffic | 2000 |
| Percentage of trucks | 15% |
| Directional distribution | 50/50 |
| Proportions of daily traffic occurring during the peak hour | 15% |
| Free flow speed | 120 km/h |
| Speed at capacity | 90 km/h |
| Jam density | 160 veh./km/lane |
| Saturation flow rate | 1800 veh./h/lane |
| Item | Cost |
|---|---|
| Earthwork cost Alt. 1 (M$) | 4 |
| Earthwork cost Alt. 2 (M$) | 60 |
| Earthwork cost Alt. 3 (M$) | 44 |
| Earthwork cost Alt. 4 (M$) | 88 |
| Earthwork cost Alt. 5 (M$) | 120 |
| Value of travel time ($/(veh. × h), cars | 30 |
| Value of travel time ($/(veh. × h), trucks | 56 |
| Value of fuel ($/L) | 0.75–4 |
| Value of CO2 emissions ($/t) | 3, 50, 100, 200, 300, 900 |
| Cost (M$) | Fuel per Year (kL) | CO2 per Year (t) | Time per Year (kveh. × h) | |
|---|---|---|---|---|
| Alt. 1 | 4 | 10,300 | 23,800 | 396.4 |
| Alt. 2 | 60 | 8500 | 19,900 | 387.1 |
| Alt. 3 | 44 | 8700 | 20,400 | 391.0 |
| Alt. 4 | 88 | 8200 | 19,100 | 385.3 |
| Alt. 5 | 120 | 8200 | 19,200 | 384.2 |
| Indifference threshold (q) | 4 | 600 | 1600 | 3.6 |
| Preference threshold (p) | 10 | 1600 | 4000 | 9.6 |
| Weight | 50–300 | 5–30 | 5–30 | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loulizi, A.; Bichiou, Y.; Rakha, H. Use of Life Cycle Cost Analysis and Multiple Criteria Decision Aid Tools for Designing Road Vertical Profiles. Sustainability 2019, 11, 7127. https://doi.org/10.3390/su11247127
Loulizi A, Bichiou Y, Rakha H. Use of Life Cycle Cost Analysis and Multiple Criteria Decision Aid Tools for Designing Road Vertical Profiles. Sustainability. 2019; 11(24):7127. https://doi.org/10.3390/su11247127
Chicago/Turabian StyleLoulizi, Amara, Youssef Bichiou, and Hesham Rakha. 2019. "Use of Life Cycle Cost Analysis and Multiple Criteria Decision Aid Tools for Designing Road Vertical Profiles" Sustainability 11, no. 24: 7127. https://doi.org/10.3390/su11247127
APA StyleLoulizi, A., Bichiou, Y., & Rakha, H. (2019). Use of Life Cycle Cost Analysis and Multiple Criteria Decision Aid Tools for Designing Road Vertical Profiles. Sustainability, 11(24), 7127. https://doi.org/10.3390/su11247127






