1. Introduction
At present, accompanied with the support of the national programmatic document “Vision and Actions on Jointly Building Silk Road Economic Belt and 21st-Century Maritime Silk Road”, China Railway Express, which refers to the international container rail lines running between China and Europe, as well as countries along “The Belt and Road”, has maintained the momentum of rapid development.
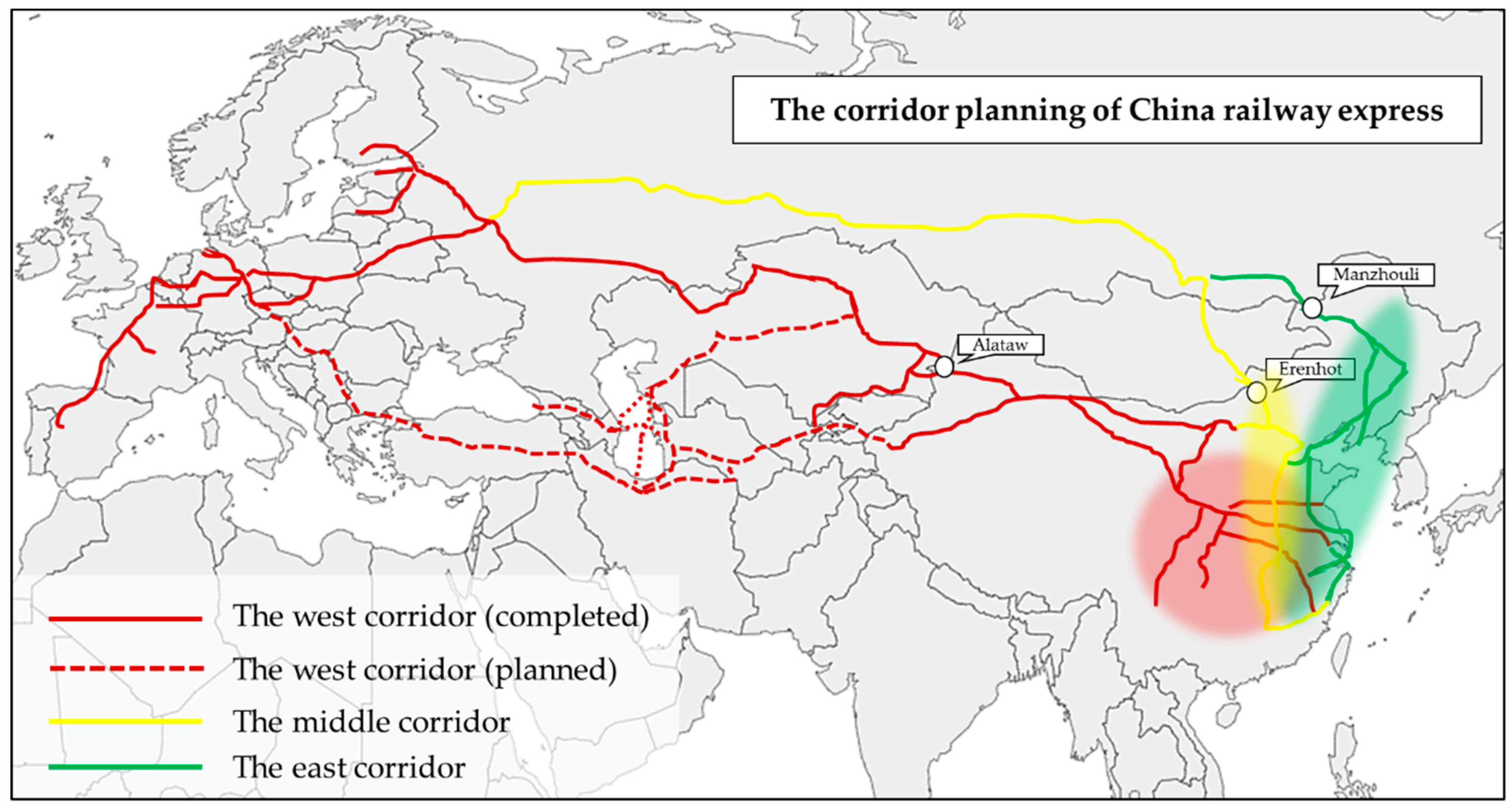
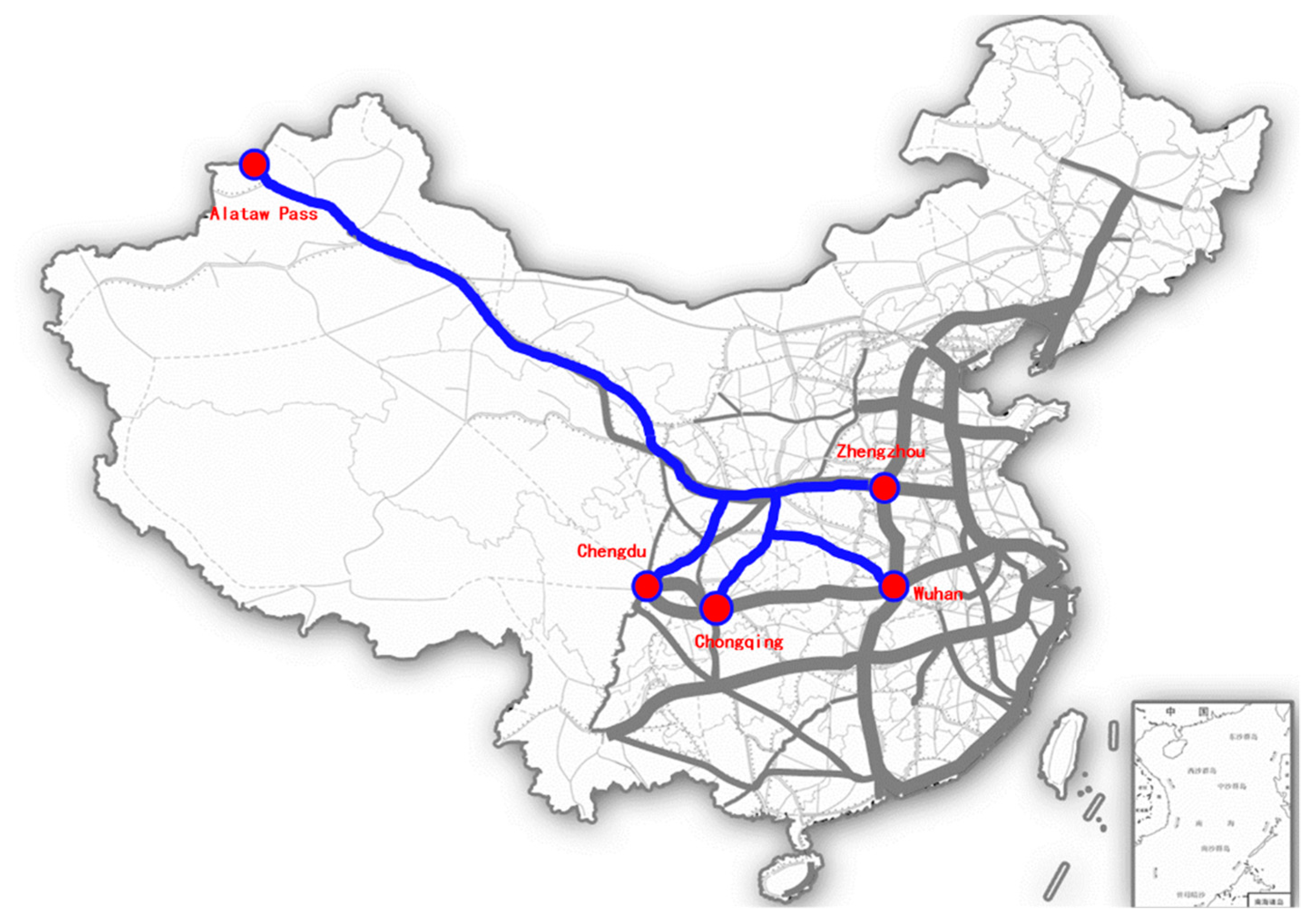
According to the requirement of construction planning, the east, middle and west corridors of the China Railway Express has been formed. The west corridor (the red line in
Figure 1), with the largest freight volume and highest benefit among the three corridors, mainly delivers goods from the central region of China towards Europe via the Alataw Pass railway station (a little through Khorgos). The middle corridor (the yellow line in
Figure 1), which mainly carries goods from central China and north China, leaves China from Erenhot Pass railway station and finally reaches Europe, whereas the goods of the east corridor (the green line in
Figure 1) mainly come from the southeast coastal areas of China and leave the country through Manzhouli Pass railway station and then continue on to Europe. By the beginning of 2019, 59 cities in China had opened their China Railway Express lines, amounting to a total of 65 lines. The total number of trains has exceeded 13,000, reaching 49 cities in 15 European countries and covering major regions of the Eurasian continent. In this paper, we chose Alataw Pass railway station in the west corridor as an example, which is the most representative case.
China Railway Express has greatly promoted China–Europe trade, but there are still problems such as the imbalance of the number of outbound and inbound trains caused by trade deficit, and the poor connection between trains resulting in a long dwell time in railway port stations, which are crucial links in transportation organization of China Railway Express, considering its long-term and sustainable development.
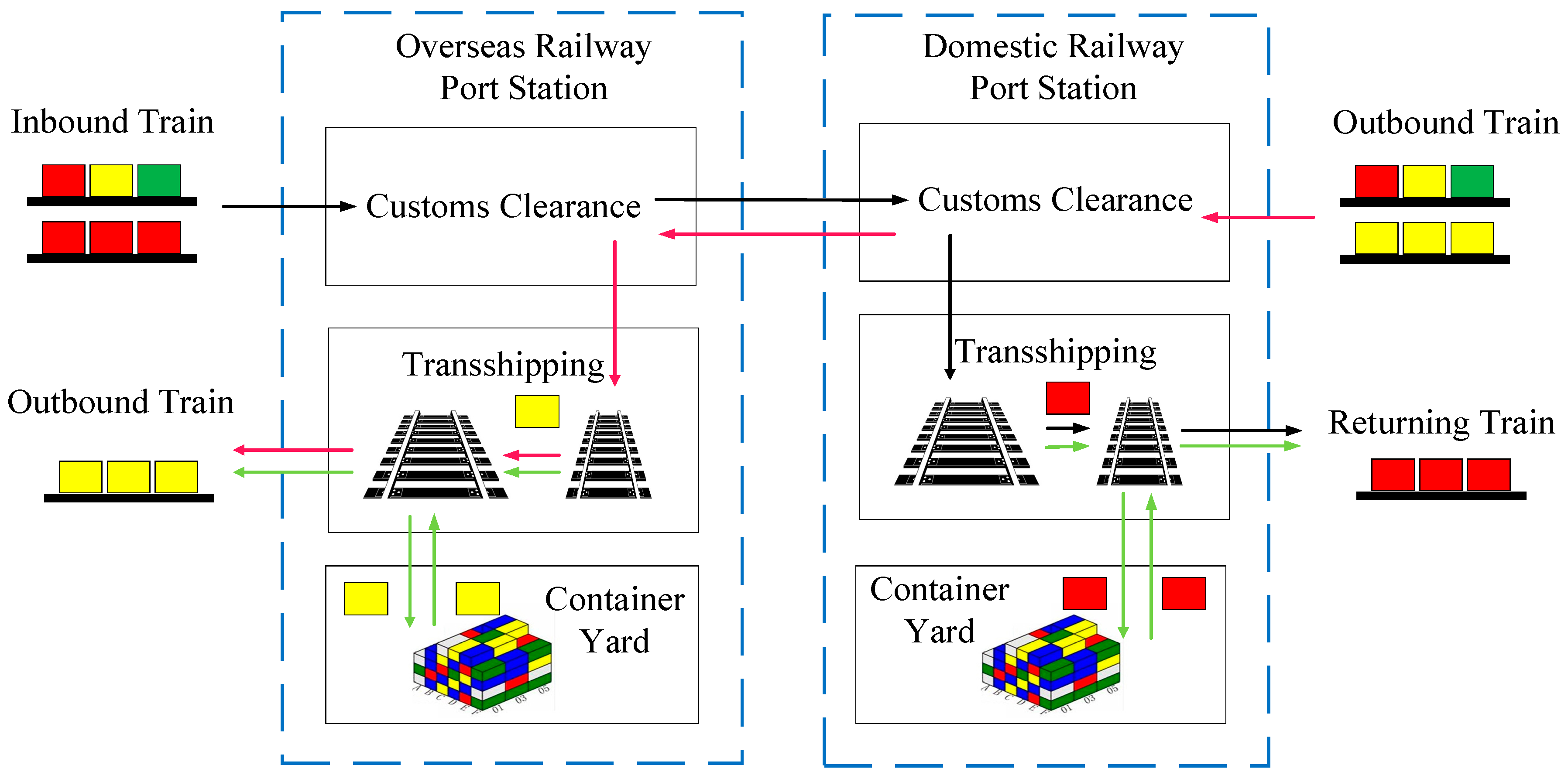
Due to the different gauges between China and Kazakhstan, as well as Russia and Mongolia, the inbound and outbound trains of China Railway Express are supposed to transship in the railway port stations. However, on account of the independent operation of China Railway Express in each city, it is possible for the trains to arrive at railway port stations intensively, which would result in the limitation of operation capacity of stations, and the transit delay time of the trains being too long to give play to the time advantage of China Railway Express over sea transportation. As a result, the efficiency of customs clearance is seriously affected.
The further development of the China Railway Express is based on the sound transportation network and advanced transshipment equipment; moreover, it needs to be guaranteed by scientific and efficient transportation organization. The problems arising in railway port stations will become a bottleneck restricting the sustainable development of China Railway Express without optimization and improvement. Given all this, this paper focuses on the operation waiting time and equipment capacity of Alataw Pass railway station, and models this problem using mathematical methods, and addresses some properties of the problem. Finally, we provide a solution algorithm to generate promising distribution organization schemes, which has important theoretical value and practical guiding significance to improve the operational efficiency of China Railway Express, while concurrently providing better services for high-volume transportation.
The rest of this paper is organized as follows: After explaining the contributions of this work in light of a literature review of transportation organization of China Railway Express and container multimodal transportation in
Section 2,
Section 3 describes the problem this paper studies and formulates the problem using mathematical methods and then states some constraint conditions. Subsequently,
Section 4 builds upon these results to introduce a heuristic procedure. The algorithm is tested through two sets of data in
Section 5. Finally, conclusions and future research directions are given in
Section 6.
2. Literature Review
With the continuous implementation and promotion of “The Belt and Road” initiative, China Railway Express, as an important carrier, has maintained the trend of rapid development. Scholars from various countries have gradually joined in the research of China Railway Express. The literature related to this paper involve two fields which are China Railway Express and container multimodal transportation.
The researches on China Railway Express started in recent years. In terms of development policy and status quo, Yang et al. compare the different performance of the China–Europe Sea–Land Express Line and the New Eurasian Land Bridge through the quantitative analysis of the questionnaire [
1]. Based on the analysis of the problems in the operation of China Railway Express, a series of corresponding strategies are listed and an index system is established from five aspects to give advice on the high quality operation management of China Railway Express [
2,
3]. In addition, Besharati et al. make a detailed analysis on the government subsidy policy of China Railway Express from the perspective of sustainable development [
4]. Wang mainly studies the difference of transport costs between rail and sea transportation, especially the main types and value of goods of China Railway Express. Then, some suggestions are put forward in view of the operation status and problems in the current transportation organization mode [
5]. Closely related to this paper, Kang analyzes reasons affecting the running speed of the China Railway Express, such as the capacity limitation of the railway port stations [
6]. Nonetheless, the author only provides conceptual theoretical suggestions on shortening the running time of the trains but does not treat this problem in much detail.
In terms of optimization of transportation organization, some researchers formulate models which take the security, cost, transit time, mode and infrastructure reliability into account to demonstrate the significant advantages of the corridors compared with the traditional sea route [
7,
8]. Jiang et al. [
9] and Li [
10] pay attention to the timeliness of China Railway Express and build mathematical models to calculate the time value advantage of different goods, and give advice on improving the time efficiency of freight trains. In the analysis of the cost structures of five typical China Railway Express routes and shipping routes of containers, Jiang et al. explore the current and the prospective choice probability of hinterland patterns of different types of goods, with and without government subsidies, applying discrete choice theory [
11]. There is also some research on a consolidation center, where Li et al. establish domestic and European nodes classification systems in which the flow of goods or containers in the same group divided by different node levels can be mutually adjusted [
12]. Fu et al. design a multi-objects optimization model for China Railway Express in central west of China and they demonstrate that Zhengzhou is the best consolidation center [
13], while Ye proves the effectiveness of the freight transportation center in Urumqi by empirical analysis compared with the direct mode of transportation organization [
14]. However, they only focus on one possible consolidation center instead of considering the layout of logistics nodes. Zhao et al. extend the previous problem by selecting 27 cities as pre-candidate consolidation centers and finally identify five cities as the optimal consolidation centers [
15]. In the works of [
16], a model of a network operation plan of trains, based on the assembly center, is proposed to ensure the stable development of China Railway Express.
In the field of container multimodal transportation, domestic and foreign scholars have carried on relevant research from many aspects. In the studies of container sea–rail intermodal transportation, Liu et al. apply a two-stage optimal model ground on revenue management to explore the problem of joint slot allocation and dynamic pricing involving container sea–rail intermodal transportation [
17]. Jin et al. put forward a series of development proposals from the theoretical point of view considering the resources in stations where containers are transited [
18]. From the perspective of quantitative analysis, some researchers use mathematical models to minimize the total transportation time during the sea–rail transshipment process considering the requirement of a fast connection in time and space [
19,
20]. Yang et al. are also interested in the problem of poor timeliness of railway container transportation. They put forward five organization modes suitable for container trains taking the idea of the passenger-like fast transport system as the core [
21].
In the studies of container yard operation, Nils et al. [
22] and Fang [
23] note the impact of resource allocation on operational efficiency in container terminals, where the optimal scheduling methods of gantry cranes are obtained to improve the container handling efficiency. Aiming to minimize the frequency of transfers within yards, Le et al. study the problem of optimizing container loading on trains in a rail–rail transshipment shunting yard [
24]. Moreover, some researchers pay attention to the train scheduling problem in rail–rail transshipment yards. Boysen et al. propose that the crux of the issue is resolving deadlocks and avoiding multiple crane picks per container move [
25], and Xie solves the problem by optimizing container prestaging and dynamic discharging/loading, subject to time windows [
26]. Stefan et al. compare the performance of four kinds of container sorting systems in rail–rail transshipment yards and provide suited scheduling policies for each system [
27]. Albareda-Sambola et al. are also interested in the rail–rail container transshipment. They use two new formulations of the acyclic graph partitioning problem to make trains packed in groups that fit in the loading area [
28]. In the works of [
29], a joint discrete-discrete copula-based model is proposed to synchronously capture the decisive factors of using a container terminal and the dwell time of containers.
Based on the literature review, on the one hand, the research of China Railway Express made by scholars at home and abroad is mainly regarding the relevant countermeasures and suggestions after analyzing the status quo and the problems. On the other hand, some scholars use mathematical models to conduct research. To be specific, most studies of China Railway Express can be partitioned into the following groups: the operation situation [
1,
2,
3,
4,
5,
6,
30,
31], optimization of transportation organization [
7,
8,
9,
10,
11,
12], as well as the consolidation center [
13,
14,
15,
16]. Less research on railway port stations is conducted. Moreover, the review finds that the research on container multimodal transportation mostly focuses on optimization of transportation organization [
17,
18,
19,
20,
21,
32], resource allocation [
22,
23,
33], yard operation optimization [
24,
25,
26,
27,
28,
29,
34], transportation path planning [
35,
36] and network optimization [
37,
38,
39]. Although some scholars pay attention to the rail–rail transshipment process, the close connection between the distribution organization scheme and container transshipment is less considered, which is of great significance to the long-term efficient development of China Railway Express.
China Railway Express itself has the characteristics of high volume, long distance and long-term, which makes it a sustainable mode of transportation. In this paper, we aim to deal with the existing problems in the railway port station and improve the transportation organization of China Railway Express. We think the improvement of container turnover efficiency is conducive to promoting mass railway transport, which is an environmentally-friendly mode of transportation in itself. The contributions of this paper are summarized as follows:
(1) This paper proposes a model for container distribution organization optimization using mathematical methods which considers spatial and temporal resource allocation.
(2) The examples of two modes of transportation organization for China Railway Express are given for validating the effectiveness of the model, and an evaluation index system is established from the perspective of the comprehensive benefits of transportation organization.
(3) This paper analyzes the change of distribution organization efficiency under different orders of magnitude, in the case of direct and assembled transportation organization modes, to adapt to the sustainable development of China Railway Express.
4. Solution Method
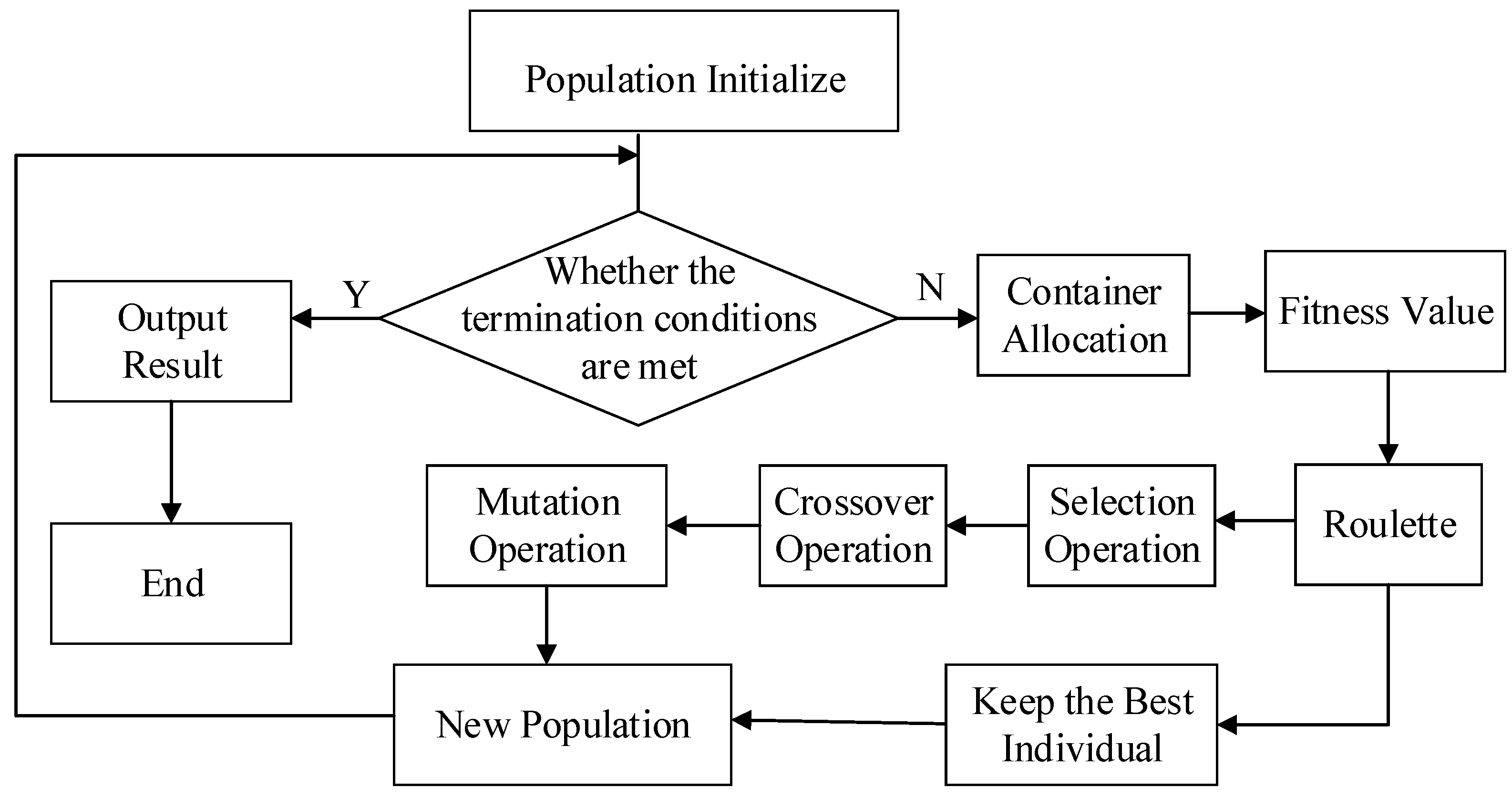
At present, a genetic algorithm is a heuristic algorithm often used to solve optimization problems. It can be used to generate a reasonable solution to optimize a goal. A genetic algorithm has no fixed rules and is easy to grasp, which has been favored by most scholars in the field of transportation. Therefore, based on the idea of a genetic algorithm, this paper explores the solution method with container allocation of the distribution organization optimization model. The process of the genetic algorithm designed in this paper is shown in
Figure 4.
The specific algorithmic process is described as follows:
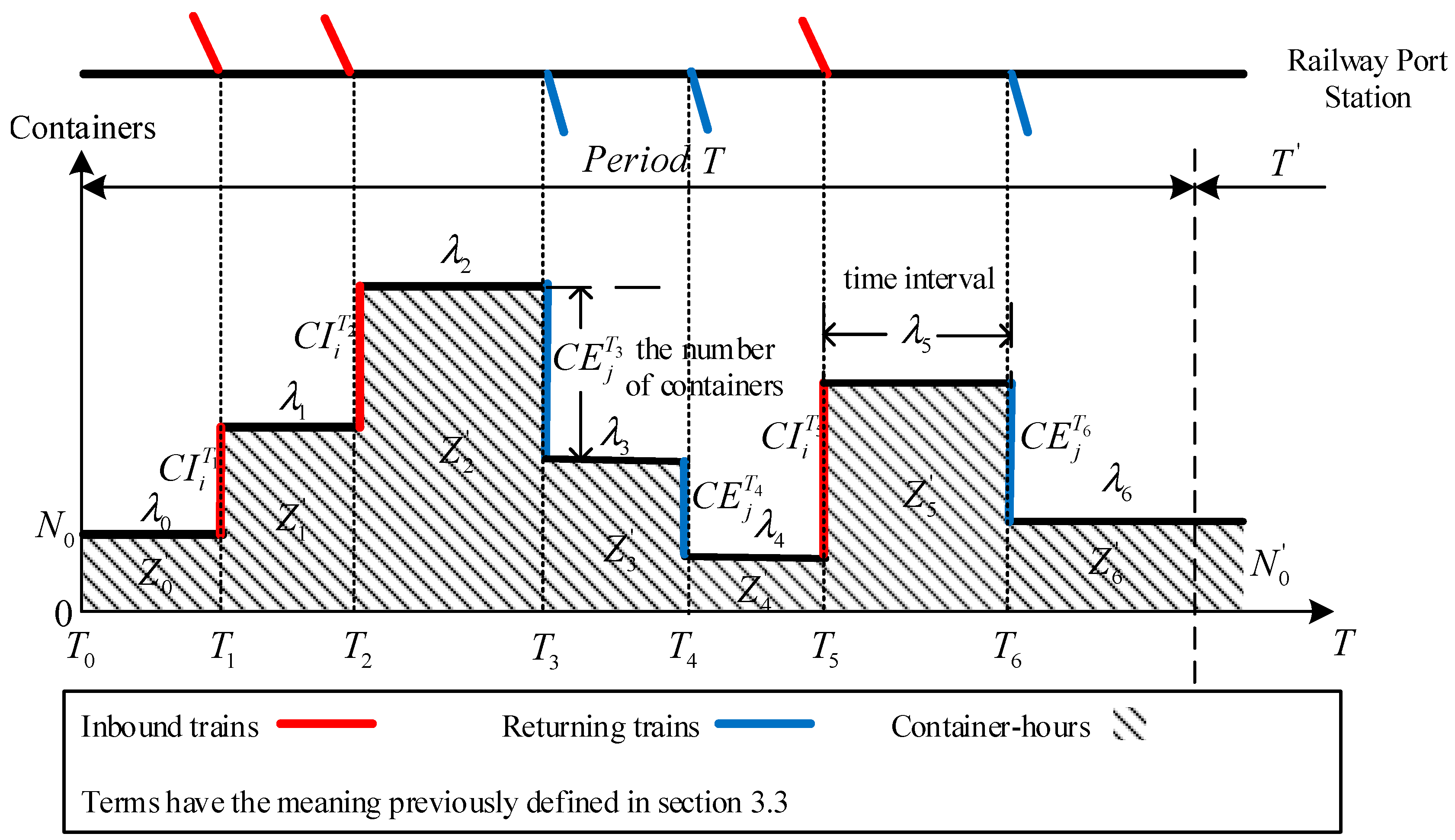
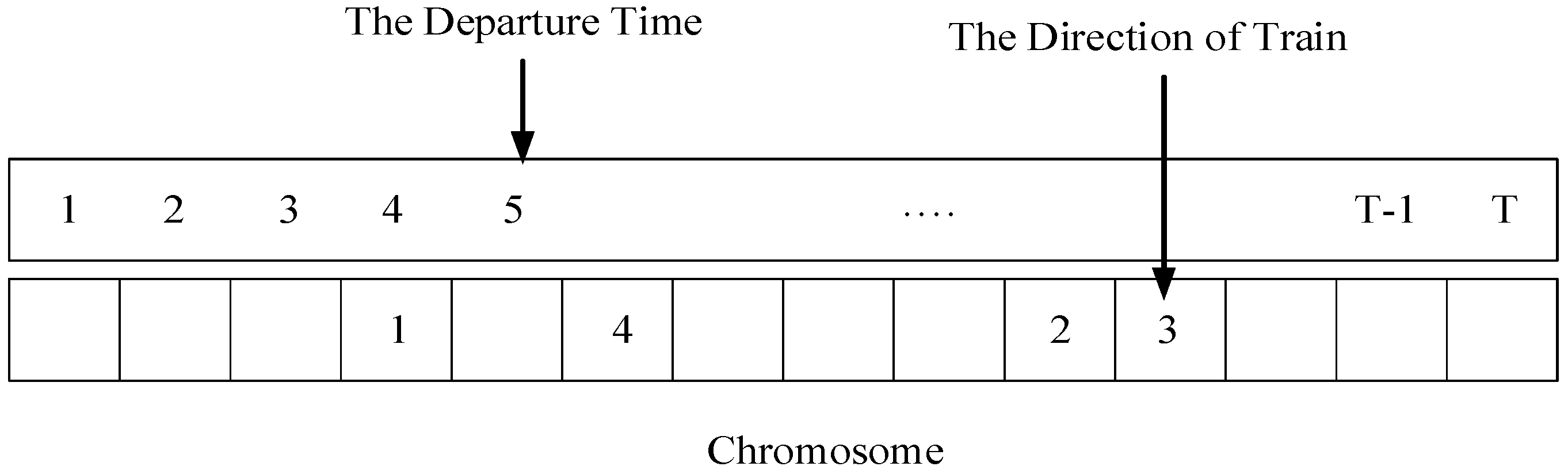
Step 0: Organization schemes of returning trains. Each chromosome represents an organization scheme, which includes the direction and the departure time of returning trains. The total number of all non-zero figures in the code represents the total number of returning trains planned to run in the period T, as shown in
Figure 5.
Step 1: Population initialization. Set up the basic data needed by the algorithm such as population size, the maximum number of iterations, cross probability and mutation probability. Then, loop through step 0 until the initial population size is met.
Step 2: Fitness calculation. Judge whether each individual satisfies the constraint conditions after obtaining the scheme from chromosome information. If so, the fitness is calculated which is the reciprocal of the objective function.
Step 3: Selection operation. During each successive generation, the selection operation is performed by preserving the excellent individuals to breed a new generation, by which the search speed can be effectively improved. In this paper, we randomly screen out individuals by means of roulette.
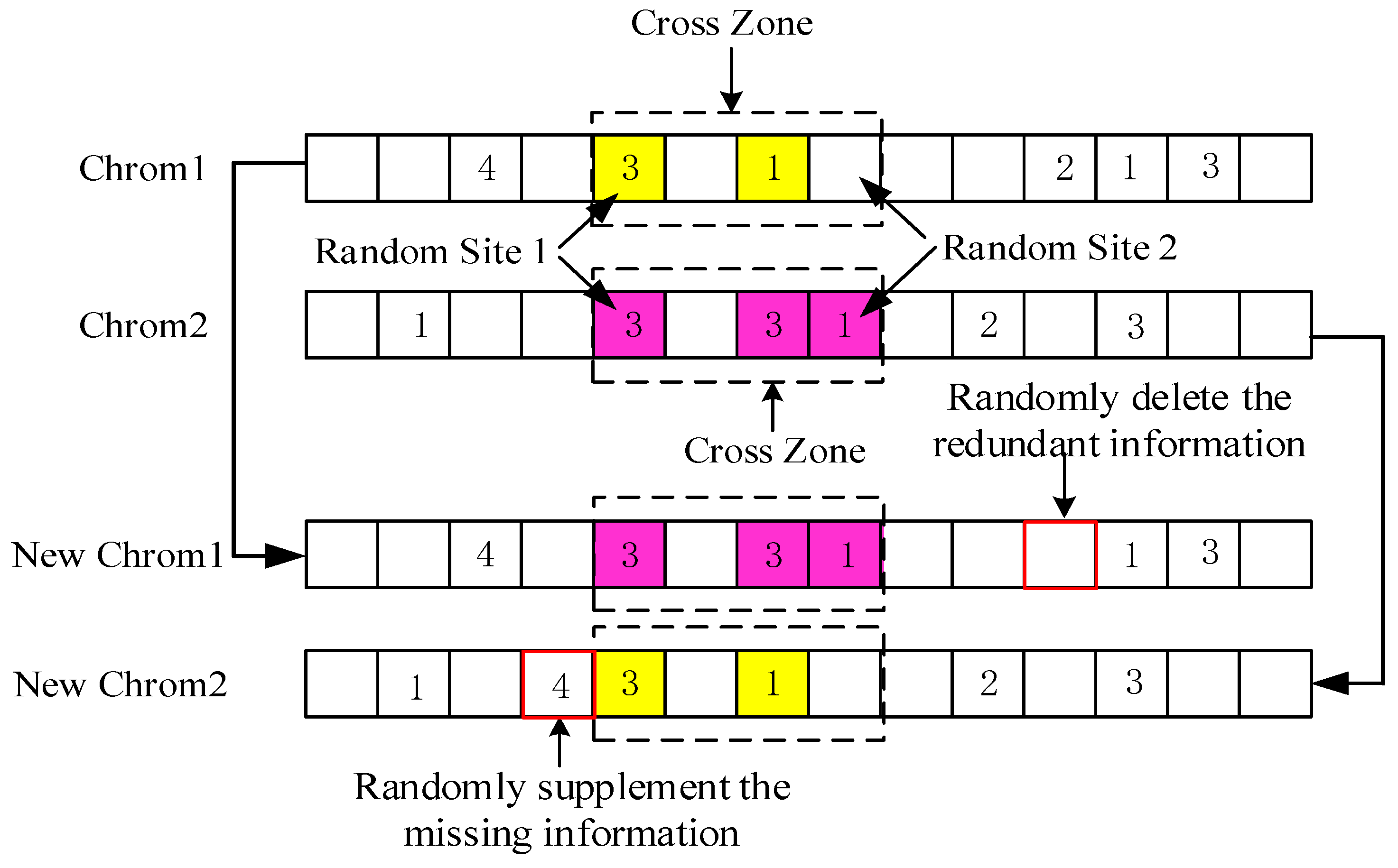
Step 4: Crossover operation. A new population is generated by exchanging some information between two chromosomes using two-sites crossover method and then mixing with the parent. Besides this, randomly select the site to supplement the missing information or randomly delete the redundant information to make the new chromosomes meet the coding requirements. An example is shown in
Figure 6.
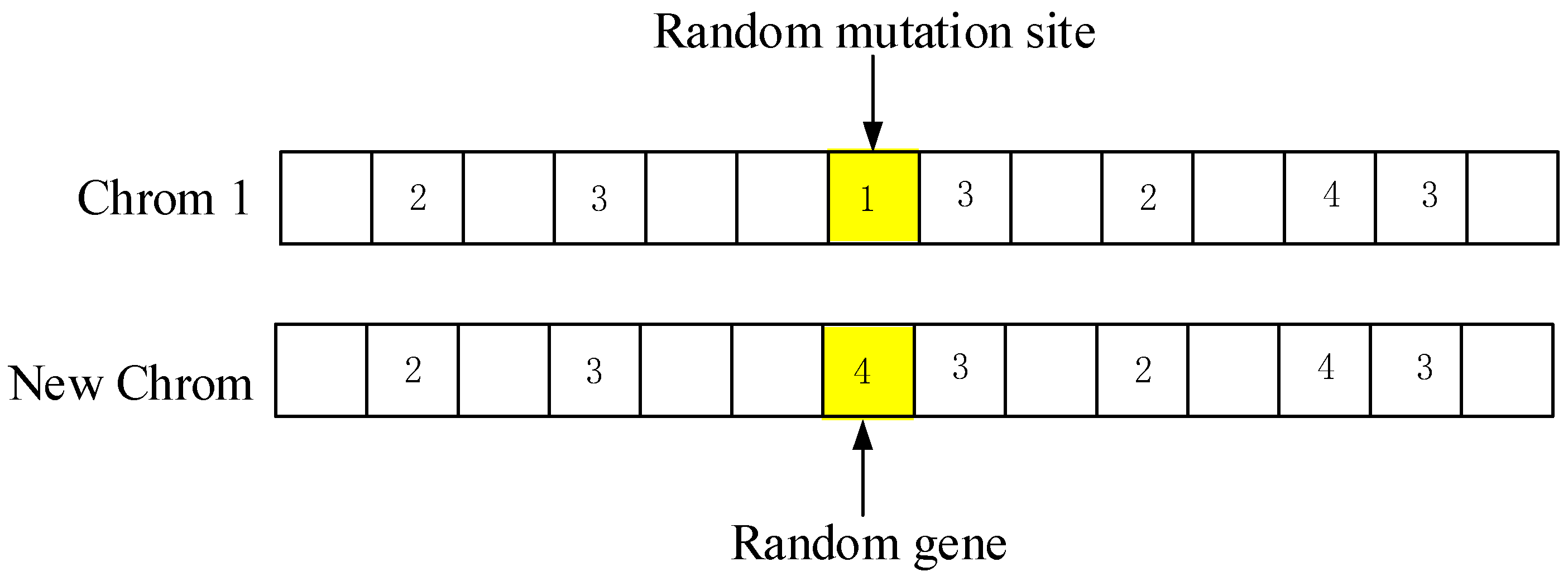
Step 5: Mutation operation. Real valued mutation is chosen to generate a new individual which is performed by randomly selecting a chromosome in population and changing the code of one site.
Figure 7 shows the detailed mutation operation process of an example.
Step 6: Termination conditions judgment. Determine whether the maximum number of iterations is met. If so, go to step 7, else return to step 2.
Step 7: Output results. The optimal individual is obtained. The end.
5. Computational Results and Discussion
In this section, the Alataw Pass railway station on the west corridor of China Railway Express is taken as an example. The tracks of standard-track yard I and II at Alataw Pass railway station are both standard tracks with 1435 mm gauge. There are 7 arrival and departure tracks and 10 shunting tracks in standard-track yard I, and 7 arrival and departure tracks and 17 shunting tracks in standard-track yard II. The wide-gauge yard, which is mainly used for inbound trains, has 10 arrival and departure tracks as well as 15 shunting tracks and 2 lead tracks. Moreover, the Alataw Pass railway station is also equipped with transshipping yards, which have 3 pairs of tracks especially for containers transshipping.
According to the different number of China Railway Express to all directions, we consider four inland stations (
Figure 8). Wuhan, Zhengzhou, Chongqing, Chengdu, are destinations which have had the largest freight volume as well as the number of trains in recent years. We respectively take experiments in case of direct and assembled transportation organization modes, according to long-term and strategic development of China Railway Express.
The experiments are performed on a Notebook with 1.90 GHz Intel Core i3 processor, with 8 GB of RAM and the programming language is MATLAB R2016a.
5.1. Direct Transportation Organization Mode
Direct transportation organization mode means the containers on each inbound train have the same destination. This mode has been adopted to the transportation organization of China Railway Express since the first line opened, which can save the time of loading and unloading, reduce the risk of transit damage, but increased the cargo assembling time at each starting station.
Through the statistical analysis, we assume one week as an operating period and 2-h as a basic time-unit, as thus, there are 84 time-units in one period. Moreover, the storage capacity of the yard is 500 containers. It is set that it takes 2 time-units, on average, for containers to complete the transshipping operation and 1 time-unit for the time interval between arrival and departure operation. Finally, based on the operation status of China Railway Express, there are 15 inbound China Railway Express arriving at Alataw Pass railway station and 13–17 returning trains are planned to run to inland stations within one operating period. The original information of inbound China Railway Express including arriving time, the number and the direction of containers is given in
Table 1.
In order to intuitively express the different effects of every container distribution organization scheme, we established an evaluation index system, shown in
Table 2, from the perspective of the comprehensive benefits of transportation organization.
To compare the results of the distribution organization optimization model with fixed-axle constraint from 35 to 45 container sets,
Table 3 shows the evaluation results of 13–16 returning trains’ distribution organization schemes.
As shown in
Table 3, when the number of returning trains is 15, which is equal to the number of arriving inbound trains, the total container-hours is the least and there are no containers remaining in the yard. When increasing the number of trains, there is no possible solution because the minimum of fixed-axle constraint is not met. When decreasing the number of returning trains, some containers are left and the total container-hours is up to 1321 and 1601. Thus, the one-to-one distribution organization scheme is of most efficiency in direct transportation organization mode. The specific scheme including the departure time, direction and the number of loaded containers of each returning train is detailed in
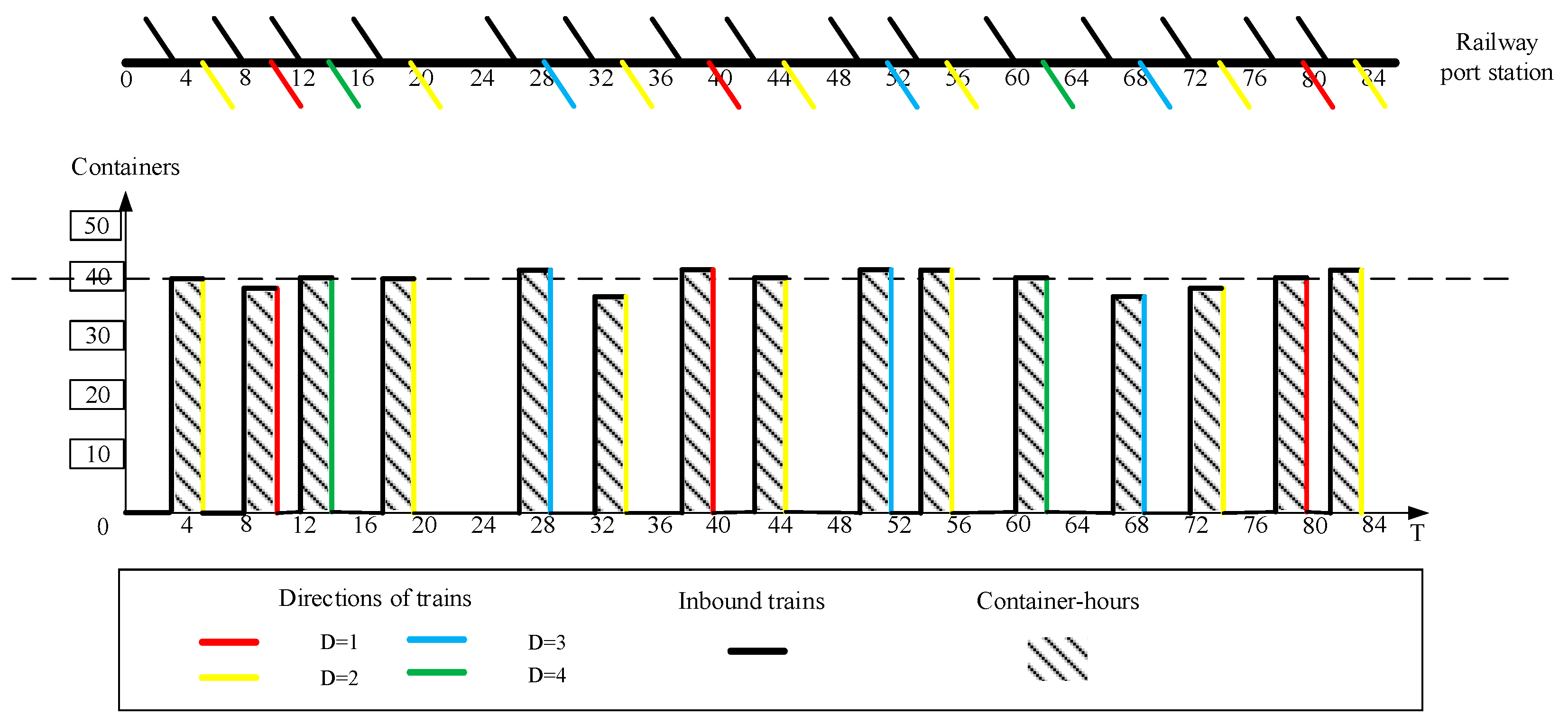
Table 4. Corresponding to
Table 4,
Figure 9 shows the distribution organization scheme of 15 returning trains in the form of an image.
At present, the direct transportation organization mode is generally adopted in China Railway Express and the number of inbound trains is currently at a lower level. The experiment results show that it is efficient to adopt a one-to-one transportation organization scheme for the inbound trains under the direct mode, which could contribute to shorten the detention time of containers in the railway port station.
5.2. Assembled Transportation Organization Mode
Assembled transportation organization mode means the containers on each inbound train have different destinations and have to be regrouped and assembled at Alataw Pass railway station prior to transporting to the inland stations. This mode has been proposed but not implemented, which can promote resource integration to improve the economic benefit of the whole transportation net; however, it increases the operational pressure on the consolidation center. With the increasing freight volume of China Railway Express, this mode has attracted more attention.
The data processing is the same as direct transportation organization mode, and the original information of inbound China Railway Express, including arriving time and the number of loaded containers towards different directions is given in
Table 5.
Table 6 shows the evaluation results of 14–17 returning trains’ transportation schemes produced by genetic algorithm.
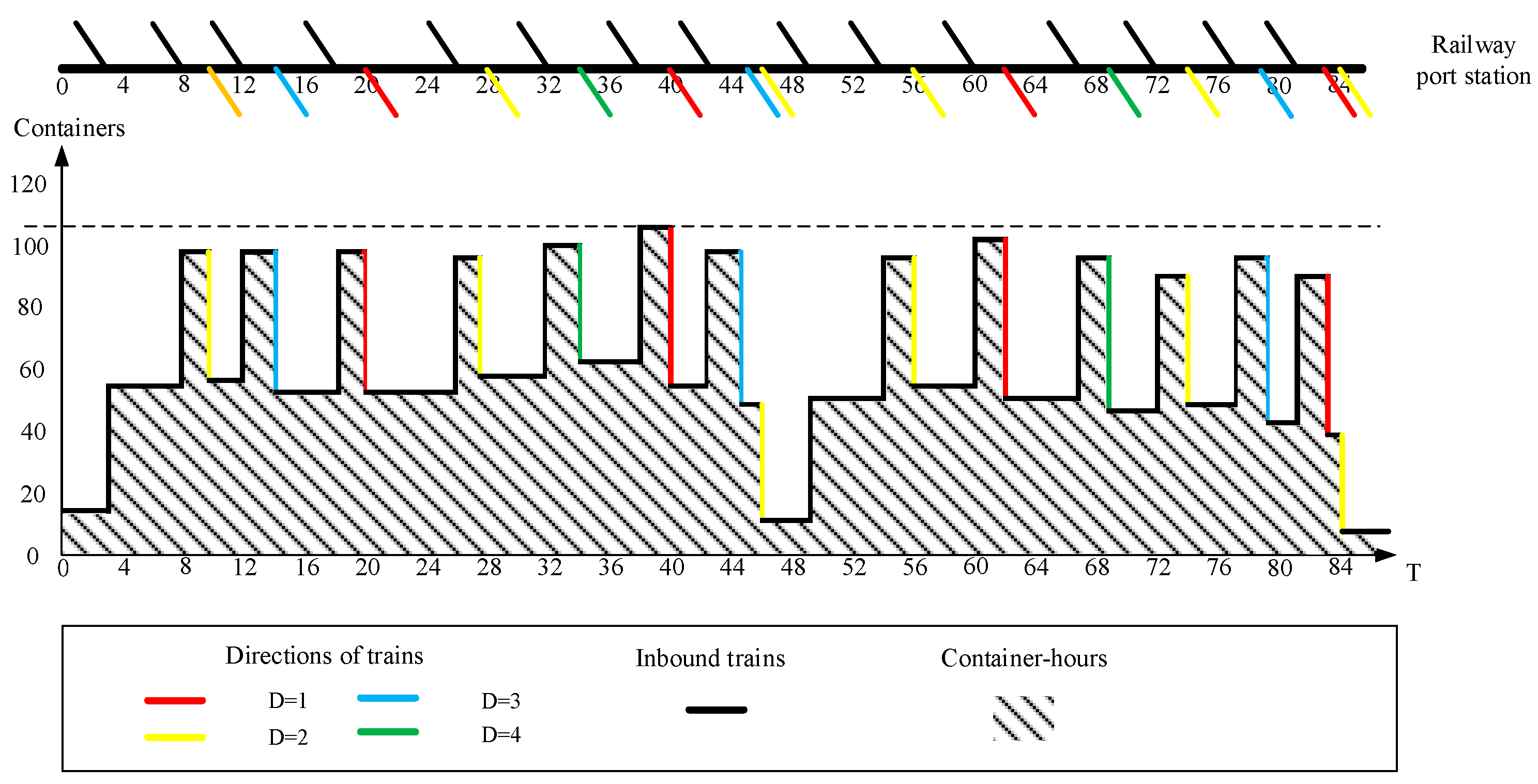
According to the results, when the number of returning trains is 15, the total container-hours is 5390, which is the most optimal solution. Whether increasing or decreasing another returning train, it does not contribute to the total container-hours but results in a rise of average container-hours, as well as a maximum number of temporary storage of containers. To be specific, when one returning train is removed, some containers have to wait to be grouped with trains that do not meet the maximum number of axles. When all the 14 returning trains meet the maximum number of axles, the containers that have not been transported can only be stuck in the storage yard, which leads to the increase of the remaining containers in the storage yard, as well as the total container-hours. In the case of 16 returning trains, some containers have to wait to be grouped as an additional train which fails to be transported in time compared with 15 returning trains. Thus, the distribution organization scheme of 15 returning trains is the most efficient in this experiment and the specific scheme is shown in
Table 7. Corresponding to
Table 7,
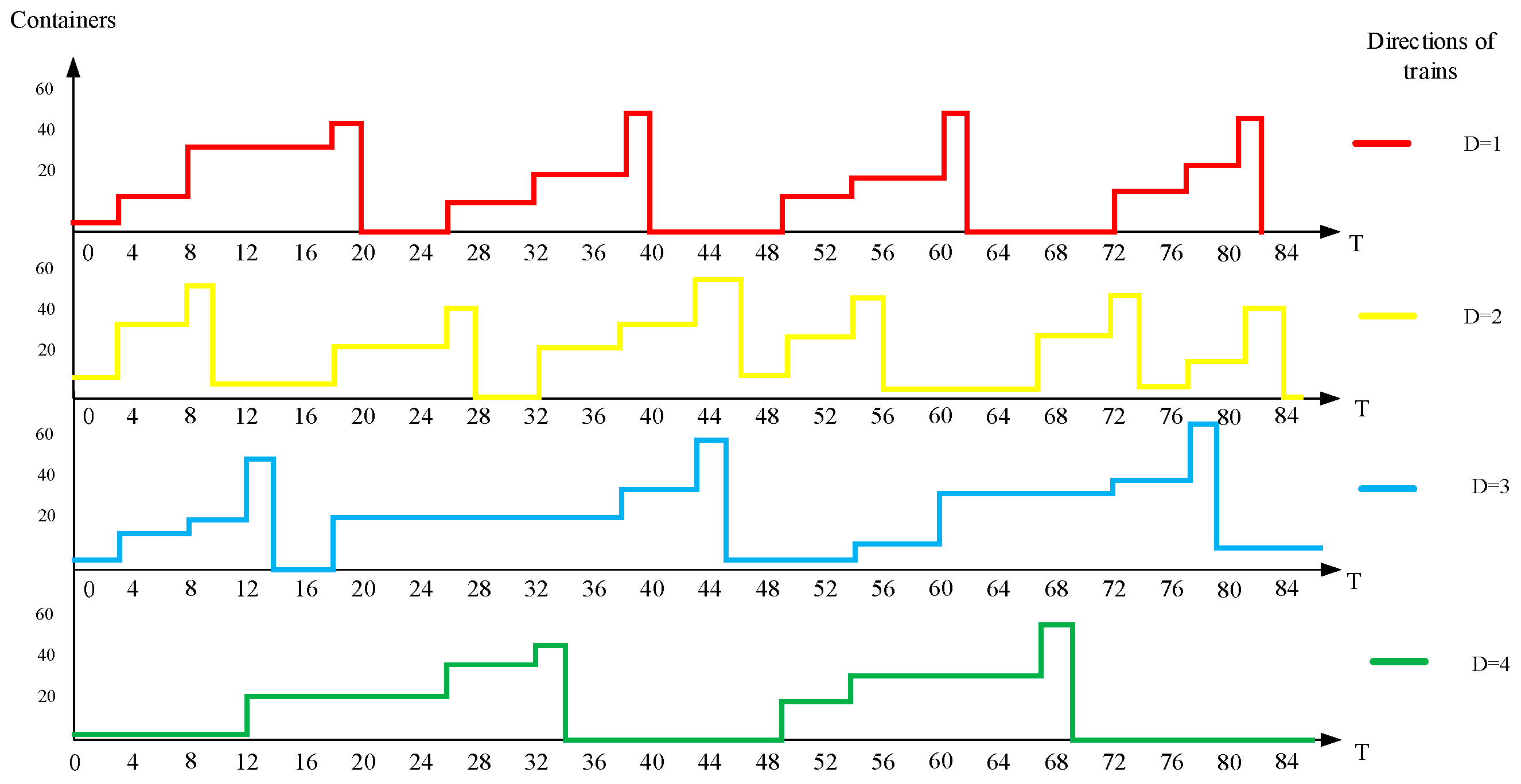
Figure 10 shows the distribution organization scheme in the form of an image and the shaded area represents the total container-hours. In order to directly show the results of the scheme in all directions, we respectively describe the change of container volume with the arrival and departure of trains in
Figure 11.
In assembled transportation organization mode, the containers on each inbound train have different destinations and have to be regrouped and assembled at Alataw Pass railway station, which results in high average container-hours compared with direct transportation organization mode. Therefore, the assembled transportation organization mode may only be applicable to the situation of a large number of inbound trains. The more inbound trains, the shorter the waiting time of the returning train to be regrouped. Through the proposed method, we can obtain the optimal operation scheme of returning trains for the inbound containers with different directions, which is conducive to improve the turnover efficiency of containers. However, this transportation organization mode has been proposed but has not been widely adopted in actual operation of China Railway Express, on account of the independence and poor cooperation between subjects of operation in each city. Therefore, our study cannot be effectively verified in the actual scenario.
5.3. Comparison of Two Modes
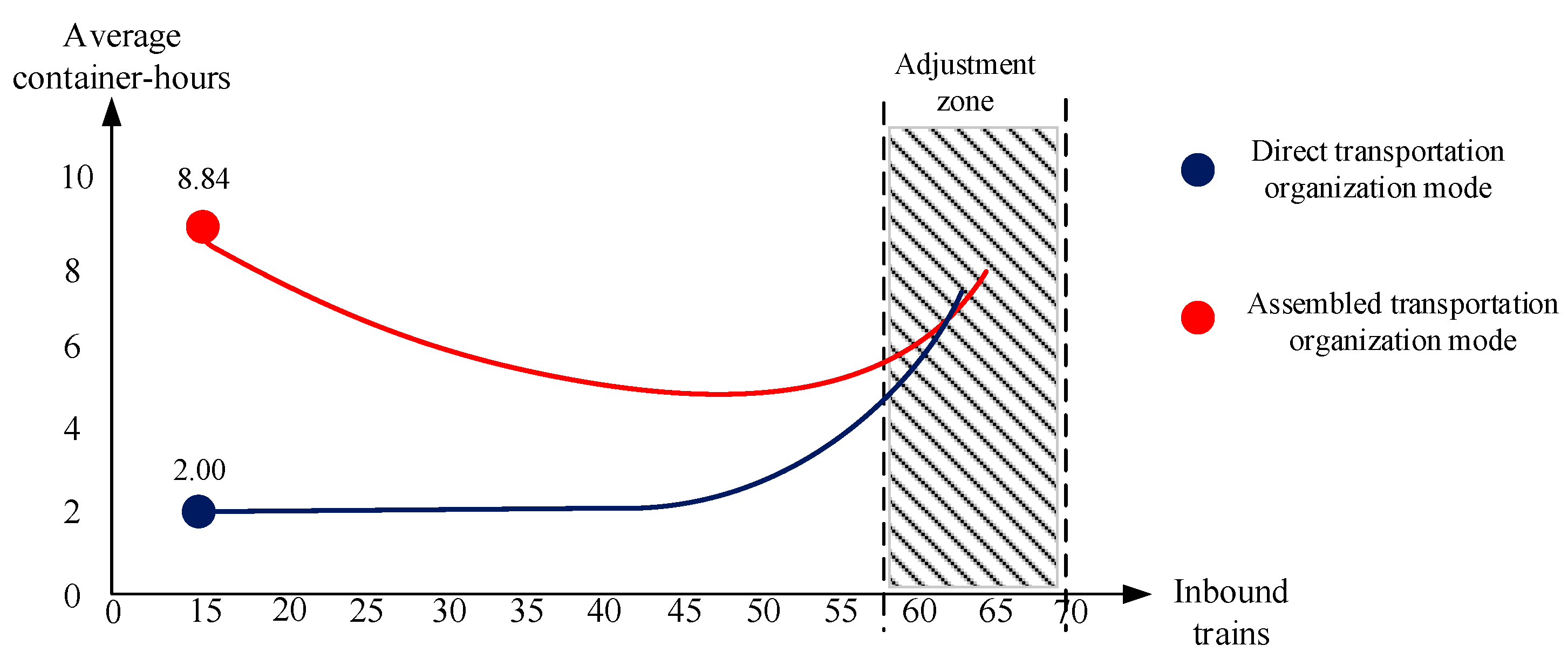
Considering the possible change of transportation organization mode of China Railway Express in the future, we respectively take experiments in the case of direct and assembled modes above. In order to compare the characteristics and differences of two modes, the average container-hours of the direct and assembled transportation organization modes of inbound trains under different orders of magnitude in one period is shown in
Figure 12.
A comparison of the two results reveals that, at first, the average container-hours in the direct transportation organization mode is much lower than that in the assembled transportation organization mode. With the increase of the number of inbound trains arriving at Alataw Pass railway station, the assembled mode starts to take on its own advantages and the average container-hours of two transportation organization modes gradually reach the same level in the adjustment zone, which suggests the possibility to change the transportation organization mode from direct mode to assembled mode.
In the works of [
11], the authors do feasibility analysis of the assembled transportation organization mode but focus on the outbound China Railway Express. Due to the extra loading and unloading operation costs and assembled waiting time, they obtained the conclusion of adopting direct mode through experiments. They analyze the impact of different travel speeds of trains and value of goods on the transportation organization mode, while we focus on the volume. Our experiments show that there is still some room for the development of the direct transportation organization mode of China Railway Express now, which would not be changed in the short term. However, in the long run, when the number of inbound trains reaches a high level, the assembled transportation organization mode would give full play to its advantages. Additionally, it is also helpful to reduce the dependence on government subsidies and promote the sustainable development of China Railway Express [
16].
6. Conclusions
In modern society, the railway is generally regarded as an environmentally-friendly mode of transportation. This paper studies a kind of long-term railway transportation mode with a large volume between developed and developing countries. We pay attention to the distribution organization optimization for inbound China Railway Express with equipment and transshipping time constraints in railway port stations, which may have an important impact on the high-volume and long-distance transportation organization and sustainable development of China Railway Express. In this paper, we formulate this problem in view of the coordination of the operation process and facilities as a mathematical model which is leveraged to develop a genetic algorithm based on container allocation. Then, computational experiments are conducted to show the efficiency and practicality of our model and algorithm. According to the proposed methods, the operation schemes are obtained and the results indicate that the one-to-one transportation organization scheme for the inbound trains in direct transportation organization mode is optimal in the short term, which could improve the turnover efficiency of containers. Furthermore, the assembled transportation organization mode may only be applicable to the situation of a large number of inbound trains in the future, due to the long waiting time of being regrouped. Though the results cannot be effectively verified in the actual scenario, it has reference value for the sustainable development of China Railway Express.
The research on China Railway Express is a long-term process, which needs to keep pace with the development of economics and society. In our current study, the transportation organization efficiency is taken as the optimization objective with no quantitative consideration of environmental assessment. However, the environmental impact may be considered at the operational level, such as crane scheduling, and we will consider incorporating environmental factors (carbon emission, etc.) into the model or establishing a quantitative environmental assessment index in further study. Moreover, the integrated transportation organization optimization of the inbound and outbound China Railway Express is also worthy of study.