Abstract
Under many circumstances, when providing full bus priority methods, urban transport officials have to operate buses in mixed traffic based on their road network limitations. In the case of Istanbul’s Metrobus lane, for instance, when the route comes to the pre-designed Bosphorus Bridge, it has no choice but to merge with highway mixed traffic until it gets to the other side. Much has been written on the relative success of implementing Ramp Metering (RM), for example ALINEA (‘Asservissement line´ aire d’entre´ e autoroutie’) and Variable Speed Limits (VSL), two of the most widely-used “merging congestion” management strategies, in both a separate and combined manner. However, there has been no detailed study regarding the combination of these systems in the face of high bus volume. This being the case, the ultimate goal of this study is to bridge this gap by developing and proposing a combination of VSL and RM strategies in the presence of high bus volume (VSL+ALINEA/B). The proposed model has been coded using microscopic simulation software—VISSIM—and its vehicle actuated programming (VAP) feature; referred to as VisVAP. For current traffic conditions, the proposed model is able to improve total travel time by 9.0%, lower the number of average delays of mixed traffic and buses by 29.1% and 81.5% respectively, increase average speed by 12.7%, boost bottleneck throughout by 2.8%, and lower fuel consumption, Carbon Monoxide (CO), Nitrogen Oxides (NOx), and Volatile Organic Compounds (VOC) emissions by 17.3% compared to the existing “VSL+ALINEA” model. The results of the scenario analysis confirmed that the proposed model is not only able to decrease delay times on the Metrobus system but is also able to improve the adverse effects of high bus volume when subject to adjacent mixed traffic flow along highway sections.
1. Introduction and Background
Nowadays, car-dependent cities with low car occupancy are facing heavy traffic congestion, resulting in delays. A sustainable solution with the aim of increasing transport capacity and decreasing traffic jams simultaneously is the implementation of effective public transport, for example, buses. Furthermore, globally, bus priority methods, for example bus lanes (BL), have become popular for increasing the utilization of bus capacity. City populations and registered vehicle owners are increasing throughout these nations, causing a number of increasingly severe traffic-related issues—congestion, variability in travel time, environmental and noise pollution, natural resource consumption and severe-fatal accident rates [1]. Improved public transport (PT) efficiency not only plays a vital role in mitigating these problems but also affects the successful development of environmentally-friendly urban areas in developing nations [2,3].
1.1. Public Transport Priority—Bus Priority
One possible low-cost measure to improve public transport services is introducing public transport priority (PTP), namely bus priority (BP) measures. BP measures can be clustered into time-based and spatially-based BP schemes [4]. The first of these so-called Transit Signal Priority (TSP) methods provides time-based priority to buses at junctions, while the second form of the method—referred to as spatially-based BP priorities—designates more space for buses, most commonly in the form of bus lanes (BL). BLs can be divided into three sub-classes according to how they are located—curbside, offset, and median. In turn, each of these can be implemented differently in terms of (i) direction of bus movement (parallel with the flow or contra-flow), (ii) separation methods (segregated or unsegregated), and (iii) operational type (static or dynamic).
A number of recent studies have analyzed the introduction and performance evaluation of new BL projects in urban areas, mostly in developed countries [5,6,7,8]. One such study by Chen et al. [7] researched the interaction between buses and general traffic flow by analyzing the variation in lane-changing patterns and driver violations. They found that ‘abnormal’ behaviors saw a 16% reduction in the saturation rate of general traffic and a 17% increase in bus travel times. In addition, increased lane-changing maneuvers close to the Bus Rapid Transit (BRT) stations caused an increase in the downstream queue discharge flows of general traffic.
1.2. Merging Congestion in Highway and Capacity Drop
Once the upstream capacity of a given segment of road exceeds downstream capacity, a bottleneck location is created. A different sense of logic informs the construction of highway bottlenecks. These can include work zones and incidents such as external capacity-reducing events, as well as the merging of on-ramp (merging) areas, lane drops and specific road buildings, for example tunnels and bridges. Bottleneck throughput or bottleneck capacity refers to the maximum number of vehicles that can be crossed over bottleneck location over a given time period, only if the upstream flow rate is smaller than or equal to the bottleneck capacity. However, if a lot of lane-changing behavior takes place or the upstream arrival flow is larger than the bottleneck throughput, congestion will begin spilling back to the upstream. Consequently, the bottleneck only functions below its nominal capacity. Researchers have long observed that capacity, however, is not a static feature of bottlenecks and that there is a reduction in the achievable capacity due to the formation of so-called ‘Capacity Drop.’ The following empirical observations have been made in several studies:
- When a bottleneck is launched, the maximum discharge flow may come to 5–20% less than nominal bottleneck throughput [9,10].
- Upstream queuing and capacity drops in bottleneck areas show a linear correlation with the acceleration process of slowed vehicles crossing the bottleneck location [11].
- There are also a strong associations between lane changing and capacity drop in particular in merging segments [12].
Recently, several congestion control strategies have been proposed and applied such as ramp metering and variable speed limit in order to prevent or shift the beginning of a bottleneck related capacity drop [13,14,15]. These traffic control measures will be discussed in detail in the following sections.
Lighthill and Whitham launched the first general investigation regarding the relationship between lane-changing behaviors and traffic flow conditions [16]. Following this, Munjal et al. evaluated the relationship between lane-changing maneuvers and the speed changes of two vehicles following one another [17]. In addition, by proposing new models in terms of speed, density, flow and lane-changing rate, it was shown that that lane-changing vehicles had remarkable effects on those vehicles following from behind [18,19]. They concluded that one of the important factors in the activation of merging bottlenecks and in capacity drops was the large amount of lane-changing in these areas [20,21,22,23,24].
Weaving and lane-changing at a freeway sections has an important impact on overall freeway performance. Weaving maneuvers can be disruptive to traffic flow depending on prevailing conditions. At a microscopic level, lane changing behavior typically deals with an individual vehicle’s lateral movement process during lane-changing [25,26]. The same can also be extended and modeled from a driver behavior perspective, in which lane-changes are typically first categorized as discretionary or mandatory and then estimated based on numerous traffic, vehicle and driver characteristic variables [27,28,29]. At a macroscopic level, lane-changing can be modeled at an aggregate level as an exchange of flow across lane boundaries as a derivative of either density perturbations between lanes or increased utility due to speed differences [22,30,31].
Lane changing can also be implemented through hybrid models, treating lane changing vehicles as moving bottlenecks with respect to their impact on the target lane [19,32]. Such hybrid models can show how lane changing can lead to capacity drop [33,34]. Jin et al. presented a new framework for modeling the effect of lane changing vehicles on the flow of traffic. Lane changing was treated as an aggregate multi-lane-group process in which all lanes are considered to be balanced in terms of traffic conditions and traffic behavior [22,35].
High bus volume can be considered a standard example of a moving bottleneck. Moving bottlenecks create different traffic conditions upstream and downstream—the upstream traffic in a congested state and downstream traffic freely flowing at a reduced volume. Another consideration is the effect of buses on traffic flow in mixed-use conditions. Buses typically travel slower than cars and could therefore create gaps in the flow of traffic, which in turn may reduce the capacity of the roadway when operating. This effect, which will hereafter be referred to as ‘capacity reduction due to bus presence,’ remains unquantified in the current literature. Giving priority to high bus volume approaching from on-ramp may improve the capacity drop and delay times of all vehicles. However, as can be gathered from existing studies, there has been no detailed research regarding the effects of giving priority to buses movement in highway merging segments. Therefore, the main objective of this study is to analyze the effects of giving priority to bus movements in highway merging segments of adjacent mixed traffic, compared to existing models. To this end, this study aims to develop a combined Variable Speed Limit (VSL) and Ramp Metering (RM) strategy, for example, ALINEA in the presence of high bus volume (hereafter referred to as VSL+ALINEA/B). Thus, the hypothesis that will be evaluated is the terms of the degree to which the integrated VSL+ALINEA/B control model can improve merging segments’ performance on highways in the presence of high bus demand approaching from on-ramp and decrease the average delay for buses and mixed traffic.
The second section of the paper offers the reader some background on the study area (Yıldız merging in Istanbul, Turkey), its microscopic simulation model and calibrated model characteristics. By describing different merging congestion control methods, such as RM and VSL, the third section presents a new integrated VSL+ALINEA/B model to control merging congestion in the presence of high bus volume. It also compares the structural difference between the existing VSL+ALINEA and the proposed VSL+ALINEA/B models. In the fourth section, the performance of the proposed VSL+ALINEA/B model and the analysis results of different scenarios for merging control in the presence of high bus volume are discussed. Finally, in Section 5, the research findings and proposals are made for possible directions for future studies.
2. Study Area and Its Microscopic Simulation Model
In order to test the highways’ merging section control method when faced with high bus volume, one segment of Istanbul’s O–1 Highway—namely the Yıldız junction—was selected as the ideal test site. Due to the distribution of residential and business districts in Istanbul, the majority of Bosporus crossings go from the Asian side to the European side in the morning hours, with the opposite flow appearing in the evening hours [36,37]. This study only considered the latter flow of traffic from the European to the Asian side. As shown in Figure 1, the Yıldız merging area of the O–1 highway consists of three lanes with mixed traffic flow for each direction. A bottleneck area forms at Yıldız junction, where one mixed traffic lane and a Metrobus lane merge into a three-lane main road flow. The driving and lane-changing behavior at this specific section is observably peculiar due to its distinct geometry and traffic composition, in particular the high volume of buses on the ramp.
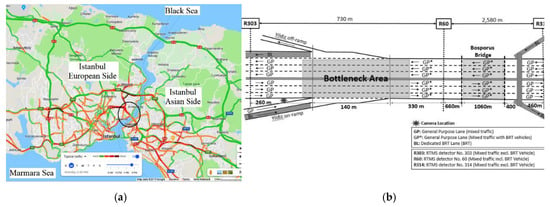
Figure 1.
(a) Bird’s-eye-view of Istanbul’s road network (Google Earth, edited by authors), (b) Layout of Yıldız on-ramp area (note: not to scale).
2.1. Data Collection
There are two Remote Traffic Microwave Sensor (RTMS) devices installed in the upstream (no. 303) and downstream (no. 60) sections of the on-ramp area. The RTMS devices measure volume, occupancy and speed for each two-minute time interval. The five working days of traffic data (13.08.18 – 17.08.18) from the RTMS detectors, provided by Istanbul Metropolitan Municipality—Traffic Control Center, has been analyzed in order to select the start and end points of the merging congestion phenomena during the peak evening hours. In this study, an uncongested-transition-congested flow condition between 2:30 and 3:30 p.m. (see Figure 2) has been modeled by traffic microsimulation software.
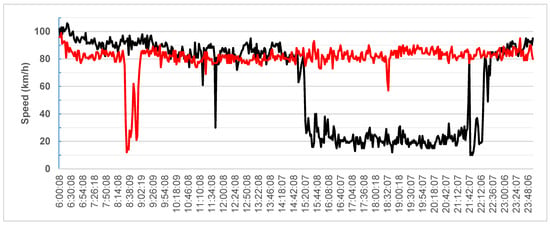
Figure 2.
Average speed changes collected by Remote Traffic Microwave Sensor (RTMS) No. 303 at the Yıldız merging area.
2.2. Existing Traffic Flow Characteristics
Before creating a microsimulation model, traffic modelers need to know the traffic flow characteristics of the case study area. Speed profile over the day represents an accurate schematic of existing traffic flow conditions, saturated and unsaturated conditions. Figure 2 shows the daily traffic speed pattern (black line: avg. flow speed of EU to Asia direction, red line: avg. flow speed of Asia to EU direction) for all the lanes of the study area obtained from detector No. 303 located before the Yıldız merging segment.
In Figure 2, the black line denotes the average speed changes over the course of the day for the crossings from the European to the Asian side, while the grey line shows the average speed changes that occur over the day for crossings from the Asian to the European side. It can be seen that free flow speed could be set to around 100 km/h while the congested flow speed is less than 20 km/h. At the crossings from the European to the Asian side, recurrent traffic congestion begins at around 3:30 p.m. in the afternoon and remains congested until 10:00 p.m. at night, resulting in a significant speed and capacity drop over the study area. The capacity flow is observed at around 1400 veh/h/lane for both directions. During the data collection period, there was recorded neither a reversible lane implementation on the bridge, nor a road re-construction, nor a maintenance project that could possibly affect the data. Based on our observations from the video files, speed reduction in peak hours caused by various reasons, namely the abnormal and aggressive lane-changing behavior of main road drivers facing two merging flows, the shockwave resulting from the entrance of the Bosporus Bridge and later toll payment section. Like many highways around the world, the travel time and delay estimation for this segment is too complex [38,39].
2.3. Study Area Modeling, Calibration and Validation
A microscopic simulation software, VISSIM [40], was used to create a microscopic model of the Yıldız merging area (see Figure 3). We set the following values for the simulation and evaluation attributes. As noted below, the total simulation time (period time) was calculated as 900 + 3600 + 300 = 4800 s. We assumed 900 s as a warm-up at the beginning and 300 s as warm-down time at the end of the simulation period. Data-collection is done for just a 60 min simulation period with a two-minute time interval (120 s) excluding warm-up periods. In order to decrease the simulation time as well, we activated ‘QuickMode’ and ‘UseMaxSimSpeed’ attributes. In order to eliminate stochastic discrepancy, in each scenario ten independent runs with the same initial condition and different seeds were made and the average of the total time were recorded. To this end, the simulation settings are as follows:
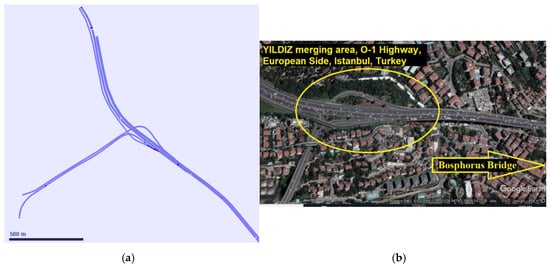
Figure 3.
Modeled study area by VISSIM (a) vs. Bird’s eye view of study area (b), source: Google Earth).
- initial random seed = 40, seed increment = 3, number of runs = 10, step time (resolution) = 10,
- Simulation time = 4800 s with max speed for Simulation (’UseMaxSimSpeed’, true and ’QuickMode’, 1).
2.4. Model Calibration
Although a wealth of microscopic traffic simulation software is available, traffic simulation studies still lack a unified perspective in terms of mimicking real-world conditions. The interactions between each element creates great complexity in microsimulation traffic models. The driving behavior and lane change model parameters have a major effect on the representativeness of the model. Having a fine-tuned and best-matched simulation model, which represents the real-life behavior of drivers, is of pivotal importance to traffic engineers. Thus, before any analysis can take place, models need to be calibrated to be able to represent real-life conditions. An automatic calibration procedure of driving behavior parameters using a metaheuristic algorithm has been proposed previously by the authors [41,42]. In this research, a calibrated model of the study area, which has been previously calibrated and validated by the authors, was used. A brief summary of objective function and calibration results has been discussed below; however, to get detailed information regarding the calibration procedure, please see the authors’ previous work [41,42].
Many single and multi-objective functions have been employee to minimize the error of simulated and observed data. The Root Mean Square Error (RMSE) and the Mean Absolute Normalized Error (MANE) fall among several multi-objective functions used in previous studies for the calibration of simulation model parameters and are widely used around the world. The developed calibration code using Genetic Algorithm (GA), Particle Swarm Optimization (PSO) and their combination (hybrid GAPSO, hybrid PSOGA), can perform the optimization process based on both single (e.g., speed only, volume only, and occupancy rate) and multi-objective functions. In order to decrease the effect of speed differences among the lanes of a main road, a weighted average speed is used in the MANE formula both for target (observed) and simulated speed data. Let us assume that there are three lanes on a main road. In this case, the weighted average speed would calculate based on the exiting traffic volume of each lane:
where
Vw.avg. = (v1*q1 + v2*q2 + v3*q3)/(q1 + q2 + q3)
- Vw.avg: Weighted average speed for n lanes,
- vi: Speed of ith lane of main road, i = (1, 2, …, n),
- qi: Traffic volume of ith lane of main road,
- n: number of lanes of main road (here n = 3).
We tried to minimize the error between simulated and observed data utilizing the MANE and RMSE objective functions formula:
w.r.t the constraints: LbXi ≤ Xi ≤ UbXi
where
- Z: General form of objective function (speed and traffic volume),
- Xi: The vector of continuous parameters (W74 and/or W99 Car following models + Lane-change model parameters),
- LbXi, UbXi: Lower and upper value of parameter Xi (e.g., CC1: Lbcc1 = 0.5 and Ubcc1 = 1.5 s),
- Vtargetj, Stargetj: Target (observed) traffic volume and speed collected by detectors,
- Vsimj, Ssimj: Simulated traffic volume and speed,
- N: Total number of data collection intervals (e.g., for half an hour observation (3600 s) with two minutes’ intervals (120 s), N = 3600/120 = 30).
Table 1 presents the MANE and RMSE values obtained. As noted in Table 1, the simulation with default values of the driving behavior and lane change parameters gave us worse MANE and RMSE values compared to simulations with calibrated parameters using any of the metaheuristic methods examined.

Table 1.
Summary of different objective function values for the optimization problem [41].
It can also be seen that hybrid GAPSO, and hybrid PSOGA algorithms have the best MANE values of 0.35 and 0.36, as well as the best RMSE values of 9.080 and 9.466, respectively. Figure 4 presents the speed profile over a selected time period including the uncongested flow condition (14:30–15:00), transition condition (15:00–15:20), and congested flow condition (>15:20). As shown, the simulated data accounting for the calibrated parameters’ values come to an acceptable fit status, while the simulated data with default parameters’ value shows a large divergence with the observed data in particular in transition and congested traffic conditions.
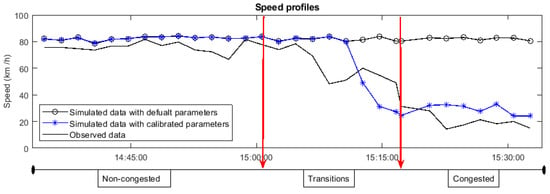
Figure 4.
Speed profiles using default and calibrated parameters’ value [41].
3. Novel and Integrated Ramp Control Model Development
Once the best-matched sets of driving behavior parameters for the study area were obtained through the proposed calibration procedure, it is then time to develop a novel and integrated control model for merging segments of highway in the presence of high bus volume. This section first provides a brief description of merging congestion controls such as VSL and RM methods, which exist globally. Following this, the study will propose a new combination of the VSL+RM model that considers bus volume in the on-ramp area.
3.1. Ramp Metering Control Strategy
RM is one of the most widely used and effective congestion control strategies available, especially when it comes to the merging of congestion on highways during rush hour periods [43]. Essentially, ramp meters consist of a signal head per lane, check-in and check-out sensors, queue override detector on the slip road and upstream and downstream detectors on the main road. One car or two cars in-green-stage RM controls are two commonly used methods globally [44]. RM systems have two main groups, referred to as local RM and coordinated (cooperative, competitive, and integral) RM. In the first category, the metering rates are decided considering local traffic conditions only while the latter uses both local and system-wide traffic information for arranging the metering rate [45]. There are also a few cases in which RM controllers have to provide preferential treatment for high occupancy vehicles (HOV) being tested in United States (US) cities or a bus bypass lane implemented in Utrecht in the Netherlands [46]. The RM controller operates as (i) off-line or open-loop, for example, fixed time ramp meters, (ii) reactive or closed-loop control, for example, real-time ramp meters and iii) proactive or predictive control that utilizes both offline and online traffic information. In this study, a closed-loop local ramp metering strategy, or ALINEA [13]—a well-studied and successful RM control algorithm—has been selected for use in the scenario analysis. The metering rate in ALINEA can be determine by:
where: k: discrete time index (1, 2, …), r(k): ALINEA metering rate at time step k, Oout (k − 1): measured occupancy (%) of downstream in the last time interval, Odes: desired occupancy (%) in downstream and KR: regulator parameter used for adjusting the constant disturbances of the feedback control (veh/h/%). Figure 5 presents a Schematic of the local ramp metering strategy, ALINEA.
r (k) = r (k − 1) + KR [Odes− Oout (k − 1)]
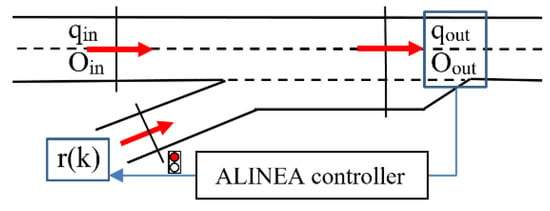
Figure 5.
Schematic of local ramp metering strategy: ALINEA.
According to References [15,47], the calculated metering rate (r) should come to the range (rmin = 200–400 veh/h, rmax = 1800 veh/h) in order to avoid the ramp closure and mainline congestion. KR should also come to a range (KRmin = 50, KRmax = 150) and after several tests showed an optimum value of KR to be 70 veh/h/% for various conditions. They also suggested that the optimum downstream location for detectors is the beginning point of congestion (usually 40 to 500 m). In this study, it is located in 150 m of downstream from the ramp nose. The desired occupancy rate is another important parameter to have accurate ALINEA control model. In this study, ALINEA performance was tested with different desired occupancy rate range (18% to 30%). Odesired = 22% was selected as the desired occupancy rate which is slightly close to the critical (capacity) occupancy in the study area. In addition, to model and implement the ALINEA control model, microsimulation software requires converting the metering rate (r) to the green time of the signal head through the following formula:
g = (r(k)/rsat).C
Here, the rsat: ramp’s saturation flow, c—cycle time and g—green-phase duration (to avoid ramp closure gmin> 0, gmax ≤ c). There are two ramp metering operating conditions; (i) one-car-per-green, and (ii) two or three-car-per-green. In this research, a one-car-per-green ALINEA operation condition has been coded in which one car on-ramp can pass during every green time. Figure 6 illustrates the ALINEA algorithm which has been coded in VisVAP. As shown in the flowchart, the algorithm first checks the number of existing lanes in the mainline (highways), then starts to calculate the metering rate based on the average observed (measured) occupancy rate through downstream detectors. Here, two conditions of ALINEA implementation in the presence of high bus volume has been examined; (1) ALINEA signal is off (no need for ramp control) but there is a bus detected on BL, and (2) ALINEA is on (one-car-per-green ramp metering) and there is a bus detected on BL. If the calculated cycle length is less than 4 s (min. cycle length to activate ramp metering), then the ramp metering signal will be switched off (condition 1). In this condition, the signal will be red only when a bus is approaching from BL (bus check-in detector). When the bus passes the ramp control area (detected by bus check-out detector), the signal will immediately turn off to avoid allocating extra delay to car flow approaching from the ramp. If the calculated cycle length is larger than 4, then the signal will be switched on (condition 2). In this condition, signal will simultaneously consider the mixed traffic flow on ramp and bus flow on BL to provide priority to bus movement once a bus was detected on BL.
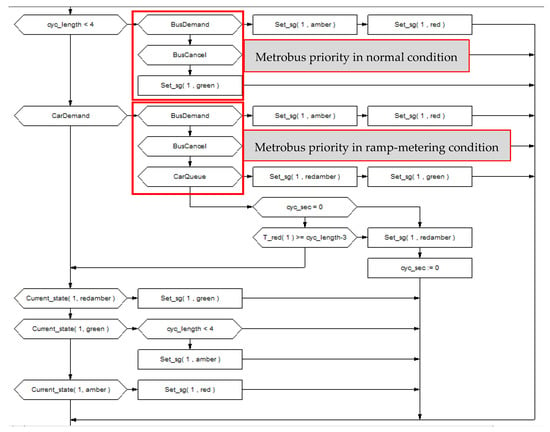
Figure 6.
Flowchart of the modified ALINEA ramp metering considering high bus volume coded in VisVap referred to as ALINEA/B.
3.2. Variable Speed Limit Control
VSL control is another effective congestion management method. All VSL control systems aim to balance traffic speed and homogenize the traffic flow according to current traffic (congestion, incidents) and weather conditions by utilizing the variable speed message [14]. It has also been used for congestion management close to work zones [48,49]. The logic behind of VSL control is that it keeps merging bottleneck throughput close to the bottleneck capacity qb <= qcapacity by creating a congestion discharge segment in the upstream of the merging area. To this end, the VSL system checks the upstream volume in mainline and on-ramp and compares this with bottleneck critical volume (see Table 2).

Table 2.
Assumed parameters value and critical volume for variable speed limit (VSL) design.
If the sum of these volumes exceeds bottleneck capacity, it tries to decrease the speed of approaching vehicles in the upstream of discharge area. It is suggested that the length of this discharge area should range between 500–700 m beginning from the merging nose [50,51]. The location of Variable Message Signs (VMS) in the upstream of the discharge area is another important component of VSL system—in this study, 850 m, due to giving the appropriate reaction time to the driver to adjust their speed based on the desired speed calculated by VSL algorithm.
The required volume and occupancy values can be measured using traffic simulation software through programming the VSL algorithm, or alternatively, can be predicted based on historical data and mathematical models known as Model Predictive Control (MPC). Via MPC, the future condition is predicted based on historical data and the use of mathematical formulas [14]. In this study, VISSIM and VisVAP was used in order to model traffic conditions and to measure the volume and occupancy rate as well as to design a VSL control algorithm. One detector per lane per vehicle class (car, minibus, bus, double-deck bus, and Metrobus) must be defined. The pseudo code below (Algorithm 1) shows the variable speed limit control algorithm developed in this study. Note that vehicle composition in this study contains car, minibus, bus, double-deck bus, and Metrobus figures. For instance, qCar1 to 3 refers to passenger car flow in Lane 1 to 3 of the highway; while qCar4r refers to passenger car flow that exists on-ramp. qCarPrev refers to passenger car flow in previous time intervals.
| Algorithm 1 Variable Speed Limit Control |
| 1: IF NOT initialized THEN |
| 2: initialized := 1; |
| 3: desSpeed := 120; |
| 4: Set Desired Speed to variable message signs; |
| 5: Start (evalInt) |
| 6: ELSE; |
| 7: IF evalInt = 60*DT THEN |
| 8: Collect data via detectors (per vehicle type per lane): |
| qCar1 := Front_ends( 21 ) * 60 / DT; Repeat for qCar2, qCar3, qCar4r |
| qCar := qCar1 + qCar2 + qCar3 + qCar4r; |
| qCarZ := (ALPHA * qCar) + ((1.0 - ALPHA) * qCarPrev); |
| 9: Repeat the same for other vehicle types (minibus, bus, double-deck bus, Metrobus); |
| 10: Clear detectors memory for the next interval; |
| 11: Qb (bottleneck volume) := qCarZ + PCUM*qMinibusZ + PCU*qBusZ + PCU* 1.2*qBus_DoDeck_MetrobusZ; |
| 12: Reset (evalInt); Start (evalInt); |
| 13: IF desSpeed >= 120 THEN |
| 14: IF Qb > QON70 THEN Compare actual Qb with speed limit critical volume (Qbcritical) |
| 15: desSpeed := 70; Set Desired Speed = 70 km/h in variable message signs; |
| 16: ELSE |
| 17: Do it for different desired speed values (100 km/h, 85 km/h, etc.); |
| 18: END |
| 19: END |
| 20: END |
| 21: END |
3.3. Existing VSL+ALINEA Model vs. Proposed VSL+ALINEA/B Model
As mentioned, RM, for example ALINEA and VSL, are two widely used and effective congestion management strategies especially for “merging congestion” of highways. According to a review of the current literature, the implementation of RM and VSL control strategies have been used both separately [52,53,54,55,56] and in a combined manner [57,58,59,60].
Generally, if the mainline upstream flow is too excessive, VSL is used to harmonize upstream flow based on bottleneck capacity or if the on-ramp flow is too heavy, RM control methods are employed. Sometimes, like in the selected study area, there is heavy demand from both mainline and on-ramp that offers a well-implemented solution in the form of a combined VSL and RM approach. There are three general forms of such VSL and RM combinations:
- Determination of metering rate before calculation of VSL values,
- Metering rate and VSL values determined simultaneously,
- Determination of VSL values before metering rate calculation (see Appendix A).
The important factors used in selecting one of the aforementioned combinations of VSL and RM are safety, drivers’ reaction and feedback (in terms of obedience and disobedience) and model complexity. The programming and code development of the first and third combination models is supposed to be simple while the second combination requires very complex programming to calculate the metering rate and VSL values at the same time.
The third model was selected to use in this study. Frequent speed changes based on pre-determined metering rates may confuse/bother drivers (first combination model) resulting in disobedience or safety level reduction in the mainline, while the calculation of a suitable metering rate based on pre-determined critical VSL can be more feasible to implement.
Having looked at the increase in using spatial bus priority schemes in recent years [4], giving priority to buses in highways on-ramp area has become a potential issue that should be evaluated. As mentioned in section one, bus lanes can be effective if implemented successfully along both roads and at junctions.
Moreover, the implementation of VSL-only, ALINEA-only control benefits transport officials to improve the mainline (highway). In the Yıldız merging area in which there are several conflicts between three kinds of flows—namely, mainline (highway), on-ramp, and buses—it is necessary to have an integrated model which is able to control all interactions.
Based on observations of the study area, numerous buses (and their very long length in the Istanbul Metrobus case) directly affects driving behavior in the mainline as well as on-ramp flow. The more lane changing, especially in merging points along urban highways, the more the capacity drops in these areas. Moreover, as mentioned in Section 1, it was found that the literature was lacking a detailed study regarding the combination of these systems considering the issue of high bus demand.
Therefore, the ultimate goal of this study is to address the gap in the literature by developing and proposing a combination of VSL and RM strategies in the face of high bus volume (e.g., Metrobus vehicles in Yıldız merging segment).
To this end, first, the third model of integrated VSL+RM, that is, the algorithm, begins with a calculation and determination of VSL, before calculating the metering rate. The demand detectors are located in dedicated BL in order to record BP requests and to send them to the ALINEA controller. The ALINEA controller calculates a suitable metering rate for on-ramp vehicles considering:
- the measured occupancy in the mainline (which is improved by VSL),
- desired occupancy rate (defined by user), and
- priority request calling by approaching buses from bus lane.
Figure 7 shows the procedure of the integrated VSL+ALINEA model modified for the high bus volume. The integrated VSL and ALINEA model accounts for high bus volume, has been coded and will be applied to the calibrated model through the VisVAP. Various scenarios —namely (i) no control, (ii) with control (ALINEA, VSL, VSL+ALINEA, and VSL+ALINEA/B)—will be tested with the calibrated model of the study area in order to evaluate the proposed model efficiency.
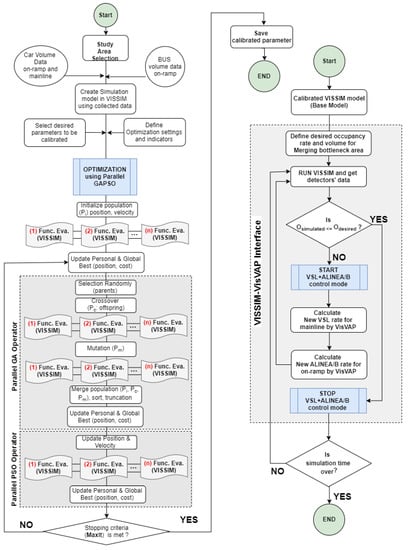
Figure 7.
Flowchart of the proposed model (integrated VSL and ALINEA/B).
4. Results and Discussions
This section discusses the results of various scenarios implemented upon the merging congestion area in the face of bus volumes. First, it describes the VSL+ALINEA/B model features implemented on study area, that is, the Yıldız merging area. Then, it examines the effectiveness of the proposed VSL+ALINEA/B model compared to the existing merging congestion control methods such as ALINEA ramp metering, VSL and VSL+ALINEA.
Figure 8 depicts the schematic of the VSL+ALINEA/B model designed for the Yıldız merging area of the O–1 highway in Istanbul. As shown, it consists of all required equipment for implementing VSL and ALINEA control models, as well as detecting buses approaching the merging area from a dedicated Metrobus lane. VSL detectors are located in the upstream of the bottleneck a distance of 700 m from the ramp nose to dynamically balance the speed of upstream flow in the mainline vis-à-vis the condition of the bottleneck. There are also VSL signs located in the downstream of the bottleneck designed in order to assign the desired speed values to all vehicles.
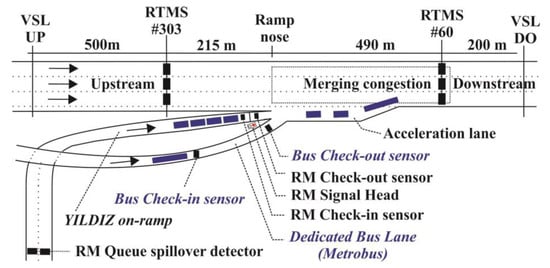
Figure 8.
Layout of the VSL+ALINEA/B model designed for the Yıldız merging area of the Istanbul’s O-1 highway (note: not to scale).
Two detectors are located in a dedicated Metrobus lane to detect approaching and departing buses. These are shown in the figure above as a bus check-in sensor and a check-out sensor. To detect and control mixed traffic coming from the ramp, ALINEA’s detectors—namely a queue spillover detector, car check-in and check-out detector are located along the Yıldız on-ramp.
Several performance measures were used to forge a precise comparison among existing merging congestion control models and the proposed VSL+ALINEA/B model. These performance measures include total travel time (sec), total travelled distance (km), average delay (sec), average speed (km/h), occupancy rate changes, bottleneck throughput (capacity), fuel consumption (liter) and emissions (grams). All results are the average of ten runs with different random seeds to decrease stochastic effects, as described in Section 2.3.
4.1. Total Travel Time
Total travel time (seconds) is the sum of the travel time of vehicles traveling within the network or that have already left the network. In general, for the whole network, the proposed VSL+ALINEA/B model can decrease total travel time by 27.6% and 9.0% compared to the No-Control scenario and the existing VSL+ALINEA model, respectively. The bar chart in Figure 9 illustrates the total travel time changes of cars according to different scenarios. It can be seen that the No-Control scenario has the highest value with big difference, while the results of other scenarios are quite similar. For cars, the proposed VSL+ALINEA/B model is able to decrease total travel time by 27.4% and 8.7% compared to No-Control scenario and the existing VSL+ALINEA model, respectively. While for Metrobus vehicles, these improvements are 28.2% and 19.0%, respectively. Detailed information regarding total travel time, total distance travelled with their corresponding statistical t-test values obtained through different scenarios can be found in Appendix A; Table A1, Figure A1, and Figure A2.
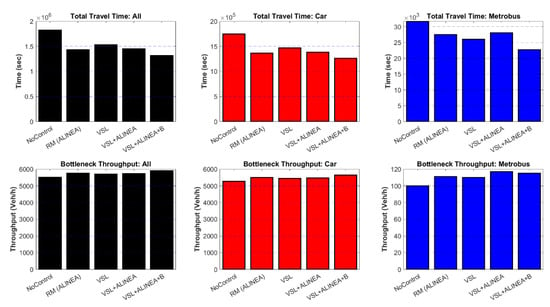
Figure 9.
The total travel time and bottleneck throughput changes of all vehicle, car, and bus in different scenarios.
4.2. Bottleneck Throughput (Capacity)
In general, for the entire network, the proposed VSL+ALINEA/B model can increase bottleneck throughput by 7.2% and 2.8% compared to the No-Control scenario and the existing VSL+ALINEA model respectively. Figure 9 also shows the bottleneck throughput of cars and buses according to various scenarios. No-Control scenario has the lowest car (5271 veh/h) and bus (100 bus/h) throughput by a larger divergence, while the proposed VSL+ALINEA/B model has the car (5644 veh/h) and bus (115 bus/h) throughput by 7.1% and 15.0% respectively. Having looked at Figure 9, it is obvious that VSL+ALINEA/B model outperformed VSL+ALINEA in terms of only car throughput, while both models have almost the same Metrobus throughput at bottleneck area.
4.3. Average Delay and Number of Stops
Table 3 gives a summary of the average delays and the number of stops in the network for various scenarios. The proposed VSL+ALINEA/B model is able to decrease the average amount of vehicle delays and total number of stops compared to the No-Control scenario by 67.1% and 50.8% respectively. Compared to the existing VSL+ALINEA model, it improves average delays and the number of stops by 29.1% and 18.4%, respectively, by decreasing the interaction between cars and buses.

Table 3.
Average delays and stops among scenarios.
The number of stops can be an appropriate performance measures representing the stop-and-go shockwaves in the network. As seen in the Table above, the number of stops for both cars and buses have been significantly decreased by 17.6% and 92.4%, respectively meaning that the network performance has been improved in terms of stop-and-go shockwaves, too. Not only does VSL+ALINEA improve the average delays and stops for buses, but also benefits cars by reducing their interaction with buses—in Yıldız ramp area in particular—for instance, in terms of conflicts between Metrobus and on-ramp flow. Figure 10 compares the average delay of cars and Metrobus according to various scenarios. The No-Control scenario for cars has the highest value, with a larger divergence than in other scenarios, while for Metrobus average delays are almost similar to ALINEA scenario. As is clear, the proposed VSL+ALINEA/B model has the lowest number of average delays in both cases cars and Metrobus compared to VSL+ALINEA which buses not having been considered. Detailed information regarding average delay and speed of the various models can be found in Appendix A (Figure A3, Figure A4, and Table A2). Statistical t-test (p-value) of VSL+ALINEA/B model given in Appendix has also better values among various scenarios.
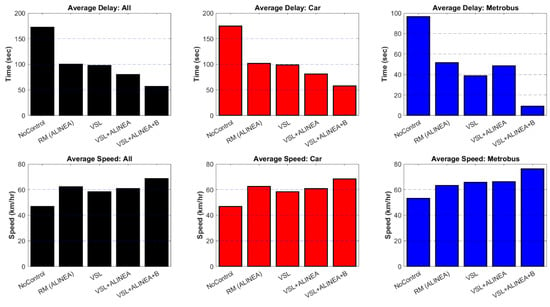
Figure 10.
Average delay and speed changes of cars and buses among different scenarios.
4.4. Spatio-Temporal Effects
4.4.1. Average Speed Changes
The average speed of the entire network is another important measure that must be considered. The bar chart in Figure 11 depicts the average speed changes of cars and the Metrobus according to the various scenarios. The No-Control scenario for both cars and the Metrobus has the lowest value by 47 and 53 km/h, respectively – with a clear divergence compared to other scenarios. The proposed VSL+ALINEA/B model has the highest average speed in both cases; cars (69 km/h) and Metrobus (76 km/h) than VSL+ALINEA, which means a better result for the proposed model. Concerning average speed changes, Figure 11 also illustrates the speed heat-map of the entire network for all vehicles in which Y-axis represents the study area divided into four segments. These are namely upstream, merging, bottleneck and downstream segments and various scenarios. The x-axis represents the simulation time (minutes) of the study area.
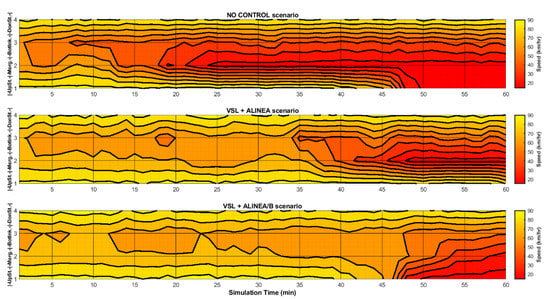
Figure 11.
Speed heat-map of the entire network for all vehicles.
As clearly seen below, the proposed VSL+ALINEA/B model is able to shift the merging congestion to the upstream position of the ramp nose (see Figure 11). It outperformed No-Control and the existing VSL+ALINEA model by providing the highest average speed in all four segments of the study area, particularly in merging and bottleneck areas.
4.4.2. Occupancy Rate Changes
The occupancy rate of the entire network as the calculation basis of the ALINEA control model is another important measure which must be considered. To this end, Figure 12 proposes the occupancy spatio-temporal graph of the entire network for all vehicles in which the Y-axis represents the study area divided into four segments. These are namely upstream, merging, bottleneck, and downstream segments and various scenarios. The x-axis represents the simulation time (minutes) of the study area.
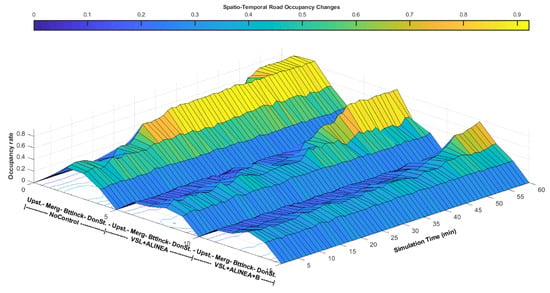
Figure 12.
Spatio-temporal graph of road occupancy of the entire network for all vehicles.
The main goal of the proposed VSL+ALINEA/B model is to decrease the occupancy rate both in value and time intervals as well as to shift potential merging congestion to the upstream of the mainline. It benefits the bottleneck area to have the highest volume close to capacity. The spatio-temporal graph above demonstrates that the proposed VSL+ALINEA/B model outperformed No-Control and the existing VSL+ALINEA model by providing the lowest occupancy rate during time intervals (SimTime) over all four segments of the study area in particular in merging and bottleneck areas.
4.5. Fuel Consumption and Emissions
In terms of sustainable and energy-efficient transport system options, fuel consumption and air-pollution relevant emission created by different models is another important performance measure which must be discussed. VERSIT+ exhaust emissions model from TNO [61] is used to calculate the fuel consumption and emission in the study area. Speed, acceleration, and weight of vehicles, location, and grade of road are the main affecting variables ae the inputs of the model. This model, first, calculates the propulsion energy of a vehicle, then estimates the corresponding fuel consumption, and lastly calculate the corresponding emission from fuel consumption using road traffic emission factors (in g/kg of fuel). Table 4 summarizes the results of fuel consumption (see also Figure 13) and emissions namely Carbon Monoxide (CO), Nitrogen Oxides (NOx), and Volatile Organic Compounds (VOC) produced by different scenarios (see also Figure 14). As seen in the Table below, the proposed model is able to reduce fuel consumption and emissions by 89.0% and 58.3%, respectively compared to No-Control scenario and by 78.2% and 17.3% compared to the existing VSL+ALINEA model.

Table 4.
Fuel consumption and Emissions summary.
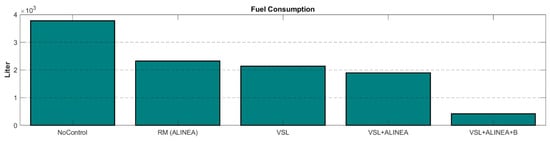
Figure 13.
Fuel consumption produced by various scenarios.
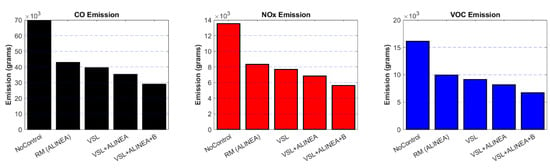
Figure 14.
Emissions (CO, NOx, VOC) produced by various scenarios.
Moreover, it gives the level of service (LOS) values obtained by different scenarios. The No-Control scenario showed the worst LOS (F), while the proposed scenario, VSL+ALINEA/B provides the highest LOS (C) compared to the other scenarios, namely ALINEA (LOS D) and even the VSL+ALINEA scenario with LOS D, which confirmed the superior performance of the proposed model. Detailed information regarding fuel consumption and emissions with their corresponding statistical t-test values produced by various scenarios can be found in Appendix A, Table A3.
Overall, the proposed VSL+ALINEA/B model has a better and acceptable result compared to all the existing models like VSL+ALINEA in terms of current traffic condition as approved by performance measures.
5. Conclusions
As can be found in the existing studies, the VSL+ALINEA model have a better performance than VSL-only and RM-only models in terms of overcoming congestion on the merging segments of highways. However, the VSL+ALINEA model performance in the presence of high bus volume approaching from the on-ramp has not yet been studied. The main objective of the current study was to find a model that works to address the limitations of the existing VSL+ALINEA model in the presence of high bus volume on-ramp. To this end, this paper presents a novel integrated VSL and ALINEA model, or the VSL+ALINEA/B model. This model has been coded and applied to the calibrated microscopic simulation model of the study area. Various scenarios, namely (i) no-control, (ii) with control (ALINEA, VSL, VSL+ALINEA, VSL+ALINEA/B) have been tested. The total travel time, total travelled distance, average delay, average speed, occupancy rate changes, bottleneck throughput, fuel consumption, and emissions were calculated for each scenario. The results of these scenario analyses showed that the proposed VSL+ALINEA/B is able to improve network performance as superior to the existing VSL+ALINEA model. The percentage values given for the performance measures below are the summary of obtained improvements gained from the VSL+ALINEA/B model compared to the existing VSL+ALINEA model:
- Total travel time by 9.0%,
- Average delays of mixed traffic and buses by 29.1% and 81.5% respectively,
- Average speed by 12.7%,
- Bottleneck throughout (capacity) by 2.8%,
- Level of service value achieved for bottleneck area: LOS C (was LOS D),
- Fuel consumption, and Emissions by 78.2%, and 17.3%, respectively.
Further research should address the following limitations of the proposed model:
- In the development of the proposed VSL+ALINEA/B model, the set of parameters used inside the VSL and ALINEA algorithms has been obtained manually after testing several sets of parameters. The development of an automatic optimization process inside the model in order to find the best sets of parameters for VSL and ALINEA remains as a potential extension of the proposed model.
- The proposed VSL+ALINEA/B model has been tested as a local on-ramp control method which can be extended and tested on a large network with several merging points.
- In this study, VISSIM software has been used to model the network, as we already have a thesis-base unlimited license to use it. However, the proposed model should be also checked using open source traffic simulation software, such as SUMO [62] considering its potential application in modeling of various traffic management scenarios [63,64].
Author Contributions
Conceptualization, N.D. and M.E.; formal analysis, N.D.; investigation, N.D., M.E.; resources, N.D., M.E.; data curation, N.D.; methodology, N.D. and M.E.; software, N.D.; validation, N.D., M.E.; visualization, N.D.; writing—original draft preparation, N.D.; writing—review and editing, M.E.; supervision, M.E.
Funding
This research received no external funding.
Acknowledgments
This study is a part of Ph.D. thesis of corresponding author from Istanbul Technical University, Turkey. We would like to thank Marijan Žura of the Traffic Technical Institute, UL-FGG (Slovenia) and Ali Sercan Kesten of Işık University (Turkey) for their kind support, valuable comments, and helpful suggestions. Authors would also like to thank the PTV-AG Karlsruhe Company for providing a thesis-based unlimited version of the VISSIM software.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
All performance measures (total travel time, total travelled distance, total delay, avg. delay, total speed, avg. speed, demand latent, and delay latent) at a network level take into account the vehicles which have already left the network and the vehicles that are still in the network at the end of the evaluation interval. The total demand of the input flows and origin-destination matrices during the simulation time results from:
Total = Vehicles in Network + vehicles which have left + vehicles which could not be used (immediately)
TTT: Total travel time (second) of vehicles traveling within the network or that have already left the network.
DistTot: Total distance travelled (km) by all vehicles in the network or of those that have already exited it.

Table A1.
Network performance results (Total Travel Time, Total Distance Travelled).
Table A1.
Network performance results (Total Travel Time, Total Distance Travelled).
| Scenario | TTT (ALL) | TTT (Car) | TTT (Metrobus) | DistTot (ALL) | DistTot (Car) | DistTot (Metrobus) | |
|---|---|---|---|---|---|---|---|
| No-Control | Avg. | 1,823,292 | 1,744,101 | 31,706 | 23,489 | 22,460 | 436 |
| No-Control | StnDev | 218,463 | 211,555 | 4529 | 480 | 477 | 36 |
| RM (ALINEA) | Avg. | 1,434,003 | 1,369,362 | 27,517 | 24,537 | 23,449 | 472 |
| RM (ALINEA) | StnDev | 122,630 | 117,737 | 3215 | 269 | 279 | 25 |
| RM (ALINEA) | p-value | 0.0699 | 0.0766 | 0.0387 | 0.0374 | 0.0483 | 0.4801 |
| RM (ALINEA) | Improve (%) | 21.4% | 21.5% | 13.2% | −4.5% | −4.4% | −8.2% |
| VSL | Avg. | 1,534,063 | 1,467,953 | 26,012 | 24,287 | 23,208 | 472 |
| VSL | StnDev | 137,064 | 131,570 | 2643 | 514 | 524 | 23 |
| VSL | p-value | 0.0292 | 0.0321 | 0.0161 | 0.0040 | 0.0055 | 0.5497 |
| VSL | Improve (%) | 15.9% | 15.8% | 18.0% | −3.4% | −3.3% | −8.2% |
| VSL+ALINEA | Avg. | 1,450,319 | 1,385,314 | 28,086 | 24,501 | 23,397 | 489 |
| VSL+ALINEA | StnDev | 172,769 | 168,220 | 1190 | 645 | 643 | 23 |
| VSL+ALINEA | p-value | 0.2087 | 0.2368 | 0.0024 | 0.0477 | 0.0580 | 0.4322 |
| VSL+ALINEA | Improve (%) | 20.5% | 20.6% | 11.4% | −4.3% | −4.2% | −12.0% |
| VSL+ALINEA/B | Avg. | 1,320,331 | 1,265,431 | 22,761 | 25,082 | 23,986 | 482 |
| VSL+ALINEA/B | StnDev | 78,948 | 78,720 | 698 | 261 | 241 | 13 |
| VSL+ALINEA/B | p-value | 0.0749 | 0.0929 | 0.0006 | 0.0030 | 0.0042 | 0.1316 |
| VSL+ALINEA/B | Improve (%) | 27.6% | 27.4% | 28.2% | −6.8% | −6.8% | −10.4% |
Bold: The average value of each scenario.
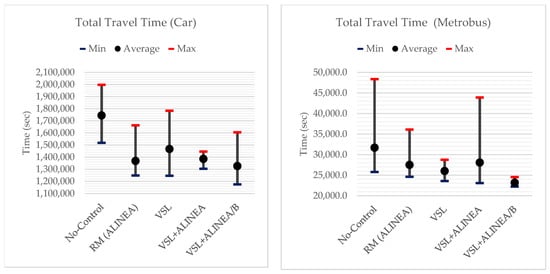
Figure A1.
Avg., Min. and Max of Total Travel Time for Car and Metrobus based on different scenarios.
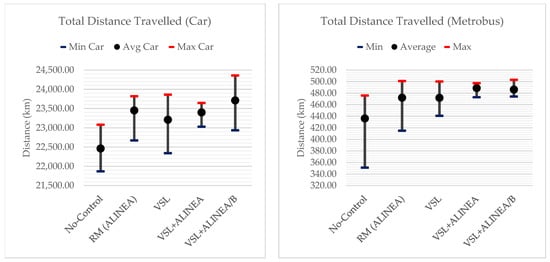
Figure A2.
Avg., Min. and Max of Total Distance Travelled by Car and Metrobus based on different scenarios.
VehAct (vehicles active) vs. VehArr (vehicles arrived): Total number of vehicles in the network at the end of the simulation. VehArr and vehicles not being used are not included in the attribute VehAct.
SpeedAvg: Average speed [km/h] can be calculated via:
SpeedAvg = Total distance DistTot/Total travel time TravTmTot
StopsTot: Total number of stops of all vehicles that are in the network or have already arrived.
StopsAvg: Average number of stops per vehicle can be calculated via:
StopsAvg = Total number of stops/(Number of veh in network + number of veh that have arrived)
DelayTot: Total delay of all vehicles in the network or of those that have already exited it. For the calculation, the quotient is obtained by subtracting the actual distance traveled in this time step and desired speed from the duration of the time step.
DelayAvg: Average delay per vehicle can be calculated via:
DelayAvg = Total delay/(Number of veh in the network + number of veh that have arrived)

Table A2.
Network performance results (Speed and Delay).
Table A2.
Network performance results (Speed and Delay).
| Scenario | Avg. Speed (All) | Avg. Speed Car | Avg. Speed Metrob | Avg. Delay (All) | Avg. Delay Car | Avg. Delay Metrob | Total Delay (All) | Total Delay Car | Total Delay Metrob | |
|---|---|---|---|---|---|---|---|---|---|---|
| No-Control | Avg. | 47 | 47 | 53 | 172 | 174 | 96 | 1,077,418 | 1,043,186 | 12,050 |
| No-Control | StnDev | 10 | 11 | 9 | 37 | 38 | 39 | 232,189 | 225,128 | 4991 |
| RM (ALINEA) | Avg. | 62 | 62 | 63 | 100 | 102 | 51 | 647,542 | 630,536 | 6275 |
| RM (ALINEA) | StnDev | 7 | 7 | 8 | 19.87 | 20.22 | 26.30 | 129,389 | 125,217 | 3318 |
| RM (ALINEA) | p-value | 0.077 | 0.089 | 0.021 | 0.053 | 0.060 | 0.029 | 0.055 | 0.062 | 0.034 |
| RM (ALINEA) | Improve (%) | 33.1% | 33.3% | 18.7% | 42.0% | 41.7% | 46.7% | 39.9% | 39.6% | 47.9% |
| VSL | Avg. | 58 | 58 | 66 | 98 | 99 | 39 | 623,657 | 604,705 | 4770 |
| VSL | StnDev | 8 | 8 | 8 | 25.80 | 26.23 | 25.34 | 162,134 | 156,885 | 3204 |
| VSL | p-value | 0.017 | 0.020 | 0.010 | 0.0008 | 0.0008 | 0.016 | 0.0007 | 0.0007 | 0.019 |
| VSL | Improve (%) | 24.7% | 24.6% | 23.4% | 43.3% | 43.2% | 59.9% | 42.1% | 42.0% | 60.4% |
| VSL+ALINEA | Avg. | 61 | 61 | 66 | 80 | 81 | 48 | 521,289 | 504,606 | 6106 |
| VSL+ALINEA | StnDev | 9 | 10 | 6 | 30.91 | 31.58 | 15.78 | 198,311 | 193,479 | 1894 |
| VSL+ALINEA | p-value | 0.175 | 0.202 | 0.0005 | 0.008 | 0.009 | 0.002 | 0.008 | 0.009 | 0.002 |
| VSL+ALINEA | Improve (%) | 30.0% | 30.0% | 24.5% | 53.6% | 53.6% | 49.9% | 51.6% | 51.6% | 49.3% |
| VSL+ALINEA/B | Avg. | 69 | 69 | 76 | 57 | 58 | 9 | 369,980 | 363,018 | 1085 |
| VSL+ALINEA/B | StnDev | 5 | 5 | 1 | 13.34 | 13.66 | 2.03 | 86,905 | 85,468 | 258 |
| VSL+ALINEA/B | p-value | 0.071 | 0.097 | 0.00005 | 0.001 | 0.002 | 0.0004 | 0.002 | 0.002 | 0.001 |
| VSL+ALINEA/B | Improve (%) | 46.5% | 46.2% | 43.1% | 67.1% | 66.7% | 90.7% | 65.7% | 65.2% | 91.0% |
Bold: The average value of each scenario.
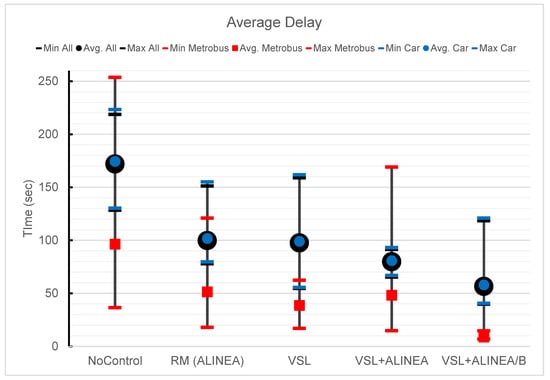
Figure A3.
Avg., Min. and Max Delay based on different scenarios.
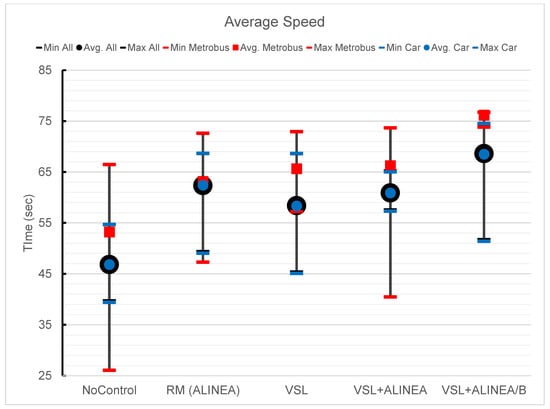
Figure A4.
Avg., Min. and Max Speed based on different scenarios.

Table A3.
Node (Merging segment) performance results.
Table A3.
Node (Merging segment) performance results.
| Scenarios | LOS (ALL) | # of All Veh. | # of Car | # of Metrobus | FUEL CONS. | EMIS. CO | EMIS. NOX | EMIS. VOC | |
|---|---|---|---|---|---|---|---|---|---|
| No-Control | Avg. | LOS F | 5509 | 5271 | 100 | 3770 | 69,613 | 13,544 | 16,133 |
| No-Control | StnDev | 112 | 112 | 11 | 146 | 10,271 | 1998 | 2380 | |
| RM (ALINEA) | Avg. | LOS D | 5759 | 5504 | 111 | 2319 | 42,822 | 8332 | 9925 |
| RM (ALINEA) | StnDev | 71 | 72 | 7 | 125.27 | 8756 | 1703 | 2029 | |
| RM (ALINEA) | p-value | 0.0362 | 0.0510 | 0.394 | 0.273 | 0.273 | 0.273 | 0.273 | |
| RM (ALINEA) | Improve (%) | −0.05 | −0.04 | −0.11 | 0.38 | 0.38 | 0.38 | 0.38 | |
| VSL | Avg. | LOS D | 5692 | 5439 | 110 | 2140 | 39,511 | 7687 | 9157 |
| VSL | StnDev | 131 | 132.00 | 7 | 130 | 9142 | 1778 | 2118 | |
| VSL | p-value | 0.0028 | 0.0039 | 0.573 | 0.003 | 0.003 | 0.003 | 0.003 | |
| VSL | Improve (%) | −0.03 | −0.03 | −0.10 | 0.43 | 0.43 | 0.43 | 0.43 | |
| VSL+ALINEA | Avg. | LOS D | 5741 | 5481 | 117 | 1902 | 35,114 | 6832 | 8138 |
| VSL+ALINEA | StnDev | 169 | 166 | 7 | 175 | 12,253 | 2384 | 2839 | |
| VSL+ALINEA | p-value | 0.0347 | 0.0422 | 0.494 | 0.173 | 0.173 | 0.173 | 0.173 | |
| VSL+ALINEA | Improve (%) | 4% | 4% | 1.7% | 0.50 | 0.50 | 0.50 | 0.50 | |
| VSL+ALINEA/B | Avg. | LOS C | 5904 | 5644 | 115 | 415 | 29,024 | 5647 | 6726 |
| VSL+ALINEA/B | StnDev | 75 | 71 | 3 | 132 | 9289 | 1807 | 2153 | |
| VSL+ALINEA/B | p-value | 0.001 | 0.002 | 0.120 | 0.144 | 0.144 | 0.144 | 0.144 | |
| VSL+ALINEA/B | Improve (%) | 7.2% | 7.1% | 15.0% | 89.0% | 58.3% | 58.3% | 58.3% | |
Bold: The average value of each scenario.
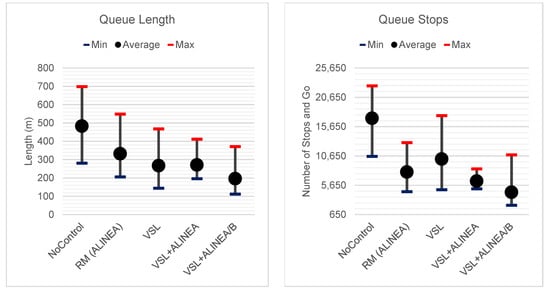
Figure A5.
Avg., Min. and Max Queue Length and Number of Stop-and-Go based on different scenarios.
References
- Beirão, G.; Cabral, J.S. Understanding attitudes towards public transport and private car: A qualitative study. Transp. Policy 2007, 14, 478–489. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Delgado, F.; Giesen, R.; Munoz, J.C. Planning, operation, and control of bus transport systems: A literature review. Transp. Res. Part B Methodol. 2015, 77, 38–75. [Google Scholar] [CrossRef]
- Kogdenko, N. Successfulness of Bus Rapid Transit Systems in Asia Ex-Post Evaluation; Master‘s Thesis, University of Groningen: Groningen, The Netherlands, 2011. [Google Scholar]
- Dadashzadeh, N.; Ergun, M. Spatial bus priority schemes, implementation challenges and needs: An overview and directions for future studies. Public Transp. 2018, 10, 545–570. [Google Scholar] [CrossRef]
- Safran, J.; Beaton, E.; Thompson, R. Factors Contributing to Bus Lane Obstruction and Usage in New York City. Transp. Res. Rec. J. Transp. Res. Board 2014, 2418, 58–65. [Google Scholar] [CrossRef]
- Xu, H.; Zheng, M. Impact of Bus-Only Lane Location on the Development and Performance of the Logic Rule-Based Bus Rapid Transit Signal Priority. J. Transp. Eng. 2012, 138, 293–314. [Google Scholar] [CrossRef]
- Chen, X.M.; Li, Z.; Jiang, H.; Li, M. Investigations of interactions between bus rapid transit and general traffic flows. J. Adv. Transp. 2015, 49, 326–340. [Google Scholar] [CrossRef]
- Yao, D.; Xu, L.; Li, J. Evaluating the performance of public transit systems: A case study of eleven cities in China. Sustainability 2019, 11, 3555. [Google Scholar] [CrossRef]
- Cassidy, M.J.; Bertini, R.L. Some traffic features at freeway bottlenecks. Transp. Res. Part B Methodol. 1999, 33, 25–42. [Google Scholar] [CrossRef]
- Chung, K.; Rudjanakanoknad, J.; Cassidy, M.J. Relation between traffic density and capacity drop at three freeway bottlenecks. Transp. Res. Part B Methodol. 2007, 41, 82–95. [Google Scholar] [CrossRef]
- Hall, F.L.; Agyemang-Duah, K. Freeway Capacity Drop and the Definition of Capacity. Transp. Res. Rec. 1991, 1320, 91–98. [Google Scholar]
- Cassidy, M.J.; Rudjanakanoknad, J. Increasing the capacity of an isolated merge by metering its on-ramp. Transp. Res. Part B Methodol. 2005, 39, 896–913. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Hadj-Salem, H.; Blosseville, J.M. ALINEA: A local feedback control law for on-ramp metering. Transp. Res. Rec. J. Transp. Res. Board 1991, 1320, 58–64. [Google Scholar]
- Khondaker, B.; Kattan, L. Variable speed limit: An overview. Transp. Lett. 2015, 7, 264–278. [Google Scholar] [CrossRef]
- Papamichail, I.; Papageorgiou, M. Traffic-responsive linked ramp-metering control. IEEE Trans. Intell. Transp. Syst. 2008, 9, 111–121. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On Kinematic Waves. II. A Theory of Traffic Flow on Long Crowded Roads. Proc. R. Soc. A Math. Phys. Eng. Sci. 1955, 229, 317–345. [Google Scholar]
- Munjal, P.; Lawrence, R.L. Propagation of on-ramp density waves on uniform unidirectional multilane freeways. Transp. Sci. 1971, 5, 257–266. [Google Scholar] [CrossRef]
- Laval, J.; Daganzo, C. Multi-Lane Hybrid Taffic Flow Model: A Theory on the Impacts of Lane-Changing Maneuvers; Working paper No. UCB-ITS-WP-2004-1; Institute of Transportation Studies, University of California at Berkeley: Berkeley, CA, USA, 2004. [Google Scholar]
- Laval, J.A.; Daganzo, C.F. Lane-changing in traffic streams. Transp. Res. Part B Methodol. 2006, 40, 251–264. [Google Scholar] [CrossRef]
- Cassidy, M.J.; Anani, S.B.; Haigwood, J.M. Study of freeway traffic near an off-ramp. Transp. Res. Part A Policy Pract. 2002, 36, 563–572. [Google Scholar] [CrossRef]
- Daamen, W.; Loot, M.; Hoogendoorn, S. Empirical Analysis of Merging Behavior at Freeway On-Ramp. Transp. Res. Rec. J. Transp. Res. Board 2010, 2188, 108–118. [Google Scholar] [CrossRef]
- Jin, W.L. A kinematic wave theory of lane-changing traffic flow. Transp. Res. Part B Methodol. 2010, 44, 1001–1021. [Google Scholar] [CrossRef]
- Choudhury, C.; Ramanujam, V.; Ben-Akiva, M. Modeling Acceleration Decisions for Freeway Merges. Transp. Res. Rec. J. Transp. Res. Board 2009, 2124, 45–57. [Google Scholar] [CrossRef]
- Long, K.; Lin, Q.; Gu, J.; Wu, W.; Han, L.D. Exploring traffic congestion on urban expressways considering drivers’ unreasonable behavior at merge/diverge sections in China. Sustainability 2018, 10, 4359. [Google Scholar] [CrossRef]
- Gipps, P.G. A model for the structure of lane-changing decisions. Transp. Res. Part B Methodol. 1986, 20, 403–414. [Google Scholar] [CrossRef]
- Lindgren, R.; Bertini, R.; Helbing, D.; Schönhof, M. Toward Demonstrating Predictability of Bottleneck Activation on German Autobahns. Transp. Res. Rec. 2006, 1965, 12–22. [Google Scholar] [CrossRef]
- Ahmed, K.I. Modeling Drivers’ Acceleration and Lane Changing Behavior. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999; pp. 46–170. [Google Scholar]
- Sun, J.; Ouyang, J.; Yang, J. Modeling and Analysis of Merging Behavior at Expressway On-Ramp Bottlenecks. Transp. Res. Rec. J. Transp. Res. Board Transp. Res. Board Natl. Acad. 2014, 2421, 74–81. [Google Scholar] [CrossRef]
- Toledo, T.; Zohar, D. Modeling Duration of Lane Changes. Transp. Res. Rec. J. Transp. Res. Board 2007, 1999, 71–78. [Google Scholar] [CrossRef]
- Munjal, P.; Pipes, L.A. Propagation of on-ramp density perturbations on unidirectional two-and three-lane freeways. Transp. Res. 1971, 5, 241–255. [Google Scholar] [CrossRef]
- Wan, X.; Jin, P.J.; Zheng, L.; Cheng, Y.; Ran, B. Empirical Analysis of Speed Synchronization of Merge Vehicle from Entrance Ramp. In Proceedings of the Transportation Research Board (TRB) 92nd Annual Meeting, Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Daganzo, C.F.; Laval, J.A. Moving bottlenecks: A numerical method that converges in flows. Transp. Res. Part B Methodol. 2005, 39, 855–863. [Google Scholar] [CrossRef]
- Ramadan, O.; Sisiopiku, V. Impact of Bottleneck Merge Control Strategies on Freeway Level of Service. Transp. Res. Procedia 2016, 15, 583–593. [Google Scholar] [CrossRef]
- Leclercq, L.; Laval, J.A.; Chiabaut, N. Capacity drops at merges: An endogenous model. Transp. Res. Part B Methodol. 2011, 45, 1302–1313. [Google Scholar] [CrossRef]
- Jin, W.L. A multi-commodity Lighthill-Whitham-Richards model of lane-changing traffic flow. Transp. Res. Part B Methodol. 2013, 57, 361–377. [Google Scholar] [CrossRef]
- Kesten, A.S.; Ergün, M.; Yai, T. An Analysis on Efficiency and Equity of Fixed-Time Ramp Metering. J. Transp. Technol. 2013, 3, 48–56. [Google Scholar] [CrossRef]
- Kesten, A.S.; Goksu, G.; Akbas, A. Dynamic ramp metering approach for an urban highway using microscopic traffic simulation. In Proceedings of the 2013 13th International Conference on ITS Telecommunications (ITST), Tampere, Finland, 5–7 November 2013; pp. 90–96. [Google Scholar]
- Pirc, J.; Turk, G.; Žura, M. Highway travel time estimation using multiple data sources. IET Intell. Transp. Syst. 2016, 10, 649–657. [Google Scholar] [CrossRef]
- Pirc, J.; Turk, G.; Žura, M. Using the robust statistics for travel time estimation on highways. IET Intell. Transp. Syst. 2015, 9, 442–452. [Google Scholar] [CrossRef]
- PTV. PTV VISSIM 10 User Manual; PTV Planug Trasport Verker AG: Karlsruhe, Germany, 2017. [Google Scholar]
- Dadashzadeh, N.; Ergun, M.; Kesten, S.; Žura, M. An automatic calibration procedure of driving behavior parameters in the presence of high bus volume. Promet Traffic Transp. 2019, 31, 491–502. [Google Scholar]
- Dadashzadeh, N.; Ergun, M.; Kesten, A.S.; Zura, M. Improving the calibration time of traffic simulation models using parallel computing technique. In Proceedings of the 2019 6th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Cracow, Poland, 5–7 June 2019; pp. 1–7. [Google Scholar]
- Shaaban, K.; Khan, M.A.; Hamila, R. Literature Review of Advancements in Adaptive Ramp Metering. Procedia Comput. Sci. 2016, 83, 203–211. [Google Scholar] [CrossRef]
- Chaudhary, N.A.; Tian, Z.; Messer, C.J.; Chu, C.-L. Ramp Metering Algorithms and Approaches for Texas; Technical Report No. FHWA/TX-05/0-4629-1; Texas Transportation Institute of the Texas A&M University: College Station, TX, USA, 2004; pp. 1–95. [Google Scholar]
- Zhang, M.; Kim, T.; Nie, X.; Jin, W.; Chu, L.; Recker, W. Evaluation of On-Ramp Control Algorithms; California PATH Research Report No. UCB-ITS-PRR-2001-36; Institute of Transportation Studies, University of California: Berkeley, CA, USA, 2001. [Google Scholar]
- Kotsialos, A.; Kosmatopoulos, E.; Papageorgiou, M. EUropean RAmp Metering Project (EURAMP)—Current Status of Ramp Metering; Deliverable d2.2; EU Publication Office: Luxembourg, 2007. [Google Scholar]
- Papageorgiou, M.; Kosmatopoulos, E.; Papamichail, I.; Wang, Y. A misapplication of the local ramp metering strategy ALINEA. IEEE Trans. Intell. Transp. Syst. 2008, 9, 360–365. [Google Scholar] [CrossRef]
- Yu, Y.; Weng, J.; Zhu, W. Optimizing Strategies for the Urban Work Zone with Time Window Constraints. Sustainability 2019, 11, 4218. [Google Scholar] [CrossRef]
- Zaidi, Z.; Radwan, E.; Harb, R. Evaluating Variable Speed Limits and Dynamic Lane Merging Systems in Work Zones: A Simulation Study. ISRN Civ. Eng. 2012, 2012, 435618. [Google Scholar] [CrossRef][Green Version]
- Hegyi, A.; De Schutter, B.; Hellendoorn, J. Optimal Traffic Control in Freeway Networks With Bottlenecks; IFAC: New York, NY, USA, 2005; Volume 38. [Google Scholar]
- Chen, D.; Ahn, S.; Hegyi, A. Variable speed limit control for steady and oscillatory queues at fixed freeway bottlenecks. Transp. Res. Part B Methodol. 2014, 70, 340–358. [Google Scholar] [CrossRef]
- Kušić, K.; Korent, N.; Gregurić, M.; Ivanjko, E. Comparison of two controllers for variable speed limit control. In Proceedings of the 2016 International Symposium ELMAR, Zadar, Croatia, 12–14 September 2016; pp. 101–106. [Google Scholar]
- Zhang, C.; Bie, Y.; Qiu, T.Z. Short-Term Demand Prediction at Freeway Bottleneck Under VSL Control. In Proceedings of the 96th Transportation Research Board Meeting, Washington, DC, USA, 5–7 January 2017; pp. 1–16. [Google Scholar]
- Conran, C.A. Modeling Microscopic Driver Behavior under Variable Speed Limits: A Driving Simulator and Integrated MATLAB-VISSIM Study. Master‘s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2017. [Google Scholar]
- Strnad, I.; Kramar Fijavž, M.; Žura, M. Numerical optimal control method for shockwaves reduction at stationary bottlenecks. J. Adv. Transp. 2016, 50, 841–856. [Google Scholar] [CrossRef]
- Shao, M.; Xie, C.; Sun, L.; Wan, X.; Chen, Z. Left-Side On-Ramp Metering for Improving Safety and Efficiency in Underground Expressway Systems. Sustainability 2019, 11, 3247. [Google Scholar] [CrossRef]
- Carlson, R.C.; Manolis, D.; Papamichail, I.; Papageorgiou, M. Integrated ramp metering and mainstream traffic flow control on freeways using variable speed limits. IFAC Proc. Vol. 2012, 45, 110–115. [Google Scholar] [CrossRef]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M. Integrated feedback ramp metering and mainstream traffic flow control on motorways using variable speed limits. Transp. Res. Part C Emerg. Technol. 2014, 46, 209–221. [Google Scholar] [CrossRef]
- Greguric, M.; Ivanjko, E.; Mandzuka, S. Cooperative ramp metering simulation. In Proceedings of the 2014 37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 26–30 May 2014; pp. 970–975. [Google Scholar]
- Sun, J.; Tang, K.; Zhang, S. Online evaluation of an integrated control strategy at on-ramp bottleneck for urban expressways in Shanghai. IET Intell. Transp. Syst. 2014, 8, 648–654. [Google Scholar] [CrossRef]
- Smit, R.; Smokers, R.; Rabé, E. A new modelling approach for road traffic emissions: VERSIT+. Transp. Res. Part D Transp. Environ. 2007, 12, 414–422. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flotterod, Y.P.; Hilbrich, R.; Lucken, L.; Rummel, J.; Wagner, P.; Wiebner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems ITSC, Maui, HI, USA, 4–7 November 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 2575–2582. [Google Scholar]
- Zambrano-Martinez, J.L.; Calafate, C.T.; Soler, D.; Cano, J.C.; Manzoni, P. Modeling and characterization of traffic flows in urban environments. Sensors 2018, 18, 2020. [Google Scholar] [CrossRef]
- Zambrano-Martinez, J.; Calafate, C.; Soler, D.; Lemus-Zúñiga, L.-G.; Cano, J.-C.; Manzoni, P.; Gayraud, T. A Centralized Route-Management Solution for Autonomous Vehicles in Urban Areas. Electronics 2019, 8, 722. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).