1. Introduction
In the past few decades, there has been a huge increase in electricity demand due to a rapid change in the environment. The traditional grid is becoming inefficient at handling such immense demand and it is undergoing various challenges like reliability, sustainability, and so forth. Moreover, 65% of produced energy is wasted during production, transmission and distribution in a conventional grid [
1]. To solve the aforementioned issues, the concept of the Smart Grid (SG) is introduced. SG incorporates bidirectional communication, auto-monitoring, auto-healing, two-way power flow and increased compatibility along with various new features in the power system. To solve the energy demand and supply gap problem, Demand Side Management (DSM) and Supply Side Management (SSM) are in focus. SSM is the energy management on the supply side. It includes production, efficient distribution and transmission of electricity. With an increase in electricity usage, challenges on the supply side are also increasing, that is, generation is quite low and old transmission infrastructure is not capable of handling such immense demand. To solve these issues, SSM is done using different approaches and techniques whereas DSM is the energy management on the user-end. Demand varies with time and it is highly unpredictable. To forecast the demand, different techniques are utilized in the literature, that is, machine learning and data mining, whereas for coordination, Game Theory (GT) is used.
DSM can be performed by implementing different strategies, that is, load shifting, valley filling, peak clipping, and so forth. Peak clipping is a type of energy management where peaks of load curve are clipped during the high price intervals for minimizing the peak demand. It only focuses on the clipping of peaks and it has very less effect on the overall demand. Valley filling fills the valley of load curve in low price rate hours. Load shifting schedules the load from peak to off-peak hours and no curtailment of load is done in load shifting strategy. This strategy is considered as one of the most efficient load management strategies [
2]. Mostly, load shifting strategy is implemented through Demand Response (DR) program. DR programs are considered as the most efficient and reliable programs [
3]. There are two kinds of DR programs: Priced-based DR (PDR) and Incentive-based DR (IDR) [
4]. Basic aim of DR program is to educate the electricity users to consume electricity in an efficient manner [
5].
Devised price signals include day ahead pricing, Real Time Pricing (RTP), Time of Use (ToU) pricing, hourly peak and Critical Peak Pricing (CPP) and non-critical peak pricing [
6]. ToU pricing tariff is a flat rate tariff, which remains fixed during specific time periods. Usually it has three peaks: off-peak, mid-peak and high peak having different prices for each peak. CPP is analogous to ToU tariff signals in case of flat prices. However, price during a specific time period can be changed because of stress events happened in the power system. RTP pricing scheme is communicated to consumers before the start of a time period and is updated after each time period. The rate of this pricing scheme depends upon the energy consumption, energy generation and response of consumers in the previous time period. RTP is the widely studied pricing scheme; as it is updated at the start of each hour [
7].
This work proposes a new load shifting technique. Moreover, coordination among the scheduled appliances is made possible to eliminate the deterioration of schedules by uncertain behavior of the user, that is, force starting or stopping of a scheduled appliance. Load shifting is conducted using a proposed Hybrid Cuckoo Earthworm Optimization (HCEO), developing a complete Energy Management System (EMS) for a home. A comparative analysis is conducted afterwards between proposed HCEO based EMS, Cuckoo Search Algorithm (CSA) based EMS and Earth Worm Algorithm (EWA) based EMS. The target of the EMS is to reduce the electricity cost. Coordination among appliances is integrated to increase the flexibility of the system using GT and a comparison is conducted among its three variants, that is, Shapley Value (SV), Nash Equilibrium (NE) and Zero Sum (ZS). Coordination allows the users to reschedule the appliances on the real time basis without disturbing their schedules of the whole day. Simulation outcomes demonstrate that our proposed technique has minimized the cost by 50.6% as compared to the unscheduled cost.
Main contributions of this paper are:
Implementation of CSA, EWA and hybrid technique “HCEO” for load shifting.
Feasible Regions (FRs) are computed for two cases: energy consumption versus electricity cost and waiting time versus electricity cost.
Comparison of these techniques is drawn based on the electricity cost, electricity consumption, PAR and appliance waiting time.
To increase the system flexibility and to enhance the comfort level, coordination among appliances is considered. Later, SV, NE and ZS are compared with each other on the basis of electricity cost, PAR, electricity consumption and appliance waiting time.
The organization of the rest of the paper is written in the following way. In
Section 2, related work is discussed. The proposed system model and its components are elaborated in
Section 3. Scheduling techniques and coordination among appliances are explained in
Section 4.
Section 5 describes the FRs along with results and discussion of both cases: coordination and without coordination. At the end,
Section 6 states the conclusion and future work.
2. Related Work
In the literature, many existing techniques are studied for the scheduling of household load through various optimization techniques. Pedram Samadi et al. [
8] propose a system model for scheduling the home appliances and for integrating the Renewable Energy Sources (RESs). For this purpose, authors implement dynamic programming to schedule the household appliances and use GT to sell surplus energy to neighbors and utility. A novel Home Energy Management System (HEMS) is proposed by Sheraz et al. [
9]. Genetic Algorithm (GA), CSA and crow search algorithms are implemented by authors for the load management of a smart building having thirty homes. Energy Storage System (ESS) is also used by authors to reduce the PAR and cost. In References [
8,
9], authors integrate RESs and ESS in their system; however, the installation and maintenance cost of RESs and ESS is not considered. In Reference [
10], a HEMS is proposed; where scheduling is performed using heuristic optimization schemes. Particle Swarm Optimization (PSO) and GA are applied for minimizing the PAR and consumers’ bill. Authors formulate the considered problem as a multiple knapsack problem and use three pricing tariffs, that is, ToU, CPP and RTP. Simulation results illustrate that GA reduces the electricity cost more than the PSO. In Reference [
11], an expert energy management system focusing on SSM is presented. Authors use Bacterial Foraging Algorithm (BFA) to schedule the multiple energy resources. Simulation results display that their proposed system reduced the operational cost of energy resources and carbon emissions. Residential, commercial and industrial users are considered in Reference [
12]. Authors propose a system to minimize the PAR and electricity cost using the Evolutionary Algorithm (EA). Finally, simulations demonstrate that large number of devices have no effect on the performance of EA.
Muralitharan et al. [
13] propose the model to decrease the cost and waiting time using multi-objective EA. Authors implement this algorithm with a threshold limit to balance the load and to avoid peaks. If the consumer load exceeds from utility’s defined threshold limit then consumer will pay extra amount in the form of penalty. In Reference [
14], efficient household load is categorized into flexible and essential load. Using this categorization, a home load management system is proposed to decrease the cost and delay of appliances. A centralized algorithm developed by the adaptive dynamic programming is used to resolve the considered optimization problem. Authors in Reference [
15] propose a Robust-Index Method (RIM) to handle the uncertainties associated with the consumers’ behavior. A major objective is to increase the user comfort. Robust indexes are calculated for different loads, which are embedded into appliance scheduling optimization problem as the constraints. This integration has helped the scheduling system in getting the optimized scheduled load.
A DR program is proposed in Reference [
16] using mixed-integer non-linear programming. The authors use the ToU pricing scheme and IDR program. Results show that 25% of cost is decreased and mostly consumers use electricity during low-price hours (off-peak hours) to get incentives from the utility. In Reference [
17], the optimization of load and electricity production in a smart home is done using a Mixed Integer Linear Programming (MILP) model. The authors use a heuristic technique for scheduling the household load in order to minimize the electricity bill. The Taguchi method is applied for performing three case studies during different time horizons. A HEMS is proposed in Reference [
18] using a Hybrid Algorithm (HBG). This algorithm is developed from GA and BFA. The authors schedule the home appliances and use three different pricing tariffs. These pricing schemes are analyzed and compared with each other on the basis of cost and waiting time. A real-time energy management model is presented in Reference [
19] using dynamic pricing scheme, the photo-voltaic module and ESSs. Main target of this work is to minimize the electricity bill. A game theoretic approach is presented in Reference [
20] for scheduling the appliances in the residential unit. For reducing the stress on the traditional grid, the idea of the locally generated RESs is presented. The simulation results depict that GT efficiently reduces the electricity cost. The authors developed a DR program in Reference [
21] for scheduling the home appliances and consider the uncertainties associated with the consumed energy and its cost.
Yang et al. [
22] propose the impact of electricity market due to the dwelling’s consumption optimization. Proposed model reduces the PAR by 35.9% and electricity cost by 34.3% with respect to baseline calculations. A decentralized approach is presented in Reference [
23] that develops a home load management module. This module is responsible for cost reduction by constantly communicating with utility server regarding load patterns. Zineb et al. in Reference [
24] propose a HEMS for the scheduling of appliances in a home with an objective to decrease the total bill and waiting time of the appliances used in the home. The authors formulate the multi-objective problem and solve it using EA. To balance the residential load curve, authors propose a system model using dynamic algorithm [
25]. An optimal residential energy management system is presented for the minimization of cost of consumers in Reference [
26]. In Reference [
27], the MILP technique is applied for the minimization of the total cost and
emission. This system is based upon the robust approach for appliance scheduling. The authors include the users’ behavior uncertainty in the proposed model to make the appliances’ schedule less sensitive to their unpredictable behavior.
A decentralized approach is used for demand scheduling of a smart home in Reference [
28]. The authors focus on the improvement of comfort levels and electricity bill reduction. For this purpose, appliance level information is collected, that is, usage, user preferences and pattern of appliances, and utilized this information for scheduling the appliances. For the privacy protection of consumers, the authors locally run the proposed technique so that data is processed at consumers’ premises and it is not shared with the utility. In Reference [
29], the authors propose an Adaptive Thermal Comfort Model (ATCM) along with appliance scheduling of a smart home. For ATCM, ventilation, heating and air conditioner are scheduled using comfort degree of user. Proposed model is solved by a new bio-inspired meta-heuristic algorithm (natural aggregation algorithm). A priority based appliances’ scheduling is performed in Reference [
30]. The authors use an evolutionary accretive comfort algorithm and consider three types of consumers with different predetermined daily budget limits. Static and dynamic priorities are allocated to the loads on the basis of the consumer’s preferences. These three scenarios are implemented and maximum user comfort level is achieved in each case.
An MILP based home load scheduling is considered in Reference [
31] along with different assets, that is, interruptible appliances, non-interruptible appliances and electric vehicles (EVs). Authors propose a model, where different connections like Vehicle to Grid (V2G), Vehicle to Neighbors (V2N) and Vehicle to Home (V2H) are possible. With this proposed model, consumers can make energy transactions, that is, V2G, V2H and V2N. These transactions can help the consumers to decrease the electricity bills. In Reference [
32], a multi-residential system with multiple appliance classes (5 classes) is considered to schedule each residence in a distributed manner using mixed integer non-linear programming. In the distributed approach, scheduling is performed at each residence level and it shares much less information with the grid in order to protect the privacy of each residence. According to the authors, the proposed model schedules the appliances optimally. In order to maintain the quality of consumers’ experience, a new smart home energy management system is proposed in Reference [
33]. The authors consider two scenarios; one with RESs and other without RESs. Cost saving through appliance scheduling and renewable power source allocation; is implemented targeted to the cost minimization. The results demonstrate that 22% cost is saved in non-RESs case and 30% cost is saved during the RESs case.
A two level optimization of multiple smart homes supported by distributed generations is performed in Reference [
34]. The authors at the first level, use local home energy management system for appliance scheduling. At the second level, global home energy management system is developed for scheduling ESS and power exchanging among smart homes. A HEMS supported by RESs, ESSs and PHEVs is presented in Reference [
35] for electricity cost savings. For this purpose, GA and multi-constraints integer programming are combined and an improved GA is proposed. Based on simulation results, proposed algorithm is robust with a high computational efficiency. The authors of Reference [
36] propose an energy management controller to classify the appliances based on their energy consumption patterns. Furthermore, the authors use heuristic techniques and fuzzy logic to reduce delay, minimize PAR and cost. However, user preferences are not considered. Muhammad et al. propose a mechanism to achieve multiple objectives through optimization technique. User cost, PAR and peak load demand are minimized; further, user discomfort is also reduced. Optimal stopping rule is used to achieve the aforementioned objectives. However, user cannot change the schedule, if the load is turned on.
Peer to peer power trading is evaluated in Reference [
37] among smart homes. Further, it is examined that the usage of RESs is increasing drastically. Unbiased cost distribution is also minimized. However, user comfort is compromised as every user has different constraints. Moreover, the authors in Reference [
38] propose a distributed mechanism to manage the power system optimally. The sole objective behind this work is to reduce the electricity bill. However, user comfort is not considered. Similar work is also done in Reference [
39]. In short, one basic problem in establishing the schedule of the appliances lies in the uncertainty of human behavior. User comfort is of vital importance; moreover, user always has an option to force start and force stop an appliance out of the schedule made. This may deteriorate the basic goal of load shifting. Furthermore, after the detailed review of existing literature, the aforementioned short comings still need to be addressed. Hence, there is a need to develop an efficient HEMS that can minimize electricity bills and can also take care of user comfort and uncertainty factors. In this paper, a two tier HEMS is proposed in order to optimize the aforementioned issues. In the first tier, a hybrid optimization technique is proposed for the load scheduling. In the second tier, to accommodate the uncertainties associated with the user at run time, rescheduling of appliances is incorporated in the proposed HEMS.
3. System Model
This paper is an extension of Reference [
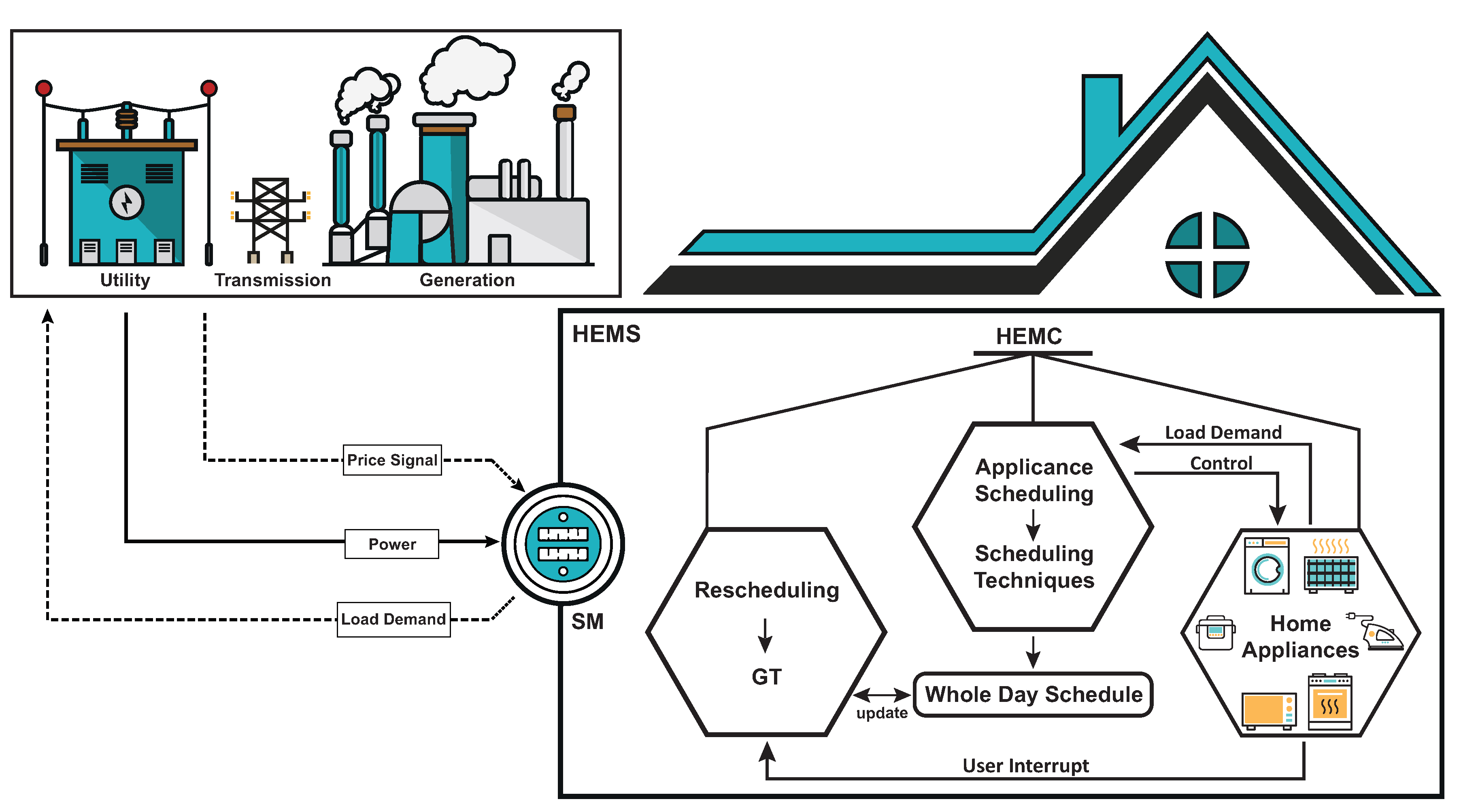
40]. This system comprises of household appliances, Smart Meter (SM) and Home Energy Management Controller (HEMC). SM is responsible for communicating to the utility in order to get the updated RTP tariff details. Based upon the appropriate pricing tariffs, HEMC performs scheduling of the household appliances using the proposed optimization technique. The purpose of the HEMC is to reduce the cost of the electricity consumed by the users. In addition, coordination is established among home appliances using the GT, as displayed in
Figure 1.
HEMC is divided into three sections. The first section is the Appliance Section (AS), which includes all appliances and this section provides information to HEMC about the status (ON/OFF) and load demand of appliances. The second section is Scheduling Section (SS), in which scheduling technique schedules the appliances keeping the objective of cost minimization. The third section is one of the most important sections of HEMC, that is, Rescheduling Section (RS). In this section, real-time coordination is performed using GT.
In SS, HEMC schedules the appliances for 24 h and it schedules each appliance to a specific time slot. Each time slot is defined as one hour during the 24 h time intervals. There are total 24 time slots, which are defined for the whole day. These time slots are scheduled as per the defined rates of the pricing schemes for the peak and off-peak hours. If peak hours are found in the schedule then appliances are scheduled to the off-peak hours. Suppose, an appliance is scheduled for a time slot of two hours; however, user switches-OFF this appliance in one hour and ten minutes. Then, the remaining time (fifty minutes) of that slot will be wasted. Instead of wasting the remaining time, rescheduling of an appliance is implemented using coordination and GT. Here again, three variants of GT (ZS, NE and SV) are compared to get optimum results. When user switches-OFF the status of an appliance before the completion of its operational time, RS obtains an interrupt from AS and then RS performs coordination among appliances. Initially, RS finds out the following information about appliances:
Which appliance has completed its operational time.
Which appliance(s) can be rescheduled.
Which appliances are already running.
After finding out this information, remaining appliances will coordinate with each other. After coordination, one or more appliances can be selected depending on the remaining operational time. In addition, this coordination will not affect the whole schedule of the day.
3.1. Appliance Classification
In order to schedule the appliances, they are categorised in three groups: Shiftable Appliances (SAs), Non-Shiftable Appliances (NSAs) and Normal Appliances (NAs). These groups are defined by the user for the set of appliances. This classification of appliances helps in scheduling the household load at their appropriate time slots. In this work, a smart home is considered; comprising of fifteen appliances. Power ratings and operational time of each appliance is different and it is given in
Table 1. Operational time is defined as the time, for which an appliance will be kept ON during a day or the daily usage of an appliance and user sets the operational time of these appliances.
3.1.1. SAs
The operational time of these appliances can be interrupted during their execution. The list of these appliances is described in
Table 1. HEMC is responsible for scheduling these appliances at an appropriate time slot during a day using proposed technique. In addition, whenever a user interrupt is generated for rescheduling, these appliances are used for rescheduling purposes.
Suppose,
represents the power rating and
depicts the status of SA then the electricity consumption of SA (
) for the full day, is expressed below;
the status of SA is represented as:
and electricity cost of SA for the whole day is computed using the equation described below:
where,
is the price signal.
3.1.2. NSAs
Washing machine and cloth dryer are included in this group, which are described in
Table 1. Both of these appliances are assumed to be scheduled one after another. As a cloth dryer is needed immediately after the operation of washing machine; therefore, it is scheduled immediately after the operation of washing machine. As these are included in NSAs, so HEMC cannot interrupt these appliances. Let, power rating of cloth dryer or washing machine is
and status of NSA appliance is
then the electricity consumption of NSA (
) during 24 h can be expressed as:
Equation (
5) represents the ON or OFF status of cloth dryer or washing machine.
The total electricity cost during 24 h of cloth dryer and washing machine can be found using following equation as:
3.1.3. NAs
The appliances which are not scheduled by HEMC, are included in this group. The household user can turn-ON these appliances during any time of the day. Let the power rating of NA is depicted by
and the status of NA is
then the energy consumption of NA (
) during 24 h is given by Equation (
7).
ON or OFF status of NA can be represented as:
and total cost of NA during 24 h is given as:
where
defines the price signal sent by the utility.
3.2. Objective Function
The major objective of this work is to minimize the electricity cost. The total cost of the appliances during the 24 h is computed by adding the electricity consumption of all three groups of appliances with respect to their price rates as expressed in Equations (
3), (
6) and (
9).
where
is the aggregated bill of all appliances for the day. Objective function is formulated as in Equation (
11).
4. Optimization Techniques
Scheduling smart appliances such that electricity cost is minimized is NP-hard problem. For such problems, heuristic algorithms are in focus of research as well as engineering industries. In this work, a hybrid algorithm is proposed based on CSA and ESA to achieve optimum results. An introduction of parent algorithms, as well as a proposed hybrid algorithm, are presented in following subsections.
4.1. CSA
CSA is inspired from the natural behavior of some species of cuckoo. Some species of cuckoo, that is,
Ani and
Guira lay eggs in other birds’ nests. Further, they remove the eggs of host birds from nests so their children can have all food. If host bird finds the alien eggs, he will either throw them out or leave the nest and make a new nest. On the basis of this natural behavior of cuckoo, CSA is formulated and it is explained in Reference [
41]. The basic rules of CSA are:
A nest is randomly selected by each cuckoo and a cuckoo lays only one egg at any time slot.
Only nests containing the best eggs will survive for the next generation.
Host nest numbers are constant and the discovery probability is .
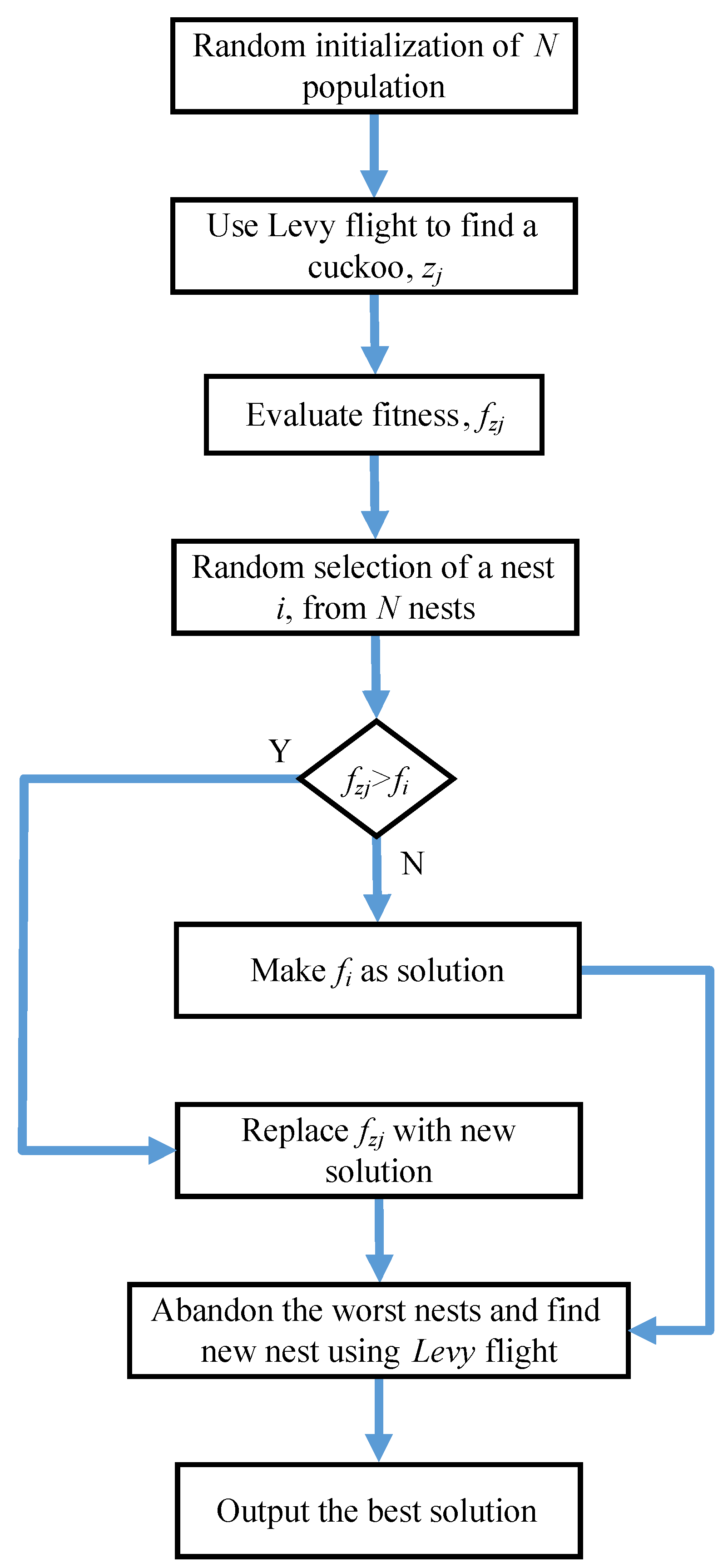
For optimization problem, cuckoo lays eggs randomly in the hosts’ nests, which are the possible solutions. Total number of host nests is the search space. A fitness function is designed for nests; therefore, each host nest is evaluated by this fitness function. Each egg in a nest represents the number of household appliances. A flowchart of CSA is presented in
Figure 2. Cuckoo performs
Levy flight to randomly lay the egg which is given as:
where,
is step size and mostly it is taken as 1.
and
represent the current and next position of cuckoo, respectively. Levy flight is a walk and its step length is random, which only depends upon its current location. It is an efficient way to explore the search space. Results of CSA are calculated and compared with the hybrid technique. The parameters used for CSA in this paper are given in
Table 2.
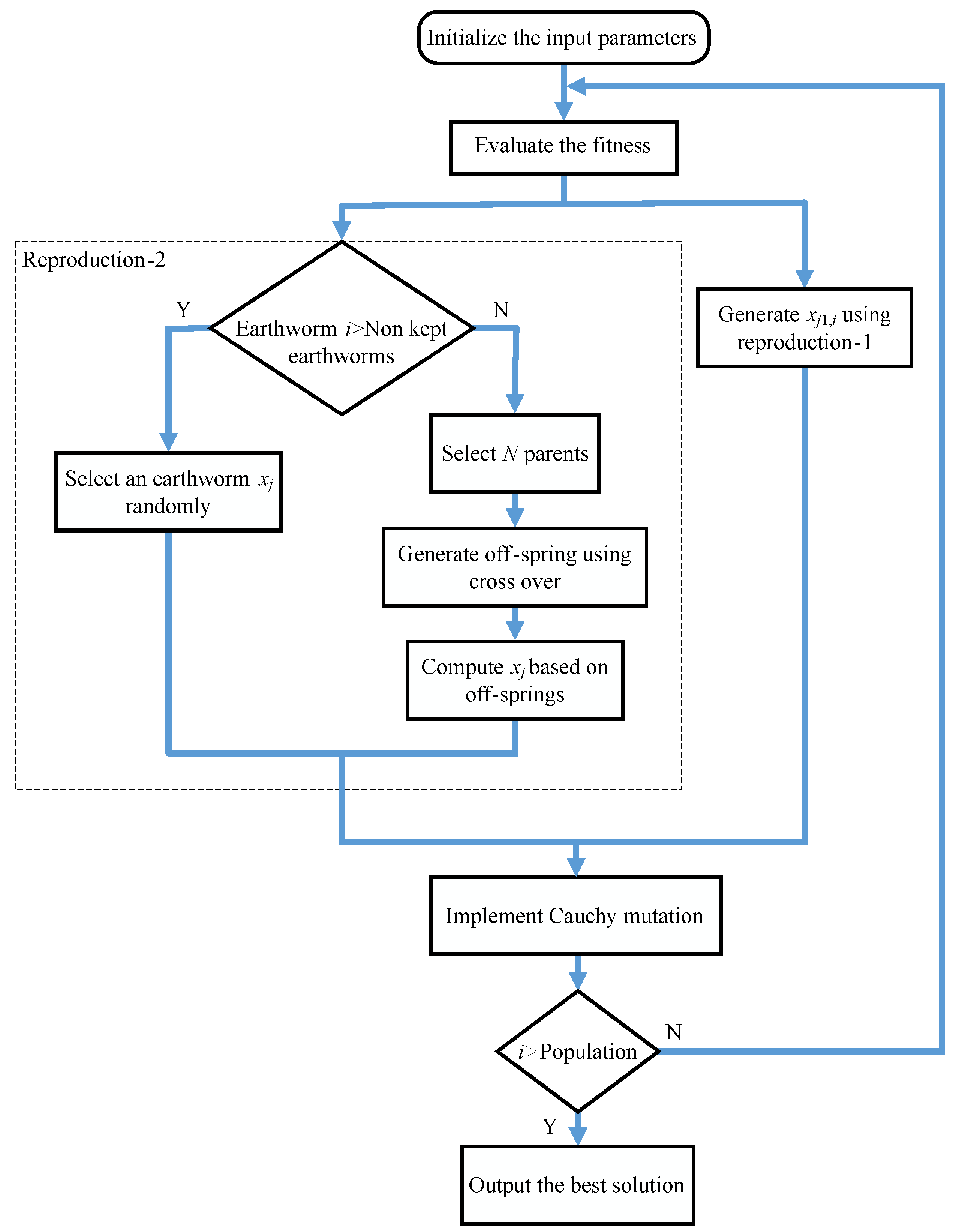
4.2. EWA
EWA is inspired from the natural behavior of earthworms, which have two types of reproductions: reproduction-1 and reproduction-2. When off-springs are produced from single parent earthworm then it is called reproduction-1 and when off-springs are produced by two parent earthworms then it is known as reproduction-2 [
42]. This technique is implemented and scheduling is performed in order to compare its results with the hybrid technique. A flowchart of EWA is presented in
Figure 3.
EWA can be summarized by following rules:
All earthworm off-springs are produced either from reproduction-1 or from reproduction-2.
Each child earthworm contains all genetic properties of its parents.
Earthworm with best fitness value will pass to next generation without increasing the population size.
Reproduction-1 is formulated as,
where
is the
ith element of
that shows the position of the earthworm
j. Similarly,
is the
ith element of
which is the new position of the earthworm
j1 and
is the similarity factor where
and
are the upper and lower limits respectively.
Reproduction-2 is an improved form of crossover. Crossover can be single point, multi-point or uniform point. In this paper, uniform crossover is used and an off-spring
is produced. After implementing above reproductions, both off-springs are combined by following equation
where
is a proportional factor which adjusts the proportion of the off-springs. At the end,
Cauchy mutation using Equation (
15) is applied to increase the search ability and to escape from the local optimal solution [
42].
where
is the weight vector and
G is a random number.
EWA is implemented for scheduling the household appliances and its results are compared with HCEO. The parameters used in this paper for EWA are given in
Table 3.
4.3. Hybrid of CSA and EWA
A hybrid technique HCEO is proposed, which is derived from EWA and CSA. As CSA is good for searching the global search space along with very few control parameters need to be tuned and EWA helps in escaping from the local optima. Therefore, these two algorithms are used to make a hybrid algorithm. Hybrid algorithms are developed in order to increase its performance as compared to the parent algorithms. Hybridization can be done by mixing the steps of parent algorithms as given in Reference [
43]. Hybridization can be loosely coupled or strongly coupled.
In strongly coupled hybridization, the flow of a technique is followed and in loosely coupled hybridization, internal steps of techniques are interchanged. In this case, few steps taken from EWA and CSA are fully opted to obtain an optimized solution as given in Algorithm 1.
HCEO’s results show that it has performed well in minimizing the electricity cost and it outperformed EWA and CSA. Results of the hybrid technique are discussed in
Section 5.
| Algorithm 1: HCEO algorithm for scheduling of a smart home |
![Sustainability 11 06287 i001]() |
4.4. GT
For maintaining the coordination among the home appliances, GT is implemented in this work. Coordination will start only if user sends an interrupt signal to switch-OFF any appliance for ending its operational time. Therefore, another decision is required for rescheduling of one or more appliances in respective time slot to minimize the effect of uncertainty.
GT concept has three main components: players, payoff and strategies. In our case, SAs are used for rescheduling because these appliances are deferrable. Appliances act as players and their cost is the payoff. Strategy is the schedule of appliances, which will be placed in that empty time slot. Three variants of GT: SV, NE and ZS are used for coordination among appliances and are compared with each other to find out the best approach. Each appliance will try to increase its payoff by implementing the best response; however, only appliances with operational time less than or equal to the empty slot time will be placed. When more than one appliances are rescheduled then sum of operational time of all appliances will be less than or equal to the empty slot time. SV calculates the operational time for each appliance and then appliances with high SV are selected to be rescheduled. SV for
kth appliance can be calculated by following formula:
where
S is the subset of
N appliances without the
kth appliance and
is the payoff of the appliances.
NE is the equilibrium point at which each player is using its best strategy to maximize its payoff. At equilibrium state, appliances with operational time less than or equal to the emptied slot time will be selected for rescheduling.
For the ZS game, two appliances are randomly selected from SAs, which can be rescheduled. Initially, SAs which have already completed their operational time, are separated from the group. Afterwards, the appliances, which are operating during the time when interrupt is generated, are separated out. Then, the remaining SAs are used as an input (players) for ZS game.
After coordination, the rescheduled appliances’ operational time is updated so that the total operational time of rescheduled appliances do not exceed their predefined operational time.
5. Simulations and Results
In this section, we will describe the simulation setup and the validation of system through its performance parameters. The list of performance parameters is: energy consumption, cost, PAR and waiting time.
5.1. Simulation Setup
For simulations, one home is considered in a residential sector, which comprises of fifteen household appliances with different power rates as described in
Table 1. Three groups are defined for these appliances in order to differentiate their operational time slots.
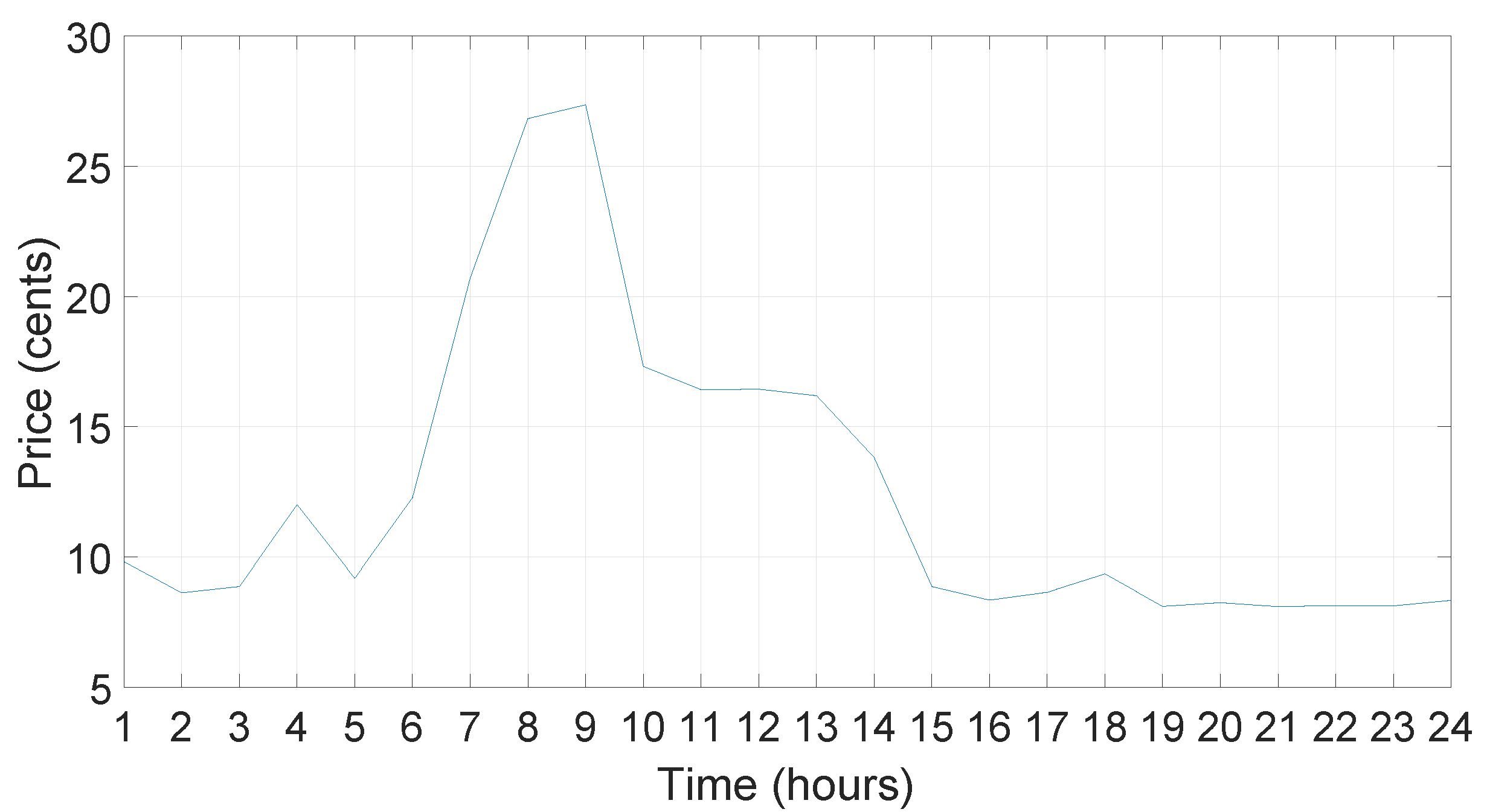
Price Signal
For simulation purposes, the RTP pricing signal is considered which is depicted in
Figure 4. This pricing signal is publicized by the utility and prices are given in cents/kWh. The maximum price is nearly 27 cents/kWh at time slot 9. On-peak hours are from time slots 6–14, because during these time slots, electricity demand is very high and as a result, electricity price is high. Time slots, in which price is low are off-peak hours, that is, from time slots 1–6 and 15–24.
5.2. FR
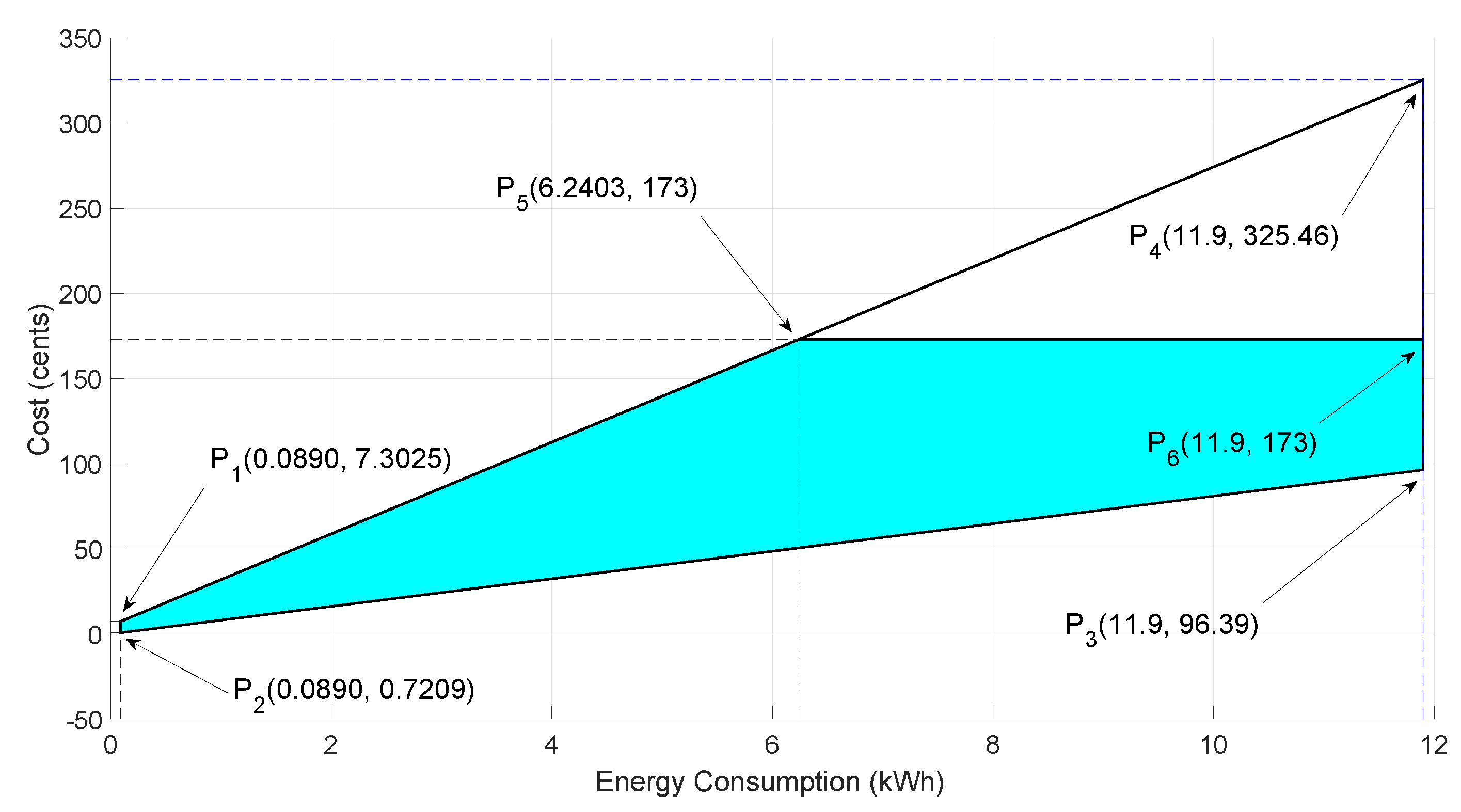
The region which satisfies all the possible values of solution and constraints of the problem is known as the FR. The power consumption cost FR is displayed in
Figure 5 where, the region is covered by P1, P2, P3 and P4, which illustrates the unscheduled versus power consumption cost. Points P1, P2, P3 and P4 are obtained as follows:
P1 (minimum energy consumption, minimum electricity cost)
P2 (minimum energy consumption, maximum electricity cost)
P3 (maximum energy consumption, minimum electricity cost)
P4 (maximum energy consumption, maximum electricity cost)
P1 (0.0890, 7.3025) and P2 (0.0890, 0.7209) tell about the maximum and minimum electricity cost at minimum unscheduled load. P3 (11.9, 96.39) and P4 (11.9, 325.46) gives the information about the maximum and minimum electricity cost at maximum unscheduled load.
The HEMC schedules the appliances and the optimal solution lies in the colored region formed by the points P1, P2, P3, P5, and P6. Points P5 (6.2403, 173) and P6 (11.9, 173) are threshold points because HEMC does not schedule any appliance above these threshold points. Therefore, optimal solution remains in the colored region. The maximum cost of HCEO in a hour is 173 cents which defines the threshold points P5 and P6.
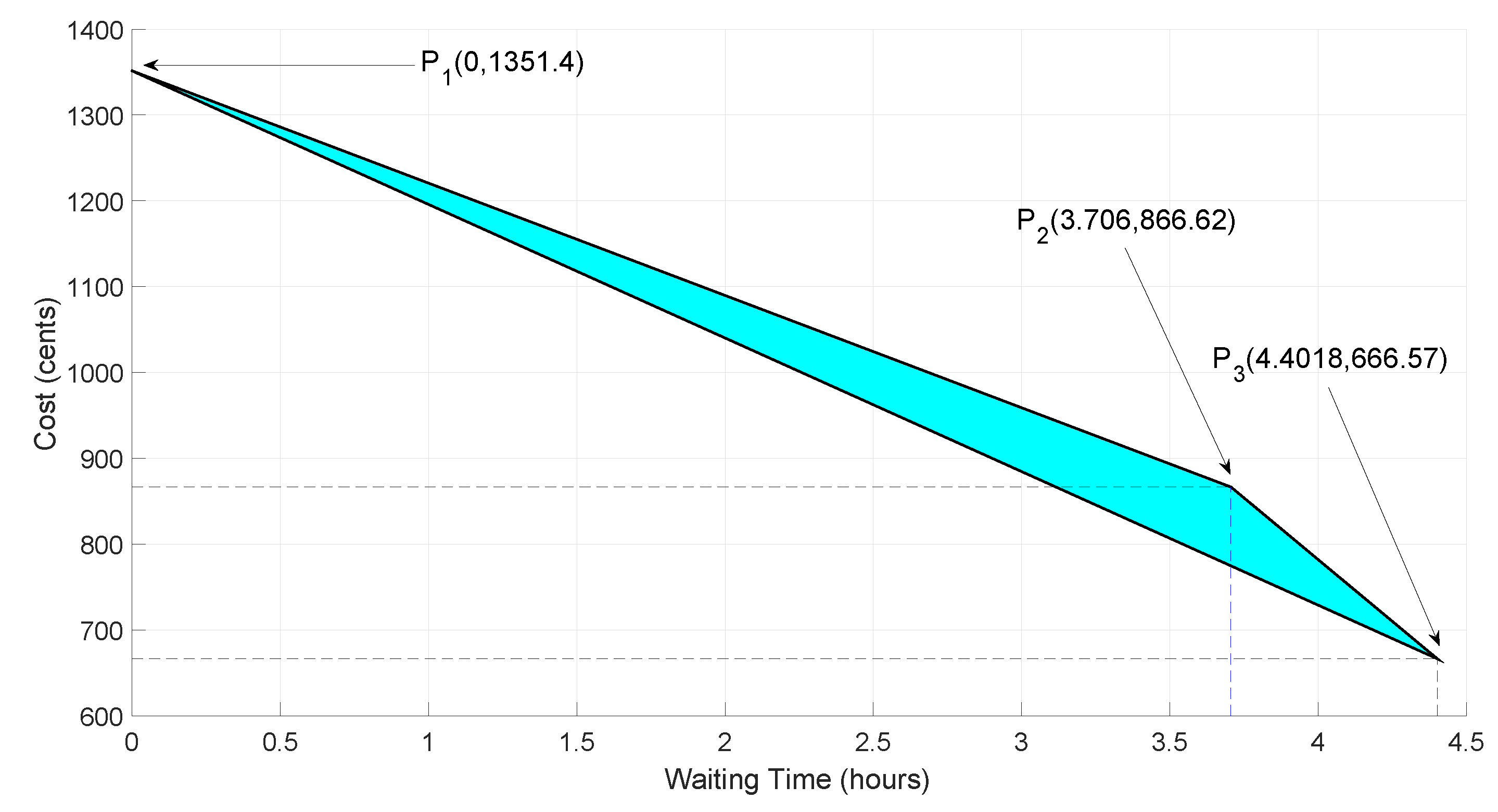
The cost-waiting time FR is illustrated in
Figure 6 where P1 (0, 1351.4), P2 (3.706, 866.62) and P3 (4.4018, 666.57) are the points which formed the FR in this scenario. Point P1 is defined as the maximum unscheduled cost with zero waiting time. P2 and P3 are minimum and maximum waiting time with respective electricity costs. HEMC keeps the waiting time of appliances within the colored region.
5.3. Results and Discussions
In order to visualize the robustness of our proposed scheme for HEMS, it is implemented in MATLAB. Algorithms: EWA, CSA and our proposed hybrid scheme are implemented and their performance is compared with each other based on four parameters: electricity cost, electricity consumption, user comfort and PAR.
5.3.1. Electricity Cost
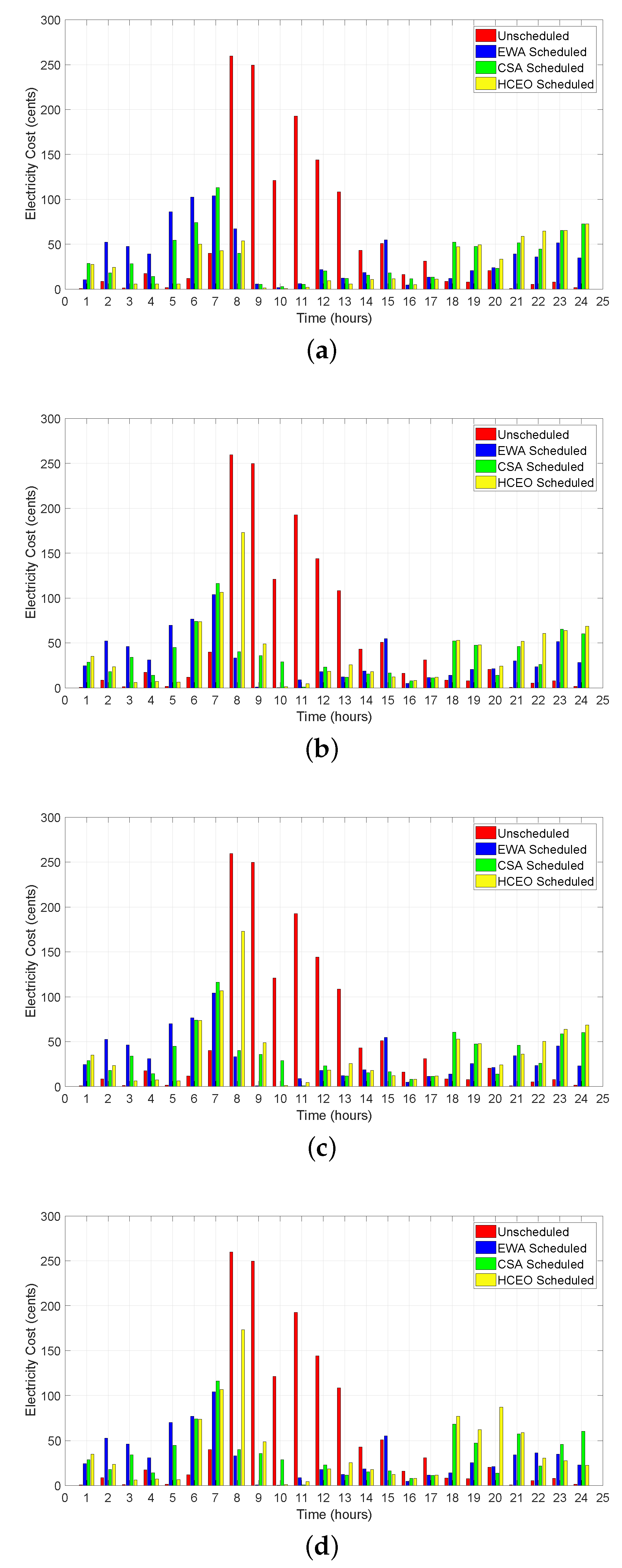
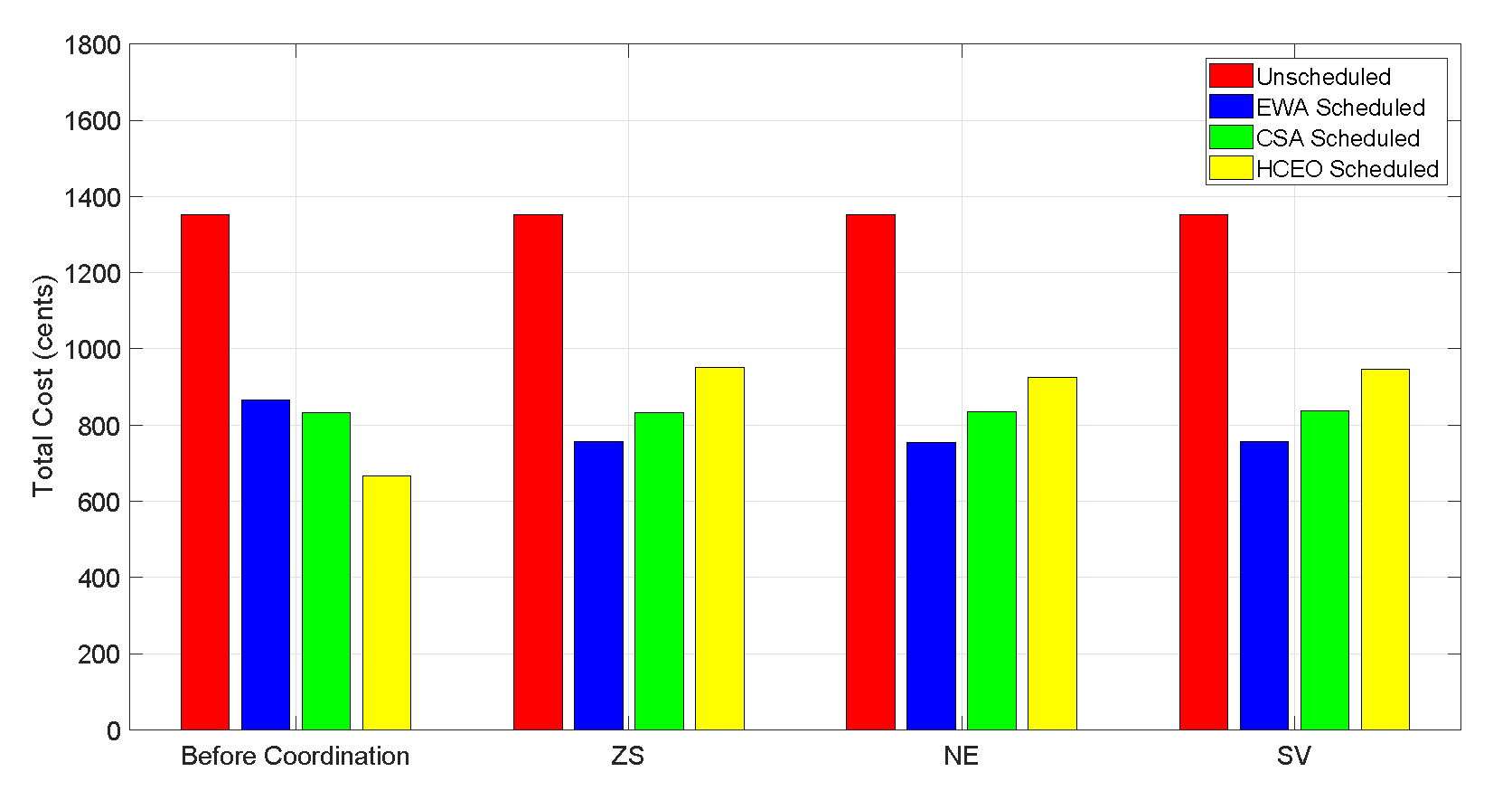
The total hourly cost of the system before and after coordination is shown in
Figure 7, which depicts that most of the load is scheduled towards off-peak hours. Maximum cost reduction is also achieved by hybrid technique. The total electricity cost of each technique is shown in
Table 4. The main target of the proposed system model is to decrease the electricity cost of a residential unit; therefore, a cost comparison of proposed hybrid technique is performed with unscheduled case and parent techniques as shown in
Figure 8. HCEO schedules the most of the energy towards low price hours more efficiently as compared to CSA and EWA as shown in
Figure 9. From this, it can be concluded that proposed hybrid technique has outperformed the other techniques for cost minimization. Proposed HCEO minimized the electricity cost by 50.6% as compared to unscheduled cost. Moreover, without coordination, cost reduction by EWA and CSA is 35.85% and 38.43% respectively.
Coordination of appliances using ZS, NE and SV for electricity cost is shown in
Figure 8. Remember that when the user switches-OFF an appliance before the finishing of its operational time then coordination is activated; otherwise no coordination takes place. For simulation purposes, some appliances are randomly switched-OFF before the completion of its time slot. After coordination results show that total cost of HCEO is increased in all three cases. The reason for this increase is the interrupt, which user has generated during on-peak hours and an appliance with high power rating is rescheduled. However, in case of other two techniques (EWA and CSA), interrupt signals are sent for low price rate hours, so their total cost is decreased in all three cases. From this, it is concluded that total cost may change a lot as in the case of the hybrid technique or maybe there is only a slight change in the total cost (in case of CSA and EWA). This change in cost totally depends upon the two factors: electricity prices during that particular time and the power consumption of the appliance which is rescheduled.
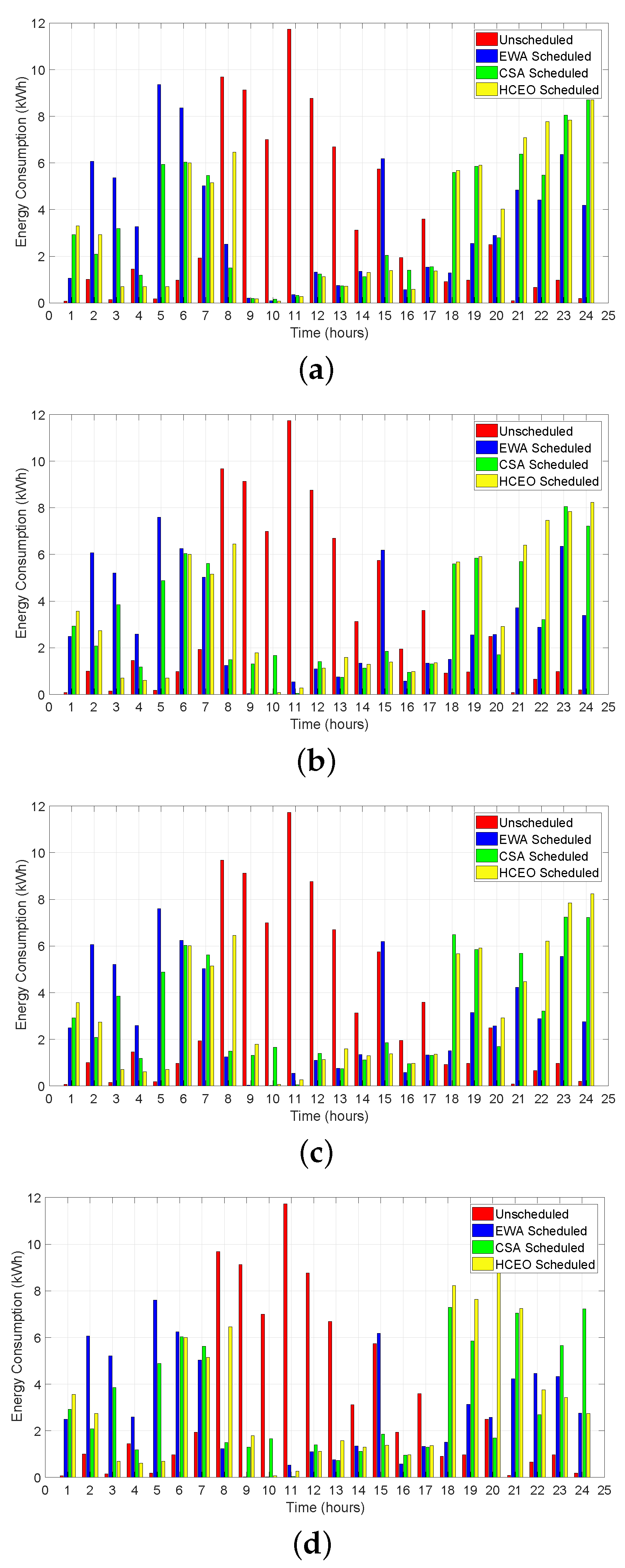
5.3.2. Energy Consumption
Figure 9 depicts per hour energy consumption of household appliances before and after coordination. During on-peak hours, when prices are high, each scheduling technique has shifted the load towards off-peak hours, where rates are relatively low. Therefore, electricity cost due to each scheduling technique is less than the unscheduled cost. In addition, these scheduling techniques have created no peaks during on-peak hours as shown in
Figure 9.
The effect of coordination among appliances through ZS, NE and SV on hourly electricity consumption can be seen in
Figure 9. It can be observed that users have generated interrupts during on-peak hours and during last hours of the day. For HCEO, interrupt signals are sent in low price rate hours and appliances with high power ratings are rescheduled as a result cost of HCEO is increased. Whereas, there is a small reduction in cost of EWA and CSA. As interrupts are generated randomly for each technique; therefore, it is generated during on-peak hours for HCEO and during off-peak hours for EWA and CSA. Practically, user generates interruptions so these are unpredictable and the timing of these interruptions effect the total electricity cost.
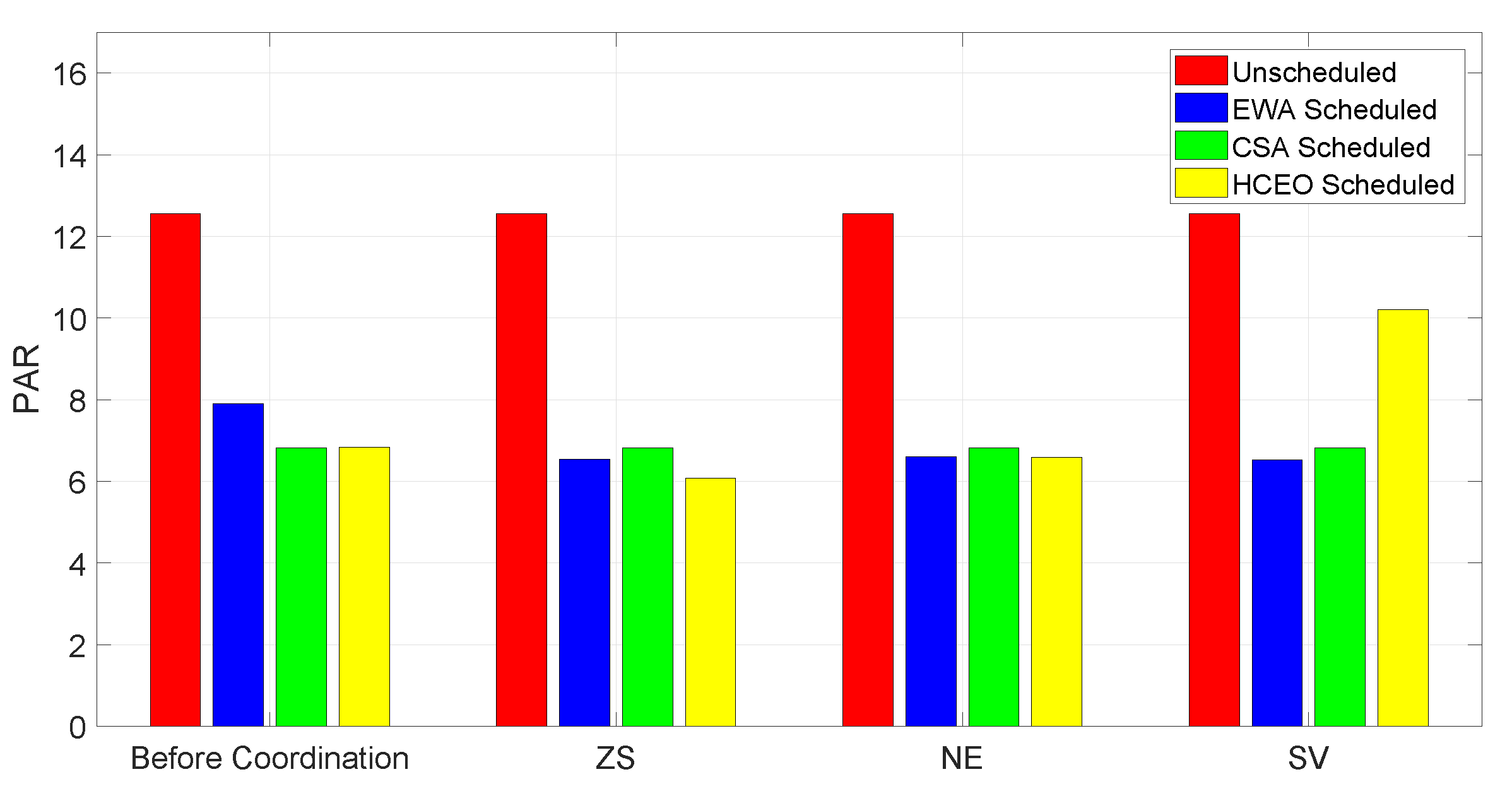
5.3.3. PAR
It is the ratio of maximum load to average load and it tells about the load peaks created during a day. This parameter helps the utilities to maintain the energy demand and supply. If PAR is high then utilities need extra generation units to meet the peak load and these generation units will be operational only during the peak hours; thus, increasing the operational cost of the utility. Low PAR is helpful in reducing the operational cost of utilities.
The PAR of each scheduling technique before coordination is demonstrated in
Figure 10 and it can be observed that PAR of CSA and HCEO is nearly same whereas, EWA has highest PAR. However, PAR of each technique is still less than the unscheduled PAR. Therefore, these scheduling techniques will help the utilities in reducing their operational cost.
After coordination through ZS and NE minute reduction in PAR is observed. However, during coordination through SV, PAR of HCEO is increased because the interrupt, which is generated during off-peak hours, has created a peak as shown
Figure 9d. Due to this reason, PAR of HCEO after coordination with SV, is increased. PAR obtained by the selected scheduling techniques with and without coordination is given in
Table 5.
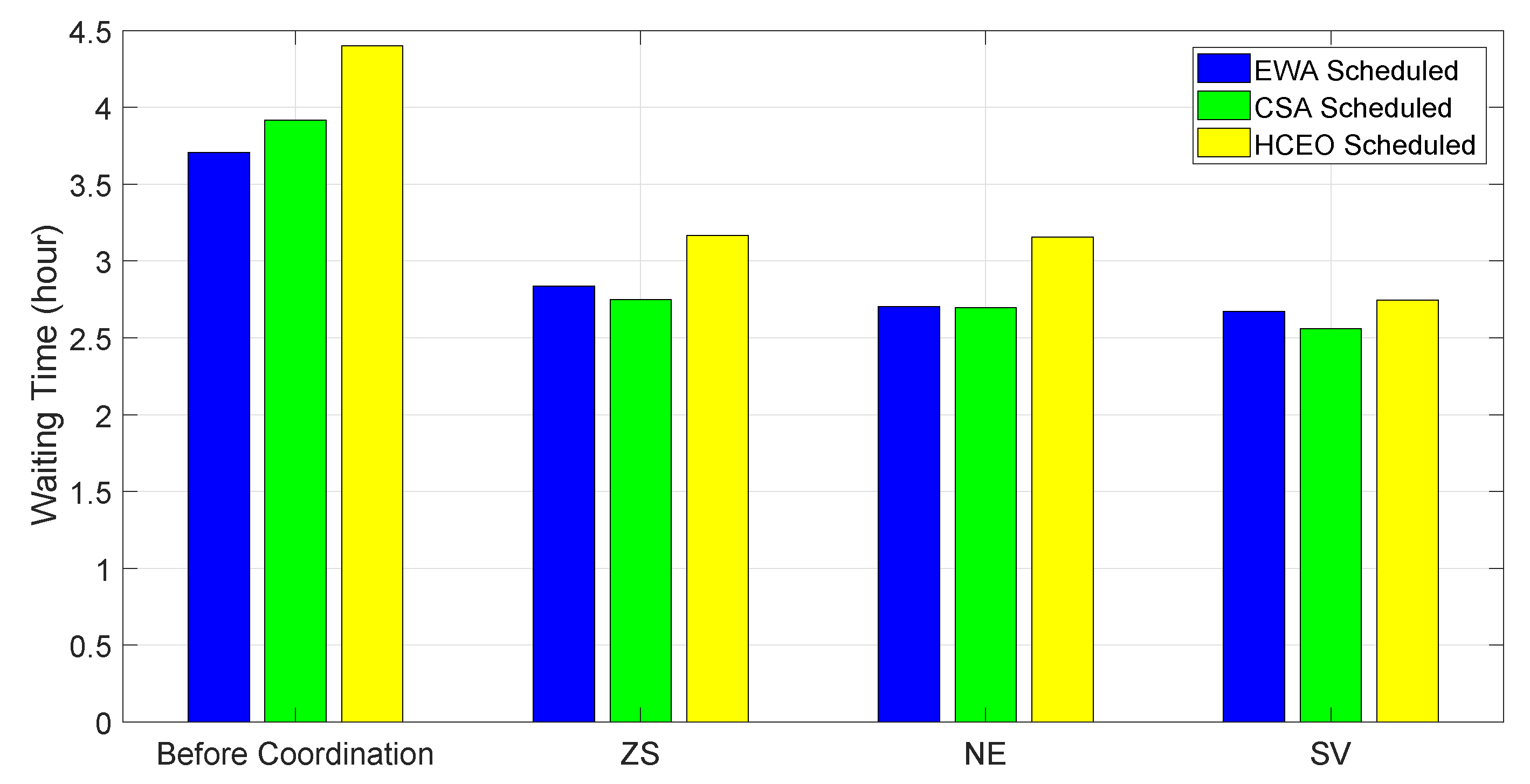
5.3.4. Waiting Time
The comfort level is measured with the help of the waiting time of appliances. The waiting time of an appliance is defined as the time interval for which a user waits for an appliance to switch ON for performing the particular task. It is evaluated for each technique as shown in
Figure 11.
The waiting time is zero for the unscheduled case; therefore, these graphs only represents the waiting time of implemented techniques before and after coordination. Before coordination, HCEO has a maximum waiting time and EWA has the lowest waiting time. HCEO has the lowest cost; however, its waiting time is high than other scheduling techniques. Therefore, if user wants to reduce electricity bill then delay of appliances will be more as compared to the normal finishing time.
The effect of coordination on waiting time of each technique is illustrated in
Figure 11. Coordination improves the comfort level of the consumers by reducing the appliances’ waiting time. It can be observed that the waiting time after coordination through each variant of GT is reduced. The waiting time of all scheduling techniques with all three variants of GT is given in
Table 6. In each technique, the maximum reduction in waiting time is achieved by SV, which is 27.93% for EWA, 34.67% reduction in case of CSA and 37.59% reduction in waiting time of HCEO.
5.4. Practical Applications Regarding the Proposed Work
The practical applications regarding to our work are specific to the electricity distribution automation management in the residential sector. These applications include demand side management and demand response programs. When our system will be implemented in these scenarios, it will greatly affect its cost and energy consumption optimization.
6. Conclusions and Future Work
This work proposes a HEMS, where load shifting strategy and appliances’ coordination are implemented for scheduling the household appliances. For scheduling, a hybrid algorithm HCEO is proposed. Later, a hybrid technique is evaluated and compared with its parent algorithms, that is, CSA and EWA. Comparison is performed on the basis of electricity cost, energy consumption, waiting time and PAR of appliances using RTP tariff. Electricity cost is decreased by 50.6% using the proposed hybrid technique HCEO as compared to the unscheduled case. In addition, the hybrid technique has also outperformed CSA and EWA in terms of cost minimization. Moreover, it has reduced the electricity consumption during on-peak hours because it has shifted high power appliances towards low price time slots. On the coordination side, ZS, NE and SV are compared with each other. These variants have reduced the waiting time of appliances as a result, user comfort is increased. SV has performed well in case of minimizing the waiting time of appliances and it has achieved the maximum reduction in waiting time of each technique as compared to ZS and NE. In the case of SV, the reduction in the waiting time of HCEO is 37.59%.
This paper can be extended by including micro-grids and their coordination for power sharing, in this proposed model. Coordination among micro-grids will help in decreasing the stress on the utility and HEMS will help in increasing user comfort.