Scheduling Sustainable Homecare with Urban Transport and Different Skilled Nurses Using an Approximate Algorithm

Abstract

The essential characteristics that distinguish homecare services from other routing and scheduling problems are relatively few patients being spread out over a large urban area, long transport times and several different services being provided. The approach that the authors present herein was developed to solve planning homecare services according to the criterion of increasing social sustainability and incorporating environmentally sustainable transport systems. The objective of this paper is to present a tool to plan the daily work carried out by a homecare service with assigned patients with specific care requirements. It relies on the resources of nurses with different qualifications by assuming costs that depend on both offering the service and the different chosen transport modes. The algorithm manages several priority rules by ensuring that homecare provider goals and standards are met. The developed algorithm was tested according to the weekly homecare schedule of a group of nurses in a medium-sized European city and was successfully used during validation to improve homecare planning decisions. The results, therefore, are not generalisable but its modular structure ensures its applicability to different cases. The algorithm provides a patient-centred visiting plan and improves transport allocation by offering nurses a better route assignment by considering the required variables and each nurse’s daily workload.

1. Introduction

Long-term care (LTC) is provided to patients with a chronic and even irreversible, illness or disability. Quite often the main goal of LTC is to keep or even improve, the quality of a patient’s remaining life [1]. Although health status is improving in OECD countries, the speed of the ageing process is likely to lead to increasing demand for LTC services [2] and the preferred place to receive such care is at home [3,4]. The ageing process is underway worldwide [5]. As older people are the primary recipients of LTC, pressure to serve demand will increase during the demographic ageing period. The complexity of developing a marginal part of the earlier healthcare system has led to different solutions in each country that has, to date, resulted in unequal access to LTC throughout Europe [6,7]. Home health care was primarily introduced into the healthcare system to take some burden off hospitals with crowded wards and also in public spending terms. However, the logistical service model was designed on an ad hoc basis [8] and LTC cannot be implemented as it currently stands in the home healthcare system. LTC incorporates a range of not strictly health-related care services to help people’s daily living over an extended period of time, such as showering/taking baths, dressing, eating, getting in/out of beds/chairs, moving around, using the toilet and controlling bladder/bowel functions, preparing meals, managing money, shopping for groceries or personal items, performing light or heavy housework, using a telephone and so forth. These services are collectively called ADL (Activities of Daily Living) and IADL (Instrumental Activities of Daily Living) [9]. Home health care and LTC are becoming inseparable from one other and the availability of services delivered at home is fundamental for frail older people as it represents the possibility of them remaining in their usual environments, despite them needing certain health care and social support.

Appropriate service delivery management is a key factor for the competitiveness of any homecare (HC) provider. Characteristics of HC services require managerial attention. Patients are relatively few but spread out over quite a large area, which makes inter-transport times long, while the type of care to be provided depends on a variety of patient requirements; for example, HC must be consistent for people with reduced mobility [10]. The process of dealing with this information includes the analysis and thorough knowledge of a series of variables, such as the types of transport that may be used; for example, maximum capacity (in physical dimensions) to be transported, analysis of public routes, location of patients, lists of patients to be visited on each route and so forth. Many researchers have pointed out that lack of appropriate tools to support the optimal routing of HC services and the complexity of their scheduling (the daily planning horizon and the combination of different transport tasks) lead to excessive organisational efforts [11,12,13]. The problem considered herein involves a daily and multimodal horizon as female nurses can choose different transport types depending on time by introducing sustainability concepts.

More than half the world´s population lives in urban areas. In 2015, there were around 34 megacities in the world (urban areas with a population exceeding 10 million people) and 75 urban areas were listed with a population of 5,000,000 or more. This indicates that supplying and supporting these urban centres is and will be, a major issue in the future [14]. As the growing use of motor vehicles in cities will continue to have a strong environmental and socio-economic impact [15], increasing pressure on urban realities has led to more interest being shown in all aspects of urban planning and its development, including all transport types (goods and people) Ros et al. [16]. Today there is growing concern about developing policies, programmes and projects that take sustainability into account [17] and refer to Centres for Sustainable Transport that define the requisites of a Sustainable Transport System [18]:

1. It allows the basic needs of individuals and societies to be met safely and in a manner consistent with both human and ecosystem health.

2. It is affordable, operates efficiently and offers a choice of various transport modes, which supports a booming economy.

3. It limits emissions and waste so that plants are able to absorb them, it minimises uses of renewable resources to sustainable levels and reuses and recycles its components and minimises noise pollution and land use.

Urban mobility must be sustainable from three main perspectives: economic, social and environmental [19]. Developments like HC must be bearable (socially and environmentally), fair (socially and economically) and feasible (environmentally and economically) [20]. Urban authorities wish to improve and support their neighbourhoods. Indeed, it is for these reasons that they restrict vehicle movements in city centres and create pedestrian-only zones or roads accessible only by public transport. However, these same urban authorities wish to offer a suitable level of HC to its fellow citizens, especially as populations in city centres tend to age and need HC services. Supplying HC in city centres has become more difficult for care and health institutions. Nevertheless, as patients require HC, demand for a rapid reliable HC chains still exists, which is expected to grow as a result of rapid urban growth and ageing populations. Changes in paradigm lead to new logistic and operational models to be sought that allow these new challenges. Homecare logistics is usually developed in an urban setting and plays a key role in city life. Thus, it is necessary to strike a balance between effective HC and the consequences of its mobility requirements [21].

This paper aims to present an approximate algorithm to improve the efficiency of urban HC services transport by grouping patients and delivering services in the shortest possible time at the lowest possible cost. Hence it is necessary to study how requests for services can be grouped and/or divided to make them suitable for subsequent HC completion. These issues are vitally important given the variability of associated services, transport routes and scheduled means of transport involved.

The next section presents the algorithm, based on the combination of the knapsack problem and the generalised assignment problem (GAP), which provides the mathematical basis to develop the proposed algorithm. The data employed to develop the Results Section in the paper were provided by the Care Centre for the Elderly (CCE). In 2017 and 2018 [22,23], the authors published particular cases or simplifications of the work herein included. Those cases made a comparison among various transport systems by making patient satisfaction a priority. This new article completely presents the algorithm by detailing the characteristics to implement it. The algorithm includes variables that refer to female nurses’ skills and allows routes to be defined according to their skills. Similarly, it develops a service cost, which contemplates the transport costs based on the possible options and the homecare-giving cost according to nurses’ skills. Calculating efficiencies in offering the homecare service is also considered. The Discussion includes the experiences gained from the study and the devised algorithm.

2. Materials and Methods

The scientific literature on HC delivery highlights the increasing need for health and social services to be more profitable and to serve an ever-growing number of requests. Therefore, scholars focus on the urge to reduce costs by minimising travel costs, waiting times and overtime through logistics and operations models, especially in relation to HC, Trautsarmwieser and Hirsh [24] conducted a literature review on daily and periodical HC. Bertels and Fahle [25] point out several key factors to assign patients to nurses using a combination of Constraint Programming and the Metaheuristic Simulated Annealing to solve scenarios with up to 50 nurses and 326 jobs. Eveborn et al. [10,26] developed a decision support system for Swedish HC service providers called Laps Care. It addresses a Set Partitioning Problem, solved by a solution approach based on repeated matching. These authors consider different transport modes (car, bicycle and walking) but not a transport mix approach. Dohn et al. [27] follow a Branch-and-Price approach to solve real-world instances with up to 15 nurses and 150 jobs. Bredstrom and Rönnqvist [28] and Rasmussen et al. [29] use Branch-and-Price Algorithms. Researchers analysed different clustering schemes in a later study done to reduce computational efforts. The use of meta-heuristics solution approaches is favoured by Bredström and Rönnqvist [30], Mankowska et al. [31] and Trautsamwieser et al. [12], who developed a Variable Neighbourhood Search Approach and model formulation for HC services in Austria by considering many legal constraints and nurse/patient satisfaction. Their work is based on time-independent travel times by focusing on rural areas where nurses have to use cars. Hiermann et al. [32] present a recent work on urban home caregivers, where a two-stage approach that combines Constraint Programming with different metaheuristics solves the real-world scenarios of an HC service provider in Vienna. Nurses choose between public transport or travelling by car based on their own preferences, while travel time data are based on estimates by the public transport service provider and Floating Car data. Fikar and Hirsch [33] propose a pooled transport service concept with designated drivers to convey nurses from one operational area to another but without encumbering them with the distress of driving and finding parking spots. Braekers et al. [34] focus on the trade-off between the often contradicting nature of the best possible patient convenience and optimal routing and formulate the problem as a Bi-objective HC Routing and Scheduling Problem. Their metaheuristic approach is designed to find a set of Pareto optimal solutions to provide decision makers with multiple options so they can choose according to their individual preferences and institutional policies.

The algorithm presented herein, according to the Branch and Bound technique, is similar to that of Clausen [35], Rouillon, Desaulniers and Soumis [36]. This technique, when applied in conjunction with decision rules to a combined problem of transport, capacity and assignment, enables an algorithm to be developed that facilitates the goal coordination possibility, such as optimising care resources and reducing transport costs (mix transport means considered). Indeed, the objective of this algorithm is to maximise the efficiency of the activities assigned to nurses and to thus maximise profits for all those stakeholders involved in the HC chain.

The algorithm is based on approaches to solve generalised assignment (GAP) and knapsack problems [37,38,39,40] but also includes some findings by Fisher et al. [41] and Snarclens de Grancy and Reimann [42]. The use of heuristics has proven especially important in the search for optimal solutions to GAP [43,44,45,46]. This has accelerated the search for solutions for the optimisation problem. To develop the HC route assignment algorithm presented herein, the authors built on the results of Ribeiro and Pradin [47], who rely on a two-phase method: firstly, selecting and assigning similar HC assistance (phase 1); secondly, establishing a new division and reallocation to minimise any possible inefficiency (phase 2) similarly to the work presented by Hiermann et al. [32], Rasmussen et al. [29]. Here the idea of Osorio and Laguna [39], who introduced different levels of efficiency of multiple resources or agents into their algorithm after assignment, is also considered. The procedure and solution to assign loads and orders to means of transport are discussed below. This assignment is determined according to the different capacities of the available care time options, patient services, minimising the division of services and improving efficiencies in-homecare services. Some authors have previously presented works to design the algorithm [48] which, in the present paper, centres on logistic and operational model aspects by emphasising their applicability to schedule the operations to be carried out by an HC unit.

From the presented literature review, it is deduced that planning HC services can be characterised by initial planning to be done some days before a given date and also before some modifications to be included or made on that particular date. The initial plan is not normally sensitive to the variable time because, conversely on the day of the operation, events take place that involve having to quickly reschedule HC activities.

Technically speaking, the considered problem can be taken as a Vehicle Routing Problem depending on transport times, where transport is multimodal as the sustainability concept and HC restrictions are introduced. HC considerations are described when contemplating the casuistry of both patients and female nurses. HC patients require one nursing service or more every day and, depending on the service type, they require a minimum nursing skill. Service type and duration are defined by the central services (CCE) as is, consequently, the input for the given problem. Patients need fluent communication with nurses to obtain satisfactory and sustainable HC. Female nurses are characterised by their skills and must inform CCE about any HC incidences they have worked on; thus, their work starts and ends at the CCE premises. Several contract types exist in terms of working day duration and hours worked at each home to confer flexibility to scheduling HC activities.

2.1. Homecare Algorithm Approach

The problem definition is summarised as that of finding the shortest path; that is to say, the transport of less weight (cost) from a fixed vertex (Care Centre for the Elderly; CCE) to the other vertexes (patients’ locations) or between two arbitrary vertices [49,50,51,52]. It is a pondered graph if we associate some values, p (v_i, v_j) with each arc of the graph. These values are called the weight or cost of their arcs (v_i, v_j). In each node $\mathrm{j}\in \mathrm{V}$, one patient P_j exist to whom one homecare-product HC_sj or more is associated, which requires one skilled nurse N_ns who can provide the homecare prescription at a cost c_sj and in a service time ${\mathrm{t}}_{\mathrm{i}}$.

As care must be provided within a time frame, a time window is required $\left[{\mathrm{a}}_{\mathrm{i}},{\mathrm{b}}_{\mathrm{i}}\right]$ that is associated with each node, within which a service is supposed to start. In the defined urban network, it is assumed for the CCE node that ${\mathrm{q}}_{0\mathrm{p}}={\mathrm{q}}_{\mathrm{n}+1\mathrm{p}}={\mathrm{S}}_0={\mathrm{S}}_{\mathrm{n}+1}=0$. Similarly, nurses work a schedule that must be considered and the time window associated with the CCE (where ${\mathrm{a}}_0={\mathrm{a}}_{\mathrm{n}+1},{\mathrm{b}}_0={\mathrm{b}}_{\mathrm{n}+1}$) represents the earliest possible departure from the CCE and the latest possible return time to the CCE, respectively. A fleet of $\mathrm{n}$ nurses of care-capacity $\mathrm{s}$ (denoted by set $\mathcal{K}= \left\{1,,,\mathrm{s}\right\}$) is based at the CCE. Unless otherwise stated, each nurse can travel at least one route.

All the HC services to be carried out, regardless of their type, are restricted by time constraints and are sometimes defined as a more or less wide interval schedule within which the care time should be located. This allows delivery to be done at the best suited time for the CCE (within this interval). Nevertheless, two variables that influence transportation can be defined as:

Transports that should leave from Origin at a given time:

Variable: Origin_Time;

Transports that must reach a Destination at a given time:

Variable: Destination_Time.

The algorithm needs to coherently and effectively plan, programme and control these two different transportation cases. As in the healthcare environment, available resources are restricted and it is very important to use them efficiently. If several possible routes exist based on the nurse type being studied, the algorithm chooses that which allows the shortest travelling time so that patients are assisted as soon as possible and resources, in this case nurses, become available sooner for the next delivery of services.

The route to the Nurse Assignment Problem with the HC service time windows is defined by taking a real urban network as a basis. Within it, we can specify:

• $\mathrm{G}=\left[\mathrm{V},\mathsf{A}\right]$ where $\mathrm{V}=\left\{0,\mathrm{n}+1\right\}\cup \left\{1,\mathrm{n}\right\}$, where 0 and n + 1 are the CCE,
• $\mathsf{A}=\left\{\left(\mathrm{i},\mathrm{j}\right):\mathrm{i}\in \mathrm{V},\mathrm{j}\in \mathrm{V};\mathrm{i}\ne \mathrm{j}\right\}$ is the arc set,
• With each arc $\left(\mathrm{i},\mathrm{j}\right)\in \mathsf{A}$ a travel cost ${\mathrm{c}}_{\mathrm{ij}}$ is associated and a travel time ${\mathrm{t}}_{\mathrm{ij}}$,
• Pj: j-th is the patient set, mainly one patient, who requires HC services given by certain nurse types N_ns from the CCE and is found in a given urban area,
• With each HC service to the patient, cost ${\mathrm{c}}_{\mathrm{sj}}$ and service time ${\mathrm{t}}_{\mathrm{sj}}$ are associated.

The algorithm introduces the following notation:

• R_ks: k-th existing routes, s-th nurse type, chosen by the CCE, in accordance with the location of patients, geography, infrastructure, the HC required, nurse-patient history and so forth. For example, when the CCE defines six routes for nurse type 1, on which the required services are to be provided to all the patients daily, then indicator k varies from 1 to 6 and this indicator will take the value 1. R_ks = (R11, R21, R31, R41, R51, R61)
• Ti: i-th type of vehicle for nurse transportation, classified according to its costs and availability for use by the CCE. For example, if the CCE is to use five different vehicle types (T1, T2,…, T5), then i varies from 1 to 5.
• N_ns: n-th number of nurses corresponding to each s-th types of nurses, classified according to their skills and their availability for care giving. For example, if the CCE is to use five nurses skilled 3 level 1 and 2 level 3, then N_ns = (N11, N21, N31, N13, N23).
• P_jks: j-th patient who requires assistance from a given (s-th) nurse type, assigned to route k by the CCE, where patients’ assignment to each route is carried out according to the proximity between patients and the route, the qualifications required for care tasks and patients’ personal preferences. One patient might require more than one different HC type, which must be carried out by a different nurse type.
• HC_msj: m-th HC issued by s-th nurse type to the j-th patient. For example, if a patient (P2) requires three HC services to be provided, two by nurse type 1 and one by nurse type 3, nurses scheduled by the CCE, then j = 2, s = 1, 3 and m = 1, 2, 3. Therefore, HCms2 = [HC112, HC212, HC322] are all the requirements issued by patient 2.
• Ck: the cost assigned to the k-th transport route (R_ks), generally by transport type (T_i). For example, if the CCE uses for nurse type 3 only routes R23 and R43 on a single day, the costs that the algorithm must consider are c2 and c4.

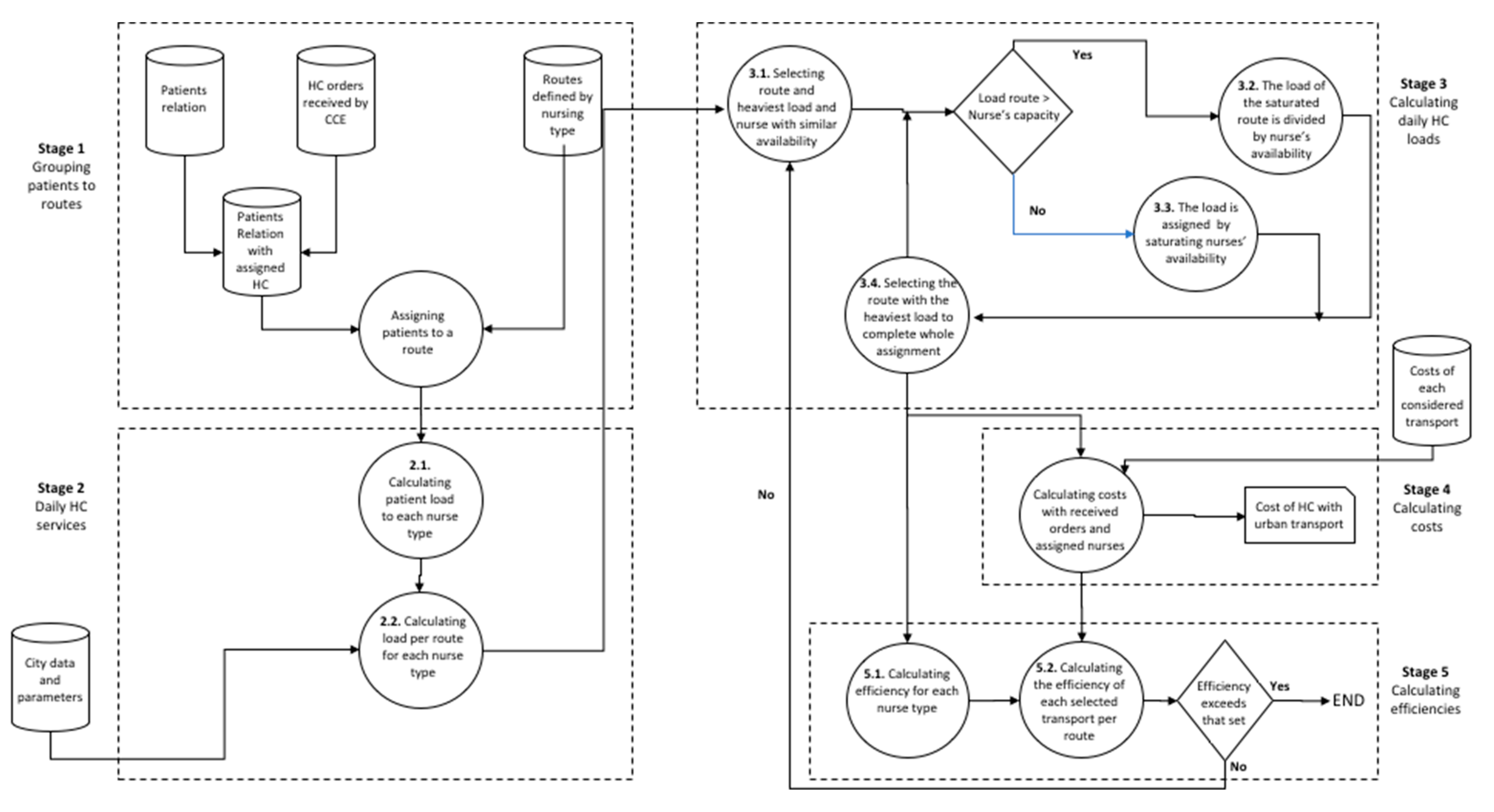
2.2. Homecare Algorithm Stages

The approximate homecare algorithm is illustrated in Figure 1.

STAGE 1. Grouping PATIENTS by the route of each nurse type. The CCE defines an initial transport route as the starting point for algorithms; patients are assigned to a particular route according to their proximity to each route and the nurse’s required competence level. The allocation of each patient (Pjs) to a route (R_ks) can be noted as P_jks, where k is the route index. Then distance matrices are produced for the available transport modes and a combination of them. The data set is only as accurate as the route planner of Google Maps and its reliability depends on the chosen location. From experience, the estimations for the subject of this study are fairly accurate.

Table 1. Homecare distribution in the city analysed in the study.

Frequency	Monday to Friday	Monday to Sunday	Tuesday to Friday
1/day	34	7	1
1/week	4
2/day	5	3
2/week	13
3/day		1
3/week	5
Total	73

shows the frequency of each HC order to be provided in the city subject under study (19).

STAGE 2. Calculating daily HC SERVICES. The daily HC load is calculated (the time required to complete the services provided to a patient j), for each patient, denoted by Load (P_jks) and the daily load for each route, Load (R_ks), defined in Stage 1.

Step 2.1.

Calculating load according to all the demand orders assigned to each nurse type (units: min):

$$\mathrm{Load}\left({\mathrm{P}}_{\mathrm{jks}}\right)={\displaystyle \sum }_{\mathrm{m}=1}^{\mathrm{d}}\mathrm{Load}\left({\mathrm{HC}}_{\mathrm{msj}}\right)$$

(1)

Step 2.2.

Calculation of load according to each route of each nurse type (units: min):

$$\mathrm{Load}\left({\mathrm{R}}_{\mathrm{ks}}\right)={{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{b}}\mathrm{Load}\left({\mathrm{P}}_{\mathrm{jks}}\right)={{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{b}}{{\displaystyle \sum }}_{\mathrm{m}=1}^{\mathrm{d}}\mathrm{Load}\left({\mathrm{HC}}_{\mathrm{msj}}\right)$$

(2)

STAGE 3. Calculating daily HOMECARE LOADS. In this stage, nurses need to provide all the loads of received requests, which are assigned to the different routes (Stage 1). In Stage 2 the algorithm still does not consider the constraints, which are built into the different steps of Stage 3.

Step 3.1.

Selecting the route with the heaviest load and the assignment of nurse N_ns with a similar time availability to this load and sufficient qualification.

N_ns is assigned if:

$$\begin{gathered} \mathrm{Load}\left({\mathrm{R}}_{\mathrm{ks}}\right)\le \mathrm{Capacity}\left({\mathrm{N}}_{\mathrm{ns}}\right) \\ \forall \mathrm{s}\to \mathrm{s}=\left\{1\dots \mathrm{a}\right\},\forall \mathrm{k}\to \mathrm{k}=\left\{1\dots \mathrm{c}\right\} \end{gathered}$$

(3)

According to the following rules:

RULE 1. Assign N_ns to the route with Load R_ks (in decreasing order), then skip to Step 3.3.

RULE 2. If Capacity N_ns < Load R_ks, go to Step 3.2.

Step 3.2.

If Load HC of a route is greater than the capacity of the non-assigned nurse’s available time, then:

$$\begin{gathered} \mathrm{Load}\left({\mathrm{R}}_{\mathrm{ks}}\right)>\mathrm{Capacity}\left({\mathrm{N}}_{\mathrm{ns}}\right) \\ \forall \mathrm{s}\to \mathrm{s}=\left\{1\dots \mathrm{a}\right\},\forall \mathrm{k}\to \mathrm{k}=\left\{1\dots \mathrm{c}\right\} \end{gathered}$$

(4)

The division of routes’ load is done as indicated in Equation (5).

$$\mathrm{Load}({\mathrm{R}}_{\mathrm{ks}})={\mathrm{Load}}_1\left({\mathrm{R}}_{\mathrm{ks}}\right)+{\mathrm{Load}}_2\left({\mathrm{R}}_{\mathrm{ks}}\right)$$

(5)

According to the following procedure:

$$\begin{gathered} {\mathrm{Load}}_1\left({\mathrm{R}}_{\mathrm{ks}}\right)=\mathrm{Capacity}\left({\mathrm{N}}_{\mathrm{ns}}\right) \\ {\mathrm{Load}}_2\left({\mathrm{R}}_{\mathrm{ks}}\right)=\mathrm{Load}({\mathrm{R}}_{\mathrm{ks}})-{\mathrm{Load}}_1\left({\mathrm{R}}_{\mathrm{ks}}\right) \\ \forall \mathrm{s}\to \mathrm{s}=\left\{1\dots \mathrm{a}\right\},\forall \mathrm{k}\to \mathrm{k}=\left\{1\dots \mathrm{c}\right\} \end{gathered}$$

(6)

Step 3.3.

If a Load HC is assigned to a route, Load (R_ks) is less than the capacity of allocated nurse N_ns. However, when failing to meet the constraint of maximum number of patients P_jsk to be visited (by exceeding that number Psk > Wsk), load is divided as follows:

$$\mathrm{Load}({\mathrm{R}}_{\mathrm{ks}})={\mathrm{Load}}_1\left({\mathrm{R}}_{\mathrm{ks}}\right)+{\mathrm{Load}}_2\left({\mathrm{R}}_{\mathrm{ks}}\right)$$

(7)

where:

$$\begin{gathered} {\mathrm{Load}}_1\left({\mathrm{R}}_{\mathrm{ks}}\right)=\mathrm{Load}\left({\mathrm{maxP}}_{\mathrm{jsk}}\right) \\ {\mathrm{Load}}_2\left({\mathrm{R}}_{\mathrm{ks}}\right)={\displaystyle \sum }_{\mathrm{non}-\mathrm{assigned}}{\mathrm{Load}}_1\left({\mathrm{R}}_{\mathrm{ks}}\right) \end{gathered}$$

(8)

$$\forall \mathrm{j}\to \mathrm{j}=\left\{1\dots \mathrm{b}\right\},\forall \mathrm{k}\to \mathrm{k}=\left\{1\dots \mathrm{c}\right\}$$

(9)

Step 3.4.

Having assigned the nurses to the route with the heaviest load, the assignment of nurses continues with the route with the next heaviest load. To do so, the procedure returns to Step 3.1. This process should be continued until all the routes with HC loads are processed. It also includes the routes that are cut because of one algorithm constraint or more.

STAGE 4. Calculating COST. With all the orders received by the CCE assigned to the selected nurses N_ns in Stage 3, attention is now paid in this section to calculate the total cost (C_t). The total cost (C_ij) comprises the transport cost of each stretch of the corresponding routes (C_k) using the selected transport type T_i (with the associated cost listed in

Table 2. Costs of each considered transport type.

Ti	Attributes	C(Ti)
T1	Walking	€0
T2	Bus	€20/month
T3	E-bikes	€9/month
T4	Taxi	€3 trip (flat rate in the city)
T5	Car	€0.19/km + parking

) and the cost of giving the HC service (C_sj) by considering the unit cost (c_sj) of the selected resource (N_s) and giving HC.

$$\mathrm{C}\mathrm{t}={\mathrm{C}}_{\mathrm{i}\mathrm{j}}+ {\mathrm{C}}_{\mathrm{s}\mathrm{j}}$$

(10)

The transport cost will be ${\mathrm{C}}_{\mathrm{i}\mathrm{j}}={\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{c}}{\mathrm{C}}_{\mathrm{k}}$

where:

$$\begin{gathered} {\mathrm{C}}_{\mathrm{k}}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{a}}{\mathsf{\delta }}_{\mathrm{i}}{\ast \mathrm{C}}_{\mathrm{i}} \\ \begin{array}{c}{\mathsf{\delta }}_{\mathrm{i}}=0;{\mathrm{if}\mathrm{T}}_{\mathrm{i}}\mathrm{is}\mathrm{not}\mathrm{used}\\ \\ {\mathsf{\delta }}_{\mathrm{i}}=1;{\mathrm{if}\mathrm{T}}_{\mathrm{i}}\mathrm{is}\mathrm{selected}\end{array} \end{gathered}$$

(11)

The HC service cost will be ${\mathrm{C}}_{\mathrm{s}\mathrm{j}}={\displaystyle \sum }_{\mathrm{s}=1}^{\mathrm{a}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{c}}_{\mathrm{s}\mathrm{j}}$

STAGE 5. Calculating EFFICIENCIES in assigning transport means. To verify an optimal transport type assignment to each nurse’s route in this stage, the efficiency associated with each transport type is calculated. The definition of efficiency depends on the CCE’s requirements, defined here as using transport type in relation to the maximum number of patients that this transport type allows to be visited on a single route.

Step 5.1.

Calculating efficiency (α) for each selected nurse N_ns in Stage 3:

$${\mathrm{N}}_{\mathrm{ns}}\to \mathsf{\alpha },\mathrm{s};\mathsf{\alpha }=\mathsf{ϵ}\left[0,1\right];\forall \mathrm{s}\to \mathrm{s}=\left\{1..\mathrm{a}\right\}$$

(12)

where:

$${\mathsf{\alpha }}_{\mathrm{nsk}}=\frac{\mathrm{Load}\left({\mathrm{N}}_{\mathrm{ns}},{\mathrm{R}}_{\mathrm{Ks}}\right)}{\mathrm{Capacity}\left({\mathrm{N}}_{\mathrm{ns}},{\mathrm{R}}_{\mathrm{Ks}}\right)}$$

(13)

Step 5.2.

If the efficiencies calculated for each T_i equal or exceed 0.7, the assignment is final as this level is considered acceptable by the CCE and, as such, the calculation with the algorithm ends. For each T_i where the efficiency calculation gives a result below 0.7, the assignment of transport type T_i should be repeated.

3. Results

Application to the studied urban area. Biking was calculated as being slower than cars or public transport (15 km/h) but still outpaced public transport on all the routes and also outpaced cars on a number of occasions. Finding the shortest route between patients implies creating distance matrices and considering the city’s specific urban characteristics for each transport mode [52]. Hence nurses’ earliest arrival time depends not only on their average attainable speed but also on the routes they are allowed to use [23].

The case presented herein is based on patients’ real data, their location in the city, the care they require and the time needed to provide such care, the constraints of the received care and the nurses available, plus the data provided by the CCE [53]. The CCE created the initial routes based on patients’ requirements, time constraints, nurse qualifications and personal preferences. The algorithm’s input can be presented as shown in

Table 3. Patient allocation to the initial route as defined by the CCE.

Patient Address	Location Code	Route (Rks)	Care Need Code	Time Required (minutes)	Pjks
Location patient 1	A000	11	Th_1_20	20	P0511
Location patient 2	A001	91	Mo-Fr_1_20	20	P5091
Location patient 3	A002	81	Tu-Th_1_30	30	P4381
Location patient 4	B001	91	Mo-Fr_1_30	30	P5691
Location patient 5	B002	121	Mo-Fr_2_30	30	P58101

. In the provided example, the origin times of all the routes are previously set and coincide with the schedules when the nurses who correspond to the CCE shifts start. Nonetheless, the algorithm was studied using other origin times (including shifts, etc.) and the algorithm obtained similar results with the same level of efficacy.

In the evaluated example, which considers three means of transport (car, buses combined with walking, e-bikes), other transport systems, such as trams or metro, were attributed to buses with walking. The study done of the times included transfer times, waiting times, busy traffic depending on the day and time, parking or locking bikes and even the frequency with which public transport arrived, which also depended on the day and time. This approach allowed sustainable mobility systems to be considered either exclusively or combined with other systems. The real example had a maximum of 10 nurses available (different skills). One of the objectives of this algorithm was to perform capacity planning for the requirements of the assigned HCs. To this end, having real knowledge about traffic and planning routes according to the real traffic situation allows a good solution to be simultaneously found but does not enable the capacity planning of available resources.

The data for Tuesday’s services in the analysed city are shown in

Table 4. Loads of the routes to be considered for assigning type 1 nurses (Tuesday).

Prioritised Routes		Algorithm Step 3.2
Route (Rks)	Time Load (minute)	Route (Rks)	Time Load (minute)
R101	667 *	R11 a	365
R11	495 *	R11 b	30
R41	300	R101 a	382
R71	207	R101 b	185
R91	200
R31	190
R21	187
R51	186
R81	177
R61	165

Note: * Load of routes that does not meet the algorithm constraints and should be “divided” (note by a or b).

.

In the case presented herein, a combination is necessary between covering the route on foot (which initially needs more time) and by public transport (despite being faster, waiting times sometimes make it less profitable). The possibility of using a private vehicle or a taxi is also considered: in both cases, routes are faster but have a very high cost. Transportation costs (see Table 2) reveal two feasible transportation types: T₂ (bus combined with walking) and T₃ (e-bikes) (see

Table 5. Data aggregated as a result of assigning routes to type 1 nurses on Monday.

	Bus + Walking				E-Bikes				Cars
Monday	Number of Patients	Care Time (hour)	Travel + Idle Time (hour)	α	Number of Patients	Care Time (hour)	Travel + Idle Time (hour)	α	Number of Patients	Care Time (hour)	Travel + Idle Time (hour)	α
Nurse 1	9	6.4	1.6	0.9	9	6.4	1.6	0.8	9	6.4	1.6	0.9
Nurse 2	5	5.1	2.9	0.8	7	7.1	0.9	0.9	5	5.1	2.9	0.7
Nurse 3	5	5.0	3.0	0.7	5	5.0	3.0	0.7	6	4.6	3.4	0.6
Nurse 4	6	4.6	3.4	0.7	6	4.6	3.4	0.6	7	7.0	1.0	0.9
Nurse 5	4	3.9	4.1	0.7	9	6.7	1.3	0.9	9	6.7	1.3	0.9
Nurse 6	9	6.0	2.1	0.9	13	7.1	0.9	0.9	12	7.0	1.0	0.9
Nurse 7	5	3.5	4.6	0.6	10	6.5	1.5	0.9	11	6.6	1.4	0.9
Nurse 8	6	3.2	4.8	0.5
Nurse 9	10	5.8	2.2	0.9
Average efficiency				0.75				0.84				0.85

). Calculating route efficiencies is a very important part of the algorithm and is considered of essential relevance by the CCE. Stage 5 finishes calculations.

Liu et al. [54] established that the services logistic chain, like that herein presented, has to face many environments that require technical, management and economic solutions. The algorithm firstly offers the cost of the solution (stage 4) but also efficient resources uses (stage 5).

In the herein presented algorithm, selecting the best outcome was done with the efficiency factor (α), as reflected in stage 5. In the studied case, efficiency was associated with the social element of sustainability (social welfare), bearing in mind that the main objective of an HC service is citizen welfare. Nonetheless, the other elements of sustainability (the economic and environmental elements) are compromised when performing the HC activity. Other aspects were considered so they would form part of the algorithm, such as factors like transport costs and the nurses’ working day (hours worked and hours not worked), as was choosing vehicles with fewer polluting emissions.

In the applications made with the algorithm, the study reduced nurses’ total working hours a day by the bus and walking combination and by comparing if nurses ride e-bikes, which respectively reduced the total time that nurses spent travelling by 5–44%. This result is applicable to an urban environment where the public transport network is sufficient and biking is allowed on a reasonable number of roads. Better HC management can support the efficient use of healthcare institutions’ resources, high-quality HC and aspirations towards liveable communities and sustainable development. The presented approach introduced sustainability into the HC value model by supporting the decision-making process [52].

4. Discussion and Conclusions

The paper aims to present an approximate algorithm to improve the efficiency of urban HC services transport by grouping patients and delivering services in the shortest possible time at the lowest possible cost. The algorithm developed herein does not address attaining an ideal (optimal) allocation of nurses to each route but bears in mind the space-time needed to attend to each patient. This is due fundamentally to the variability included in transport times, which depends on the selected transportation system type. Nevertheless, it offers a good assignment of routes to nurses by considering the aforementioned variables, plus each nurse’s daily availability. The paper sheds light on how the use of multiple transport modes can influence resource allocation, patient satisfaction and HC providers’ cost management.

The presented algorithm has several advantages over other planning transport systems, including the sustainability of the HC transport system and better controls journeys and the improved use of resources. Shorter waiting times for patients help improve patient expectations, which also falls in line with the CCE’s general strategy. This is determined to improve the services for patients by attempting to keep costs as low as possible. This algorithm offers the possibility of making progress in knowing which variables influence route assignment for HC. Future studies can explore other options to combine transport modes for HC nurses; for example, enabling switches from the public transport network to the city bike system on the same route, where it is reasonable thanks to time/cost considerations.

This approximate algorithm provides a good solution within the HC services frame in urban areas as it allows the constraints and data provided by different transport modes to be included and even the possibility of including multimodal transport that represents cities’ current trend to be sustainable. More importantly, patient satisfaction is guaranteed as they are provided in advance with a more refined plan for their HC service/s, waiting times are minimised and they do not experience stress while waiting for an indefinite time or enduring unnecessary delays. Extending options in HC planning and making it more efficient can make HC accessible and affordable to frail people who would otherwise be left without help.

The people in charge of designing policies in urban settings must consider many mobility systems with which they can organise transport in an urban area to maintain stakeholders’ economic feasibility in the city and to ensure social sustainability for cities. The solution presented herein reinforces sustainable transport system guidelines by consistently accessing more humanised health and the ecosystem, which is more efficiently operative at a lower cost.

Regarding sustainability and in line with the TBL approach [54], the following benefits are obtained using the developed HC algorithm:

-

Social benefits by making the healthcare HC service feasible by taking services to patients, which increases the perceived welfare [6,7]. The algorithm prioritises scheduling nurses to the same patients, an aspect that enhances the reliability of the provided HC service

-

Economic benefits (in the long term), as transport costs are a variable of the algorithm and form an intrinsic part of a country’s social and healthcare policies. The algorithm links the economic aspects to the environmental ones that the HC service requires

-

Environmental benefits (in the short- and mid-terms), by considering a means of transport offer that addresses minimum emissions and is ecological by factoring in an activity that is increasingly present in urban areas of cities.

In sustainability terms, it is important to point out that the present article is about a developed algorithm which, despite its main leitmotif being to reduce HC system costs by considering different transport systems, is based on the constraints imposed by patients as to the times that their HC requires as the routes initially defined by the CCE are based on HC and welfare criteria.