A Comparative Study on the Influence of DC/DC-Converter Induced High Frequency Current Ripple on Lithium-Ion Batteries

1. Introduction

Battery energy systems for stationary storages as well as for electric vehicles that are based on lithium-ion batteries are widely regarded as one of the key technologies to realize the energy transition [1]. A determined shift could mitigate the most severe aspects of climate change so that in recent years the research on battery materials, modelling, ageing, systems and integration has been thriving [2]. Yet, amongst others, a lot of open questions remain in the field of diagnosing batteries connected to power electronics in practical conversion systems although they are already comprehensively used in stationary systems and electric vehicles alike. Batteries, connected to power electronics that play a vital role in stabilising voltage quality and power delivery have been considered for many years as an important part of so called microgrids that could be a method to secure the energy supply in power grids with highly distributed feed-ins [3,4,5]. Moreover, as electric vehicles will have spread extensively, their battery packs are considered to be used to buffer peaks in power demand or dips in power supply [6] in vehicle to grid systems thus demanding sophisticated charging and discharging systems that are based on various power electronic circuits [7,8,9]. In summary, every battery in battery energy systems is in some way connected to power electronics, especially DC/DC-converters. They are based on controlling semiconducting, transistor-based high frequency switches to modulate the desired voltage or current respectively. Therefore, if costly and bulky filtering measures were not installed, the cells would be under severe high frequency switching stress. High frequency current waves, called ’current ripple’, would be induced on the batteries and could lead to battery ageing mechanisms that are still unknown or render known ageing mechanisms more severe. If the results showed no further influence and therefore implied that current ripple does not shorten the battery life, the results could still lead to improvements in the design of battery energy systems as filters that are normally used to even out ripple, e.g., in [9,10,11], could be reduced in size or even be omitted. It is expected that the severity of current ripple rises with future converters that are based on silicon carbide (SiC) that operate at very high frequencies of several tens or even hundreds of kilohertz [12]. However, the common usage of switching frequencies considerably higher than a few kilohertz are not expected to excite electrochemical reactions thus high frequency current ripple is not expected to have any severe impact on battery ageing just as it is suggested by the following overview.

In the last years, a small amount of research groups have dealt with those particular questions in various ways: In [13], De Breucker at al. investigate the influence of current ripple, induced by a DC/DC-converter connected to a high voltage battery pack that could occur in a plug-in hybrid vehicle. Based on the switching frequency of 8 kHz the double layer is supposed to be mainly influenced by the ripple. Instead, their results show that the temperature plays a much more important role. It should be noted, that only two battery packs have been investigated. In comparison, the authors of [14] superimpose sinusoidal current waves with different frequencies up to 14.8 kHz on the DC current that charges and discharges 15 different 18,650 lithium-ion cells with a nickel cobalt aluminium oxide positive electrode (NCA) in a more detailed ageing test. It is argued that the aforementioned heat generation, leading to faster battery ageing, might also be caused by the imposed ripple current. Yet, a direct formula or factor is not given. A second study that deals with the effects of superimposed sinusoidal current waves can be found in [15]. Instead of NCA, more than 18 commercial cells with a positive electrode that is made of nickel manganese cobalt oxide (NMC) are used. Again, the authors stress that elevated temperatures cover possible effects originating from small current ripple. Finally, Bessman et al. give a short but comprehensive review of additional research in this particular field in [16]. Moreover, they carry out measurements with underlying triangular waves using twelve larger prismatic cells that are more comparable to cells that are used in high energy and/or high power battery storage systems. Compared to the other studies and most of those further mentioned within them, the work that is presented in [14] stands out since it is one of the very few that suggests a significant connection between current ripple and accelerated ageing. Moreover, most explanations remain vague and have to be categorised only as well thought-out assumptions. Thus, this present study has two goals: On the one hand, it is a further investigation on the effects of current ripple induced by practical DC/DC-converters on cylindrical 18,650 NMC lithium-ion batteries. The results of comparative cyclic ageing tests using ripple currents and comparatively unperturbed DC-current respectively, are shown and analysed thoroughly. On the other hand, the authors try to give further explanations as to why it turns out to be quite challenging to find reliable answers to the specific question of how exactly alternating currents affect battery ageing. The particular approach at hand is organised as follows: Section 2 is a detailed description about the hardware setup, the design of the cyclic ageing tests and the investigated battery are introduced. For the ageing tests, a DC/DC-converter to cycle the batteries has been developed. Its working principle and control algorithms are introduced shortly. Furthermore, regarding the test procedure, the converter is accompanied by conventional battery test equipment, that delivers mostly undistorted DC-currents, so that correspondent ageing tests with DC-currents that do not have significant current ripple can be carried out. Those ageing tests follow a set of rules that are established to be able to analyse the preassigned ageing parameters, to make the ageing tests as comparable as possible and to narrow down side effects that could overlay the influence of current ripple. In Section 3 the ageing results for a representative batch of ageing parameters is given, described in detail and more uncommon methods are introduced shortly. The depiction of the ageing results is focused on the comparison between the conventionally aged cells and those aged with ripple current. Subsequently, the results are discussed and analysed critically at the ends of each subsection. To conclude, in Section 4 the results are classified and rated. Based on this, further advice for the practical use of batteries that are connected to power electronics is given so that future battery energy storage systems can be used in an optimal way.

2. Experimental

In this chapter, the circuit for the cyclic ageing tests is proposed, the setup is shown and the design of the ageing tests is elaborated. The battery that has been used in every ageing test is a commercially available ’LG 18650 HE4’ cylindrical 18,650 lithium-ion battery with a graphite anode and a cathode made out of cobalt-, nickel- and manganese oxide (NMC). Its nominal capacity is $C_{\mathrm{N}}=2.5\mathrm{Ah}$, measured at a 1 C discharge from the end-of-charge voltage $U_{\mathrm{EOC}}=4.2\mathrm{V}$ to the end-of-discharge voltage $U_{\mathrm{EOD}}=2.5\mathrm{V}$.

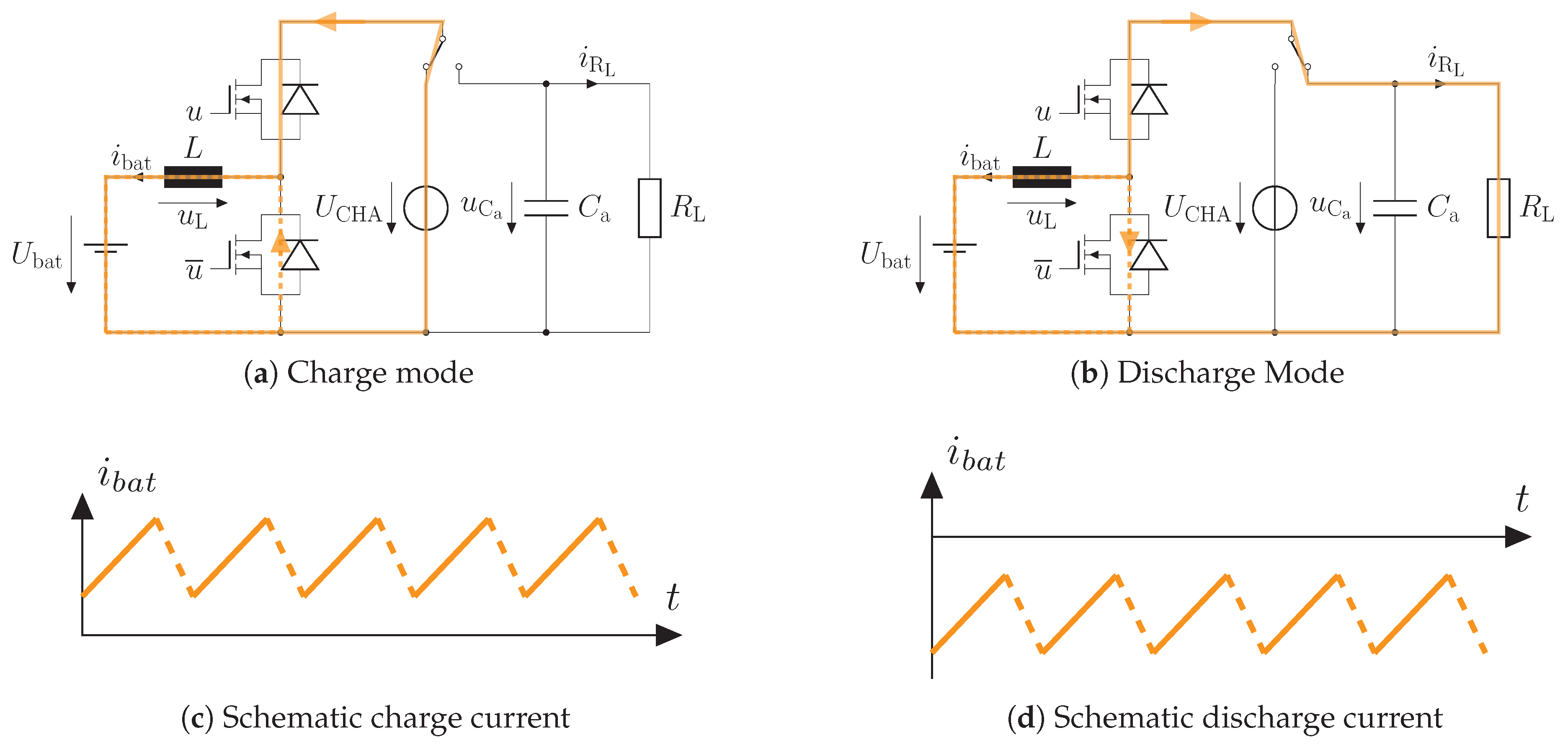
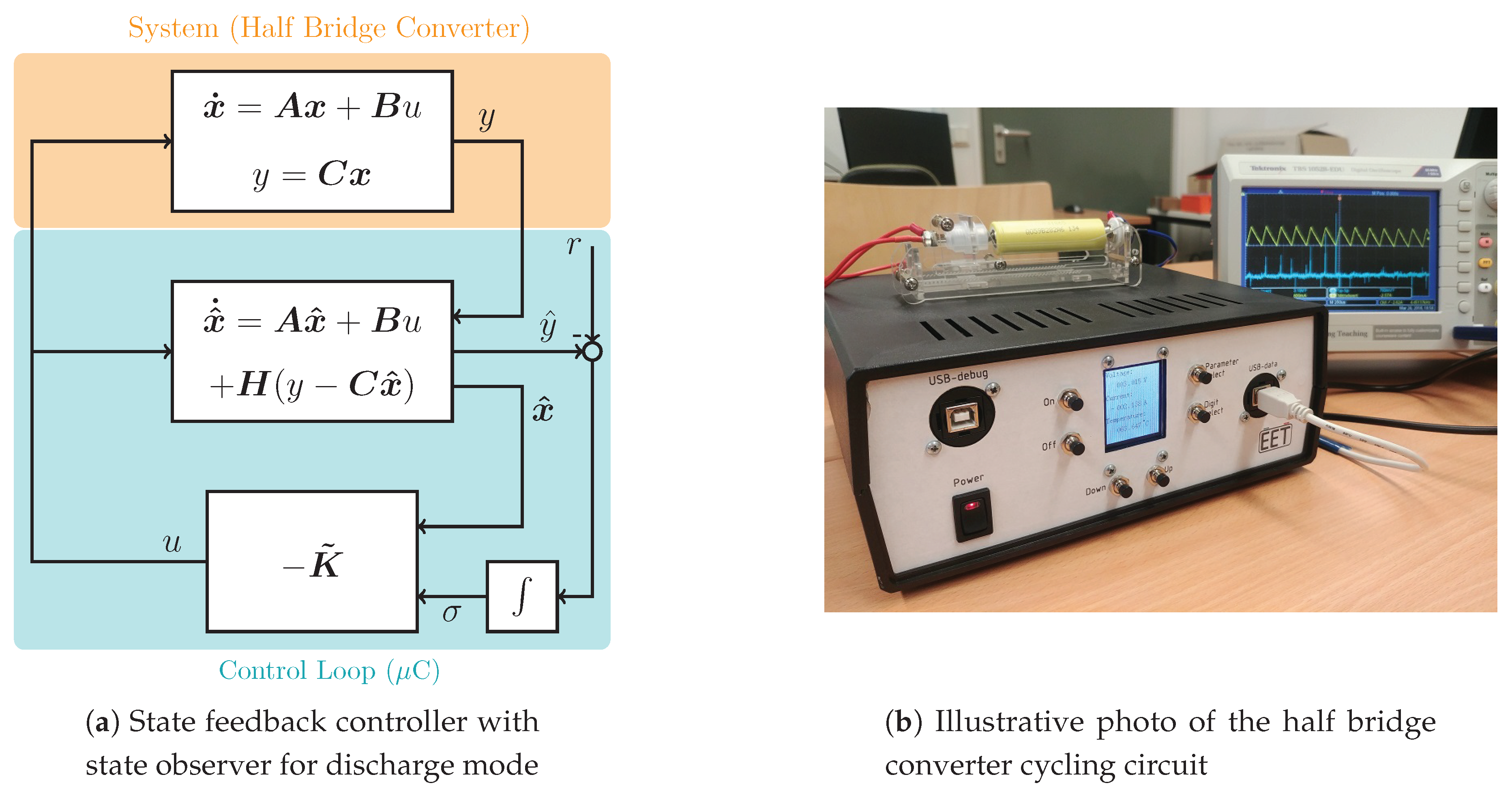
2.1. Ripple Current Test Circuit

The short literature overview in the introduction has already been a glimpse of how challenging the investigation of the influence of current ripple on battery ageing appears to be. First of all, well suited test equipment has to be found. Keeping the focus on the selected literature, the authors of [14,15,16] use signal generators to induce sinusoidal or triangular waves on the DC-current flowing in and out of the batteries. This is a very viable approach since the spectra only consist of the fundamental wave in case of the sinusoidal excitation or in the well known form of odd harmonics that decline in orders of $1/n^2$ in case of triangular ripple currents. Thus, these methods have the highest potential for reproducibility but cannot be seen as a practical approach. Especially a pure sinusoidal excitation should be considered carefully as a recent study [17], has shown, that using higher harmonics is a feasible tool to analyse the electrode reactions. Thus, an impact of higher current harmonics on the quality of the electrode reactions cannot be excluded. At the cost of higher noise and a slight signal dependency on the state of the circuit, actual DC/DC-converters might also be used as cycling circuits that induce ripple currents on the batteries as De Breucker et al. have done in [14]. They use a half-bridge converter with a high voltage battery pack. Although one can expect the most practical results, it comes with a lot of constraints such as expected noise because of the voluminous setup and very high currents or voltages, respectively. Besides, a high voltage system is more hazardous and makes repeated tests with more cells or battery packs quite costly.

In this paper, a reasonable compromise is found: Using the widely known half bridge converter as shown for example in [18] at low voltage as a foundation to cycle single cells is still a practical approach that is cheap, scalable and does not have to deal with high voltage and severe noise. Figure 1 shows the basic working principle of the circuit. The battery is located at the low side and is connected directly to the smoothing inductance. At the high-side a 12 V voltage source or a resistive load with a smoothing capacitor are connected to the circuit with a simple switch, depending on whether the the battery is charged or discharged, respectively. Low- and high-side are interconnected with field-effect transistors (FET) and their internal body diodes. In Figure 1a,b, the current flow is given, depending on the operation mode. Assuming lossless and ideally fast switches, an ideal inductor, that $U_{\mathrm{CHA}}$ is a constant voltage source, that $U_{\mathrm{bat}}$ and $u_{C_{\mathrm{a}}}$ are approximately constant or rather their time constants are large compared to the switching frequency the differential equation

$$\begin{array}{c}\hfill -L\frac{\mathrm{d}{i}_{\mathrm{bat}}}{\mathrm{d}t}=u_{\mathrm{L}}=\underset{\mathrm{charge}\mathrm{mode}}{\underbrace{U_{\mathrm{bat}}-u{U}_{\mathrm{CHA}}}}\mathrm{or}\underset{\mathrm{discharge}\mathrm{mode}}{\underbrace{(U_{\mathrm{bat}}-u{u}_{C_{\mathrm{a}}})}}\end{array}$$

(1)

with $u\in \left\{0,1\right\}$ yields the linearly rising and falling current wave, that is depicted in Figure 1c,d respectively. Thus, the battery current is basically a triangular wave that is induced on a mean value ${\overline{i}}_{\mathrm{bat}}$ comparable with the approach in [16].

Combining the differential equation

$$\begin{array}{c}\hfill C_{\mathrm{a}}\frac{\mathrm{d}{u}_{C_{\mathrm{a}}}}{\mathrm{d}t}=\frac{1}{R_{\mathrm{L}}}{u}_{C_{\mathrm{a}}}\end{array}$$

(2)

that affects the system while discharging the battery with Equation (1) yields the full dynamic description of the circuit model in the upper half of Figure 1. However, it is more convenient to separate the equations as indicated by the switch on top of the circuit diagram and design independent control algorithms for charging and discharging, i.e., for the highlighted paths in Figure 1a,b respectively. In both cases, the output variable is the same as the state variable $i_{\mathrm{bat}}$. The control loop is based on a state feedback controller taken from a textbook such as [19]. It is designed so that the output asymptotically follows the desired value ${\overline{i}}_{\mathrm{bat}}$, i.e., the charge or discharge current of the battery. As the other state variable $u_{C_{\mathrm{a}}}$, that does not appear while charging, is not measured while discharging, a state observer, e.g., as in [19], has to be added. A full block diagram is shown in Figure 2a. As indicated in the picture, the control algorithms are carried out on a microcontroller. In this case, it is an ’ARM Cortex-M4’ on an ’Infineon XMC4700 Relax Kit’. Moreover, an interface is implemented so that the cycling circuit is able to communicate with a PC via USB. The incoming measurements on the PC are gathered, visualised in real time and continuously saved with a GUI that is implemented in LabView. On top of that, the case comes with basic I/O-features and a status display. A representative photo of the circuit is shown in Figure 2b.

2.2. Ageing Test Structure

In order to be able to relate ageing phenomena with ripple current, the ageing tests are based on comparison with ageing results of identical ageing tests, that are conducted as a reference test on the conventional test system ’Arbin BTS2000’. It is not the aim of this work to formulate a comprehensive ageing model for the tested battery. That is why the ageing matrix, depicted in

Table 1. Distribution of the cells between the four different ageing tests. $\overline{SOC}$ and $\vartheta$ are kept constant at 50% and 35 °C, respectively.

	Test Systems
$\Delta \mathit{DOD}$	Conventional	Ripple Current
100%	$C_1$, $C_2$, $C_3$, $C_4$	$R_1$, $R_2$, $R_3$, $R_4$, $R_5$, $R_6$
10%	$C_5$, $C_6$	$R_7$, $R_8$

, only consists of two different cycle depths $\Delta DO{D}_1$ = 100% and $\Delta DO{D}_2$ = 10%. Moreover, every cell that has been exposed to ripple current is marked with the letter R in a dark yellow or light orange, respectively. Consequently, the cells that are aged by the conventional tests system are marked with a dark green C. $\Delta DO{D}_1$ has been chosen as one cycle depth so that the ripple current might cause higher ageing rates because of higher or respectively lower high-frequency overpotentials, that shortly deep discharge or overcharge the battery respectively and might remain undetected by a battery management system in a practical application. As it is presented in [20], very low or very high SOC affect rapid SEI-growth, the occurence of Inhomogeneities, co-intercalation of solvents or accelerated decomposition in general. Thus, the main question to be answered is: Is it possible and if so, how is it possible to separate ageing effects and connect them solely to the current ripple? Besides, batteries that are aged with deep full cycles age much faster, see e.g., [21], so that the experiment becomes statistically more evaluable faster due to the possibility to test larger amounts of cells at the same time. In contrast, it is commonly accepted by now that low cycle depths such as $\Delta DO{D}_2$ around a low or medium $\overline{SOC}$ result in much slower ageing rates. Thus, superimposed ageing mechanisms such as the current ripple appear much stronger so that it should be easier to detect its expected influence. This mindset draws through the other parameters of the ageing tests as well. All tests are conducted in a temperature controlled environment in an oven (Memmert UF55) at an only slightly elevated temperature of 35 °C so that calendar ageing is reduced to a minimum as indicated in [22]. Besides, the mean state of charge is always $\overline{SOC}$ = 50% and the cells are always cycled with a current rate of $I_{\mathrm{cyc}}=2.5\mathrm{A}$ which translates to a current rate of 1 C compared to the nominal capacity of $C_{\mathrm{N}}=2.5\mathrm{Ah}$. At this current rate and a switching frequency of $f_{\mathrm{S}}=5\mathrm{kHz}$. the amplitude of the current ripple is going to be around $0.29I_{\mathrm{cyc}}$ at $\overline{SOC}$ = 50%, ranging from $0.22I_{\mathrm{cyc}}$ at the discharge cut-off voltage of $2.5\mathrm{V}$ to $0.32I_{\mathrm{cyc}}$ at the charge cut-off voltage of $4.2\mathrm{V}$, dependant on the battery’s terminal voltage.

In Figure 3a, the general structure of every ageing test is depicted. It mainly consists of three parts: The cycling with one hundred full cycles at a time, periodical check-up measurements to obtain updated ageing parameters, cycling tests and occasional electrochemical impedance spectroscopy (EIS) to gather information on the dynamic behaviour of the tested battery. It should be further noted that for $C_1$ and $R_1$ check up tests have been done every fifty full cycles to have some information about the influence of the check up tests on battery ageing and about the probability of missed information if the check-ups are to far apart from each other. Just as the reference ageing tests, the check-up tests for the rippled batteries are also conducted at the conventional cell tester to minimize differences induced by different test equipment. The general structure and course of the check-up is depicted in Figure 3b. Within the tests, the remaining capacity after a full discharge with 1 C = 2.5 A is measured at the beginning. Afterwards, the cell is fully discharged and charged with a much smaller current, i.e., $\left|I\right|$ = 0.2 C = 0.5 A, to obtain information that can be used to calculate the differential voltage analysis (DVA) [23]. The rest of the check-up consists of partial discharges and charges and subsequent relaxations over thirty minutes so that the evolution of the cell’s inner resistance is also taken care of, albeit not shown in this article as the results do not contribute anything unique to the evaluation. If the cell is still functional, it will be cycled again. In this work, an arbitrary limit such as eighty percent remaining capacity is not used as it is unclear, whether there is any severe ageing because of current ripple, that appears in the nonlinear part of battery ageing [24]. Therefore, ageing tests are not necessarily ended at typical limits.

In addition to that, the dynamic impedance is measured with a Zahner IM6ex every two hundred cycles at three different states of charge, i.e., $SO{C}_1$ = 80%, $SO{C}_2$ = 50%, $SO{C}_3$ = 20% with a bandwidth of $f\in \left[100\mathrm{mHz}100\mathrm{kHz}\right]$.

3. Results and Discussion

The following section deals with the comparison of the capacity loss, the differential voltage analysis (DVA), the impedance and the distribution of relaxation times (DRT) between the cells, that are either exposed to ripple current or the cells that are cycled with the conventional test system. For each method, the battery groups, related by cycle depth, are compared to each other. Normally, it is refrained from investigating each individual cell as the amount of different potentially affecting parameters renders such assumptions pointless. It is assumed that only a possibly resulting general trend leads to representative and reproducible results.

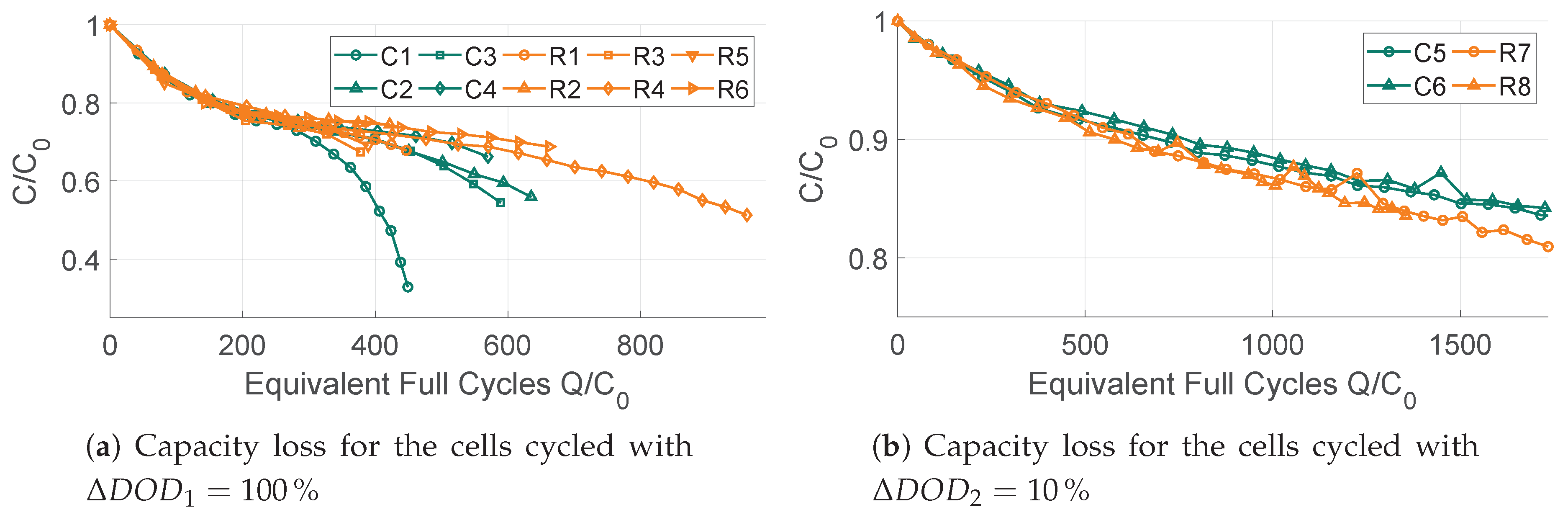
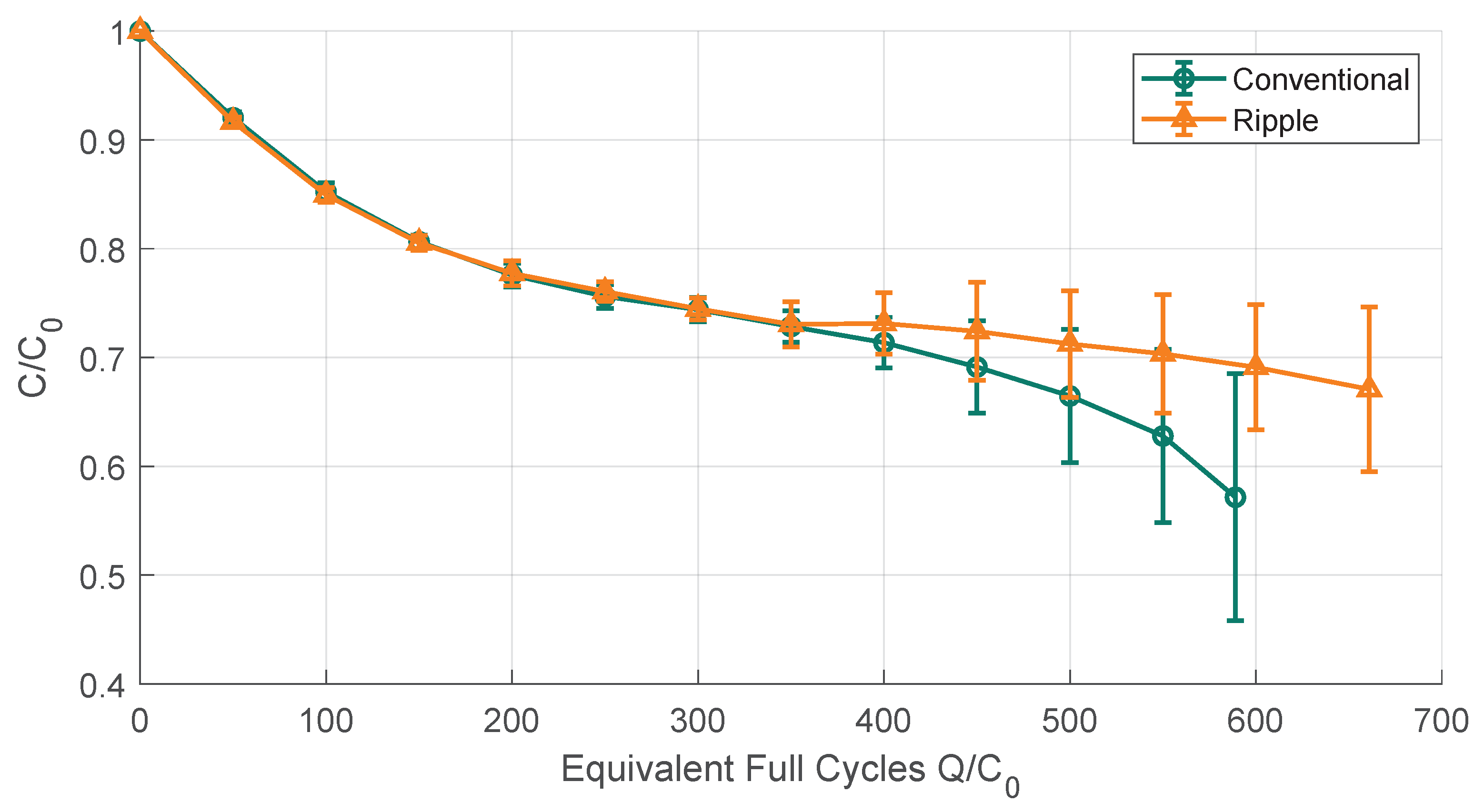
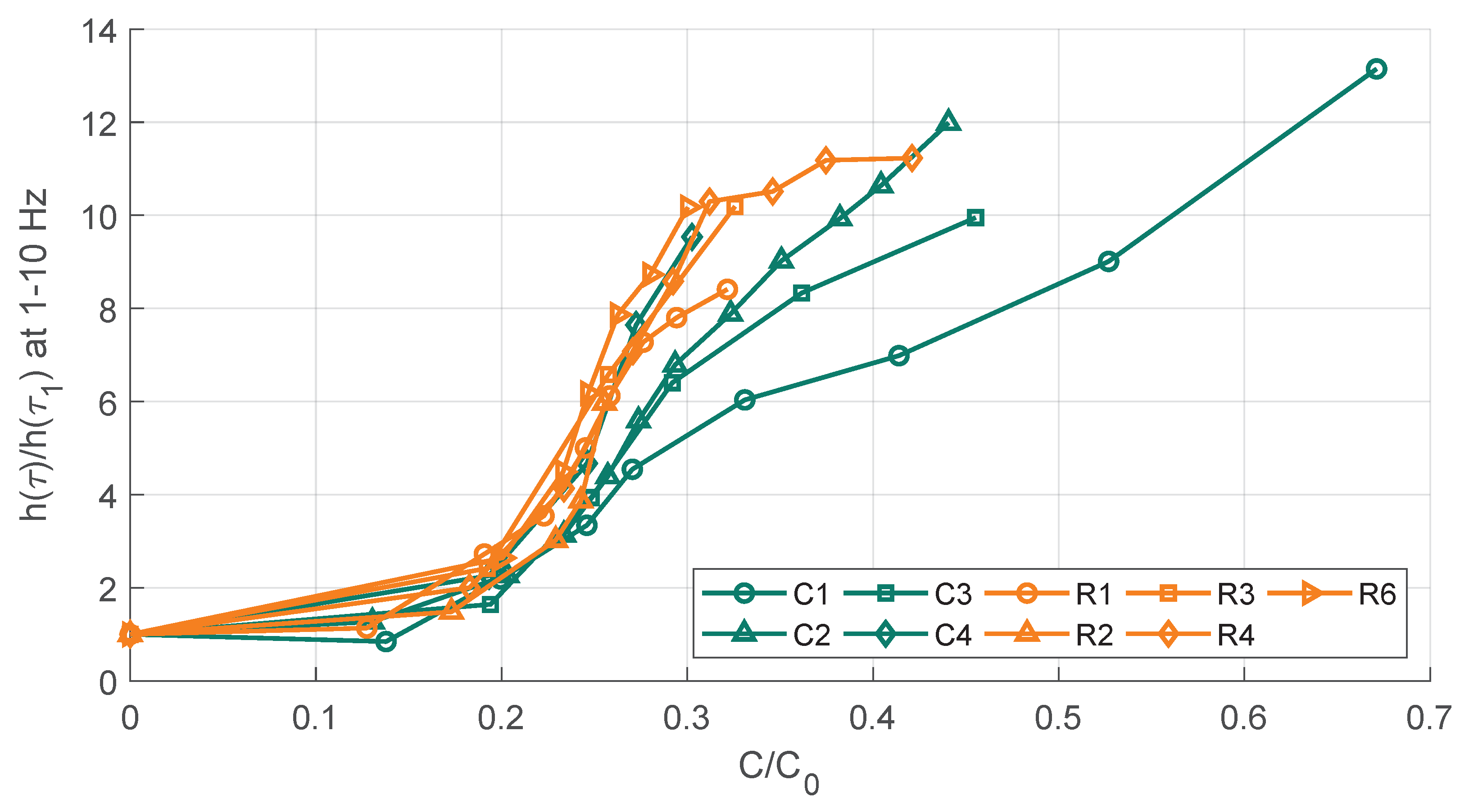
3.1. Capacity Loss

The capacity diminution is seen as one of the most important parameters to define ageing as it is directly connected to electric vehicle range or the amount of time a storage system can operate. Accordingly, the capacity fade is also referred to as the ’state of health’ (SOH) such as in e.g., [20,25] so that the remaining capacity is directly linked to the remaining usability of the battery in practical applications. In Figure 4, the capacity evolution for each tested cell is depicted. The Figure 4a represents the cells that have been cycled with $\Delta DO{D}_1$ = 100% whereas Figure 4b shows the evolution of the capacity for the cells with a much lower $\Delta DO{D}_2$ of 10%. To reduce the business of Figure 4a due to the higher amount of tested cells, the same measurements are shown in Figure 5 as mean values with errorbars, that represent the upper and lower bounds of confidence intervals for a probability of 95%. It should be noted that the markers in Figure 5 are arbitrarily set at every fifty equivalent full cycles as the results have been interpolated to make the statistical analysis possible. Besides, the suddenly increasing slope of the ripple current graph in Figure 5 comes from premature cell failure of R2, R3 and R5 as indicated in Figure 4a. Throughout all tests a major similarity can be noted: The capacity drops quite steeply in the beginning of the tests. Interestingly, the capacity depletion of the cells cycled with $\Delta DO{D}_1$ slows down at roughly $0.8C_0$ which is a common reference point for the transition between linear and nonlinear ageing [24,26]. Later on, the typical spread between faster and severely faster aged cells as reported in [27] is observable. Furthermore, it becomes visible in the last part of the graph that the rippled cells and the conventionally aged cells are grouped respectively which is easier to distinguish in Figure 5. At the same time, the upper and lower error bounds become much larger. However, this grouping should not be over-interpreted as it only occurs at late stages of battery life beyond a $SOH$ of approximately 70% and is expected to be linked to premature cell failures (see above) and the volatile region of nonlinear battery ageing that could also be due to statistical spread induced by production tolerance as investigated in [27].

The aforementioned grouping is also visible for $\Delta DO{D}_2$, as seen in Figure 4b. In opposition to the fully cycled cells, R7 and R8 age a bit faster than the conventionally aged reference cells C5 and C6. Moreover, the contradictory observation between Figure 4b and Figure 5 cannot be explained satisfactorily in another way than statistical spread. It is assumed, that an absence of the unexpected early failure of cells R2, R3 and R5 would have led to a more similar trend of the mean values. Moreover, the uncertainty of the statistical approach rises as the number of analysed cells diminish. Therefore, the analysis of the capacity loss leads to the assumption that the effect of a deep cycle depth greatly outmatches the influence of current ripple whereas the influence of current ripple could be visible for the partially cycled cells instead.

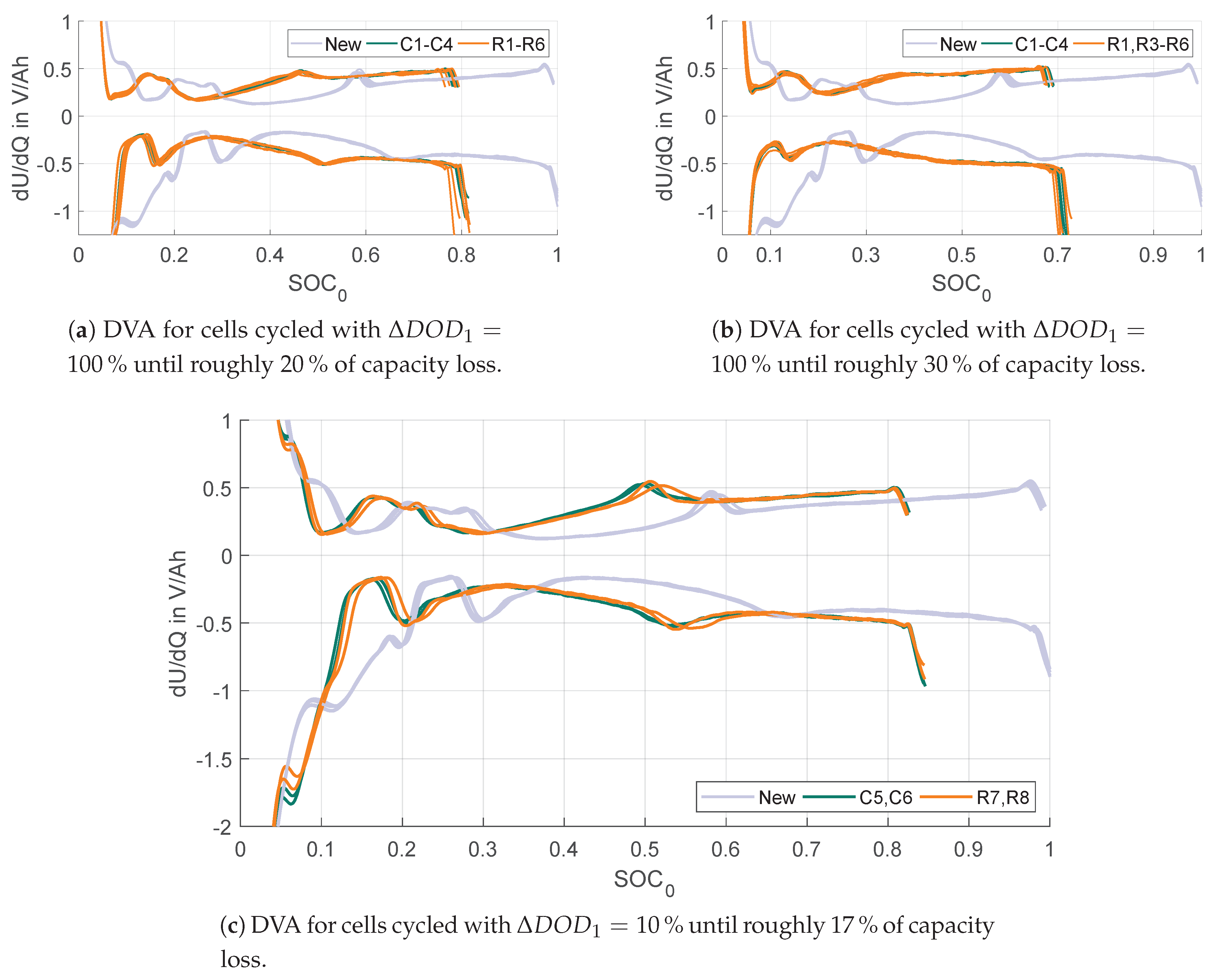
3.2. Differential Voltage Analysis (DVA)

In recent years, the differential voltage analysis (DVA) has become a common tool to analyse the behaviour of the electrodes of a lithium-ion battery, primarily the behaviour of the anode [23,28]. It is based on the derivation of the voltage with respect to the transferred charge or the respective SOC. Characteristic local maxima or minima, respectively, correlate with the phase changes of the graphite that is commonly used as an anode material such as within the investigated cell. Thus, the ageing effects are visible in the depiction of the DVA-curves. However, the phase changes are only clearly visible for very low charge or discharge currents that do not cause high and therefore overlapping overpotentials. In this study, a current of $I_{\mathrm{DVA}}=0.5\mathrm{A}$ which translates to $0.2C_0$ is used as a compromise between visibility of characteristic elements and measurement time.

In Figure 6, three exemplary graphics are shown to illustrate the results of the DVA. The pictures are separated by $\Delta DO{D}_{1/2}$ and the respective $SOH$, as on the left side in Figure 6a, the cells cycled with $\Delta DO{D}_1$ are shown after a capacity loss of roughly 20% whereas on the right side in Figure 6b the cells cycled with $\Delta DO{D}_1$ are shown by the time the cells approximately reached a capacity loss of 30%. As it can be seen in Figure 4a, the cells are not necessarily cycled with the same amount of cycles at that particular point. Besides, one cell is left out in Figure 6b. The rippled cell R2 has broken down before it has reached the desired capacity drop of 30%, so that it is not shown in this particular picture. For further comparison, the DVA-curves, obtained at the initial check-up are also shown in light grey for each cell. They overlap each other well which is an indicator for the highly precise and reliable manufacturing of the cells. As it can be seen in Figure 6a,b, the overlapping continues as the cells age. This is expected until the cells reach a $SOH$ of 80% and is even maintained in regions beyond a typical capacity loss of 20%. As long as the DVA is executed for cells with the same capacity loss, even a distinction between rippled cells and conventionally aged cells is impossible let alone cells of the same group. In Figure 6c, it is possible to spot the different curves. However, the grouping that has been reported for the capacity loss is not as clearly visible as before. As a reason of the aforementioned very minor differences, especially for cells cycled with $\Delta DO{D}_1$, the only further analysis the plots could be used for, is the analysis of cyclic ageing effects in general as the diminution of the local extrema due to degradation of the anode and shortening due to capacity loss are typical features. However, the authors refrain from this as it is not in the scope of this work and discussed thoroughly in the literature [23,28,29]. In addition to that, a look at Figure 6 in accordance with [29] reveals that, given the same $SOH$, i.e., the same capacity loss, substantial changes of the anode surface and therefore the voltage plateaus of its intercalation reaction are mostly linked to the cycle depth. This is one reason why the $SOH$ has been used as the control variable to pick the proper check-up test for comparison. Thus, current ripple does not seem to contribute in a way the cycle depth already does on its own to the loss of active material or loss of active lithium, respectively as it would have been observable in the DVA-curves otherwise.

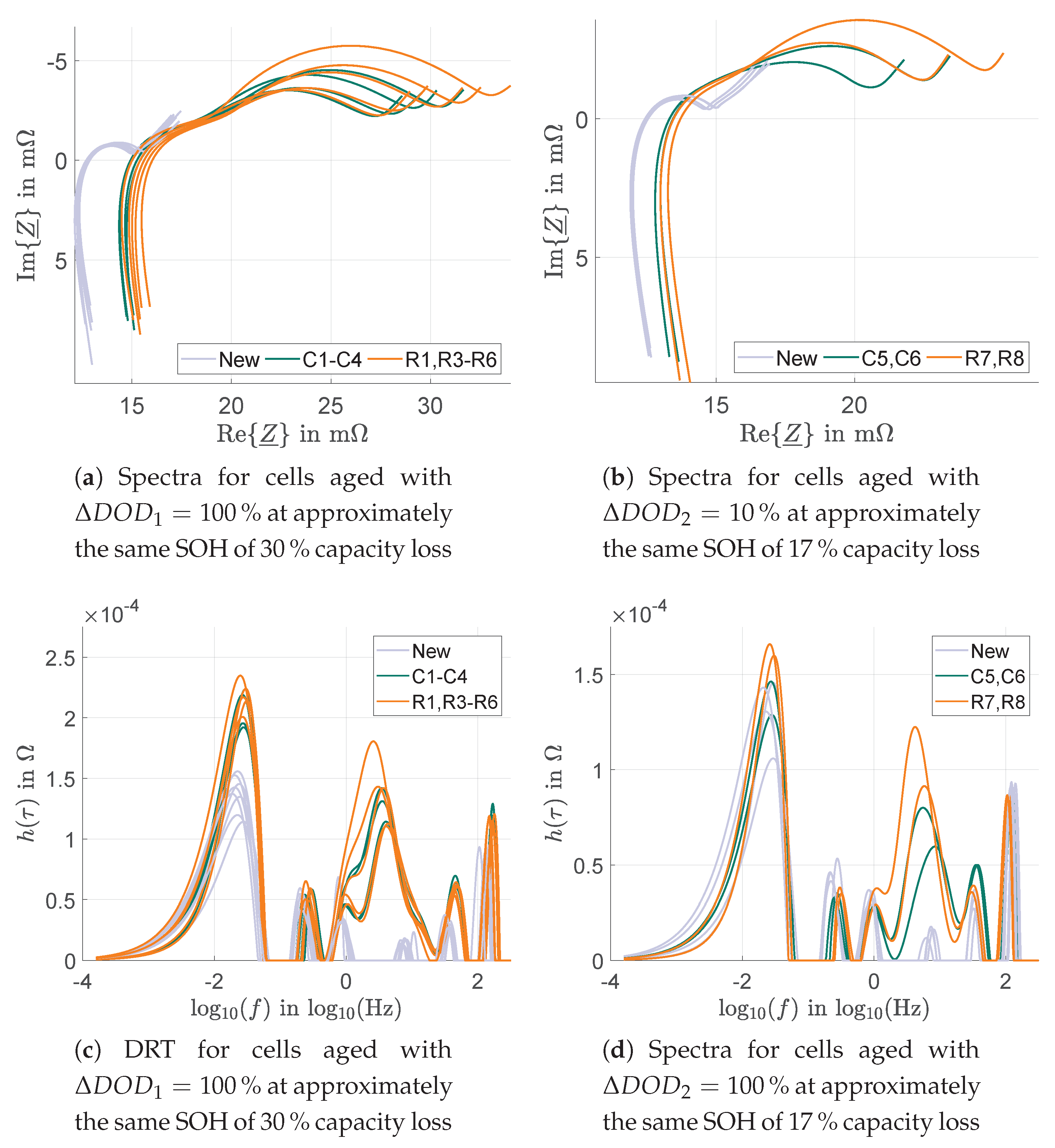
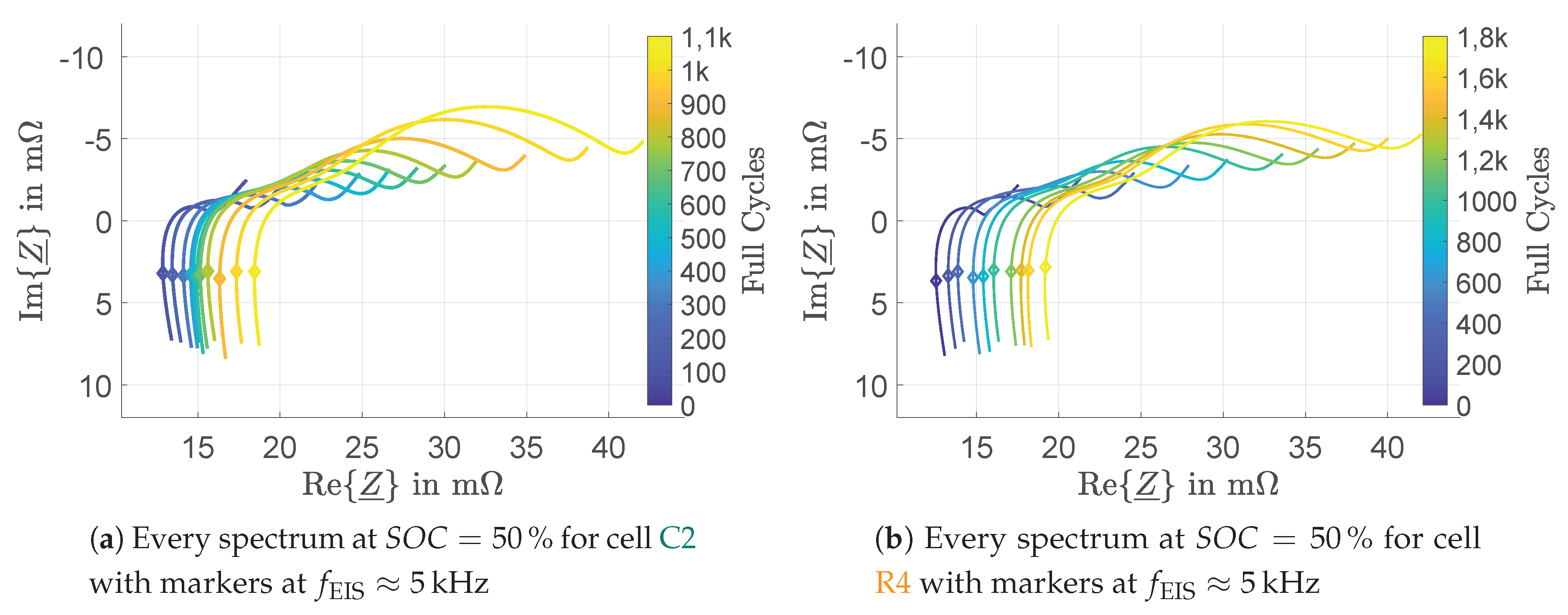
3.3. Impedance Measurements

For a lot of years, the electrochemical impedance spectroscopy (EIS) has been one of the most widely used methods to analyse any electrochemical system [30]. Based on the assumption that electrochemical systems are approximately linear and time-invariant (LTI), a galvanostatic excitation with a sinusoidal current over a broad band of frequencies $\omega$ yields the impedance

$$\begin{array}{c}\hfill \underline{Z}\left(\omega \right)=\frac{\underline{U}\left(\omega \right)}{\underline{I}\left(\omega \right)}.\end{array}$$

This impedance can be used to derive a dynamical model of the measured cell or to analyse ageing effects as the behaviour of the impedance is directly linked to corresponding characteristics of the cell such as the electrode reactions or diffusion. The trend of the impedance is normally visualised as a Nyquist plot in the complex plane. This visualisation can be seen in Figure 7a,b in the same way as the results for the DVA are presented in Figure 6, i.e., at the same SOH to minimize unwanted discrepancies between the groups of cells because of different capacity losses. A picture that shows the spectra at $SOH=80\%$ is omitted as it does not supply any further information compared to the impedance spectra shown at a capacity loss of $30\%$. The shown frequency range is $f_{\mathrm{EIS}}\in \left[1\mathrm{mHz}10\mathrm{kHz}\right]$ since high frequency parts above $10\mathrm{kHz}$ do not show any distinguishable differences between the aged cells. Moreover, the inductive reactance rises significantly at higher frequencies so that this area has been also cut due to better visibility of the capacitive area. Furthermore, general statements about the alteration of the spectrum because of cyclic ageing are neglected again to keep the focus on the comparison. As expected, the intersection of the real axis, often referred to as the inner resistance $R_{\mathrm{i}}$, e.g., in [30], rises as the cells age. It should be noted that the spread between the initial intersections has been equalised in Figure 7a,b to improve comparability. Taking this into account, a further grouping is visible as most inner resistances of the rippled cells have grown slightly larger compared to the conventionally aged cells. More information is gathered, if the polarisation of the electrodes is taken into account. Considering the new cells, the representation of the electrodes cannot be distinguished. This changes as the batteries age since both flattened semicircles separate from each other and become wider. Except for one rippled cell in each group, i.e., R6 and R8, no clear differentiation between the rippled and the conventionally aged cells is observed. Moreover, it is challenging to derive the most prominent time constants that cause the spectra at hand, yet this valuable information is a nominal asset to compare rippled and non-rippled cells even further.

To achieve this goal and to validate whether the slight outlier mentioned before is also visible in other ways, the calculation of the distribution of relaxation times (DRT) has proven to be a suitable tool to analyse impedance spectra further [33]. As explained in [30], the polarisation of dielectric materials such as electrolytes can neither be fully described by a single time constant nor a single $RC$-circuit, respectively but rather as a distribution of time constants that is often referred to as the distribution of relaxation times. It is explained by the representation of the impedance as

$$\begin{array}{c}\hfill \underline{Z}\left(\omega \right)=R_0+R_{\mathrm{pol}}{\int }_0^{\infty }\frac{g\left(\tau \right)}{1+j\omega \tau }\mathrm{d}\tau \end{array}$$

(3)

with the inner resistance $R_0$ and the distribution function $g\left(\tau \right)$ that is usually normalised by

$$\begin{array}{c}\hfill {\int }_0^{\infty }g\left(\tau \right)\mathrm{d}\tau =1\end{array}$$

so that the polarisation resistance $R_{\mathrm{pol}}$, that represents the width of the semicircle in typical impedance spectra of batteries is separated from the distribution. Thus, $g\left(\tau \right)$ needs to be calculated. Considering measurements with a limited amount of m data points $\underline{Z}\left(\omega \right)$ over a limited set of m excitation frequencies $\omega$ and an arbitrarily chosen amount of n time constants ${\tau }_k$, the integral becomes the discrete sum

$$\begin{array}{c}\hfill \underline{Z}\left(\omega \right)=R_0+R_{\mathrm{pol}}{\displaystyle \sum _{k=1}^n}\frac{g\left({\tau }_k\right)}{1+j\omega {\tau }_k}.\end{array}$$

(4)

As mentioned in [34], this task requires the calculation of an ill posed problem because the improper ’Fredholm integral’ in Equation (3) or the corresponding sum in Equation (4) has to be calculated. According to [31,32,34] a promising approach is the ’Tikhonov-regularisation’ that converts Equation (3) to the optimisation problem

$$\begin{array}{c}\hfill \min \left\{\Vert \mathbf{A}\mathbf{x}-{\mathbf{b}\Vert }^2+{\Vert \lambda \mathbf{x}\Vert }^2\right\}.\end{array}$$

It consists of the matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, representing the unweighted $RC$-elements with the arbitrarily chosen time constants ${\tau }_k$, whose quantity and bandwidth should surpass those of the angular frequencies ${\omega }_i$ of the measurement [32], the vector $\mathbf{b}\in {\mathbb{R}}^m$, representing the measured impedance $\underline{Z}\left({\omega }_i\right)$ and the optimisation factor $\lambda$ that has to be chosen carefully, [31,34]. The distribution function $g\left(\tau \right)$ is stored in $\mathbf{x}$ after a successful numerical optimisation with a feasible solving method such as the non-negative least squares (NNLS) algorithm [31]. Much more detailed information on the calculation of the DRT is found in [31], too.

In the lower part of Figure 7 the result of the DRT-analysis is shown in correspondence to the spectra in the upper part. Thus, the graphs basically show the same measurement. However, the prominently contributing time constants are clearly visible in Figure 7c,d. Besides, it should be noted that the bandwidth shown in these depictions corresponds to the a priori chosen time constants ${\tau }_k$ and ranges from $0.1\mathrm{mHz}$ to roughly $300\mathrm{Hz}$ to get the most meaningful representation. A broader bandwidth of the time constants up to several MHz is used to extend the DRT to the inductive branch in adaption to [31], modelled as a distribution of $RL$-circuits which are proposed in [35]. However, these results are not shown as they do not provide any further useful information. Instead of $g\left(\tau \right)$,

$$\begin{array}{c}\hfill h\left(\tau \right)=R_{\mathrm{pol}}g\left(\tau \right)\end{array}$$

is shown on the vertical axis. In both figures, five major peaks can be detected that are in good accordance with the literature, for example [30] or [33]. The first peak from left to right represents the diffusion branch. As in the spectra, no distinctive difference between rippled cells and conventionally aged ones is found. In general, the rise of the peak over the battery ageing implies a flattening of the diffusion branch that is not detected without any further analysis in the spectra. The following peaks are directly connected to the polarisation of the electrodes with two smaller peaks that most likely represent the polarisation at the cathode and the larger peak in the middle corresponding to the main anode reaction. These peaks mainly shape the capacitive parts of the spectra. The last peak is connected to the interfaces between the current collectors and the active mass. Generally, the observations considering the spectra can be validated by the DRT. Again, cells R6 and R8 are prominent. Their middle peaks are clearly elevated as compared to the other cells.

Another approach to visualise the information given in the impedance data is shown in Figure 8. In this picture, the normalised height of the largest peak in the middle of the DRT, representing the polarisation of the anode, is plotted against the capacity loss as shown in Figure 4a for cells cycled with $\Delta DO{D}_1$. A slight grouping just as in Figure 4a is detectable as an addition to the general observation that the polarisation of the anode starts to get worse more rapidly as the capacity deterioration is getting slower. In this picture, R5 is not shown because the initial EIS-measurement at zero cycles is missing so that a relative examination is not possible.

As expected, the polarisation of the electrodes changes over time as the cell reactions are constrained more and more which leads to a rising real part at lower frequencies as the batteries age. In [20], most of these changes in the dynamic behaviour of the electrodes are linked to SEI-growth which is most prominently accelerated by a high SOC and higher temperatures. Thus, as the rather small amplitude of the current ripple does not lead to periodic overcharges due to transient higher overpotentials that are not recognized by the test circuit, different temperatures while cycling should lead to different ageing curves. Given the well known fact, that the temperature is linked to ohmic losses calculated by multiplying the square of the root mean square value (hereafter: RMS-value) of the current with the internal resistance, a different RMS-value should lead to a different temperature because the RMS-value represents the equivalent DC-value of the alternating current that would convert the same amount of energy at a resistive load which is solely heat. The RMS-value of a purely direct current is the same as the mean value that is used to charge and discharge the batteries whereas the RMS-value of a triangular wave as in Figure 1 is calculated by

$$\begin{array}{c}\hfill I_{\mathrm{RMS},\mathrm{R}}=I_{\min ,\mathrm{R}}+\frac{1}{\sqrt{3}}\Delta I_{\mathrm{R}}\end{array}$$

so that it is higher than the mean value which could lead to higher temperatures compared to an undistorted direct current. However, further measurements have shown that the difference in surface temperature of the cells between rippled and conventionally aged cells is below 2 K. This fits the observation that the ripple current does not have any clear influence on the dynamic battery behaviour that exceeds the influence of cyclic ageing in general. The advantage of the DRT that the most influential processes at the electrodes are visible separately further supports the aforementioned claim as no clear deviation between the cell groups is visible for any kind of diffusion or reaction process. Moreover, no direct connection between ripple current and the outliers, visible in Figure 7a–d, respectively could be found. It is expected that these cells represent the unpredictable spread that occurs in later parts of battery ageing [27]. To conclude, the spectra are used as a further possible explanation as to why the ripple does not have any severe impact. The assumption, e.g., in [14,16], that the excitation frequency of the current ripple, i.e., the switching frequency of the DC/DC-converter, has the highest impact on the dynamic behaviour of the battery if it is still in its capacitive range and thus provoking unwanted reactions at the electrodes could be another explanation for the lack of impact of high frequency current ripple on battery ageing. Switching frequencies of practical DC/DC-converters are typically located at several kilohertz which usually corresponds to the inductive branch of the battery as illustrated in Figure 9. In these drawings, the trends over ageing of the impedance spectra of two arbitrarily chosen batteries C2 and R4 with and without ripple current are depicted. Moreover, an excitation frequency of $5\mathrm{kHz}$ that is also the switching frequency of the converter is marked for each spectrum. Neither does the mark change position significantly nor does the inductive branch show any clear alteration because of ageing. As stated by [35,36], the inductive branch is mostly affected by the geometry of the cell and the current collectors which does not change due to cyclic ageing not to mention current ripple.

4. Conclusions

In this article, the influence of practical DC/DC-converter induced high frequency current ripple on the ageing of conventional 18650 lithium-ion batteries is investigated. After numerous ageing tests, the measurements strongly indicate that there is no significant effect of half bridge converter induced current ripple on battery ageing that outmatches the influence of a deep $DOD$. However, by reducing the influence of the cycle depth by using $\Delta DO{D}_2$ = 10%, slight deviations between conventionally aged and rippled cells are visible, regardless of the measurement as seen in Figure 4b, Figure 6c and Figure 7b,d. Yet, a distinct relation between current ripple and these deviations remains debatable. These statements incorporate themselves into the literature and support the findings of [16] and the literature overview within. In addition to further literature, e.g., [13,14,15] the research at hand is able to provide some more attempts to explain whether current ripple could be harmful in general and why the detection of any current ripple affected ageing parameters is rather difficult.

Investigating the influence of current ripple or, more generally speaking, the influence of AC-excitation on battery ageing implies cyclic ageing tests that most likely influence battery ageing more than alternating currents as long as the ageing test is made from a practical perspective. The amplitude of the current should stay within the battery specifications and the current profile itself is orientated to reproduce typical practical dimensions, i.e., limited current ripple. In concordance with [14,16], it is expected that alternating currents with amplitudes beyond battery specifications or at least designed in a way so that the effective value is drastically higher than the mean value lead to elevated heating of the batteries. However, overextending this approach would lead to accelerated ageing because of higher temperatures resulting from the high rms-value of the ripple currents. For comparison: In this study, the temperatures of the rippled cells are elevated by not more than 2 K compared to the conventionally cycled cells. It is expected that ageing tests that overextend on the deviation of the effective value from the mean value of the ripple current would reveal that the battery ageing would be influenced much more by the presence of considerably elevated temperatures than the influence of ripple currents. On top of that, the influence of elevated temperatures has already been discussed satisfactorily in the literature, e.g., in [21]. Moreover, such studies would be comparable to the result of this study that a large $DOD$ affects ageing much more than current ripple. In general, indicated by the slight deviations between the cells cycled with $\Delta DO{D}_2$ = 10%, assumed influences of current ripple are only visible if other ageing influences are minimised.

Further Work

This article joins its solid foundation of referred literature, e.g., [13,15,16], that collectively doubt the influence of current ripple or alternating current on battery ageing. However, generalisation and transferability remain problematic as the vast amount of possible parameters connected to ripple currents that could influence battery ageing produce countless combinations that could be tested. For example, different DC/DC-converters with different current wave of forms such as bidirectional flyback converters or resonant converters could lead to new insights. Besides, changing the switching frequency could lead to different results as indicated in Section 2 in the same way different cell geometries, cell sizes and electrode materials or even electrolytes could lead to alternative behaviour if ripple current is induced. Nonetheless, the likelihood of current ripple not needing to be addressed carefully in practical applications could lead to lower development cost and less filtering effort in future energy storage systems. In [37,38] the component costs of power electronic systems are evaluated. Although the authors do not take batteries into account, their research is appropriate for a rough estimate. According to the studies, a cost reduction up to 20% or even 30% in some cases could be achieved because lighter and more compact filter capacitors and inductors could be used. By adding batteries, these values would be reduced fairly, yet smaller filter capacitors and inductors still most likely lead to cheaper, lighter and more compact energy storage systems which could be a crucial, prospective benefit in highly competitive markets such as the automobile industry.