Analysis for Spatio-Temporal Variation Characteristics of Droughts in Different Climatic Regions of the Mongolian Plateau Based on SPEI
Abstract
1. Introduction
2. Materials and Methods
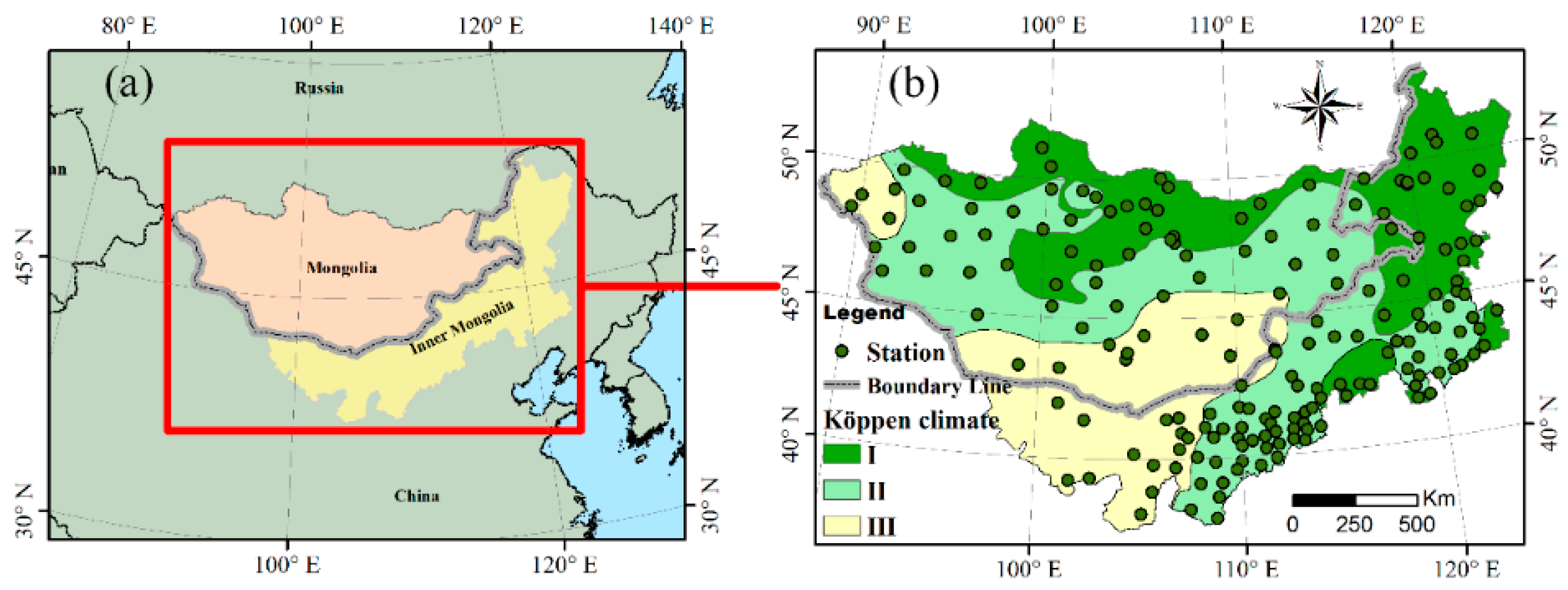
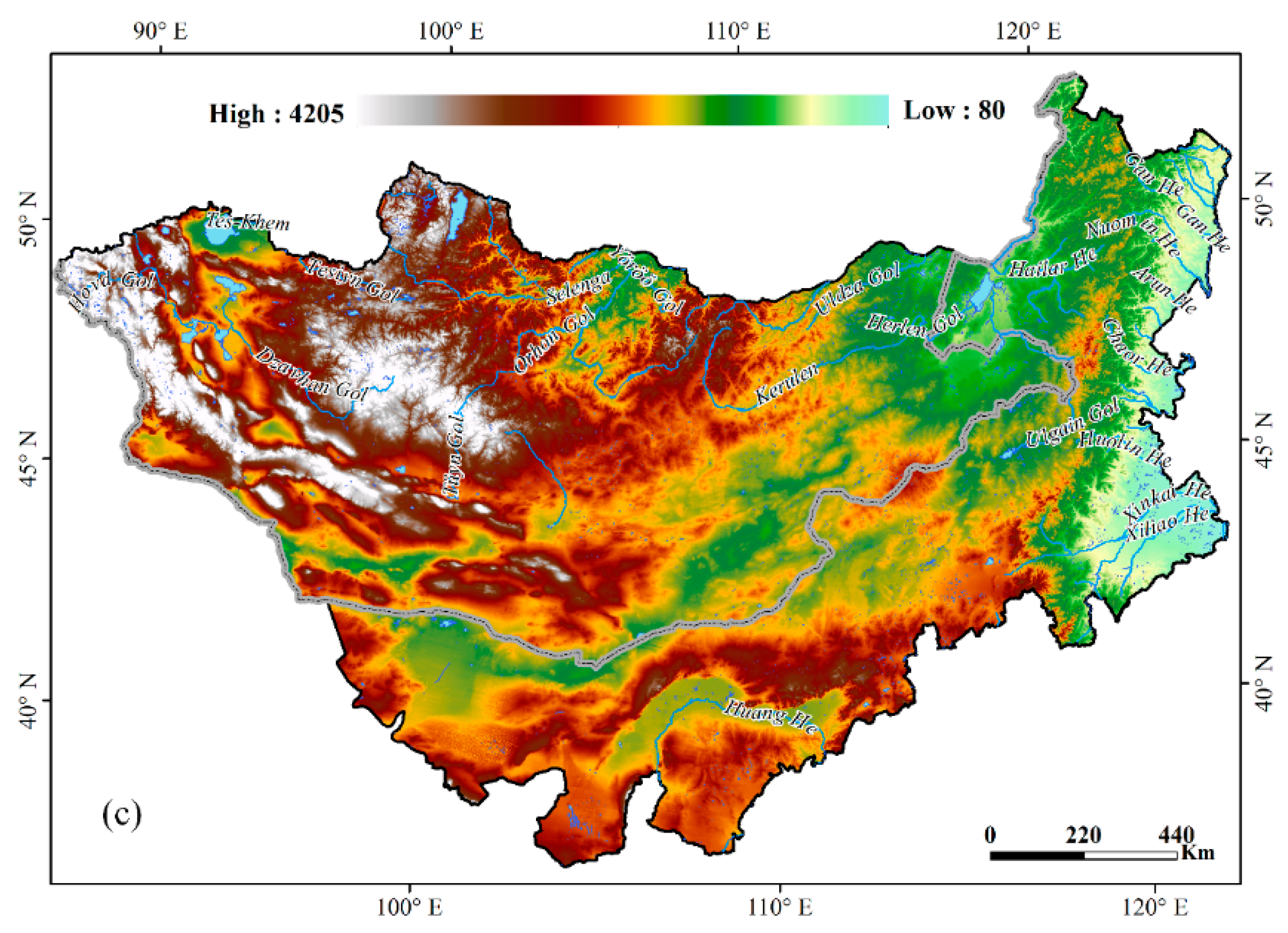
2.1. Description of Study Area
2.2. Data Sources
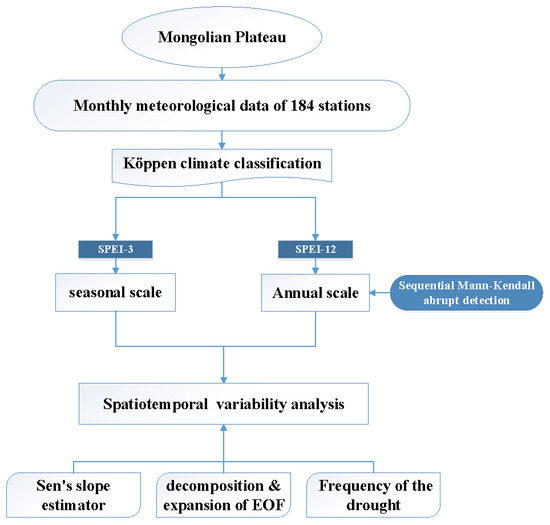
2.3. Methodology
2.3.1. Standardized Precipitation-Evapotranspiration Index (SPEI)
- (1)
- Calculate the potential evapotranspiration PET by the Penman–Monteith model:where PET is the potential evapotranspiration (mm/d); is the Net irradiance (), G is the heat flux density of soil ; T is the average air temperature (); is the slope of the temperature varying with the saturated water vapor pressure ; is the Psychrometric constant ; is the wind speed 2 m above the ground; is the saturated water vapor pressure (kPa) and is the actual water vapor pressure (kPa).
- (2)
- Calculate the water balance:where is the precipitation (mm); and is the potential evaporation (mm/d); is the difference between precipitation and evapotranspiration. according to the linear decreasing weight scheme, the cumulative water deficit series at different time scales are established.where k is time scale (monthly); n is number of the month.
- (3)
- The water balance is normalized into a log-logistic probability distribution to calculate the SPEI index series as follows:where α is the scale parameter, β is the shape parameter, and γ is the origin parameters, for D values in the range .is a Gamma function about . Thereby, the cumulative function of probability density of is obtained.
- (4)
- With F(x), the SPEI can easily be obtained as the standardized values of F(x).where for and P is the probability of exceeding a determined D value, . If , then P is replaced by and the sign of the resultant SPEI is reversed. The constants are , , , , . In this paper, we used the SPEI package of R language to calculate SPEI-3 and SPEI-12. The drought severity was classified according to the SPEI, as shown in Table 1.
2.3.2. Trend Analyzed Method
- (1)
- Mann–Kendall (MK) test
- (2)
- Sen’s Slope detection method
- (3)
- The Sen’s slope detection method can reduce or avoid the influence of data missing and abnormality on the statistical results [30,31,32]. The Sen slope formula is as follows (Equations (11) and (12)):where Xi and Xj are the sequence values at the i-th and j-th, respectively, 1 < i < j < n, and n is the sequence length. The Sen’s slope is the median value of slope, determined by the parity of the total number of Sij determined by the sequence length n, where k is an integer related to the length of the sequence, N = n(n − 1)
2.3.3. Sequential Mann–Kendall Abrupt Detection Method
2.3.4. Empirical orthogonal function (EOF)
3. Results
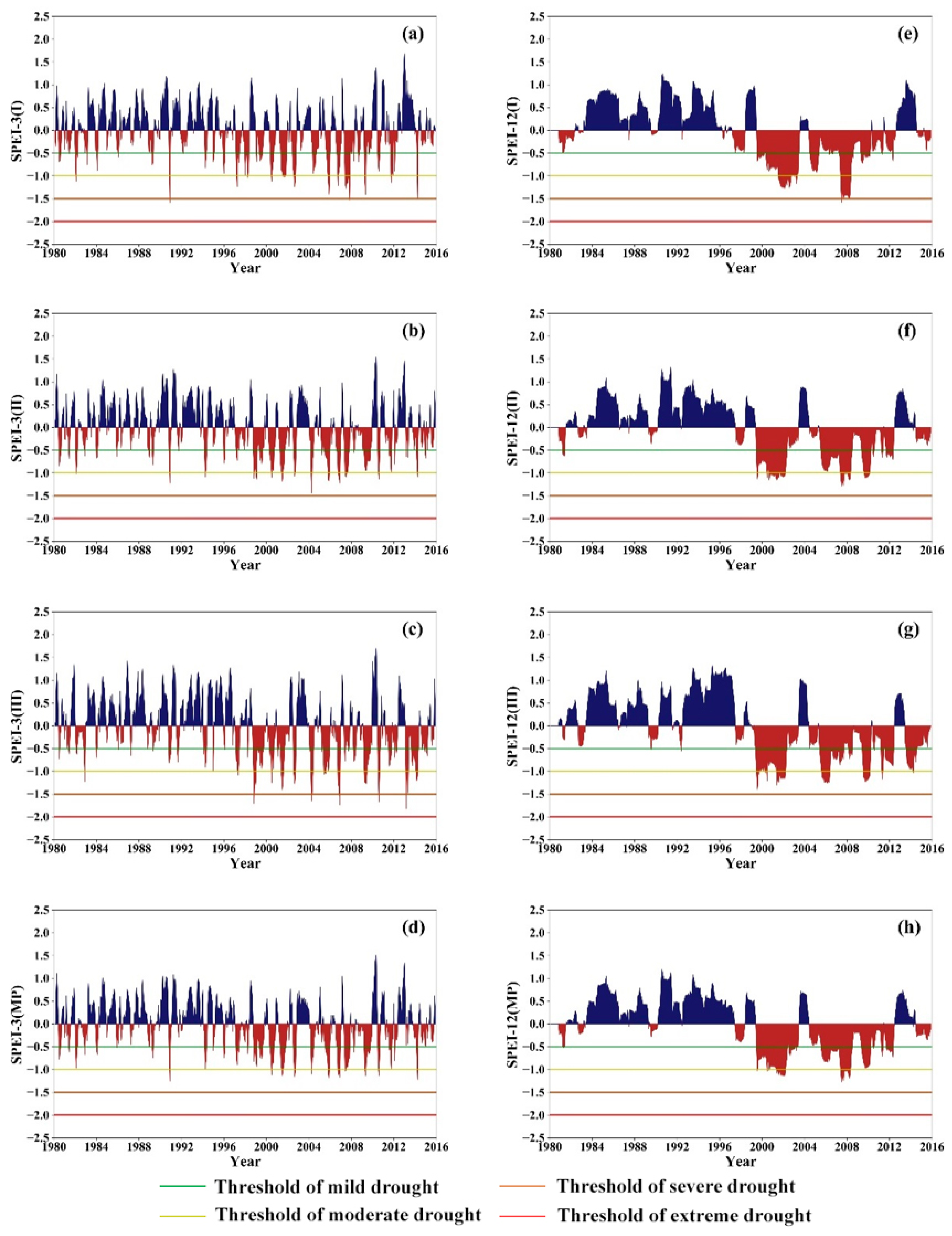
3.1. Identify Drought Period Within Different Climatic Regions of the Mongolian Plateau
3.2. Temporal Variability of Droughts
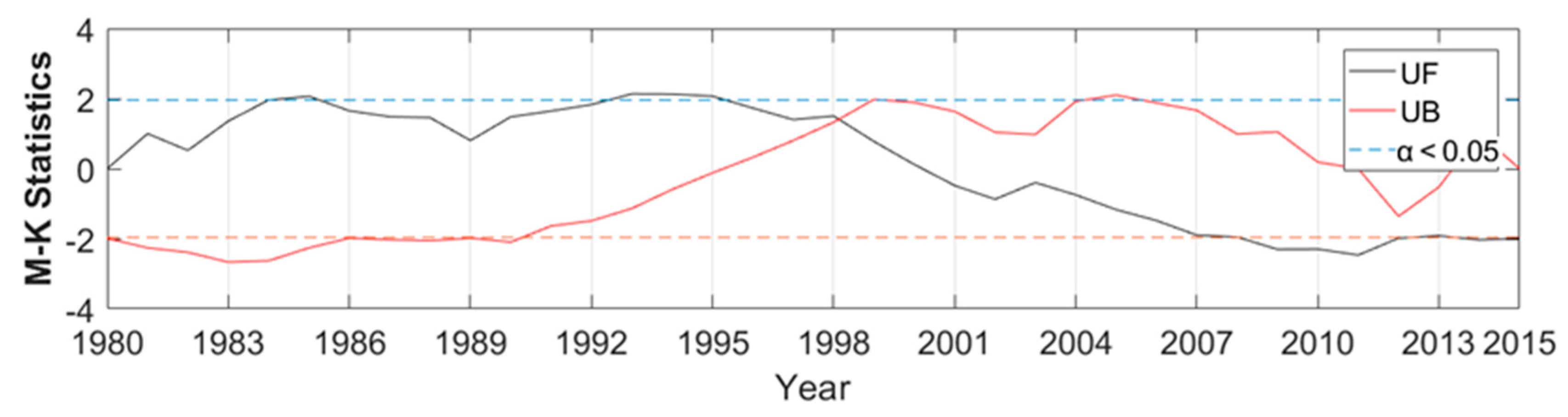
3.2.1. M–K Abrupt Change Analysis Based on SPEI-12 and Slope Analysis Before and After Abrupt Change
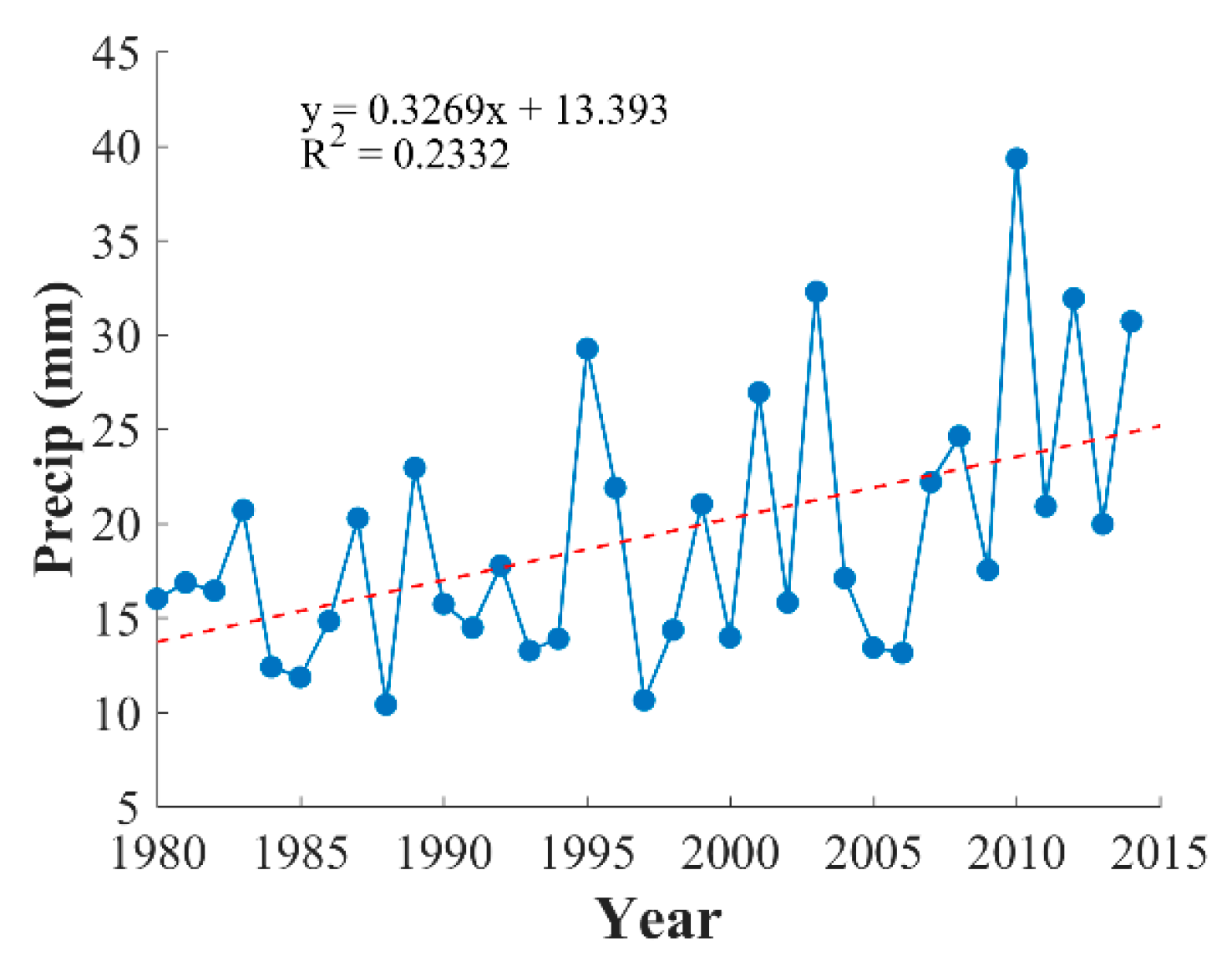
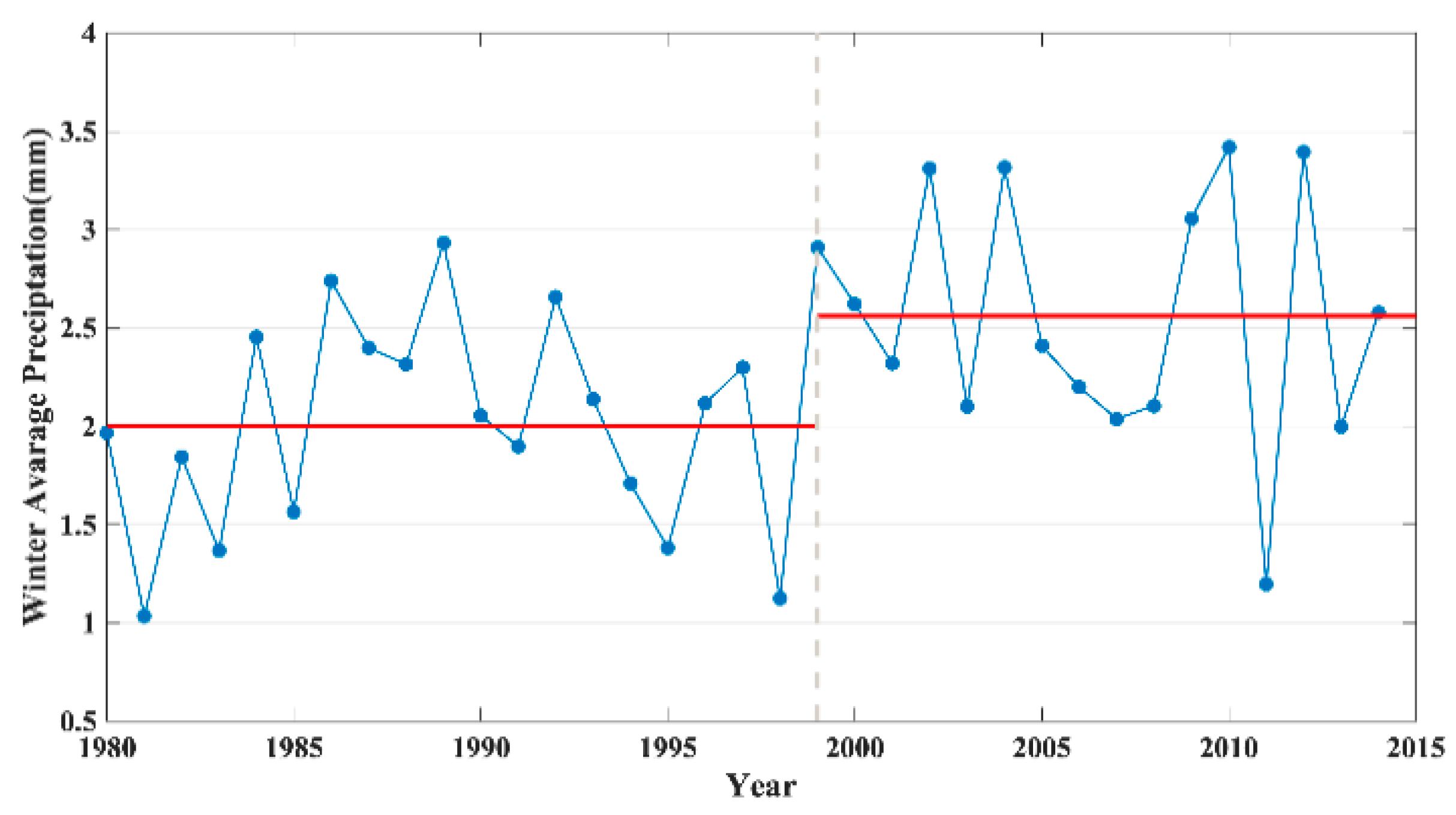
3.2.2. Seasonal Variability
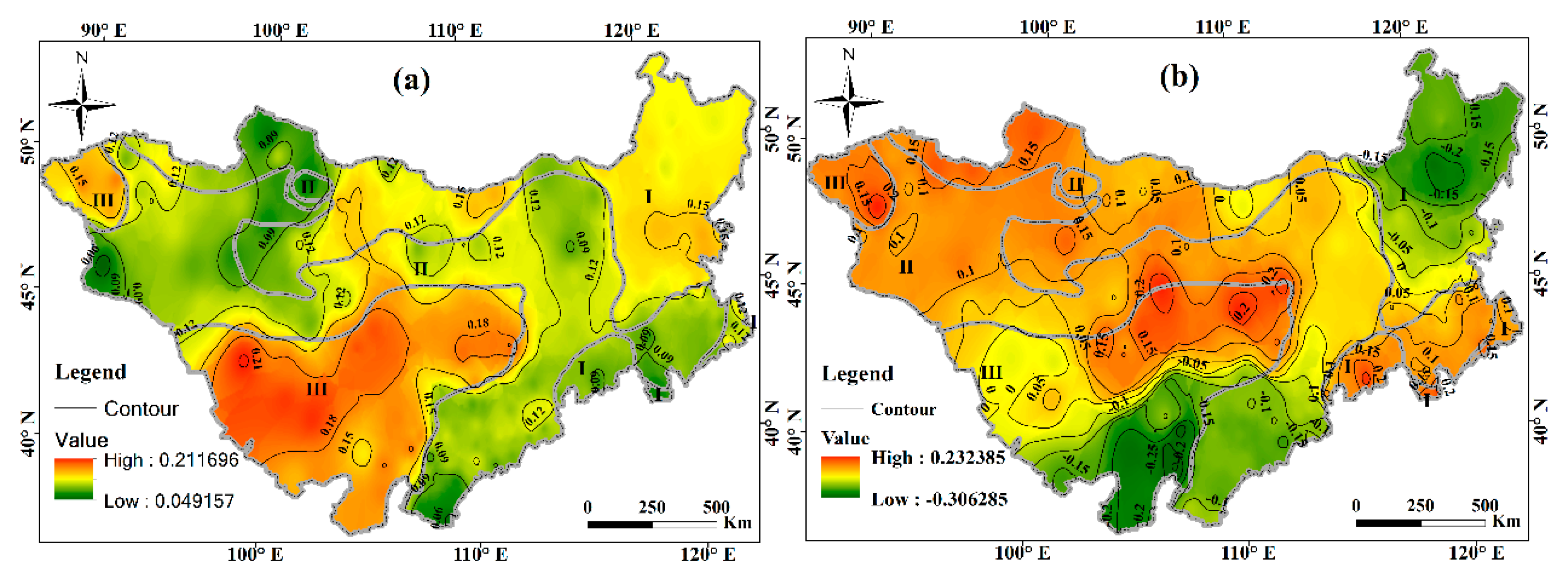
3.3. Spatial Variability of Droughts
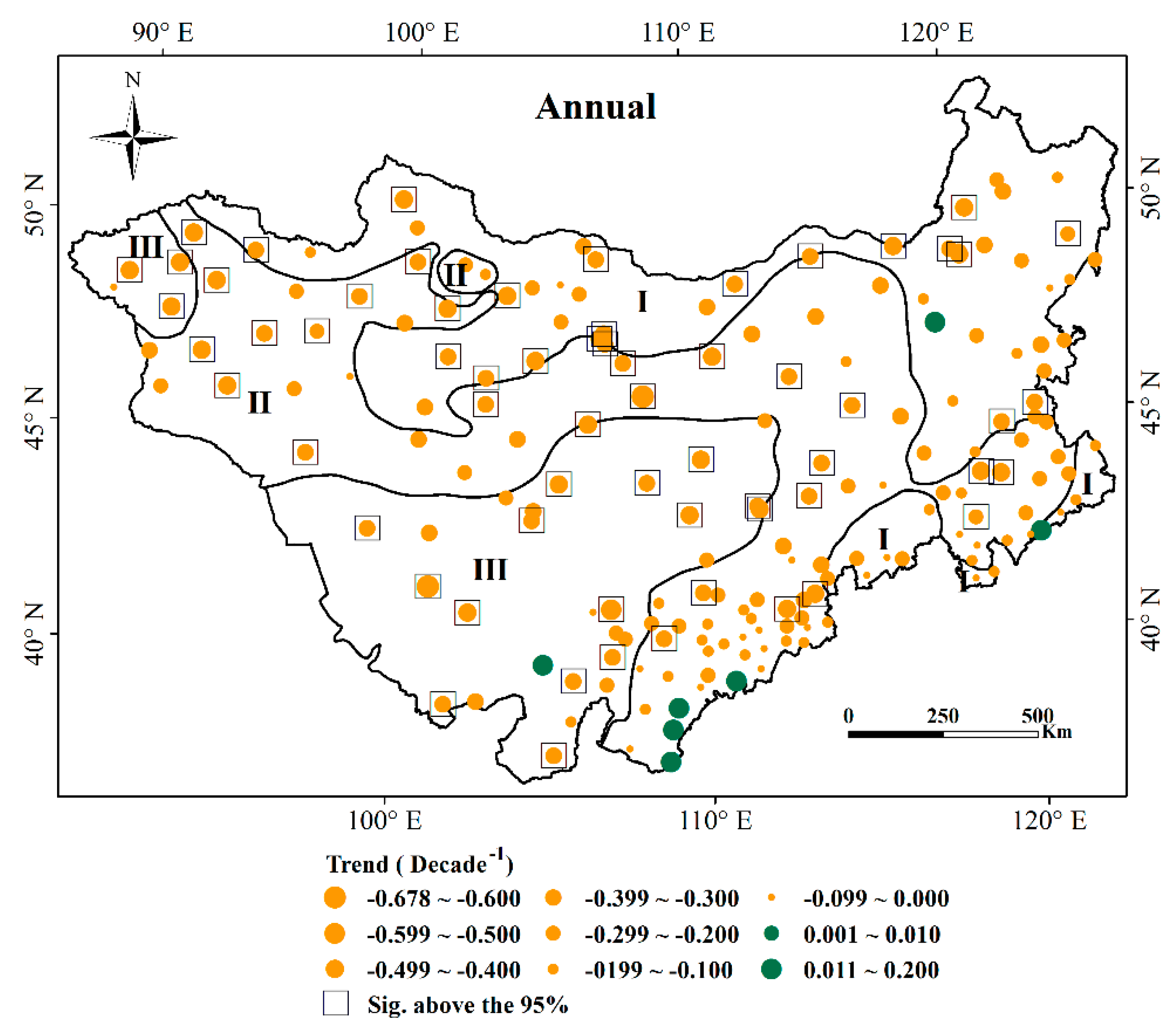
3.3.1. Annual Drought Trend Detected by SPEI Analysis
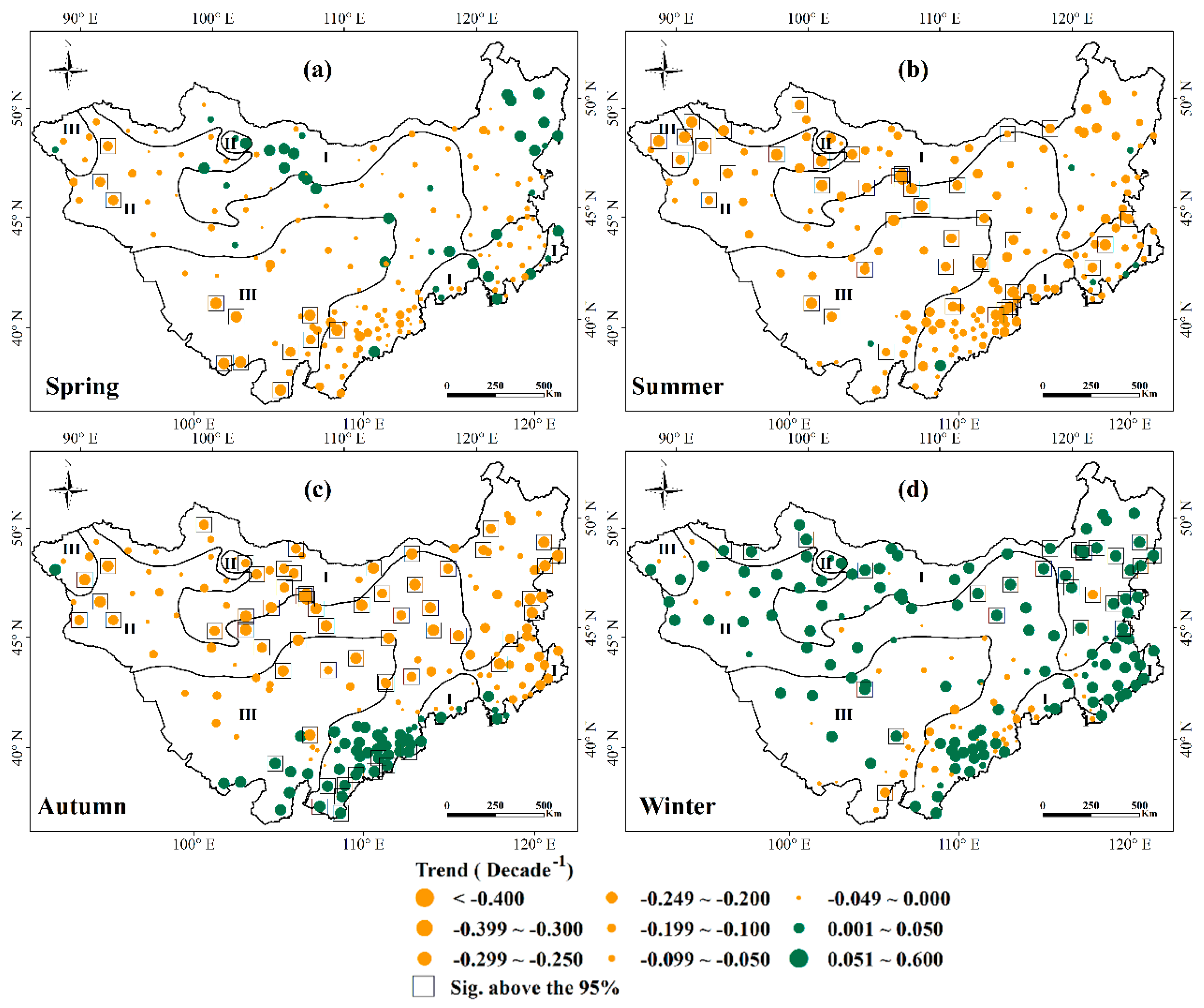
3.3.2. Seasonal Trend of SPEI in Different Climatic Regions
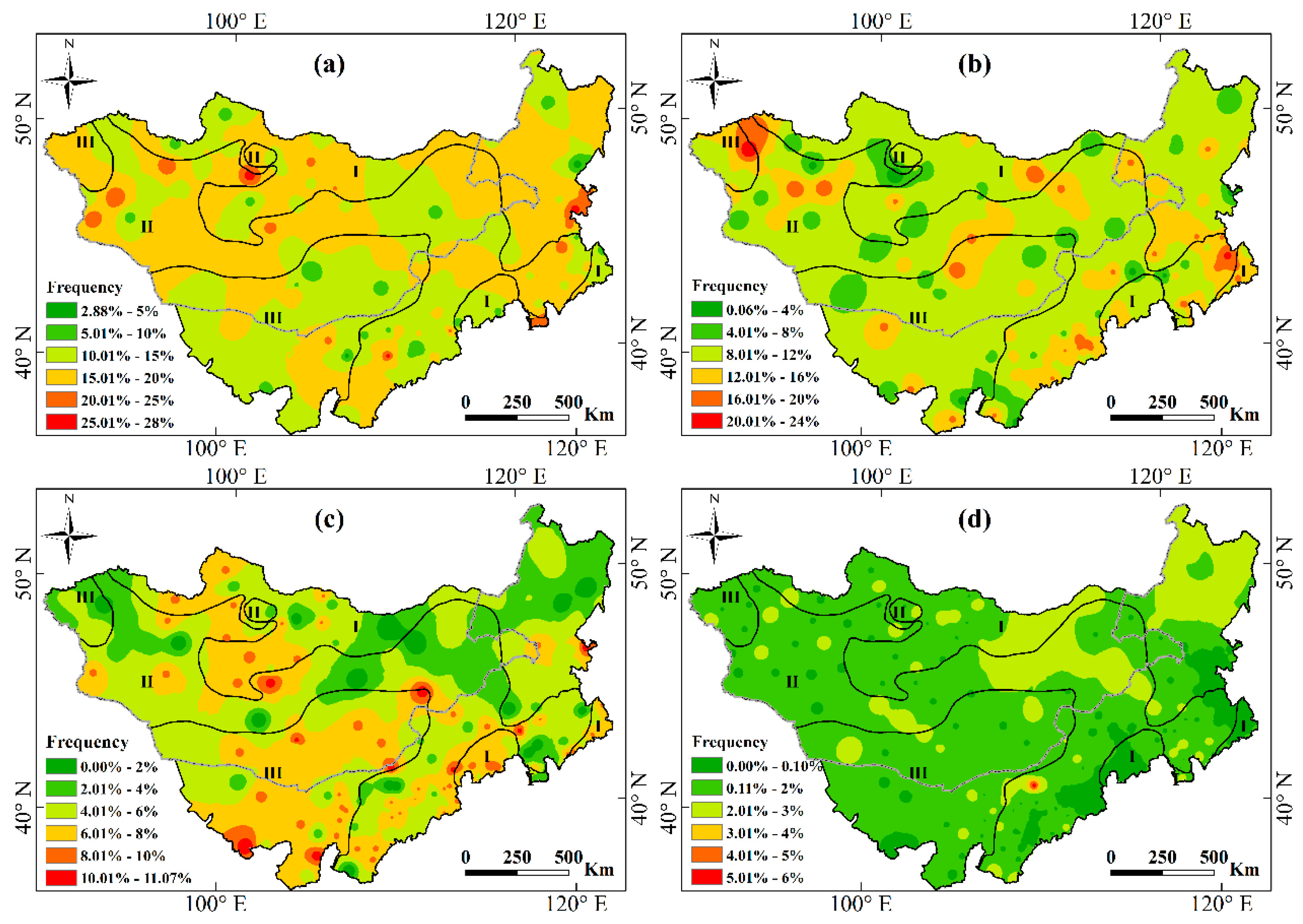
3.3.3. Spatial Distribution of the Drought Frequency Categorized by Relative Severity
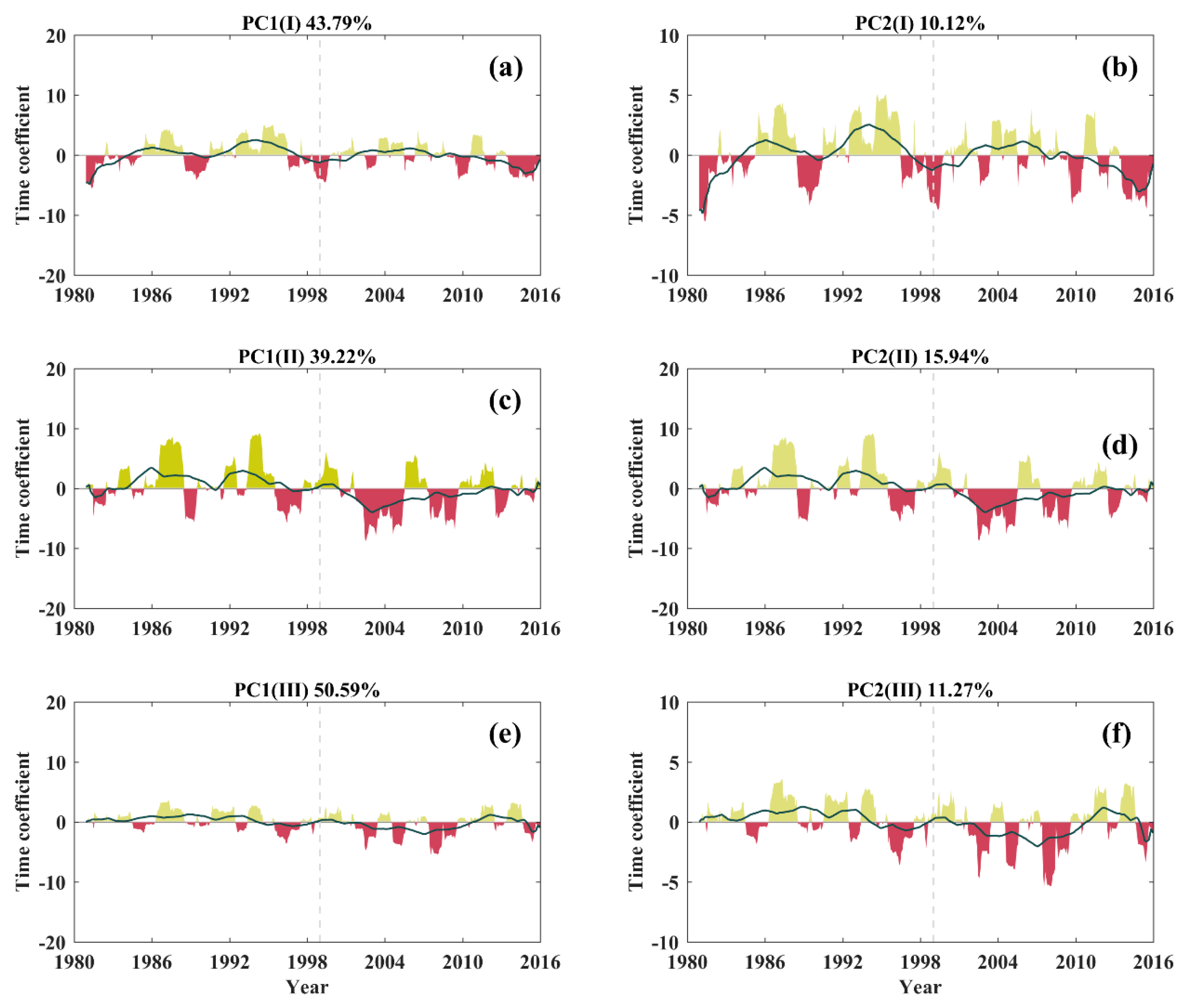
3.4. Spatial Distribution Characteristics of Droughts (Decomposition and Expansion of EOF)
4. Discussion
4.1. Aridification Trend of the Mongolian Plateau under the Background of Climate Change
4.2. Drought Variations in Different Climatic Regions at the Seasonal Scale and Their Impacts
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pachauri, R.K.; Meyer, L. Climate Change 2014 Synthesis Report-Summary for Policymakers; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2014. [Google Scholar]
- Cao, G.; Hou, P. Assessment of the ecological security based on the ecological carrying capacity. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7285–7288. [Google Scholar]
- Wang, R.; Bowling, L.C.; Cherkauer, K.A.; Cibin, R.; Her, Y.; Chaubey, I. Biophysical and hydrological effects of future climate change including trends in CO2, in the St. Joseph River watershed, Eastern Corn Belt. Agric. Water Manag. 2016, 180, 280–296. [Google Scholar] [CrossRef]
- Huang, J.; Guan, X.; Ji, F. Enhanced cold-season warming in semi-arid regions. Atmos. Chem. Phys. 2012, 12, 5391–5398. [Google Scholar] [CrossRef]
- Rotenberg, E.; Yakir, D. Contribution of semi-arid forests to the climate system. Science 2010, 327, 451–454. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Huang, J.; Ji, M.; Ran, J. Dryland expansion in northern China from 1948 to 2008. Adv. Atmos. Sci. 2015, 32, 870–876. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Wilhite, D.A. Droughts: A Global Assessment; Routledge: Abingdon, UK, 2016. [Google Scholar]
- Wilhite, D.A.; Svoboda, M.D.; Hayes, M.J. Understanding the complex impacts of drought: A key to enhancing drought mitigation and preparedness. Water Resour. Manag. 2007, 21, 763–774. [Google Scholar] [CrossRef]
- Zarch, M.A.A.; Sivakumar, B.; Sharma, A. Droughts in a warming climate: A global assessment of Standardized precipitation index (SPI) and Reconnaissance drought index (RDI). J. Hydrol. 2015, 526, 183–195. [Google Scholar] [CrossRef]
- Council, A. AMS statement on meteorological drought. Bull. Am. Meteorol. Soc. 2004, 85, 771–773. [Google Scholar]
- Miao, L.; Fraser, R.; Sun, Z.; Sneath, D.; He, B.; Cui, X. Climate impact on vegetation and animal husbandry on the Mongolian plateau: A comparative analysis. Nat. Hazards 2016, 80, 727–739. [Google Scholar] [CrossRef]
- Bao, G.; Bao, Y.; Qin, Z.; Xin, X.; Bao, Y.; Bayarsaikan, S.; Zhou, Y.; Chuntai, B. Modeling net primary productivity of terrestrial ecosystems in the semi-arid climate of the Mongolian Plateau using LSWI-based CASA ecosystem model. Int. J. Appl. Earth Obs. 2016, 46, 84–93. [Google Scholar] [CrossRef]
- Dorjsuren, M.; Liou, Y.; Cheng, C. Time Series MODIS and in Situ Data Analysis for Mongolia Drought. Remote Sens. 2016, 8, 509. [Google Scholar] [CrossRef]
- Du, T.; Kang, S.; Sun, J.; Zhang, X.; Zhang, J. An improved water use efficiency of cereals under temporal and spatial deficit irrigation in north China. Agric. Water Manag. 2010, 97, 66–74. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, G.; Guo, E. Spatial distribution and temporal variation of drought in Inner Mongolia during 1901–2014 using Standardized Precipitation Evapotranspiration Index. Sci. Total Environ. 2019, 654, 850–862. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Kang, W.; Wang, T. Drought variability in Inner Mongolia of northern China during 1960–2013 based on standardized precipitation evapotranspiration index. Environ. Earth Sci. 2016, 75, 145. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, N.; Ji, Z.; Gu, X.; Fan, B. Temporal and Spatial Patterns of Droughts Based on Standard Precipitation Index (SPI) in Inner Mongolia during 1981–2010. J. Nat. Resour. 2013, 28, 1694–1706. [Google Scholar]
- Gao, R.; Li, F.; Wang, X.; Liu, T.; Du, D.; Bai, Y. Spatiotemporal variations in precipitation across the Chinese Mongolian plateau over the past half century. Atmos. Res. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Guo, E.; Dong, Z.; Quan, L. Estimation of Variability Characteristics of Regional Drought during 1964–2013 in Horqin Sandy Land, China. Water 2016, 8, 543. [Google Scholar] [CrossRef]
- Sternberg, T.; Middleton, N.; Thomas, D. Pressurised pastoralism in South Gobi, Mongolia: What is the role of drought? Trans. Inst. Br. Geogr. 2009, 34, 364–377. [Google Scholar] [CrossRef]
- Wang, H.; He, S. The North China/Northeastern Asia Severe Summer Drought in 2014. J. Clim. 2015, 28, 6667–6681. [Google Scholar] [CrossRef]
- Wang, R.; Cherkauer, K.; Bowling, L. Corn Response to Climate Stress Detected with Satellite-Based NDVI Time Series. Remote Sens. 2016, 8, 269. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.; Gao, Z.; Ning, J.; Shi, R.; Gao, W. Monitoring Drought in the Monglian Plateau Based on NDVI-Ts General Space, 2000–2010; SPIE—The International Society for Optical Engineering: Bellingham, WA, USA, 2013. [Google Scholar]
- Yan, H.; Wang, S.; Wang, J.; Lu, H.; Guo, A.; Zhu, Z.; Myneni, R.B.; Shugart, H.H. Assessing spatiotemporal variation of drought in China and its impact on agriculture during 1982–2011 by using PDSI indices and agriculture drought survey data. J. Geophys. Res. Atmos. 2016, 121, 2283–2298. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Response to comment on ‘Candidate Distributions for Climatological Drought Indices (SPI and SPEI)’. Int. J. Climatol. 2016, 36, 2132–2138. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- El-Shaarawi, A.H.; Piegorsch, W.W. Encyclopedia of Environmetrics; John Wiley & Sons: Hoboken, NJ, USA, 2001; Volume 1. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Angulo-Martínez, M. A Multiscalar Global Drought Dataset: The SPEIbase: A New Gridded Product for the Analysis of Drought Variability and Impacts. Bull. Am. Meteorol. Soc. 2010, 91, 1351–1356. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann—Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Gerstengarbe, F.; Werner, P.C. Estimation of the beginning and end of recurrent events within a climate regime. Clim. Res. 1999, 11, 97–107. [Google Scholar] [CrossRef]
- Kaihatu, J.M.; Handler, R.A.; Marmorino, G.O.; Shay, L.K. Empirical orthogonal function analysis of ocean surface currents using complex and real-vector methods. J. Atmos. Ocean. Technol. 1998, 15, 927–941. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, M. Climatic characteristics of strong and very strong sandstorms in the middle and west parts of Inner Mongolia. Plateau Meteorol. 2003, 1, 6. [Google Scholar]
- Fan, Q.; Wang, C.; Zhang, D.; Zang, S. Environmental Influences on Forest Fire Regime in the Greater Hinggan Mountains, Northeast China. Forests 2017, 8, 372. [Google Scholar] [CrossRef]
- Philip, G.M.; Watson, D.F. A precise method for determining contoured surfaces. APPEA J. 1982, 22, 205–212. [Google Scholar] [CrossRef]
- Watson, D.F. A refinement of inverse distance weighted interpolation. Geoprocessing 1985, 2, 315–327. [Google Scholar]
- Hu, W.; Niu, H.; Zhang, D.; Wu, Z.; Chen, C.; Wu, Y.; Shang, D.; Hu, M. Insights into a dust event transported through Beijing in spring 2012: Morphology, chemical composition and impact on surface aerosols. Sci. Total Environ. 2016, 565, 287–298. [Google Scholar] [CrossRef]
- Hagemann, S.; Chen, C.; Clark, D.; Folwell, S.; Gosling, S.N.; Haddeland, I.; Hannasaki, N.; Heinke, J.; Ludwig, F.; Voss, F. Climate change impact on available water resources obtained using multiple global climate and hydrology models. Earth Syst. Dynam. 2013, 4, 129–144. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Jongman, B.; Veldkamp, T.; Hallegatte, S.; Bangalore, M.; Ward, P. Disaster Risk, Climate Change, and Poverty: Assessing the Global Exposure of Poor People to Floods and Droughts; The World Bank: Washington, DC, USA, 2015. [Google Scholar]
- Liljedahl, A.K.; Boike, J.; Daanen, R.P.; Fedorov, A.N.; Frost, G.V.; Grosse, G.; Hinzman, L.D.; Iijma, Y.; Jorgenson, J.C.; Matveyeva, N. Pan-Arctic ice-wedge degradation in warming permafrost and its influence on tundra hydrology. Nat. Geosci. 2016, 9, 312. [Google Scholar] [CrossRef]
- Gu, G.; Adler, R.F.; Huffman, G.J.; Curtis, S. Tropical rainfall variability on interannual-to-interdecadal and longer time scales derived from the GPCP monthly product. J. Clim. 2007, 20, 4033–4046. [Google Scholar] [CrossRef]
- John, V.O.; Allan, R.P.; Soden, B.J. How robust are observed and simulated precipitation responses to tropical ocean warming? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Jiang, L.G.; Yao, Z.J.; Huang, H.Q. Climate variability and change on the Mongolian Plateau: Historical variation and future predictions. Clim. Res. 2016, 67, 1–14. [Google Scholar] [CrossRef]
- Zou, X.K.; Zhai, P.M. Relationship between vegetation coverage and spring dust storms over northern China. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific Interdecadal Climate Oscillation with Impacts on Salmon Production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Schlesinger, M.E.; Ramankutty, N. An oscillation in the global climate system of period 65–70 years. Nature 1994, 367, 723–726. [Google Scholar] [CrossRef]
- Qin, M.; Li, D.; Dai, A.; Hua, W.; Ma, H. The influence of the Pacific Decadal Oscillation on North Central China precipitation during boreal autumn. Int. J. Climatol. 2018, 38, e821–e831. [Google Scholar] [CrossRef]
- Qin, F.Y.; Jia, G.S.; Yang, J.; Na, Y.T.; Hou, M.T. Spatiotemporal variability of precipitation during 1961–2014 across the Mongolian Plateau. J. Mt. Sci. 2018, 15, 992–1005. [Google Scholar] [CrossRef]
- Tong, S.; Li, X.; Zhang, J.; Bao, Y.; Bao, Y.; Na, L.; Si, A. Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci. Total Environ. 2019, 649, 75–89. [Google Scholar] [CrossRef]
- Ma, Y.; Mao, R.; Feng, S.; Gong, D.; Kim, S. Does the recent warming hiatus exist over Northern Asia for winter wind chill temperature? Int. J. Climatol. 2017, 37, 3138–3144. [Google Scholar] [CrossRef]
- Nandintsetseg, B.; Shinoda, M.; Erdenetsetseg, B. Contributions of multiple climate hazards and overgrazing to the 2009/2010 winter disaster in Mongolia. Nat. Hazards 2018, 92, 109–126. [Google Scholar] [CrossRef]
| Grade | Type | SPEI Value |
| 0 | Normal | more than −0.5 |
| 1 | Mild drought | (−1.00, −0.5] |
| 2 | Moderate drought | (−1.50, −1.00] |
| 3 | Severe drought | (−2.00, −1.50] |
| 4 | Extreme drought | less than −2.00 |
| Periods | Areas | Slope | 1980–1998 Average SPEI-12 | 1999–2015 Average SPEI-12 |
|---|---|---|---|---|
| Year | I | −0.0243 * | 0.3711 | −0.4083 |
| II | −0.0241 * | 0.3499 | −0.3838 | |
| III | −0.0307 * | 0.4330 | −0.4768 | |
| MP | −0.0234 * | 0.3685 | −0.4070 |
| Zone | Season | Slope | 1980–1998 Average SPEI-3 | 1999–2015 Average SPEI-3 |
|---|---|---|---|---|
| Ⅰ | Spring | –0.0011 | 0.0094 | 0.0019 |
| Summer | –0.0231 * | 0.3594 | –0.3939 | |
| Autumn | –0.0235 * | 0.2887 | –0.3050 | |
| Winter | 0.0241 * | –0.1872 | 0.2389 | |
| Ⅱ | Spring | –0.0157 | 0.1377 | –0.1352 |
| Summer | –0.0232 * | 0.3671 | –0.3999 | |
| Autumn | –0.0055 | 0.0846 | –0.0668 | |
| Winter | 0.0090 | –0.0690 | 0.1094 | |
| Ⅲ | Spring | –0.0247 * | 0.2134 | –0.2253 |
| Summer | –0.0257 * | 0.4043 | –0.4387 | |
| Autumn | –0.0177 | 0.1257 | –0.1279 | |
| Winter | –0.0016 | 0.0202 | 0.0198 | |
| MP | Spring | –0.0138 | 0.1086 | –0.1076 |
| Summer | –0.0236 * | 0.3684 | –0.4051 | |
| Autumn | –0.0139 | 0.1559 | –0.1529 | |
| Winter | 0.0098 | –0.0911 | 0.1294 |
| Mode-1 | Mode-2 | Mode-3 | Mode-4 | Mode-5 | Mode-6 | Mode-7 | Cumulated Explained Variance | |
|---|---|---|---|---|---|---|---|---|
| Ⅰ | 43.79% | 10.12% | 7.75% | 5.76% | 3.33% | 3.09% | 2.65% | 76.48% |
| Ⅱ | 39.22% | 15.94% | 5.39% | 5.10% | 3.60% | 3.28% | 2.75% | 75.28% |
| Ⅲ | 50.59% | 11.27% | 6.82% | 4.51% | 3.33% | 3.19% | 2.42% | 82.14% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Zhang, J.; Wang, R.; Zhang, M.; Bao, Y.; Guo, E.; Wang, Y. Analysis for Spatio-Temporal Variation Characteristics of Droughts in Different Climatic Regions of the Mongolian Plateau Based on SPEI. Sustainability 2019, 11, 5767. https://doi.org/10.3390/su11205767
Jin L, Zhang J, Wang R, Zhang M, Bao Y, Guo E, Wang Y. Analysis for Spatio-Temporal Variation Characteristics of Droughts in Different Climatic Regions of the Mongolian Plateau Based on SPEI. Sustainability. 2019; 11(20):5767. https://doi.org/10.3390/su11205767
Chicago/Turabian StyleJin, Laiquan, Jiquan Zhang, Ruoyu Wang, Minghua Zhang, Yuhai Bao, Enliang Guo, and Yongfang Wang. 2019. "Analysis for Spatio-Temporal Variation Characteristics of Droughts in Different Climatic Regions of the Mongolian Plateau Based on SPEI" Sustainability 11, no. 20: 5767. https://doi.org/10.3390/su11205767
APA StyleJin, L., Zhang, J., Wang, R., Zhang, M., Bao, Y., Guo, E., & Wang, Y. (2019). Analysis for Spatio-Temporal Variation Characteristics of Droughts in Different Climatic Regions of the Mongolian Plateau Based on SPEI. Sustainability, 11(20), 5767. https://doi.org/10.3390/su11205767