An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products
Abstract
1. Introduction
2. Literature Review
2.1. Low-Carbon Product Design
2.2. Remanufacturing
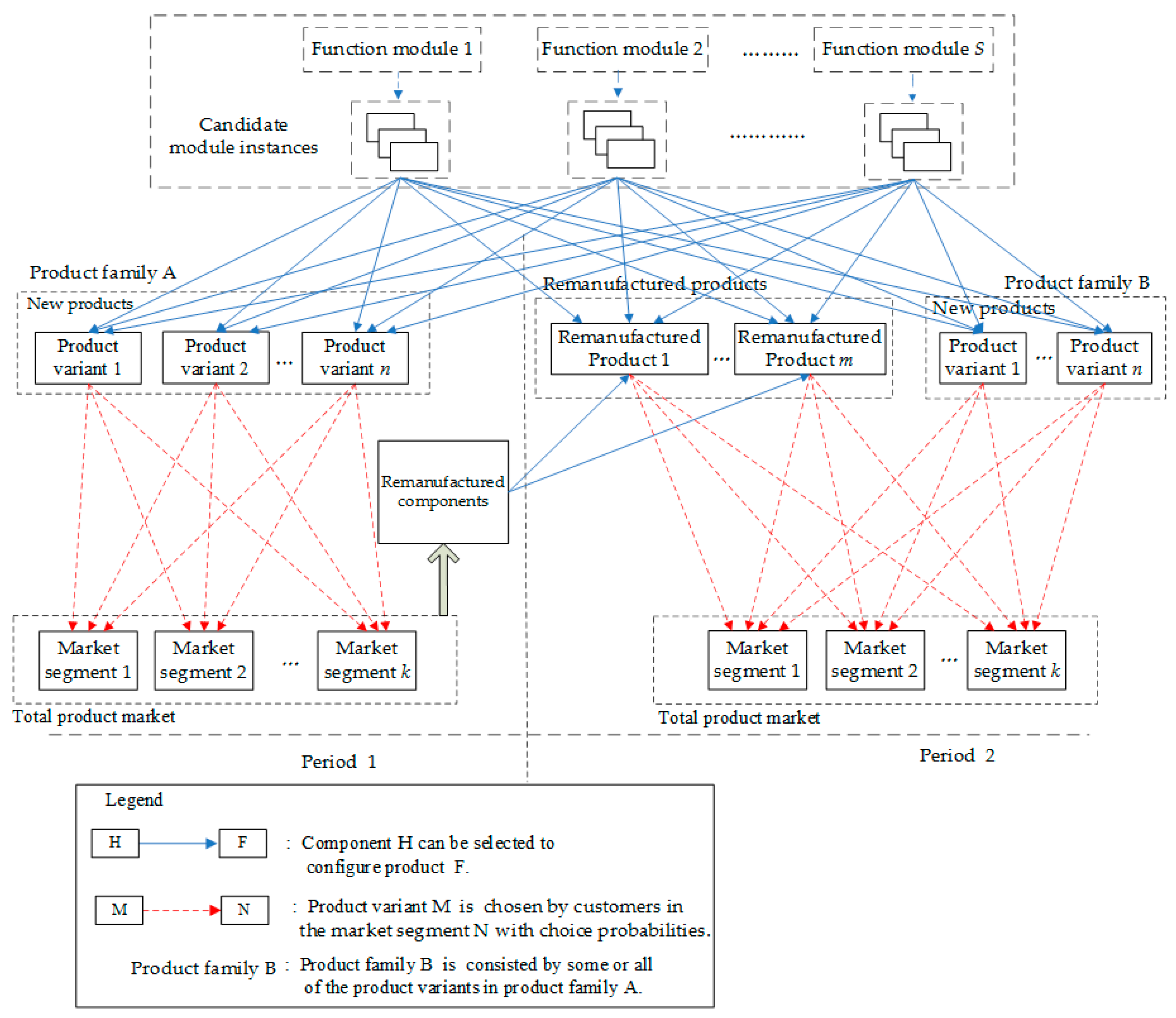
3. Problem Description
- Number of product variants and remanufactured products;
- Module instance (component) configuration of each product variant and each remanufactured product;
- Selling prices of each product variant and each remanufactured product in periods 1 and 2; and
- Selection of remanufacturing technology (remanufacturing parameters) for remanufacturing of used components.
4. Development of an Optimization Model
4.1. Customer Preference Modeling with Utility Function
4.2. Product Demand Model
4.3. Cost Models
4.4. GHG Emission Models
4.5. Constraints
4.5.1. Selection Constraint of Module Instances.
4.5.2. Selection Constraint of Remanufactured Components for Remanufactured Products
4.5.3. Product Reliability Constraint
4.6. Formulation of the Optimization Model
| Total profit of a company | |
| Total expected revenue of a company | |
| C | Total cost of production |
| E | Total GHG emission of production |
| Binary decision variable such that if the rth product variant is produced, and otherwise | |
| Binary decision variable such that if the hth remanufactured product is produced, and otherwise | |
| Binary decision variable such that if the jth instance of ith module is selected for rth product variant, and otherwise | |
| Binary decision variable such that if the jth instance of ith module is selected for hth remanufactured product, and otherwise | |
| Binary decision variable such that if the jth instance of ith module is remanufactured for hth remanufactured product, and otherwise | |
| Sale price of rth product variant in period 1 | |
| Sale price of rth product variant in period 2 | |
| Sale price of hth remanufactured product |
5. Solution Methodology
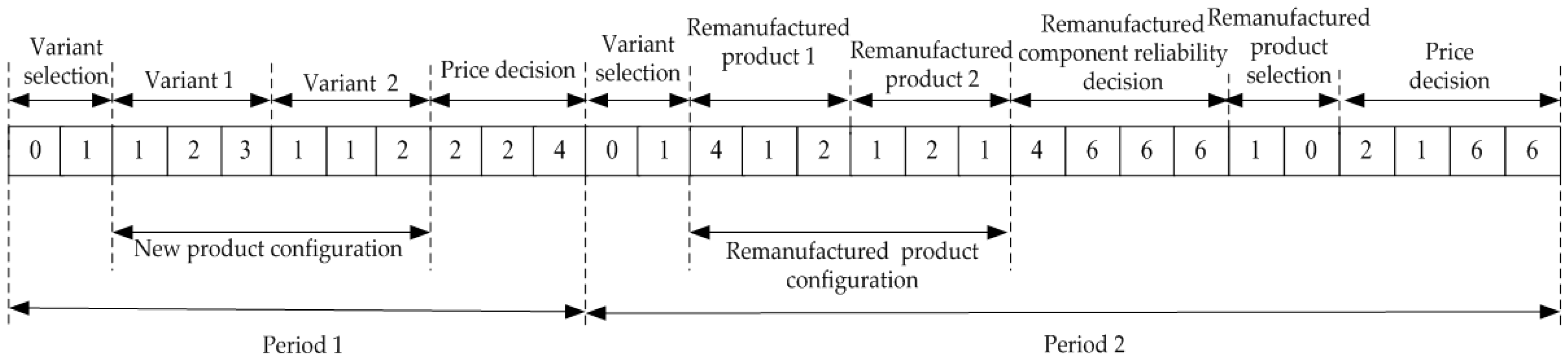
5.1. Chromosome Representation
5.2. Fitness Function
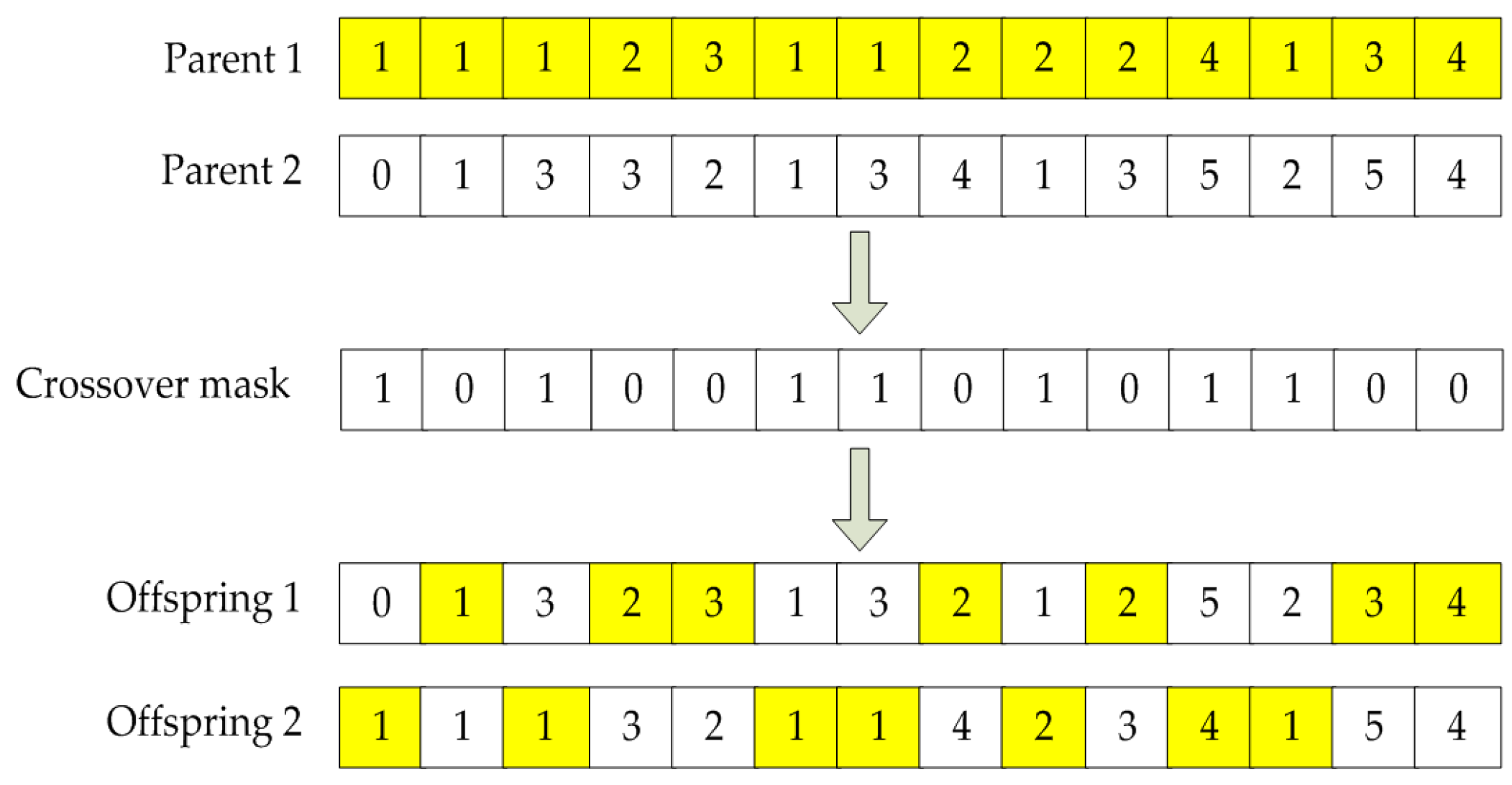
5.3. Genetic Operators
5.4. Constraints Handling
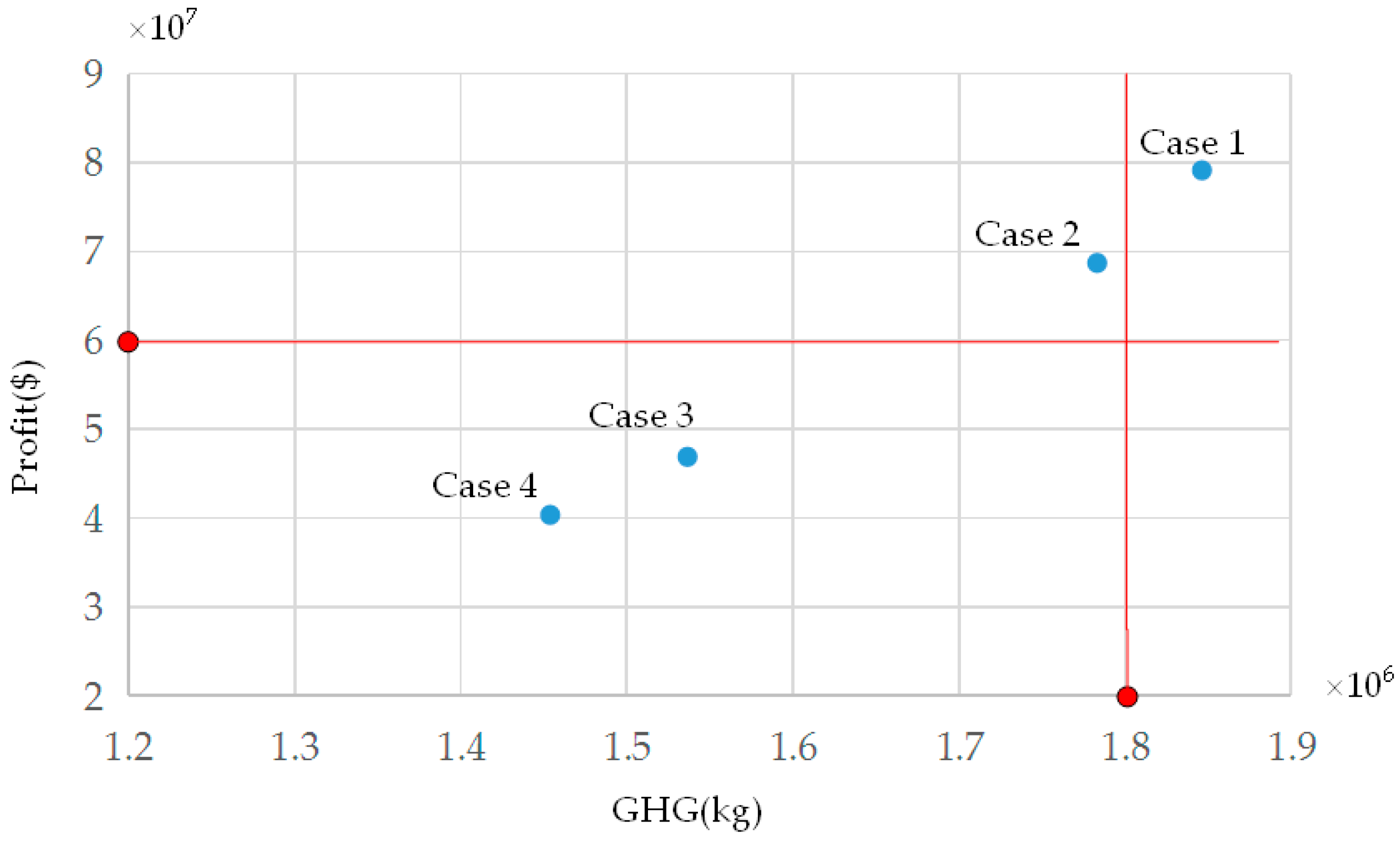
6. Case Study
6.1. Sensitivity Analysis of GHG Emission Weight
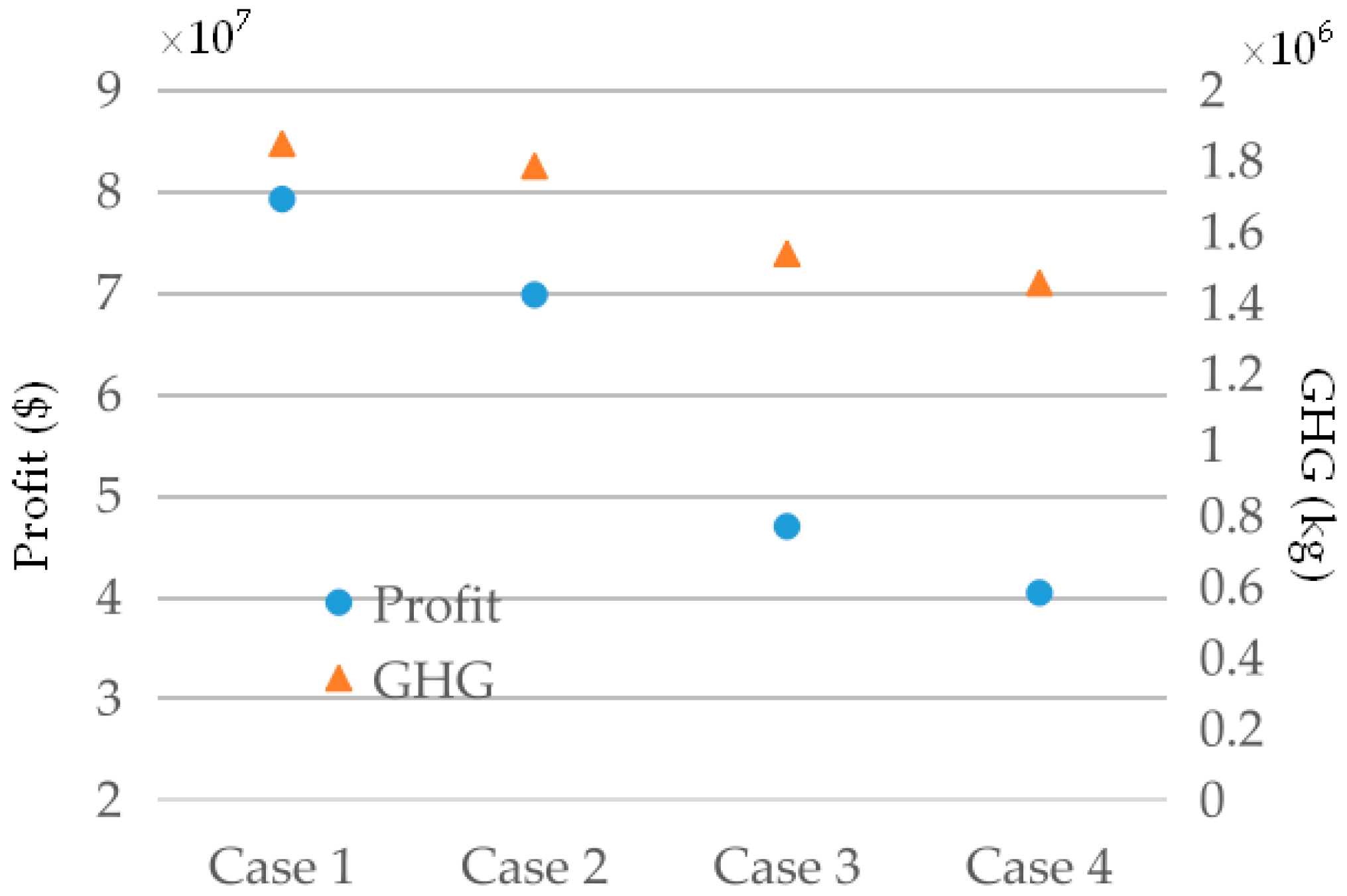
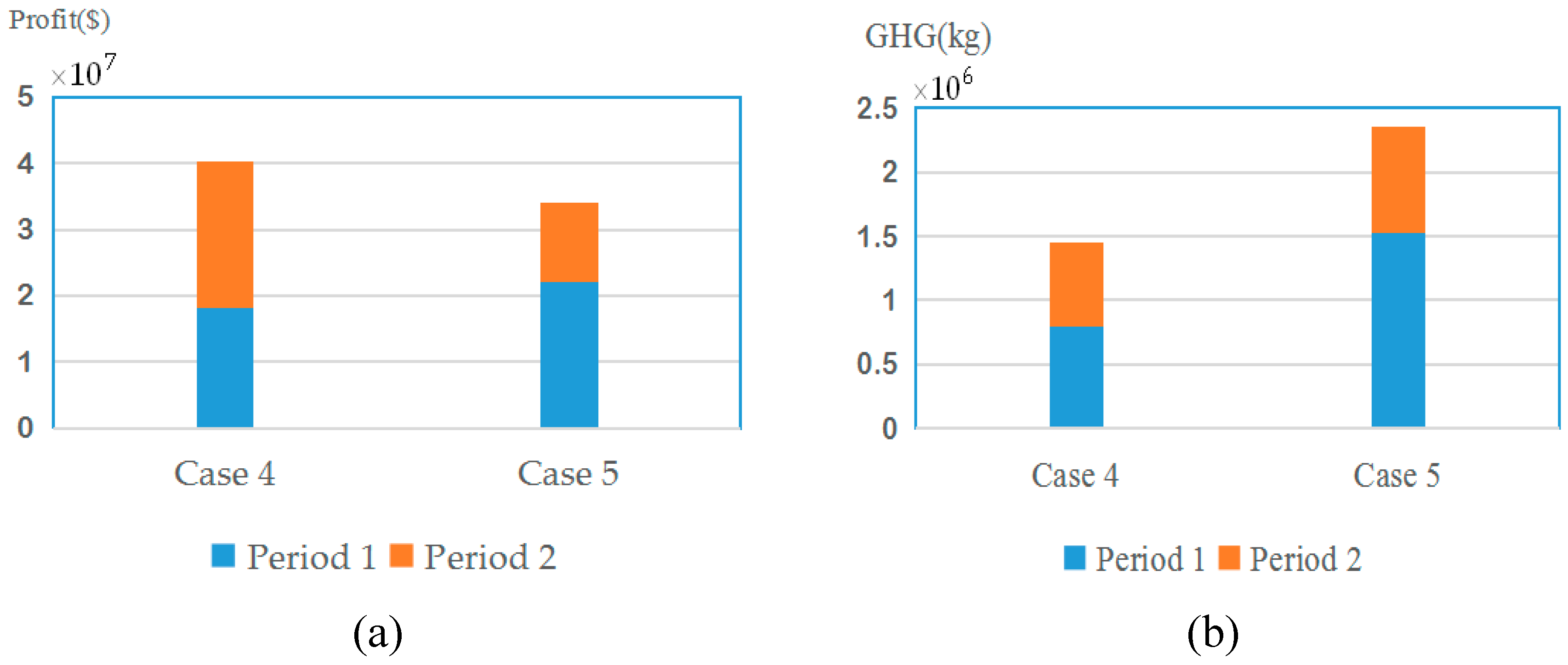
6.2. Analysis to the Effect on Low-Carbon Product Family Design with or without Considering Remanufactured Products
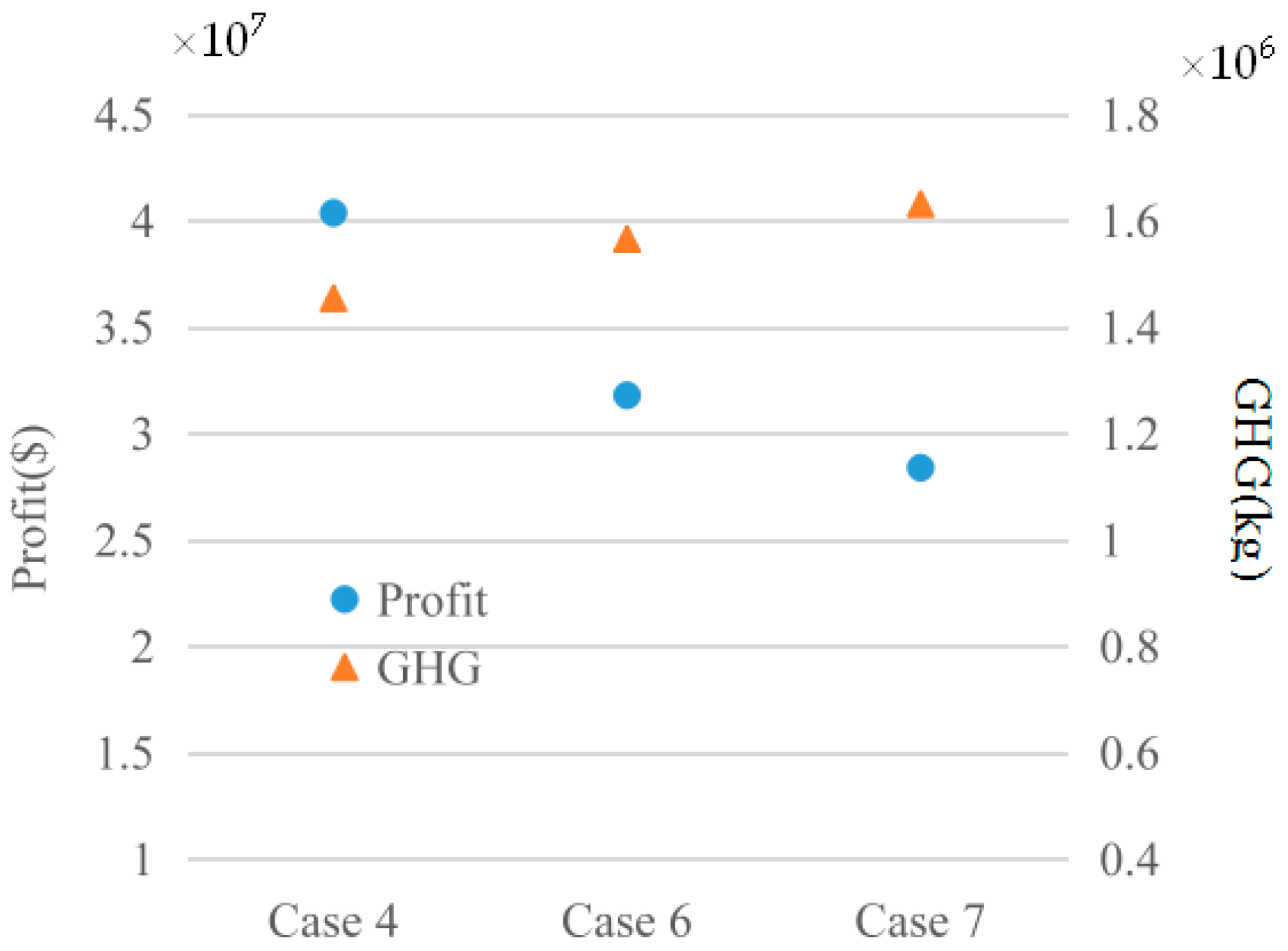
6.3. The Influence of Reliability Threshold Value of a Product on Optimization Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change (IPCC). IPCC Fourth Assessment Report: Climate Change 2007; Cambridge University Press: New York, NY, USA, 2007; pp. 447–496. [Google Scholar]
- Mascle, C.; Zhao, H.P. Integrating environmental consciousness in product/process development based on life-cycle thinking. Int. J. Prod. Econ. 2008, 112, 5–17. [Google Scholar] [CrossRef]
- Kengpol, A.; Boonkanit, P. The decision support framework for developing ecodesign at conceptual phase based upon iso/tr 14062. Int. J. Prod. Econ. 2011, 131, 4–14. [Google Scholar] [CrossRef]
- Ferrer, G.; Swaminathan, J.M. Managing new and differentiated remanufactured products. Eur. J. Oper. Res. 2010, 203, 370–379. [Google Scholar] [CrossRef]
- Sutherland, J.W.; Adler, D.P.; Haapala, K.R.; Kumar, V. A comparison of manufacturing and remanufacturing energy intensities with application to diesel engine production. CIRP Ann.-Manuf. Technol. 2008, 57, 5–8. [Google Scholar] [CrossRef]
- Song, J.S.; Lee, K.M. Development of a low-carbon product design system based on embedded GHG emissions. Resour. Conserv. Recycl. 2010, 54, 547–556. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, X.B. Low-carbon technologies integrated innovation strategy based on modular design. Energy Procedia 2011, 5, 2509–2515. [Google Scholar] [CrossRef][Green Version]
- Su, J.C.P.; Chu, C.; Wang, Y. A decision support system to estimate the carbon emission and cost of product designs. Int. J. Precis. Eng. Manuf. 2012, 13, 1037–1045. [Google Scholar] [CrossRef]
- Kuo, T.C.; Chen, H.M.; Liu, C.Y.; Tu, J.C.; Yeh, T.C. Applying multi-objective planning in low-carbon product design. Int. J. Precis. Eng. Manuf. 2014, 15, 241–249. [Google Scholar] [CrossRef]
- Xu, Z.Z.; Wang, Y.S.; Teng, Z.R.; Zhong, C.Q.; Teng, H.F. Low-carbon product multi-objective optimization design for meeting requirements of enterprise, user and government. J. Clean. Prod. 2015, 103, 747–758. [Google Scholar] [CrossRef]
- He, B.; Wang, J.; Huang, S.; Wang, Y. Low-carbon product design for product life cycle. J. Eng. Des. 2015, 26, 321–339. [Google Scholar] [CrossRef]
- Chiang, T.A.; Che, Z.H. A Decision-Making Methodology for Low-Carbon Electronic Product Design. Decis. Support Syst. 2015, 71, 1–13. [Google Scholar] [CrossRef]
- He, B.; Tang, W.; Wang, J.; Huang, S.; Deng, Z.Q.; Wang, Y. Low-carbon conceptual design based on product life cycle assessment. Int. J. Adv. Manuf. Technol. 2015, 81, 863–874. [Google Scholar] [CrossRef]
- Jiao, J.; Simpson, T.W.; Siddique, Z. Product family design and platform-based product development: A state-of-the-art review. J. Intell. Manuf. 2007, 18, 5–29. [Google Scholar] [CrossRef]
- Francalanza, E.; Borg, J.C.; Constantinescu, C. A case for assisting ’Product Family’ manufacturing system designers. Procedia CIRP 2012, 3, 376–381. [Google Scholar] [CrossRef]
- Bryan, A.; Wang, H.; Abell, J. Concurrent Design of Product Families and Reconfigurable Assembly Systems. J. Mech. Des. 2013, 135, 051001. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, D.B.; Yin, L.L.; Salido, M.A.; Giret, A.; Xu, Y.C. Bi-objective optimization for low-carbon product family design. Robot. Comput.-Int. Manuf. 2016, 41, 53–65. [Google Scholar] [CrossRef][Green Version]
- Tang, D.B.; Wang, Q.; Ullah, I. Optimisation of product configuration in consideration of customer satisfaction and low carbon. Int. J. Prod. Res. 2017, 55, 3349–3373. [Google Scholar] [CrossRef]
- Kim, S.; Moon, S.K. Sustainable platform identification for product family design. J. Clean. Prod. 2017, 143, 567–581. [Google Scholar] [CrossRef]
- Xiao, W.X.; Du, G.; Zhang, Y.Y.; Liu, X.J. Coordinated optimization of low-carbon product family and its manufacturing process design by a bilevel game-theoretic model. J. Clean. Prod. 2018, 184, 754–773. [Google Scholar] [CrossRef]
- Mangun, D.; Thurston, D.L. Incorporating component reuse, remanufacture, and recycle into product portfolio design. IEEE Trans. Eng. Manag. 2002, 49, 479–490. [Google Scholar] [CrossRef]
- Debo, L.G.; Toktay, L.B.; Wassenhove, L.N.V. Joint life-cycle dynamics of new and remanufactured products. Prod. Oper. Manag. 2006, 15, 498–513. [Google Scholar] [CrossRef]
- Vorasayan, J.; Ryan, S.M. Optimal price and quantity of refurbished products. Prod. Oper. Manag. 2006, 15, 369–383. [Google Scholar] [CrossRef]
- Kwak, M.; Kim, H.M. Assessing product family design from an end-of-life perspective. Eng. Optim. 2011, 43, 233–255. [Google Scholar] [CrossRef]
- Kwak, M.; Kim, H.M. Market positioning of remanufactured products with optimal planning for part upgrades. J. Mech. Des. 2013, 135, 1–10. [Google Scholar] [CrossRef]
- Debo, L.G.; Toktay, L.B.; Wassenhove, L.N.V. Market Segmentation and Product Technology Selection for Remanufacturable Products. Manag. Sci. 2005, 51, 1193–1205. [Google Scholar] [CrossRef]
- Ferguson, M.E.; Toktay, L.B. The Effect of Competition on Recovery Strategies. Prod. Oper. Manag. 2006, 15, 351–368. [Google Scholar] [CrossRef]
- Jin, Y.; Muriel, A.; Lu, Y. When to Offer Lower Quality or Remanufactured Versions of a Product. Decis. Sci. 2016, 47, 699–719. [Google Scholar] [CrossRef]
- Liu, B.; Holmbom, M.; Segerstedt, A.; Chen, W. Effects of carbon emission regulations on remanufacturing decisions with limited information of demand distribution. Int. J. Prod. Res. 2015, 53, 532–548. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W.; Liu, B. Manufacturing/remanufacturing decisions for a capital-constrained manufacturer considering carbon emission cap and trade. J. Clean. Prod. 2017, 140, 1118–1128. [Google Scholar] [CrossRef]
- Yenipazarli, A. Managing new and remanufactured products to mitigate environmental damage under emissions regulation. Eur. J. Oper. Res. 2016, 249, 117–130. [Google Scholar] [CrossRef]
- Simpson, T. A Concept Exploration Method for Product Family Design. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 1998. [Google Scholar]
- Perera, H.S.; Nagarur, N.; Tabucanon, M.T. Component part standardization: A way to reduce the life-cycle costs of products. Int. J. Prod. Econ. 1999, 60–61, 109–116. [Google Scholar] [CrossRef]
- Kwak, M. Green Profit Design for Lifecycle. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2012. [Google Scholar]
- Hsu, T.H.; Chu, K.M.; Chan, H.C. The fuzzy clustering on market segment. In Proceedings of the IEEE International Conference on Fuzzy Systems, San Antonio, TX, USA, 7–10 May 2000. [Google Scholar]
- Jiao, J.X.; Zhang, Y. Product portfolio planning with customer-engineering interaction. IIE Trans. 2005, 37, 801–814. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.K.; Ma, H. Joint procurement and production decisions in remanufacturing under quality and demand uncertainty. Int. J. Prod. Econ. 2009, 120, 5–17. [Google Scholar] [CrossRef]
- Wang, K.; Choi, S.H. A holonic approach to flexible flow shop scheduling under stochastic processing times. Comput. Oper. Res. 2014, 43, 157–168. [Google Scholar] [CrossRef]
| - | Segment 1 | Segment 2 | Segment 3 |
|---|---|---|---|
| Demand quantity (PCS) period 1/2 | 250,000/40,0000 | 400,000/360,000 | 650,000/380,000 |
| Utility of competitor product 1 | 85.48 | 98.27 | 156.87 |
| Utility of competitor product 2 | 120.47 | 110.62 | 107.58 |
| Module | Module Instance (Component) (Price, $) | Utility in Segment 1 | Utility in Segment 2 | Utility in Segment 3 | Variable Unit Cost ($) | Variable Unit Emission (g) | GHG Emission (g) | Reliability |
|---|---|---|---|---|---|---|---|---|
| M1 | M1,1 (82.45) | 160.65 | 164.40 | 155.20 | 8 | 3 | 40.9 | 0.988 |
| M1,2 (75.48) | 152.31 | 153.29 | 147.45 | 8 | 5 | 37.2 | 0.983 | |
| M1,3 (70.47) | 145.52 | 148.85 | 140.10 | 10 | 3 | 35.4 | 0.985 | |
| M1,4 (65.08) | 140.56 | 138.30 | 134.90 | 10 | 3 | 30.3 | 0.985 | |
| M2 | M2,1(76.58) | 110.23 | 108.21 | 115.87 | 7 | 1 | 217 | 0.999 |
| M2,2 (70.25) | 105.87 | 103.49 | 107.46 | 8 | 3 | 210 | 0.997 | |
| M2,3 (65.08) | 100.68 | 97.84 | 98.45 | 8 | 1 | 220 | 0.999 | |
| M2,4 (57.49) | 97.89 | 89.27 | 84.87 | 9 | 2 | 198 | 0.998 | |
| M3 | M3,1 (39.08) | 50.57 | 52.87 | 47.59 | 7 | 5 | 282 | 0.987 |
| M3,2 (32.14) | 45.98 | 47.85 | 44.12 | 7 | 5 | 254 | 0.988 | |
| M3,3 (28.79) | 41.45 | 38.98 | 35.87 | 8 | 3 | 264 | 0.986 | |
| M4 | M4,1 (240.89) | 300.54 | 298.47 | 307.56 | 6 | 3 | 362 | 0.995 |
| M4,2 (218.87) | 285.25 | 281.28 | 291.58 | 6 | 1 | 358 | 0.996 | |
| M4,3 (200.08) | 274.87 | 270.79 | 284.26 | 8 | 1 | 341 | 0.998 | |
| M5 | M5,1 (15.76) | 27.9 | 28.45 | 27.5 | 7 | 2 | 157 | 0.986 |
| M5,2 (13.14) | 24.86 | 24.47 | 20.89 | 8 | 3 | 134 | 0.985 | |
| M5,3 (11.42) | 22.14 | 18.49 | 16.45 | 8 | 4 | 130 | 0.982 | |
| M6 | M6,1(56.11) | 97.56 | 89.45 | 97.25 | 6 | 1 | 450 | 0.998 |
| M6,2 (50.98) | 88.47 | 84.87 | 89.82 | 6 | 2 | 431 | 0.998 | |
| M6,3 (44.38) | 80.78 | 77.69 | 74.39 | 6 | 3 | 425 | 0.997 |
| Module instance | Reliability | Utilities in Segment 1/2/3 | Remanufacturing Unit Cost/GHG Emission |
|---|---|---|---|
| M2,1 | 1st: 0.978 | 77.16/75.74/81.10 | 22.97/65.1 |
| 2st: 0.959 | 66.13/64.92/69.52 | 15.31/43.4 | |
| M2,2 | 1st: 0.985 | 74.10/72.44/75.22 | 21.07/63 |
| 2st: 0.968 | 63.52/62.09/64.47 | 14.05/42 | |
| M2,3 | 1st: 0.985 | 70.04/68.48/68.91 | 19.52/66 |
| 2st: 0.968 | 60.40/58.70/59.07 | 13.01/44 | |
| M2,4 | 1st: 0.987 | 68.52/62.48/59.40 | 17.24/59.4 |
| 2st: 0.959 | 58.73/53.56/50.92 | 11.49/39.6 | |
| M3,1 | 1st: 0.978 | 35.39/37/33.31 | 11.72/84.6 |
| 2st: 0.959 | 30.34/31.72/28.55 | 7.81/56.4 | |
| M3,2 | 1st: 0.968 | 32.18/33.49/30.88 | 9.64/76.2 |
| 2st: 0.949 | 27.58/28.71/26.47 | 6.42/50.8 | |
| M3,3 | 1st: 0.968 | 29.01/27.28/25.10 | 8.63/79.2 |
| 2st: 0.948 | 24.87/23.98/21.52 | 5.75/52.8 | |
| M5,1 | 1st: 0.969 | 19.53/19.91/19.25 | 4.72/47.1 |
| 2st: 0.947 | 16.74/17.07/16.5 | 3.15/31.4 | |
| M5,2 | 1st: 0.988 | 17.40/17.12/14.62 | 3.94/40.2 |
| 2st: 0.969 | 14.91/14.68/12.53 | 2.62/26.8 | |
| M5,3 | 1st: 0.988 | 15.49/12.94/11.51 | 3.42/39 |
| 2st: 0.965 | 13.28/11.09/9.87 | 2.28/26 | |
| M6,1 | 1st: 0.990 | 68.29/62.61/68.07 | 16.83/135 |
| 2st: 0.975 | 58.53/53.67/58.35 | 11.22/90 | |
| M6,2 | 1st: 0.990 | 61.92/59.40/62.87 | 15.29/129.3 |
| 2st: 0.982 | 53.08/50.92/53.89 | 10.19/86.2 | |
| M6,3 | 1st: 0.98 | 56.54/54.38/52.07 | 13.31/127.5 |
| 2st: 0.97 | 48.46/46.61/44.63 | 8.87/85 |
| Module Instance Configuration | Launched in Period | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Product | M1 | M2 | M3 | M4 | M5 | M6 | 1 | 2 | |
| Case 1 | variant 1 | 1 | 1 | 1 | 3 | 1 | 2 | Yes | Yes |
| variant 2 | 2 | 1 | 2 | 3 | 2 | 3 | Yes | Yes | |
| variant 3 | 2 | 4 | 3 | 1 | 3 | 2 | Yes | Yes | |
| Remanufactured 1 | 3 | 1r−1 | 1r−1 | 2 | 1r−1 | 2 | - | Yes | |
| Remanufactured 2 | 4 | 1r−1 | 3 | 2 | 1r−1 | 3 | - | Yes | |
| Case 2 | variant 1 | 4 | 1 | 2 | 2 | 2 | 2 | Yes | Yes |
| variant 2 | 4 | 4 | 1 | 3 | 2 | 1 | Yes | Yes | |
| variant 3 | 3 | 1 | 1 | 2 | 1 | 1 | Yes | Yes | |
| Remanufactured 1 | 2 | 4 | 1r−1 | 3 | 1r−1 | 1r−1 | - | Yes | |
| Remanufactured 2 | 3 | 1r−1 | 1r−1 | 3 | 1r−1 | 2 | - | Yes | |
| Remanufactured 3 | 3 | 1r−1 | 1r−1 | 3 | 1r−1 | 1r−1 | - | Yes | |
| Case 3 | variant 1 | 1 | 3 | 3 | 2 | 3 | 2 | Yes | Yes |
| variant 2 | 4 | 1 | 3 | 3 | 3 | 2 | Yes | Yes | |
| variant 3 | 4 | 1 | 1 | 2 | 1 | 1 | Yes | Yes | |
| Remanufactured 1 | 2 | 4 | 1r−1 | 3 | 1r−2 | 2 | - | Yes | |
| Remanufactured 2 | 3 | 3 | 1r−1 | 3 | 1r−2 | 3 | - | Yes | |
| Remanufactured 3 | 1 | 1r−2 | 1 | 3 | 1r−2 | 2 | - | Yes | |
| Case 4 | variant 1 | 1 | 4 | 3 | 3 | 1 | 3 | Yes | Yes |
| variant 2 | 1 | 2 | 3 | 3 | 3 | 1 | Yes | Yes | |
| variant 3 | 2 | 1 | 2 | 3 | 1 | 2 | Yes | Yes | |
| Remanufactured 1 | 1 | 4 | 3 | 3 | 1r−2 | 2 | - | Yes | |
| Remanufactured 2 | 3 | 3 | 3 | 3 | 1r−2 | 3 | - | Yes | |
| Remanufactured 3 | 1 | 1r−1 | 3 | 2 | 1 | 3 | - | Yes | |
| Product | Module Instance Configuration | Launched in Period | ||||||
|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | 1 | 2 | |
| variant 1 | 1 | 4 | 1 | 3 | 1 | 2 | Yes | Yes |
| variant 2 | 3 | 1 | 3 | 3 | 3 | 2 | Yes | Yes |
| variant 3 | 4 | 1 | 1 | 3 | 1 | 1 | Yes | Yes |
| Remanufactured 1 | 2 | 4 | 4 | 3 | 1r−2 | 2 | - | Yes |
| Remanufactured 2 | 2 | 1r−2 | 2 | 2 | 1 | 3 | - | Yes |
| - | Product | Module Instance Configuration | Launched in Period | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | 1 | 2 | ||
| Case 6 | variant 1 | 4 | 4 | 2 | 3 | 2 | 3 | Yes | Yes |
| variant 2 | 4 | 1 | 3 | 2 | 3 | 3 | Yes | Yes | |
| variant 3 | 4 | 1 | 1 | 2 | 1 | 1 | Yes | Yes | |
| Remanufactured 1 | 2 | 4 | 1r−1 | 3 | 1r−1 | 2 | - | Yes | |
| Remanufactured 2 | 1 | 3 | 1r−1 | 3 | 1r−1 | 2 | - | Yes | |
| Remanufactured 3 | 1 | 1r−2 | 2 | 2 | 1 | 3 | - | Yes | |
| Case 7 | variant 1 | 2 | 3 | 3 | 2 | 3 | 3 | Yes | Yes |
| variant 2 | 3 | 3 | 3 | 2 | 1 | 3 | Yes | Yes | |
| variant 3 | 4 | 1 | 1 | 2 | 1 | 1 | Yes | Yes | |
| Remanufactured 1 | 2 | 4 | 1r−1 | 3 | 3 | 2 | - | Yes | |
| Remanufactured 2 | 3 | 3 | 1r−1 | 3 | 3 | 3 | - | Yes | |
| Remanufactured 3 | 1 | 1r−1 | 1 | 3 | 1 | 2 | - | Yes | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Tang, D.; Li, S.; Yang, J.; Salido, M.A.; Giret, A.; Zhu, H. An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products. Sustainability 2019, 11, 460. https://doi.org/10.3390/su11020460
Wang Q, Tang D, Li S, Yang J, Salido MA, Giret A, Zhu H. An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products. Sustainability. 2019; 11(2):460. https://doi.org/10.3390/su11020460
Chicago/Turabian StyleWang, Qi, Dunbing Tang, Shipei Li, Jun Yang, Miguel A. Salido, Adriana Giret, and Haihua Zhu. 2019. "An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products" Sustainability 11, no. 2: 460. https://doi.org/10.3390/su11020460
APA StyleWang, Q., Tang, D., Li, S., Yang, J., Salido, M. A., Giret, A., & Zhu, H. (2019). An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products. Sustainability, 11(2), 460. https://doi.org/10.3390/su11020460






