Nonlinear Predictive Control for a Boiler–Turbine Unit Based on a Local Model Network and Immune Genetic Algorithm
Abstract
1. Introduction
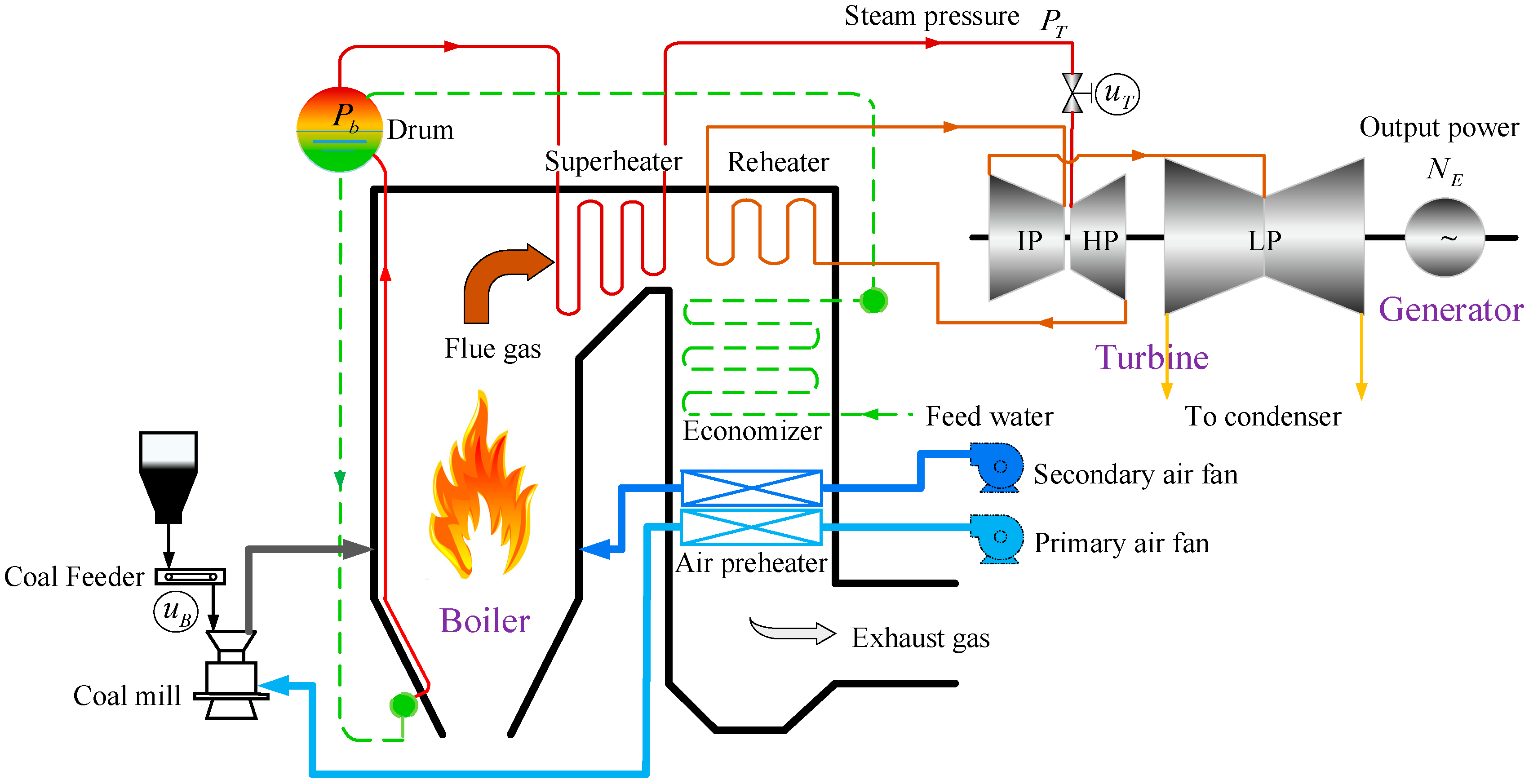
2. System Description
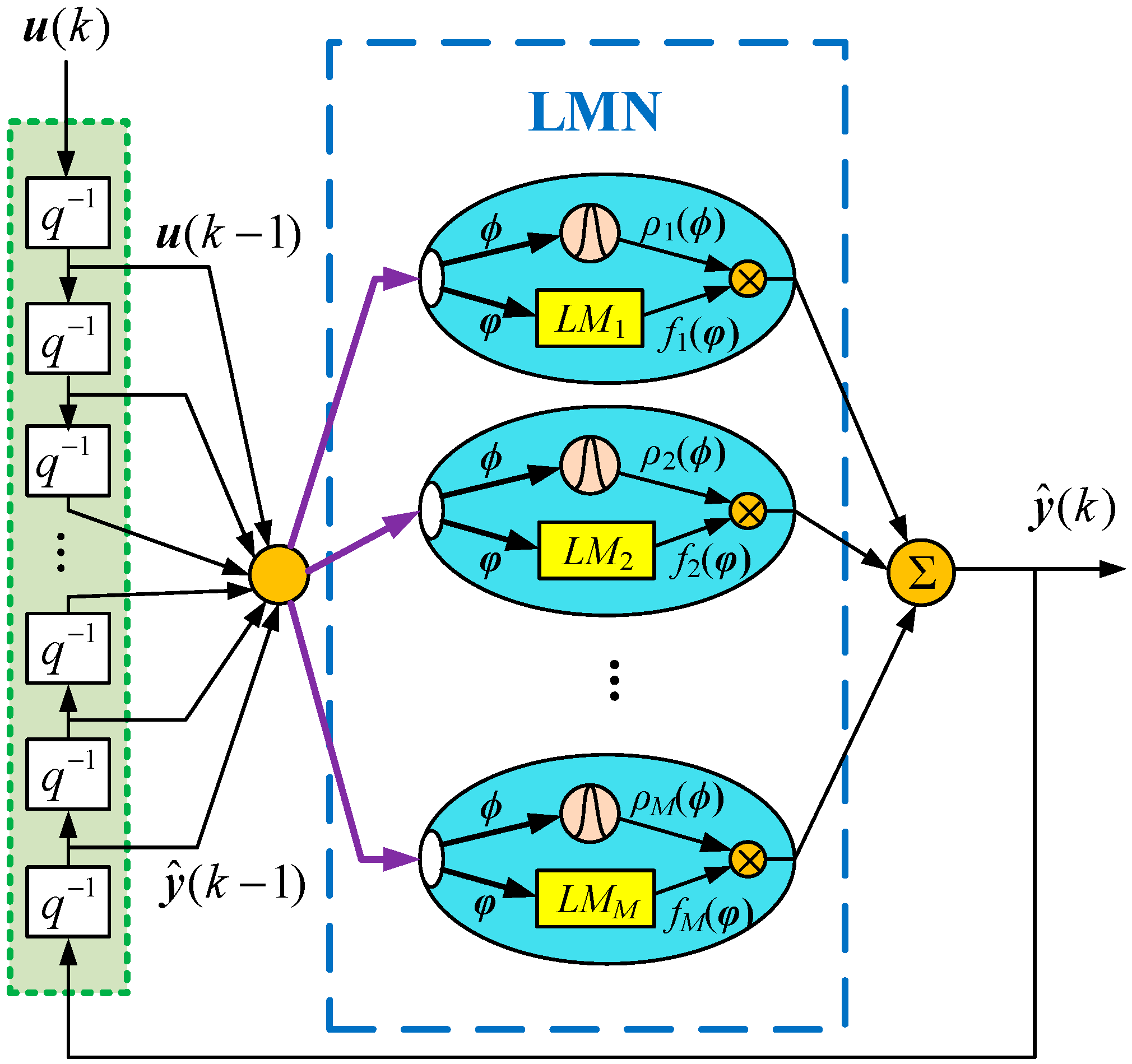
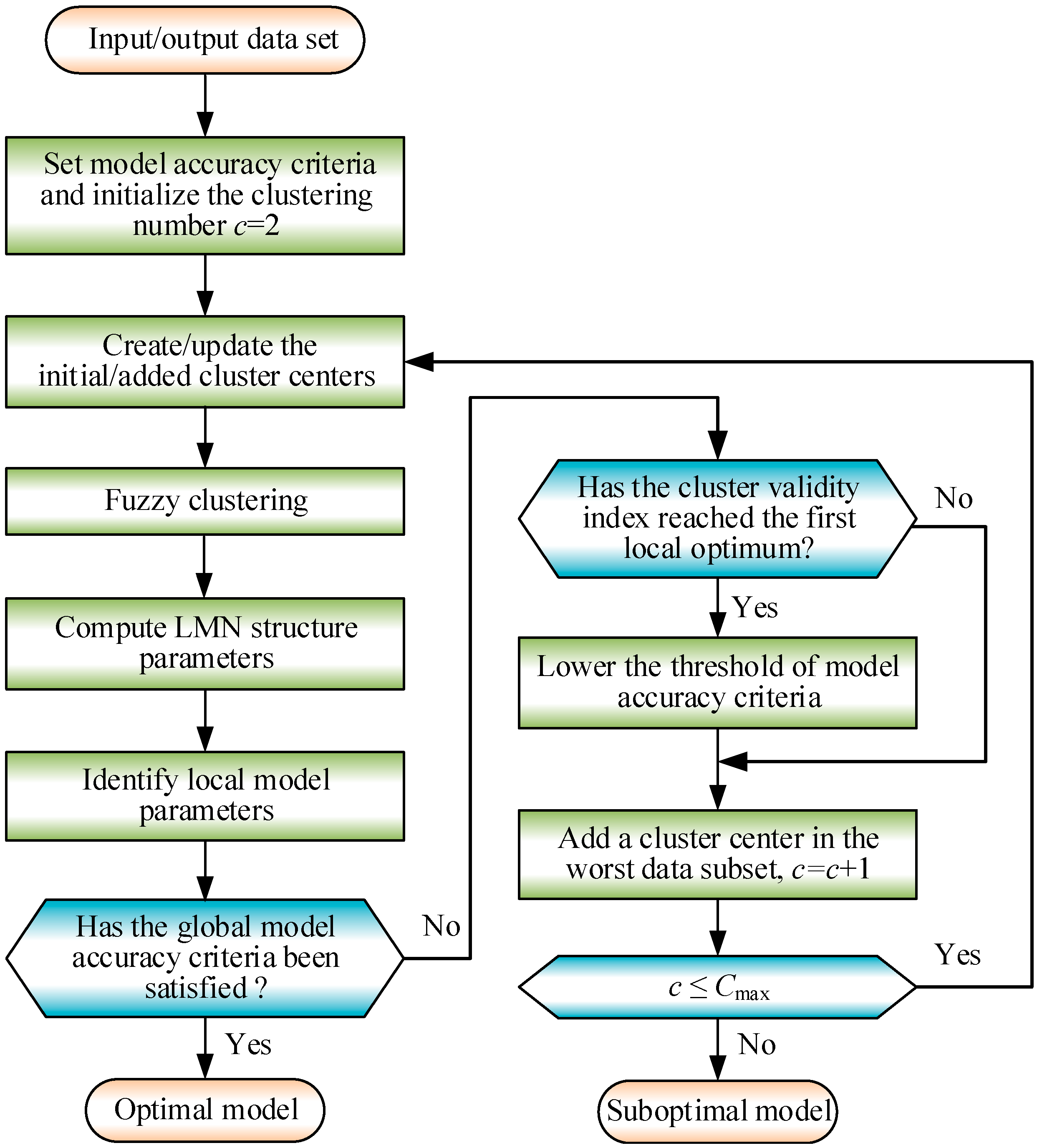
3. Data-Driven Modeling of the B-T Unit
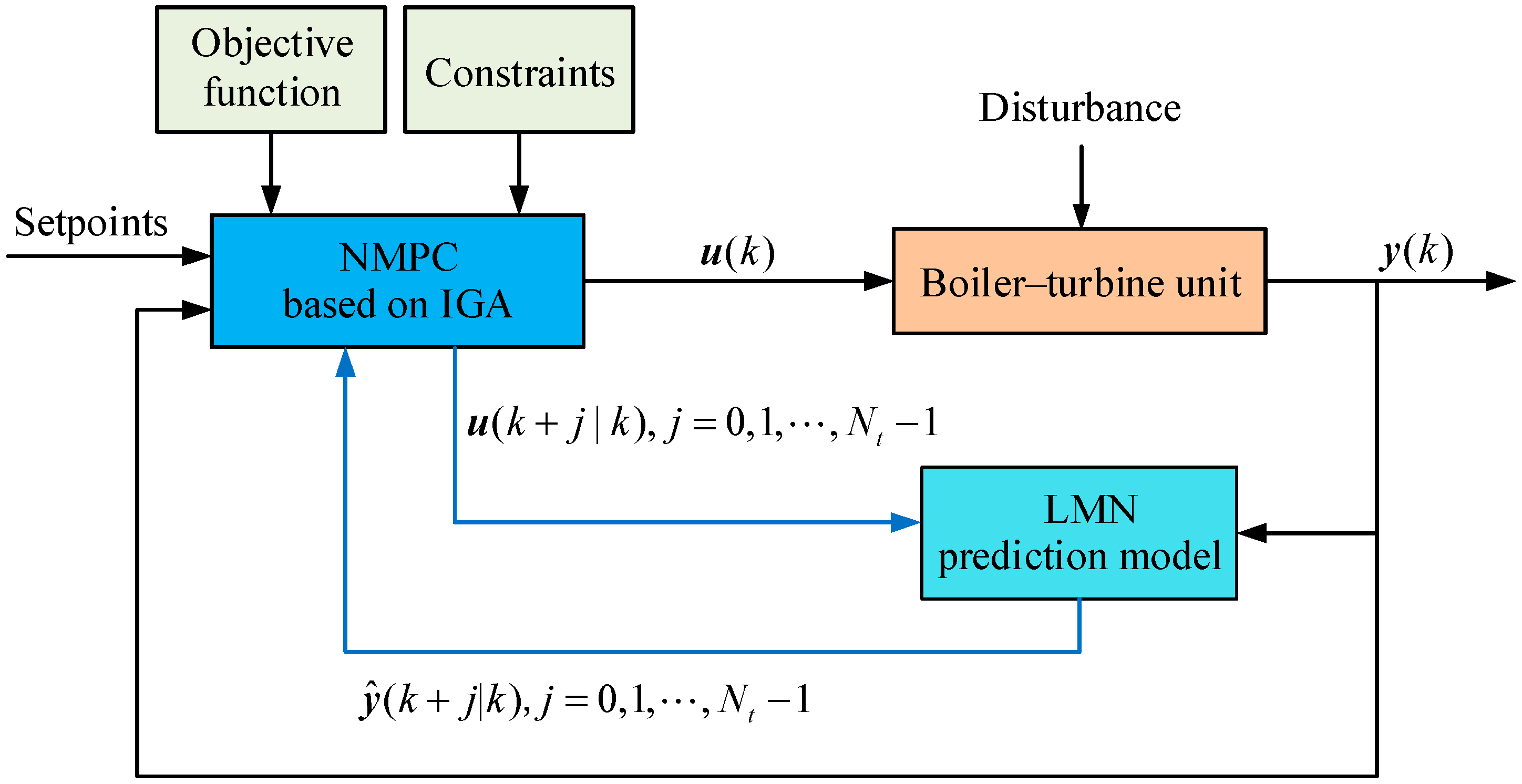
4. Nonlinear Predictive Control Based on IGA Optimization
4.1. State-Space Representation of the Prediction Model
4.2. Nonlinear Optimization Problem Formulation
4.2.1. Objective Function
4.2.2. Steady-State Target
4.2.3. Terminal Penalty Matrix
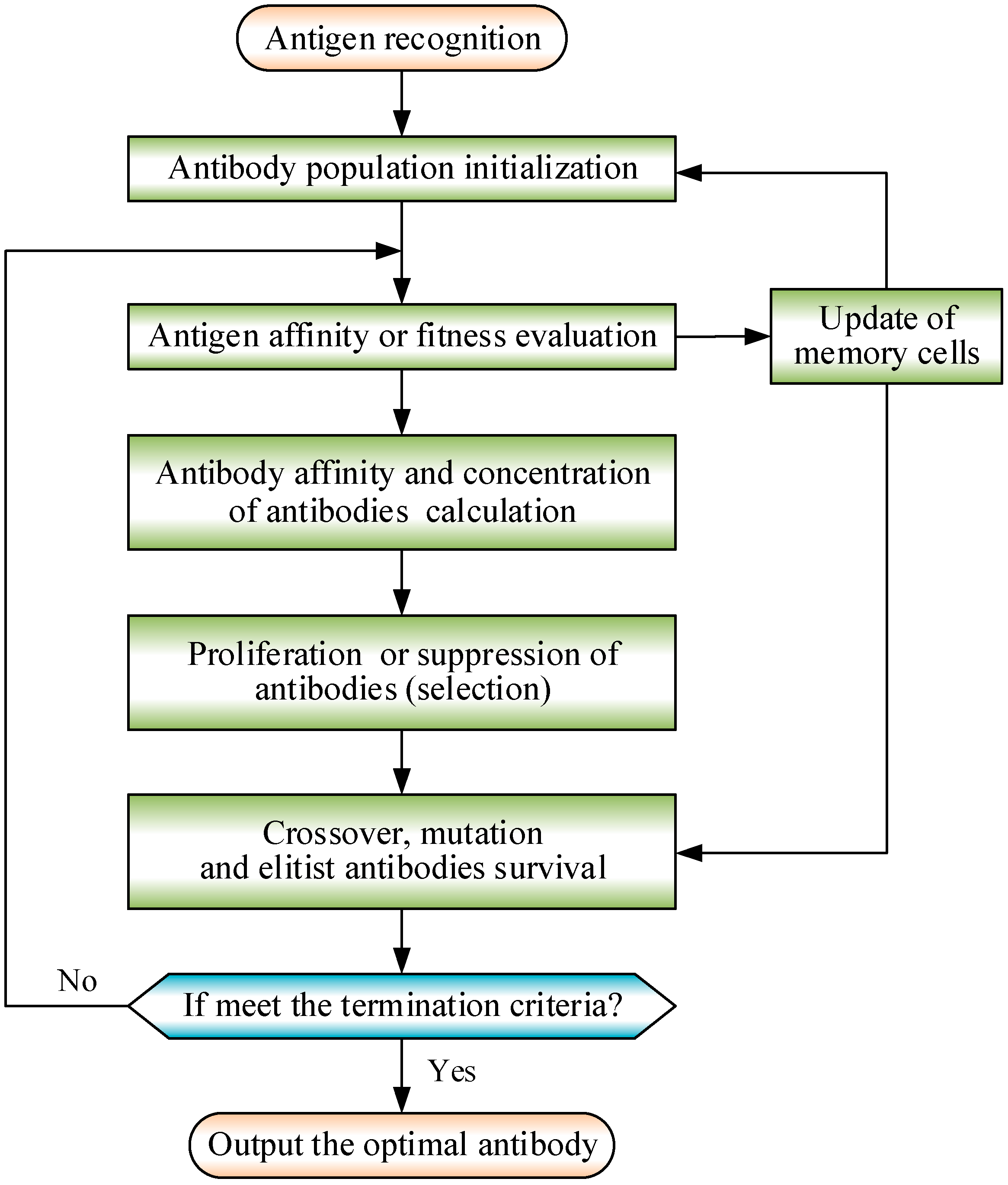
4.3. Receding Horizon Optimization Based on IGA
4.4. Implementation of the NMPC based on an LMN and IGA
| Algorithm 1. Implementation procedure of the NMPC based on an LMN and IGA |
| Off-line part: S01. The LMN model of the nonlinear B-T unit is identified based on the data-driven modeling method and converted into the global model shown in (8) as the prediction model; S02. Linear local models in the LMN are converted into the state-space form (13) and the candidate terminal penalty matrix and gain matrix of the local controller are calculated by (14) and (15) for each local model. S03. The parameters and weighting matrices in the objective function (10)., the parameters in IGA, along with the control and control move constraints are given. Online part: S1. At the current instant k, the scheduling vector and the current state are obtained according to the measured input and output of the system, forming the optimization problem (12); S2. IGA is used to solve (12) to obtain the optimal or sub-optimal control sequence ; S3. The output of the system is obtained by applying the control input to the plant; S4. Let , go to S1 and proceed to the calculation for the next sampling period. |
5. Simulation Results
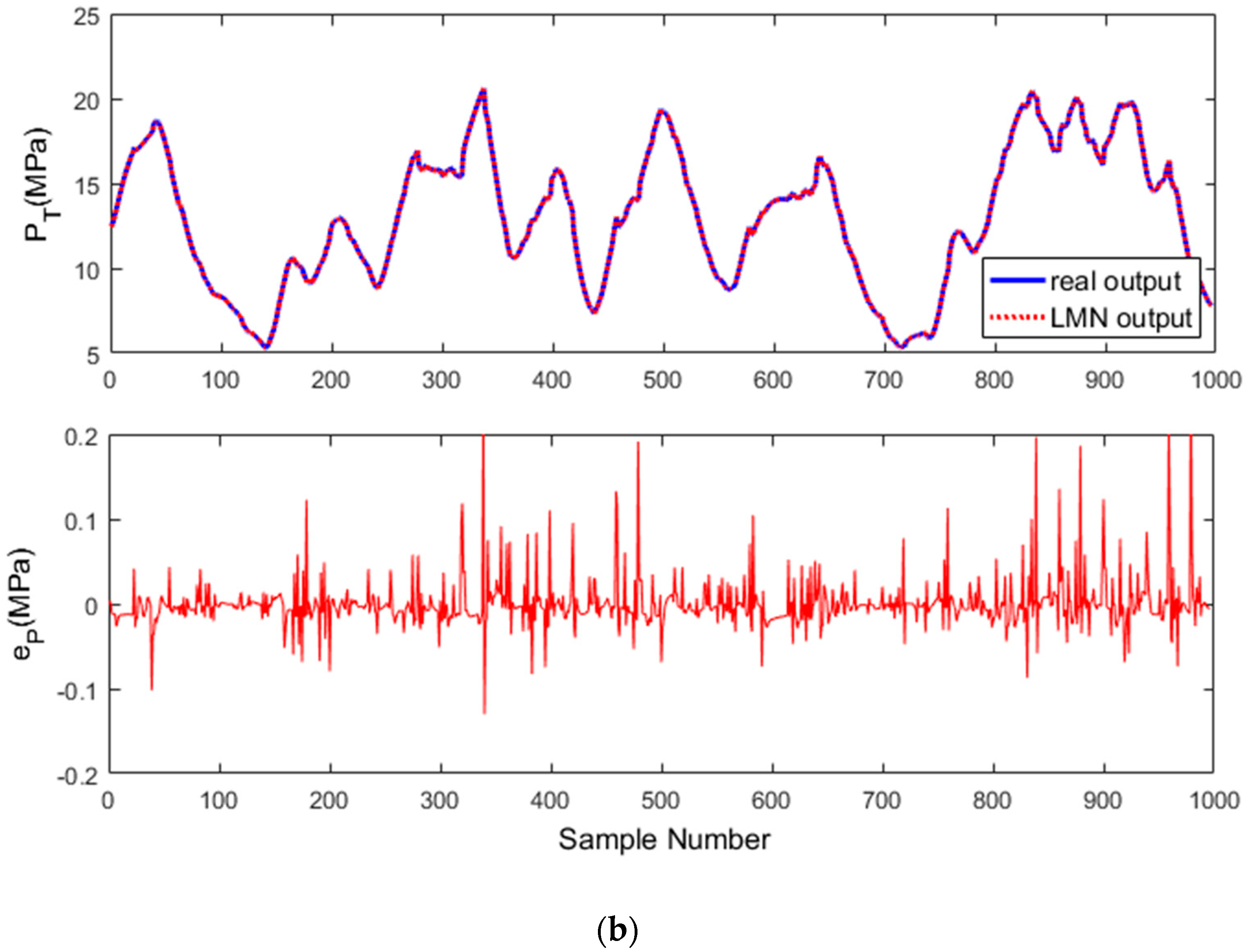
5.1. Model Identification and Test for the B-T Unit
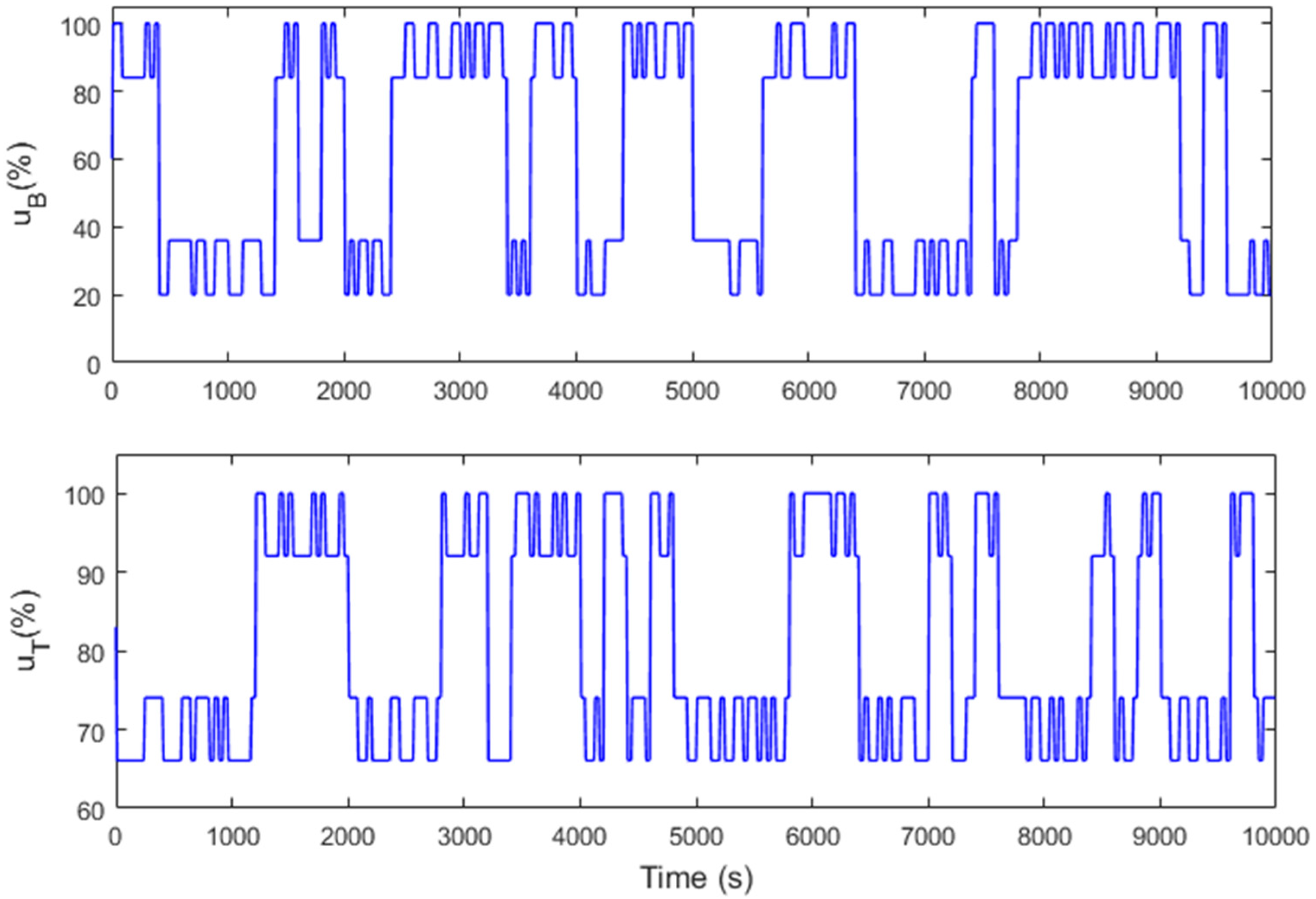
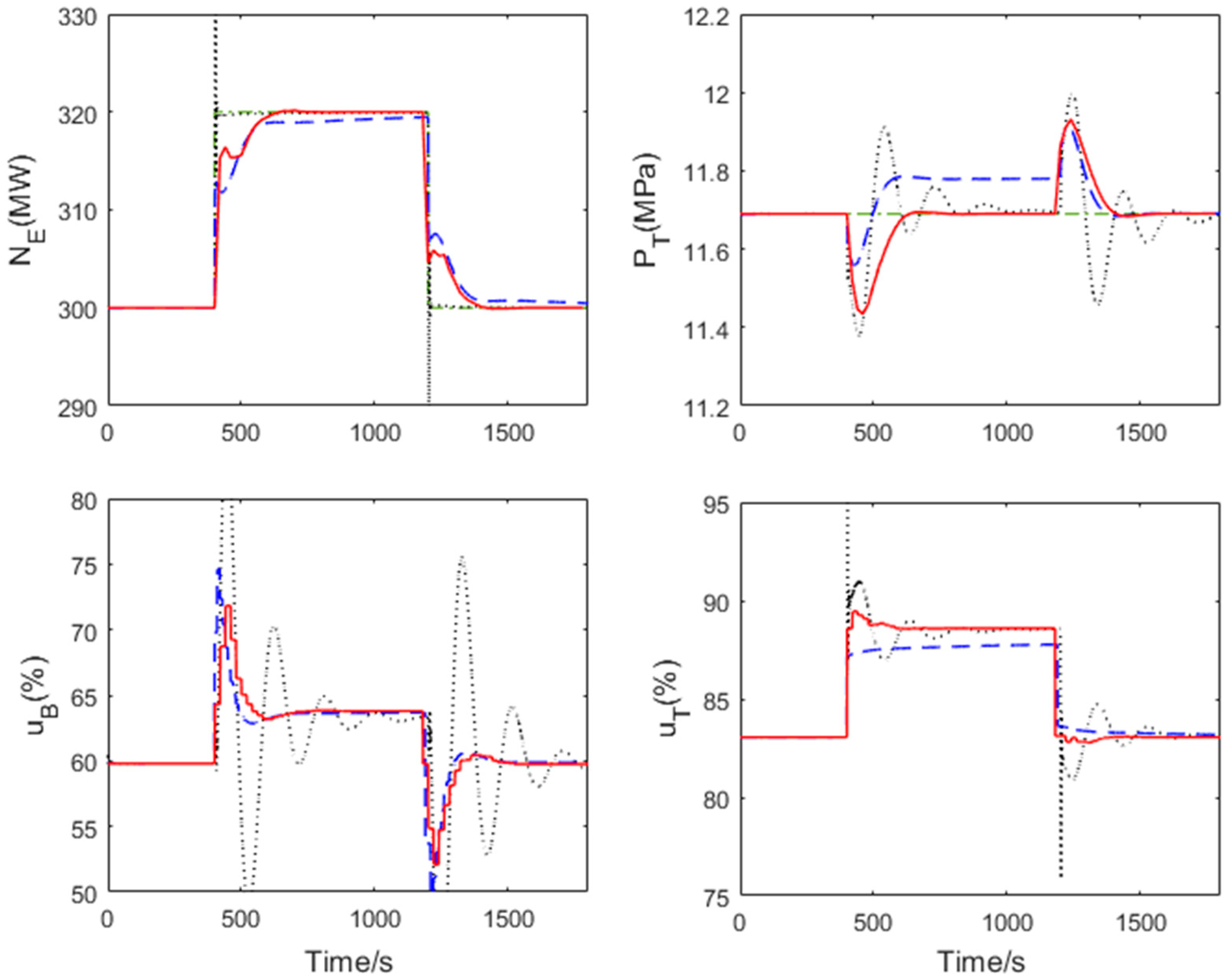
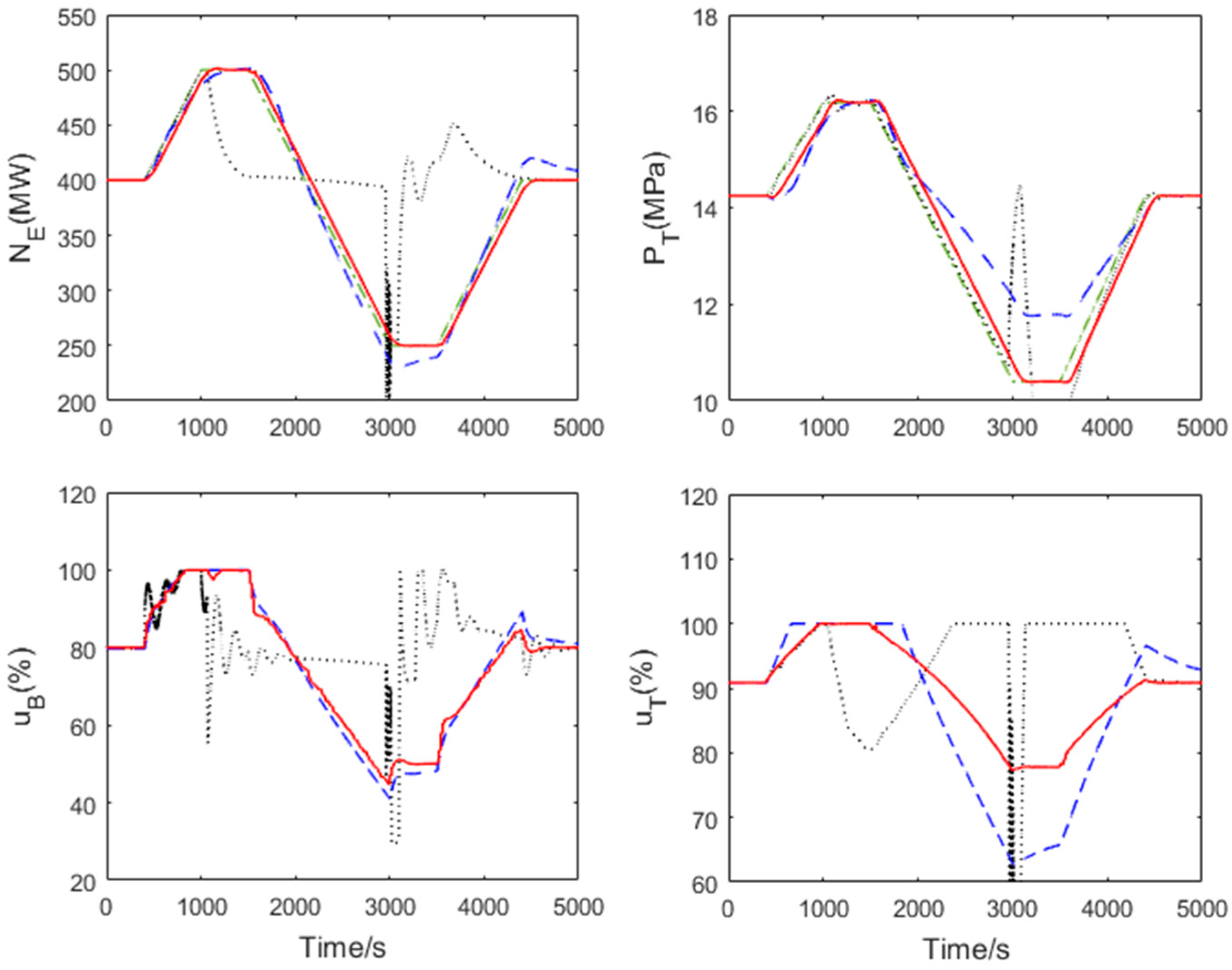
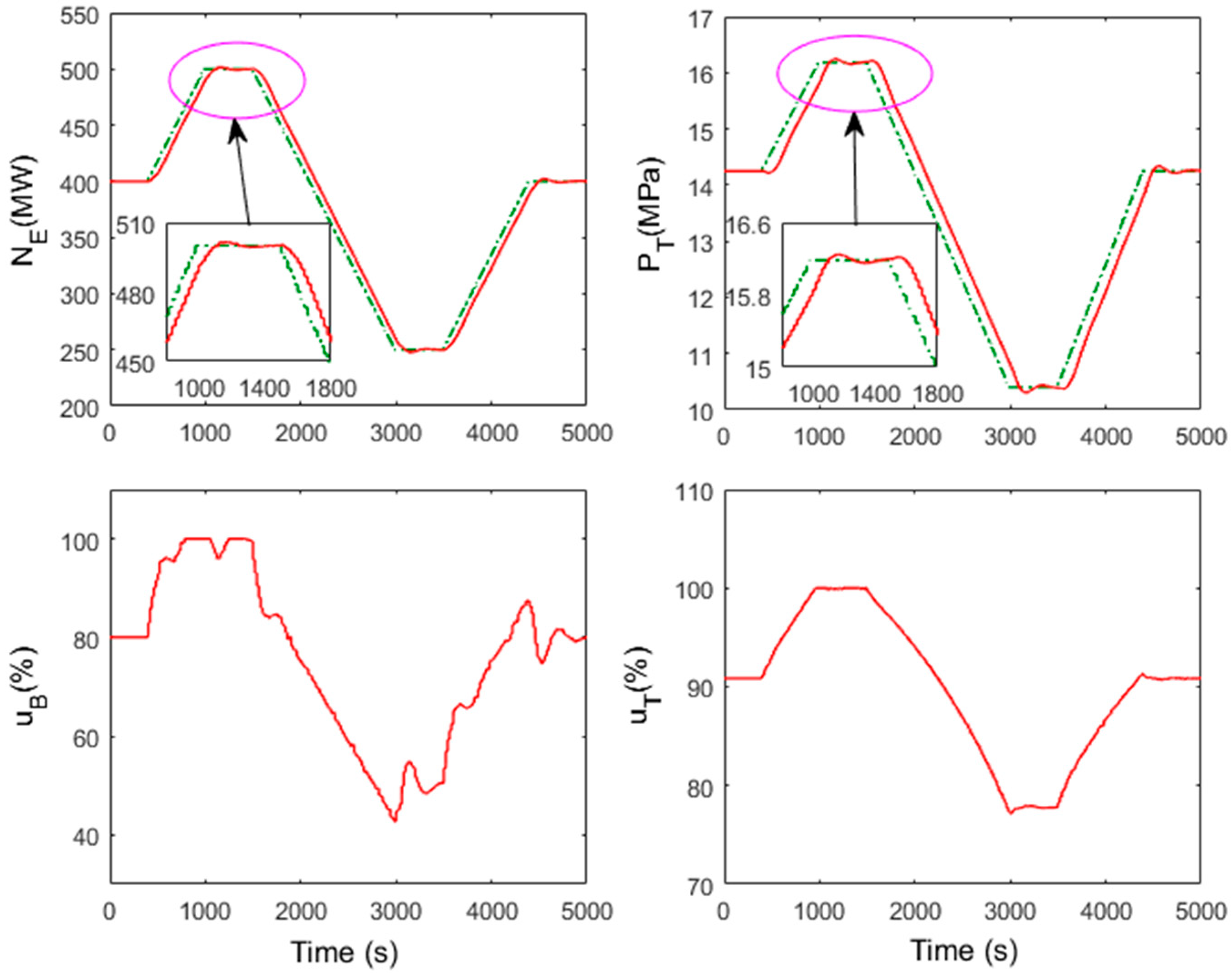
5.2. Validation of the NMPC Control Strategy
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Local Linear Models in the LMN of the B-T Unit
Appendix B. The Gain of Local Controllers and Terminal Penalty Matrices for the B-T Unit
References
- Wang, W.; Li, L.; Long, D.; Liu, J.; Zeng, D.; Cui, C. Improved boiler-turbine coordinated control of 1000 MW power units by introducing condensate throttling. J. Process. Control 2017, 50, 11–18. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Lee, K.Y.; Xue, Y. Control-oriented modeling and analysis of direct energy balance in coal-fired boiler-turbine unit. Control Eng. Pract. 2016, 55, 38–55. [Google Scholar] [CrossRef]
- Sun, L.; Hua, Q.; Shen, J.; Xue, Y.; Li, D.; Lee, K.Y. Multi-objective optimization for advanced superheater steam temperature control in a 300 MW power plant. Appl. Energy 2017, 208, 592–606. [Google Scholar] [CrossRef]
- Wang, W.; Jing, S.; Sun, Y.; Liu, J.; Niu, Y.; Zeng, D.; Cui, C. Combined heat and power control considering thermal inertia of district heating network for flexible electric power regulation. Energy 2019, 169, 988–999. [Google Scholar] [CrossRef]
- Dimeo, R.; Lee, K.Y. Boiler-turbine control system design using a genetic algorithm. IEEE Trans. Energy Convers. 1995, 10, 752–759. [Google Scholar] [CrossRef]
- Zhang, S.; Taft, C.W.; Bentsman, J.; Hussey, A.; Petrus, B. Simultaneous gains tuning in boiler/turbine PID-based controller clusters using iterative feedback tuning methodology. ISA Trans. 2012, 51, 609–621. [Google Scholar] [CrossRef]
- Sayed, M.; Gharghory, S.M.; Kamal, H.A. Gain tuning PI controllers for boiler turbine unit using a new hybrid jump PSO. J. Electr. Syst. Inf. Technol. 2015, 2, 99–110. [Google Scholar] [CrossRef]
- Moon, U.C.; Lee, K.Y. Step-response model development for dynamic matrix control of a drum-type boiler–turbine system. IEEE Trans. Energy Convers. 2009, 24, 423–430. [Google Scholar] [CrossRef]
- Moon, U.C.; Lee, K.Y. An adaptive dynamic matrix control with fuzzy-interpolated step-response model for a drum-type boiler-turbine system. IEEE Trans. Energy Convers. 2011, 26, 393–401. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Steam power plant configuration, design, and control. Wiley Interdiscip. Rev. Energy Environ. 2015, 4, 537–563. [Google Scholar] [CrossRef]
- Lee, K.Y.; Van Sickel, J.H.; Hoffman, J.A.; Jung, W.H.; Kim, S.H. Controller design for a large-scale ultrasupercritical once-through boiler power plant. IEEE Trans. Energy Convers. 2010, 25, 1063–1070. [Google Scholar] [CrossRef]
- Lee, K.Y.; Heo, J.S.; Hoffman, J.A.; Kim, S.-H.; Jung, W.-H. Modified predictive optimal control using neural network-based combined model for large-scale power plants. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Kong, X.; Liu, X.; Lee, K. An Effective Nonlinear Multivariable HMPC for USC Power Plant Incorporating NFN-based Modeling. IEEE Trans. Ind. Inform. 2016, 12, 555–666. [Google Scholar] [CrossRef]
- Keshavarz, M.; Yazdi, M.B.; Jahed-Motlagh, M. Piecewise affine modeling and control of a boiler–turbine unit. Appl. Therm. Eng. 2010, 30, 781–791. [Google Scholar] [CrossRef]
- Wang, G.; Yan, W.; Chen, S.; Zhang, X.; Shao, H. Multi-model Predictive Control of Ultra-supercritical Coal-fired Power Unit. Chin. J. Chem. Eng. 2014, 22, 782–787. [Google Scholar] [CrossRef]
- Li, Y.; Shen, J.; Lee, K.Y.; Liu, X. Offset-free fuzzy model predictive control of a boiler–turbine system based on genetic algorithm. Simul. Model. Pract. Theory 2012, 26, 77–95. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X. Nonlinear fuzzy model predictive iterative learning control for drum-type boiler–turbine system. J. Process. Control 2013, 23, 1023–1040. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Data-Driven Modeling and Predictive Control for Boiler–Turbine Unit. IEEE Trans. Energy Convers. 2013, 28, 470–481. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Data-driven modeling and predictive control for boiler–turbine unit using fuzzy clustering and subspace methods. ISA Trans. 2014, 53, 699–708. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Fuzzy modeling and stable model predictive tracking control of large-scale power plants. J. Process. Control 2014, 24, 1609–1626. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Hierarchical optimization of boiler–turbine unit using fuzzy stable model predictive control. Control Eng. Pract. 2014, 30, 112–123. [Google Scholar] [CrossRef]
- Pan, L.; Luo, J.; Cao, C.; Shen, J. L1 adaptive control for improving load-following capability of nonlinear boiler–turbine units in the presence of unknown uncertainties. Simul. Model. Pract. Theory 2015, 57, 26–44. [Google Scholar] [CrossRef]
- Ghabraei, S.; Moradi, H.; Vossoughi, G. Multivariable robust adaptive sliding mode control of an industrial boiler–turbine in the presence of modeling imprecisions and external disturbances: A comparison with type-I servo controller. ISA Trans. 2015, 58, 398–408. [Google Scholar] [CrossRef] [PubMed]
- Moradi, H.; Abbasi, M.H.; Moradian, H. Improving the performance of a nonlinear boiler–turbine unit via bifurcation control of external disturbances: A comparison between sliding mode and feedback linearization control approaches. Nonlinear Dyn. 2016, 85, 229–243. [Google Scholar] [CrossRef]
- Tian, Z.; Yuan, J.; Xu, L.; Zhang, X.; Wang, J. Model-based adaptive sliding mode control of the subcritical boiler-turbine system with uncertainties. ISA Trans. 2018, 79, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Ghabraei, S.; Moradi, H.; Vossoughi, G. Design & application of adaptive variable structure & H∞ robust optimal schemes in nonlinear control of boiler-turbine unit in the presence of various uncertainties. Energy 2018, 142, 1040–1056. [Google Scholar]
- Sun, L.; Zhang, Y.; Li, D.; Lee, K.Y. Tuning of Active Disturbance Rejection Control with application to power plant furnace regulation. Control. Eng. Pract. 2019, 92, 104122. [Google Scholar] [CrossRef]
- Sun, L.; Shen, J.; Hua, Q.; Lee, K.Y. Data-driven oxygen excess ratio control for proton exchange membrane fuel cell. Appl. Energy 2018, 231, 866–875. [Google Scholar] [CrossRef]
- Su, Z.G.; Zhao, G.; Yang, J.; Li, Y.G. Disturbance Rejection of Nonlinear Boiler-Turbine Unit Using High-Order Sliding Mode Observer. IEEE Trans. Syst. ManCybern. Syst. 2018, 1–12. [Google Scholar] [CrossRef]
- Sun, L.; Hua, Q.; Li, D.; Pan, L.; Xue, Y.; Lee, K.Y. Direct energy balance based active disturbance rejection control for coal-fired power plant. ISA Trans. 2017, 70, 486–493. [Google Scholar] [CrossRef]
- Tian, Z.; Yuan, J.; Zhang, X.; Kong, L.; Wang, J. Modeling and sliding mode predictive control of the ultra-supercritical boiler-turbine system with uncertainties and input constraints. ISA Trans. 2018, 76, 43–56. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, X.; Shen, J. Extended state observer based fuzzy model predictive control for ultra-supercritical boiler-turbine unit. Appl. Therm. Eng. 2017, 118, 90–100. [Google Scholar] [CrossRef]
- Zeng, D.; Zhao, Z.; Chen, Y.; Liu, J. A practical 500MW boiler dynamic model analysis. Proc. CSEE 2003, 23, 149–152. [Google Scholar]
- Johansen, T.A.; Foss, B.A. A NARMAX model representation for adaptive control based on local models. Modeling Identif. Control 1992, 13, 25–39. [Google Scholar] [CrossRef][Green Version]
- Gregorčič, G.; Lightbody, G. Nonlinear system identification: From multiple-model networks to Gaussian processes. Eng. Appl. Artif. Intell. 2008, 21, 1035–1055. [Google Scholar] [CrossRef]
- Hametner, C.; Jakubek, S. Local model network identification for online engine modelling. Inf. Sci. 2013, 220, 210–225. [Google Scholar] [CrossRef]
- Prasad, G.; Swidenbank, E.; Hogg, B. A Local Model Networks Based Multivariable Long-Range Predictive Control Strategy for Thermal Power Plants. Automatica 1998, 34, 1185–1204. [Google Scholar] [CrossRef]
- Zhu, H.; Shen, J.; Li, Y. Satisfactory fuzzy clustering-based multi-model modeling method for thermal process. Electr. Mach. Control 2016, 20, 94–103. [Google Scholar]
- Li, N.; Li, S.Y.; Xi, Y.G. Multi-model predictive control based on the Takagi–Sugeno fuzzy models: A case study. Inf. Sci. 2004, 165, 247–263. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing, LLC.: Dane County, WI, USA, 2013. [Google Scholar]
- Fan, H.; Zhang, Y.F.; Su, Z.G.; Wang, B. A dynamic mathematical model of an ultra-supercritical coal fired once-through boiler-turbine unit. Appl. Energy 2017, 189, 654–666. [Google Scholar] [CrossRef]
- Jiao, L.; Wang, L. A novel genetic algorithm based on immunity. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2000, 30, 552–561. [Google Scholar] [CrossRef]
- Xu, X.; Li, C. Research on immune genetic algorithm for solving the job-shop scheduling problem. Int. J. Adv. Manuf. Technol. 2007, 34, 783–789. [Google Scholar] [CrossRef]
- Zhu, H.; Shen, J.; Miao, G. An Improved Multi-Population Immune Genetic Algorithm. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 3155–3160. [Google Scholar]
- Guo, H.Y.; Li, Z.L. Structural damage identification based on Bayesian theory and improved immune genetic algorithm. Expert Syst. Appl. 2012, 39, 6426–6434. [Google Scholar] [CrossRef]
- Zhu, H.; Shen, J.; Wang, P.; Li, Y. Fuzzy optimization control based on immune genetic algorithm and its simulating study. J. Southeast Univ. 2005, 35, 64–68. [Google Scholar]
- Garduno-Ramirez, R.; Lee, K.Y. Compensation of control-loop interaction for power plant wide-range operation. Control Eng. Pract. 2005, 13, 1475–1487. [Google Scholar] [CrossRef]
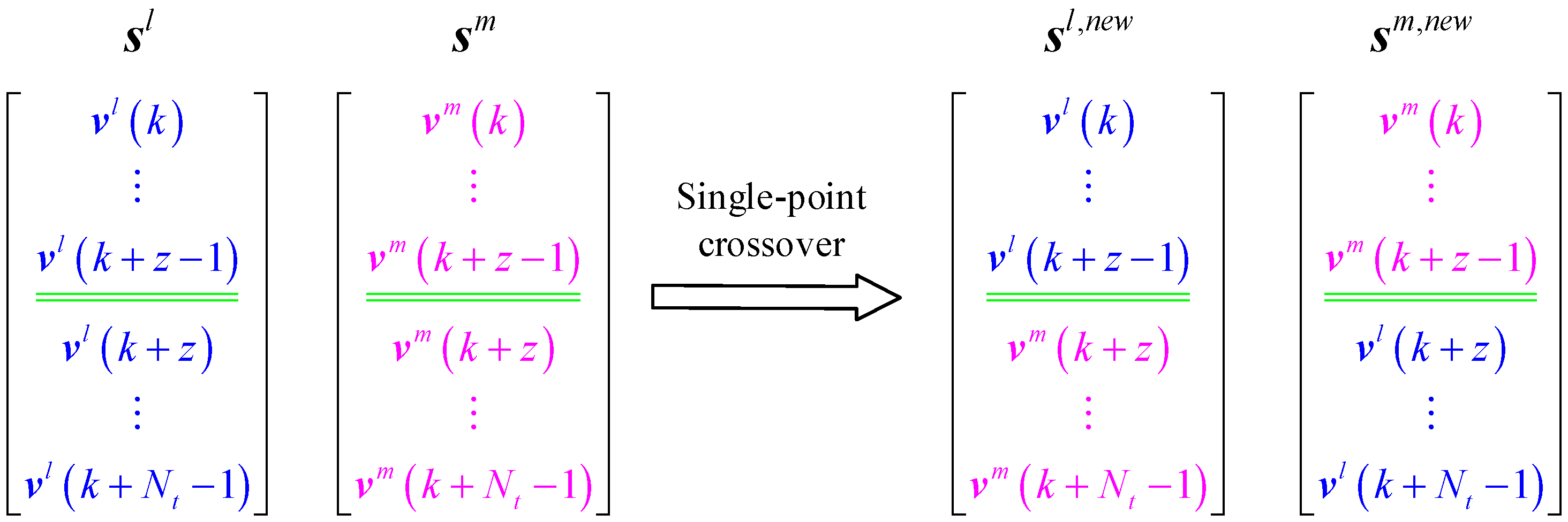



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Zhao, G.; Sun, L.; Lee, K.Y. Nonlinear Predictive Control for a Boiler–Turbine Unit Based on a Local Model Network and Immune Genetic Algorithm. Sustainability 2019, 11, 5102. https://doi.org/10.3390/su11185102
Zhu H, Zhao G, Sun L, Lee KY. Nonlinear Predictive Control for a Boiler–Turbine Unit Based on a Local Model Network and Immune Genetic Algorithm. Sustainability. 2019; 11(18):5102. https://doi.org/10.3390/su11185102
Chicago/Turabian StyleZhu, Hongxia, Gang Zhao, Li Sun, and Kwang Y. Lee. 2019. "Nonlinear Predictive Control for a Boiler–Turbine Unit Based on a Local Model Network and Immune Genetic Algorithm" Sustainability 11, no. 18: 5102. https://doi.org/10.3390/su11185102
APA StyleZhu, H., Zhao, G., Sun, L., & Lee, K. Y. (2019). Nonlinear Predictive Control for a Boiler–Turbine Unit Based on a Local Model Network and Immune Genetic Algorithm. Sustainability, 11(18), 5102. https://doi.org/10.3390/su11185102





