Development of a Refined Analysis Method for Earthquake-Induced Pounding between Adjacent RC Frame Structures
Abstract
1. Introduction
2. Beam-Column Element Model
2.1. Concrete and Steel Materials
2.2. Verification of Element Model
3. Integration of Pounding in the Element Model
3.1. Contact Element
3.2. Compression Deformation
3.3. Pounding Force
3.4. Integration into System Equation
4. Pounding Analysis for RC Frames
4.1. Building Information and Selected Ground Motions
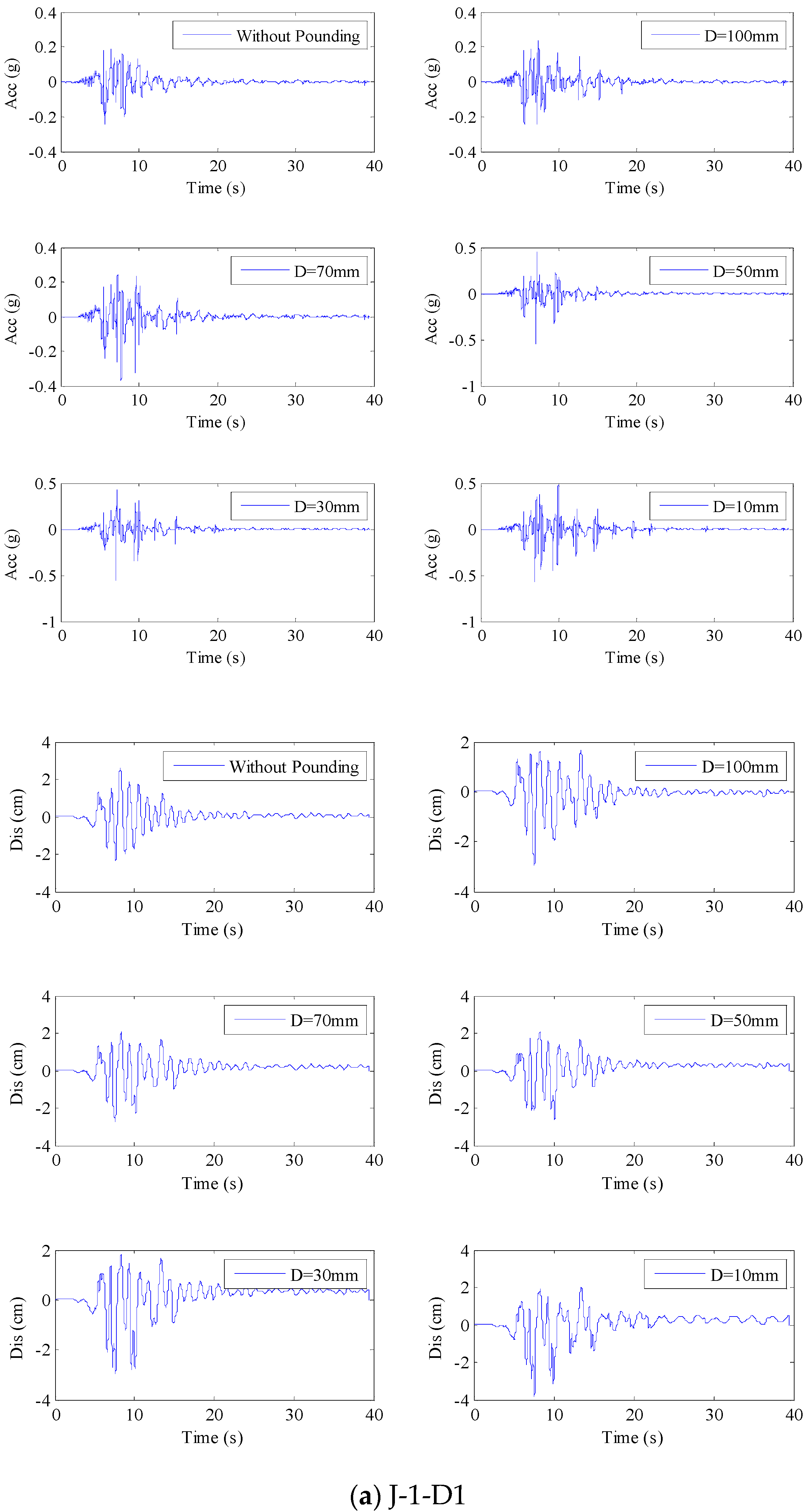
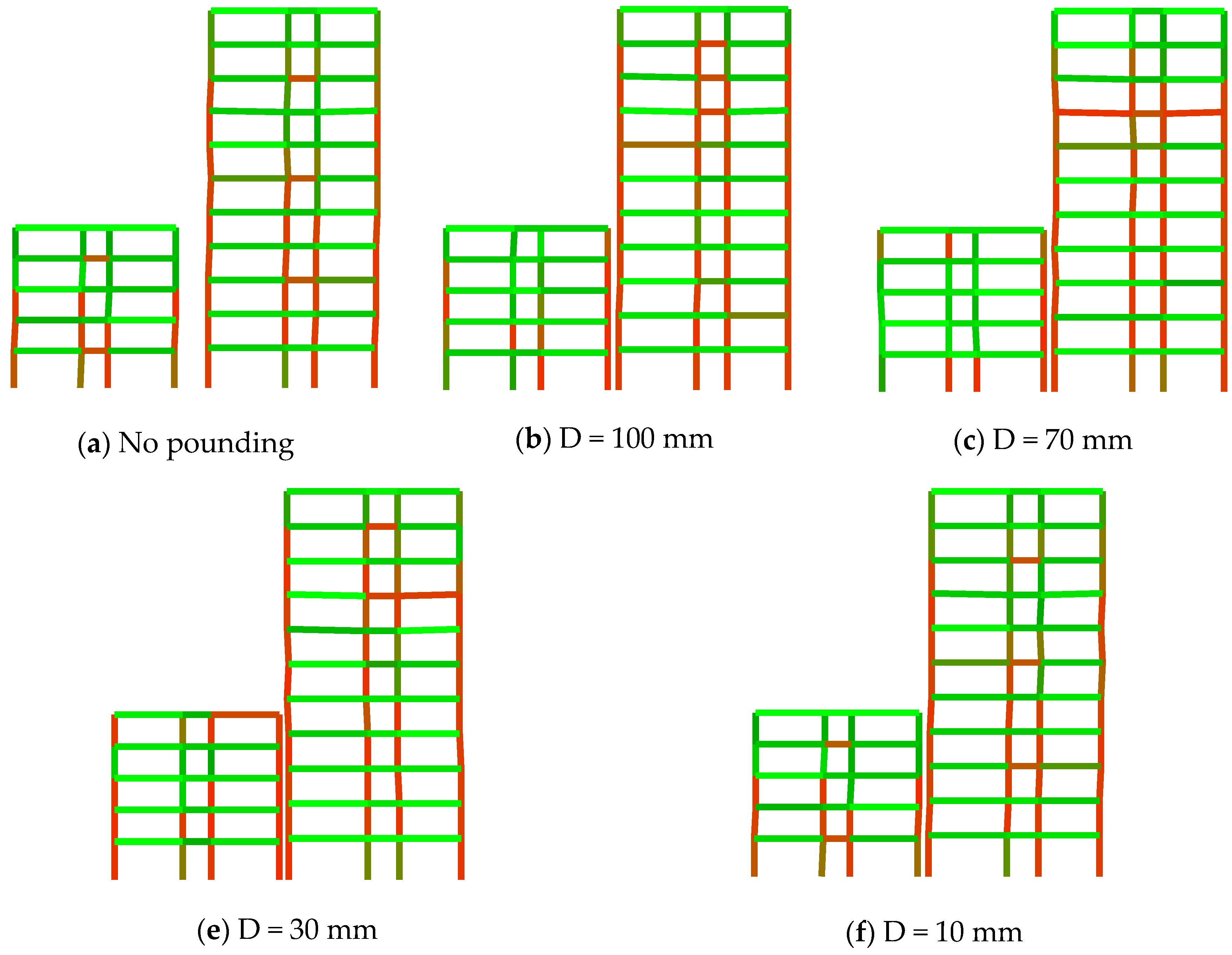
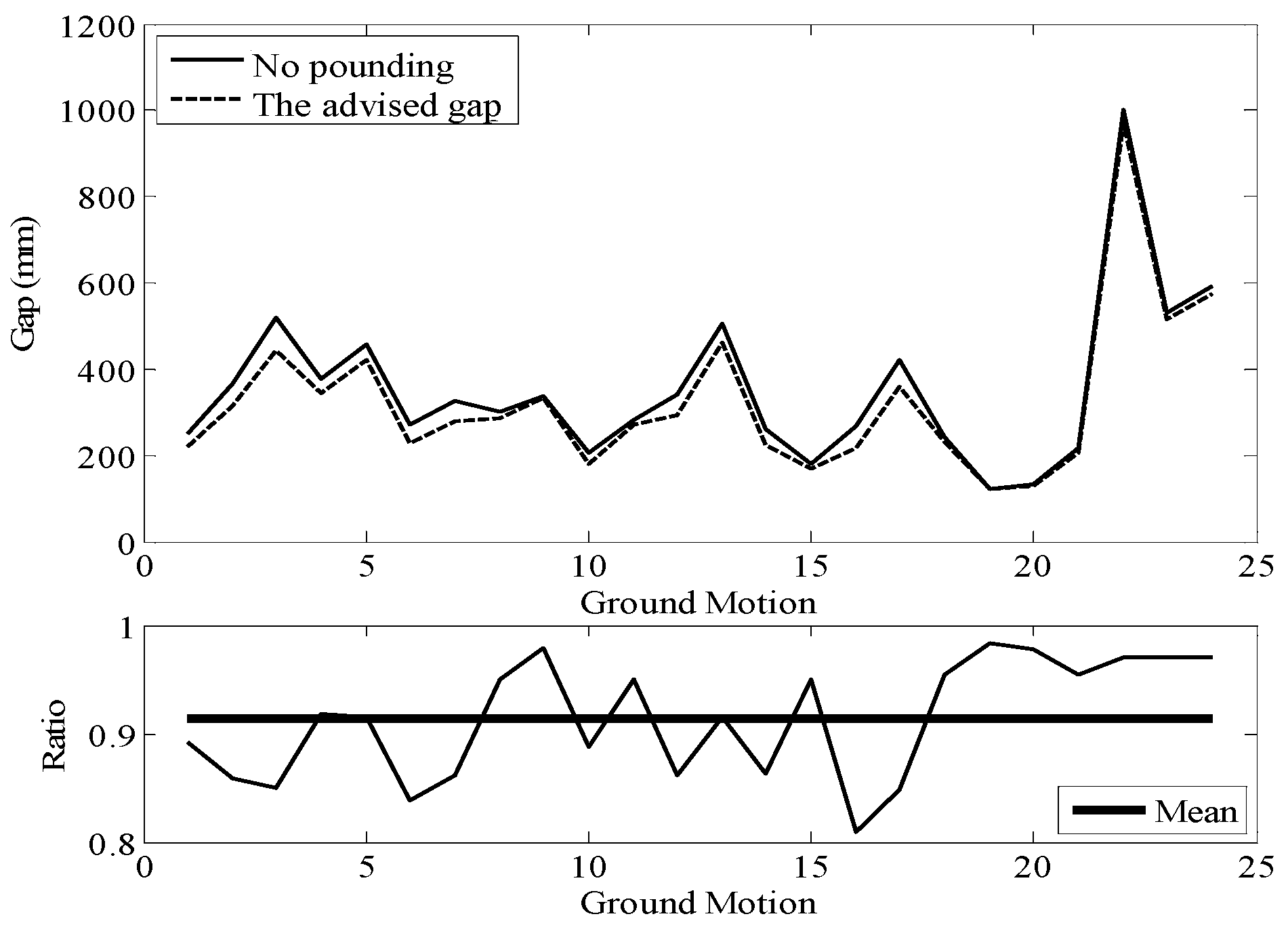
4.2. Pounding Analysis and the Rational Separation Gap
5. Conclusions
- (1)
- The fiber beam-column element model is adopted and the element section discretized into concrete and reinforcement fibers with hysteretic models while considering bucking behaviors. The formulas that integration of the beam-column element and Hertz-damp contact element are proposed. The pounding can be considered either at the level between the story slab to slab or at the level between story slab to mid-column.
- (2)
- The application of the proposed method in pounding analyses to provide a rational seismic separation gap between two adjacent RC frame structures is conducted. It seems that the structural damage may not linearly vary as the separation gap reduces, but it may remain nearly unchanged when the separation gap is larger than a threshold value. The threshold value is smaller than the required separation gap meaning no pounding occurs. This value can be set as the rational seismic separation gap.
- (3)
- The proposed method can be used in damage analysis for structures which may be influenced by pounding or used to provides a rational seismic separation gap in a probabilistic way by analyses of a series of ground motion records at a specific earthquake intensity, in order to increase the safety and sustainability of a structure in earthquakes.
Author Contributions
Funding
Conflicts of Interest
References
- Rojas, F.R.; Anderson, J.C. Pounding of an 18-story building during recorded earthquakes. J. Struct. Eng. 2012, 138, 1530–1544. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A.; Karamaneas, C.E. Use of collision shear walls to minimize seismic separation and to protect adjacent buildings from collapse due to earthquake-induced pounding. Earthq. Eng. Struct. Dyn. 2008, 37, 1371–1388. [Google Scholar] [CrossRef]
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Wang, C.J.; Shih, M.H. Performance study of a bridge involving sliding decks and pounded abutment during a violent earthquake. Eng. Struct. 2007, 29, 802–812. [Google Scholar] [CrossRef]
- Hu, M.; Han, Q.; Wen, J.; Bai, Y. Seismic failure of multi-span simply supported RC slab-on-grider bridge in 2008 Wenchuan earthquake: Case study. Eng. Fail. Anal. 2019, 95, 140–153. [Google Scholar] [CrossRef]
- Cole, G.L.; Dhakal, R.P.; Turner, F.M. Building pounding damage observed in the 2011 Christchurch earthquake. Earthq. Eng. Struct. Dyn. 2012, 41, 893–913. [Google Scholar] [CrossRef]
- Chouw, N.; Hao, H. Study of SSI and non-uniform ground motion effect on pounding between bridge girders. Soil Dyn. Earthq. Eng. 2005, 25, 717–728. [Google Scholar] [CrossRef]
- Shrestha, B.; Hao, H. Building pounding damages observed during the 2015 Gorkha earthquake. J. Perform. Constr. Facil. 2018, 32. [Google Scholar] [CrossRef]
- Filiatrault, A.; Wangner, P. Analytical prediction of experimental building pounding. Earthq. Eng. Struct. Dyn. 1995, 24, 1131–1154. [Google Scholar] [CrossRef]
- Jankowski, R. Experimental study on earthquake-induced pounding between structural elements made of different building materials. Earthq. Eng. Struct. Dyn. 2009, 39, 343–354. [Google Scholar] [CrossRef]
- Chau, K.T.; Wei, X.X.; Guo, X.; Shen, C.Y. Experimental and theoretical simulations of seismic poundings between two adjacent structures. Earthq. Eng. Struct. Dyn. 2003, 32, 537–554. [Google Scholar] [CrossRef]
- Pantelides, C.P.; Ma, X. Linear and nonlinear pounding of structural systems. Comput. Struct. 1998, 66, 79–92. [Google Scholar] [CrossRef]
- Muthukumar, S.; DesRoches, R. A Hertz contact model with non-linear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 2006, 35, 811–828. [Google Scholar] [CrossRef]
- Dimitrakopoulos, E.; Makris, N.; Kappos, A.J. Dimensional analysis of the earthquake-induced pounding between adjacent structures. Earthq. Eng. Struct. Dyn. 2009, 38, 867–886. [Google Scholar] [CrossRef]
- Cole, G.; Dhakal, R.; Carr, A.; Bull, D. An investigation of the effects of mass distribution on pounding structures. Earthq. Eng. Struct. Dyn. 2011, 40, 641–659. [Google Scholar] [CrossRef]
- Crozet, V.; Politopoulos, I.; Yang, M.; Martinez, J.M.; Erlicher, S. Sensitivity analysis of pounding between adjacent structures. Earthq. Eng. Struct. Dyn. 2018, 47, 219–235. [Google Scholar] [CrossRef]
- Jankowski, R. Earthquake-induced pounding between equal height buildings with substantially different dynamic properties. Eng. Struct. 2008, 30, 2818–2829. [Google Scholar] [CrossRef]
- Matsagar, V.A.; Jangid, R.S. Seismic response of base-isolated structures during impact with adjacent structures. Eng. Struct. 2003, 25, 1311–1323. [Google Scholar] [CrossRef]
- Agarwal, V.K.; Niedzwecki, J.M.; Van de Lindt, J.W. Earthquake induced pounding in friction varying base isolated buildings. Eng. Struct. 2007, 29, 2825–2832. [Google Scholar] [CrossRef]
- Komodromos, P. Simulation of the earthquake-induced pounding of seismically isolated buildings. Comput. Struct. 2008, 86, 618–626. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Komodromos, P. Earthquake-induced poundings of a seismically isolated building with adjacent structures. Eng. Struct. 2010, 32, 1937–1951. [Google Scholar] [CrossRef]
- Moustafa, A.; Mahmoud, S. Damage assessment of adjacent buildings under earthquake loads. Eng. Struct. 2014, 61, 153–165. [Google Scholar] [CrossRef]
- Bao, Y.; Becker, T.C. Inelastic response of base-isolated structures subjected to impact. Eng. Struct. 2018, 171, 86–93. [Google Scholar] [CrossRef]
- Efraimiadou, S.; Hatzigeorgiou, G.D.; Beskos, D.E. Structural pounding between adjacent buildings subjected to strong ground motions. Part I: The effect of different structures arrangement. Earthq. Eng. Struct. Dyn. 2013, 42, 1509–1528. [Google Scholar] [CrossRef]
- Carr, A.J. Ruaumoko—Inelastic Dynamic Analysis Program; University of Canterbury: Christchurch, New Zealand, 2008. [Google Scholar]
- Pratesi, F.; Sorace, S.; Terenzi, G. Analysis and mitigation of seismic pounding of a slender R/C bell tower. Eng. Struct. 2014, 71, 23–34. [Google Scholar] [CrossRef]
- Chujo, T.; Yoshikado, H.; Sato, Y.; Naganuma, K.; Kaneko, Y. Experimental and analytical investigations of seismic pounding of adjacent 14-story reinforced concrete buildings damaged in 1985 mexico earthquake. J. Adv. Concr. Technol. 2016, 14, 753–769. [Google Scholar] [CrossRef][Green Version]
- Jankowski, R. Non-linear FEM analysis of earthquake-induced pounding between the main building and the stairway tower of the Olive View Hospital. Eng. Struct. 2009, 31, 1851–1864. [Google Scholar] [CrossRef]
- Jeng, V.; Tzeng, W.L. Assessment of seismic pounding hazard for Taipei City. Eng. Struct. 2000, 22, 459–471. [Google Scholar] [CrossRef]
- Lin, J.H.; Weng, C.C. Probability analysis of seismic pounding of adjacent buildings. Earthq. Eng. Struct. Dyn. 2001, 30, 1539–1557. [Google Scholar] [CrossRef]
- Wang, S.S.; Hong, H.P. Quantiles of critical separation distance for nonstationary seismic excitations. Eng. Struct. 2006, 28, 985–991. [Google Scholar] [CrossRef]
- Smith, I.M.; Griffiths, D.V. Programming the Finite Element Method, 4th ed.; JohnWiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Spacone, E.; Filippou, F.C.; Taucer, F.F. Fiber beam-column model for non-linear analysis of R/C frames: Part, I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Flexural members with confined concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. ACI J. Proc. 1982, 79, 13–27. [Google Scholar]
- Yassin, M.H.M. Nonlinear Analysis of Prestressed Concrete Structures under Monotonic and Cyclic Loads. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of Analysis for Cyclically Loaded Reinforced Concrete Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements Under Combined Normal Force and Bending. In Symposium Report of Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads; IABSE: Lisbon, Portugal, 1973; pp. 15–22. [Google Scholar]
- Spacone, E. Flexibility-Based Finite Element Models for the Nonlinear Static and Dynamic Analysis of Concrete Frame Structures. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Talaat, M.M. Computational Modeling of Progressive Collapse in Reinforced Concrete Frame Structures. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2007. [Google Scholar]
- Bae, S.; Mieses, A.M.; Bayrak, O. Inelastic buckling of reinforcing bars. J. Struct. Eng. 2005, 131, 314–321. [Google Scholar] [CrossRef]
- Monti, G.; Nuti, C. Nonlinear cyclic behaviour of reinforcing bars including buckling. J. Struct. Eng. 1992, 118, 3268–3284. [Google Scholar] [CrossRef]
- Lu, X.Z. Newsletter for Quasi-Static Collapse Test of RC Frame. Available online: http://www.collapse-prevention.net/download/NewsLetter02_2011-06-28.rar (accessed on 15 June 2019).
- Van Mier, J.G.M.; Paruijssers, A.F.; Reinhardt, H.W.; Monnier, T. Load-time response of colloding concrete bodies. J. Struct. Eng. 1991, 117, 354–374. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- Ye, K.; Li, L.; Zhu, H. A note on the Hertz contact model with nonlinear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 2009, 38, 1135–1142. [Google Scholar] [CrossRef]
- Zhao, D.H.; Liu, Y. Improved damping constant of Hertz-Damp model for pounding between structures. Math. Probl. Eng. 2016, 2016, 9161789. [Google Scholar] [CrossRef]
- CECS160. General Rule for Performance-Based Seismic Design of Buildings; China Planning Press: Beijing, China, 2004. [Google Scholar]
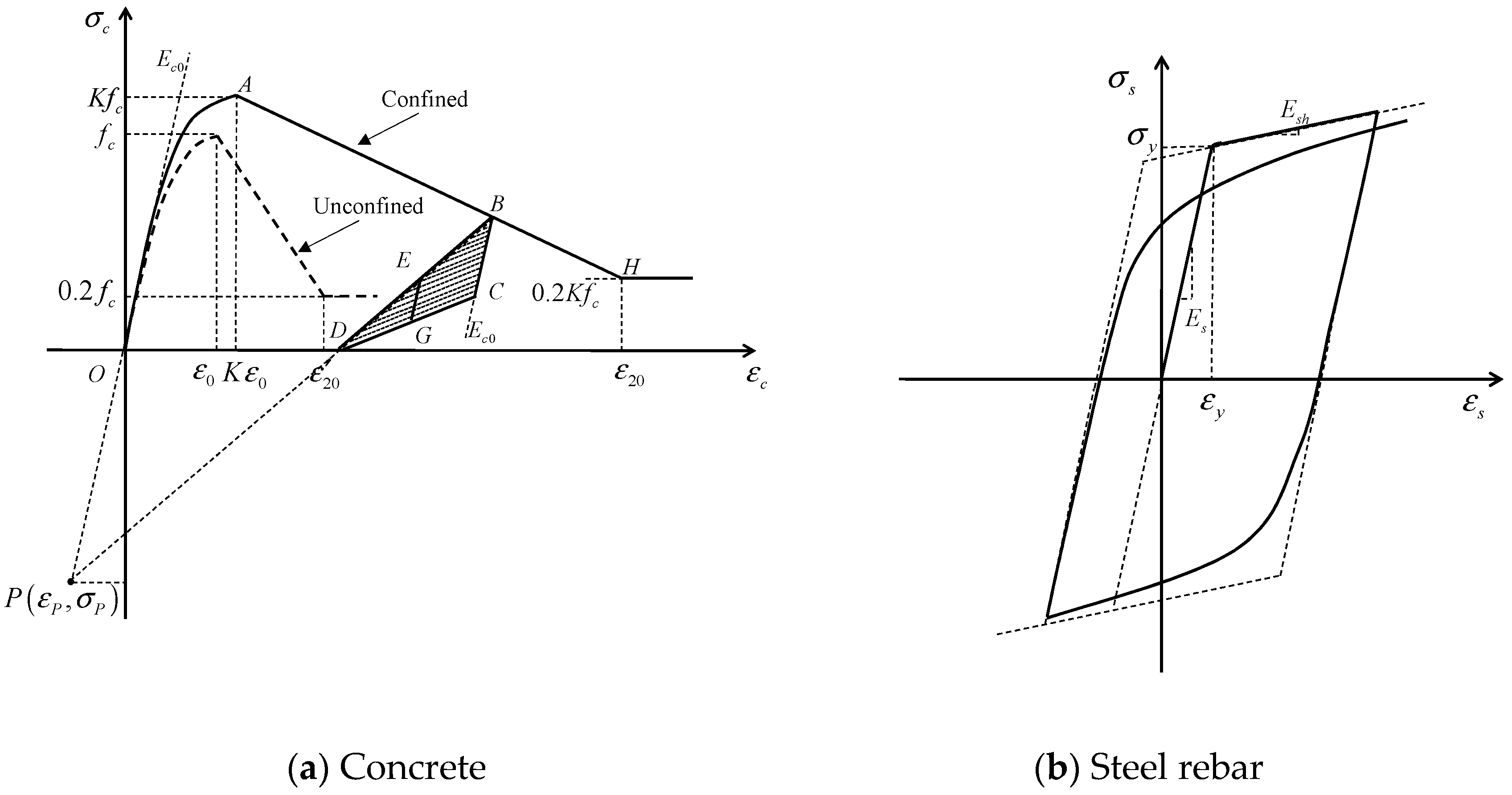
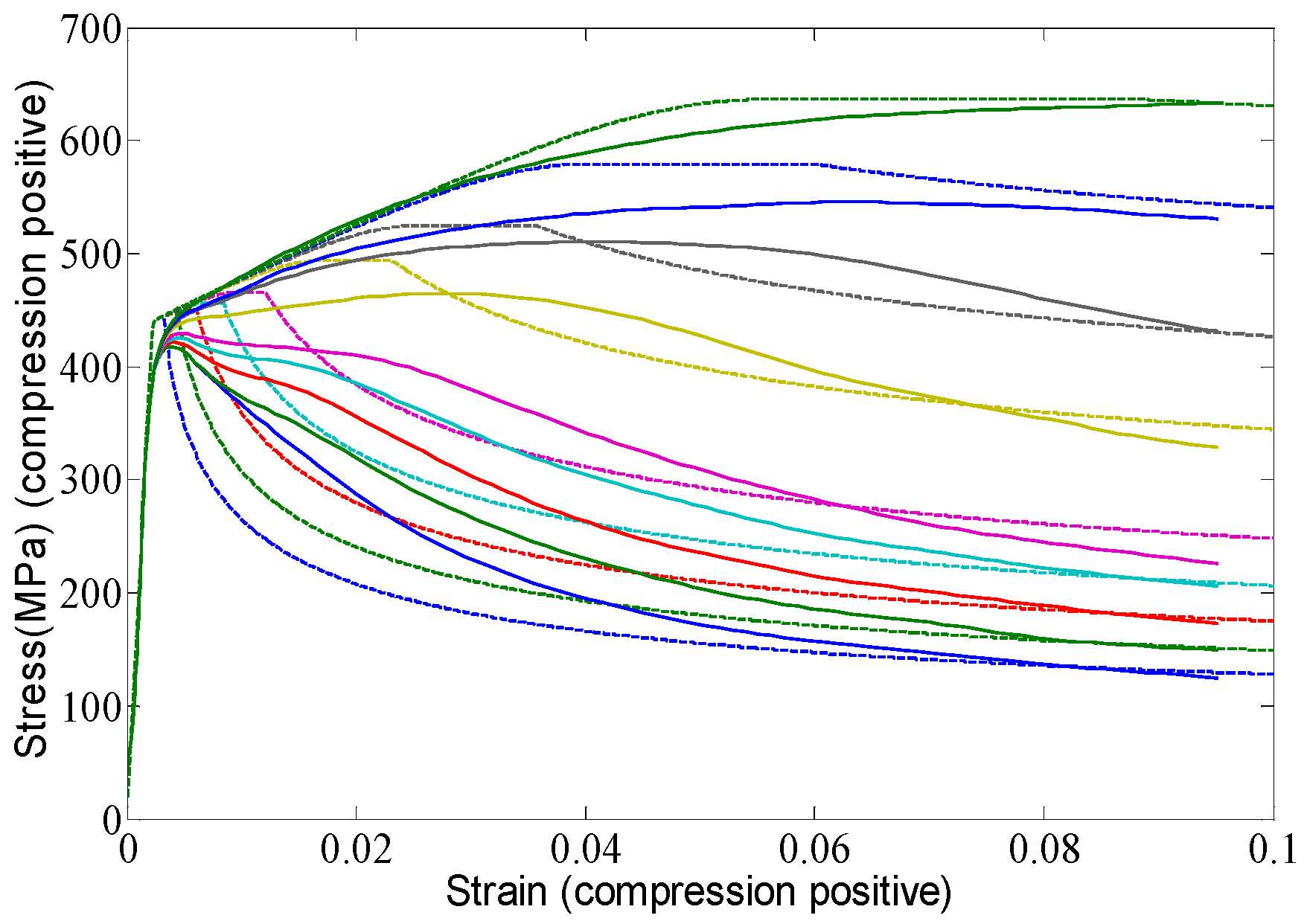
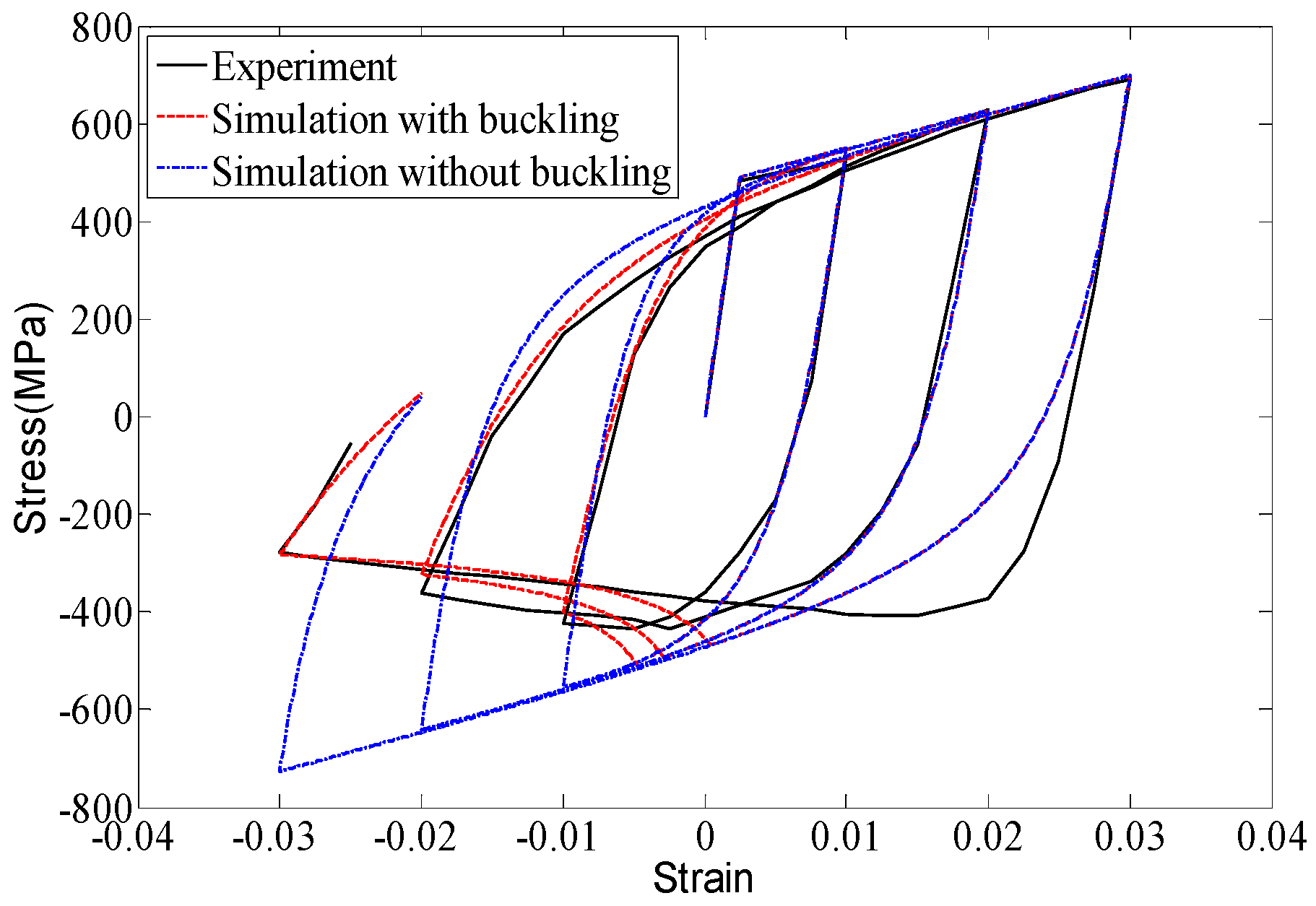
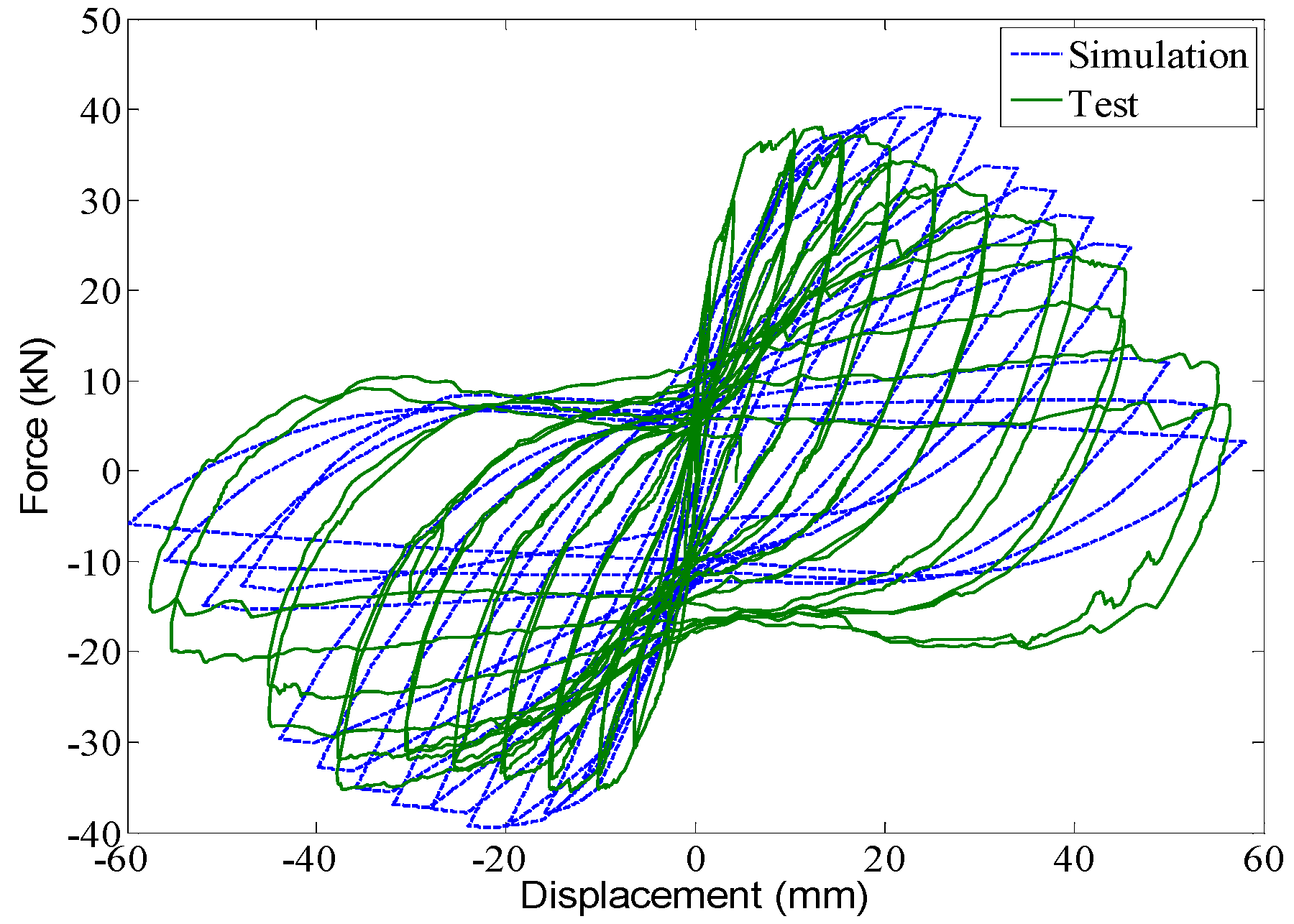

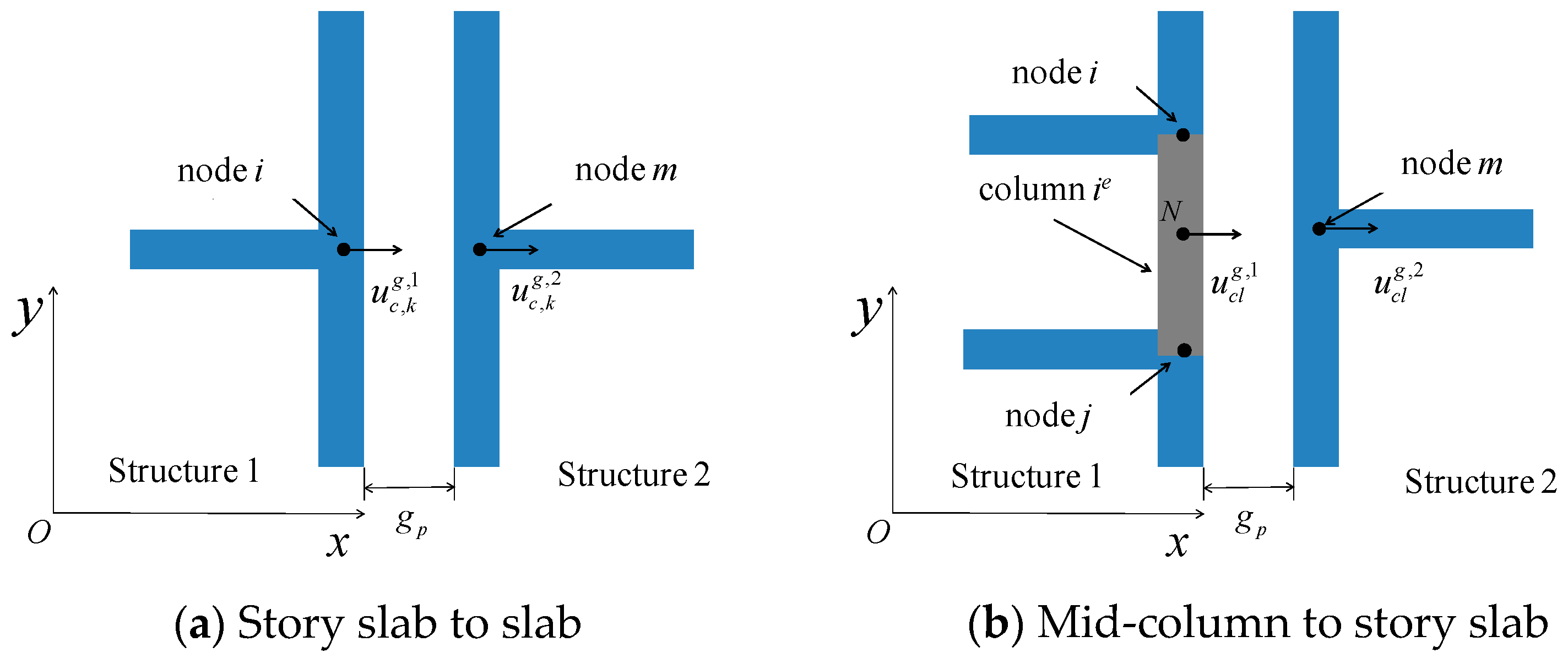




 1).
1).
 1).
1).

| Frame | Floor | Concrete Type | Cross-Section Size (mm × mm) Height × Width | Beam Ends Area (mm2) | Middle Beam Area (mm2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AB | BC | CD | A | B | C | D | AB | BC | CD | |||
| J-1 | 1–4 | C30 | 500 × 250 | 400 × 250 | 500 × 250 | 1008 | 1008 | 1008 | 1008 | 763 | 763 | 763 |
| 5 | C30 | 500 × 250 | 400 × 250 | 500 × 250 | 763 | 763 | 763 | 763 | 763 | 603 | 763 | |
| J-2 | 1–4 | C30 | 600 × 250 | 400 × 250 | 500 × 250 | 1610 | 1964 | 1964 | 1473 | 833 | 1074 | 833 |
| 5–6 | C30 | 600 × 250 | 400 × 250 | 500 × 250 | 1610 | 1964 | 1964 | 1473 | 833 | 833 | 710 | |
| 7–10 | C30 | 600 × 250 | 400 × 250 | 500 × 250 | 1256 | 1256 | 1256 | 1256 | 833 | 710 | 603 | |
| 11 | C30 | 600 × 250 | 400 × 250 | 500 × 250 | 942 | 942 | 942 | 829 | 833 | 710 | 603 | |
| Frame | Floor | Concrete Type | Cross-Section Size (mm × mm) | Area (mm2) | ||
|---|---|---|---|---|---|---|
| Side Column | Middle Column | Side Column | Middle Column | |||
| J-1 | 1–5 | C30 | 500 × 500 | 500 × 500 | 2512 | 2512 |
| J-2 | 1–6 | C30 | 600 × 600 | 600 × 600 | 3807 | 3807 |
| 7–11 | C30 | 550 × 550 | 550 × 550 | 3411 | 3411 | |
| Number | Earthquake | Station | Direction |
|---|---|---|---|
| 1 | 1979, Imperial Valley, CA | El Centro, Array #5 | 140 |
| 2 | 1979, Imperial Valley, CA | El Centro, Array #5 | 230 |
| 3 | 1979, Imperial Valley, CA | Centro, Array #10 | 50 |
| 4 | 1979, Imperial Valley, CA | Centro, Array #10 | 320 |
| 5 | 1979, Imperial Valley, CA | Meloland Overpass FF | 270 |
| 6 | 1985, Michoacan, Mexico | La Union | 90 |
| 7 | 1985, Michoacan, Mexico | La Union | 180 |
| 8 | 1992, Landers-28 June | Amboy | 0 |
| 9 | 1992, Landers-28 June | Joshua Tree-Fire Station | 0 |
| 10 | 1994, Northridge | Canoga Park | S74E |
| 11 | 1994, Northridge | Canoga Park | S16W |
| 12 | 1992, Landers-28 June | Yermo-Fire Station | 270 |
| 13 | 1992, Landers-28 June | Yermo-Fire Station | 360 |
| 14 | 1949, Western Washington | Olympia Hwy Test Lab | 356 |
| 15 | 1995, Kobe | Takarazuka | 0 |
| 16 | 1995, Kobe | Takarazuka | 90 |
| 17 | 1979, Imperial Valley, CA | El Centro, Array #6 | 140 |
| 18 | 2001, Yongsheng, China | Qina | NS |
| 19 | 2001, Yongsheng, China | Qina | WE |
| 20 | 1976, Tangshan, China | Hujialou | NS |
| 21 | 1976, Tangshan, China | Hujialou | WE |
| 22 | 1996, Atushen, China | Xikeer | WE |
| 23 | 1976, Tangshan aftershock, China | Tianjin Hospital | NS |
| 24 | 1976, Tangshan aftershock, China | Tianjin Hospital | WE |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, S. Development of a Refined Analysis Method for Earthquake-Induced Pounding between Adjacent RC Frame Structures. Sustainability 2019, 11, 4928. https://doi.org/10.3390/su11184928
Yang Y, Li S. Development of a Refined Analysis Method for Earthquake-Induced Pounding between Adjacent RC Frame Structures. Sustainability. 2019; 11(18):4928. https://doi.org/10.3390/su11184928
Chicago/Turabian StyleYang, Yongqiang, and Shuang Li. 2019. "Development of a Refined Analysis Method for Earthquake-Induced Pounding between Adjacent RC Frame Structures" Sustainability 11, no. 18: 4928. https://doi.org/10.3390/su11184928
APA StyleYang, Y., & Li, S. (2019). Development of a Refined Analysis Method for Earthquake-Induced Pounding between Adjacent RC Frame Structures. Sustainability, 11(18), 4928. https://doi.org/10.3390/su11184928






