Identifying Spatial Patterns of Retail Stores in Road Network Structure
Abstract
1. Introduction
2. Methodology
2.1. Network-Based Kernel Density Estimation
2.2. Closeness Centrality Index
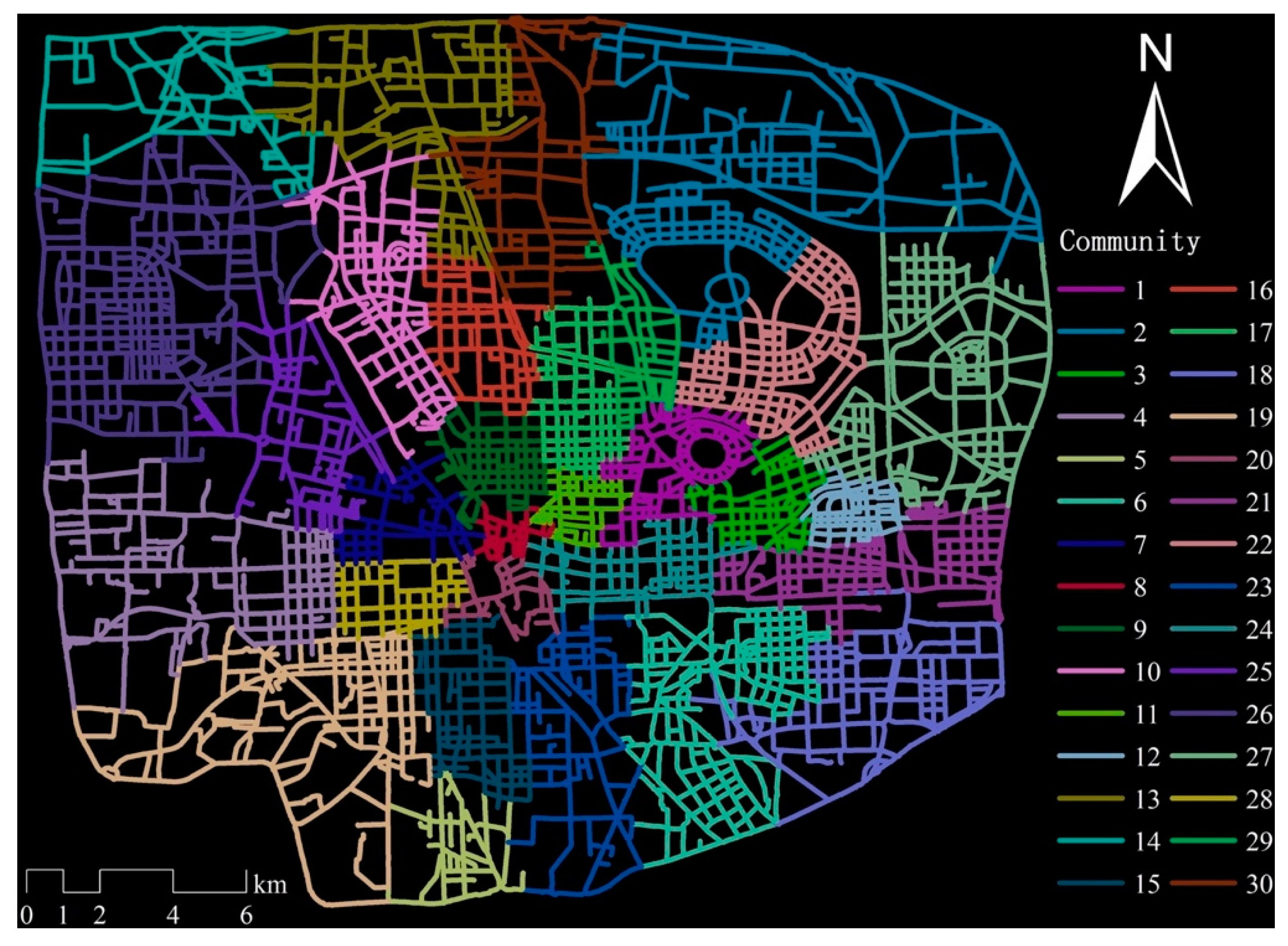
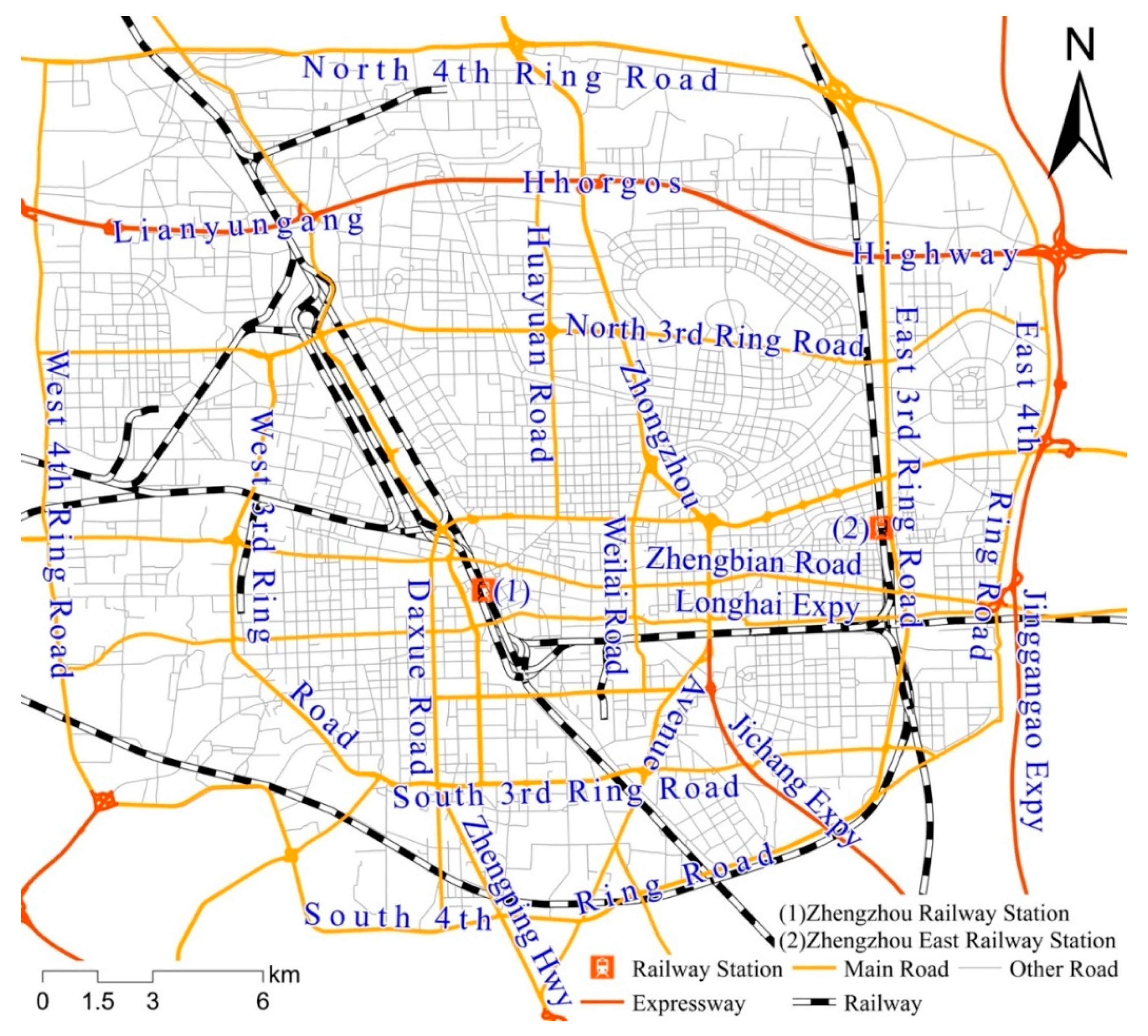
3. Study Area and Data
4. Results and Discussion
4.1. Descriptive Statistics for Retail Stores
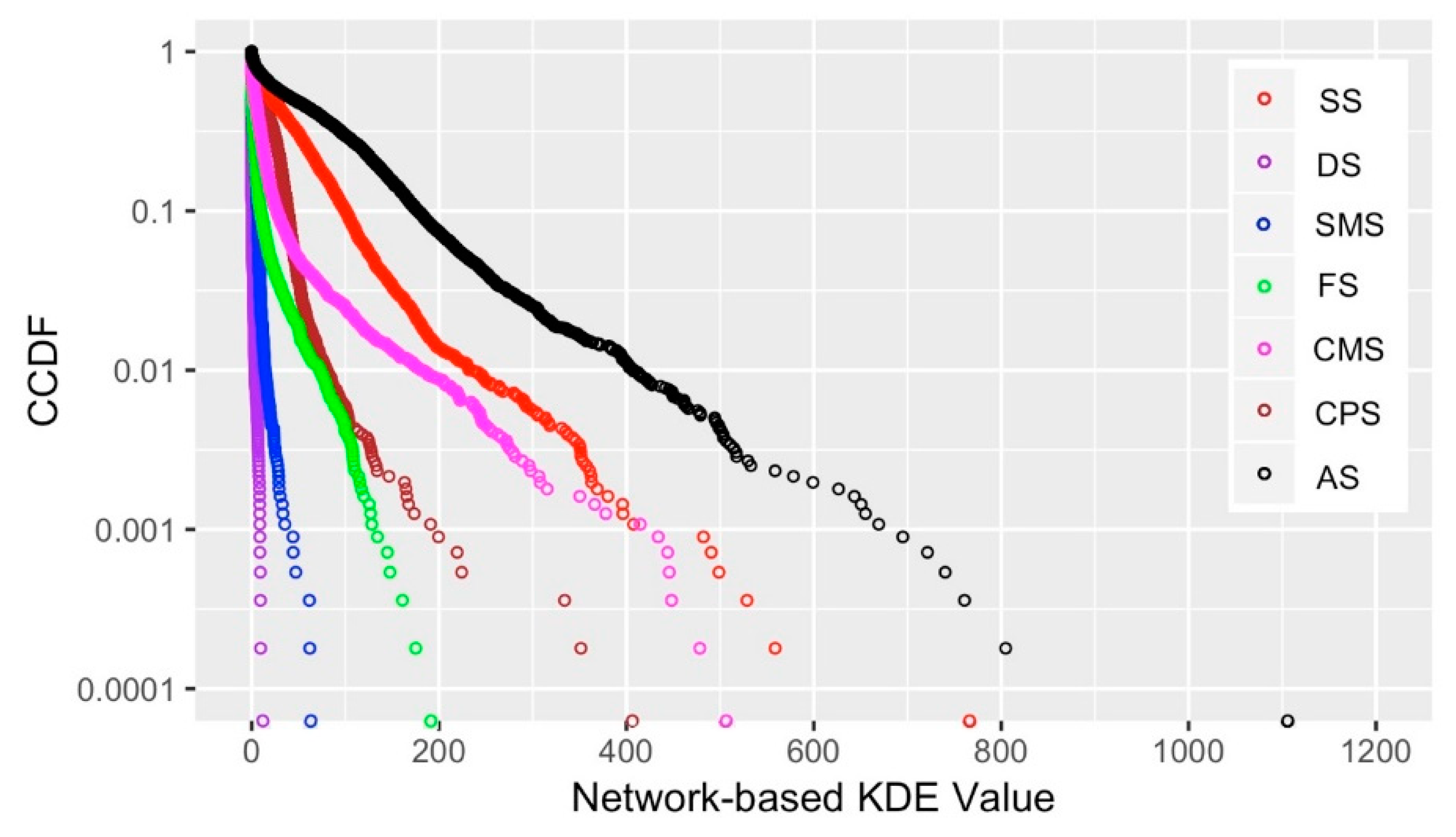
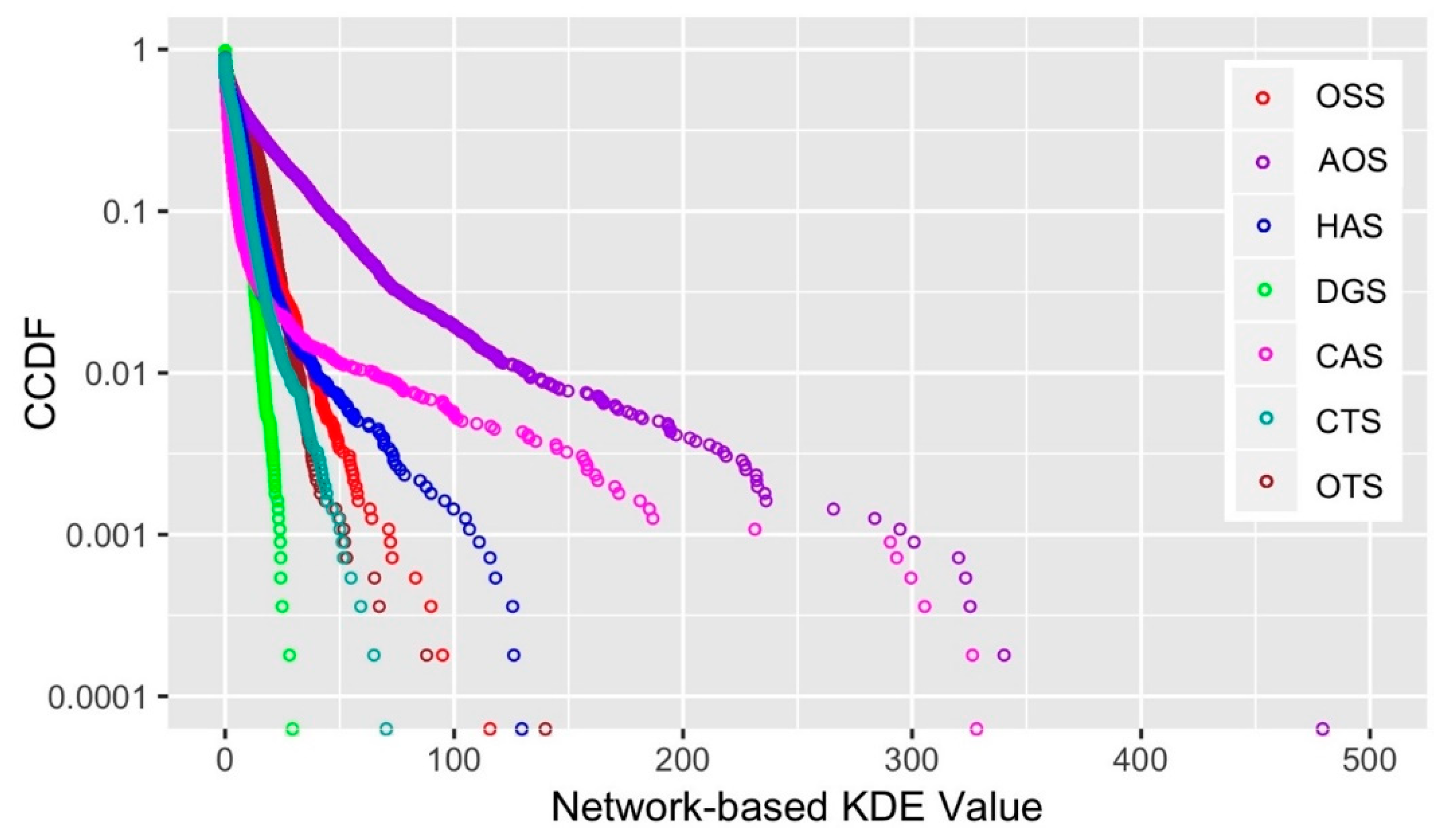
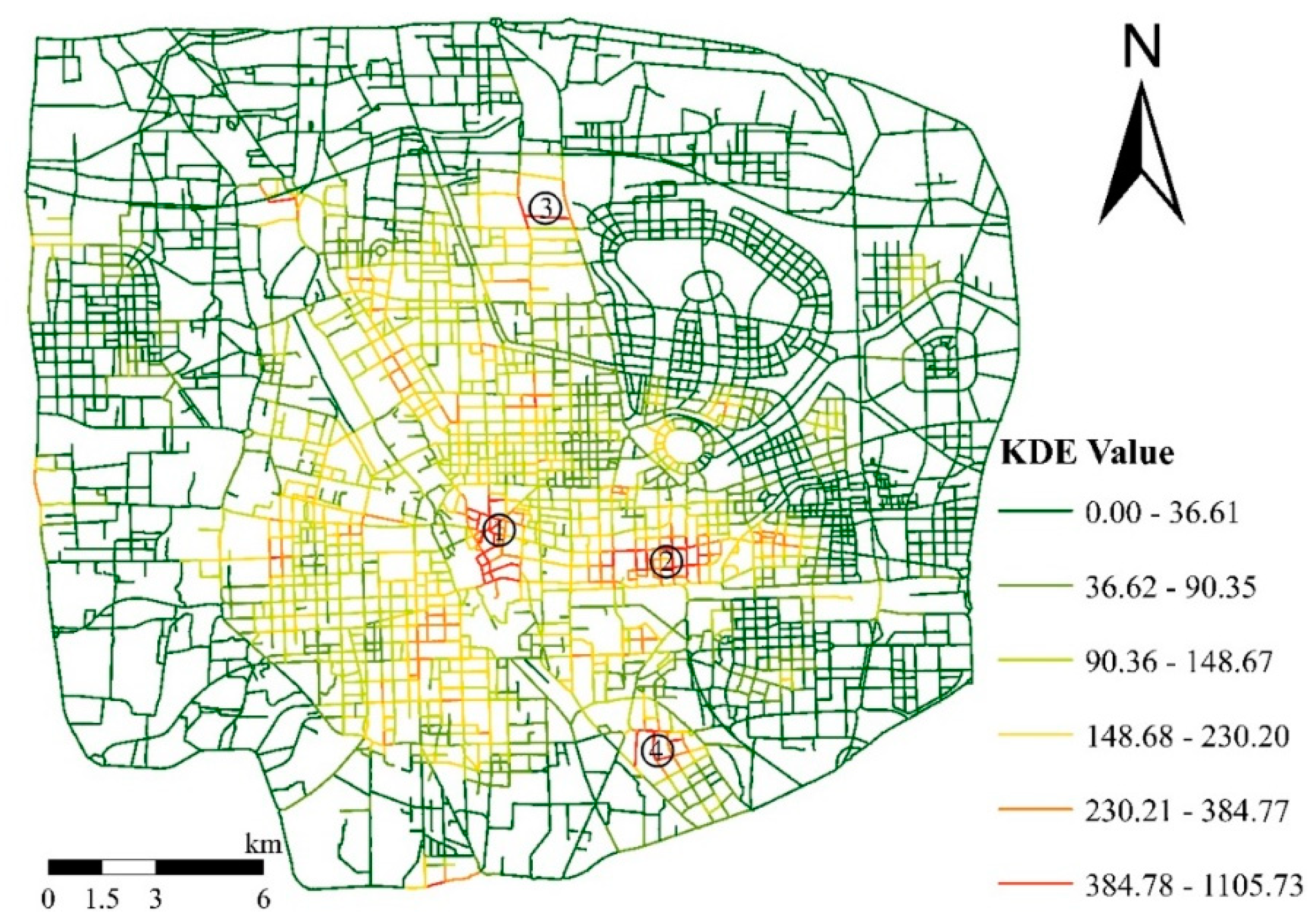
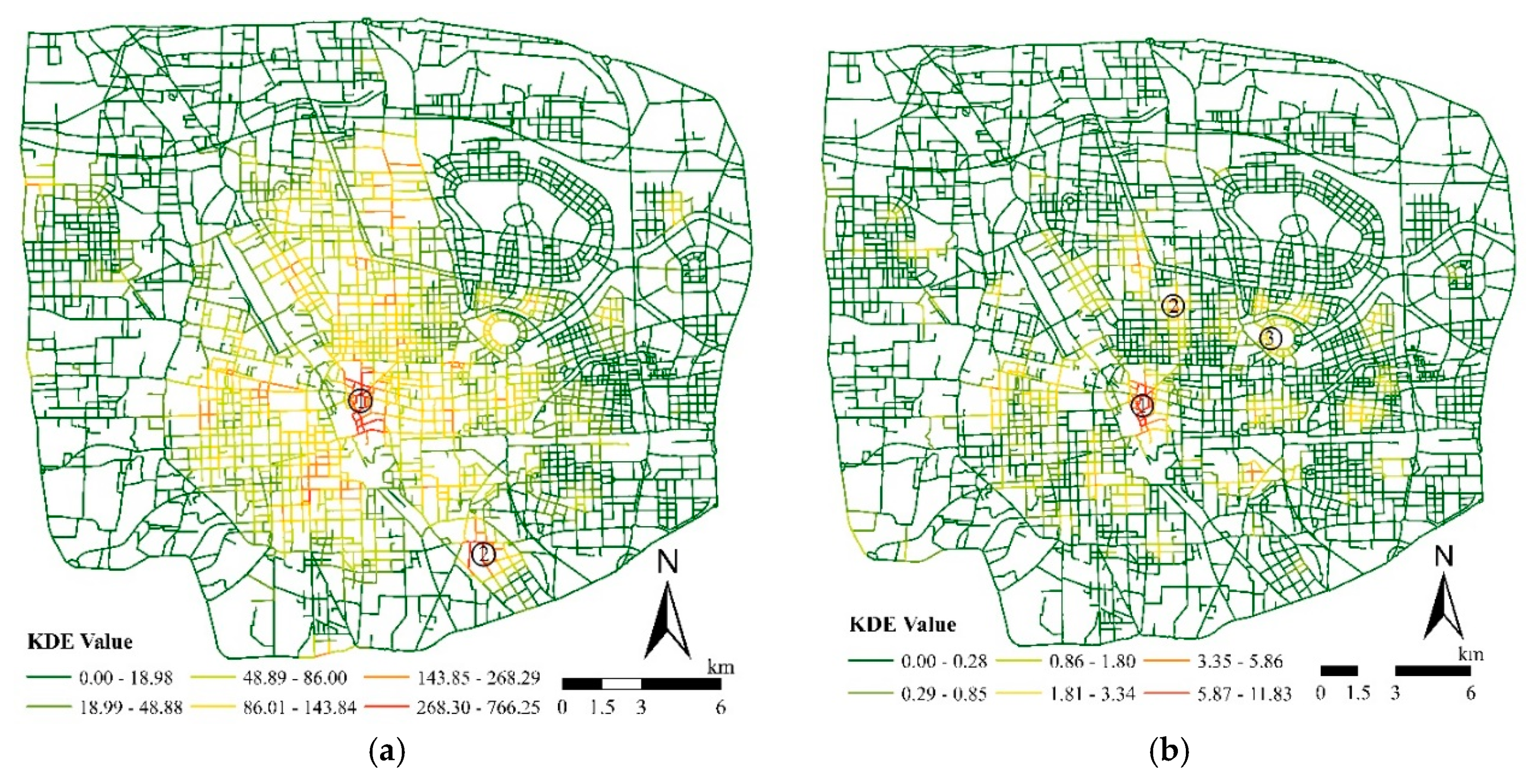
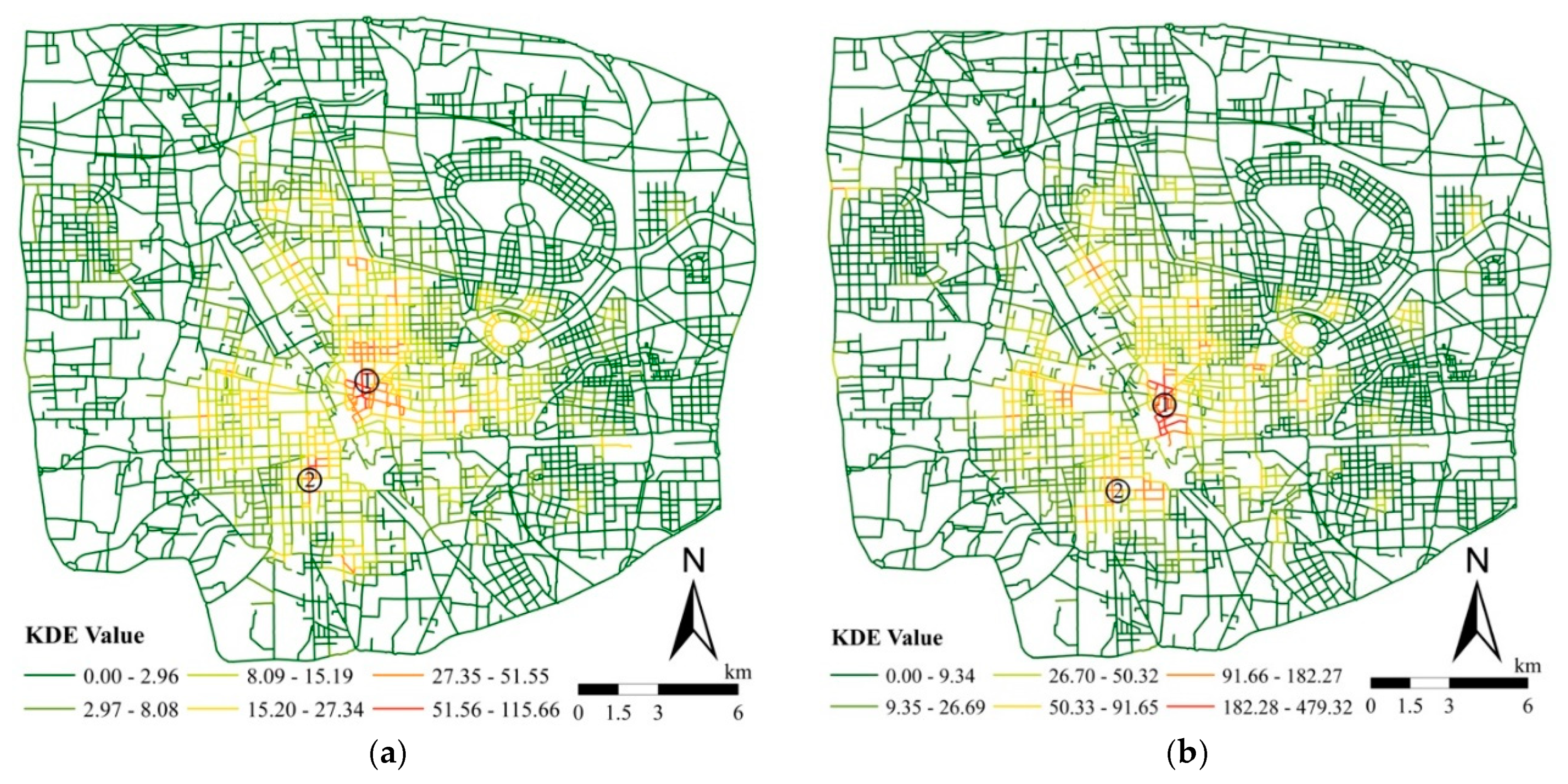
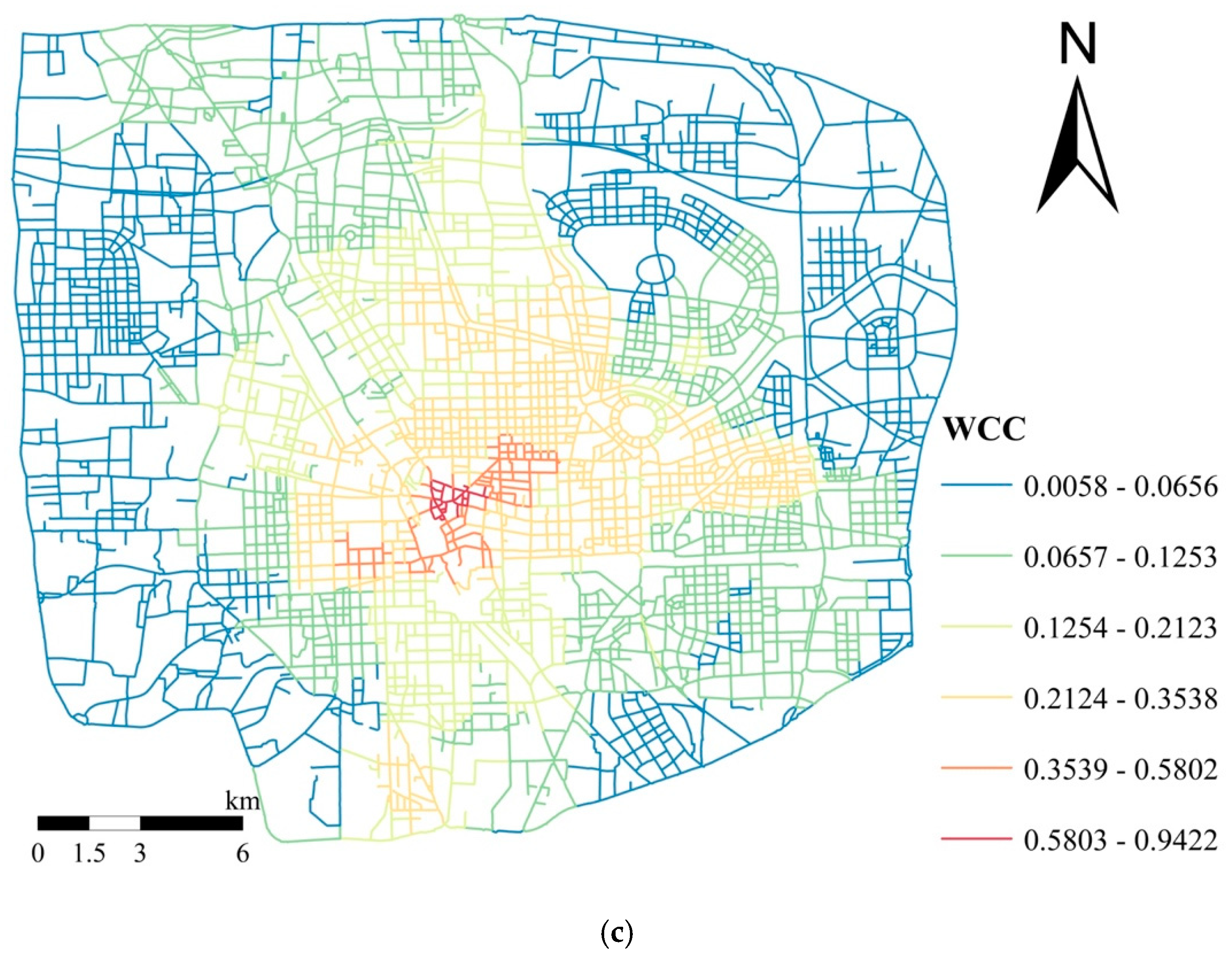
4.2. Network-Based Spatial Patterns of Retail Stores
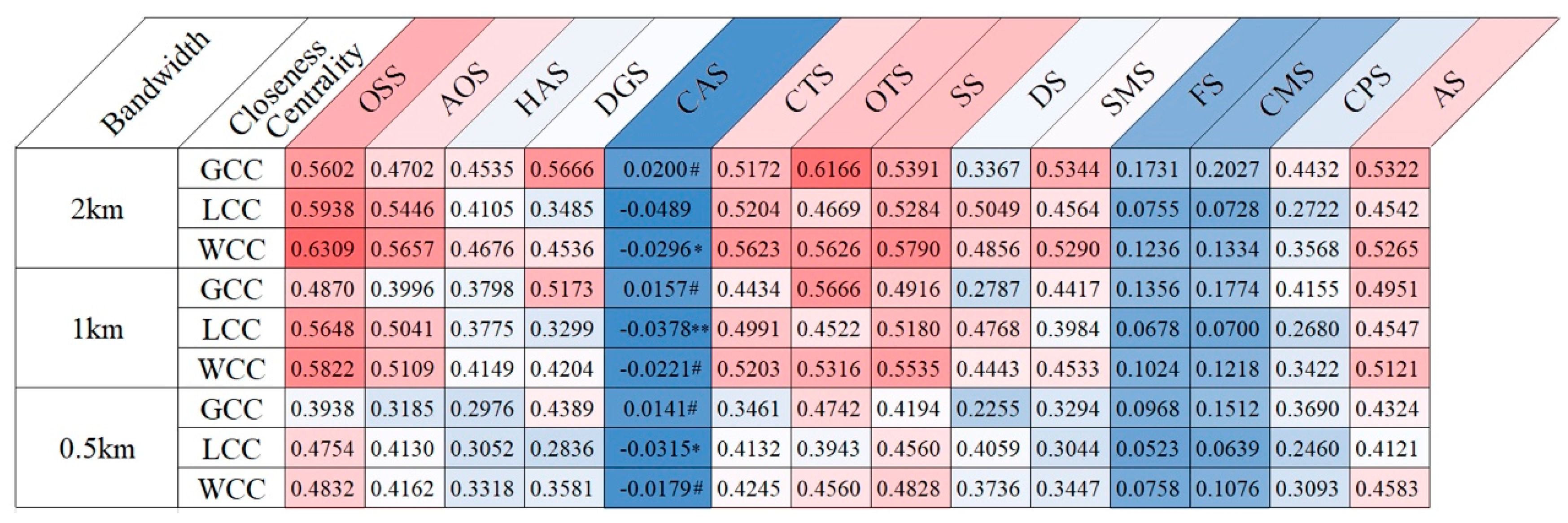
4.3. Correlations between NKDE and Closeness Centrality
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barry, R.B.; Joel, R.E.; Patrali, M.C. Retail Management: A Strategic Approach, 13th ed.; Pearson Education: Harlow, UK, 2018; pp. 22–42. [Google Scholar]
- Glaeser, E.L.; Kolko, J.; Saiz, A. Consumer city. J. Econ. Geogr. 2001, 1, 27–50. [Google Scholar] [CrossRef]
- Wang, S. China’s New Retail Economy: A Geographic Perspective; Routledge: New York, NY, USA, 2014; pp. 10–60. [Google Scholar]
- Goldman, A. The transfer of retail formats into developing economies: The example of China. J. Retail. 2001, 77, 221–242. [Google Scholar] [CrossRef]
- Thomas, W.; Susan, G.M. Retail gravitation and economic impact: A market-driven analytical framework for bike-share station location analysis in the United States. Int. J. Sustain. Transp. 2016, 10, 247–259. [Google Scholar]
- Les, D.; Michalis, P.; Alex, S. Estimating attractiveness, hierarchy and catchment area extents for a national set of retail centre agglomerations. J. Retail. Consum. Serv. 2016, 28, 78–90. [Google Scholar]
- Michael, F.G. LACS: A Location-Allocation Mode for Retail Site Selection. J. Retail. 1984, 60, 84–100. [Google Scholar]
- Norat, R.T.; Amparo, B.P.; Juan, B.V.; Francisco, M.V. The retail site location decision process using GIS and the analytical hierarchy process. Appl. Geogr. 2013, 40, 191–198. [Google Scholar]
- Mike, G. The Poetics of Cities: Designing Neighborhoods That Work; The Ohio State University Press: Columbus, OH, USA, 1995; pp. 1–16. [Google Scholar]
- Michael, F.D. The geometry of central place theory. Geogr. Ann. B 1965, 47, 111–124. [Google Scholar]
- Gordon, F.M. Agglomeration and central place theory: A review of the literature. Int. Reg. Sci. Rev. 1984, 9, 1–42. [Google Scholar]
- Guy, C. The Retail Development Process. Location, Property and Planning; Routeledge: London, UK, 1994; pp. 12–36. [Google Scholar]
- Sergio, P.; Emanuele, S.; Valentino, I.; Roberto, M.; Vito, L.; Alessio, C.; Wang, F.H.; Salvatore, S. Street centrality and densities of retail and services in Bologna, Italy. Environ. Plan. B 2009, 36, 450–465. [Google Scholar]
- Sergio, P.; Vito, L.; Wang, F.H.; Salvador, R.; Emanuele, S.; Salvatore, S.; Alessio, C.; Eugenio, B.; Francisco, C.; Berta, C. Street centrality and the location of economic activities in Barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar]
- Wang, F.H.; Chen, C.; Xiu, C.L.; Zhang, P.Y. Location analysis of retail stores in Changchun, China: A street centrality perspective. Cities 2014, 41, 54–63. [Google Scholar] [CrossRef]
- Lin, G.; Chen, X.X.; Liang, Y.T. The location of retail stores and street centrality in Guangzhou, China. Appl. Geogr. 2018, 100, 12–20. [Google Scholar] [CrossRef]
- He, S.W.; Yu, S.; Wei, P.; Fang, C.L. A spatial design network analysis of street networks and the locations of leisure entertainment activities: A case study of Wuhan, China. Sustain. Cities Soc. 2019, 44, 880–887. [Google Scholar] [CrossRef]
- Chen, X. Take the edge off: A hybrid geographic food access measure. Appl. Geogr. 2017, 87, 149–159. [Google Scholar] [CrossRef]
- Matthew, C.; Steve Ti Tim, H.; Taner, O. Public Places Urban Spaces, The Dimensions of Urban Design, 2nd ed.; Routledge: New York, NY, USA, 2012; pp. 180–190. [Google Scholar]
- Jacobs, J. The Death and Life of Great American Cities: The Failure of Town Planning; Random House: New York, NY, USA, 1961; pp. 1–25. [Google Scholar]
- Stephen, M. Streets and Patterns; Routledge: New York, NY, USA, 2005; pp. 235–258. [Google Scholar]
- Shen, Y.; Kayvan, K. Urban function connectivity: Characterisation of functional urban streets with social media check-in data. Cities 2016, 55, 9–21. [Google Scholar] [CrossRef]
- Okabe, A.; Okunuki, K. A computational method for estimating the demand of retail stores on a street network and its implementation in GIS. Trans. GIS 2001, 5, 209–220. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: London, UK, 1989; pp. 1–32. [Google Scholar]
- Hillier, B. Space Is the Machine: A Configurational Theory of Architecture; Space Syntax: London, UK, 2007; pp. 21–52. [Google Scholar]
- Itzhak, O.; Ran, G. Spatial patterns of retail activity and street network structure in new and traditional Israeli cities. Urban Geogr. 2016, 37, 629–649. [Google Scholar]
- Wang, F.H.; Antipova, A.; Sergio, P. Street centrality and land use intensity in Baton Rouge, Louisiana. J. Transp. Geogr. 2011, 19, 285–293. [Google Scholar] [CrossRef]
- Wang, S.; Xu, G.; Guo, Q.S. Street Centralities and Land Use Intensities Based on Points of Interest (POI) in Shenzhen, China. ISPRS. Int. J. Geo-Inf. 2018, 7, 425. [Google Scholar] [CrossRef]
- Kevin, L. The Image of the City; MIT Press: Boston, MA, USA, 1960; pp. 1–26. [Google Scholar]
- Ian, S.; Nikhil, N.; Carlo, R.; Raphäel, P. Green streets− Quantifying and mapping urban trees with street-level imagery and computer vision. Landsc. Urban Plan. 2017, 165, 93–101. [Google Scholar]
- Li, X.J.; Zhang, C.R.; Li, W.D.; Robert, R.; Meng, Q.Y.; Zhang, W.X. Assessing street-level urban greenery using Google Street View and a modified green view index. Urban For. Urban Green. 2015, 14, 675–685. [Google Scholar] [CrossRef]
- Long, Y.; Liu, L. How green are the streets? An analysis for central areas of Chinese cities using Tencent Street View. PLoS ONE 2017, 12, e0171110. [Google Scholar]
- Gong, F.Y.; Zeng, Z.C.; Zhang, F.; Li, X.J.; Edward, N.; Leslie, K.N. Mapping sky, tree, and building view factors of street canyons in a high-density urban environment. Build. Environ. 2018, 134, 155–167. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, Z.X. Measuring visual enclosure for street walkability: Using machine learning algorithms and Google Street View imagery. Appl. Geogr. 2016, 76, 147–153. [Google Scholar] [CrossRef]
- Li, X.J.; Carlo, R.; Ian, S. Quantifying the shade provision of street trees in urban landscape: A case study in Boston, USA, using Google Street View. Landsc. Urban Plan. 2018, 169, 81–91. [Google Scholar] [CrossRef]
- Li, X.J.; Carlo, R. Mapping the spatio-temporal distribution of solar radiation within street canyons of Boston using Google Street View panoramas and building height model. Landsc. Urban Plan. 2018. [Google Scholar] [CrossRef]
- Hao, J.W.; Zhu, J.; Zhong, R. The rise of big data on urban studies and planning practices in China: Review and open research issues. J. Urban Manag. 2015, 4, 92–124. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, N.H.; Wu, L.; Liu, Y. Street as a big geo-data assembly and analysis unit in urban studies: A case study using Beijing taxi data. Appl. Geogr. 2017, 86, 152–164. [Google Scholar] [CrossRef]
- Wu, L.; Zhi, Y.; Sui, Z.W.; Liu, Y. Intra-urban human mobility and activity transition: Evidence from social media check-in data. PLoS ONE 2014, 9, e97010. [Google Scholar] [CrossRef]
- Pucci, P.; Fabio, M.; Paolo, T. Mapping Urban Practices through Mobile Phone Data; Springer: Berlin, Germany, 2015; pp. 21–70. [Google Scholar]
- Yuan, J.; Zheng, Y.; Xie, X. Discovering regions of different functions in a city using human mobility and POIs. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 1–9. [Google Scholar]
- Gao, S.; Janowicz, K.; Couclelis, H. Extracting urban functional regions from points of interest and human activities on location-based social networks. Trans. GIS 2017, 21, 446–467. [Google Scholar] [CrossRef]
- Hu, T.Y.; Yang, J.; Li, X.C.; Gong, P. Mapping urban land use by using landsat images and open social data. Remote Sens. 2016, 8, 151. [Google Scholar] [CrossRef]
- Liu, X.P.; He, J.L.; Yao, Y.; Zhang, J.B.; Liang, H.L.; Wang, H.; Hong, Y. Classifying urban land use by integrating remote sensing and social media data. Int. J. Geogr. Inf. Sci. 2017, 31, 1675–1696. [Google Scholar] [CrossRef]
- Biłozor, A.; Kowalczyk, A.M.; Bajerowski, T. Theory of Scale-Free Networks as a New Tool in Researching the Structure and Optimization of Spatial Planning. J. Urban Plan. Dev. 2018, 144, 04018005. [Google Scholar] [CrossRef]
- Kowalczyk, A.M. The analysis of networks space structures as important elements of sustainable space development. In Proceedings of the International Conference on Environmental Engineering, Saulėtekio, Lithuania, 27–28 April 2017; pp. 1–6. [Google Scholar]
- Xie, Z.X.; Yan, J. Kernel density estimation of traffic accidents in a network space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef]
- Christopher, L. Spatial Data Analysis: An Introduction for GIS Users; Oxford University Press: London, UK, 2010; pp. 102–169. [Google Scholar]
- Tang, L.L.; Kan, Z.H.; Zhang, X.; Sun, F.; Xue, Y.; Li, Q.Q. A network Kernel Density Estimation for linear features in space–time analysis of big trace data. Int. J. Geogr. Inf. Sci. 2016, 30, 1717–1737. [Google Scholar] [CrossRef]
- Okabe, A.; Kokichi, S. Spatial Analysis along Networks: Statistical and Computational Methods; John Wiley & Sons: Chichester, UK, 2012; pp. 171–190. [Google Scholar]
- She, B.; Zhu, X.Y.; Ye, X.Y.; Guo, W.; Su, K.H.; Jay, L. Weighted network Voronoi Diagrams for local spatial analysis. Comput. Environ. Urban Syst. 2015, 52, 70–80. [Google Scholar] [CrossRef]
- Stanley, W.; Katherine, F. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994; pp. 1–35. [Google Scholar]
- Linton, C.F. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar]
- Emanuele, S.; Matheus, V.; Luciano, F.C.; Alessio, C.; Sergio, P.; Vito, L. Urban street networks, a comparative analysis of ten European cities. Environ. Plan. B 2013, 40, 1071–1086. [Google Scholar]
- Sergio, P.; Paolo, C.; Vito, L. The network analysis of urban streets: A primal approach. Environ. Plan. B 2006, 33, 705–725. [Google Scholar]
- Newman, M.E. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Huang, L.P.; Yang, Y.J.; Gao, H.P.; Zhao, X.H.; Du, Z.W. Comparing Community Detection Algorithms in Transport Networks via Points of Interest. IEEE Access 2018, 6, 29729–29738. [Google Scholar] [CrossRef]
- Stanislav, S.; Riccardo, C.; Alexander, B.; Carlo, R. General optimization technique for high-quality community detection in complex networks. Phys. Rev. 2014, 90, 1–8. [Google Scholar]
- Ghalmane, Z.; El Hassouni, M.; Cherifi, C.; Cherifi, H. Centrality in modular networks. EPJ Data Sci. 2019, 8, 1–27. [Google Scholar] [CrossRef]
- Andres, S.; Michael, M. Urban network analysis: A new toolbox for measuring city form in ArcGIS. In Proceedings of the 2012 Symposium on Simulation for Architecture and Urban Design, Orlando, FL, USA, 26–29 March 2012; pp. 1–15. [Google Scholar]
- Wang, X.F.; John, T. Zhengzhou—Political economy of an emerging Chinese megacity. Cities 2019, 84, 104–111. [Google Scholar] [CrossRef]
- Jiang, B. Street hierarchies: A minority of streets account for a majority of traffic flow. Int. J. Geogr. Inf. Sci. 2009, 23, 1033–1048. [Google Scholar] [CrossRef]
- Alexander, E.; Michael, L.; Kay, W.A. Graph-theoretical analysis of the Swiss road and railway networks over time. Netw. Spat. Econ. 2009, 9, 379–400. [Google Scholar]
| Store Type | Store Subtype | Store Count | Road Count | Average Stores Per Street | Line Cell Count | Average Stores Per Line Cell |
|---|---|---|---|---|---|---|
| Specialty stores (SS) | Office supply stores (OSS) | 4285 | 897 | 4.7770 | 1374 | 3.1186 |
| Apparel shop stores (AOS) | 15456 | 1245 | 12.4145 | 1829 | 8.4505 | |
| Home appliance stores (HAS) | 4919 | 1035 | 4.7527 | 1626 | 3.0252 | |
| Drug stores (DGS) | 3142 | 979 | 3.2094 | 1555 | 2.0206 | |
| Car stores (CAS) | 3811 | 434 | 8.7811 | 795 | 4.7937 | |
| Cosmetics stores (CTS) | 3569 | 860 | 4.1500 | 1367 | 2.6108 | |
| Other stores (OTS) | 6587 | 1491 | 4.4178 | 2156 | 3.0552 | |
| Subtotal | 41769 | 2285 | 18.2796 | 3335 | 12.5244 | |
| Department stores (DS) | 249 | 121 | 2.0579 | 179 | 1.3911 | |
| Supermarkets (SMS) | 2377 | 823 | 2.8882 | 1375 | 1.7287 | |
| Furniture stores (FS) | 4211 | 492 | 8.5589 | 803 | 5.2441 | |
| Construction material stores (CMS) | 13271 | 1147 | 11.5702 | 1887 | 7.0329 | |
| Consumer product stores (CPS) | 16900 | 1966 | 8.5961 | 2967 | 5.6960 | |
| All Stores (AS) | 78777 | 2652 | 29.7048 | 3934 | 20.0247 | |
| Store Type | Store Subtype | Average | Median | Maximum | Standard Deviation |
|---|---|---|---|---|---|
| Specialty stores (SS) | Office supply stores (OSS) | 6.2003 | 3.2650 | 115.6580 | 8.5152 |
| Apparel shop stores (AOS) | 17.6005 | 6.6483 | 479.3170 | 29.8941 | |
| Home appliance stores (HAS) | 6.1540 | 3.5878 | 129.5320 | 9.3261 | |
| Drug stores (DGS) | 3.8343 | 2.2271 | 29.3573 | 4.1453 | |
| Car stores (CAS) | 4.0902 | 1.1406 | 328.1910 | 16.7913 | |
| Cosmetics stores (CTS) | 4.7676 | 3.1391 | 70.3148 | 5.9746 | |
| Other stores (OTS) | 8.2742 | 5.9976 | 139.8360 | 8.4355 | |
| Subtotal | 40.3303 | 22.3597 | 766.2540 | 52.1403 | |
| Department stores (DS) | 0.3422 | 0.0388 | 11.8333 | 0.8177 | |
| Supermarkets (SMS) | 3.1721 | 2.3872 | 63.3645 | 3.6940 | |
| Furniture stores (FS) | 5.5538 | 1.5317 | 191.4990 | 13.9360 | |
| Construction material stores (CMS) | 14.4089 | 5.1197 | 506.5090 | 35.1740 | |
| Consumer product stores (CPS) | 17.9092 | 12.5695 | 406.3060 | 20.4603 | |
| All Stores (AS) | 74.5491 | 45.1345 | 1105.7300 | 88.6215 | |
| Store Type | Store Subtype | GCC | LCC | WCC |
|---|---|---|---|---|
| Specialty stores (SS) | Office supply stores (OSS) | 0.5602 *** | 0.5938 *** | 0.6309 *** |
| Apparel shop stores (AOS) | 0.4702 *** | 0.5446 *** | 0.5657 *** | |
| Home appliance stores (HAS) | 0.4535 *** | 0.4105 *** | 0.4676 *** | |
| Drug stores (DGS) | 0.5666 *** | 0.3485 *** | 0.4536 *** | |
| Car stores (CAS) | 0.0173 # | −0.0489 *** | −0.0296 * | |
| Cosmetics stores (CTS) | 0.5172 *** | 0.5204 *** | 0.5623 *** | |
| Other stores (OTS) | 0.6166 *** | 0.4669 *** | 0.5626 *** | |
| Subtotal | 0.5391 *** | 0.5284 *** | 0.5790 *** | |
| Department stores (DS) | 0.3367 *** | 0.5049 *** | 0.4856 *** | |
| Supermarkets (SMS) | 0.5344 *** | 0.4564 *** | 0.5290 *** | |
| Furniture stores (FS) | 0.1731 *** | 0.0755 *** | 0.1236 *** | |
| Construction material stores (CMS) | 0.2027 *** | 0.0728 *** | 0.1334 *** | |
| Consumer product stores (CPS) | 0.4432 *** | 0.2722 *** | 0.3568 *** | |
| All Stores (AS) | 0.5322 *** | 0.4542 *** | 0.5265 *** | |
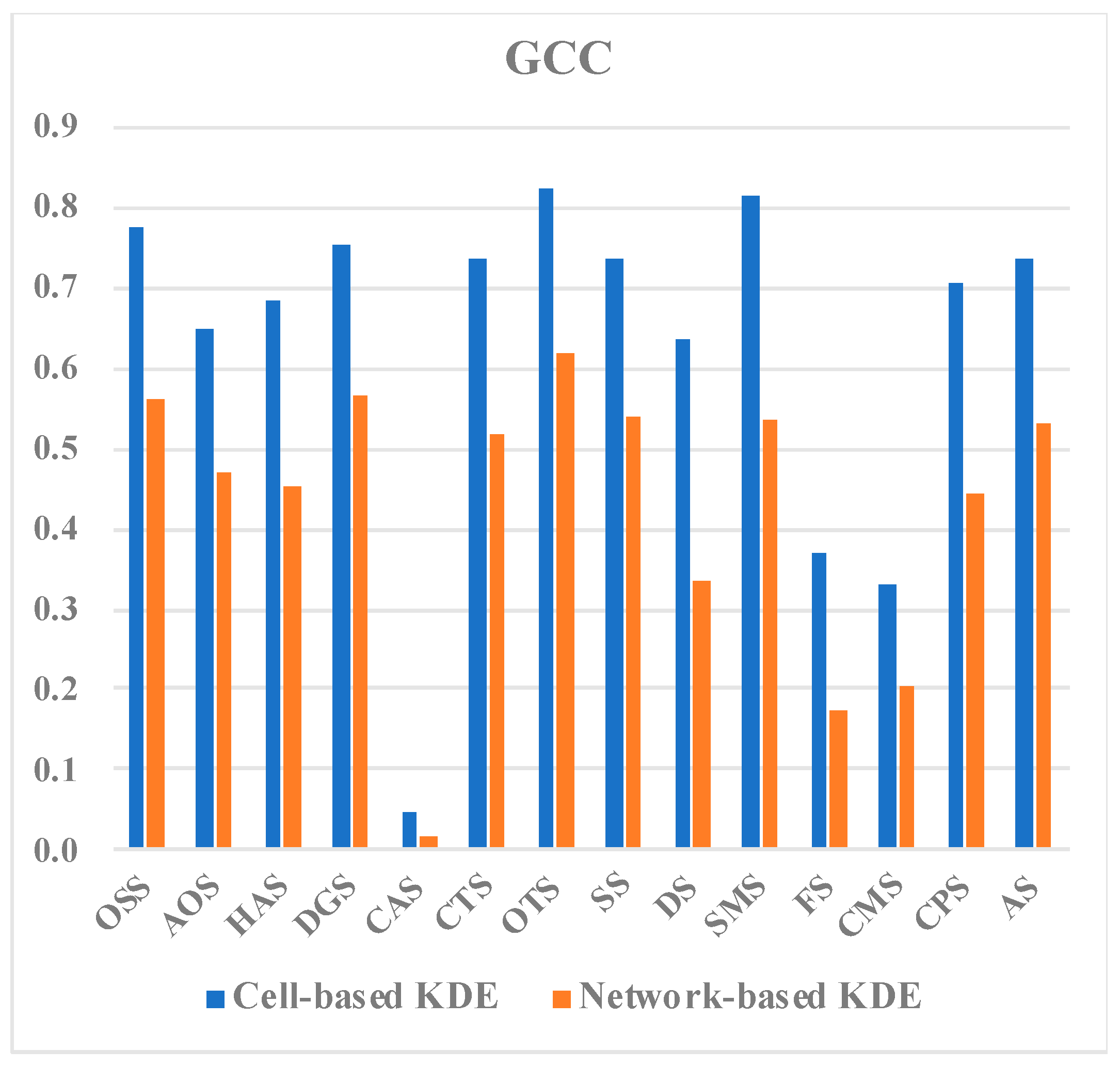
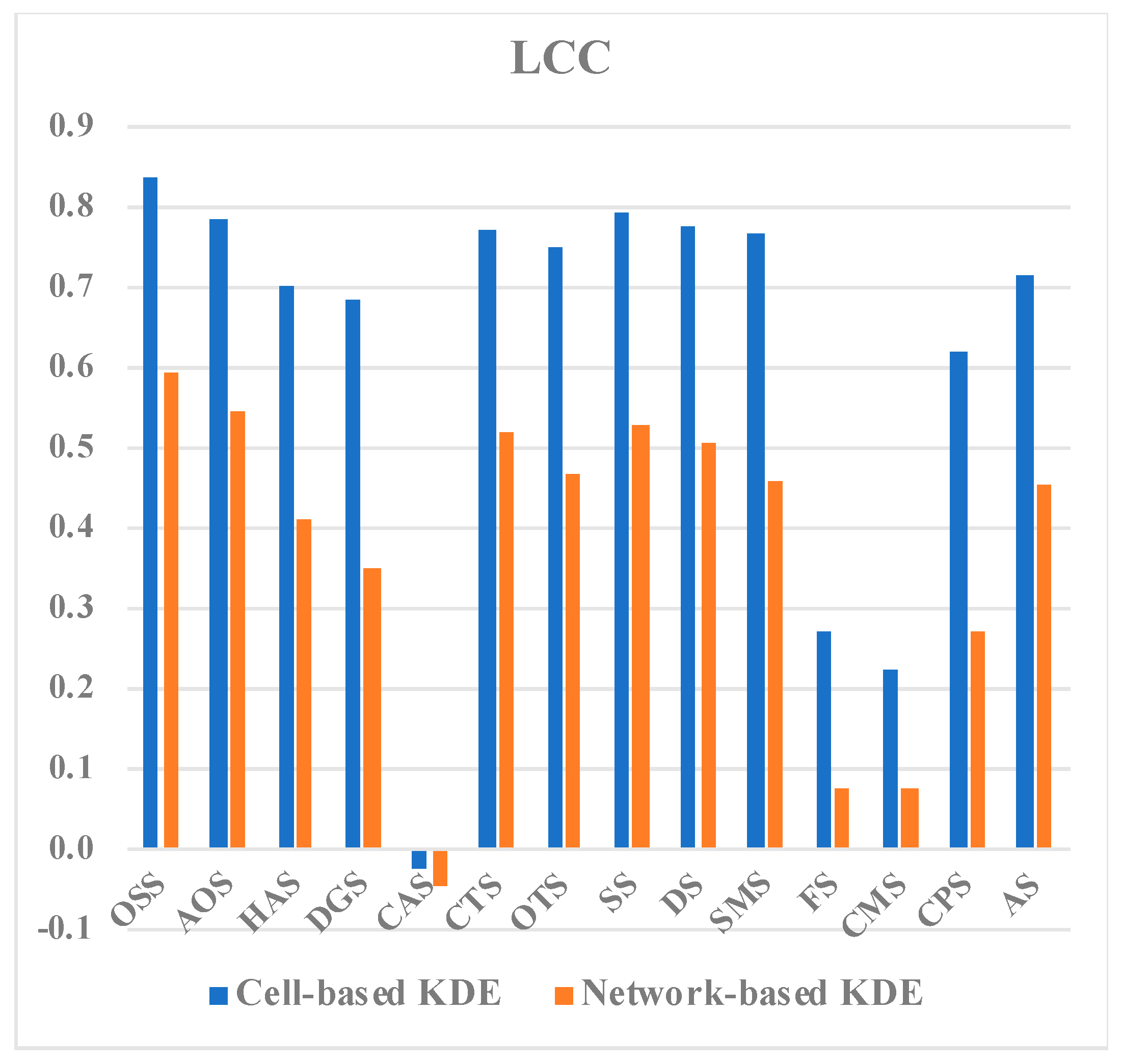
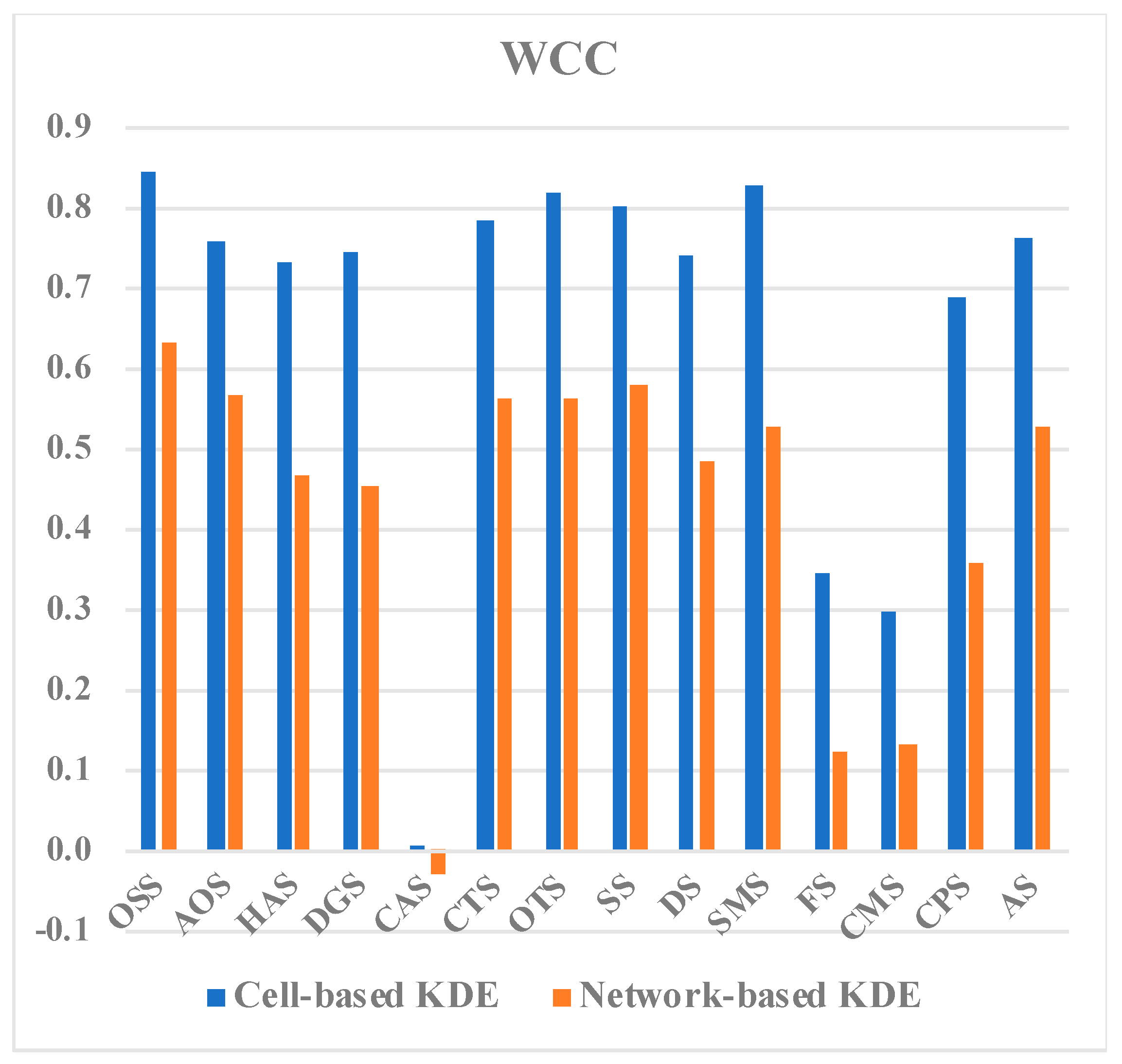
| Store Type | GCC | LCC | WCC | |
| SS | OSS | 0.7772 *** | 0.8390 *** | 0.8461 *** |
| AOS | 0.6487 *** | 0.7850 *** | 0.7591 *** | |
| HAS | 0.6842 *** | 0.7001 *** | 0.7339 *** | |
| DGS | 0.7556 *** | 0.6845 *** | 0.7439 *** | |
| CAS | 0.0458 *** | -0.0252 *** | 0.0068 # | |
| CTS | 0.7370 *** | 0.7709 *** | 0.7865 *** | |
| OTS | 0.8251 *** | 0.7482 *** | 0.8187 *** | |
| Subtotal | 0.7381 *** | 0.7914 *** | 0.8041 *** | |
| DS | 0.6354 *** | 0.7740 *** | 0.7395 *** | |
| SMS | 0.8138 *** | 0.7650 *** | 0.8283 *** | |
| FS | 0.3720 *** | 0.2710 *** | 0.3429 *** | |
| CMS | 0.3325 *** | 0.2206 *** | 0.2954 *** | |
| CPS | 0.7055 *** | 0.6189 *** | 0.6874 *** | |
| AS | 0.7383 *** | 0.7128 *** | 0.7630 *** | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Cui, C.; Miao, C.; Wang, H.; Chen, X. Identifying Spatial Patterns of Retail Stores in Road Network Structure. Sustainability 2019, 11, 4539. https://doi.org/10.3390/su11174539
Han Z, Cui C, Miao C, Wang H, Chen X. Identifying Spatial Patterns of Retail Stores in Road Network Structure. Sustainability. 2019; 11(17):4539. https://doi.org/10.3390/su11174539
Chicago/Turabian StyleHan, Zhigang, Caihui Cui, Changhong Miao, Haiying Wang, and Xiang Chen. 2019. "Identifying Spatial Patterns of Retail Stores in Road Network Structure" Sustainability 11, no. 17: 4539. https://doi.org/10.3390/su11174539
APA StyleHan, Z., Cui, C., Miao, C., Wang, H., & Chen, X. (2019). Identifying Spatial Patterns of Retail Stores in Road Network Structure. Sustainability, 11(17), 4539. https://doi.org/10.3390/su11174539






