1. Introduction
The multifunctionality of forests in Europe stems from the diversity of tree species and ecosystems. Indicatively, forests serve as a regulatory tool for hydrologic cycles, provide refuges for biodiversity, contribute raw material for medicinal and forest products, prevent soil destruction, and satisfy recreational, spiritual, and aesthetic value needs [
1]. However, the most significant impact is related to climate change mitigation, since it contributes greatly to exchanges in energy, water, carbon dioxide, and other chemical substances [
1,
2]. The significant contribution of forests to climate change mitigation has become recognized in the existing literature recently [
3]. Given that the destruction of forests reduces the ability of the Earth to absorb CO
2 from the atmosphere [
4], an effort was initiated for its limitation. This effort was established with the negotiation of the Montreal UNFCCC CoP held in 2005, in which the dominant motto for forest management is “Reducing emissions from deforestation and forest degradation” (REDD).
In Europe, forests correspond to 37% of the terrestrial surface with ecological, economical, and soci-ocultural impacts, as mentioned above [
5,
6], while eastern and central European countries do still have large and relatively undisturbed forests compared to western European countries [
7,
8].
Within the last couple of centuries in the name of societal modernization and urbanization, deforestation has become a necessary tool, which permanently converts forest land into other land uses [
9].
A high level of deforestation is globally considered an anthropogenic environmental problem [
9,
10]. The impacts of this problem are more severe for less developed countries, and less extended for developed countries. Indeed, developed countries are exerting intense efforts for afforestation, which led to an increase in the forest area, estimated at 1% from 1990 to 2005 [
11]. The linkage among deforestation, forest degradation, and climate change is attributed to fewer trees absorbing less greenhouse gases (GHGs); therefore, deforestation is indirectly causing increased quantities of carbon dioxide emissions [
12,
13]. In addition, according to macro-sociologists, carbon dioxide emissions may be indicative of marketable outsourcing production for developing countries [
13]. Deforestation in global terms is related to the cooling effect and the warming carbon cycle, due to changes in albedo and evapotranspiration [
14].
Deforestation in the European Union (EU) constitutes an environmental issue of adverse negative impacts within the last few decades. Motivation policies for deforestation are characterized by complexity and are differentiated from region to region and from country to country. One of the major reasons for deforestation in the EU, according to the FAO (2016) [
15], is related to the agricultural expansion for the production of specific food commodities (accounting for 80%), while the issues of urbanization/infrastructure interpret less than 10% of deforestation each.
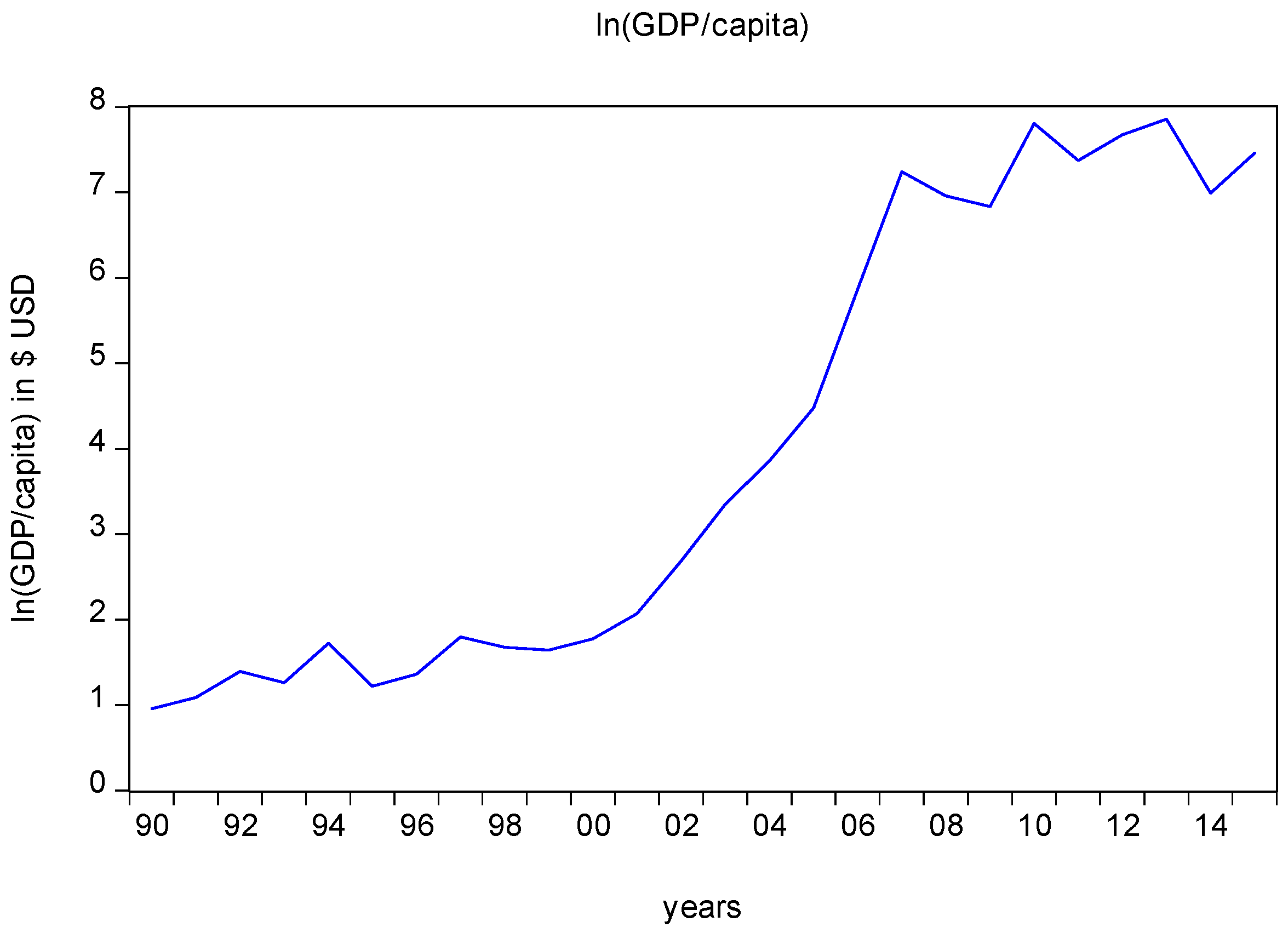
Bulgaria is selected as the country to be studied, since it has become a new member state in the EU in 2007 and it is ranked fourth among EU members in terms of gross domestic product (GDP) growth for the last decade. The change from a highly centralized, planned economy to an open, market-based, upper-middle income economy has become achievable after a decade of slow economic restructuring and growth, high indebtedness, and a loss of savings. The time period until its entrance into the EU was characterized by an exceptionally high economic growth and improved living standards. However, in the last decade, few positive impacts were implemented. Particularly, the global economic crisis of 2008 and a period of political instability in the period 2013–2014 urged the Bulgarian government to achieve the objectives of growth and shared prosperity.
Today, for Bulgaria, the most importance issues to be addressed are those of raising productivity and handling the rapid demographic change. Particularly, higher productivity growth is critical to accelerate convergence, as Bulgaria’s income per capita is only 47% of the EU average, which is the lowest in the EU.
Furthermore, in Bulgaria, according to statistics provided by the FAO [
15], 36.1% or about 3,927,000 ha of the total area is forested, 8.6% (338,000.00) of which is classified as primary forest, which is the mostly bioversatile and carbon-dense forest area. In addition, 815,000 ha are forest plantations. Besides, deforestation has currently become a significant issue, since Bulgaria’s forests contain 202 million metric tons of carbon in living forest biomass.
The overexploitation of forests—being not accompanied by a project for sustainable management—as well as a lack of effective surveillance of forests and forest areas in Bulgaria resulted in losing an average of 30,000 ha or 0.90% per year [
16].
Common methods of deforestation for Bulgaria are burning trees and clear cutting. These practices are considered controversial, since they leave the land completely barren. Degradation and deforestation may well lead to a devastating chain of events both locally and globally, including the loss of species, the water cycle (trees are important to the water cycle, since they absorb rain fall and produce water vapor that is released into the atmosphere), soil erosion, life quality, and floods during winter.
The low income is encouraging the government to implement institutional and legislative changes, such as low tax rates and promotional investments. On the other hand, the country’s forest cover has been expanding gradually, at an annual rate of 0.6% over the period 1990–2015 [
17], while as an EU member, Bulgaria is required to implement the EU Timber Regulation, which came into force in March 2013.
Another major alarming problem with the forests in Bulgaria is illegal logging. Among the types of illegal logging are the illegal lending of forest area and damage of forest stands to obtain extended harvesting volume at a lower price.
Nowadays, the legislation has become strict regarding the activities and rights related to forest management and timber harvesting. The state forestry staff should control logging activities, but all the violations in forests are caused by a lack of governance and enforcement of existing regulations and laws, thus necessitating cooperation among forest employees. Moreover, low salaries have led to high rates of corruption in terms of state forest services as well as to limited and ineffective control mechanisms [
16]. It is noteworthy that deforestation and forest degradation account for approximately 20–25% of global anthropogenic greenhouse gas (GHG) emissions, which are the major source of emissions from developing countries [
18]. Deforestation in Bulgaria, as among all ex-socialist countries, and especially in private forests, is becoming limited according to statistical data, which is attributed to the modernization, urbanization, and immigration phenomena that were initiated in the period of socialism. In Bulgaria, data are available only for the case of afforestation, but not for deforestation. An indirect conclusion can be reached through the change in the land area covered by forests as well as the afforestation rate. Particularly, a decrease in the afforestation rate was observed during the 1990s, when the afforested areas per year were decreased under 10,000 ha year
−1, and after 2009, under 5000 ha year
−1. The major reasons for this decrease are the following: the large mastered areas for afforestation, the development of silvicultural systems with natural regeneration priority, chronic economic crises, as well as a lack of resources.
There are plentiful studies addressing the environmental Kuznets curve (EKC) hypothesis, where deforestation has been used as a proxy for environmental degradation, given the direct effects of growth on natural capital, in order productive agrarian efforts and policies to be promoted [
19]. A lack of data for the deforestation area was the reason that the authors in this study used the GHG emissions generated by deforestation as an index for environmental degradation.
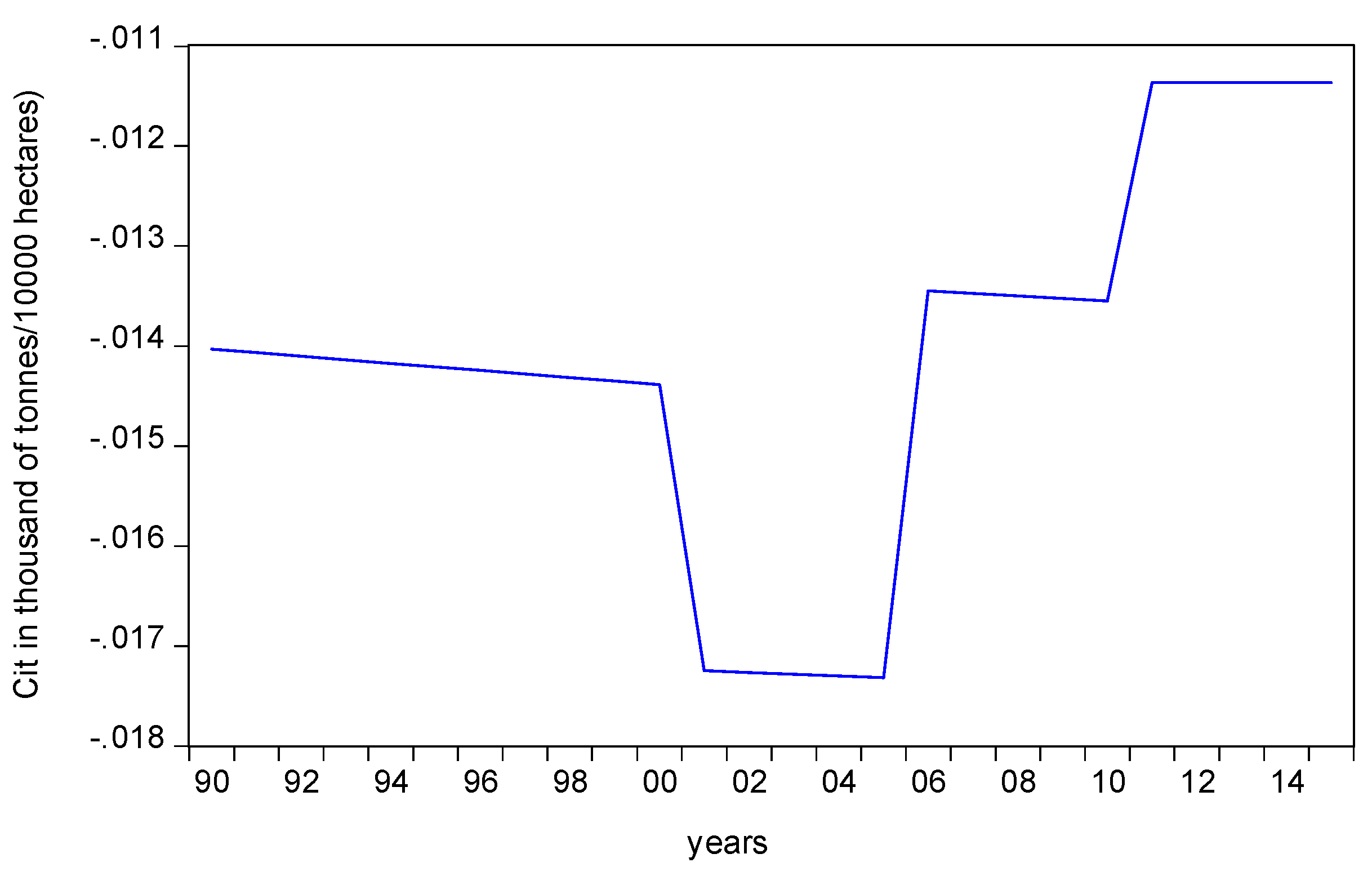
In this research context, the extended deforestation and the carbon emissions generated by deforestation are related to the GDP per capita (as motivation for income improvement). This scientific background can be a subject of econometric study under the framework of the EKC on providing policy tools to enable a strategy design that can provide alternative and more profitable sources of income. In this study, the ARDL bounds cointegration technique was deployed, and it validated the reversed N Kuznets pattern for the data applied. The novelty of the study stands on the use of the GHG emissions generated by deforestation for a country with many particularities regarding the issue of deforestation, including a lack of data, suffering from the problem of illegal logging, and strong motivation for afforestation. The study is organized as follows:
Section 2 describes the existing literature,
Section 3 outlines the methodology,
Section 4 provides and discusses the results, and the concluding remarks are succinctly presented in
Section 5.
4. Results
The results of the methodology are provided in the following
Table 2,
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7. In the first step of the analysis, two different unit roots tests were implemented, namely the DF-GLS unit root test and the DF break unit root test. The results of those tests are provided in
Table 2 and
Table 3, respectively.
According to these findings, the first unit root test confirmed that the variables used in the model—that is, deforestation as a proxy for environmental degradation and economic growth, respectively—are I(1), which is non-stationary in levels and stationary in first differences.
The second unit root test employed, which takes into consideration the existence of structural breaks, does also confirm that the variables are I(1), as evident in
Table 3. Furthermore, this test provides the potential structural breaks of the time-series studied. Based on these, potential explanations for the structural breaks were identified. The year 2006 is a significant hallmark, since it coincides with the end of the privatization of the state-owned firms. This is significant for GDP per capita and deforestation due to a reduction in the foreign direct investments (FDI). In addition, regarding the year 2002, the mechanisms of coordination and management for the implementation of the strategy on structural funds have been refined. Finally, the year 2005 corresponds to when the Kyoto protocol was entered into force, specifically on 16 February 2005, which may adequately interpret the behavior of the carbon emissions equivalent generated by deforestation for the case of Bulgaria.
Having empirically confirmed that the time series studied are not I(2), the ARDL methodology was well deployed. The ARDL model selected based on the Akaike criterion, was ARDL (1,0,2,1). In the next step, the estimated F test suggests that the null hypothesis according to which no level relationships exist cannot be accepted, a result implying the existence of a long-run relationship among the variables studied, as evident in
Table 4.
The next step in the analysis involves the estimation of the cointegrating relationship (long-run relationship) model based on the ARDL bounds test and is provided in
Table 5.
The estimated error correction term that describes the speed of convergence to the steady state is the following: Cit − (−10.4642*GDP_CAPITA + 2.0064*(GDP)2 − 0.1017*(GDP)3 − 3.0495). The coefficients of the long-run relation are found to be statistically significant (for 10% level of significance), while the signs of the coefficients are as follows; λ1 < 0, λ2 > 0, and λ3 < 0. Therefore, the signs validate the reversed N Kuznets curve pattern. This pattern implies that emissions would begin to rise again once a second income turning point is passed.
The estimation of the error correction model is provided in
Table 6. The negative coefficients of ECT
t–1 are corroborating the short-term relationship in the model. The coefficient of the ECT
t–1 is indicative of the speed of convergence from short-term disequilibrium to the long-term equilibrium in the approximately 15.5 months in the linear ARDL model. The negative (positive) coefficients of DGDP
t–1 (DGDP
t–12) do not confirm the existence of the EKC hypothesis (inverted U pattern) with a one-year lag in the model. Subsequently, the inversed N Kuznets curve is also fully validated for the case of Bulgaria in the short run.
In the short term, it is shown that the statistical significance of the cubic form implies the validity of the N Kuznets curve pattern (not inverted N Kuznets, contrary to the long term). Regarding the diagnostic tests as observed in
Table 7, we conducted the Breusch Godfrey autocorrelation test and ARCH heteroscedasticity of the estimated model residuals.
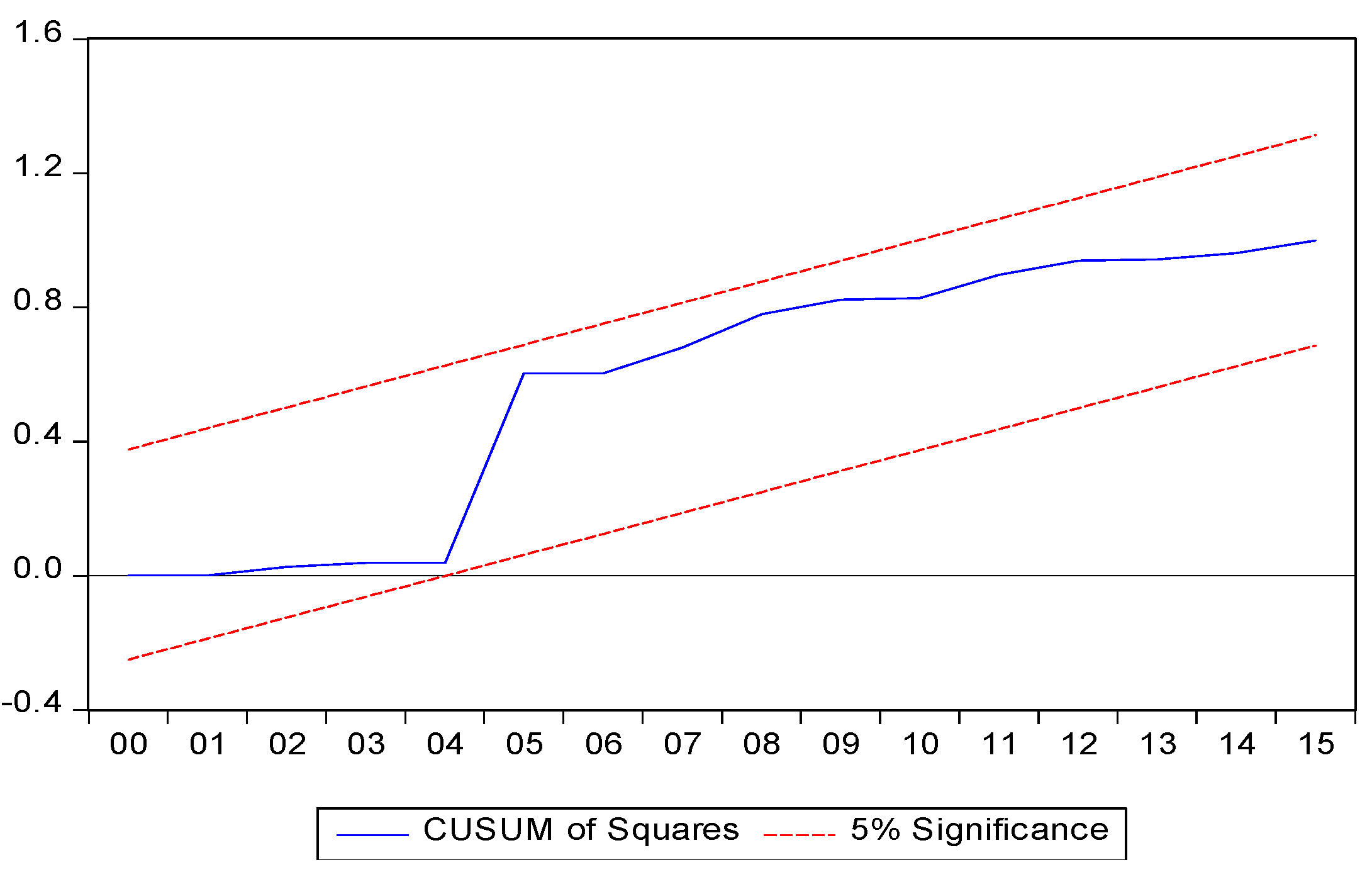
The last step in the analysis involves the study of the parameter’s stability with the Cumulative d CUSUM square (CUSUMsq) tests, the results of which are illustrated in
Figure 3. Specifically, in
Figure 3, the particular plot lies within the critical bounds at a 5% significance level, which indicates that the estimated model is stable in the research period.
Furthermore, the parameter stability CUSUM of squares and the diagnostic tests provided in
Table 7 confirm the robustness of the linear ARDL estimates test.
5. Conclusions
Among EU members, Bulgaria was selected as one of the newly entrant economies, having a high growth rate and specific condition in the deforestation process. This study investigated the validity of EKC in alignment with the ARDL approach of carbon emissions generated due to deforestation (in thousands of tonnes per 1000 ha of deforested ex forest land) as an index of environmental degradation, and the per capita GDP (in thousand of USD dollars) as an index for income. According to these findings, a reverted N Kuznets curve pattern was validated, which was a result implying two different income thresholds for change in the behavior of carbon emissions. This result was validated not only for the long-term period, but also for the N pattern relationship for the short term. Having confirmed the validity of the opposite N-shaped EKC implies that the economic growth initially will improve environmental quality to a certain income level, where the relationship will be positive before it once again becomes negative. This finding is not only interesting, but also challenging to interpret. Possibly, it could be a consequence of the initial environmentally-friendly attitude of the Bulgarian economy and its limitations toward deforestation as well as the efforts aiming to afforestation, compensating for the increased emissions caused by the scale effect. The results were based on carbon emissions generated by deforestation, and these may well efficiently and indirectly describe the forest land situation in Bulgaria, and contribute effectively to the design and implementation of environmental policies that are capable of eliminating the deforestation problem in Bulgaria.
The process of afforestation could provide a solution to the problem of deforestation—namely, a reduction in GHG emissions and an increased absorption of environmental pollutants. In addition, policies and measures design and implementation should promote the efficiency of human activities in order to ensure that the economic losses attributed to the limited exploitation of forest resources are limited.
The state’s efforts for afforestation (a plausible explanation for the findings) were outperformed by the illegal logging, and the low wages of the civil servants in the forest service may also lead to a higher quantity of carbon emissions generated by deforestation. Therefore, initiatives should be taken for the counteraction of these behaviors that can be achieved by seminars, in order for residents to be better informed, and a provision of motivation for them to pursue a limitation in deforestation. This motivation could include, among others, economic incentives for the conversion of forestland to agricultural uses such as taxes or subsidies. Furthermore, clearly defined and enforced property rights to timberlands could also provide an effective solution to the limitation of the problem.
To synopsize the novel institutional measures that should be taken, we aim to limit the degradation of forest resources, which in turn will bring about a decrease in the carbon emissions generated by deforestation. Furthermore, the smooth forest land use with alternative methodologies may well lead to quality environmental improvement and the prosperity of rural and urban surrounding areas.
The specific conditions that dominate in Bulgaria despite the country complying with the agri-environmental measures adopted by the EU may also interpret the opposite N pattern of environmental performance–GDP per capita relationship, necessitating a more insightful study regarding the formation of the variables and the evolution of this relationship. For that reason, the findings of this study contradict the findings of Zambrano-Monserrate et al. [
67] that confirmed the validity of EKC for other five European countries with the same methodology for a longer time horizon. Based on the aforementioned results, the environmental policies mainly for the case of Bulgaria should be directed to the expansion of forest land, since forestry production and agricultural exports may increase jointly, allowing a significant progress for environmental protection inside the continent.
The study also unveiled a remarkable conclusion regarding the shape of the EKC, thus suggesting research intensification in order for the pollution–income relationship to be identified. The relationship may well be studied in alignment with an alternative methodology while considering other possible shapes than those already examined and expected in other EKC core studies. It is important to further investigate the relationship between income and environmental degradation in order to combat climate change and reach sustainable economic development.
Conclusively, regarding suggestions for the future research, the implementation of a different nonlinear ARDL methodology on available data could provide more concise and accurate results, as well as the implementation of panel data analysis to support researchers with more general results regarding the agro-environmental EU policy for more countries.