Uncertainty Assessment in Drought Severities for the Cheongmicheon Watershed Using Multiple GCMs and the Reliability Ensemble Averaging Method
Abstract
1. Introduction
2. Methodology
2.1. Study Area and SWAT Formulation
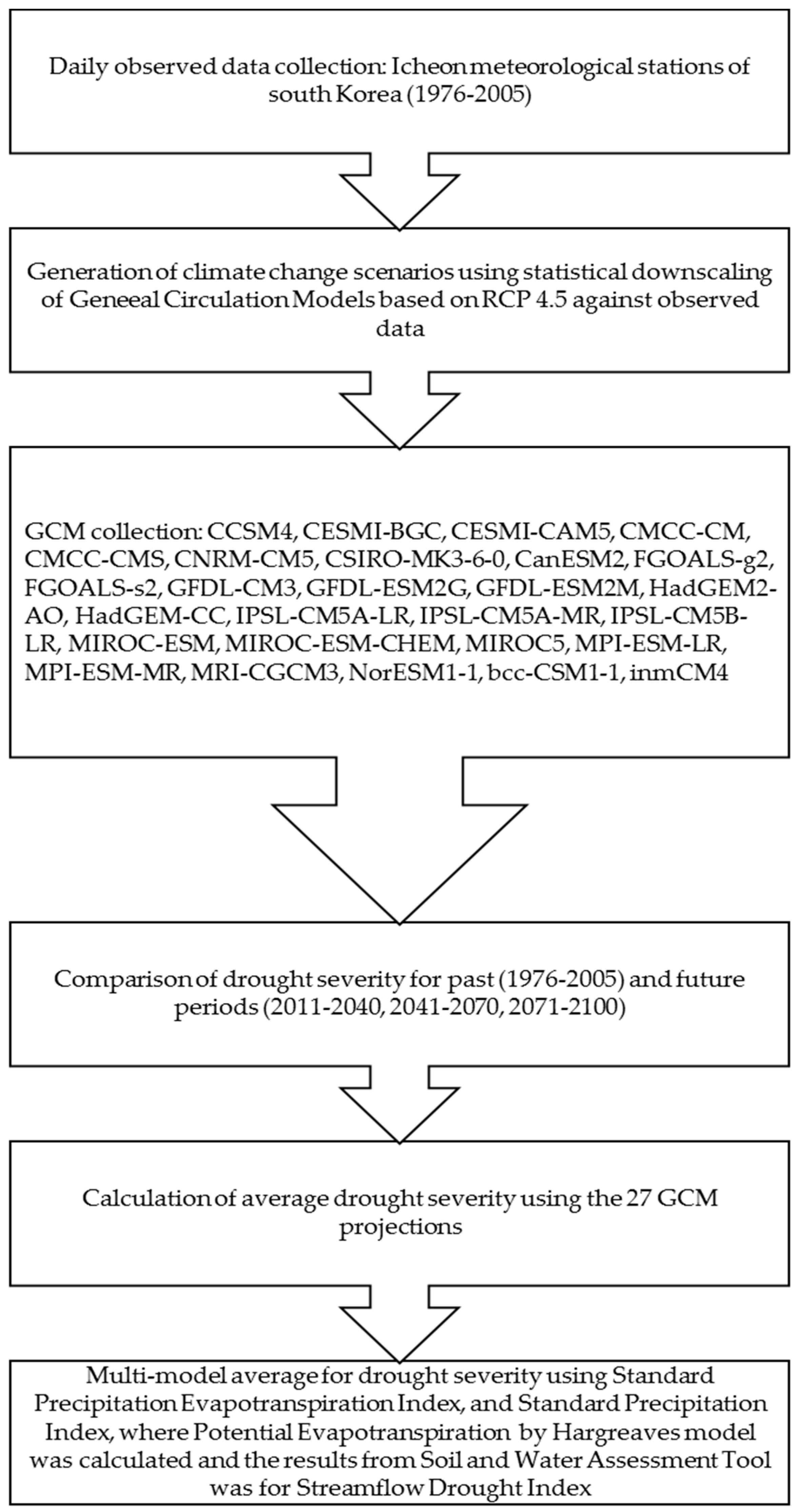
2.2. Procedures
2.3. Downscaling of GCM Simulations
2.4. Simulated Data Analysis
2.5. Performance-Based Method for Reliability Ensemble Averaging (REA)
2.6. SPI, SDI and SPEI Drought Indices
3. Results
3.1. Evaluation of Model Performances
3.2. REA Model Weights Based on Model Performance RMSE
3.3. REA Model Weights of Drought Projection
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hattermann, F.F.; Weiland, M.; Huang, S.; Krysanova, V.; Kundzewicz, Z.W. Model-supported impact assessment for the water sector in central Germany under climate change—A case study. Water Resour. Manag. 2011, 25, 3113. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Harun, S.B.; Chung, E.S.; Wang, X. Climate change uncertainties in seasonal drought severity-area-frequency curves: Case of arid region of Pakistan. J. Hydrol. 2019, 570, 473–485. [Google Scholar] [CrossRef]
- Ning, L.; Riddle, E.E.; Bradley, R.S. Projected changes in climate extremes over the Northeastern United States. J. Clim. 2015, 28, 3289–3310. [Google Scholar] [CrossRef]
- Noor, M.; Ismail, T.; Shahid, S.; Chung, E.S.; Sung, J.H. Uncertainty in rainfall intensity duration frequency curves of peninsular Malaysia under changing climate scenarios. Water 2018, 10, 1750. [Google Scholar] [CrossRef]
- Thomas, G.H. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar]
- Chung, E.S.; Park, K.; Lee, K.S. The relative impacts of climate change and urbanization on the hydrological response of a Korean urban watershed. Hydrol. Process. 2011, 25, 544–560. [Google Scholar] [CrossRef]
- Ning, L.; Mann, M.E.; Crane, R.; Wagener, T.; Najjar, R.G.; Singh, R. Probabilistic projections of anthropogenic climate change impacts on precipitation for the Mid-Atlantic region of the United States. J. Clim. 2012, 25, 5273–5291. [Google Scholar] [CrossRef]
- Thompson, I.R.; Green, A.I.; Kingston, D.G.; Gosling, S.N. Assessment of uncertainty in river flow projections for the Mekong River using multiple GCMs and hydrological models. J. Hydrol. 2007, 486, 1–30. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J.; Chen, Y.; Li, Z.; De Maeyer, P. Impact of GCM structure uncertainty on hydrological processes in an arid area of China. Hydrol. Res. 2017, 49, 893–907. [Google Scholar] [CrossRef]
- Graham, L.P.; Hagemann, S.; Jaun, S.; Beniston, M. On interpreting hydrological change from regional climate models. Clim. Chang. 2007, 81, 97–122. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of average, uncertainty range, and reliability of regional climate changes from AOGCM simulations via the “Reliability Ensemble Averaging” (REA) method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Coppola, E.; Giorgi, F.; Rauscher, S.; Piani, C. Model weighting based on mesoscale structures in precipitation and temperature in an ensemble of regional climate models. Clim. Res. 2010, 44, 121–134. [Google Scholar] [CrossRef]
- Suh, M.-S.; Oh, S.-G.; Lee, D.-K.; Cha, D.-H.; Choi, S.-J.; Jin, C.-S.; Hong, S.-Y. Development of new ensemble methods based on the performance skills of regional climate models over South Korea. J. Clim. 2012, 25, 7067–7082. [Google Scholar] [CrossRef]
- Casanova, S.; Ahrens, B. On the weighting of multimodel ensembles in seasonal and short-range weather forecasting. Mon. Weather Rev. 2009, 137, 3811–3822. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kwon, H.-H.; Jang, H.-W.; Kim, T.-W. Future Changes in Drought Characteristics under Extreme Climate Change over South Korea. Adv. Meteorol. 2016, 2016, 1–19. [Google Scholar] [CrossRef]
- Minville, M.; Brissette, F.; Leconte, R. Uncertainty of the impact of climate change on the hydrology of a nordic watershed. J. Hydrol. 2008, 358, 70–83. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Wilhite, D.A. Chapter 1 Drought as a natural hazard: Concepts and definitions. In Drought: A global Assessment; Wilhite, D.A., Ed.; Routledge: London, UK, 2000; Volume I. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; López-Moreno, J.I.; Azorin-Molina, C.; Revuelto, J.; Morán-Tejeda, E.; Sanchez-Lorenzo, A. Performance of drought Indices for ecological, agricultural, and hydrological applications. Earth Interact. 2012, 16, 1–27. [Google Scholar] [CrossRef]
- Liu, S.; Kang, W.; Wang, T. Drought variability in Inner Mongolia of northern China during 1960–2013 based in standardized precipitation evapotranspiration index. Environ. Earth Sci. 2016, 75, 145. [Google Scholar] [CrossRef]
- Kim, D.; Hong, S.J.; Han, D.; Choi, C.; Kim, H.S. Analysis of future meteorological drought index considering climate change in Han-River basin. J. Wetl. Res. 2016, 18, 432–447. [Google Scholar] [CrossRef]
- Park, M.; Lee, O.; Park, Y.; Kim, S. Future drought projection in Korea under AR5 RCP climate change scenarios. J. Korean Soc. Hazard Mitig. 2015, 15, 423–433. [Google Scholar] [CrossRef]
- Kim, S.H.; Chung, E.S. Peak drought index analysis of Cheongmicheon watershed using meteorological and hydrological drought index. J. Korea Water Resour. Assoc. 2017, 50, 65–73. [Google Scholar]
- Won, K.J.; Chung, E.-S. Drought analysis of Cheongmicheon watershed using meteorological, agricultural and hydrological drought indices. J. Korea Water Resour. Assoc. 2016, 49, 509–518. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geograph. Rev. 1948, 55–94. [Google Scholar] [CrossRef]
- McKee, T.B.; Doeskin, N.J.; Kleist, J. Drought monitoring with multiple time scales. In Proceedings of the 9th Conference on Applied Climatology, Dallas TX, USA, 15–20 January 1995; pp. 233–236. [Google Scholar]
- Tigkas, M.; Vangelis, H.; Tsakiris, G. DrinC: a software for drought analysis based on indices. Earth Sci Inform. 2015, 8, 697–709. [Google Scholar] [CrossRef]
- Gudmundsson, L. Statistical Transformations for Postprocessing Climate Model Output. R Package Version 1.0-4. Available online: http://www.rcran.r-project.org/web/packages/qmap/ (accessed on 3 May 2016).
- Maraun, D. Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Maurer, E.P.; Pierce, D.W. Bias correction can modify climate model simulated precipitation changes without adverse effect on the ensemble mean. Hydrol. Earth Syst. Sci. 2014, 18, 915–925. [Google Scholar] [CrossRef]
- Alam, S.; Ali, M.M.; Islam, Z. Future streamflow of Brahmaputra River basin under synthetic climate change scenarios. J. Hydrol. Eng. 2016, 1943–5584. [Google Scholar] [CrossRef]
- Muhammad, E.T.; Moon-Hwan, L.; Deg-Hyo, B. Uncertainty and reliability analysis of CMIP5 climate projections in South Korea using REA method. In Proceedings of the 12th International Conference on Hydro informatics, HIC Procedia Engineering, Incheon, Korea, 21–26 August 2016; Kim, J.H., Kim, H.S., Yoo, D.G., Eds.; pp. 650–655. [Google Scholar]
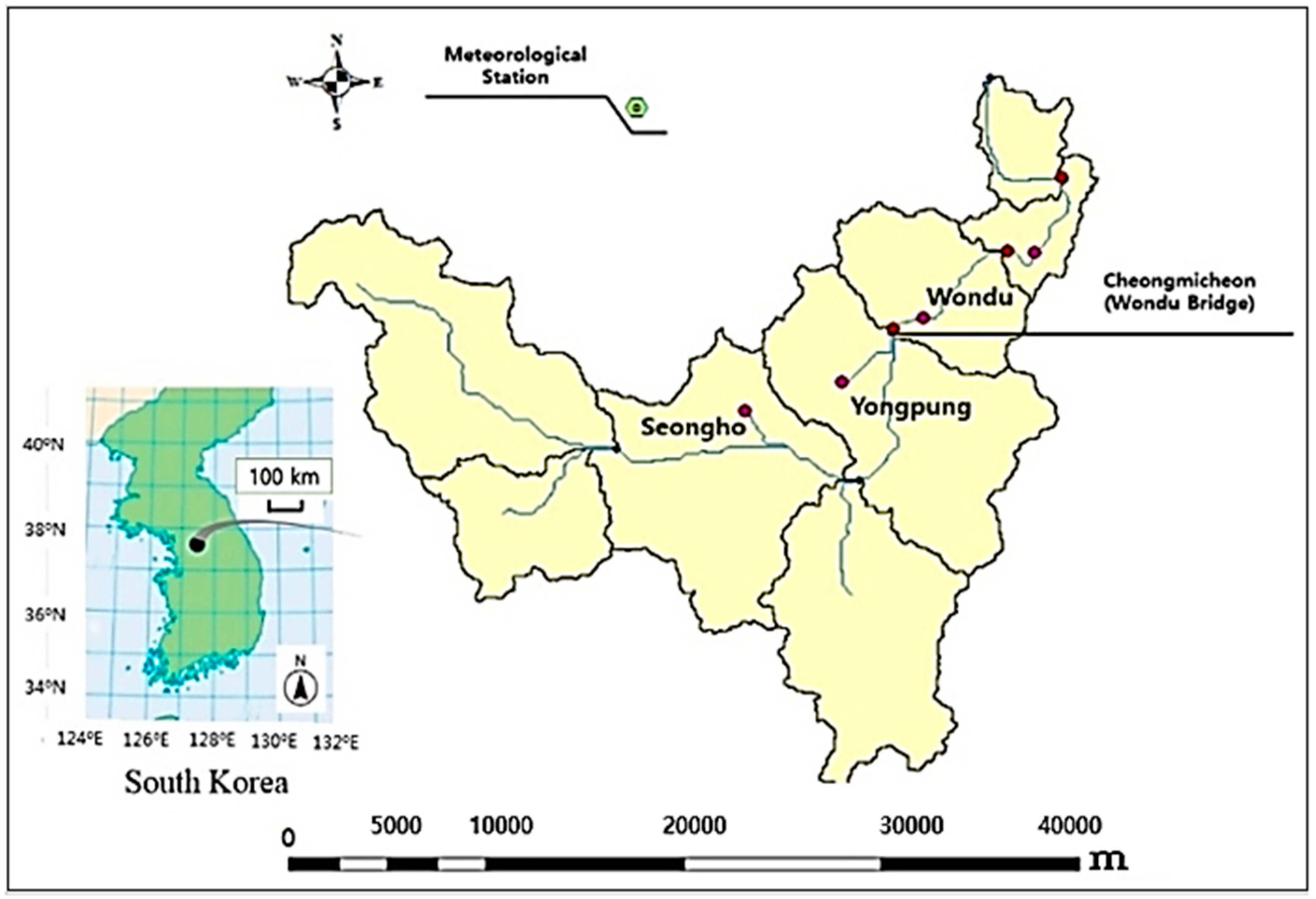
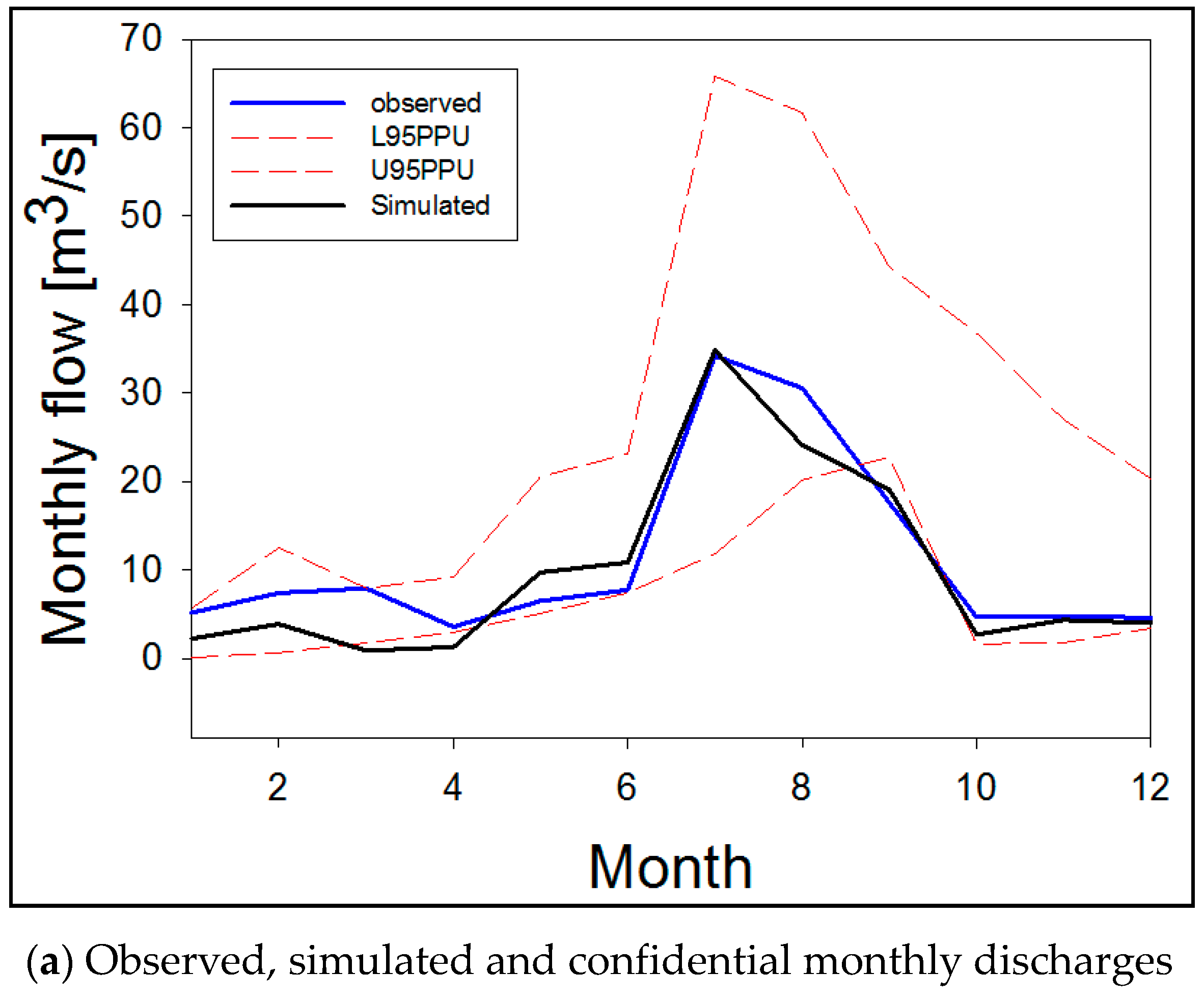
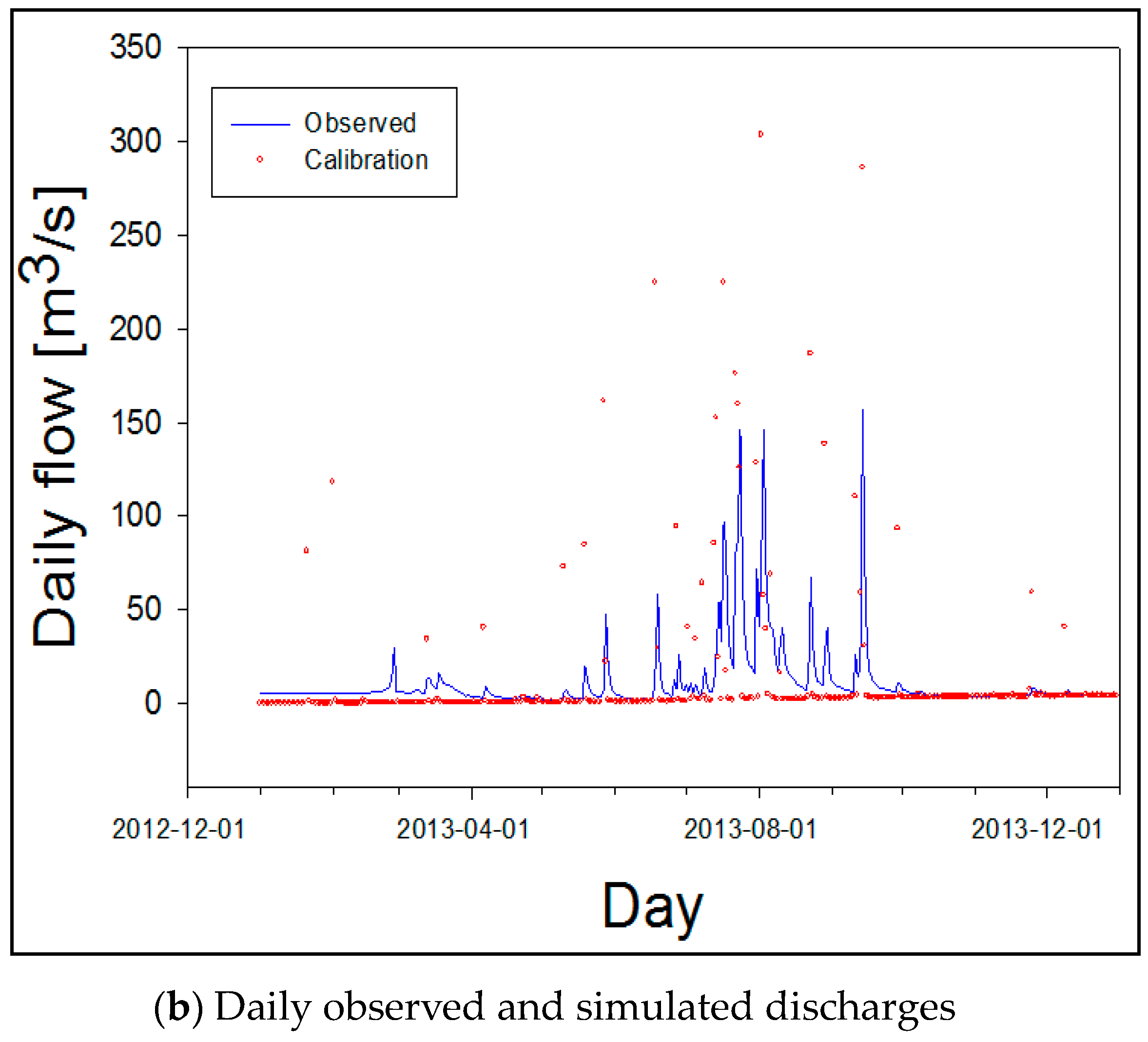
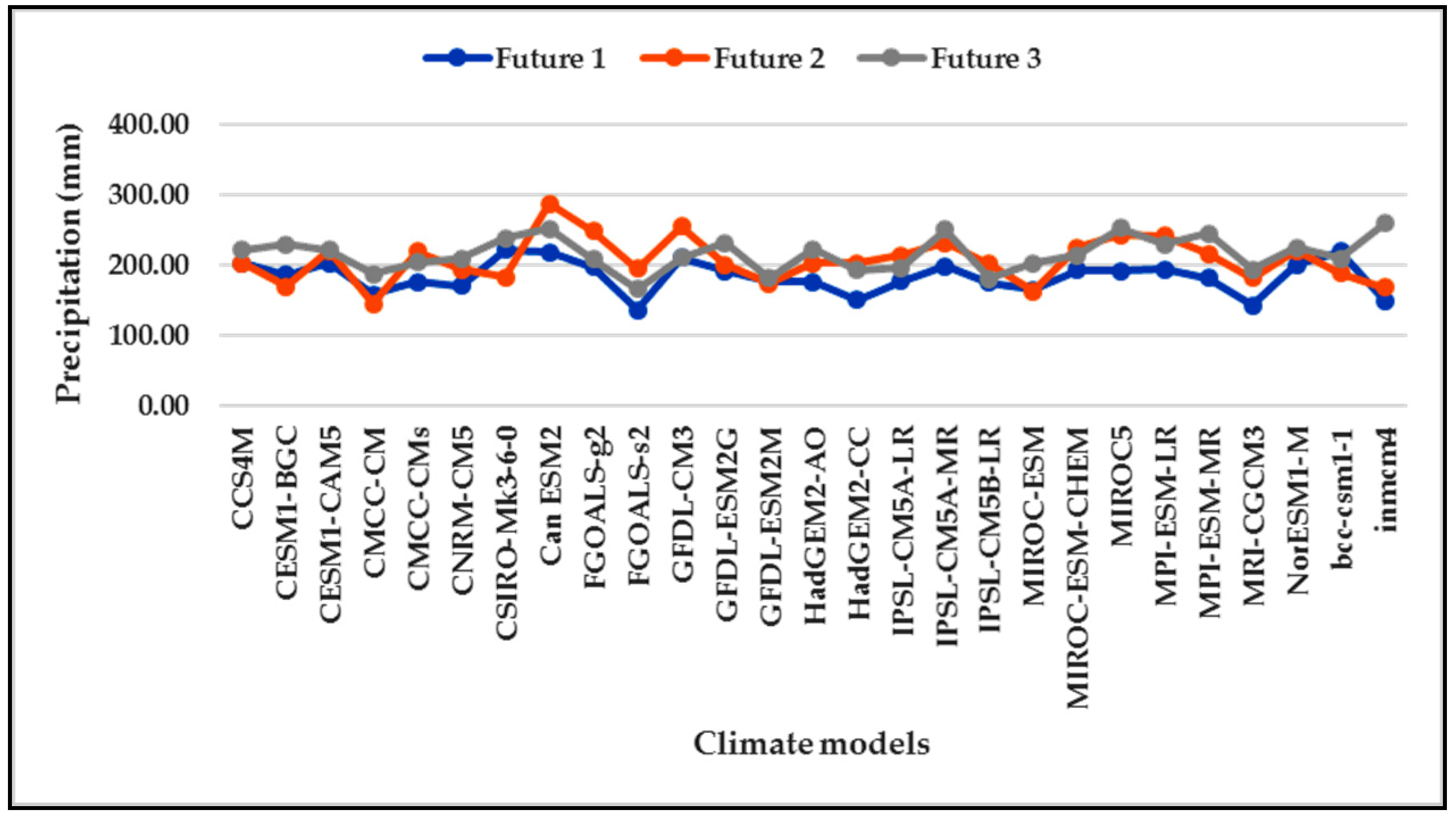
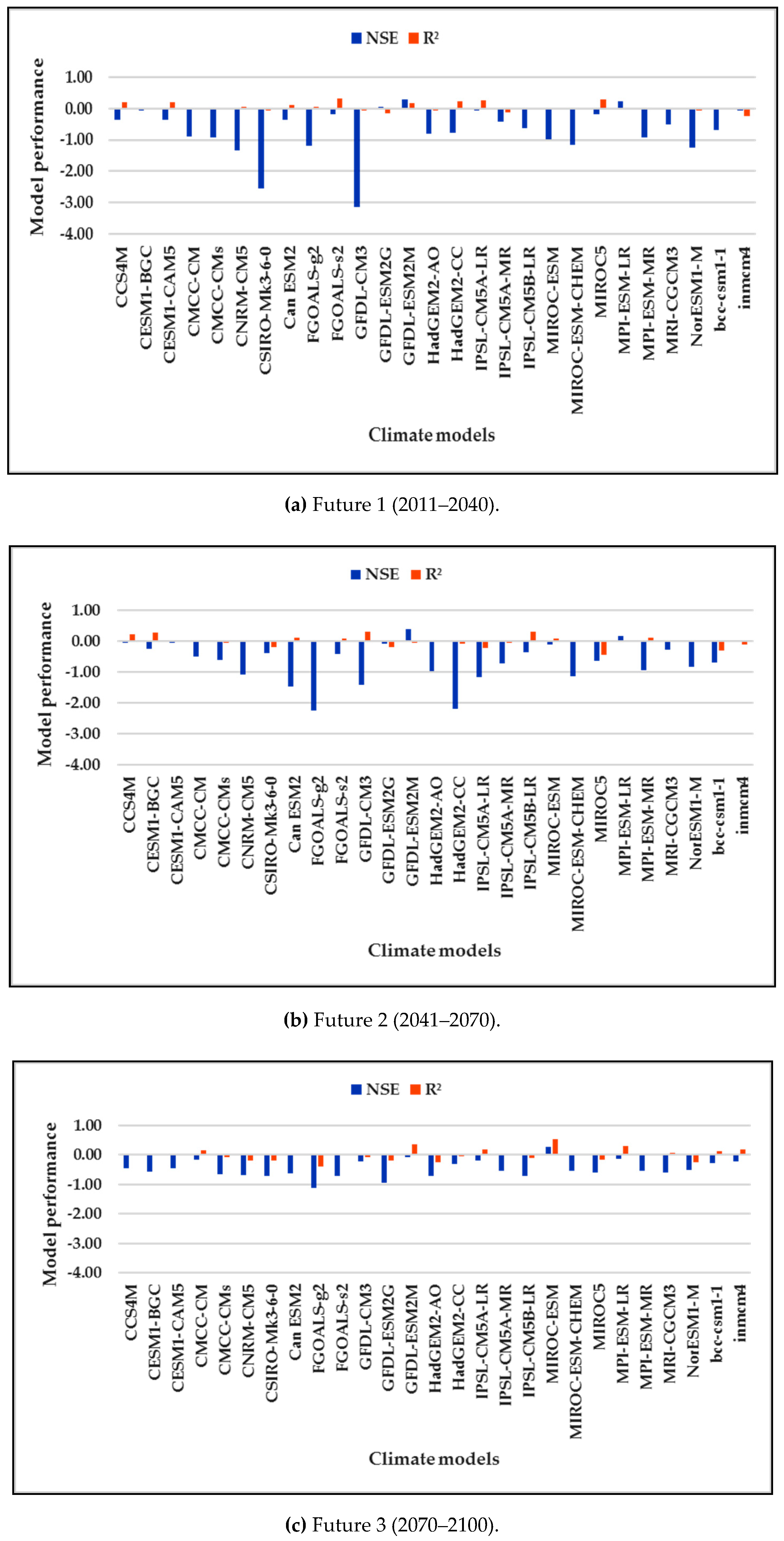
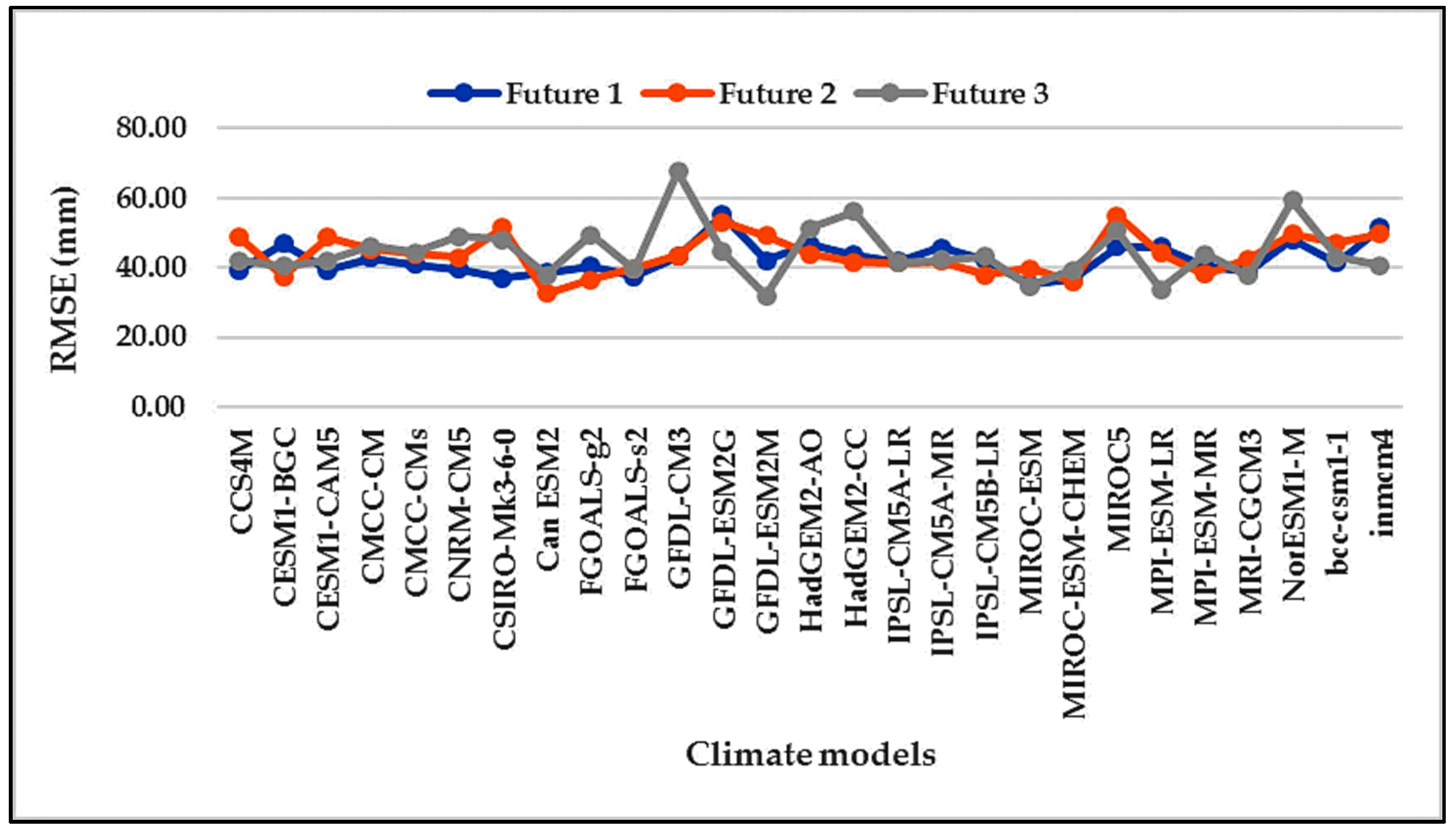
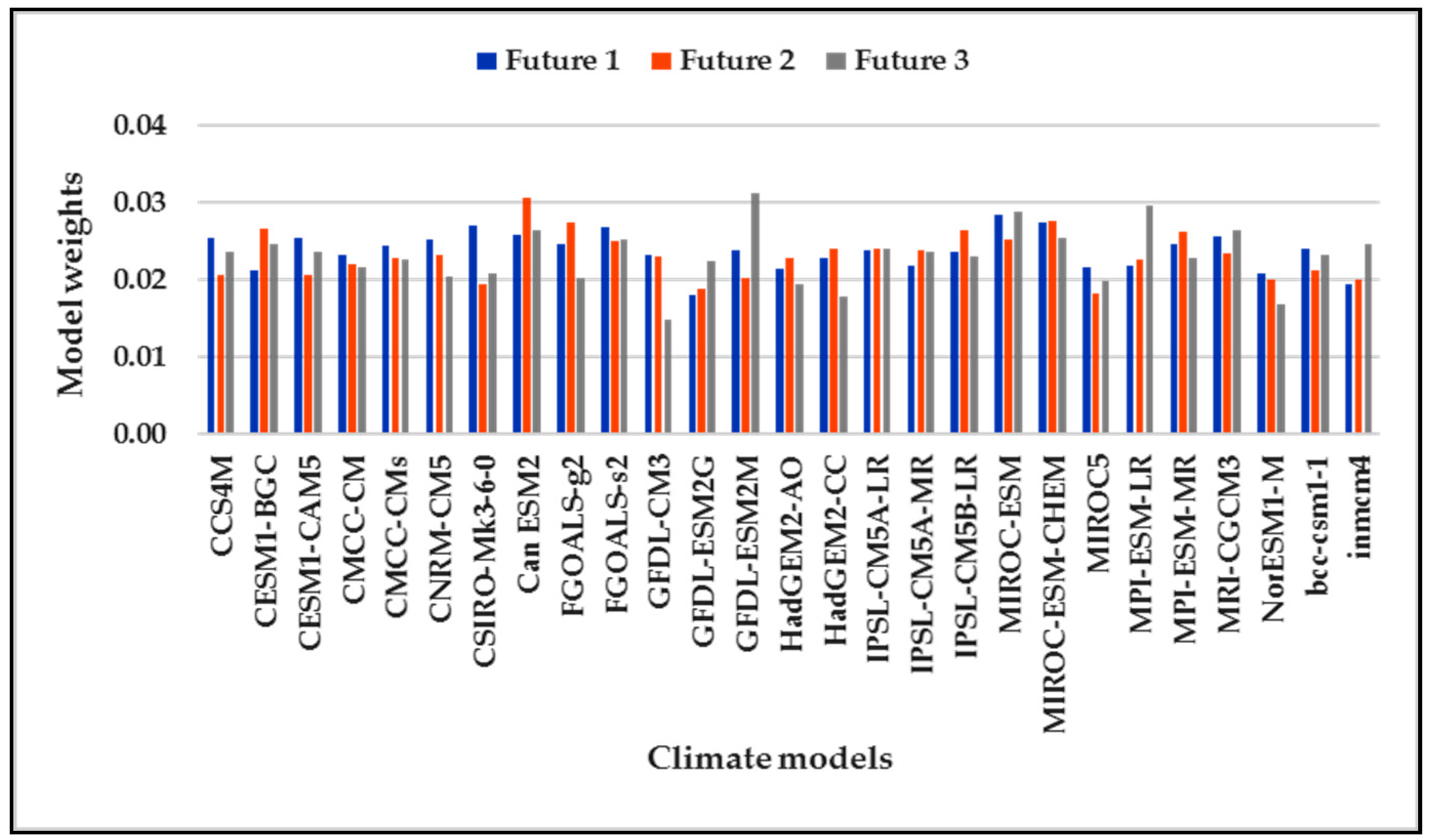
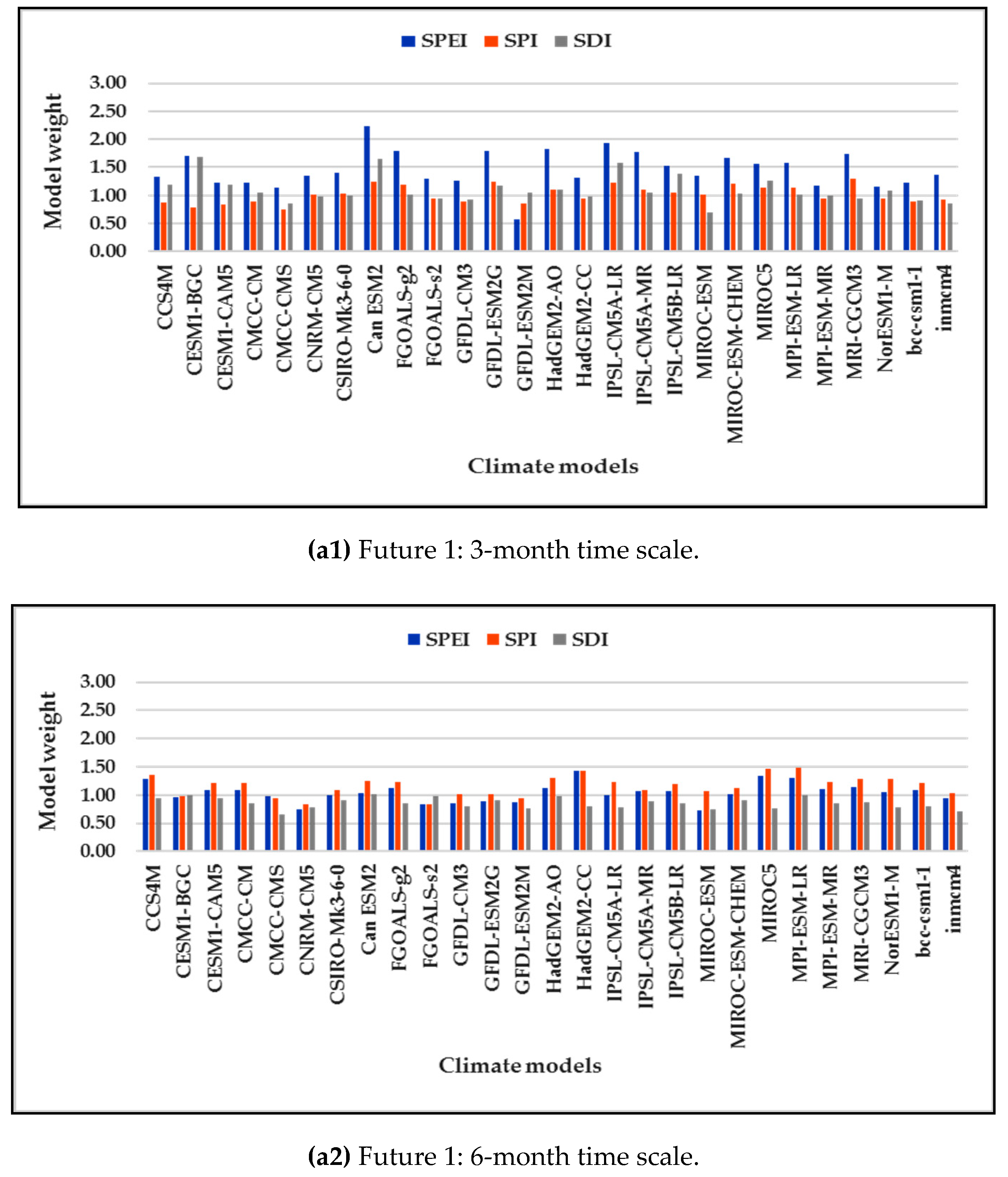
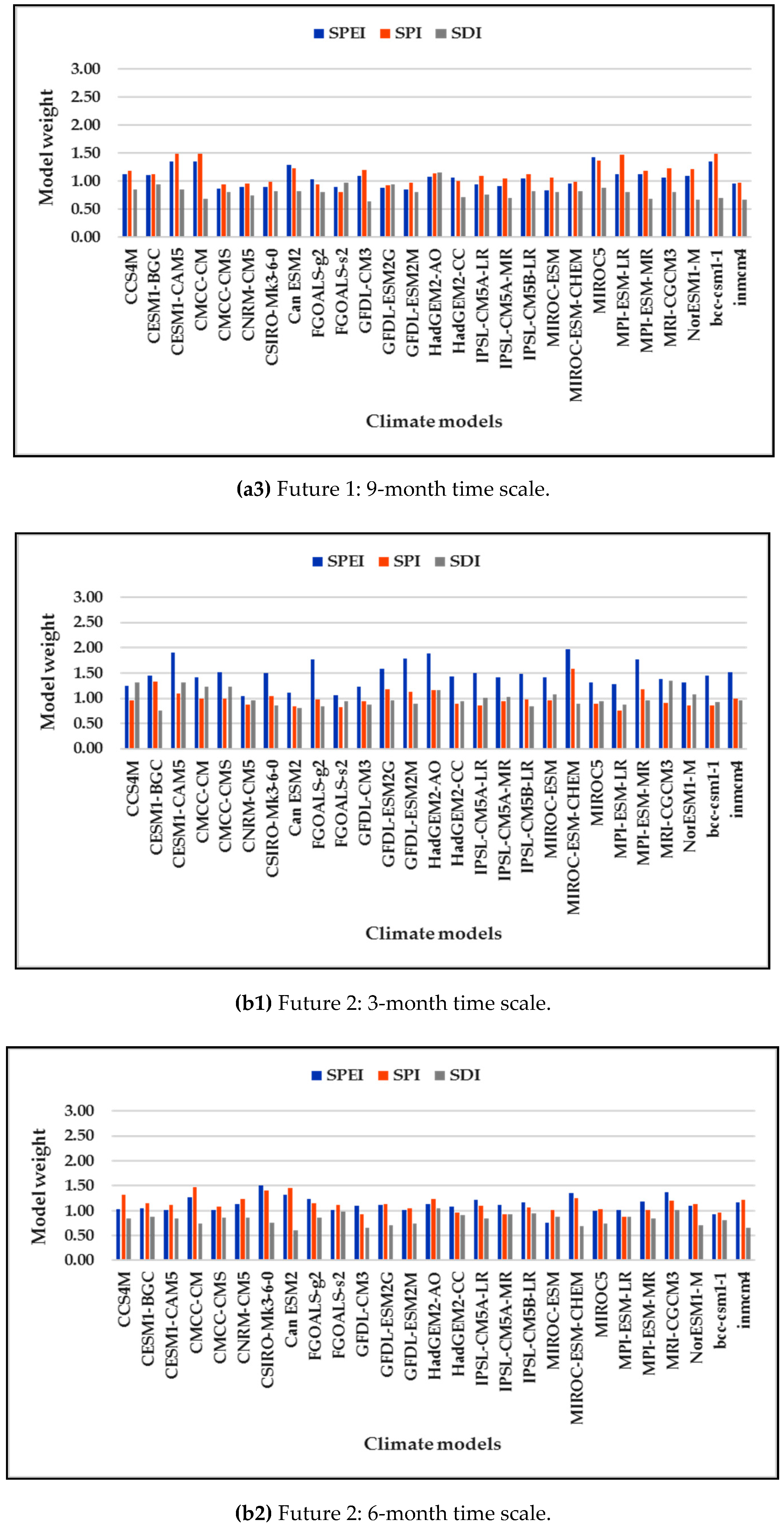
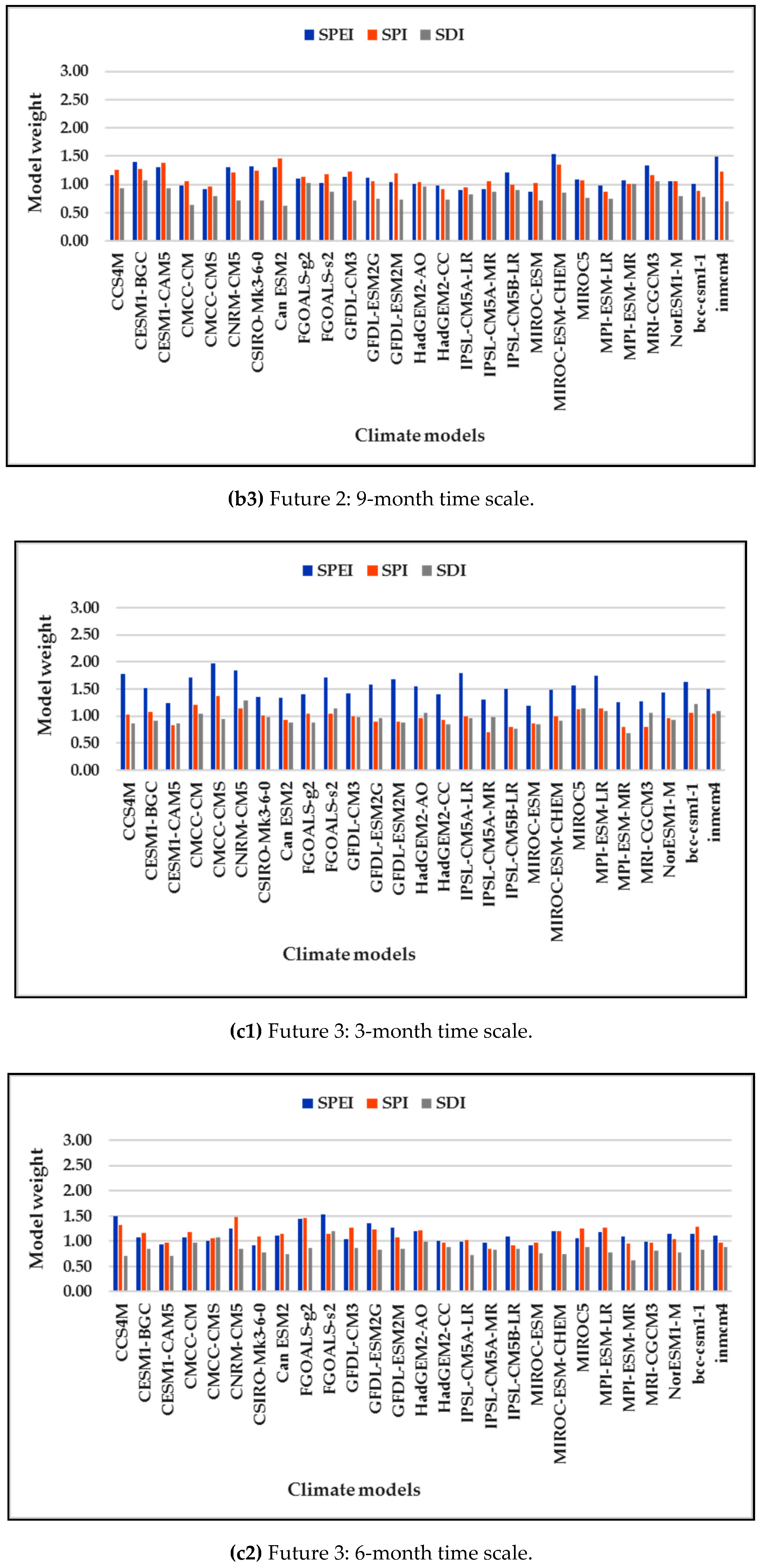
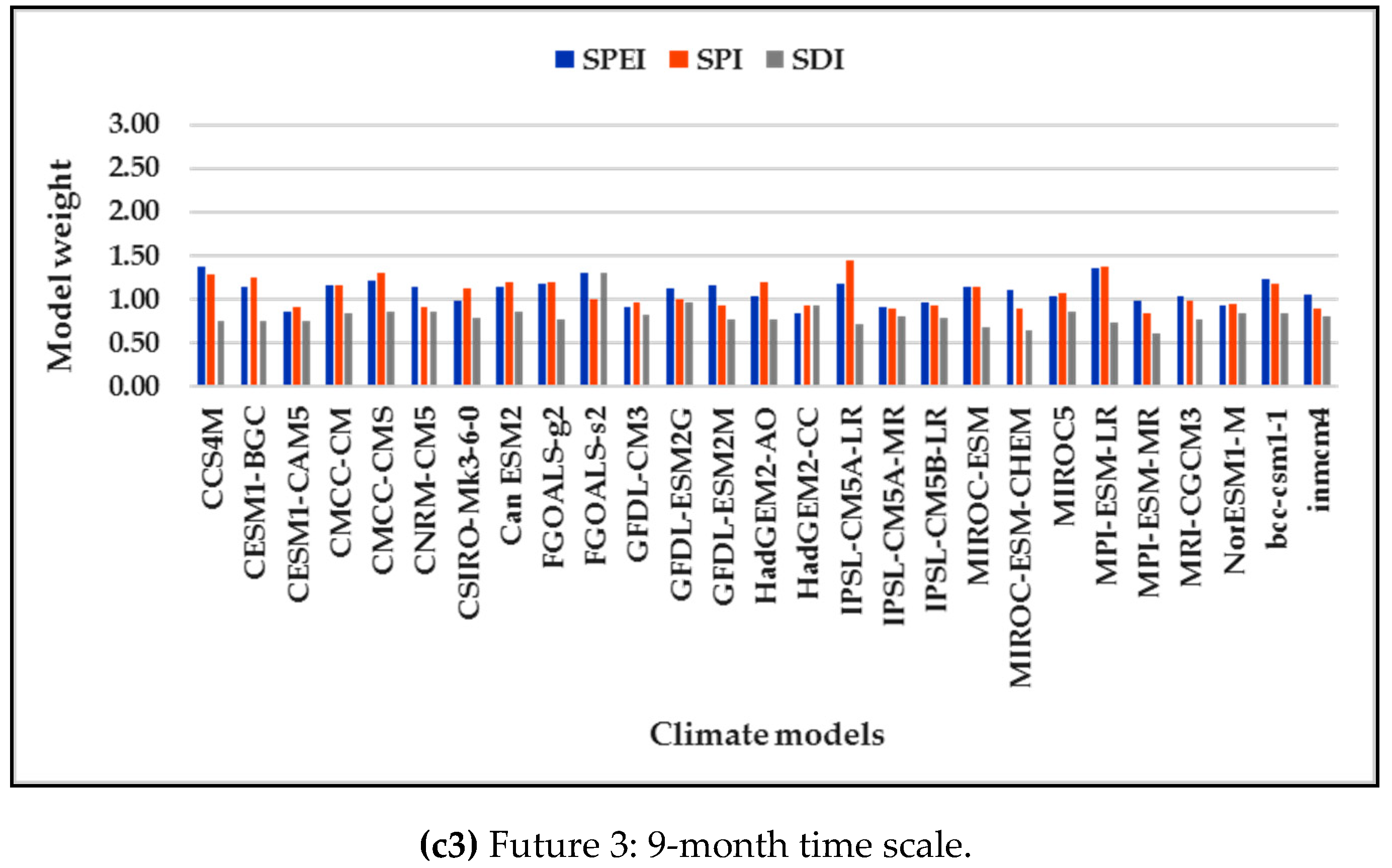
| No. | Input Parameter used SWAT-CUP Calibration Process | Fitted Value | Description |
|---|---|---|---|
| 1 | R__CN2.mgt | 56.741997 | Soil Conservation Service runoff curve number for moisture condition II |
| 2 | V__ALPHA_BF.gw | 0.153 | Base flow alpha factor (days) |
| 3 | V__GW_DELAY.gw | 292.5 | Groundwater delay time (days) |
| 4 | V__GWQMN.gw | 565 | Threshold depth of water in the shallow aquifer required for return flow to occur (mm) |
| 5 | V__GW_REVAP.gw | 0.18938 | Groundwater “revap” or percolation coefficient describing how readily water from the shallow aquifer can move into the capillary fringe where it is available for evaporation (unitless) |
| 6 | V__ESCO.hru | 0.731 | Soil evaporation compensation factor |
| 7 | V__CH_N2.rte | −0.00039 | Manning’s n value for main channel |
| 8 | R__SOL_K(..).sol | 790 | Saturated hydraulic conductivity(mm/hour) |
| 9 | R__SOL_AWC(..).sol | 0.747 | Soil available water storage capacity (mm H2O/mm soil) |
| 10 | V__CH_K2.rte | 89.491791 | Effective hydraulic conductivity in the main channel (mm hr-1) |
| 11 | R__SOL_AWC(..).sol | 0.975 | Available water capacity of the soil layer (mm H2O /mm soil) |
| 12 | V__REVAPMN.gw | 490.5 | Threshold depth of water in the shallow aquifer for “revap” or percolation to the deep aquifer to occur (mm) |
| 13 | V__RCHRG_DP.gw | 0.531 | Deep aquifer percolation fraction |
| 14 | V__OV_N.hru | 5.43819 | Manning’s “n” value for overland flow |
| 15 | V__SLSUBBSN.hru | 32.259998 | Average slope length (m) |
| 16 | V__SMFMX.bsn | 1.06 | Melt factor for snow |
| 17 | V__SMTMP.bsn | 11.559999 | Snow melt base temperature °C |
| 18 | V__ALPHA_BNK.rte | 0.005 | Base-flow alpha factor for bank storage |
| 19 | V__SFTMP.bsn | −11.400001 | Plants uptake compensation factor |
| No. | GCM | Modelling Centre (Or Group) |
|---|---|---|
| 1 | CCSM4 | National Center for Atmospheric Research |
| 2 | CESMI-BGC | Community Earth System Model Contributors |
| 3 | CESMI-CAM5 | National Science Foundation, Department of Energy, National Center for Atmospheric Research, USA |
| 4 | CMCC-CM | Centro Euro-Mediterraneo per I Cambiamenti Climatici |
| 5 | CMCC-CMS | Centro Euro-Mediterraneo per I Cambiamenti Climatici |
| 6 | CNRM-CM5 | Centre National de Recherches Météorologiques/Centre Européen de Recherche et Formation Avancée en Calcul Scientifique et Formation Avancée en Calcul Scientifique |
| 7 | CSIRO-MK3 | Commonwealth Scientific and Industrial Research Organization, Queensland Climate |
| 8 | CanESM2 | Canadian Centre for Climate Modelling and Analysis |
| 9 | FGOALS-g2 | LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences (China) |
| 10 | FGOALS-s2 | LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences (China) |
| 11 | GFDL-CM3 | NOAA Geophysical Fluid Dynamics Laboratory |
| 12 | GDFL-ESM2G | NOAA Geophysical Fluid Dynamics Laboratory |
| 13 | GDFL-ESM2M | NOAA Geophysical Fluid Dynamics Laboratory |
| 14 | HadGEM2-AO | National Institute of Meteorological Research/Korea Meteorological Administration |
| 15 | HadGEM2-CC | Met Office Hadley Centre |
| 16 | IPSL-CM5A-LR | Institut Pierre-Simon Laplace |
| 17 | IPSL-CM5A-MR | Institut Pierre-Simon Laplace |
| 18 | IPSL-CM5B-LR | Institut Pierre-Simon Laplace |
| 19 | MIROC-ESM | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies |
| 20 | MIROC-ESM-CHEM | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies |
| 21 | MIROC5 | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies |
| 22 | MPI-ESM-LR | Max-Planck-Institut für Meteorologie (Max Planck Institute for Meteorology) |
| 23 | MPI-ESM-MR | Max-Planck-Institut für Meteorologie (Max Planck Institute for Meteorology) |
| 24 | MRI-CGCM3 | Meteorological Research Institute |
| 25 | NorESM1-M | Norwegian Climate Centre |
| 26 | bcc-CSM1-1 | Beijing Climate Center, China Meteorological Administration |
| 27 | inmCM4 | Institute for Numerical Mathematics |
| Future 1 (2011–2040) | Future 2 (2041–2070) | Future 3 (2071–2100) | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (mm) | NSE | R2 | RMSE (mm) | NSE | R2 | RMSE (mm) | NSE | R2 |
| 42.50 | −0.71 | 0.04 | 43.78 | −0.67 | 0.00 | 44.45 | −0.48 | 0.01 |
| Indices | Future 1 (2011–2040) | Future 2 (2041–2070) | Future 3 (2071–2100) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3-month | 6-month | 9-month | 3-month | 6-month | 9-month | 3-month | 6-month | 9-month | |
| SPEI | 0.73 | 0.99 | 0.96 | 0.70 | 0.90 | 0.91 | 0.67 | 0.90 | 0.93 |
| SPI | 1.00 | 0.88 | 0.90 | 1.03 | 0.90 | 0.91 | 1.04 | 0.90 | 0.96 |
| SDI | −0.95 | −1.18 | −1.26 | −1.02 | −1.24 | −1.24 | −1.05 | −1.21 | −1.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulai, P.J.; Chung, E.-S. Uncertainty Assessment in Drought Severities for the Cheongmicheon Watershed Using Multiple GCMs and the Reliability Ensemble Averaging Method. Sustainability 2019, 11, 4283. https://doi.org/10.3390/su11164283
Abdulai PJ, Chung E-S. Uncertainty Assessment in Drought Severities for the Cheongmicheon Watershed Using Multiple GCMs and the Reliability Ensemble Averaging Method. Sustainability. 2019; 11(16):4283. https://doi.org/10.3390/su11164283
Chicago/Turabian StyleAbdulai, Patricia Jitta, and Eun-Sung Chung. 2019. "Uncertainty Assessment in Drought Severities for the Cheongmicheon Watershed Using Multiple GCMs and the Reliability Ensemble Averaging Method" Sustainability 11, no. 16: 4283. https://doi.org/10.3390/su11164283
APA StyleAbdulai, P. J., & Chung, E.-S. (2019). Uncertainty Assessment in Drought Severities for the Cheongmicheon Watershed Using Multiple GCMs and the Reliability Ensemble Averaging Method. Sustainability, 11(16), 4283. https://doi.org/10.3390/su11164283






