1. Introduction
High-speed railway (HSR) has many advantages, such as large transportation capacity, fast speed, less land occupation, low energy consumption, low pollution, etc. As a green mode of transportation, HSR has been developing rapidly in many countries, and this is particularly the case in China. In 2018, China’s HSR operating mileage exceeded 29,000 km, ranking first in the world. Despite the rapid development of HSR in China, the China Railway Corporation (CRC) still faces a significant debt problem, due to the large investment in HSR construction. If the HSR operation continues to lose money, it will have a huge impact on the sustainable development of HSR construction, slowing down the development between cities and between urban and rural areas. Therefore, the revenue management of HSR is crucial for the sustainable development and operation of HSR [
1]. Developed countries, such as France, Japan and Germany, have introduced the concept of revenue management in their HSR operations to gain more revenue in order to realize long-term development [
2]. However, China’s HSR is relatively deficient in this aspect, which causes some problems in the seating rate as it fluctuates with time for some rail lines leading to either insufficient or wasted seat capacity [
3]. The maximum revenue of CRC has not been realized.
Pricing and seat allocation are the two core issues of revenue management. At present, the pricing of China’s HSR is generally guided by the government, who uses the fixed price, and the fixed price cannot guide or regulate passenger flow. In terms of seat allocation, basically, the method of fixed seat allocation is adopted, namely, determining the number of seats for each origin–destination (OD) pair for each train throughout the sales period [
4]. The fixed seat allocation method cannot be adjusted in time according to time-varying demand, and, thus, the transportation capacity cannot be rationally utilized. Existing pricing and seat allocation methods can hardly adapt to the dynamic market, which is not conducive to maximize revenue and realize the development of HSR. Therefore, formulating a scientific and reasonable HSR pricing mechanism and a flexible seat allocation system based on revenue management has become a key issue to improve the utilization rate of transportation resources, which needs to be solved urgently for the future development of China’s HSRs.
Revenue management means “selling the right product at the right time and selling it to the right person at the right price” in order to maximize revenue [
5]. Dynamic pricing refers to setting different prices for the same product over time according to consumers’ different willingness to pay in different time periods. Due to consumers’ heterogeneous valuations, dynamic pricing over time can occur as a strategy to cater to consumers’ willingness to pay in different time periods to obtain more benefits [
6]. As an important strategy in revenue management, dynamic pricing can play a critical role in guiding and regulating demand. It has been studied in many areas, especially in the aviation field. In these studies, one type of research is based on the assumption that the market is monopolistic [
7,
8]. In the process of these studies, monopoly companies used different price policies to induce and guide demand to achieve the maximum total expected revenue. Later, many studies were devoted to obtaining bid price control strategies [
9,
10]. These studies used Markov Decision Process (MDP) model to describe the dynamic airline revenue management problem and obtained bid-price control strategies.
Currently, most of the pricing studies on HSR are mainly borrowed from the aviation field, but there are many differences between the two fields. For example, airlines are a point-to-point mode of passenger transport, and the ticket prices between different OD pairs are mostly independent, which can be determined separately [
11]. However, each train has multiple stops, which can generate demand between many different OD pairs, and this leads to the correlation of ticket prices among different OD pairs. Besides, we need to determine a price for each OD, so the scale of the decision variable for HSR is too large. Therefore, if the MDP model is applied to HSR, the solution to the problem becomes very complicated, and so the Markov method is unsuitable for HSR pricing. Due to the difficulty and complexity of the pricing of HSR, the optimal pricing problem of HSR has not been fully studied and implemented compared with the airline industry [
12]. Alexander [
13] summarized the railway passenger revenue management model before 2010. Crevier et al. [
14] put forward a bi-level programming model that can optimize service pricing and railway vehicle routes at the same time. Lin [
15] studied the pricing problem based on uncertain demand. However, most of the existing railway pricing problems are still based on a single OD pair or single train, which leads to the poor practical application of existing research.
Customer choice behavior plays an important role in estimating customer demand. Understanding passengers’ choice behavior can help authorities improve their service levels. New ideas for the sustainable development of HSR are also being investigated. A great deal of the literature studied the factors influencing customer choice behavior, and they divided the factors into two aspects: Personal attributes and trip attributes [
16,
17,
18,
19,
20,
21,
22,
23,
24,
25]. At present, more and more scholars are considering the impact of passengers’ travel choice behavior [
26,
27,
28]. These studies simulated the travel behavior of passengers by constructing corresponding functions to predict demand and provided a good basis for future optimal pricing research.
Another core issue of revenue management is seat allocation. You [
29] studied the seat control problem of two-class pricing on a multi-segment passenger train. Jiang et al. [
30] proposed a dynamic adjustment method for seat allocation. However, these studies attempted to solve the deterministic seat allocation problem of railways on the basis of fixed ticket, while the uncertainty of passenger demand has not been resolved. In practice, passenger demand is changing dynamically, so research based on stochastic passenger demand is more in line with the actual situation. Wang et al. [
4] considered passengers’ discrete random demand and proposed a stochastic seat allocation model to optimize the train capacity utilization based on the random selection behavior of passengers. However, the research was on the basis of fixed ticket prices. Existing studies on the seat allocation of HSR usually ignore the adjustment of price to demand, which leads to the separation of seat allocation and ticket pricing.
In the past few decades, pricing and seat allocation issues have often been treated separately, and there is a gap in the literature regarding joint pricing and seat allocation models [
31,
32]. However, the two issues are interrelated and complementary, and it is necessary to optimize them jointly. Weatherford [
33] first stressed the importance of considering prices and suggested them as decision variables for seat allocation problems. Cote et al. [
34] proposed a joint model for solving pricing and seat allocation problems in networks with competitors. They assumed that demand was deterministic and focused on fare optimization. The research mentioned above only considered one time period and did not consider the changes in demand caused by price changes.
On the railway side, there are even fewer studies on the joint optimization of the ticket price and seat allocation. The joint optimization method for pricing and seat allocation developed in our work is similar to that adopted by Hetrakul and Cirillo [
31]. Hetrakul and Cirillo [
31] proposed a latent class choice-based model system to jointly optimize price and seat allocation considering multiple time periods. Compared with Hetrakul and Cirillo [
31], our research mainly has the following differences: (1) They did not consider the situation of multiple train stop plans, but the situation in real life is much more complicated; and (2) they treated the traffic demand of each day as a deterministic value. In practice, passenger demands are complex and changeable. Hence, it is more practical to consider the elastic demand of passengers. Therefore, our research takes into account the complex situation of multiple trains and multiple stops and considers the elastic demand of passengers varying with price, which is more in line with the actual situation.
In summary, due to the complexity of the solution, the current studies of optimal pricing for HSR usually only consider the case of single train multi-OD pairs or multiple trains and single OD pair, which is quite different from the actual situation. At present, due to the complex interaction between ticket pricing and seat allocation, they are generally studied separately. However, pricing and seat control problems are highly correlated in the revenue management problem, so these two decision problems need to be considered jointly.
Unlike other studies, our research has the following innovations: (1) We comprehensively consider multiple trains with multi-OD pairs, which is more realistic and challenging; (2) considering passenger’s elastic demand, we propose an innovative model to simultaneously optimize the pricing and seat allocation for HSR based on revenue management. The goal of our model is to maximize the expected revenue; additionally, we construct an elastic function of demand with respect to prices, which is more in line with reality.
This paper proceeds as follows:
Section 2 lists the model assumptions and the variable definition and presents the mathematical model formulation;
Section 3 provides the algorithms to solve the proposed model;
Section 4 describes the numerical experiments; and
Section 5 concludes the paper.
3. Solution Algorithm
To simplify the objective function and facilitate subsequent solutions, we transform the joint optimization model built in
Section 2 into the following equivalent model (I):
where function (21) maximizes the total expected revenue, Constraint (22) represents the maximum seat capacity constraint of the train segment, Constraint (23) represents the ticket limit of each OD pair, Constraint (24) is the ticket price constraint of the train, Constraint (25) judges whether the train
provides passenger service in
, and Constraint (26) is the non-negative integer constraint of seat number allocation.
The optimization model we constructed requires the joint optimization of two variables: Ticket price and seat allocation. In the heuristic algorithm, the Artificial Bee Colony (ABC) algorithm is good at solving multivariable optimization problem [
36]. Therefore, we will use the ABC algorithm to solve this.
The ABC algorithm is a bionic intelligent computing method proposed by Karaboga [
37], which simulates a bee colony finding an excellent honey source. Compared to other heuristic algorithms, such as genetic algorithms and particle swarm algorithms, the prominent advantage of the ABC algorithm is that global and local searching are carried out in each iteration, so the probability of finding an optimal solution is greatly increased, and the local optimization is avoided to a large extent [
1]. In addition, the ABC algorithm has fewer controlled parameters and is easy to realize. In recent years, it has been gradually applied to the numerical optimization of functions, target recognition, neural network silk training and other aspects, and has achieved good test results.
We use the ABC algorithm to solve model (I). A honey source is used to represent a price combination for different ticketing periods. The published prices
are known, and the discount set
is given in advance, according to Equation (2), the executive price set
is also known. We randomly generate
initial price combinations:
,
.
δ = 1, 2, …,
SN.
SN is the number of honey sources. Both the number of Employed Bees and the number of Onlooker Bees are
,
. The maximum number of iterations is
, and the maximum number of search stops for one honey source is
.
where
is the price of train
h between
during the
ticketing period in the
price combination.
Then the elastic passenger flow can be calculated by Equation (13). We then substitute the corresponding ticket price and elastic passenger flow into the model (I), and model (I) will become the model with as the decision variable. In this way, the transformed model can be changed from MINLP model to mixed-integer linear programming (MILP) model by algorithm solving process.
We give an initial value, if , the excess passenger flow is rejected in the current ticketing period. If , the value of is adjusted to be . Calculate the expected revenue corresponding to each group of ticket price, and the nectar amount is the expected revenue corresponding to the honey source.
Then, the Employed Bees and the Onlooker Bees successively search in the neighborhood to find new price combinations for each ticketing period. The neighborhood search process is as follows:
where
is the updated price of train
h between
during the
ticketing period in the
price combination;
is a random number between
;
is the price of train
h between
during the
ticketing period in the
price combination,
;
is randomly determined.
The ticket prices obtained after the neighborhood search of the Employed Bees and the Onlooker Bees are defined as the candidate honey sources. We calculate the nectar amount of each candidate honey source and compare it with that of the corresponding original nectar amount and keep the honey source with a higher nectar amount through greedy criterion. The probability of a honey source being selected by the Onlooker Bees is
where
is the fitness value function of the
honey source, which is proportional to the nectar amount of the
honey source.
If the number of times the honey source is searched by the Employed Bees and the Onlooker Bees (the number of consecutive stays) exceeds , and no honey source with higher fitness is found, the honey source will be abandoned, and the corresponding Employed Bee will be changed into a Scout Bee. Each iteration produces at most one Scout Bee, which randomly searches to generate a new initial price honey source.
The specific steps of the algorithm are as follows:
Step 1: Select the line, according to the historical ticket sales data, obtain relevant information about the line, and give the initial seat number of each OD pair at each ticketing period;
Step 2: Set the initial parameters of the ABC algorithm: , , , , number of continuous stays of each honey source , and number of iterations ;
Step 3: Randomly generate initial honey source, and calculate the nectar amount corresponding to each initial honey source;
Step 4: Each Employed Bee collects a new honey source according to Equation (28). Calculate the nectar amount corresponding to each new honey source, retain the honey source according to the greedy criterion, and update the number of ;
Step 5: Each Onlooker Bee selects a honey source according to Equation (29), and searches for a new honey source according to Equation (28). Calculate the nectar amount corresponding to each new honey source, retain the honey source according to the greedy criterion, and update the number of ;
Step 6: If exceeds , the Employed Bee corresponding to the honey source becomes a Scout Bee, and the Scout Bee randomly searches to generate a new honey source;
Step 7: Record the nectar amount of all current honey sources, update the number of iterations . If , end the iteration; otherwise, return to Step 4;
Step 8: Output the maximum nectar amount; the corresponding ticket price and seat allocation combination scheme is required.
4. Results and Analysis
In this section, we provide numerical experiments to evaluate the model. We will describe the experiment data in
Section 4.1. The numerical results are presented in
Section 4.2.
4.1. Basic Data
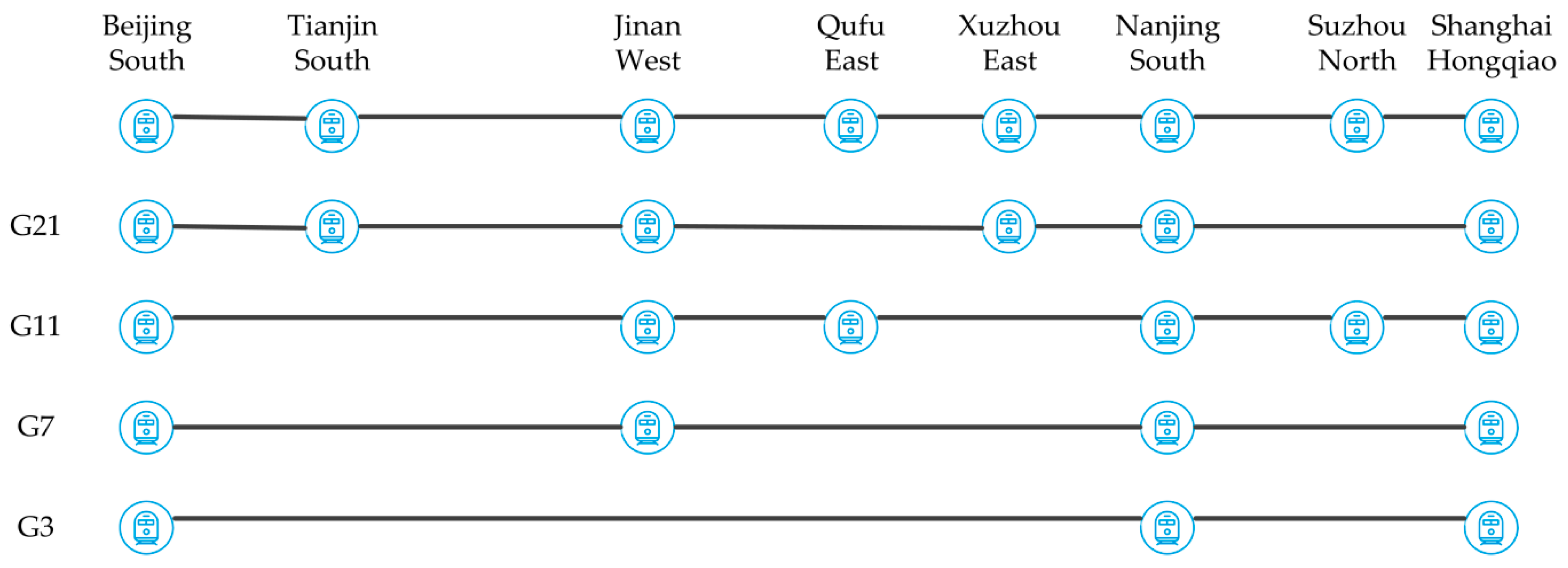
Our model is applicable to all HSR pricing systems, and the Beijing–Shanghai line in China was just chosen as an example to verify the validity of the model. At the same time, we consider the situation of multiple trains and multiple stops, so we randomly select four trains with different stop plans on the line to verify the accuracy of the model and algorithm. The trains we select are G21, G11, G7, G3. All of the four trains depart from Beijing South Station, and stop at different intermediate stations and finally arrive at Shanghai Hongqiao Station. As shown in
Figure 1, in the rail network of this case, there are eight stations on the line; namely, Beijing South, Tianjin South, Jinan West, Qufu East, Xuzhou East, Nanjing South, Suzhou North and Shanghai Hongqiao. We take the average value of the total passenger ticket revenue of the four trains from 5 June 2017 to 11 June 2017 as the case for empirical analysis.
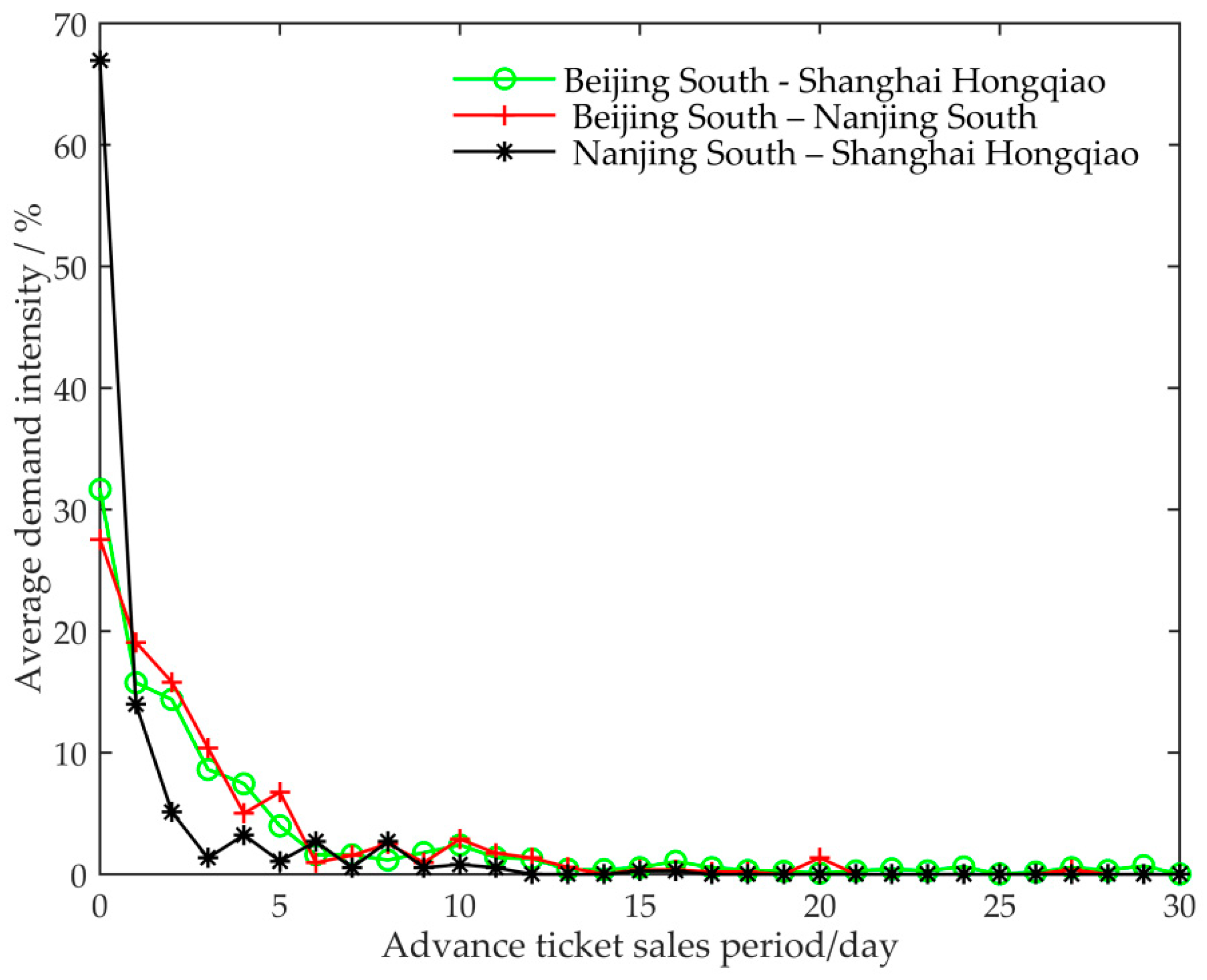
Through the analysis of the passenger ticket data from 1 August 2016 to 31 July 2017, we obtain the purchase rules of different sections of passengers.
Because the average demand intensity curve of each segment has a high similarity, in order to understand the commonality and characteristics of the ticket purchase rules of each segment, we select the statistical results of some segments to display, as shown in
Figure 2.
It can be seen from
Figure 2 that the ticket purchase rules of the passengers in the pre-sale period have certain similarities; that is, the demand intensity is weak from 30 days to 11 days before departure. However, it begins to increase slowly from 10 days to 3 days, and it increases rapidly in the last 1–2 days before departure, and peaks on the day of departure. According to this rule, the pre-sale period is divided into the following four time periods: Eleven days to thirty days before departure
; ten days to three days before departure
; two days to one day before departure
; and the departure date
.
Taking a single seat type (second-class seat) into consideration, the total train capacity is set at 1066. The highest price is the published price, and the current price is 83% of the published price. We set the price discount set as {0.58, 0.61, 0.64, 0.67, 0.70, 0.73, 0.76, 0.79, 0.82, 0.85, 0.88, 0.91, 0.94, 0.97, 1.00}. The values of other parameters for the example are as follows: , , , , , , .
4.2. Computational Results
We use Python language programming to solve the model; the total revenue of the four trains is ¥ 2,247,980, which is 5.92% higher than the total revenue of ¥ 2,122,355.5 under the fixed price case.
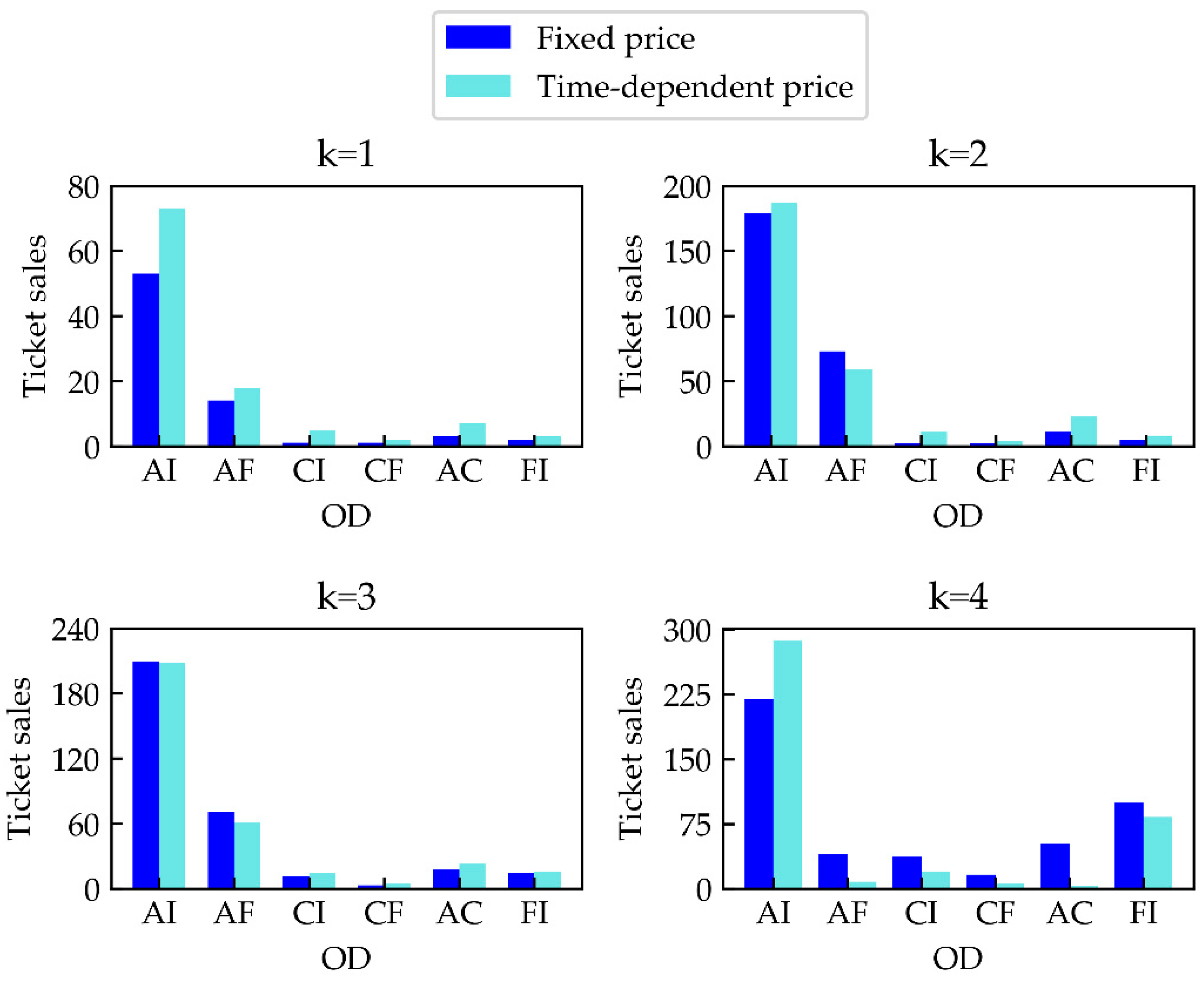
Table 2 shows the optimal prices for each ticketing period. Taking G7 as an example,
Figure 3 shows the comparison of the ticket sales of each OD of the train under fixed price and time-dependent price cases.
Table 3 shows the comparison of the total passenger flow of partial OD of each train under fixed price and time-dependent price cases.
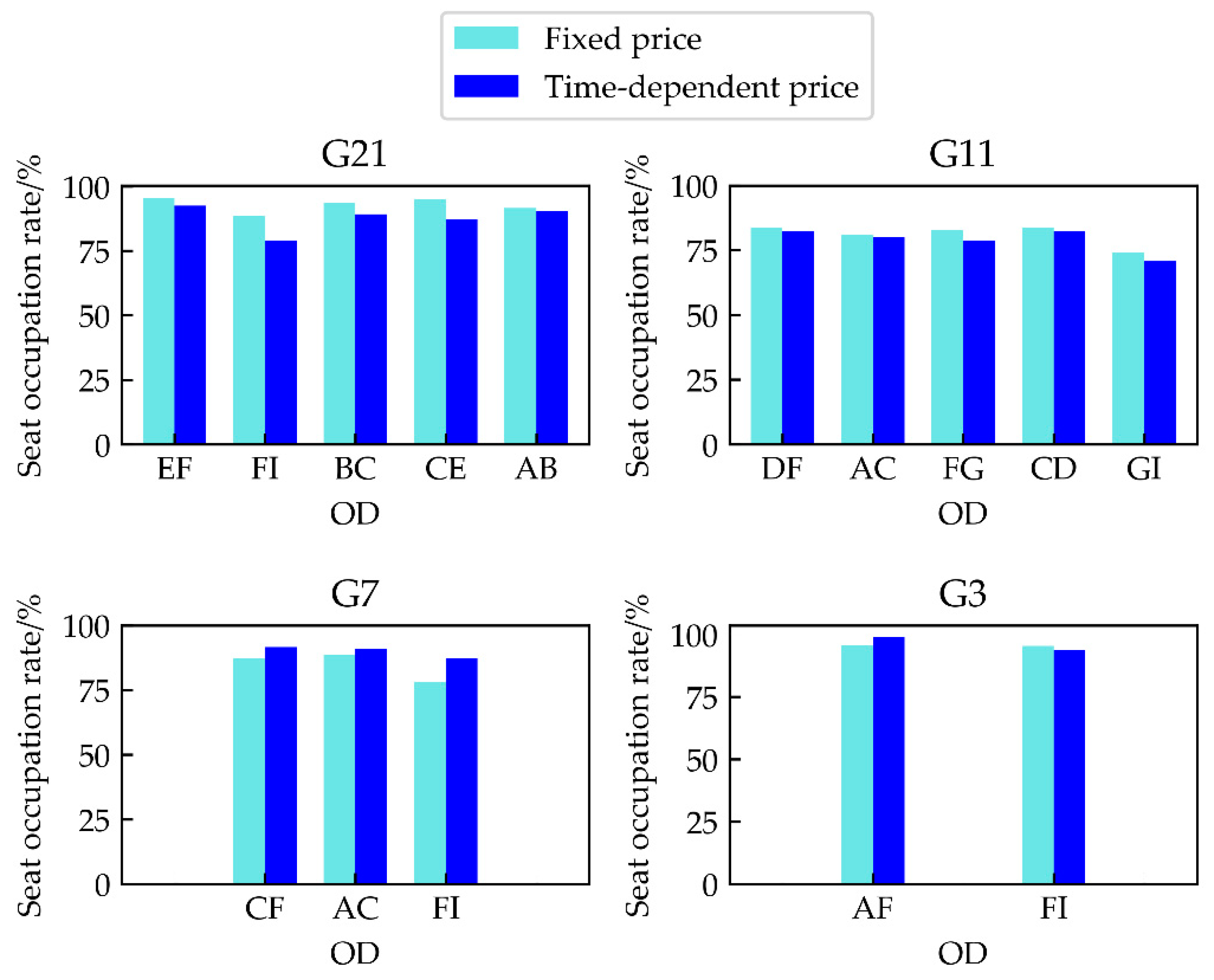
Figure 4 shows the comparison of the seat occupation rate of each train segment under fixed price and time-dependent price cases. We attach different values to the initial seat number,
Table 4 gives a comparison of the price and seat allocation of G3 based on different initial seat numbers and
Table 5 gives a comparison of the percentage increase in total revenue based on different initial seat numbers (in all the figures and tables, A–G represent Beijing South, Tianjin South, Jinan West, Qufu East, Xuzhou East, Nanjing South and Suzhou North, respectively, and I represents Shanghai Hongqiao). We define the existing fixed price and ticket allocation scheme as the initial Scheme I for comparison, and the scheme that only optimizes the ticket price is defined as Scheme II, and the scheme we propose in the paper is the existing Scheme III.
Table 6 gives the results of the ticket revenue under different schemes.
The model can determine the optimal ticket price for each OD in each ticketing period according to the characteristics of passenger flow demand in different ticketing periods and the elastic changes of passenger demand with price fluctuations. As can be seen from
Table 2, the HSR tickets are sold at fluctuating upward prices, and this is in line with the idea of revenue management. The core idea of revenue management is to “sell the right products at the right time and at the right price to the right people” [
5]. In the early stage of the ticketing period, passengers are more sensitive to prices and have greater demand elasticity. At this time, selling tickets at a lower price can attract more passengers to purchase tickets to enhance revenue. On the other hand, the closer the departure time is, the lower the sensitivity of passengers’ travel demand to price, and the smaller the demand elasticity, and, thus, we set the ticket at a higher price so that the tickets with a higher price can be sold in the later stage of the ticketing period, which can also achieve the effect of increasing revenue.
By adjusting the ticket price during different ticketing periods, the passenger demand of each OD will elastically change, so that the seat number allocated for each OD in each ticketing period will also change. Taking G7 as an example, as shown in
Figure 3, at the beginning of the ticketing period (i.e.,
), the seat number allocated to each OD is less than the seat number allocated at the end of the ticketing period (i.e.,
). This is also in line with the idea of revenue management, leaving more seats to passengers who are willing to pay a higher price to get more benefits. Generally, we can see that in the early stage of ticketing period, because of the lower price, it will attract more people to buy tickets (i.e.,
, more passengers bought tickets under the time-dependent price than under the fixed price). The demand for passengers at a single fixed price is usually limited by the number of tickets allocated by each OD, while the time-dependent pricing is used to actively guide and adjust the changes in passenger demand by adjusting the price. Passengers have more choices for prices and can choose the appropriate price in the appropriate ticketing period according to their needs. At the same time, it can be seen that the time-dependent pricing scheme also give priority to meeting the needs of long-distance passengers (e.g., AI between Beijing South and Shanghai Hongqiao), and this can also achieve the goal of increasing total revenue.
It can be seen from
Table 3 that after optimization, the passenger flow of some OD segments has increased, while some have declined.
Figure 4 shows that the seat occupation rate is decreased for G21 and G11, but increased for G7 and G3 with a time-dependent ticket price, and in general, the utilization rate of the seat capacity is high. The total passenger flow before and after optimization has not changed much, but the plan has gained more benefits after optimization, indicating that it is not the case that the more tickets are sold, the higher the revenue, but a greater revenue will be obtained by selling tickets to passengers who are more willing to pay a high price.
According to the historical ticket sales data, we randomly select historical data for different six months and separately calculate the average value of each month as the initial seat allocation values in six cases, and we take them as scenarios I–VI respectively. Taking G3 as an example,
Table 4 shows the price and seat allocation of G3 under different scenarios and
Table 5 shows the percentage increase of total revenue under different scenarios.
It can be seen from
Table 4 and
Table 5 that in the different initial seat allocation scenarios, the seat allocation number and the price in each ticketing period are relatively stable and the floating amount of the percentage increase of total revenue is 0.30% at most. The optimal solution obtained by the algorithm is stable. Therefore, this shows that the algorithm we use in this paper is less dependent on the initial solution and can get a stable optimal solution.
In
Table 6, (II–I) = (Scheme II–Scheme I)/Scheme I × 100%, represents the percentage increase in revenue after optimizing ticket price; (III–II) = (Scheme III–Scheme II)/Scheme II × 100%, indicates the percentage increase in revenue after the optimization of the seat allocation based on the optimization of price; (III–I) = (Scheme III–Scheme I)/Scheme I × 100%, indicates the percentage increase in revenue after using joint optimization of pricing and seat allocation. It can be seen from
Table 6 that the joint optimization model of pricing and seat allocation is better than the single optimization model of price and can increase the revenue to a greater extent.
4.3. Sensitivity Test
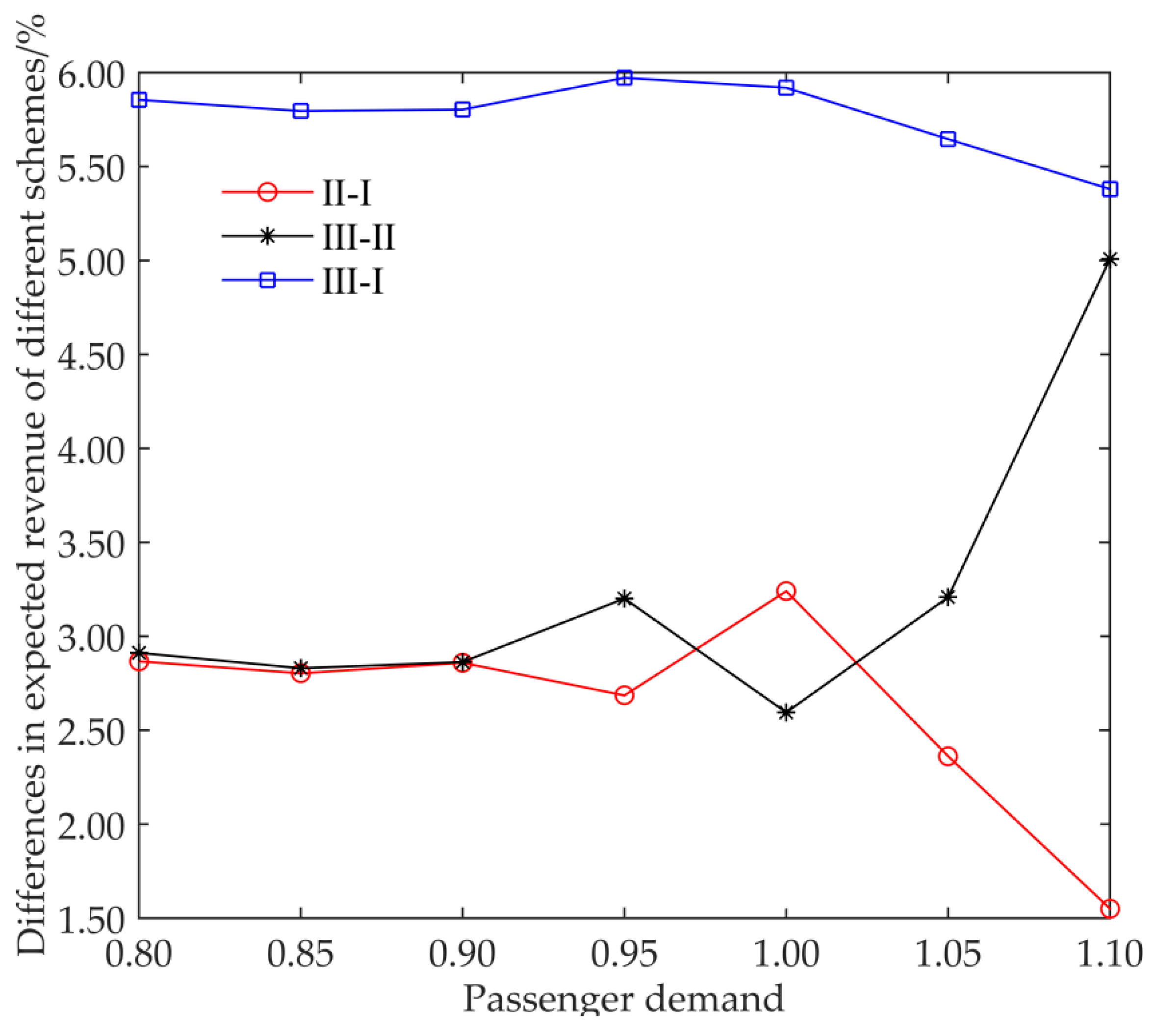
We study the changes in the ratio of revenue increase of different schemes under different demand intensities, as shown in
Figure 5.
Figure 5 shows the expected revenue results and differences in passenger tickets under different schemes when the passenger demand is 0.8–1.1 times that of the initial passenger flow. The following observations are obtained from the sensitivity test:
(1) When the passenger flow increases to a certain value, the revenue generated by the scheme only considering optimizing fare will decrease (i.e., when the passenger flow reaches a certain value, the II–I curve will decrease). This is because, when the demand for passenger flow is large, most of the seats are fully utilized, and sometimes the passenger demand is greater than the capacity of the HSR. At this time, if the scheme considering optimizing fares only is carried out, there may be many people buying low-priced tickets in the early stage of the ticketing period. Since there is no optimization of the seat allocation, the requested demand will be met under the premise of satisfying the transportation capacity. By the end of the ticketing period, the HSR fare will rise. Since a large number of low-priced tickets have been sold in the early stage of the ticketing period, at this time, there may be a situation in which some requests for the purchase of high-priced tickets are rejected, due to the limitation of transportation capacity, and this may cause a certain loss of revenue.
(2) According to the analysis of the demand intensity of passenger flow, it is found that under any demand intensity level, the scheme of optimizing the ticket seat number based on the optimized price can make the expected ticket revenue become better, and its percentage of increase in revenue increases as the intensity of demand increases (i.e., the III–II curve keeps rising with the increase in passenger flow intensity).
(3) Under any demand intensity level, the increase in the revenue from the scheme that jointly optimizes pricing and seat allocation is significantly higher than that from the scheme that only optimizes fares (i.e., the values of (III–I) are always obviously higher than the values of (II–I)). This is because our scheme will dynamically adjust the number of seats allocated to each ticketing period according to the change in the demand intensity of passenger flow during each ticketing period to achieve the purpose of adjusting and guiding demand. At the same time, our scheme can avoid a high-priced ticket being sold at a low price in the early stage of ticketing period on the basis of fully satisfying the travel demand, meaning that the revenue can be greatly improved.
It can be seen from the above analysis that compared with a single optimization model of price, the joint optimization model of pricing and seat allocation proposed in this paper can better achieve the goal of improving the expected revenue. Additionally, when the passenger flow demand is large, the effect of our model is more remarkable.
5. Discussion and Conclusions
In this paper, we aim to optimize HSR operation based on revenue management. In particular, we propose an innovative model to simultaneously optimize the pricing and seat allocation for HSRs; i.e., determining the optimal price and seat allocation for each OD of each train during each ticketing period.
We first analyze passengers’ ticket purchase behavior based on historical ticket data and divide the ticketing period accordingly. Next, we identify the key factors that influence passengers’ choice behavior and construct the elastic passenger demand function that changes with the ticket price. Then, we simulate the passenger’s choice behavior among trains based on the Logit model. After that, we establish a joint optimization model of pricing and seat allocation for HSR, transform it into an equivalent model that is easy to solve, and design a heuristic algorithm to solve it according to the characteristics of the model. Finally, we present some numerical experiments to verify the feasibility and validity of the proposed model and solution algorithm.
The conclusions of this paper have demonstrated the following:
Compared with the existing pricing and seat allocation method, the joint optimization method proposed in this paper considers the elastic passenger flow affected by ticket price which can formulate time-dependent prices to respond to the purchasing patterns of passengers, so as to guide and adjust passenger flow actively, and at the same time, make passengers more satisfied with HSR travel, which is more conducive to the long-term development of HSR.
After numerical verification, we find that under different demand intensities, compared with a single optimization model of price, the joint optimization model proposed in this paper can adapt to fluctuations in demand, and can always generate greater revenue. This can help provide scientific and reasonable decision-making suggestions for railway operation departments and develop a more flexible fare mechanism and a scientific seat allocation system. This will help the HSR to provide higher-quality and richer passenger transportation services in the future to realize sustainable development.
This paper provided a new way of thinking for the railway operation department to reasonably set time-dependent prices to increase revenue and provided a scientific basis for the sustainable operation of the railway. However, this article is based on the assumption that the passengers’ refund and change behavior are not considered. The situation in real life may be more complicated, which can be a direction for future research. In addition, this article only considers the second-class seats of HSR; the HSR also provides a certain number of first-class seats and business seats. The joint optimization of pricing and seat allocation for heterogeneous seats could be another future research direction.