Abstract
This paper proposes a discrete optimisation model and a heuristic algorithm to solve the landfill siting problem over large areas. Besides waste transport costs and plant construction and maintenance costs, usually considered in such problems, the objective function includes economic compensation for residents in the areas affected by the landfill, to combat the NIMBY (Not In My Back Yard) syndrome or, at least, reduce its adverse effects. The proposed methodology is applied to a real-scale case study, the region of Campania, Italy, where waste management is a thorny problem. Numerical results show that the proposed algorithm may be used to obtain a solution to the problem, albeit sub-optimal, with acceptable computing times, and the proposed model tends to locate landfills in sparsely populated sites.
1. Introduction
NIMBY (Not In My Back Yard) syndrome [1] is a widespread phenomenon related to the strong opposition of a community to some public-interest interventions in a local area, mainly “undesirable plants”, such as landfills, incinerators and thermoelectric power plants. Local communities often “fight” against public authorities and their decisions, even with violent demonstrations and roadblocks. In this context, landfills are probably the most controversial facilities; in addition to social costs, they can lead to a reduction in property values in adjacent zones [2]. Hence residents living in the surrounding areas should be assured of economic compensation [3]. Such an approach should be able to compensate the inhabitants involved for all external and social costs produced by the plant and incurred primarily or exclusively by themselves, such as air pollution (due to the plant and to the vehicles transporting waste), noise, foul-smelling air, soil availability (directly occupied or indirectly influenced by the plant), the already cited reduction in property values and possible health effects (whether real or imaginary, depending largely on plant location and design).
Decision-makers should consider compensation costs just like other costs (construction, maintenance, waste transportation, etc.). In this paper, we formulate an optimisation model for solving the landfill siting problem, where economic compensation is also explicitly considered. Some preliminary results of this research have been published in [4].
The landfill siting problem can be considered a variant of the classical p-median problem [5,6,7]; more precisely, the problem can be formulated as a location problem with demand-dependent costs [8]. A review of p-median problems was published in [6], where the main solution algorithms were also examined. This paper focuses mainly on the proposed approach, especially evaluating the effects on the optimal solutions of considering economic compensation within the objective function; a comparison between methods, models and algorithms for solving location problems lies outside the scope of this paper.
The objectives of this paper were to propose a model for optimising landfill location that explicitly considers compensation costs for inhabitants affected by the plant and an algorithm that can solve the problem efficiently in acceptable computing times even when the problem at hand occurs on a large scale. Moreover, the methodology is tested on a real-scale case study, the region of Campania, where waste management has been, and still is, a thorny problem.
The paper is structured as follows: Section 2 examines the background of landfill siting problems; Section 3 illustrates the proposed methodology, based on an optimisation model and a solution algorithm; Section 4 summarises the numerical results on a real-scale case; Section 5 discusses the results; finally, Section 6 draws the main conclusions.
2. Background
In this section, the background to the landfill siting problem is explored. A literature review on the more general location problem would deserve its own treatment; here, we refer only to papers cited in the introduction.
The importance of considering social aspects in waste management problems, as well as public acceptance so as to limit NIMBY syndrome effects, was underlined in [9]. Simsek et al. [10] proposed a landfill site screening procedure which considered NIMBY syndrome constraints, without providing, however, compensation costs for inhabitants.
Waste management models were reviewed in [11], where the models are classified into: (i) models based on cost-benefit analysis; (ii) models based on life-cycle analysis; and (iii) models based on multicriteria decision analysis. The authors concluded that joint consideration of environmental, economic and social aspects of the problem is an important aim to be pursued in the waste management approach, whilst emphasising the importance of people’s acceptance in such kinds of decisions.
Several papers propose multicriteria approaches [12,13,14] for solving location problems of undesirable plants. Melachrinoudis et al. [15] developed a dynamic (multiperiod) multicriteria mixed integer programming model; they considered a planning horizon and that some parameters of the problem (population, costs, etc.) could change over time, taking into account past data and future projections. The model considered four objectives: minimising total cost, minimising risk for the population, minimising risk for the ecosystem and minimising inequity. Hokkanen and Salminen [16] applied the ELECTRE III multicriteria approach to choose a solid waste management system in a Finnish region, bearing in mind that the energy potential of the waste in question should be used within the region. Cheng et al. [17] proposed an integration of a multicriteria approach and inexact mixed integer linear programming for selecting an optimal landfill site and a waste-flow-allocation pattern; the objective was to minimise total costs and several different multicriteria methods were tested (weighted addition, weighted product, co-operative game theory, TOPSIS and complementary ELECTRE). Public acceptance was considered one of the criteria adopted in the procedure. Vasiloglou [18] proposed a decision-making process in which broad community participation and acceptance was explicitly considered. Kontos et al. [19] proposed a spatial methodology based on multicriteria analysis for siting a landfill that identifies land suitability on a grading scale; the methodology, which used an analytical hierarchy process for estimating the weights of the criteria, was applied to the island of Lemnos. Chang et al. [20] proposed a fuzzy multicriteria analysis integrated with a GIS; in an initial stage, a GIS-based spatial analysis identifies the potential areas that are then examined with fuzzy multicriteria analysis. Xi et al. [21] integrated an optimisation approach with multicriteria decision analysis for supporting long-term planning of solid waste management in the City of Beijing (China); also here, fuzzy theory was adopted inside the multicriteria analysis model. A GIS-based multicriteria analysis for siting a landfill in the Polog region of Macedonia was proposed in [22]; in the multi-criteria decision framework, environmental and economic factors were standardised using fuzzy membership functions, and combined by integrating analytic hierarchy process and ordered weighted average techniques. Gbanie et al. [23] modelled the landfill location problem using GIS and multicriteria analysis, and applied the proposed approach to a case study in Sierra Leone; the multicriteria-GIS approach integrated the weighted linear combination and the ordered weighted average techniques.
A landfill site selection based on fuzzy inference was proposed in [24]. Sumathi et al. [25] proposed GIS-based procedures that combined the use of GIS with a multicriteria analysis, Zamorano et al. [26] applied the procedure to a case study in Southern Spain and Simsek et al. [10] explicitly considered NIMBY syndrome constraints. Other case studies can be found in [27,28,29,30,31].
Eiselt [32] compared actual and optimal landfill locations, while Eiselt and Marianov [33] proposed a procedure for jointly locating landfills and transfer stations. Finally, Guiqin et al. [34] introduced an analytic hierarchy process (AHP) for selecting landfill sites.
To our best knowledge, limiting local opposition to the location of a landfill was not previously considered a real cost to bear; this paper proposes a methodology for including this aspect of the problem inside the optimisation procedure.
3. Methodology
The landfill siting problem assumes that: (i) several landfills have to be located in a large geographical area for receiving the waste produced therein, (ii) the location of all waste sources is known and (iii) the annual production from each source is known. Moreover, we consider that there is at least one waste source for each municipality and its location is known; this point may represent a local plant where waste produced in the municipality is collected and compacted before being transferred to landfill; more waste sources can be assumed in large cities. Finally, we assume that all eligible sites in the region were already identified and located, so as to respect some technical (geological, hydro-geological, etc.), territorial (accessibility, altitude, etc.), social and political constraints.
The proposed approach considers three kinds of costs: (i) landfill construction/maintenance costs, (ii) waste transportation costs and (iii) compensation costs. The cost of a landfill depends on the annual quantity of waste that it receives (including the construction costs, which are appropriately amortised); each eligible site may have a different function that relates its annual cost with the waste quantity to be received. The transportation cost is assumed dependent only on ton-km of transported waste, and other more complex approaches considering the different vehicles used and/or the kind of road used can be introduced, without significant impacts on the proposed approach. Finally, compensation costs for residents affected by the plants are also included. They represent compensation given by society to those directly affected by the negative impacts of each landfill, and could be paid in different ways: tax exemptions, reductions in energy costs, monetary investments for improving the urban environment and the quality of life (e.g., parks and gardens, sustainable transit systems, building renovation).
3.1. Optimisation Model
The mathematical model is formulated as follows:
where:
xopt = Arg x min (Σi yci(wi(x)) xi + Σj dj,min(x) wpj ctr + Σi resi wi(x) ccomp)
s.t. xi ∈ {0, 1} ∀ i
1 ≤ Σi xi ≤ lmax
- i indicates an eligible site;
- j indicates a waste source;
- x is the vector of decision variables xi;
- xopt is the optimal solution;
- xi is a binary variable that is equal to 1 if a landfill is located in site i, 0 otherwise;
- wi(x) is the annual waste quantity allocated to site i;
- yci(.) is a function used for calculating the annual cost of the landfill located in site i; it depends on the annual waste quantity to be treated, wi(x);
- dj,min(x) indicates the distance between a waste source j and the nearest landfill;
- wpj indicates the annual production of waste source j;
- ctr indicates the cost per ton-km of transported waste (€/ton-km);
- resi indicates the number of residents that have to be compensated for a landfill located in site i;
- ccomp is the annual compensation cost per ton of waste per resident (€/ton);
- lmax is the maximum number of landfills.
Even if other options are possible, in this model, we assume that the waste produced by source j, wpj, is sent to the nearest landfill. Under this assumption, we can write:
where:
wi(x) = Σj wpj ai,j(x)
- ai,j(x) is equal to 1 if, under configuration x, site i is the nearest to source j (di,j = dj,min), 0 otherwise, with di,j indicating the distance between site i and source j.
This model is a binary non-linear optimisation model that belongs to the class of location problems with demand-dependent costs [8]. This problem is NP-hard like all location problems on general graphs [5,35,36].
3.2. Solution Algorithm
In the literature, plant location problems are solved with several methods and algorithms, most of which are heuristic or metaheuristic; a literature review can be found in [6]. Indeed, solving the problem with exact approaches is possible only for small or simple case studies. Many metaheuristic methods are proposed in the literature [37] for solving this problem, such as genetic algorithms [38,39,40,41,42], simulated annealing [43,44,45,46,47] and Tabu search [45,47,48,49,50,51,52,53]. Extensive literature is also available for heuristic algorithms [45,48,50,54].
For solving the Equations (1)–(3), we propose to use a heuristic algorithm that can lead to a solution, albeit sub-optimal, in an acceptable computing time also for large problems. This algorithm uses a multi-start technique [55] and a variant of a greedy heuristic [54] that is based on exhaustive monodimensional searches. Multi-start procedures are commonly used in combinatorial problems when the objective function is not convex; Resende and Werneck [55], among others, applied this approach to p-median problems.
It is worth noting that the landfill location problems usually have a large number of decisional variables (one for each possible location site) and a very small maximum number of landfills to be set up. For example, the application that will be carried out in the next section will have 551 possible sites but a maximum of only five landfills. Therefore, it is possible to simplify the management of the solution algorithm by transforming the binary model into a discrete model. Indeed, we may introduce lmax pointer variables, χk, that assume an integer value between 0 and n, where n is the number of possible locations. Each pointer variable indicates site i, χk = i, where a landfill is provided; otherwise, χk = 0 indicates that the pointer variable is not associated to any site i and thus the number of landfills in this solution is lower than the maximum. Figure 1 shows an example of the above approach.
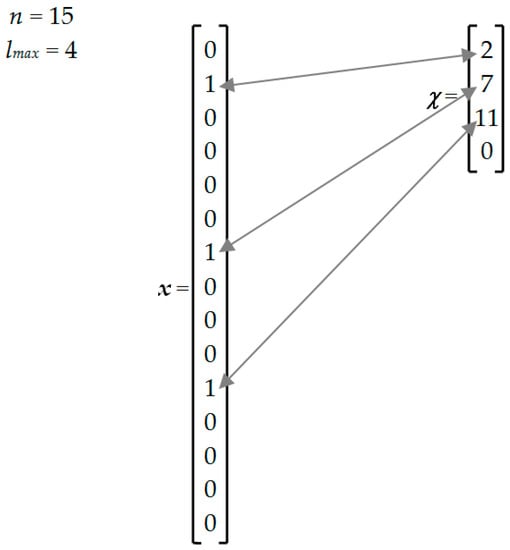
Figure 1.
Decision variables and pointer variables.
Adopting this approach, each solution x can be represented by a vector of pointer variables, χ, and the optimisation model can be formulated as follows:
χopt = Arg χ min (Σi yci(wi(χ)) xi(χ) + Σj dj,min(χ) wpj ctr + Σi resi wi(χ) ccomp)
s.t. 0 ≤ χk ≤ n ∀ k
χk integer ∀ k
Σk χk ≥ 1
Using the pointer variables allows the constraint (3) to be included directly within the model and the search to be limited only to solutions that respect it. Indeed, solutions that exceed the maximum number of landfills are automatically excluded, and at least one landfill is provided considering that the transportation cost is assumed to be infinity (actually, a very large number) if there are no landfills.
The solution algorithm is articulated as follows.
Phase 0—Initialisation. Set the counter of iterations to 0. Set all variables χk to 0. Set the objective function value to a very large number, M.
Phase 1—Mono-dimensional exhaustive search (1st cycle). Examine all solutions obtained by changing the first pointer from 0 to n, identify the best one and set the first pointer to the corresponding value. Repeat the procedure for the other pointers, assuming the previous pointer values are fixed. End when the optimal value of a pointer is equal to 0 (no other landfills) or when all pointers have been exhaustively explored. In this phase, the algorithm examines at most lmax × n solutions.
Phase 2—Mono-dimensional exhaustive search (2nd cycle). Repeat phase 1 starting from the last pointer values, until the best solution at the end of the exhaustive search is equal to that generated in the previous phase or a maximum number of solutions have been examined.
Figure 2a reports the structure of the algorithm. Since the problem is not convex and the proposed algorithm is heuristic, the algorithm leads to a local optimum. For exploring the solution set, we propose to apply a multi-start technique; this method generates randomly different solutions that are used as starting points for the second cycle (see Figure 2b). The complexity of each mono-dimensional exhaustive search is O(lmax × n).
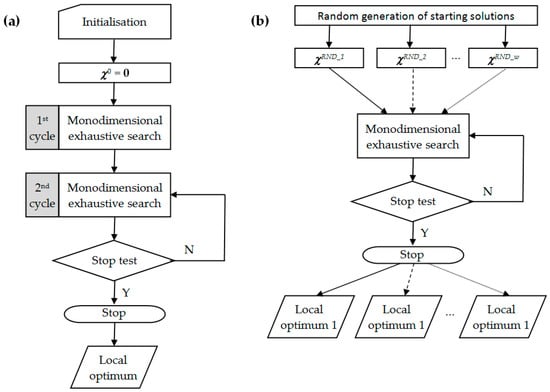
Figure 2.
Algorithms: (a) base; (b) multistart.
4. Numerical Results
We tested the proposed approach on a large area corresponding to the region of Campania (southern Italy). This region (13,590 km2) has 551 municipalities, about 5.8 million inhabitants and its capital is Naples (about 1 million inhabitants). We assumed 551 waste sources, one per municipality, whose waste production was obtained from official data [56]. We also assumed 551 eligible sites, one inside each municipal area, and that a landfill located in an area will affect only people living in the same municipality. In Figure 3a the territories, with their centroid nodes, are reported, while Figure 3b reports the road network graph, representing about 6000 km of roads, used for calculating the distances between sources and eligible sites. All maps in this paper were generated with the software QGIS and are geo-referenced with the coordinate reference system WGS84/UTM Zone 32. Moreover, we have assumed a compensation cost equal to 0.0001 €/ton per resident and an average transportation cost of 0.4 €/ton-km (obtained from some regional tenders regarding waste management).
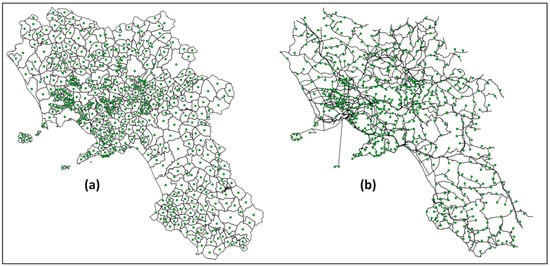
Figure 3.
Case study: (a) municipal boundaries and centroids; (b) road network.
The annual cost of a landfill was calculated using the method proposed in [33]:
where:
yci(wi(χ)) = c0 + wi(χ) c1(wi(χ))
- c0 is a fixed cost of the landfill (€/year);
- c1 is a variable cost per waste ton (€/ton-year), depending on wi for considering the scale economy.
According to the formula proposed in [33] and converting the values of coefficients from dollars to Euros, we assumed: c0 = 220,000 and c1(wi(χ)) = 428.015 wi(χ)−0.209.
With these assumptions, we tested the proposed algorithm considering the three terms of the objective function (transportation costs; construction/maintenance costs; compensation costs) and then only the first two terms. The results are summarised in Table 1 and Figure 4.

Table 1.
Optimal solutions.
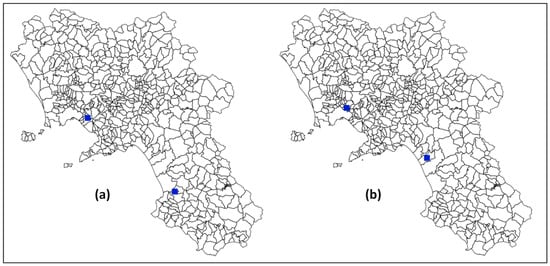
Figure 4.
Optimal landfill location: (a) with comp. costs; (b) without comp. costs.
The algorithm, starting from all pointers equal to 0, examined 1654 solutions in about 21 min; in Figure 5, the objective function values corresponding to solutions examined by the algorithm are reported. In this test, the multi-start procedure, starting from 15 random solutions, led to the same solution. Moreover, an exhaustive search among all solutions that have only two landfills (151,525 solutions, computing time about 32 h) led to the same results. However, it does not ensure that the algorithm leads to the global optimum.
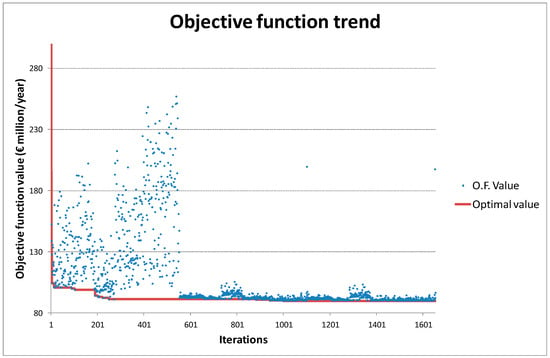
Figure 5.
Objective function values of examined solutions.
By comparing results with and without compensation costs, we can underline that the proposed approach leads to a solution where the population affected by the undesirable plant is lower: indeed, Casoria and Battipaglia have 77,642 and 50,798 inhabitants, respectively, while Massa di Somma and Giungano only have 5449 and 1253 inhabitants, respectively. The methodology, therefore, should be able to limit NIMBY syndrome effects, since the directly involved people are less, and to limit the total compensation costs, since they are proportional to involved inhabitants.
Finally, we assumed different landfill construction/maintenance yearly cost functions, in order to explore how the solution changes with significant changes in costs. We used the same function adopted above, modifying only the term c1(wi(χ)) by substituting the value 428.015 with the following values: 600, 500, 400, 300, 200 and 100. Figure 6 shows the landfill year costs generated under such assumptions.
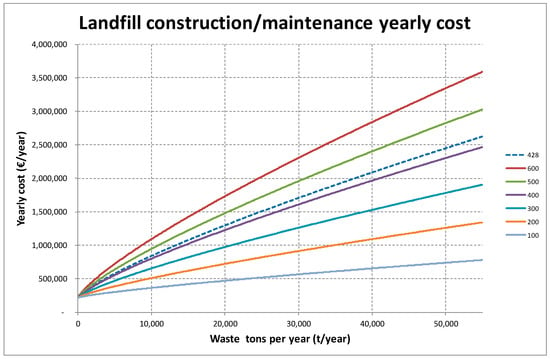
Figure 6.
Landfill construction/maintenance costs with different costs.
Table 2 summarises the results corresponding to different landfill construction/maintenance cost functions, identified by a different value of the coefficient c1. As expected, solutions with more landfills correspond to lower amounts of the coefficient (5 or 4, if c1 is between 100 and 300; between 1 and 3, if c1 is between 400 and 600), i.e., lower construction/annual maintenance costs. On comparing the results with and without compensation costs, it can be shown that the total number of landfills does not differ so markedly (only in two cases does the model lead to a different number of landfills) although the number of inhabitants involved is very different. Some municipalities recur in the optimal solution; if we consider the compensation costs, this is due to a promising combination of position and inhabitants, while in the other case only the location influences the results.

Table 2.
Results with different landfill construction/maintenance costs.
As a percentage of total annual costs, the compensation costs vary from 1.3% to 5.3% (see Figure 7), while the increase between the solutions with and without compensation costs varies between 3.0% and 11.5% (see Figure 8). Inhabitants of municipalities affected by landfills are summarised in Figure 9: the differences between considering compensation costs or otherwise are very substantial. In Figure 10 and Figure 11, the optimal locations in the different cases are reported.
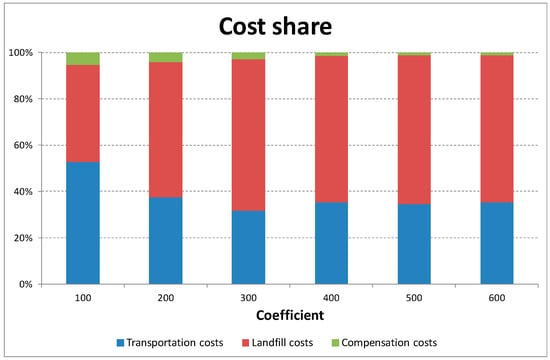
Figure 7.
Cost share.
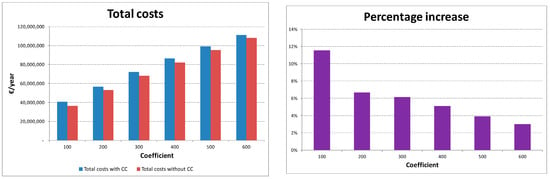
Figure 8.
Comparison of total costs.
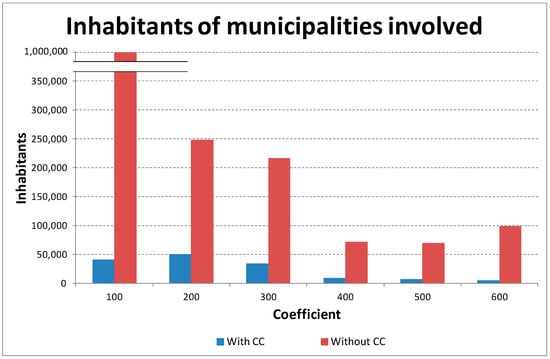
Figure 9.
Inhabitants of municipalities affected by the landfills.
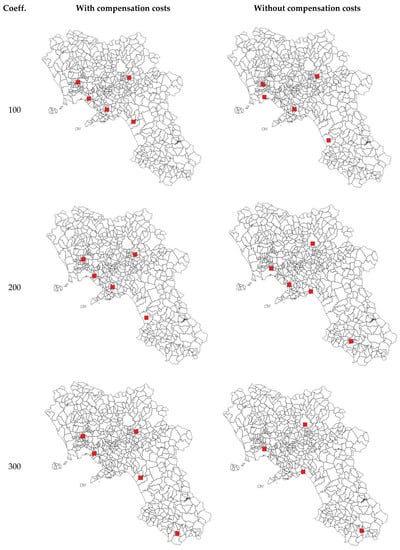
Figure 10.
Optimal locations (1/2).
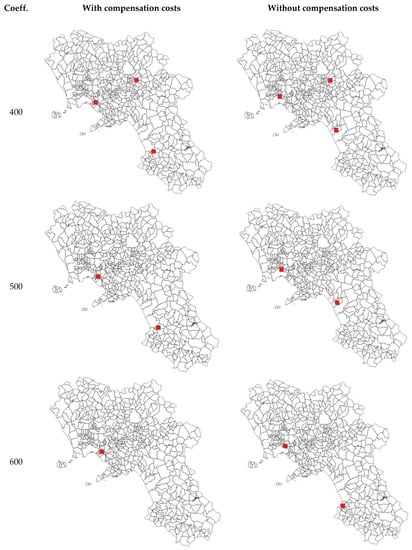
Figure 11.
Optimal locations (2/2).
5. Discussion
The location of undesirable plants, especially of landfills, is a complex problem in several respects: (1) mathematical, since the problem is NP-Hard; (2) technical, since the choice of the specific location has to consider several aspects such as the kind of soil, the presence or otherwise of aquifers, landslide risk, hydrogeological risk, accessibility and so on; (3) economic, related to construction, maintenance and transportation costs; (4) environmental, such as the general impacts on air quality, noise, soil pollution and fauna; (5) social, related to the external costs produced by the landfill that are incurred by the local population (smelly air, reduction in property values, noise, etc.) and the inevitable inequity of the interventions (only some people are affected by a plant that is required to satisfy the needs of a vast community). Social problems lead to the strong opposition of local communities to the construction and operation of the plant, the well-known NIMBY syndrome.
The approach proposed in this paper tries to solve some social aspects of the problem, contrasting the local opposition by economically compensating the people affected by the plant. This compensation, if it is directly included in the objective function, leads the solution towards locations that impact on smaller local communities. For instance, an analysis of our results shows (see Figure 9 and Table 2) a large difference in the size of the population involved with and without considering the compensation costs.
Other crucial aspects of the problem regard the external costs of landfills. While some social and environmental external costs for the host communities can be offset economically, as herein proposed, other impacts, such as on local flora and fauna [57], are not explicitly considered in this study. These impacts can be considered and limited in two ways: (1) to select, after a specific in-depth study, as possible landfill hosting sites only those that generate minor impact on flora and fauna; (2) to propose a method for including in the landfill costs also those on flora and fauna, changing the formulation of yci(wi(χ)). In this second case, a specific study on the economic value of such impacts has to be preliminarily conducted.
Estimation of the economic compensation for the host community is an important point to examine; indeed, it significantly influences the final result and the political acceptability of the intervention. Here we assumed that each inhabitant would be compensated proportionally to the amount of waste addressed to the landfill and that each plant affects only the residents of the hosting municipality, regardless of the distance. These simplifications are compatible with a “real-scale” (and not “real”) case study and can be removed in future researches, which will require specific in-depth studies. In the literature, numerous studies proposed methods for determining willingness to accept (WTA) compensation for hosting undesirable plants. Usually, direct surveys are necessary for estimating the willingness to accept compensation; examples involving waste disposal infrastructures can be found in [58,59,60]. In [59], the authors highlighted the importance of the distance on the compensation and its acceptance. The acceptance of compensation is higher for those who live further away from the site; on the contrary, residents closer to the plant tend to refuse compensation and prefer to continue the opposition. This suggests, as a matter of course, that higher compensation should be granted to residents in the areas closest to the plant. To use a value of WTA from the literature is seldom possible; on the contrary, a different value should be used for different municipalities, since social factors significantly influence the value in question [61]. Numerous other case studies can be found in the literature; herein we refer to [62,63,64,65,66,67].
The proposed methodology is general and transferable since it can be easily applied to other large areas. Indeed, all necessary data are easily obtainable and the social problems related to the location of landfills are common to all regions of the world. A preliminary phase requires identification of all feasible locations that respect the technical prescriptions (it is possible to use multi-hazard assessment maps as well [68,69]) and the corresponding local communities affected by the plant. Moreover, surveys for estimating the compensation costs would also be required. In our test, that has to be considered a “real-scale” case study but not a “real” case study; it was not possible to perform the preliminary phase: all municipalities were assumed as possible sites and the population of each municipality is considered affected only if the plant is located in its own territory. Except for this simplification, all data used are real, as well as the road network.
It is essential also to underline that another significant contribution for reducing the local opposition can be given by inclusive decision-making processes, which involve the local communities in the political decisions, negotiating possible solutions.
The choice of the case study is not casual. Waste management in the region of Campania has been, and is partly still, a critical problem from environmental, social and political points of view. Officially, the crisis started in 1994 and ended in 2011; it was preliminarily due to the oversaturation of the available landfills and then to the difficulty to propose and implement an effective regional waste management plan. The crisis had a loud echo in the national and international press. During this period, several NIMBY syndrome phenomena have occurred, such as local opposition to the waste-to-energy plant of Acerra, to the landfills provided in Naples (Chiaiano and Pianura districts) and Terzigno. During the same period, numerous investigations by the judiciary showed that organised crime had infiltrated the waste business. Today, the situation is better, also thanks to the higher percentage of separate waste collection, although the risk of a new crisis is ever-present. The waste crisis in Campania has also been the subject of numerous studies in the scientific literature. Herein we cite only [70,71,72,73,74,75,76].
6. Conclusions
The methodology proposed in this paper aims to limit the opposition from local communities to undesirable plants. Giving economic compensation to local communities affected by an undesirable plant is common practice, but often policy-makers grant such benefits after the decision has already been taken. Considering economic compensation like other project costs can lead to solutions that can be better accepted and may result in compensation costs that can be lower overall.
This is confirmed by the results obtained in this paper. Comparison between the solution with and without compensation costs showed that the solutions differed significantly in terms of the number of people to be compensated, while, by examining the landfill locations, the corresponding optimal sites are not so distanced.
It should be stressed that the proposed approach increases the overall cost of the solution; this is due to the compensation costs and, almost always, also to increases in other costs. This additional cost is about 4.5% in the case study, and varies from 3.0% and 11.5% with different assumptions on landfill costs. Given that public opposition often generates significant delays in construction, opening and operation of plants, this approach could indeed reduce the real cost of the overall waste management cycle. Moreover, if the policy-maker compensates those affected by the waste facility after the choice of the location, such costs will be significantly higher than those obtained with the proposed approach.
From the point of view of computational efforts, considering compensation costs or otherwise does not produce significant effects. Finally, the proposed heuristic algorithm is able to lead to a (local) optimal solution in acceptable computing times in a large-scale case study.
Future research efforts would be best spent on removing some simplifying assumptions that we have considered in this paper and testing the model on a “real” case, instead of a “real-scale” case, where the actual possible locations and construction/maintenance costs are considered. In particular, a specific study would be necessary for evaluating the compensations, with different values depending on the social factors of residents and distance from the plant. This study will require specific surveys, GIS-based approaches and multidisciplinary competencies (environmental, hydro-geological, economic, social, etc.). Finally, the proposed algorithm could be compared with other algorithms proposed in the literature, such as genetic algorithms, scatter searches and simulated annealing.
Funding
This research received no external funding.
Acknowledgments
The author is grateful to the Editor and three anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Shen, H.W.; Yu, Y.H. Social and Economic Factors in the Spread of the NIMBY Syndrome against Waste Disposal Sites in Taiwan. J. Environ. Plan. Man. 1997, 40, 273–282. [Google Scholar] [CrossRef]
- Li, R.Y.M.; Li, H.C.Y. Have Housing Prices Gone with the SmellyWind? Big Data Analysis on Landfill in Hong Kong. Sustainability 2018, 10, 341. [Google Scholar] [CrossRef]
- Jenkins, R.R.; Maguire, K.M.; Morgan, C. Host Community Compensation and Municipal Solid Waste Landfills; Working Paper #02-04; U.S. Environmental Protection Agency, National Center for Environmental Economics (NCEE): Washington, DC, USA, 2002.
- Gallo, M. A model and algorithm for solving the landfill siting problem in large areas. In Optimization and Decision Science: Methodologies and Applications. ODS 2017; Sforza, A., Sterle, C., Eds.; Springer: Cham, Switzerland, 2017; Volume 217, pp. 267–274. [Google Scholar]
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems, Part II: The p-medians. SIAM J. Appl. Math. 1979, 37, 539–560. [Google Scholar] [CrossRef]
- ReVelle, C.S.; Eiselt, H.A.; Daskin, M.S. A bibliography of some fundamental problem categories in discrete location science. Eur. J. Oper. Res. 2008, 184, 817–848. [Google Scholar] [CrossRef]
- Daskin, M.S.; Mass, K.L. The p-Median problem. In Location Science; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer: Cham, Switzerland, 2015; pp. 21–45. [Google Scholar]
- Averbakh, I.; Berman, O.; Drezner, Z.; Wesolowsky, G.O. The Plant Location Problem with Demand-Dependent Setup Costs and Centralized Allocation. Eur. J. Oper. Res. 1998, 111, 543–554. [Google Scholar] [CrossRef]
- Joos, W.; Carabias, V.; Winistoerfer, H.; Stuecheli, A. Social aspects of public waste management in Switzerland. Waste Manag. 1999, 19, 417–425. [Google Scholar] [CrossRef]
- Simsek, C.; Elci, A.; Gunduz, O.; Taskin, N. An improved landfill site screening procedure under NIMBY syndrome constraints. Landsc. Urban Plan. 2014, 132, 1–15. [Google Scholar] [CrossRef]
- Morrisey, A.J.; Browne, J. Waste management models and their application to sustainable waste management. Waste Manag. 2004, 24, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Greco, S.; Ehrgott, M.; Figueira, J.R. Multiple Criteria Decision Analysis. State of the Art Surveys, 2nd ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Department for Communities and Local Government. Multi-Criteria Analysis: A Manual; Communities and Local Government, Eland House: London, UK, 2009.
- Tsolaki-Fiaka, S.; Bathrellos, G.D.; Skilodimou, H.D. Multi-Criteria Decision Analysis for an Abandoned Quarry in the Evros Region (NE Greece). Land 2018, 7, 43. [Google Scholar] [CrossRef]
- Melachrinoudis, E.; Min, H.; Wu, X. A multiobjective model for the dynamic location of landfills. Locat. Sci. 1995, 3, 143–166. [Google Scholar] [CrossRef]
- Hokkanen, J.; Salminen, P. Choosing a solid waste management system using multicriteria decision analysis. Eur. J. Oper. Res. 1997, 98, 19–36. [Google Scholar] [CrossRef]
- Cheng, S.; Chan, C.W.; Huang, G.H. An integrated multi-criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Eng. Appl. Artif. Intell. 2003, 16, 543–554. [Google Scholar] [CrossRef]
- Vasiloglou, V.C. New tool for landfill location. Waste Manag. Res. 2004, 22, 427–439. [Google Scholar] [CrossRef] [PubMed]
- Kontos, T.D.; Komilis, D.P.; Halvadakis, C.P. Siting MSW landfills with a spatial multiple criteria analysis methodology. Waste Manag. 2005, 25, 818–832. [Google Scholar] [CrossRef] [PubMed]
- Chang, N.-B.; Parvathinathan, G.; Breeden, J.B. Combining GIS with fuzzy multicriteria decision-making for landfill siting in a fast-growing urban region. J. Environ. Manag. 2008, 87, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Xi, B.D.; Su, J.; Huang, G.H.; Qin, X.S.; Jiang, Y.H.; Huo, S.L.; Ji, D.F.; Yao, B. An integrated optimization approach and multi-criteria decision analysis for supporting the waste-management system of the City of Beijing, China. Eng. Appl. Artif. Intell. 2010, 23, 620–631. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Donevska, K.R.; Mitrovski, C.D.; Frizado, J.P. Integrating multi-criteria evaluation techniques with geographic information systems for landfill site selection: A case study using ordered weighted average. Waste Manag. 2012, 32, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Gbanie, S.P.; Tengbe, P.B.; Momoh, J.S.; Medo, J.; Kabba, V.T.S. Modelling landfill location using Geographic Information Systems (GIS) and Multi-Criteria Decision Analysis (MCDA): Case study Bo, Southern Sierra Leone. Appl. Geogr. 2013, 36, 3–12. [Google Scholar] [CrossRef]
- Al-Jarrah, O.; Abu-Qdais, H. Municipal solid waste landfill siting using intelligent system. Waste Manag. 2006, 26, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Sumathi, V.R.; Natesan, U.; Sarkar, C. GIS-based approach for optimized siting of municipal solid waste landfill. Waste Manag. 2008, 28, 2146–2160. [Google Scholar] [CrossRef] [PubMed]
- Zamorano, M.; Molero, E.; Hurtado, A.; Grindlay, A.; Ramos, A. Evaluation of a municipal landfill site in Southern Spain with GIS-aided methodology. J. Hazard. Mater. 2008, 160, 473–481. [Google Scholar] [CrossRef] [PubMed]
- Chabuk, A.; Al-Ansari, N.; Hussain, H.M.; Knutsson, S.; Pusch, R.; Laue, J. Combining GIS Applications and Method of Multi-Criteria Decision-Making (AHP) for Landfill Siting in Al-Hashimiyah Qadhaa, Babylon, Iraq. Sustainability 2017, 9, 1932. [Google Scholar] [CrossRef]
- Al-Anbari, M.A.; Thameer, M.Y.; Al-Ansari, N. Landfill Site Selection by Weighted Overlay Technique: Case Study of Al-Kufa, Iraq. Sustainability 2018, 10, 999. [Google Scholar] [CrossRef]
- Yousefi, H.; Javadzadeh, Z.; Noorollahi, Y.; Yousefi-Sahzabi, A. Landfill Site Selection Using a Multi-Criteria Decision-Making Method: A Case Study of the Salafcheghan Special Economic Zone, Iran. Sustainability 2018, 10, 1107. [Google Scholar] [CrossRef]
- Chen, F.; Li, X.; Yang, Y.; Hou, Y.; Liu, G.-J.; Zhang, S. Storing E-waste in Green Infrastructure to Reduce Perceived Value Loss through Landfill Siting and Landscaping: A Case Study in Nanjing, China. Sustainability 2019, 11, 1829. [Google Scholar] [CrossRef]
- Chabuk, A.; Al-Ansari, N.; Ezz-Aldeen, M.; Laue, J.; Pusch, R.; Hussain, H.M.; Knutsson, S. Two Scenarios for Landfills Design in Special Conditions Using the HELP Model: A Case Study in Babylon Governorate, Iraq. Sustainability 2018, 10, 125. [Google Scholar] [CrossRef]
- Eiselt, H.A. Locating landfills-Optimization vs. reality. Eur. J. Oper. Res. 2007, 179, 1040–1049. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Marianov, V. A bi-objective model for the location of landfills for municipal solid waste. Eur. J. Oper. Res. 2014, 235, 187–194. [Google Scholar] [CrossRef]
- Guiqin, W.; Li, Q.; Guoxue, L.; Lijun, C. Landfill site selection using spatial information technologies and AHP: A case study in Beijing, China. J. Environ. Manag. 2009, 90, 2414–2421. [Google Scholar]
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems, Part I: The p-centers. SIAM J. Appl. Math. 1979, 37, 513–538. [Google Scholar] [CrossRef]
- Hochbaum, D.S. When are NP-hard location problems easy? Ann. Oper. Res. 1984, 1, 201–214. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Sandblom, C.-L. Decision Analysis, Location Models, and Scheduling Problems; Springer: New York, NY, USA, 2004. [Google Scholar]
- Kratica, J.; Tosic, D.; Filipovic, V.; Ljubic, I. Solving the simple plant location problem by genetic algorithm. RAIRO-Oper. Res. 2001, 35, 127–142. [Google Scholar] [CrossRef]
- Jaramillo, J.H.; Bhadury, J.; Batta, R. On the use of genetic algorithms to solve location problems. Comput. Oper. Res. 2002, 29, 761–779. [Google Scholar] [CrossRef]
- Alp, O.; Erkut, E.; Drezner, Z. An Efficient Genetic Algorithm for the p-Median Problem. Ann. Oper. Res. 2003, 122, 21–42. [Google Scholar] [CrossRef]
- Maric, M. An efficient genetic algorithm for solving the multi-level uncapacitated facility location problem. Comput. Inform. 2010, 29, 183–201. [Google Scholar]
- Fernandes, D.R.M.; Rocha, C.; Aloise, D.; Ribeiro, G.M.; Santos, E.M.; Silva, A. A simple and effective genetic algorithm for the two-stage capacitated facility location problem. Comput. Ind. Eng. 2014, 75, 200–208. [Google Scholar] [CrossRef]
- Murray, A.T.; Church, R.L. Applying simulated annealing to location-planning models. J. Heuristics 1996, 2, 31–53. [Google Scholar] [CrossRef]
- Bornstein, C.T.; Azlan, H.B. The use of reduction tests and simulated annealing for the capacitated plant location problem. Locat. Sci. 1998, 6, 67–81. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, Z.; Wesolowsky, G.O. Location of Facilities on a Network with Groups of Demand Points. IIE Trans. 2001, 33, 637–648. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, Z.; Wesolowsky, G.O. The Facility and Transfer Plant Location Problem. Int. Trans. Oper. Res. 2005, 12, 387–402. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, A. Location of congested capacitated facilities with distance sensitive demand. IIE Trans. 2006, 38, 213–221. [Google Scholar] [CrossRef]
- Delmaire, H.; Dìaz, J.A.; Fernandez, E.; Ortega, M. Reactive GRASP and Tabu Search Based Heuristics for the Single Source Capacitated Plant Location Problem. INFOR 1998, 37, 194–225. [Google Scholar] [CrossRef]
- Al-Sultan, K.S.; Al-Fawzan, M.A. A Tabu Search Approach to the Uncapacitated Facility Location Problem. Ann. Oper. Res. 1999, 86, 91–103. [Google Scholar] [CrossRef]
- Mladenovic, N.; Labbé, M.; Hansen, P. Solving the p-center problem with tabu search and variable neighborhood search. Networks 2003, 42, 48–64. [Google Scholar] [CrossRef]
- Ghosh, D. Neighborhood Search Heuristics for the Uncapacitated Facility Location Problem. Eur. J. Oper. Res. 2003, 150, 150–162. [Google Scholar] [CrossRef]
- Sun, M. A tabu search heuristic procedure for the capacitated facility location problem. J. Heuristics 2012, 18, 91–118. [Google Scholar] [CrossRef]
- Ho, S.C. An iterated tabu search heuristic for the Single Source Capacitated Facility Location Problem. Appl. Soft Comput. 2015, 27, 169–178. [Google Scholar] [CrossRef]
- Whitaker, R. A Fast Algorithm for the Greedy Interchange of Large-Scale Clustering and Median Location Problems. INFOR 1983, 21, 95–108. [Google Scholar] [CrossRef]
- Resende, M.G.C.; Werneck, R.F. A Hybrid Heuristic for the p-Median Problem. J. Heuristics 2004, 10, 59–88. [Google Scholar] [CrossRef]
- ISPRA Catasto Rifiuti. Available online: http://www.catasto-rifiuti.isprambiente.it/index.php_?pg=provincia&aa=2015®id=Campania (accessed on 25 February 2019).
- Chan, Y.S.G.; Chu, L.M.; Wong, M.H. Influence of landfill factors on plants and soil fauna—An ecological perspective. Environ. Pollut. 1997, 97, 39–44. [Google Scholar] [CrossRef]
- Caplan, A.; Grijalva, T.; Jackson-Smith, D. Using choice question formats to determine compensable values: The case of a landfill-siting process. Ecol. Econ. 2007, 60, 834–846. [Google Scholar] [CrossRef][Green Version]
- Ferreira, S.; Gallagher, L. Protest responses and community attitudes toward accepting compensation to host waste disposal infrastructure. Land Use Policy 2010, 27, 638–652. [Google Scholar] [CrossRef]
- Giaccaria, S.; Frontuto, V. Perceived health status and environmental quality in the assessment of external costs of waste disposal facilities. An empirical investigation. Waste Manag. Res. 2012, 30, 864–870. [Google Scholar] [CrossRef] [PubMed]
- Jones, N.; Evangelinos, K.; Halvadakis, C.P.; Iosifides, T.; Sophoulis, C.M. Social factors influencing perceptions and willingness to pay for a market-based policy aiming on solid waste management. Resour. Conserv. Recy. 2010, 54, 533–540. [Google Scholar] [CrossRef]
- Lu, W.; Peng, Y.; Webster, C.; Zuo, J. Stakeholders’ willingness to pay for enhanced construction waste management: A Hong Kong study. Renew. Sustain. Energy Rev. 2015, 47, 233–240. [Google Scholar] [CrossRef]
- Challcharoenwattana, A.; Pharino, C. Wishing to finance a recycling program? Willingness-to-pay study for enhancing municipal solid waste recycling in urban settlements in Thailand. Habitat Int. 2016, 51, 23–30. [Google Scholar] [CrossRef]
- Gallagher, L.; Ferreira, S.; Convery, F. Host community attitudes towards solid waste landfill infrastructure: Comprehension before compensation. J. Environ. Plan. Man. 2008, 51, 233–257. [Google Scholar] [CrossRef]
- Hong, J.; Jung, M.J.; Kim, Y.-B.; Seo, Y.-C.; Koo, J. Analysis of the compensation system at the Environmental-Adverse-Effect Zone of a large-scale waste landfill site. J. Mater. Cycles Waste Manag. 2012, 14, 351–359. [Google Scholar] [CrossRef]
- Liu, J.; Teng, Y.; Jiang, Y.; Gong, E. A cost compensation model for construction and demolition waste disposal in South China. Environ. Sci. Pollut. Res. 2019, 26, 13773–13784. [Google Scholar] [CrossRef]
- Ren, X.; Che, Y.; Yang, K.; Tao, Y. Risk perception and public acceptance toward a highly protested Waste-to-Energy facility. Waste Manag. 2016, 48, 528–539. [Google Scholar] [CrossRef]
- Bathrellos, G.; Skilodimou, H.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef] [PubMed]
- Skilodimou, H.D.; Bathrellos, G.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Multi-hazard assessment modeling via multi-criteria analysis and GIS: A case study. Environ. Earth Sci. 2019, 78, 21. [Google Scholar] [CrossRef]
- D’Alisa, G.; Burgalassi, D.; Healy, H.; Walter, M. Conflict in Campania: Waste emergency or crisis of democracy. Ecol. Econ. 2010, 70, 239–249. [Google Scholar] [CrossRef]
- Cantoni, R. The waste crisis in Campania, South Italy: A historical perspective on an epidemiological controversy. Endeavour 2016, 40, 102–113. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, S.P. A political geography of ‘waste wars’ in Campania (Italy): Competing territorialisations and socio-environmental conflicts. Political Geogr. 2018, 67, 46–55. [Google Scholar] [CrossRef]
- Di Nola, M.F.; Escapa, M.; Ansah, J.P. Modelling solid waste management solutions: The case of Campania, Italy. Waste Manag. 2018, 78, 717–729. [Google Scholar] [CrossRef]
- Esposito, F.; Nardone, A.; Fasano, E.; Scognamiglio, G.; Esposito, D.; Agrelli, D.; Ottaiano, L.; Fagnano, M.; Adamo, P.; Beccaloni, E.; et al. A systematic risk characterization related to the dietary exposure of the population to potentially toxic elements through the ingestion of fruit and vegetables from a potentially contaminated area. A case study: The issue of the "Land of Fires" area in Campania region, Italy. Environ. Pollut. 2018, 243, 1781–1790. [Google Scholar]
- Cembalo, L.; Caso, D.; Carfora, V.; Caracciolo, F.; Lombardi, A.; Cicia, G. The “Land of Fires” ToxicWaste Scandal and Its Effect on Consumer Food Choices. Int. J. Environ. Res. Public Health 2019, 16, 165. [Google Scholar] [CrossRef]
- Garofalo, A.; Castellano, R.; Agovino, M.; Punzo, G.; Musella, G. How Far is Campania from the Best-Performing Region in Italy? A Territorial-Divide Analysis of Separate Waste Collection. Soc. Indic. Res. 2019, 142, 667–688. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).