Stochastic Drone Fleet Deployment and Planning Problem Considering Multiple-Type Delivery Service
Abstract
1. Introduction
- (1)
- This paper studies a new stochastic DFDP with uncertain parcel demand, which determines (i) the drone fleet deployment, i.e., the numbers of different types of drones deployed, (ii) the drone service module, and (iii) the numbers of parcels delivered by drones and couriers under each scenario of demand.
- (2)
- For the problem, a novel two-stage stochastic programming formulation is proposed and a classic sample average approximation (SAA) method is first employed. Since SAA is very time-consuming, a hybrid genetic algorithm (GA) is further developed to achieve computational efficiency.
- (3)
- A case study based on the delivery service of Ele.me in Shanghai Jinshan industrial park in China demonstrates the applicability of the proposed methods. Computational results show that, under a given number of scenarios, the hybrid GA outperforms SAA in terms of total computational time with high solution quality.
2. Literature Review
2.1. Operational-Level Drone Routing Problem
2.2. Tactical-Level Drone Facility Location and Drone Fleet Deployment Problem
2.3. Fleet Deployment and Planning Problem
3. Problem Description and Formulation
3.1. Problem Description
3.2. Formulation
- -
- : Number of drones of type deployed on service route , and .
- -
- : A binary variable equal to 1 if there is a drone of type deployed on service route , 0 otherwise, and .
- -
- : A binary variable equal to 1 if the service module is selected on route , 0 otherwise, and .
- -
- : Number of parcels of category transported by drones on leg of route under realized .
- -
- : A nonnegative integral variable used to linearize , and .
- -
- : A nonnegative integral variable used to linearize , and , .
- -
- : The recourse function value, i.e., the labor cost, with given , and under realized during the planning time period.
4. Solution Approaches
4.1. SAA
4.2. Hybrid GA
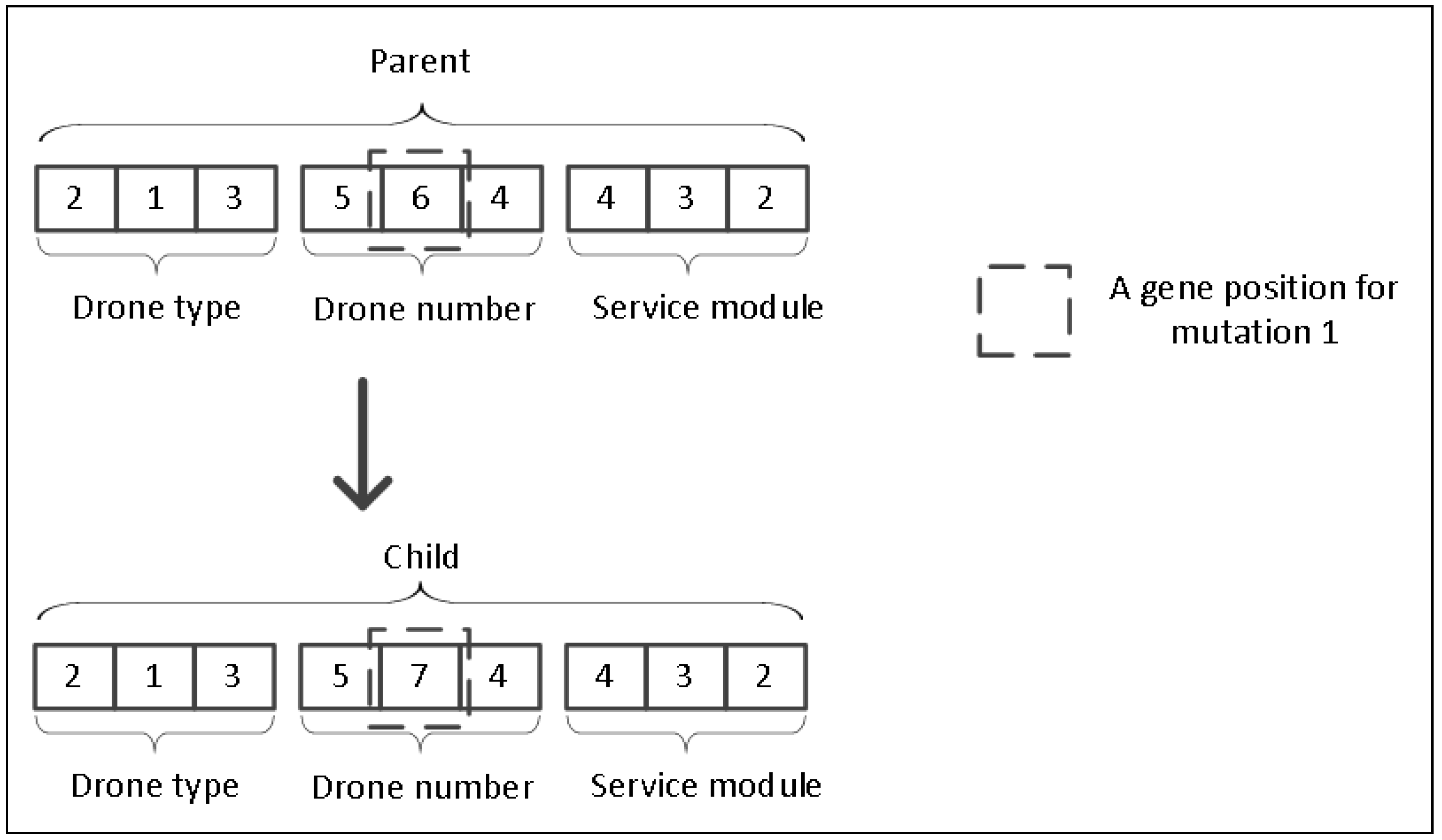
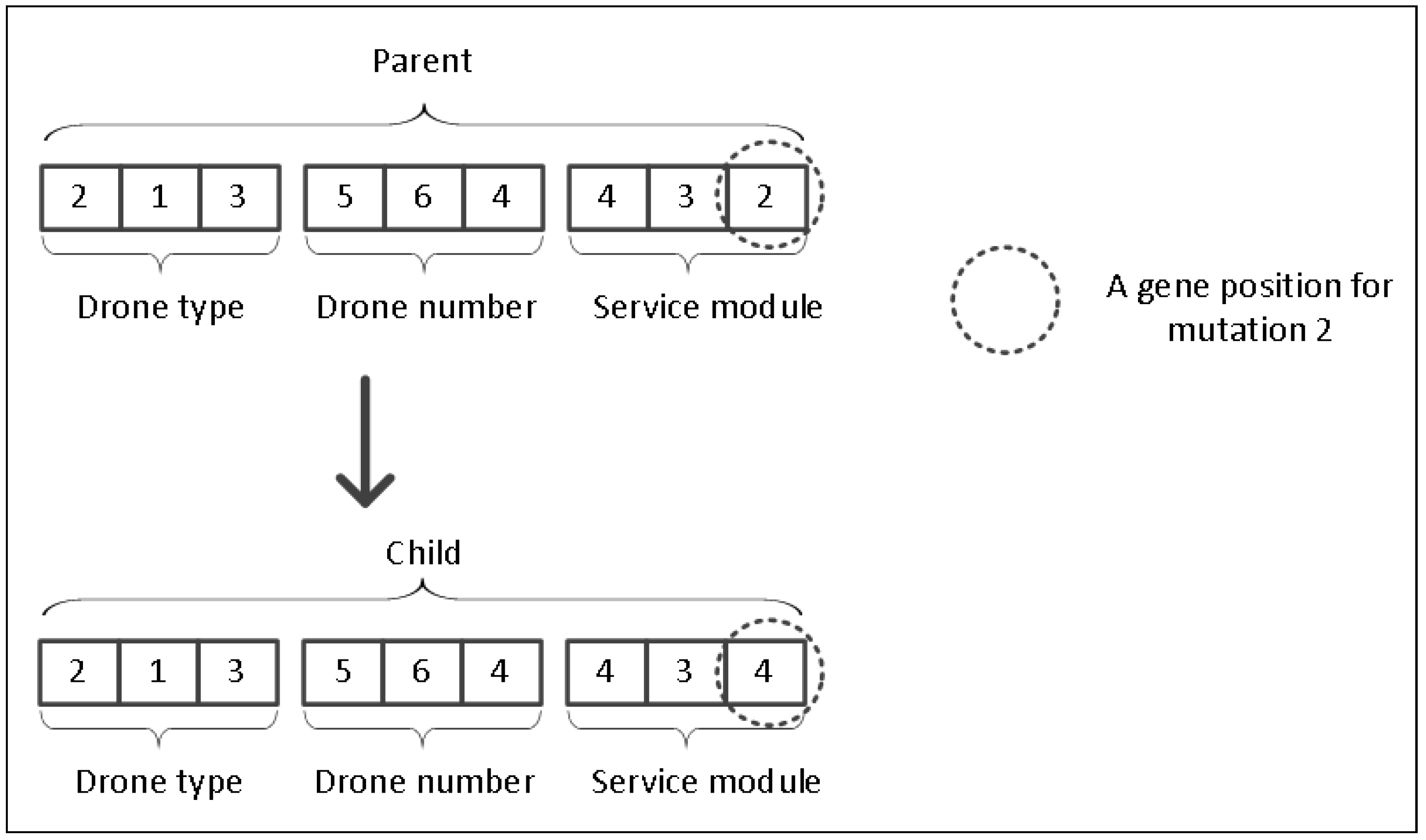
4.2.1. Coding
4.2.2. Crossover and Mutation
5. Computational Experiments
5.1. Data Generation
5.2. Computational Results
- (1)
- with the increase of the number of scenarios, the computational time of SAA increases dramatically;
- (2)
- given the same number of scenarios, the computational time of the hybrid GA is smaller than SAA with high solution quality;
- (3)
- with the increase of average drone speed and the total flight time, the number of drones deployed and the total cost decrease;
- (4)
- when the volume and weight capacities of drones increase, the number of drones deployed and the total cost decrease;
- (5)
- when the time intervals decrease, the number of drones deployed increases; and
- (6)
- the developed hybrid GA outperforms the SAA in terms of the computational time with high solution quality.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sikeridis, D.; Tsiropoulou, E.E.; Devetsikiotis, M.; Papavassiliou, S. Wireless powered Public Safety IoT: A UAV-assisted adaptive-learning approach towards energy efficiency. J. Netw. Comput. Appl. 2018, 123, 69–79. [Google Scholar] [CrossRef]
- Hong, I.; Kuby, M.; Murray, A.T. A range-restricted recharging station coverage model for drone delivery service planning. Transp. Res. Part Emerg. Technol. 2018, 90, 198–212. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Aleem, Z. The Chinese Version of Amazon Is Already Using Drones to Deliver Stuff to Customers; Vox Media, Inc.: New York, NY, USA, 2017. [Google Scholar]
- Rose, C. Amazon’s Jeff Bezos looks to the future. CBS News, 1 December 2013. [Google Scholar]
- Hu, Y. Your takeaway order in Shanghai might soon be delivered by a drone. Urban Family, 31 May 2018. [Google Scholar]
- Pymnts. Ele.me Clared to Use Food Delivery Drones in China. 2018. Available online: https://www.pymnts.com/news/delivery/2018/eleme-food-delivery-drones-china/ (accessed on 31 May 2018).
- Scott, J.; Scott, C. Drone delivery models for healthcare. In Proceedings of the 50th Hawaii International Conference on System Sciences, Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Nejad, M.G.; Rismanchian, F.; Izbirak, G. Application of hierarchical facility location problem for optimization of a drone delivery system: a case study of Amazon prime air in the city of San Francisco. Int. J. Adv. Manuf. Technol. 2018, 95, 3141–3153. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Chow, J.Y. Dynamic UAV-based traffic monitoring under uncertainty as a stochastic arc-inventory routing policy. Int. J. Transp. Sci. Technol. 2016, 5, 167–185. [Google Scholar] [CrossRef]
- Tavana, M.; Khalili-Damghani, K.; Santos-Arteaga, F.J.; Zandi, M.H. Drone shipping versus truck delivery in a cross-docking system with multiple fleets and products. Expert Syst. Appl. 2017, 72, 93–107. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 70–85. [Google Scholar] [CrossRef]
- Furini, F.; Persiani, C.A.; Toth, P. The time dependent traveling salesman planning problem in controlled airspace. Transp. Res. Part Methodol. 2016, 90, 38–55. [Google Scholar] [CrossRef]
- Keeney. How Can Amazon Charge $1 for Drone Delivery. 2015. Available online: https://ark-invest.com/research/drone-delivery-amazon (accessed on 5 May 2015).
- Perdikaki, O.; Kostamis, D.; Swaminathan, J.M. Timing of service investments for retailers under competition and demand uncertainty. Eur. J. Oper. Res. 2016, 254, 188–201. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer: New York, NY, USA, 2011. [Google Scholar]
- Liu, M.; Liu, X.; Zhang, E.; Chu, F.; Chu, C. Scenario-based heuristic to two-stage stochastic program for the parallel machine ScheLoc problem. Int. J. Prod. Res. 2019, 57, 1706–1723. [Google Scholar] [CrossRef]
- Francis, P.; Smilowitz, K.; Tzur, M. The period vehicle routing problem with service choice. Transp. Sci. 2006, 40, 439–454. [Google Scholar] [CrossRef]
- Guenard, N.; Hamel, T.; Mahony, R. A practical visual servo control for an unmanned aerial vehicle. IEEE Trans. Robot. 2008, 24, 331–340. [Google Scholar] [CrossRef]
- McGonigle, A.; Aiuppa, A.; Giudice, G.; Tamburello, G.; Hodson, A.; Gurrieri, S. Unmanned aerial vehicle measurements of volcanic carbon dioxide fluxes. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Dunford, R.; Michel, K.; Gagnage, M.; Piégay, H.; Trémelo, M.L. Potential and constraints of Unmanned Aerial Vehicle technology for the characterization of Mediterranean riparian forest. Int. J. Remote Sens. 2009, 30, 4915–4935. [Google Scholar] [CrossRef]
- Baluja, J.; Diago, M.P.; Balda, P.; Zorer, R.; Meggio, F.; Morales, F.; Tardaguila, J. Assessment of vineyard water status variability by thermal and multispectral imagery using an unmanned aerial vehicle (UAV). Irrig. Sci. 2012, 30, 511–522. [Google Scholar] [CrossRef]
- Herissé, B.; Hamel, T.; Mahony, R.; Russotto, F.X. Landing a VTOL unmanned aerial vehicle on a moving platform using optical flow. IEEE Trans. Robot. 2011, 28, 77–89. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Unmanned aerial vehicle with underlaid device-to-device communications: Performance and tradeoffs. IEEE Trans. Wirel. Commun. 2016, 15, 3949–3963. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Thomas, B.W. Same-day delivery with heterogeneous fleets of drones and vehicles. Networks 2018, 72, 475–505. [Google Scholar] [CrossRef]
- Campbell, J.F.; Sweeney, D.; Zhang, J. Strategic Design for Delivery with Trucks and Drones; Supply Chain Analytics Report SCMA; SCMA-2017-0201; University of Missouri-St. Louis: St. Louis, MO, USA, 2017. [Google Scholar]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization approaches for the traveling salesman problem with drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Venkatachalam, S.; Sundar, K.; Rathinam, S. Two-stage stochastic programming model for routing multiple drones with fuel constraints. arXiv 2017, arXiv:1711.04936. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile unmanned aerial vehicles (UAVs) for energy-efficient internet of things communications. IEEE Trans. Wirel. Commun. 2017, 16, 7574–7589. [Google Scholar] [CrossRef]
- Sikeridis, D.; EleniTsiropoulou, E.; Devetsikiotis, M.; Papavassiliou, S. Self-Adaptive Energy Efficient Operation in UAV-Assisted Public Safety Networks. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Wang, S.; Meng, Q. Liner ship route schedule design with sea contingency time and port time uncertainty. Transp. Res. Part B 2012, 46, 615–633. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, S. Liner ship fleet deployment with week-dependent container shipment demand. Eur. J. Oper. Res. 2012, 222, 241–252. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Robust bunker management for liner shipping networks. Eur. J. Oper. Res. 2015, 243, 789–797. [Google Scholar] [CrossRef]
- Kleywegt, A.J.; Nori, V.S.; Savelsbergh, M.W.P. The Stochastic Inventory Routing Problem with Direct Deliveries. Transp. Sci. 2002, 36, 94–118. [Google Scholar] [CrossRef]
- Pagnoncelli, B.K.; Ahmed, S.; Shapiro, A. Sample Average Approximation Method for Chance Constrained Programming: Theory and Applications. J. Optim. Theory Appl. 2009, 142, 399–416. [Google Scholar] [CrossRef]
- Ralph, D.; Xu, H. Convergence of stationary points of sample average two-stage stochastic programs: A generalized equation approach. Math. Oper. Res. 2011, 36, 568–592. [Google Scholar] [CrossRef]
- Verweij, B.; Ahmed, S.; Kleywegt, A.J.; Nemhauser, G.; Shapiro, A. The sample average approximation method applied to stochastic routing problems: a computational study. Comput. Optim. Appl. 2003, 24, 289–333. [Google Scholar] [CrossRef]
- Wang, W.; Ahmed, S. Sample average approximation of expected value constrained stochastic programs. Oper. Res. Lett. 2008, 36, 515–519. [Google Scholar] [CrossRef]
- Bertsimas, D.; Gupta, V.; Kallus, N. Robust sample average approximation. Math. Program. 2017, 171, 217–282. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Polat, O.; Gupta, S.M. A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem. Ann. Oper. Res. 2016, 242, 321–354. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in natural and artificial systems. Q. Rev. Biol. 1975, 6, 126–137. [Google Scholar]
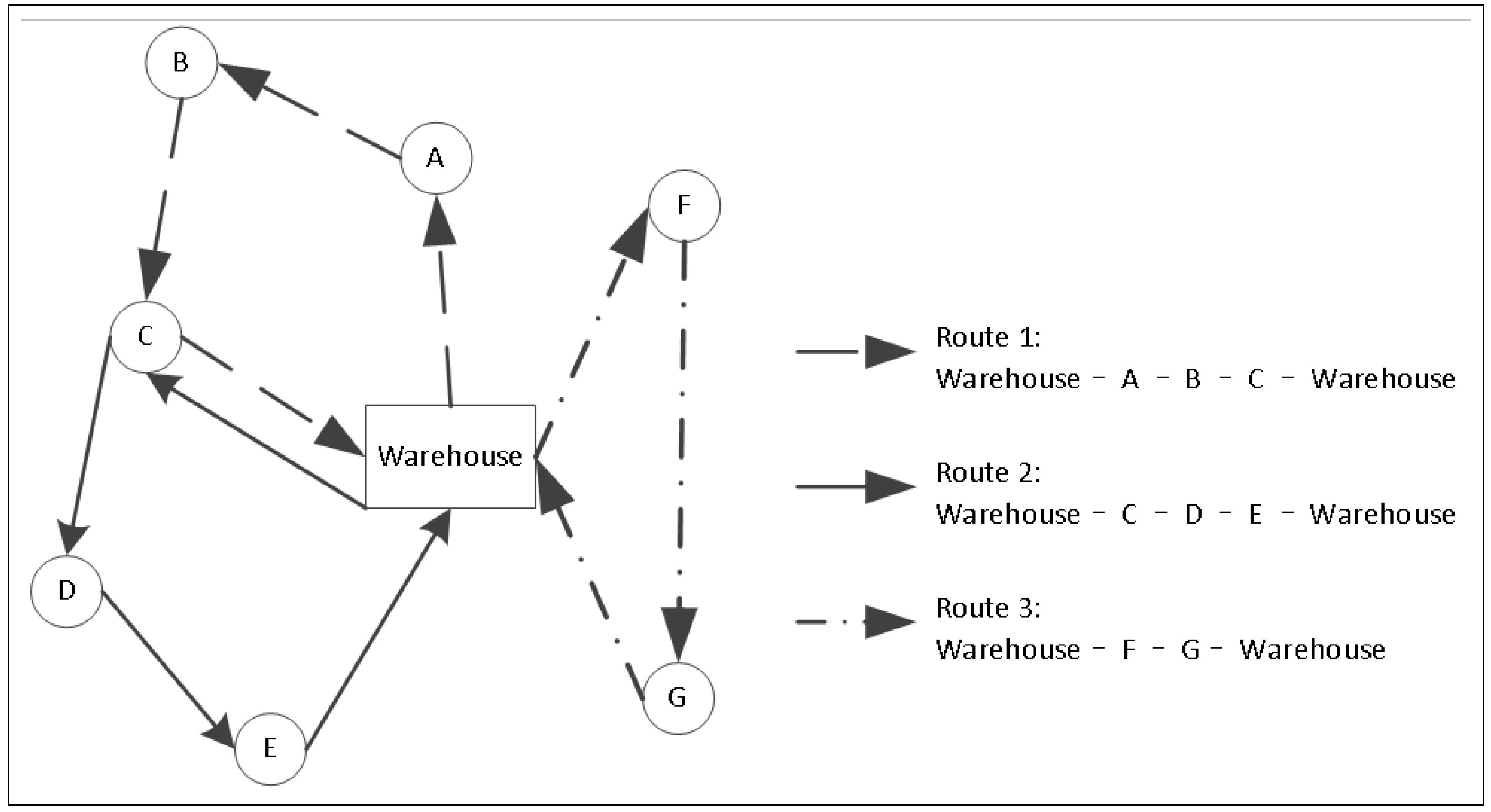
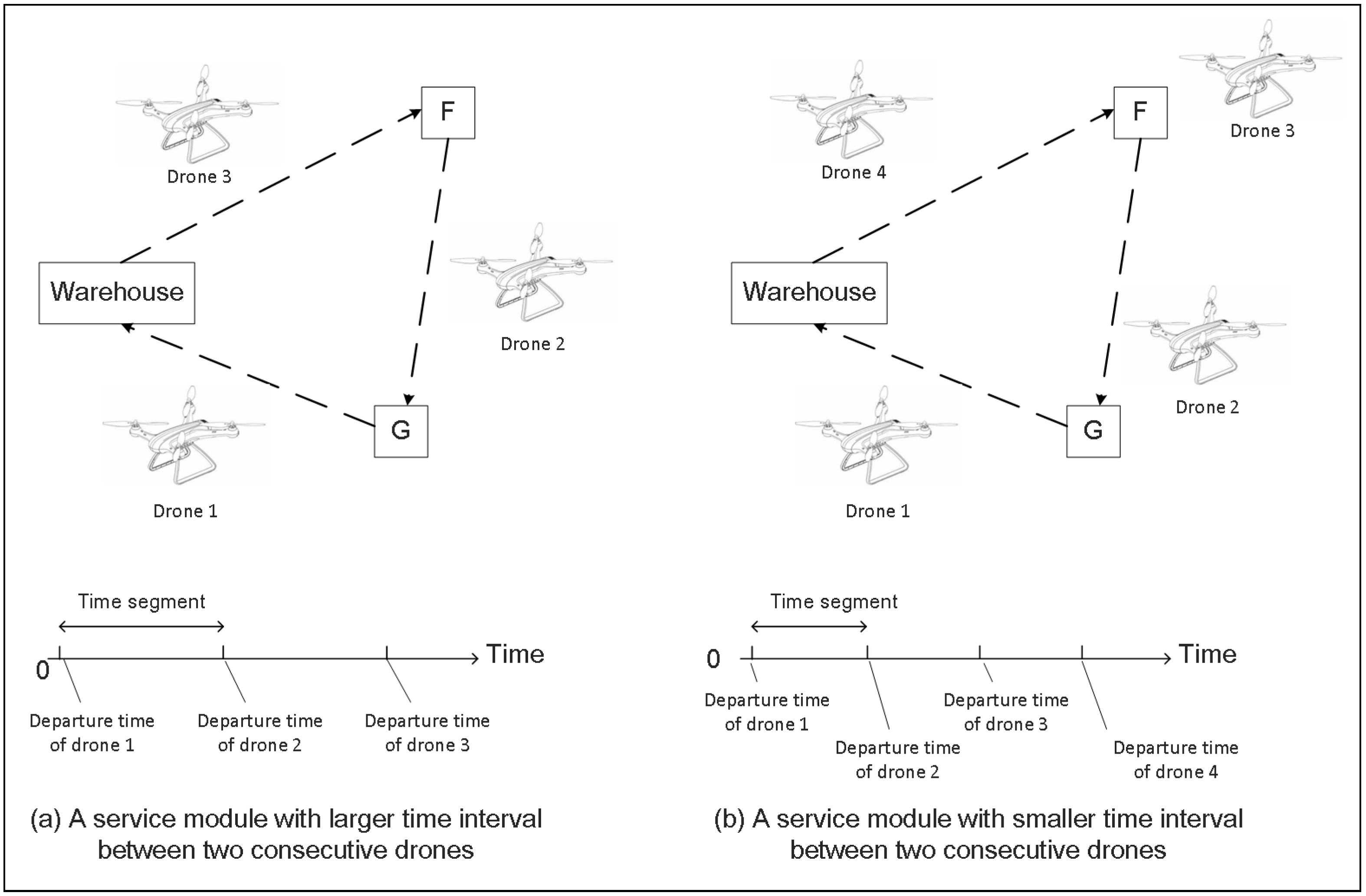
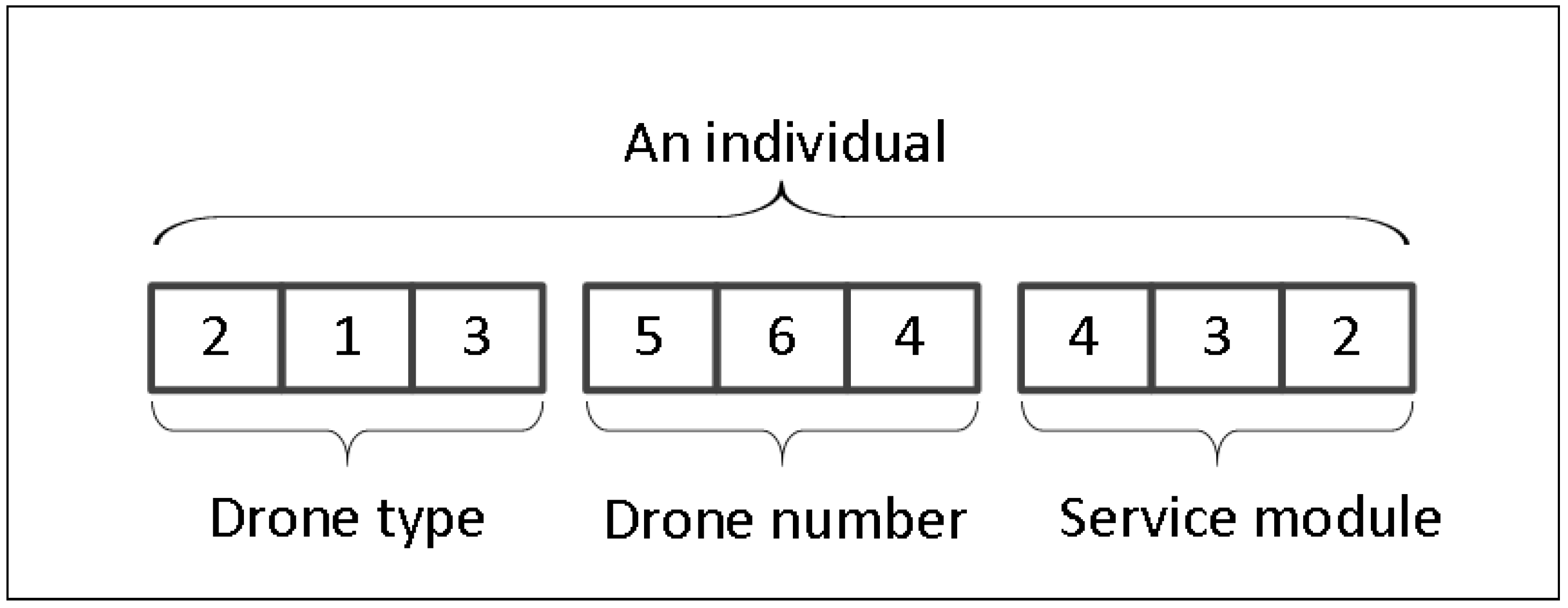
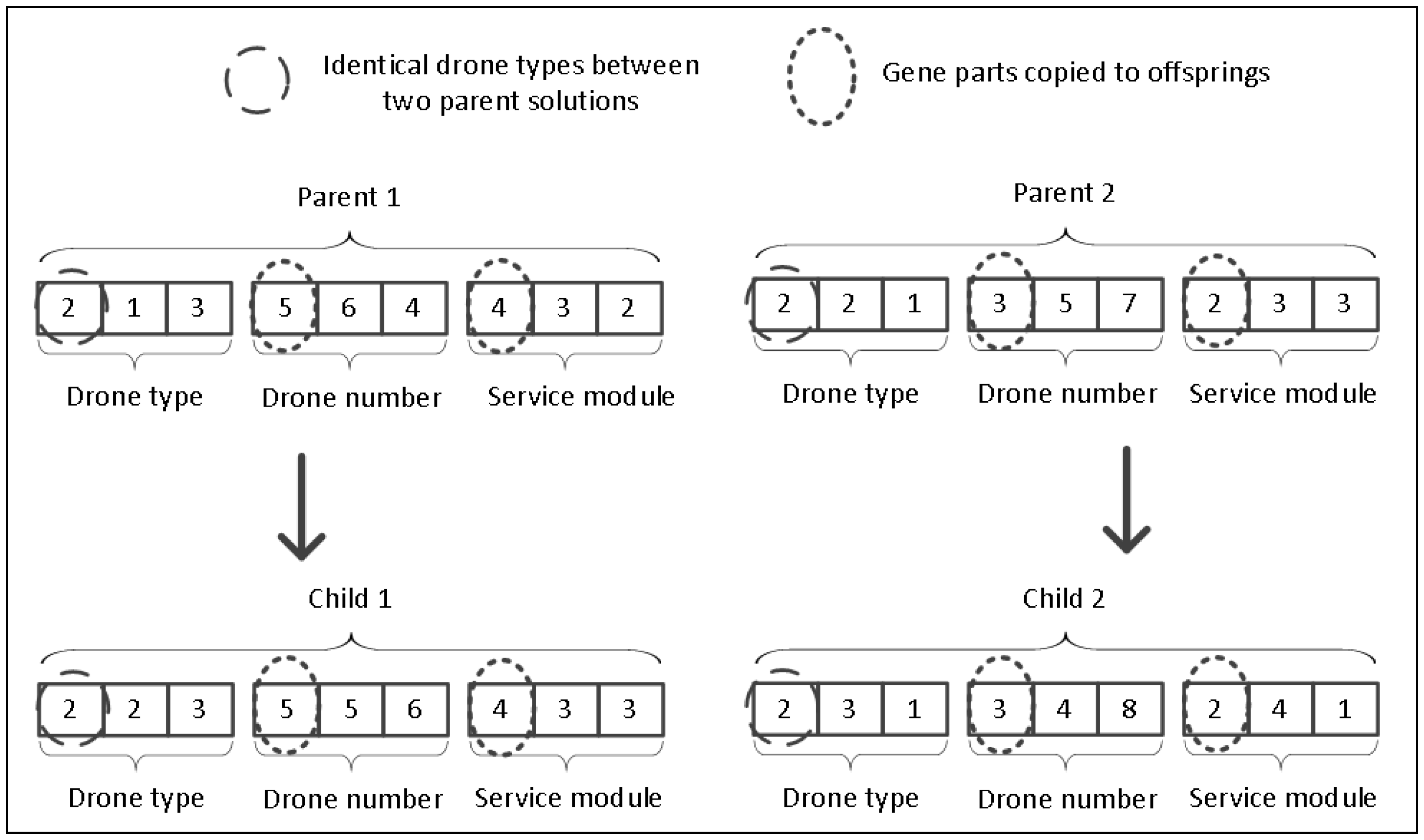
| i: | Index of legs on a service route. |
| : | Set of service routes indexed by r. |
| : | Set of all drone types indexed by l. |
| : | Set of drone service modules indexed by k. |
| : | Set of parcel categories indexed by h. |
| : | Number of customers visited by service route . |
| : | Set of customers on service route , and . |
| : | Service frequency in the planning time period under service module . |
| : | Time interval between two consecutive drones under service module . |
| : | Volume capacity of a drone of type . |
| : | Weight capacity of a drone of type . |
| : | Total travel time of a drone of type on service route . |
| : | Fixed leasing (or amortized purchasing) cost in the planning time period of a drone of type . |
| : | Variable cost for operating a drone of type per flight on each route. |
| : | Cost for a courier handling a parcel of category on the i-th leg of service route . |
| : | Stochastic demand per time unit of category on leg i of route . |
| : | Volume of a parcel of category . |
| : | Weight of a parcel of category . |
| D: | Number of time units in the planning time period. |
| M: | A large enough number. |
| Parameter | Value (Hybrid GA) |
|---|---|
| Population size | 50 |
| Generation number | 20 |
| Crossover probability | 0.9 |
| Mutation 1 probability | 0.2 |
| Mutation 2 probability | 0.8 |
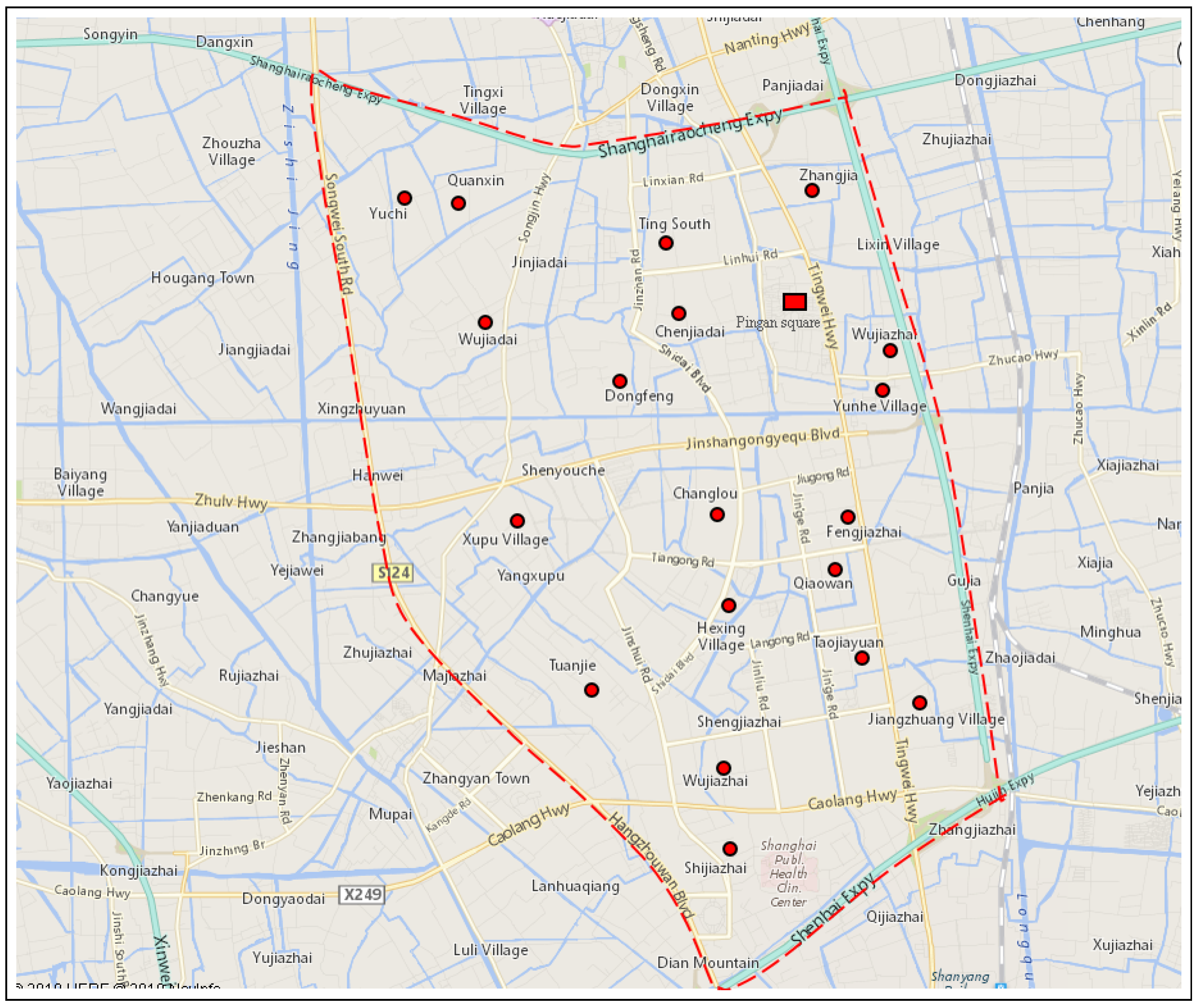
| ID | Service Routes |
|---|---|
| 1 | Pingan Square → Yunhe Village → Wujiazhai → Zhangjia → Ting South → Pingan Square |
| 2 | Pingan Square → Chenjiadai → Dongfeng → Wujiadai →Yuchi → Quanxin → Ting South → Pingan Square |
| 3 | Pingan Square → Dongfeng → Xupu Village → Tuanjie → Changlou → Pingan Square |
| 4 | Pingan Square → Changlou → Hexing Village → Qiaowan → Pingan Square |
| 5 | Pingan Square → Changlou → Fengjiazhai → Hexing Village → Taojiayuan → Qiaowan → Pingan Square |
| 6 | Pingan Square → Hexing Village → Wujiazhai → Shijiazhai → Jiangzhunag Village → Pingan Square |
| 7 | Pingan Square → Zhangjia → Wujiazhai → Yunhe Village → Fengjiazhai → Changlou → Dongfeng → Chenjiadai → Pingan Square |
| 8 | Pingan Square → Ting South → Wujiadai → Xupu Village → Tuanjie → Hexing Village → Qiaowan → Pingan Square |
| 9 | Pingan Square → Taojiayuan → Jiangzhuang Village → Yunhe village → Pingan Square |
| 10 | Pingan Square → Hexing Village → Wujiazhai → Shijiazhai → Tuanjie → Changlou → Pingan Square |
| 11 | Pingan Square → Xupu Village → Wujiadai → Yuchi → Quanxin → Chejiadai → Pingan Square |
| Drone Type | Capacity | |||
|---|---|---|---|---|
| Volume (m) | Weight (kg) | Operating Cost (Yuan) | Average Speed (km/h) | |
| 1 | 1 | 30 | 350 | 20 |
| 2 | 2 | 35 | 420 | 30 |
| 3 | 3 | 40 | 490 | 40 |
| Parcel Category | Volume (m) | Weight (kg) | Labor Cost Per Parcel Per Kilometer (Yuan) |
|---|---|---|---|
| 1 | 0.01 | 1 | 0.2 |
| 2 | 0.02 | 2 | 0.4 |
| 3 | 0.01 | 2 | 0.3 |
| 4 | 0.02 | 1 | 0.3 |
| Route | Deterministic Situation | SAA | HGA | |||
|---|---|---|---|---|---|---|
| Service module | Service Module | Service Module | ||||
| 1 | 2 | 2 | 4 | 1 | 4 | 1 |
| 2 | 2 | 2 | 3 | 1 | 3 | 1 |
| 3 | 2 | 2 | 3 | 1 | 3 | 1 |
| Obj | 5003 | 4900 | 4987 | |||
| SAA | HGA | |||||
|---|---|---|---|---|---|---|
| Obj () | Time (s) | Obj () | Time (s) | |||
| 3 | 50 | 7.3531 | 56.0 | 50 | 7.5165 | 48.2 |
| 5 | 50 | 6.3544 | 119.3 | 50 | 6.3795 | 66.9 |
| 10 | 50 | 6.8960 | 462.7 | 50 | 7.0713 | 79.8 |
| 15 | 50 | 6.9026 | 2883.2 | 50 | 6.9867 | 89.5 |
| 20 | 50 | 7.1125 | 3600.0 | 50 | 7.1602 | 112.4 |
| 25 | - | - | - | 50 | 7.0799 | 138.6 |
| 30 | - | - | - | 50 | 7.0001 | 164.2 |
| 35 | - | - | - | 50 | 6.9762 | 189.4 |
| 40 | - | - | - | 50 | 6.8648 | 249.8 |
| 50 | - | - | - | 50 | 6.8782 | 308.7 |
| Average | 50 | 6.9237 | 1424.2 | 50 | 6.9913 | 144.8 |
| Lower bound | 50 | 6.3544 | 56.0 | 50 | 6.3795 | 48.2 |
| Upper bound | 50 | 7.3531 | 3600.0 | 50 | 7.5165 | 308.7 |
| Increase of the | SAA with 10 Scenarios | HGA with 50 Scenarios | ||||
|---|---|---|---|---|---|---|
| Average Drone Speed | Time (s) | Obj() | Time (s) | Obj() | ||
| 0 | 50 | 463.2 | 6.8960 | 50 | 312.7 | 6.8782 |
| 5 | 44 | 465.3 | 6.2485 | 44 | 306.3 | 6.8488 |
| 10 | 42 | 468.9 | 6.1849 | 42 | 317.9 | 6.8390 |
| 15 | 39 | 472.1 | 6.2458 | 39 | 317.2 | 6.8243 |
| 20 | 35 | 471.6 | 6.2346 | 36 | 318.3 | 6.8047 |
| 25 | 34 | 465.8 | 6.1793 | 34 | 306.6 | 6.7998 |
| 30 | 30 | 466.9 | 6.1345 | 31 | 309.9 | 6.7802 |
| Average | 39.1 | 467.7 | 6.3034 | 39.4 | 312.7 | 6.8250 |
| Increase of Volume | SAA with 10 Scenarios | HGA with 50 Scenarios | ||||
|---|---|---|---|---|---|---|
| and Weight Capacities | Time (s) | Obj() | Time (s) | Obj() | ||
| (0, 0) | 50 | 467.5 | 6.8960 | 50 | 313.3 | 6.8782 |
| (0.5, 5) | 37 | 472.6 | 6.7510 | 37 | 311.0 | 6.8145 |
| (0.5, 10) | 37 | 468.9 | 6.2560 | 37 | 309.8 | 6.8145 |
| (1, 5) | 37 | 469.8 | 6.2346 | 36 | 320.4 | 6.8047 |
| (1, 10) | 37 | 470.6 | 6.1793 | 37 | 322.7 | 6.7998 |
| Average | 39.6 | 469.9 | 6.4634 | 39.4 | 315.4 | 6.8223 |
| Decrease of | SAA with 10 Scenarios | HGA with 50 Scenarios | ||||
|---|---|---|---|---|---|---|
| Time Intervals | Time (s) | Obj() | Time (s) | Obj() | ||
| 0 | 50 | 466.1 | 6.8960 | 50 | 314.6 | 6.8782 |
| 1 | 62 | 464.2 | 2.4349 | 62 | 310.4 | 2.9725 |
| 2 | 81 | 478.1 | 0.9162 | 81 | 313.4 | 1.2973 |
| 3 | 117 | 472.9 | 0.5733 | 117 | 319.5 | 0.5769 |
| 4 | 229 | 469.8 | 1.1221 | 228 | 320.3 | 1.1221 |
| Average | 107.8 | 470.22 | 2.3885 | 107.6 | 315.6 | 2.5694 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Liu, X.; Zhu, M.; Zheng, F. Stochastic Drone Fleet Deployment and Planning Problem Considering Multiple-Type Delivery Service. Sustainability 2019, 11, 3871. https://doi.org/10.3390/su11143871
Liu M, Liu X, Zhu M, Zheng F. Stochastic Drone Fleet Deployment and Planning Problem Considering Multiple-Type Delivery Service. Sustainability. 2019; 11(14):3871. https://doi.org/10.3390/su11143871
Chicago/Turabian StyleLiu, Ming, Xin Liu, Maoran Zhu, and Feifeng Zheng. 2019. "Stochastic Drone Fleet Deployment and Planning Problem Considering Multiple-Type Delivery Service" Sustainability 11, no. 14: 3871. https://doi.org/10.3390/su11143871
APA StyleLiu, M., Liu, X., Zhu, M., & Zheng, F. (2019). Stochastic Drone Fleet Deployment and Planning Problem Considering Multiple-Type Delivery Service. Sustainability, 11(14), 3871. https://doi.org/10.3390/su11143871





