Abstract
Since its origins, the idea of sustainability has always been linked to forest management. However, nowadays, sustainable forest management has usually been approached by defining a set of criteria and indicators. This paper aims to address sustainability in forest management including a set of criteria encompassing the most common decisions: whether the stands are even or uneven-aged, and the optimal silviculture that should be applied in each stand. For this purpose, a lexicographic goal programming model with two priority levels has been defined, into which six different criteria are integrated. Each criterion corresponds to a particular pillar (economic, technical, or environmental). Furthermore, also incorporated into the model are the preferences of diverse stakeholders, both for the criteria considered in the analysis and for the most suitable silvicultural alternatives to be applied in each stand. This methodology has been applied to a case study in Spain, and the results show much more attractive solutions than the current forest management planning, allowing the obtainment of multi-aged systems that could be favourable for other ecosystem services.
1. Introduction
The concept of sustainability in a forestry perspective has a development history that dates over 300 years back in time [1], without the author himself having supplied any definition of this term [2]. In some respects, this idea at that time was the first conservation principle ever formulated [3]. In recent decades, it has spread in an exceptional manner to other areas [4]. To some authors, the sustainability concept is currently belonging to the field of social ethics [5]. Nowadays, it continues to be a forceful message with a wide representation in diverse disciplines [6]. In synthesis, von Carlowitz’s premise promoted the concept of not exhausting resources in order to bequeath them to future generations, safeguarding finite natural resources for future generations [7].
In order to integrate sustainability into forest management, it has been customary to define a multidisciplinary ensemble of criteria and indicators in order to arrive at a consensus as to what sustainable forest management should be like [8], although sometimes it is not easy to transfer this idea to a strategic level [9]. It has been successfully applied on different spatial scales, using more or less aggregated information. Thus, there are indicators for sustainable forest management focused at a national or supranational level [10,11], or at a management unit level [12,13]. Further, in order to include this concept of sustainability in forest management, tools like certification systems aimed at ensuring sustainable management in forests have been developed. Thus, the systems most used nowadays simply require compliance with a series of indicators [14]. However, although it is commonly believed that a certification scheme implies a sustainability attribute, this direct relationship is not always clear [15].
On the basis of the literature consulted, it has been verified that the definition of sustainable forest management was usually of a static nature. That is to say, the studies in question contained only one measurement of the indicators, without taking into account their temporal evolution, in spite of this component being included in the definition of the word sustainability [16]. However, only in some studies has it been proposed to measure a set of criteria over the entire planning horizon covering forest management in a certain case study [17,18,19]. Given the extensive length of rotations in many forest systems, it is necessary to have a set of indicators available whose values are known in each period or, at least, are quantifiable at the end of the planning horizon.
Given the multidimensional nature intrinsic to the concept of sustainability, and as has been mentioned previously, the need to apply multifunctional management requires the use of Multi-Criteria Decision-Making (MCDM) techniques. These methodologies have been widely employed to solve typical forest management problems [20,21,22]. Moreover, multicriteria methods have been applied prolifically to tackle aspects related to sustainability [23,24,25,26], even dealing with aggregation problems and dynamic sustainability indicators [27]. These methodologies are also recommendable for integrating different ecosystem services into the decision-making process [28,29,30]. Finally, it is fitting to insist that these methods permit the solution of the emergent problem of how to aggregate the indicators on which the idea of sustainability is based [31].
Bearing in mind that sustainability is difficult to define in precise terms [32,33], the main objective of this study is to present a flexible model, based on multicriteria techniques. These kinds of models permit the redefinition of sustainability in a forest system, not at one specific moment, but through the evolution of the indicators considered throughout the planning horizon. This new view of sustainability should address the multifunctionality of forest systems, which implies defining a diverse set of criteria and indicators, choosing the best silvicultural alternative for each stand, and enabling the stakeholders involved to have their opinion integrated into it. It should be emphasized that some authors have affirmed that the rigidity of the concept of a normal forest does not ensure the idea of sustainability in force today [34], which would justify using the approach proposed here in order to adapt this notion to the present-day context. Finally, in the following Sections, we will introduce terms like “criterion”, “objective”, “indicator” and “index”. In order to avoid misinterpretations, and following [35], under an MCDM umbrella, criteria are the objectives or goals to be considered relevant for a certain decision-making situation. However, if applicable, we have considered a hierarchy between criteria and indicators. Indicators are parameters or sub-criteria which can be measured, and which correspond to a particular criterion. Besides, some sustainability measurements can be defined as a synthetic, aggregate, or composite index, and the value achieved by this index is a proxy of the respective sustainability goodness.
2. Theoretical Background
2.1. Framework
The stages of the model proposed are condensed in Figure 1A. The first step involves defining both the sustainability indicators selected for the planning horizon chosen, and the different silvicultural alternatives put forward. Applying both the indicators and the silvicultural alternatives to the case study, precise information is made available for the formulation of a strategic forest planning model. If each criterion considered is optimized separately, the pay-off matrix can be set up and the degree of conflict between the different criteria verified [35]. If no solution is supplied by the pay-off matrix, coming from the optimization of a single criterion is acceptable. The following step is to construct an MCDM model, integrating the opinions of the stakeholders (DMs) on some aspects. In that way, compromise solutions that could be accepted by the decision-maker will be obtained.
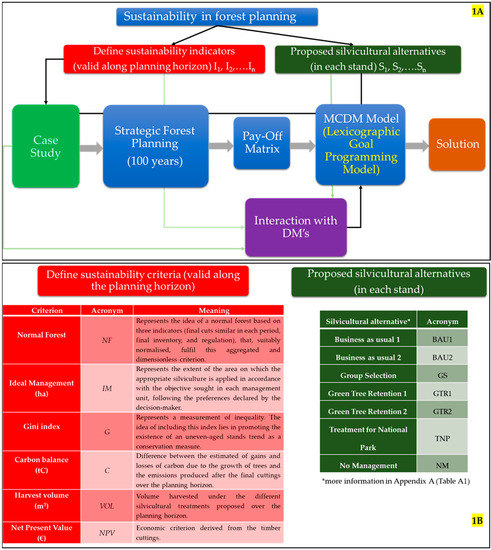
Figure 1.
Framework for integrating sustainability into forest planning (1A). Sustainability criteria and silvicultural alternatives proposed (1B).
As previously mentioned, the methodology to be applied is based on MCDM techniques, because the latter are highly appropriate when facing this type of problem. However, although, under the MCDM umbrella, a large set of techniques co-exist [36], due to the nature of the problem, only those that can solve continuous-type problems will be apt. This circumstance implies that those techniques that aim to choose the best solution out of a finite set of alternatives would not be valid for this case. From the MCDM techniques that fulfil the above condition, goal programming has been selected. This methodology adds flexibility to forest management models [37], and it has been used quite frequently to tackle this type of problem [31]. The basics of goal programming can be seen in [38,39,40].
Among the variants of this technique typically employed [39], we chose Lexicographic Goal Programming (LGP), also known as Non-Archimedean or pre-emptive goal programming [41]. The selection of this technique is justified because it allows the decision-making centre to show an order of preference for each of the goals defined. In addition, the idea of defining sustainability by means of a conceptual hierarchy [42] fits the LGP notion perfectly. This hierarchy manifests itself in the definition of different levels of priority to which each goal is attached. This means that the preferences are initially assigned to each goal following an established order, and that the achievement of a goal situated at a certain level of priority is infinitely preferred to the fulfilment of one located at a lower priority level. In short, this type of modelling implies accepting that there are no finite trade-offs among the goals placed at one priority level with respect to goals placed at lower ones [35]. Consequently, the results obtained for the goals situated at lower priority levels cannot worsen those of the goals at higher priority levels [43]. The mathematical formulation can be seen in Appendix B. Once the goals are defined [44], the variant of the weighted goal programmed is selected to solve the problem at each priority level [45], this being the most common option when electing this goal programming variant [46].
With the methodology shown in Appendix B, a model is obtained which permits the evaluation of the different criteria or indicators considered for defining sustainability over the defined time period, in the context of strategic forest planning [9]. The preferences introduced into the model will only take into account the opinion of the stakeholders and exclude intergenerational justice components from the analysis [47]. In addition, only criteria for which values can be obtained throughout the entire planning horizon are considered [31]. That is to say, if the evolution over time of a certain criterion cannot be modelled, it is not included in the analysis. Further, it is assumed that the silvicultural alternatives that can be applied in each of the stands are known with certainty. The model proposed is totally deterministic, and the introduction of elements of risk and/or uncertainty is not considered [48,49,50]. Finally, although, in previous work, diverse climate change scenarios have been analyzed in the same case study [51,52], the latter will not be included in this work, although the results for some ecosystem services like carbon sequestration could be altered according to the different scenarios contemplated [53].
The next step is to design a strategic forest planning model (see Appendix B). In order to assess the degree of conflict between the criteria considered, a pay-off matrix was developed starting from the results of the strategic forest planning model. This is a usual step in the application of multicriteria techniques in forest management problems [54,55]. The pay-off matrix is a square matrix, whose dimension coincides with the number of objectives considered. This matrix is obtained by optimizing the six objectives separately and computing the values of the criteria for each of the corresponding optimal solutions, thus having a dimension equal to the number of objectives that exist [35]. The main diagonal includes the optimum values that each objective can reach, known as the ideal point. By definition, this vector in the objective space is infeasible, but plays a decisive role as a point of reference [56]. Other cells of the matrix contain the anti-ideal (nadir) points, which would be the worst results obtained for each of the objectives. Concerning the criteria considered, it is appropriate to clarify that VOL, NPV, IM and C are criteria belonging to the type “the more, the better”, while NF and G are criteria belonging to the type “the less, the better”, following the term used in [35].
2.2. Theory Review
The primordial concept of sustainability has marked the development of forest science both in Europe and in the U.S.A. [57], and it has become a leading component of forest management over the last 250 years [58]. Similarly, it has been considered to be an integral part of forest management [33] and has been accepted almost unanimously by foresters [59]. Generally, in the past, sustainability was based on a few basic principles in accordance with the type of forest management practiced at the time, which was centered on the “normal forest” or “normality” concept [60], established at the end of the 18th century by German foresters [61]. In fact, it was characterized by being a mono-objective management, focused only on timber production, usually in regular stands, in which one or a few main species prevailed [62], and to which a silviculture with a fixed rotation was applied [63]. In addition, a single decision-maker made the corresponding decisions with the aim of perpetuating the idea of a fully-regulated forest [57,64]. Finally, as a result, and unlike what happens nowadays [65], restrictions to final harvest were very lenient.
The concept of sustainability has been modified and updated due, among other reasons, to the changes in the role played by forests in society [66,67]. Besides that, the demand for goods and services coming from forest systems has been continuously increasing [68], meaning that, today, forest management is much more polyhedral (or multi-faceted, according to [69]) than it was three centuries ago, and includes other ecosystem services not contemplated in the original idea of sustainability, such as in the case of biodiversity [70]. Indeed, some authors have recently gone beyond the theory of von Carlowitz and defined forests as a “multifunctional bioeconomic system” [71]. Thus, numerous authors maintain that the new paradigms associated with sustainability should promote multifunctionality in forest management [72]. At the same time, the idea of sustainability in forest management has been linked to that of resilience [73]. In this regard, although the expression “sustainable” has for many years been on a par with forest management [74], nowadays it has been assumed that the latter should achieve certain goals with respect to economic, social and environmental pillars and, also, balancing present and future demands [75]. Some authors even propose the concept of “ecologically sustainable forest management” to give prominence to a type of forest management that perpetuates ecosystem integrity [76].
The way forest management has evolved has required the reformulation of the original sustainability concept [1] into the idea of a “regulated forest” (the organization of a forest property to provide a sustained yield of timber products forms [57]), by integrating the abovementioned pillars, but taking into account that, on some occasions, the trade-offs between different criteria are not fully known [77]. That is why sustainability should not be defined by only focusing on the conception of its being concentrated on “sustained yield”, one of the objectives most sought after in forest management [78], or on other similar concepts [47]. Namely, this idea should be generalized starting from a case in which not all the forest should be associated with the idea of even-aged stands into which different silvicultural alternatives are established [63]; other ecosystem services are integrated, as well as timber production; and the preferences of the different stakeholders in the decision-making process are included. In effect, a multi-aged structure in forest stands is associated with the idea of long-term sustainability [79], incorporating multiple uses into different stands even with variable rotations [32]. Lastly, the inclusion of different silvicultural alternatives in the analysis is basically justified for two reasons. First, because different forest management strategies promote biodiversity [80], and, second, because silviculture as a science has to respond to the demands of society and not only concentrate on timber production [81].
3. Materials and Methods
3.1. Case Study
The case study corresponds to Valsaín forest, which is in the Central Mountain Range of Spain. The forest area covers about 7206 ha and mainly composed of pure Scots pine (Pinus sylvestris L.) stands, although there are other species less represented in the area such as Quercus pyrenaica L. and Ilex aquifolium L. The first management plan was developed in 1889, and the main objective was timber production. Since 1940, in order to achieve this objective, a uniform shelterwood system with a rotation of 120 years and a 20 years regeneration period has been proposed [52]. However, in recent years, this management has become more multifunctional [25], and the silvicultural treatment was turned into a shelterwood group system [52]. Nowadays, other aspects such as biodiversity conservation are of great importance. Thus, there are several endangered species in the area, like the black vulture (Aegypius monachus (Linnaeus, 1766)). The number of nests of this species is around 131, and harvest limitations have been introduced in order to protect them. In short, around each nest, a restricted area without management of 3.14 ha has been established as a buffer protection. Finally, there are several protection features in this forest, such as the declaration of the Sierra de Guadarrama National Park in 2013, where commercial cuttings have been forbidden, and which affects 3326 ha.
3.2. Silvicultural Alternatives
In order to deal with this complexity, seven silvicultural strategies have been proposed to maintain the adaptability of forests to different conditions [81], and to provide different ecosystem services. The set of possible treatments considers the nature of the stands forming the case study, and all of them have been discussed and approved by the forest manager. A priori, the seven treatments (see Figure 1B and Appendix A, Table A1) could be applied to every stand.
The first alternative is based on a shelterwood group system. The treatment spans 40 years, cutting every ten years, and it would be the “business as usual” alternative (BAU). After the final cut, 2% of the stand volume remains as dispersed trees for at least one rotation. In order to model this alternative, we have considered the schedule and cutting intensity traditionally used in Valsaín forest [82]. BAU has been divided into two new alternatives: BAU1, embracing light thinning, and a more intensive option with strong thinning (BAU2). The third alternative, called Group selection (GS), consists of 2 cuttings with medium patch sizes of 1 hectare. After final cutting, 5% of the stand volume remains as residual trees.
Another two silvicultural alternatives are based on the idea of Green Tree Retention (GTR). Two GTR alternatives with different retention percentages are proposed, before applying BAU1 or BAU2. In short, either 15% of the volume is maintained in an aggregated way as mature forest patches (GTR1), or 30% of it (GTR2). These figures are similar to those proposed for this species in Spain [83]. These patches could simulate the protection buffers discussed above for the protection of the black vulture species.
For the area now included in the National Park, we have proposed an alternative (TNP) similar to BAU, but with a main difference: the final cut is excluded, due to prohibitions in all Spanish National Parks. Moreover, in this case, the rotation has been increased (up to 140 years) in relation to the other treatments, as a conservation measure [84]. Finally, a no management alternative (NOM) has been incorporated in order to facilitate the possibility of creating mature forest stands in the future, given that these stands are allowed to grow naturally, thus forming reserve areas.
3.3. Criteria Considered
As mentioned above, the criteria to be introduced should evaluate sustainability based on the multifunctionality intrinsic to forest systems. First, two technical criteria have been defined. The first of these corresponds to a synthetic index that encompasses the classic idea of a normal forest (NF). In short, this criterion embraces tree indicators: one associated with the notion of even-flow policy, another with the idea of regulation or regulated forest [57], and, finally, a third one related to a suitable ending forest inventory, which ensures the perpetuation of the forest. In order to aggregate the above indicators under the normal forest concept, the procedure used in [85] was followed. In addition, a criterion called Ideal Management (IM) has been introduced. It can be quantified by the amount of area (in hectares) to which the silviculture suitable for each stand, according to the criterion optimized in each case, is applied. Therefore, calculating this criterion consists of minimizing the deviations of the silviculture used, compared to that which would be preferred in terms of the characteristics of the stands and in accordance with the preferences reflected by a decision-maker.
On another side, two environmental criteria have been defined. The first one refers to the possibility that, at the end of the planning horizon, there is a multi-aged forest. To enable a comparison of the degree of irregularity between different prescriptions, the Gini index (G) was employed. The latter is frequently used to measure the degree of inequality in different variables, generally with economic data, although applications in many fields have been described [86]. It supplies values in the interval [0 1] and has been defined in such a way that values close to 0 imply the existence of multi-aged stands, whereas values close to 1 ensure an even-aged structure. The second environmental criterion considered was the carbon balance (C), defined as the difference between the estimated gains and losses of carbon due to the growth of trees and their removal (default method, following [87]) throughout the planning horizon. This criterion will be computed in physical units (tons of carbon).
With respect to the production criteria, the Net Present Value (NPV) and the volume (VOL) associated with the final cuttings (cubic meters) over the planning horizon have been considered. Regarding NPV (€), the incomes provided referred only to timber sales. We have considered a fixed maintenance cost (11.6 €/ha), and different harvesting costs in relation to the silvicultural treatment applied. Following data provided from the current forest management plan, the timber price considered was 28 €/m3. We have considered a real discount rate of 2%. Concerning the criteria considered, it is appropriate to clarify that VOL, NPV, IM and C are criteria belonging to the type “the more, the better”, while NF and G are criteria belonging to the type “the less, the better”, following the terms used in [35]. Figure 1B shows the six criteria considered with their acronyms, meanings, and the units in which they are expressed.
3.4. Multi-Criteria Model
When analyzing the solutions shown in the Pay-off matrix, if no solution is preferable, it is necessary to look for a satisficing compromise solution, making the harvest scheduling more sustainable. As we have said before, the technique chosen was Lexicographic Goal Programming (LGP), the second most used GP variant in forest management applications [88].
The first issue to decide in this type of model is how to select the number of priority levels that one wants to establish. Starting from the premise that it should be a limited number and that there should not be as many priorities as the number of criteria [89], in this case, two priority levels have been fixed. In the first one, three goals most directly related to silvicultural aspects have been included, while in the second, NF, IM and G are considered. Namely, given that there are no finite trade-offs among goals placed at the two priority levels [88], it is assumed to be a priority to achieve the goals at the first level before optimizing the criteria situated at the second priority level [90]. The target for each goal was established at 70% with respect to the ideal value obtained in the pay-off matrix. This percentage has been employed in the literature [91], and its use avoids the drawback of not obtaining optimal alternatives if the targets are closer to ideal values [92]. Finally, the complete model can be found in Appendix B, and for its resolution the software LINGO 13.0 [93] has been used.
3.5. Interactive Process
In this study, we interacted with two decision-makers (DM1 and DM2). First, as mentioned above (Equations (A2) and (A3)), it was considered appropriate to introduce preferential weights for each of the six goals contemplated in the analysis. For this purpose, the interaction was with the forest manager (DM1), and his opinion was asked on the six criteria using a survey based on pairwise comparisons, with Saaty’s verbal scale [94] (see Appendix A, Table A3). This way of obtaining the decision-maker’s preferences is recommended for integrating them into GP models [95]. These pairwise comparisons are typically used in the forest context [96].
On another side, and with the aim of obtaining the IM criterion, the engineer in charge of carrying out the last forest management planning (DM2) was contacted. Taking into account the silvicultural alternatives considered (see Appendix A, Table A1) the objective was to establish the suitability of each one for being applied to each stand. For this purpose, the 288 stands in the forest have been grouped into seven categories generated as a combination of a series of factors: production, protection, National Park, districts with nests or the presence of mixed stands. Once the categories were defined, in a first contact with DM2, we selected a set of 2–3 preferred alternatives for each stand. Later, after a second interaction with the same expert, some weights were obtained to weight the different silvicultural alternatives for their suitability, attending to the characteristics and nature of the stand in which they were found (see Appendix A, Table A2). To obtain the weights assigned to each silvicultural alternative in each stand, the same procedure as that employed with DM1 was used (see Appendix A, Table A3).
4. Results
Beginning with the pay-off matrix, Table 1 shows the results of the optimization of the six criteria separately. In Table 1, ideal values (principal diagonal of the matrix) are shown in bold type, while anti-ideal (or least desired ones) are underlined. The main diagonal includes the maximum values that each criterion can reach, known as the ideal point. Other parts of the matrix contain the anti-ideal points, which would be the worst results obtained for each of the criteria. Finally, to increase the informative character of this matrix, several additional rows were included by measuring the area occupied when each criterion is optimized by each of the silvicultural treatments described, as well as the average rotation.

Table 1.
Pay-off matrix (ideal values in bold; anti-ideal values underlined).
The results given in this table show the ideal and anti-ideal values reached by the criteria, according to the optimized criterion (per columns). First, it can be seen that some objectives do not reach ideal values (NF, IM, G). Then, the level of conflict existing between the different criteria, mainly between NF and IM, and between C and G, can be observed, as well as the fact that the results are fairly similar in relation to carbon balance, because the percentage for this criterion varies the least compared to the rest. In synthesis, it can be noted that there is no solution corresponding to the optimization of a single criteria that appears to be sufficiently attractive. In short, the results of this pay-off matrix justify the setting up of an MCDM model in order to achieve solutions that are more balanced from the point of view of sustainability.
However, before revealing the results of those models, the result of the first interaction with DM1 to obtain the preferential weights associated with the criteria is shown (Table 2). Note that the sum of the weights for each priority level is equal to 1. Finally, Appendix A (Table A2) contains the weights obtained throughout the second interactive process with DM2 for the seven categories, in which the stands and the silvicultural alternatives associated with them have been grouped.

Table 2.
Preferential weights associated with the criteria after DM1 interaction.
Next, Table 3 displays the solutions obtained for the two priority levels proposed. It can be noted that the solutions at the second priority level (U2) are the same as the values found in the preceding solution (U1), whereas the values of the three criteria included in U2 improve in comparison with those obtained in U1. Further, to facilitate comparisons, the same auxiliary rows have been included. In general, it can also be seen that the areas assigned to each silvicultural alternative are notably modified when moving from U1 to U2.

Table 3.
Results obtained in the resolution of model LGP (in bold the results for the six goals considered).
In the auxiliary rows in Table 3, the area selected by the model for each silvicultural alternative is indicated. Also, this solution of the LGP model can be compared with the value proposed by the DM2 (the area pointed out as being the one preferred for applying each silviculture), information which is available on Appendix A (Table A2). In Figure 2 the difference (in surface) between both areas (applied or selected by the model and preferred) can be noted. However, it should be taken into account that the area preferred exceeds the value of the total forest area, because, for each stand, a set of 2–3 possible silvicultural treatments were proposed.
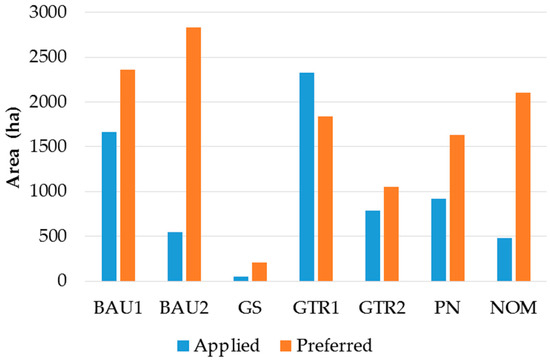
Figure 2.
Relation between the silviculture applied in the forest and the deviation of when it would be preferred, according to the categories defined.
5. Discussion
The method here proposed for evaluating sustainability in forest management has the advantage of following the evolution of the criteria over the planning horizon [19], but it could also be adapted when including spatial constraints [97]. In that case, it could be suitable to design a model simultaneously integrating strategic and tactical planning [98]. Furthermore, the methodology proposed could be extended to incorporate the preferences of a group of stakeholders for addressing sustainability [99,100]. Some authors suggest compiling the forest managers’ preferences on silvicultural aspects in a goal programming model [101], although the way these individual preferences would be aggregated is still an open question [102]. Finally, although the inclusion of dynamic aspects could trigger highly specific models, limiting their transference to others [103], we do not believe that this could happen in the proposal presented in this study due to its potential adaptation to other works, with other criteria and indicators.
The results presented in Table 3 allow us to observe the differences in relation to the values achieved for the indicators situated at the first priority level, at forest level. Thus, Figure 3 shows how the values of the criteria NF, IM and G obtained in the pay-off matrix are modified (Table 1), with respect to those obtained in the solution of the LGP model (Table 3).
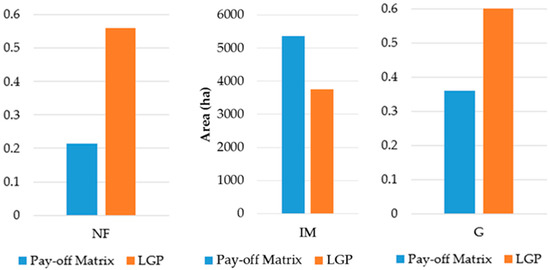
Figure 3.
Comparison between the results of the pay-off matrix and those obtained in the LGP model, for the criteria NF, IM and G.
As could be expected, in the comparison between models (Figure 3), the values of the criteria obtained in the LGP model are lower than the ideal ones reached in the pay-off matrix. These reductions indicate the opportunity cost associated with the simultaneous consideration of the six criteria defined in this model, instead of the values proposed in the individual optimization of each criterion. Thus, taking into account that the NF and G values (located at each end of the graphic) are adimensional and that they represent indicators of the less-the-better type, in the LGP solution their values are 2.7 and 1.6 times worse, respectively, compared to that obtained in the pay-off matrix. Finally, the IM criterion’s value of 5358 ha, which represents the area managed by the most suitable treatment in each management unit (according to DM2), was reduced to 3750 ha in the LGP solution; i.e., about 30% of the area under ideal management (IM) is taken advantage of in LGP, using a different silvicultural treatment from the one that a priori was preferred for application in these areas.
From a sustainability perspective, it has been implicitly assumed up to now that the criteria selected functioned within weak sustainability parameters [31]. Namely, a certain degree of compensation between the different indicators was presumed, although the LGP method implies that there is no finite trade-off between the different indicators of the different criteria considered [89]. However, in the literature, aggregated sustainability indexes based on multicriteria techniques including premises associated with strong sustainability can be found; i.e., it is found that there cannot be compensation between the criteria [104], nor can a certain degree of compensation between criteria even be chosen [105,106].
The methodology proposed here is open to incorporating other silvicultural alternatives. In our case study, GS has been proposed in order to favor the development of multi-aged stands [79], and GTR has been suggested in order to maintain multiple forest values [76], including biodiversity conservation [107], and, especially, to promote silvicultural treatments compatible with the protection of wildlife species [108]. The percentages of mature forest chosen here are those most frequently used in the literature [109,110]. Another silvicultural alternative (TNP) embraces the prohibition of final cuts (this forbiddance is mandatory in all Spanish National Parks). Maintaining this type of protected area is highly beneficial for certain species, and this justifies not employing a conventional silvicultural alternative [111].
On another side, and as mentioned above, other criteria could be integrated into the model, if considered to be appropriate. For example, we are aware that, unlike other studies [112,113], no criterion expressly linked to the social pillar of sustainability has been proposed. Although one study made in the same case study [114] did suggest two recreation indicators, it has not been possible to transfer this idea to our analysis. Along these lines, some studies point to an underrepresentation of social type indicators as being common [103].
Again, and aside from the significance of the Gini coefficient proposed here, which has been applied as an indicator of forest structural heterogeneity [115,116], we have attempted to define our own biodiversity criterion [117] that could be integrated into the LGP model. In fact, one of the objectives in the case study [118] is focussed on the conservation of the black vulture, an umbrella species [119], which is catalogued as “near threatened” at the global level [120]. For this reason, we pursue the possibility that, at the end of the planning horizon, there is a multi-aged forest. The inclusion of this criterion (Gini coefficient) under an environmental pillar is justified when the forest managers aim to promote the existence of uneven-aged stands as a biodiversity conservation measure [63,79].
However, it has not been possible to model the evolution of this species over 100 years, due to the lack of information available for predicting these values, so it has not been included in the analysis. Furthermore, it would have been necessary to determine the impact of the different silvicultural alternatives on the vulture populations, because it has been demonstrated that they have an influence on some requirements of the nesting of this species [121]. The lack of consideration of this criterion illustrates the difficulty in finding criteria compatible with the information assembly over the planning horizon, in spite of the availability of suitable methodologies for their possible integration into the model proposed. However, some studies have been developed under the goal programming technique successfully integrating aspects related to biodiversity [122,123]. Lastly, the methodology proposed here can also be extended, incorporating other silvicultural alternatives centred on other ecosystem services different from timber production [124].
Furthermore, the results of the LGP model permit one to obtain an overall value of sustainability derived from the resolution of that model, making it act as an aggregated index of the sustainability of forest management, assimilating the procedure reported in [125]. Indeed, if the objective is to compare sustainability between similar forests, or between parts of the same one, the solution of the LGP model could allow them to be ranked in terms of greater or lesser aggregate achievement. In [12,13], some examples of this extension are shown. Finally, the opportunity cost in terms of sustainability (gains or losses of sustainability) could also be calculated, by obligating a single silvicultural alternative to be used in some part of the case study. This circumstance can be of interest when, as can be seen in this case, the solutions notably vary with respect to the area that each silvicultural treatment has to cover, and this also happens in other studies [126].
In addition to incorporating new sustainability criteria, one aspect of the methodology proposed here that should be highlighted lies in the combination of flexibility and complexity that can be incorporated, for example, in terms of the silvicultural alternatives considered. The advantage of this flexibility is indispensable for tackling typical contemporary challenges in forest management [127,128]. Since there is no single specific definition of the idea of complexity in silviculture [129], some authors affirm that the impact of certain forest practices on forest system dynamics can compromise their sustainability [81]. Thus, the consideration of diverse silvicultural alternatives for approaching different criteria would lead to what some authors already call “complex adaptive systems” [130]. Lastly, this methodology can be applied at different levels (spatial or temporal) at which it is desired to carry out the planning and silviculture [128], contributing to the flexibility of the proposed methodology.
6. Conclusions
In this study, a flexible methodology was proposed to address sustainability in forest management. It includes the possibility of incorporating different criteria, or even synthetic indicators, multiple silvicultural alternatives for each stand and the preferential weights of different stakeholders. The solutions of these multi-criteria models allow the decision-maker to select, in terms of sustainability, the optimal silvicultural alternative for each stand along the planning horizon, the degree of multi-aged forest proposed and the fulfilment of the normal forest ideal.
The results obtained in the case study show different solutions from the ideal values shown in the pay-off matrix, with those supplied by the LGP model being much more attractive. Moreover, it can be seen how the areas devoted to each silvicultural alternative are notably modified in each of the solutions obtained. Finally, the flexibility of the model leads us to believe that this methodology could easily be extended to other case studies and planning levels, both temporal and spatial.
Author Contributions
M.E. carried out all the research, wrote the manuscript and performed the modelling issues. M.P. wrote the manuscript, focusing on silvicultural alternatives. L.D.-B. coordinated the study and wrote the manuscript, focusing on sustainability topics.
Funding
This work was funded by the Ministry of Economy and Competitiveness of Spain under project AGL2015-68657-R. Additionally, this research was partially financed by the European Union’s H2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 691149–SuFoRun.
Acknowledgments
The authors thank Javier Donés, Marisol Redondo and Marta Piñuela (Valsaín forest staff) for their continuous support. The authors deeply appreciate the comments and suggestions raised by Carlos Romero. Thanks are also given to Patricia Riquelme (Sierra de Guadarrama National Park) and Miguel Cabrera, and to Diana Badder for editing the English. Additionally, this manuscript has been proofread by PRS and MDPI. Thanks are given to the Editor and the reviewers for their helpful comments and criticisms, which have greatly improved the presentation and accuracy of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Set of possible silvicultural alternatives to be applied in the case study.
Table A1.
Set of possible silvicultural alternatives to be applied in the case study.
| Silvicultural Alternative | Age | Operation | Intensity (%) | Standing Volume (%) |
|---|---|---|---|---|
| BAU1 | 40–60–80 | Light thinnings | From below | |
| 120–180 | Seeding cutting | 50 | ||
| Secondary cutting 1 | 12 | |||
| Secondary cutting 2 | 12 | |||
| Final cutting | 24 | 2 | ||
| BAU2 | 40–60–80 | Strong thinnings | From below | |
| 120–180 | Seeding cutting | 50 | ||
| Secondary cutting 1 | 12 | |||
| Secondary cutting 2 | 12 | |||
| Final cutting | 24 | 2 | ||
| GS | 40–60–80 | Light thinnings | From below | |
| 120–180 | Seeding cutting | 60 | ||
| Final cutting | 35 | 5 | ||
| GTR1 | 40–60–80 | Light thinnings | From below | |
| 80–120 | Retention | 15 | 15 | |
| 120–180 | Seeding cutting | 45 | ||
| Secondary cutting 1 | 10 | |||
| Secondary cutting 2 | 10 | |||
| Final cutting | 18 | 2 | ||
| GTR2 | 40–60–80 | Strong thinnings | From below | |
| 80–120 | Retention | 30 | 30 | |
| 120–180 | Seeding cutting | 35 | ||
| Secondary cutting 1 | 10 | |||
| Secondary cutting 2 | 10 | |||
| Final cutting | 13 | 2 | ||
| TNP | 40–60–80 | Light thinnings | From below | |
| 140–180 | Seeding cutting | 40 | ||
| Secondary cutting 1 | 10 | |||
| Secondary cutting 2 | 10 | |||
| No Final cuttings | 40 | |||
| NOM | NO Management |
BAU1: Business As Usual 1, BAU2: Business As Usual 2, GS: Group Selection, GTR1: Green-Tree Retention1, GTR2: Green-Tree Retention2, TNP: Treatment for the National Park, NOM: NO Management.

Table A2.
Weights for the set of possible silvicultural treatments (7) in each category (7).
Table A2.
Weights for the set of possible silvicultural treatments (7) in each category (7).
| Categories | Definition | Set of Alternatives | Weights |
|---|---|---|---|
| 1 | Productive stands | BAU1 | 0.188 |
| BAU2 | 0.081 | ||
| GTR1 | 0.731 | ||
| 2 | Under protection stands | NOM | 0.9 |
| TNP | 0.1 | ||
| 3 | Mixed stands | GS | 0.875 |
| NOM | 0.125 | ||
| 4 | Mixed stands with nests | GS | 0.055 |
| GTR1 | 0.173 | ||
| GTR2 | 0.772 | ||
| 5 | Mixed stands in the National Park (NP) | GS | 0.149 |
| TNP | 0.785 | ||
| NOM | 0.066 | ||
| 6 | Stands with nests | GTR1 | 0.25 |
| GTR2 | 0.75 | ||
| 7 | Stands with nests in the National Park (NP) | GTR2 | 0.149 |
| TNP | 0.785 | ||
| NOM | 0.066 |
BAU1: Business As Usual 1, BAU2: Business As Usual 2, GS: Group Selection, GTR1: Green-Tree Retention1, GTR2: Green-Tree Retention2, TNP: Treatment for the National Park, NOM: NO Management.

Table A3.
Scale of relative importance [94].
Table A3.
Scale of relative importance [94].
| Intensity of Importance | Definition |
|---|---|
| 1 | Equal importance |
| 3 | Moderate importance |
| 5 | Strong importance |
| 7 | Demonstrated importance |
| 9 | Extreme importance |
| 2, 4, 6, 8 | Intermediate values |
Appendix B
Appendix B.1. Lexicographic Goal Programming Formulation
[…]
Starting from priority levels (Equation (A1)), for each of the priority levels cited, some functions are defined (Equations (A2) and (A3)), composed of the unwanted deviation variables corresponding to the goals (Equation (A4)) situated at those priority levels. is the target level for the qth goal, and are the negative and positive deviations from the target value of the qth goal. is used if is unwanted, otherwise is used , if it is unwanted, otherwise . The parameters and are the weights reflecting preferential and normalising purposes attached to the achievement of the qth goal.
Appendix B.2. Strategic Planning
Following Figure 1A, a strategic forest planning model was designed with a planning horizon of 100 years, divided into 10-year periods, which is a typical timeframe in models with slow-growing species, especially with Scots pine [118]. In short, a timber harvest scheduling model following Model I methodology [121] was built. Initially, Model I requires the definition of the decision variables or prescriptions, which need to encompass all possible management regimes to be considered, taking into account the rotation length and the silvicultural alternatives put into the model, which will remain unaltered throughout the planning horizon [33]. This strategic planning model was fed with the information available in the last forest management plan [82]. In addition, the abovementioned silvicultural alternatives were included in this general model, and we fixed an interval for rotations of between 120 and 180 years. The lowest limit corresponds to the current rotation length for Scots pine in the Sierra de Guadarrama [52], while the upper limit was established at 180 years in order to provide mature forest habitats, which are essential for the survival of several endangered species [84,131]. On the other hand, it is convenient to clarify that, in addition to the endogenous restrictions two exogenous restrictions have been introduced: a minimum harvest area for each silvicultural treatment, and a minimum commercial volume from final cuttings (TNP not included) per period. Finally, considering the rotation length and the 288 stands defined in Valsaín Forest, a set of 11,148 prescriptions was generated.
Appendix B.3. Definition of Model Inputs
Constants
is the length of the planning horizon.
is the time period.
is the number of periods into which the planning horizon is divided.
is the time span that defines the final age class.
is the number of final age classes, taking into account the range of years in which regeneration can occur.
is the total forest area.
is the area in stand .
is the minimum harvest area when prescriptions are selected.
is the minimum harvest area when prescriptions are selected.
is the minimum harvest area when prescriptions are selected.
is the minimum harvest area when prescriptions are selected.
is the minimum harvest area when prescriptions are selected.
is the minimum volume harvested per period.
and are the minimum and maximum harvest ages during the planning horizon, respectively.
is the volume harvested per hectare in stand , prescription at period .
is the initial forest inventory on site index.
is the Black Vulture Nest protection area.
is the initial investment and is the cash-flow per year.
is the discount rate.
is the parameter that expresses the density of wood in tons per m3 (0.5) and the percentage of carbon content (50%) existing in dry biomass, whose value is obtained through .
Index Sets
is the number of stands.
is the number of prescriptions, defining a complete treatment schedule for each stand, following the Model I structure (Johnson and Scheurman, 1977).
is the number of initial age classes.
is the index of periods.
is the site index.
is the number of priority levels.
Variables
is the area harvested at prescription in stand .
is the area harvested by at prescription in stand .
is the area harvested by at prescription in stand .
is the area harvested by at prescription in stand .
is the area harvested by at prescription in stand .
is the area harvested by at prescription in stand .
is the area harvested by at prescription in stand .
is the area selected for at prescription in stand .
is a binary variable to force decision variable to take either a zero value or a value greater than, or equal to, the minimum harvest area designated by parameters , , , and .
is the area belonging to s final age class at the ending period.
is the ending forest inventory from site index .
is the total standing volume at prescription in stand .
is the cumulative percentage of the number of trees per hectare for each stand .
is the cumulative percentage of volume.
is the carbon capture at prescription in stand .
are the carbon emissions produced by cuttings at prescription in stand .
is the normalized vector (as the difference between ideal and anti-ideal values) for each criterion .
Appendix B.4. Definition of LGP Model
Criteria
is the normal forest as an aggregated normalized function of the even flow harvest volume per period (), the forest ending inventory for each site class () and the area control for each age class ().
is the ideal management to be applied in each stand .
is the gini index as an inequaluty measure.
is the volume harvested at the end of the planning horizon.
is the Net Present Value at the end of the planning horizon.
is the carbon balance at the end of the planning horizon.
Achievement function
Goals
(1) Normal Forest ()
(2) Ideal Management ()
(3) Gini index ()
(4) Carbon balance ()
(5) Harvest volume ()
(6) Net Present Value ()
The following constraints were introduced into the LGP model. First, endogenous ones were introduced to ensure that the area chosen by the model cannot exceed the available area in each stand. Second, a minimum harvest area was proposed for each treatment, since, as the treatments propose cutting sequences at several periods (2–4), a minimum area necessary for the intervention (5 ha for BAU1 and BAU2, and 10 ha for GTR1 and GTR2) for each of them, was considered. In the case of GS, this minimum area refers to the size of the gaps in which the thinnings are applied. Finally, for TPN and NOM, no amount of minimum area was imposed for their application. The last constraint ensures a minimum harvested volume per period, according to the current forest management plan and the timber harvested in past years.
Subject to:
(7) Area accounting
(8) Auxiliary variables domain
(9) Minimum harvest area per treatment
(10) Minimum and maximum harvest age
(11) Minimum harvested volume per period
(12) Non-negativity constraints
References
- von Carlowitz, H. Sylvicultura Oeconomica Oder Haußwirthliche Nachricht und Naturgemäßige Anweisung zur Wilden Baum-Zucht; Johann Friedrich Braun (2 Bände): Leipzig, Germany, 1713. [Google Scholar]
- Grober, U. The discovery of sustainability: The genealogy of a term. In Theories of Sustainable Development; Enders, J.C., Remig, M., Eds.; Routledge: Abingdon, UK, 2015; pp. 6–15. [Google Scholar]
- Robin, L. A history of global ideas about environmental justice. In Natural Resources and Environmental Justice. Australian Perspectives; Lukasiewicz, A., Dovers, S., Robin, L., McKay, J., Schilizzi, S., Graham, S., Eds.; CSIRO Publishing: Clayton South, Australia, 2017; pp. 13–25. [Google Scholar]
- Bettencourt, L.; Kaur, J. Evolution and structure of sustainability science. Proc. Natl. Acad. Sci. USA 2011, 108, 19540–19545. [Google Scholar] [CrossRef] [PubMed]
- Schuler, A. Sustainability and biodiversity- forest historical notes on two main concerns of environmental utilization. In Assessment of Biodiversity for Improved Forest Planning; Bachmann, P., Köhl, M., Paivinen, R., Eds.; Springer Science: Dordrecht, The Netherlands, 1998; pp. 353–360. [Google Scholar]
- Caradonna, J.L. Routledge Handbook of the History of Sustainability; Routledge: Abingdon, UK, 2018; 443p. [Google Scholar]
- Zenner, E.K. The Ongoing Story of Silviculture on Our Natural Public Forestlands. J. For. 2014, 112, 611–616. [Google Scholar] [CrossRef]
- Raison, R.J.; Brown, A.; Flinn, D. Criteria and Indicators for Sustainable Forest Management; CABI Publishing: Wallingford, UK, 2001; 427p. [Google Scholar]
- Spies, J.; Devisscher, T.; Bulkan, J.; Tansey, J.; Griess, V. Value-oriented criteria, indicators and targets for conservation and production: A multi-party approach to forest management planning. Biol. Conserv. 2019, 230, 151–168. [Google Scholar] [CrossRef]
- Grainger, A. Forest sustainability indicator systems as procedural policy tools in global environmental governance. Glob. Environ. Chang.-Hum. Policy Dimens. 2012, 22, 147–160. [Google Scholar] [CrossRef]
- Linser, S.; Wolfslehner, B.; Asmar, F.; Bridge, S.R.J.; Gritten, D.; Guadalupe, V.; Jafari, M.; Johnson, S.; Laclau, P.; Robertson, G. 25 Years of Criteria and Indicators for Sustainable Forest Management: Why Some Intergovernmental C&I Processes Flourished While Others Faded. Forests 2018, 9, 515. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Alfranca, O.; Bertomeu, M.; Ezquerro, M.; Giménez, J.C.; González-Pachón, J.; Romero, C. Using quantitative techniques to evaluate and explain the sustainability of forest plantations. Can. J. For. Res. 2016, 46, 1157–1166. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Alfranca, O.; González-Pachón, J.; Romero, C. Ranking of industrial forest plantations in terms of sustainability: A multicriteria approach. J. Environ. Manag. 2016, 180, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Rametsteiner, E.; Simula, M. Forest Certification—An Instrument to Promote Sustainable Forest Management? J. Environ. Manag. 2003, 67, 87–98. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Jalón, S.G. Certifying Forests to Achieve Sustainability in Industrial Plantations: Opinions of Stakeholders in Spain. Forests 2017, 8, 502. [Google Scholar] [CrossRef]
- Helms, J.A. The Dictionary of Forestry; Society of American Foresters: Bethesda, MD, USA, 1998; 203p. [Google Scholar]
- Briceño-Elizondo, E.; Jäger, D.; Lexer, M.J.; García-Gonzalo, J.; Peltola, H.; Kellomäki, S. Multi-criteria evaluation of multi-purpose stand treatment programmes for Finnish boreal forests under changing climate. Ecol. Ind. 2008, 8, 26–45. [Google Scholar] [CrossRef]
- Nelson, E.; Mendoza, G.; Regetz, J.; Polasky, S.; Tallis, H.; Cameron, D.; Chan, K.M.; Daily, G.C.; Goldstein, J.; Kareiva, P.M.; et al. Modeling multiple ecosystem services, biodiversity conservation, commodity production, and tradeoffs at landscape scales. Front. Ecol. Environ. 2009, 7, 4–11. [Google Scholar] [CrossRef]
- Mönkkonen, M.; Juutinen, A.; Mazziotta, A.; Miettinen, K.; Podkopaev, D.; Reunanen, P.; Salminen, H.; Tikkanen, O.-P. Spatially dynamic forest management to sustain biodiversity and economic returns. J. Environ. Manag. 2014, 134, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Martins, H.; Borges, J.G. Addressing collaborative planning methods and tools in forest management. For. Ecol. Manag. 2007, 248, 117–118. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Romero, C. Making forestry decisions with multiple criteria: A review and an assessment. For. Ecol. Manag. 2008, 255, 3222–3241. [Google Scholar] [CrossRef]
- Uhde, B.; Hahn, W.A.; Griess, V.; Knoke, T. Hybrid MCDA methods to integrate multiple ecosystem services in forest management planning: A critical review. J. Environ. Manag. 2015, 56, 373–388. [Google Scholar] [CrossRef] [PubMed]
- Cinelli, M.; Coles, S.R.; Kirwan, K. Analysis of the potentials of multi criteria decision analysis methods to conduct sustainability assessment. Ecol. Ind. 2014, 46, 138–148. [Google Scholar] [CrossRef]
- Lozano-Oyola, M.; Blancas Peral, F.; Lozano, M.; Caballero, R. Sustainable tourism indicators as planning tools in cultural destinations. Ecol. Ind. 2012, 18, 659–675. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res. 2017, 258, 607–616. [Google Scholar] [CrossRef]
- Stojčić, M.; Zavadskas, E.K.; Pamučar, D.; Stević, Ž.; Mardani, A. Application of MCDM Methods in Sustainability Engineering: A Literature Review 2008–2018. Symmetry 2019, 11, 350. [Google Scholar] [CrossRef]
- Pérez, F.; Molinos-Senante, M.; Gómez, T.; Caballero, R.; Sala-Garrido, R. Dynamic goal programming synthetic indicator: An application for water companies sustainability assessment. Urban Water J. 2018, 15, 592–600. [Google Scholar] [CrossRef]
- Langer, A.; Irauschek, F.; Pérez, S.; Pardos, M.; Zlatanov, T.; Öhman, K.; Nordström, E.-M.; Lexer, M. Value-based ecosystem service trade-offs in multi-objective management in European mountain forests. Ecosyst. Serv. 2017, 26, 245–257. [Google Scholar] [CrossRef]
- Blattert, C.; Lemm, R.; Thees, O.; Hansen, J.; Lexer, M.; Hanewinkel, M. Segregated versus integrated biodiversity conservation: Value-based ecosystem service assessment under varying forest management strategies in a Swiss case study. Ecol. Ind. 2018, 95, 751–764. [Google Scholar] [CrossRef]
- Müller, A.; Knoke, T.; Olschewski, R. Can Existing Estimates for Ecosystem Service Values Inform Forest Management? Forests 2019, 10, 132. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Belavenutti, P.; Ezquerro, M.; González-Pachón, J.; Nobre Ribeiro, S.; Romero, C. Measuring the sustainability of a natural system by using multi-criteria distance function methods: Some critical issues. J. Environ. Manag. 2018, 214, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Toman, M.A.; Ashton, M.S. Sustainable forest ecosystems and management: A review article. For. Sci. 1996, 42, 366–377. [Google Scholar]
- Davis, L.S.; Johnson, K.M.; Bettinger, P.; Howard, T.E. Forest Management, 4th ed.; McGraw-Hill: New York, NY, USA, 2001; 816p. [Google Scholar]
- Morgenstern, E.K. The origin and early application of the principle of sustainable forest management. For. Chron. 2007, 83, 485–489. [Google Scholar] [CrossRef]
- Romero, C.; Rehman, T. Multiple Criteria Analysis for Agricultural Decisions, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003; 186p. [Google Scholar]
- Zopounidis, C.; Pardalos, P.M. Handbook of Multicriteria Analysis; Springer: Berlin, Germany, 2010; 455p. [Google Scholar]
- Buongiorno, J.; Gilles, J.K. Decision Methods for Forest Resource Management; Academic Press: San Diego, CA, USA, 2003; 439p. [Google Scholar]
- Ignizio, J.; Romero, C. Goal Programming. In Encyclopedia of Information Systems; Four Volume Set; Bidgoli, H., Ed.; Academic Press: San Diego, CA, USA, 2002; pp. 489–500. [Google Scholar]
- Jones, D.; Tamiz, M. Practical Goal Programming; Springer: New York, NY, USA, 2010; 170p. [Google Scholar]
- Jones, D.; Romero, C. Advances and New Orientations in Goal Programming. In New Perspectives in Multiple Criteria Decision Making, Multiple Criteria Decision Making; Doumpos, M., Rui Figueira, J., Greco, S., Zopounidis, C., Eds.; Springer: Cham, Switzerland, 2019; pp. 231–246. [Google Scholar]
- Ignizio, J.P.; Romero, C. Goal Programming. Encycl. Inf. Syst. 2003, 2, 489–500. [Google Scholar] [CrossRef]
- Fischer, J.; Manning, A.; Steffen, W.; Rose, D.B.; Daniell, K.; Felton, A.; Garnett, S.; Gilna, B.; Heinsohn, R.; Lindenmayer, D.; et al. Mind the sustainability gap. Trends Ecol. Evol. 2007, 22, 621–624. [Google Scholar] [CrossRef]
- Zeleny, M. Multiple Criteria Decision Making; McGraw-Hill: New York, NY, USA, 1982; 563p. [Google Scholar]
- Romero, C. A general structure of achievement function for a goal programming model. Eur. J. Oper. Res. 2004, 153, 675–686. [Google Scholar] [CrossRef]
- Benítez-Fernández, A.; Ruiz, F. A Meta-Goal Programming Approach to Cardinal Preferences Aggregation in Multicriteria Problems. Omega 2019, in press. [Google Scholar] [CrossRef]
- Caballero, R.; Núñez, T.; Ruiz, F. Goal Programming: Realistic targets for the near future. J. Multi-Criteria Decis. Anal. 2009, 16, 79–110. [Google Scholar] [CrossRef]
- Hahn, A.; Knoke, T. Sustainable development and sustainable forestry: Analogies, differences, and the role of flexibility. Eur. J. For. Res. 2010, 129, 787–801. [Google Scholar] [CrossRef]
- von Detten, R. Sustainability as a guideline for strategic planning? The problem of long-term forest management in the face of uncertainty. Eur. J. For. Res. 2011, 130, 451–465. [Google Scholar] [CrossRef]
- Hahn, A.; Härtl, F.; Irland, L.; Kohler, C.; Moshammer, R.; Knoke, T. Financially optimized management planning under risk aversion results in even-flow sustained timber yield. For. Policy Econ. 2014, 42, 30–41. [Google Scholar] [CrossRef]
- Pasalodos-Tato, M.; Mäkinen, A.; Garcia-Gonzalo, J.M.; Borges, J.G.; Lamas, T.; Eriksson, L.O. Assessing uncertainty and risk in forest planning and decision support systems: Review of classical methods and introduction of innovative approaches. For. Syst. 2013, 22, 282–303. [Google Scholar] [CrossRef]
- Mina, M.; Bugmann, H.; Cordonnier, T.; Irauschek, F.; Klopcic, M.; Pardos, M.; Cailleret, M. Future ecosystem services from European mountain forests under climate change. J. Appl. Ecol. 2017, 54, 389–401. [Google Scholar] [CrossRef]
- Pardos, M.; Perez, S.; Calama, R.; Alonso, R.; Lexer, J.M. Ecosystem service provision, management systems and climate change in Valsain forest, Central Spain. Reg. Environ. Chang. 2017, 17, 17–32. [Google Scholar] [CrossRef]
- Başkent, E. Exploring the effects of climate change mitigation scenarios on timber, water, biodiversity and carbon values: A case study in Pozantı planning unit, Turkey. J. Environ. Manag. 2019, 238, 420–433. [Google Scholar] [CrossRef]
- Hernandez, M.; Gomez, T.; Molina, J.; Leon, M.A.; Caballero, R. Efficiency in forest management: A multiobjective harvest scheduling model. J. For. Econ. 2014, 20, 236–251. [Google Scholar] [CrossRef]
- Xavier, A.M.; Costa Freitas, M.B.; Fragoso, R. Management of Mediterranean forests—A compromise programming approach considering different stakeholders and different objectives. For. Policy Econ. 2015, 57, 38–46. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Martell, D.; Romero, C.; Weintraub, A. The optimal rotation of a flammable forest stand when both carbon sequestration and timber are valued: A multi-criteria approach. Nat. Hazards 2014, 72, 375–387. [Google Scholar] [CrossRef]
- Franklin, J.F.; Johnson, K.N.; Johnson, D.L. Ecological Forest Management; Waveland Press: Long Grove, IL, USA, 2018; 646p. [Google Scholar]
- Schraml, U.; Detten, R.V. Forestry or “the art of flying blind”. Sustainability in an era of global change. In Sustainable Forest Management in a Changing World. A European Perspective; Spathelf, P., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 217–238. [Google Scholar]
- Hauhs, M.; Langel, H. Sustainability in Forestry: Theory and a historical case study. In Sustainable Forest Management; von Gadow, K., Pukkala, T., Tomé, M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000; pp. 69–98. [Google Scholar]
- Johnston, D.R.; Grayson, A.J.; Bradley, R.T. Forest Planning; Faber and Faber Limited: London, UK, 1967; 541p. [Google Scholar]
- Osmaston, F.C. The Management of Forests; George Allen and Unwin Ltd.: London, UK, 1968; 384p. [Google Scholar]
- Ciancio, O.; Nocentini, S. Biodiversity conservation and systemic silviculture: Concepts and applications. Plant Biosyst.—Int. J. Deal. Asp. Plant Biol. 2011, 145, 411–418. [Google Scholar] [CrossRef]
- Puettmann, K.J.; Wilson, S.M.; Baker, S.C.; Donoso, P.J.; Drossler, L.; Amente, G.; Harvey, B.D.; Knoke, T.; Lu, Y.; Nocentini, S.; et al. Silvicultural alternatives to conventional even-aged forest management—What limits global adoption? For. Ecosyst. 2015, 2, 8. [Google Scholar] [CrossRef]
- Kangas, A.; Kurttila, M.; Hujala, T.; Eyvindson, K.; Kangas, J. Decision Support for Forest Management, 2nd ed.; Springer: Berlin, Germany, 2015; 307p. [Google Scholar]
- Kašpar, J.; Marušák, R.; Hlavatý, R. A Forest Planning Approach with Respect to the Creation of Overmature Reserved Areas in Managed Forests. Forests 2015, 6, 328–343. [Google Scholar] [CrossRef]
- Wiersum, K.F. 200 years of sustainability in forestry: Lessons from history. Environ. Manag. 1995, 19, 321–329. [Google Scholar] [CrossRef]
- Rytteri, T.; Peltola, T.; Leskinen, L.A. Co-production of forestry science and society: Evolving interpretations of economic sustainability in Finnish forestry textbooks. J. For. Econ. 2016, 24, 21–36. [Google Scholar] [CrossRef]
- Pretzsch, H.; Knoke, T. Forest management planning in mixed-species forests. In Mixed-Species Forests. Ecology and Management; Pretzsch, H., Forrester, D.I., Bauhus, J., Eds.; Springer: Berlin, Germany, 2017; pp. 503–544. [Google Scholar]
- Parrot, L.; Kange, H. An introduction to complexity science. In Managing Forests as Complexity Adaptive Systems; Messier, C., Puettmann, K.J., Coates, D., Eds.; Routledge: Abingdon, UK, 2014; pp. 17–32. [Google Scholar]
- Eyvindson, K.; Repo, A.; Mönkkönen, M. Mitigating forest biodiversity and ecosystem service losses in the era of bio-based economy. For. Policy Econ. 2018, 92, 119–127. [Google Scholar] [CrossRef]
- Langenberger, G.; Lippe, M. Forestry. In Bioeconomy: Shaping the Transition to a Sustainable, Biobased Economy; Lewandowski, I., Ed.; Springer: Cham, Germany, 2018; pp. 124–141. [Google Scholar]
- Shannon, M.A.; Buttoud, G.; Päivinen, R. Science is Endogenous to Sustainable Forestry—Implications for Scientists and Policymakers. In Sustainable Forestry: From Monitoring and Modelling to Knowledge Management and Policy Science; Reynolds, K.M., Thompson, A.J., Köhl, M., Shannon, M.A., Ray, D., Reynolls, K., Eds.; CABI: Wallingford, UK, 2007; pp. 1–13. [Google Scholar]
- Rist, L.; Moen, J. Sustainability in forest management and a new role for resilience thinking. For. Ecol. Manag. 2013, 310, 416–427. [Google Scholar] [CrossRef]
- Bettinger, P.; Boston, K.; Siry, J.P.; Grebner, D. Forest Management and Planning, 2nd ed.; Academic Press: San Diego, CA, USA, 2017; 362p. [Google Scholar]
- Higman, S.; Mayers, J.; Bass, S.; Judd, N.; Nussbaum, R. The Sustainable Forestry Handbook, 2nd ed.; Earthscan: London, UK, 2005; 332p. [Google Scholar]
- Lindenmayer, D.B.; Franklin, J.F.; Lohmus, A.; Baker, S.C.; Bauhus, J.; Beese, W.; Brodie, A.; Kiehl, B.; Kouki, J.; Pastur, G.M.; et al. A major shift to the retention approach for forestry can help resolve some global forest sustainability issues. Conserv. Lett. 2012, 5, 421–431. [Google Scholar] [CrossRef]
- Mori, A.S.; Lertzman, K.P.; Gustafsson, L. Biodiversity and ecosystem services in forest ecosystems: A research agenda for applied forest ecology. J. Appl. Ecol. 2017, 54, 12–27. [Google Scholar] [CrossRef]
- Nordström, E.-M.; Nieuwenhuis, M.; Başkent, E.; Biber, P.; Black, K.; Borges, J.; Bugalho, M.; Corradini, G.; Corrigan, E.; Eriksson, L.; et al. Forest decision support systems for the analysis of ecosystem services provisioning at the landscape scale under global climate and market change scenarios. Eur. J. For. Res. 2019, 1–21. [Google Scholar] [CrossRef]
- O’Hara, K.L. Multiaged Silviculture. Managing for Complex Forest Stand Structures; Oxford University Press: Oxford, UK, 2014; 213p. [Google Scholar]
- Augustynczik, L.D.A.; Asbeck, T.; Basile, M.; Bauhus, J.; Storch, I.; Mikusiński, G.; Yousefpour, R.; Hanewinkel, M. Diversification of forest management regimes secures tree microhabitats and bird abundance under climate change. Sci. Total Environ. 2018, 650, 2717–2730. [Google Scholar] [CrossRef] [PubMed]
- Puettmann, K.J.; Coates, K.D.; Messier, C. A Critique of Silviculture: Managing for Complexity; Island Press: Washington, DC, USA, 2009; 188p. [Google Scholar]
- Cabrera, M. Proyecto de 7ª Revisión de la Ordenación del Monte Número 2 del Catálogo de los de Utilidad Pública de la Provincia de Segovia “Pinar” de Valsaín; Organismo Autónomo Parques nacionales, Ministerio de Medio Ambiente: Madrid, Spain, 2010; 365p.
- Bravo, F.; Diaz-Balteiro, L. Evaluation of new silvicultural alternatives for Scots pine stands in Northern Spain. Ann. For. Sci. 2004, 61, 163–169. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Franklin, J.F. Conserving Forest Biodiversity: A Comprehensive Multiscaled Approach; Island Press: Washington, DC, USA, 2002; 351p. [Google Scholar]
- Aldea, J.; Martínez-Peña, F.; Romero, C.; Diaz-Balteiro, L. Participatory Goal Programming in Forest Management: An Application Integrating Several Ecosystem Services. Forests. 2014, 5, 3352–3371. [Google Scholar] [CrossRef]
- Farris, F. The Gini Index and Measures of Inequality. Am. Math. Mon. 2010, 117, 851–864. [Google Scholar] [CrossRef]
- Pasalodos-Tato, M.; Almazán Riballo, E.; Montero, G.; Diaz-Balteiro, L. Evaluation of tree biomass carbon stock changes in Andalusian forests: Comparison of two methodologies. Carbon Balance Manag. 2017, 8, 125–134. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Goal programming in forest management: Customising models for the decision-maker’s preferences. Scand. J. For. Res. 2013, 28, 166–173. [Google Scholar] [CrossRef]
- Romero, C. Handbook of Critical Issues in Goal Programming; Pergamon Press: Oxford, UK, 1991; pp. 13–21. [Google Scholar]
- Romero, C. Extended lexicographic goal programming: A unifying approach. Omega 2001, 29, 63–71. [Google Scholar] [CrossRef]
- Giménez, J.C.; Bertomeu, M.; Diaz-Balteiro, L.; Romero, C. Optimal harvest scheduling in eucalyptus plantations under a sustainability perspective. For. Ecol. Manag. 2013, 291, 367–376. [Google Scholar] [CrossRef]
- Ballestero, E.; Romero, C. Multiple Criteria Decision Making and its Applications to Economic Problems; Springer Science+Business Media: New York, NY, USA, 1998. [Google Scholar]
- LINGO User´s Guide; LINDO Systems Inc.: Chicago, IL, USA, 2006; 820p.
- Saaty, T.L. A scaling method for priorities in hierarchical structure. J. Math. Psychol. 1977, 15, 317–332. [Google Scholar] [CrossRef]
- González-Pachón, J.; Romero, C. Goal programming: From constrained regression to bounded rationality theories. In Handbook of Multicriteria Analysis; Zopounidis, C., Pardalos, P.M., Eds.; Springer: Berlin, Germany, 2010; pp. 311–328. [Google Scholar]
- Eyvindson, K.; Öhman, K.; Nordström, E.-M. Using uncertain preferential information from stakeholders to assess the acceptability of alternative forest management plans. J. Multi-Criteria Decis. Anal. 2018, 25, 43–52. [Google Scholar] [CrossRef]
- Gómez, T.; Huelin, M.; Molina, J.; León, M.A.; Aldana, M.; Caballero, R. A multiobjective model for forest planning with adjacency constraints. Ann. Oper. Res. 2011, 190, 75–92. [Google Scholar] [CrossRef]
- Belavenutti, P.; Romero, C.; Diaz-Balteiro, L. Integrating Strategic and Tactical Forest- Management Models within a Multicriteria Context. For. Sci. 2018, 65, 178–188. [Google Scholar] [CrossRef]
- Nordström, E.M.; Romero, C.; Eriksson, L.O.; Öhman, K. Aggregation of preferences in participatory forest planning with multiple criteria: An application to the urban forest in Lycksele, Sweden. Can. J. For. Res. 2009, 39, 1979–1992. [Google Scholar] [CrossRef]
- Ortiz-Urbina, E.; González-Pachón, J.; Diaz-Balteiro, L. Decision-Making in Forestry: A Review of the Hybridisation of Multiple Criteria and Group Decision-Making Methods. Forests 2019, 10, 375. [Google Scholar] [CrossRef]
- Bagdon, B.A.; Huang, C.-H.; Dewhurst, S. Managing for ecosystem services in northern Arizona ponderosa pine forests using a novel simulation-to-optimization methodology. Ecol. Model. 2016, 324, 11–27. [Google Scholar] [CrossRef]
- Rönnqvist, M.; D’Amours, S.; Weintraub, A.; Jofre, A.; Gunn, E.; Haight, R.G.; Martell, D.; Murray, A.T.; Romero, C. Operations Research challenges in forestry: 33 open problems. Ann. Oper. Res. 2015, 232, 11–40. [Google Scholar] [CrossRef]
- Castro, L.; Härtl, F.; Moreno, W.; Calvas, B.; Izquierdo, L.; Knoke, T. Integrated bio-economic models as tools to support land-use decision making: A review of potential and limitations. J. Bioecon. 2018, 20, 183–211. [Google Scholar] [CrossRef]
- Blancas Peral, F.; Caballero, R.; Lozano, M.; Oyola, M.; Pérez, F. Goal programming synthetic indicators: An application for sustainable tourism in Andalusian coastal counties. Ecol. Econ. 2010, 69, 2158–2172. [Google Scholar] [CrossRef]
- Ruiz, F.; Cabello, J.M.; Gladish, B. Building Ease-of-Doing-Business synthetic indicators using a double reference point approach. Technol. Forecast. Soc. Chang. 2017, 131, 130–140. [Google Scholar] [CrossRef]
- Ruiz, F.; El Gibari, S.; Cabello, J.M.; Gómez-Núñez, T. MRP-WSCI: Multiple Reference Point based Weak and Strong Composite Indicators. Omega 2019, in press. [Google Scholar] [CrossRef]
- Augustynczik, L.D.A.; Yousefpour, R.; Rodriguez, L.C.; Hanewinkel, M. Conservation Costs of Retention Forestry and Optimal Habitat Network Selection in Southwestern Germany. Ecol. Econ. 2018, 148, 92–102. [Google Scholar] [CrossRef]
- Bauhus, J.; Puettmann, K.; Messier, C. Silviculture for old-growth attributes. For. Ecol. Manag. 2009, 258, 525–537. [Google Scholar] [CrossRef]
- Holloway, G.L.; Smith, W.P.; Halpern, C.B.; Gitzen, R.A.; Maguire, C.C.; West, S.D. Influence of forest structure and experimental green-tree retention on northern flying squirrel (Glaucomys sabrinus) abundance. For. Ecol. Manag. 2012, 285, 187–194. [Google Scholar] [CrossRef]
- Sullivan, T.; Sullivan, D.S. Green-tree retention and recovery of an old-forest specialist, the southern red-backed vole (Myodes gapperi), 20 years after harvest. Wildl. Res. 2018, 44, 669–680. [Google Scholar] [CrossRef]
- Nolet, P.; Kneeshaw, D.; Messier, C.; Béland, M. Comparing the effects of even- and uneven-aged silviculture on ecological diversity and processes: A review. Ecol. Evol. 2018, 8, 1217–1226. [Google Scholar] [CrossRef] [PubMed]
- Eggers, J.; Holmström, H.; Lämås, T.; Lind, T.; Öhman, K. Accounting for a Diverse Forest Ownership Structure in Projections of Forest Sustainability Indicators. Forests 2015, 6, 4001–4033. [Google Scholar] [CrossRef]
- Pang, X.; Nordström, E.-M.; Böttcher, H.; Trubins, R.; Mörtberg, U. Trade-offs and synergies among ecosystem services under different forest management scenarios—The LEcA tool. Ecosyst. Serv. 2017, 28, 67–79. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Alonso, R.; Martínez-Jaúregui, M.; Pardos, M. Selecting the best forest management alternative by aggregating ecosystem services indicators over time: A case study in Central Spain. Ecol. Ind. 2017, 72, 322–329. [Google Scholar] [CrossRef]
- O’Hara, K.; Hasenauer, H.; Kindermann, G. Sustainability in multi-aged stands: An analysis of long-term plenter systems. Forestry 2007, 80, 163–181. [Google Scholar] [CrossRef]
- Adnan, S.; Maltamo, M.; Coomes, D.A.; Valbuena, R. Effects of plot size, stand density, and scan density on the relationship between airborne laser scanning metrics and the Gini coefficient of tree size inequality. Can. J. For. Res. 2017, 47, 1590–1602. [Google Scholar] [CrossRef]
- Ezquerro, M.; Pardos, M.; Diaz-Balteiro, L. Operational research techniques used for addressing biodiversity objectives into forest management: An overview. Forests 2016, 7, 229. [Google Scholar] [CrossRef]
- Ezquerro, M.; Pardos, M.; Diaz-Balteiro, L. Integrating variable retention systems into strategic forest management to deal with conservation biodiversity objectives. For. Ecol. Manag. 2019, 433, 585–593. [Google Scholar] [CrossRef]
- Iglesias-Merchan, C.; Diaz-Balteiro, L.; de la Puente, J. Road traffic noise impact assessment in a breeding colony of cinereous vultures (Aegypius monachus) in Spain. J. Acoust. Soc. Am. 2016, 139, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Opo, R.; Fernandez-Olalla, M.; Margalida, A.; Arredondo, A.; Guil, F. Effect of methodological and ecological approaches on heterogeneity of nest-site selection of a long-lived vulture. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Fargallo, J.A.; Blanco, G.; Soto-Largo, E. Forest management effects on nesting habitat selected by Cinereous Vultures (Aegypius monachus) in central Spain. J. Raptor Res. 1998, 32, 202–207. [Google Scholar]
- Bertomeu, M.; Romero, C. Managing forest biodiversity: A zero-one goal programming approach. Agric. Syst. 2001, 68, 197–213. [Google Scholar] [CrossRef]
- Corrigan, E.; Nieuwenhuis, M. Using Goal-Programming to Model the Effect of Stakeholder Determined Policy and Industry Changes on the Future Management of and Ecosystem Services Provision by Ireland’s Western Peatland Forests. Sustainability 2017, 9, 11. [Google Scholar] [CrossRef]
- Campos, P.; Caparrós, A.; Cerdá, E.; Diaz-Balteiro, L.; Herruzo, A.C.; Huntsinger, L.; Martín-Barroso, D.; Martínez- Jauregui, M.; Ovando, P.; Oviedo, J.L.; et al. Multifunctional natural forest silviculture economics revised: Challenges in meeting landowners’ and society’s wants: A review. For. Syst. 2017, 26, eR01S. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Romero, C. In search of a natural systems sustainability index. Ecol. Econ. 2004, 49, 401–405. [Google Scholar] [CrossRef]
- Pereira, S.; Prieto, A.; Calama, R.; Diaz-Balteiro, L. Optimal management in Pinus pinea L. Stands combining silvicultural schedules for timber and cone production. Silva Fenn. 2015, 49, 1–16. [Google Scholar] [CrossRef]
- D’Amato, A.; Jokela, E.; O’Hara, K.; Long, J.N. Silviculture in the United States: An Amazing Period of Change over the Past 30 Years. J. For. 2018, 116, 55–67. [Google Scholar] [CrossRef]
- Fahey, R.T.; Alveshere, B.C.; Burton, J.I.; D’Amato, A.W.; Dickinson, Y.L.; Keeton, W.S.; Kern, C.C.; Larson, A.J.; Palik, B.J.; Puettmann, K.J.; et al. Shifting conceptions of complexity in forest management and silviculture. For. Ecol. Manag. 2018, 421, 59–71. [Google Scholar] [CrossRef]
- Messier, C.; Puettmann, K.J.; Coates, K.D. Managing Forests as Complex Adaptive Systems: Building Resilience to the Challenge of Global Change; Routledge: New York, NY, USA, 2013; 368p. [Google Scholar]
- Messier, C.; Bauhus, J.; Doyon, F.; Maure, F.; Sousa-Silva, R.; Nolet, P.; Mina, M.; Aquilué, N.; Fortin, M.-J.; Puettmann, K. The functional complex network approach to foster forest resilience to global changes. For. Ecosyst. 2019, 6, 21. [Google Scholar] [CrossRef]
- Filyushkina, A.; Strange, N.; Lof, M.; Ezebilo, E.E.; Boman, M. Applying the Delphi method to assess impacts of forest management on biodiversity and habitat preservation. For. Ecol. Manag. 2018, 409, 179–189. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).