Return Strategies and Online Product Customization in a Dual-Channel Supply Chain
Abstract
1. Introduction
2. Literature Review
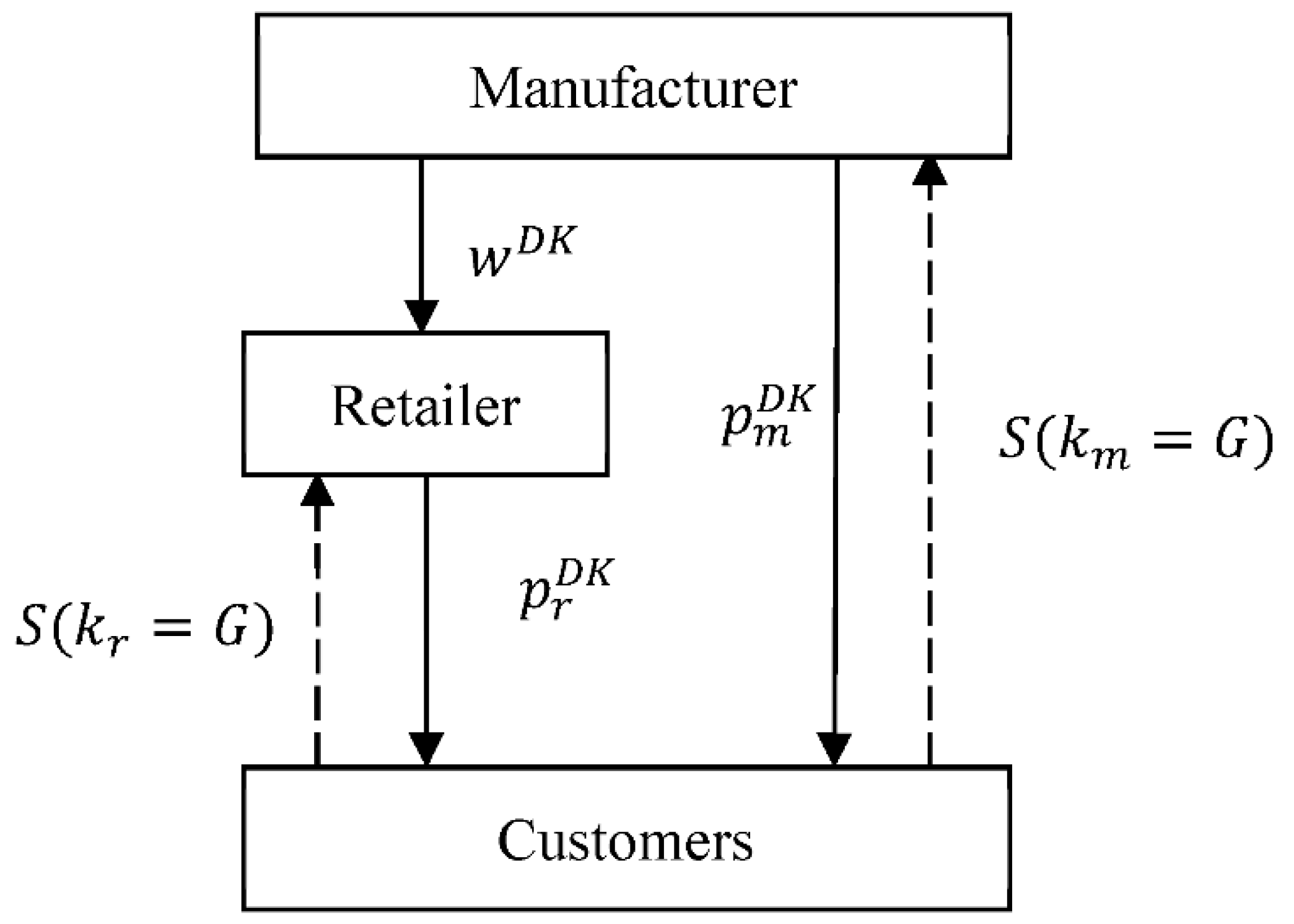
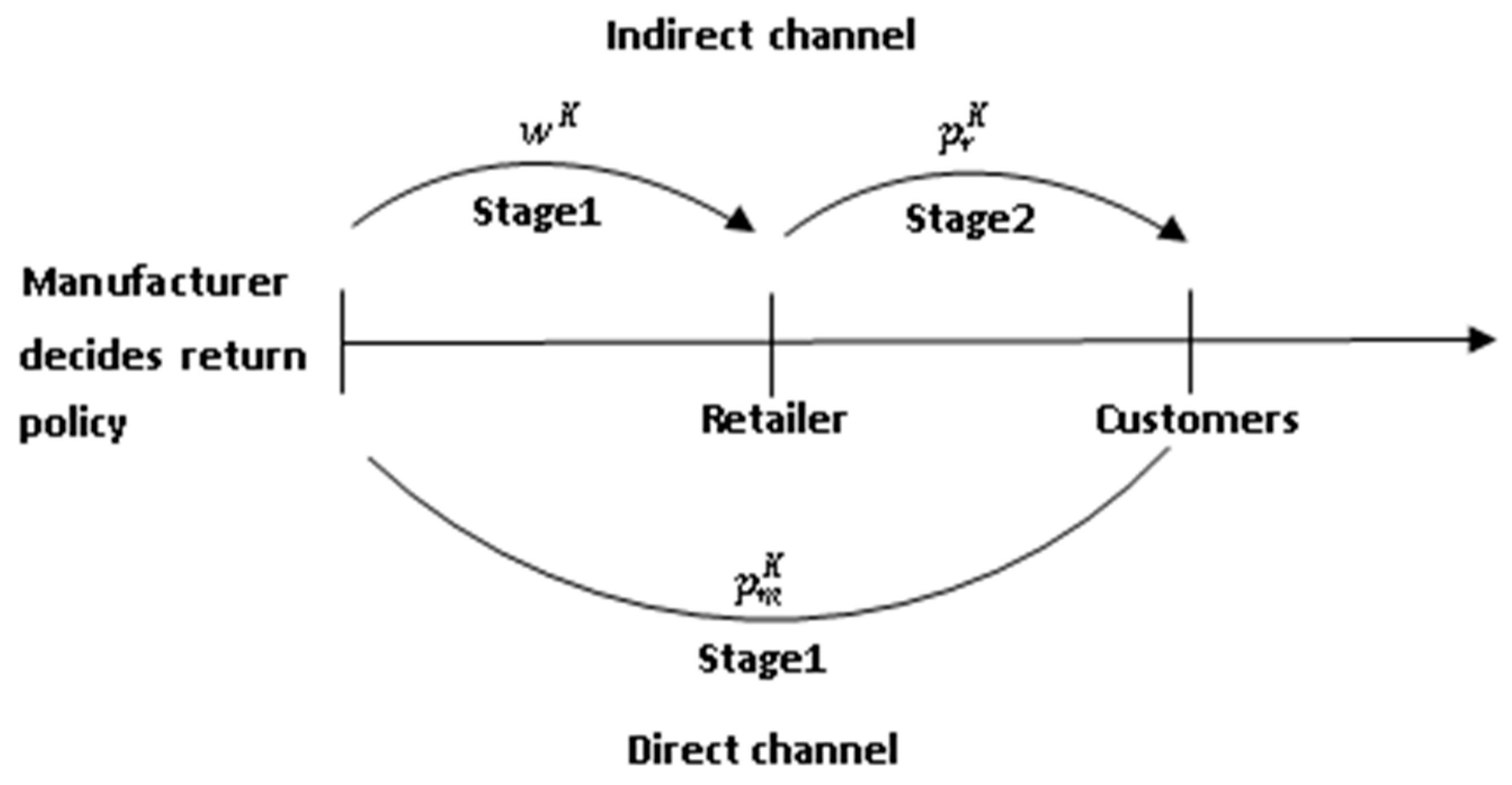
3. Dual-Channel Model
4. Analysis
4.1. Third-Stage Game: Customer’s Choice
4.2. Second-Stage Decision: The Price Choice of the Retailer and Manufacturer
4.3. First-Stage Decision: Return Policy Decision for Each Channel
- (a)
- ifand
- (b)
- if.
4.4. Impact of the Return Strategy in the Dual-Channel Supply Chain
- (a)
- and
- (b)
- If,If,.
- (1)
- Ifand, and
- (2)
- If,and.
- (1)
- If,; while,and
- (2)
- If,; while,.
5. Implementation of Product Customization in the Online Channel
5.1. Equilibrium Solution
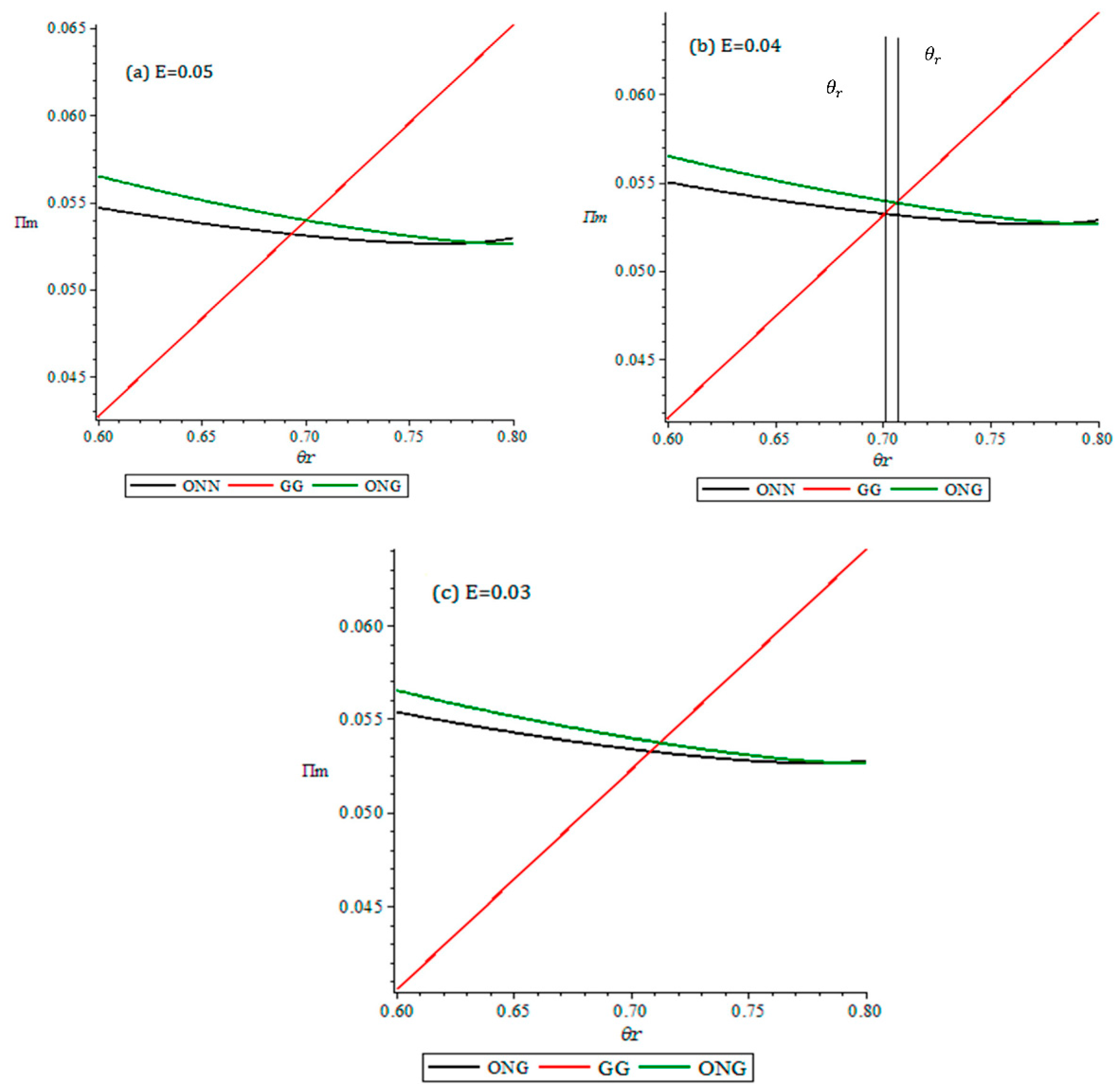
5.2. Channel Selection and the Impact of Personalized Customization
- (1)
- Whenit is beneficial for manufacturers to open online customization channels, regardless of the return policy adopted.
- (2)
- WhenONG is the optimal decision for the manufacturer.
- (3)
- When, maintaining an ordinary dual-channel structure and implementing MBG policies in both channels are the best decisions for manufacturers.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| K | NN | GN | NG | GG |
|---|---|---|---|---|
| DK | NN | GN | NG | GG |
|---|---|---|---|---|
References
- Li, W.; Chen, J.; Liang, G. Money-back guarantee and personalized pricing in a Stackelberg manufacturer’s dual-channel supply chain. Int. J. Prod. Econ. 2018, 197, 84–98. [Google Scholar] [CrossRef]
- Zhang, G.P.; Xia, Y.; Xiao, T. The Impact of Product Returns and Retailer’s Service Investment on Manufacturer’s Channel Strategies. Decis. Sci. 2016, 48, 918–955. [Google Scholar]
- Chen, J.; Bell, P.C. Implementing market segmentation using full-refund and no-refund customer returns policies in a dual-channel supply chain structure. Int. J. Prod. Econ. 2012, 136, 56–66. [Google Scholar] [CrossRef]
- Mostard, J.; Teunter, R. The newsboy problem with resalable returns: A single period model and case study. Eur. J. Oper. Res. 2006, 169, 81–96. [Google Scholar] [CrossRef]
- Ofek, E.; Katona, Z.; Sarvary, M. Bricks & clicks: The impact of product returns on the strategies of multi-channel retailers. Mark. Sci. 2011, 30, 42–60. [Google Scholar]
- Mukhopadhyay, S.K.; Setoputro, R. Reverse logistics in e-business: Optimal price and return policy. Int. J. Phys. Distrib. Logist. Manag. 2004, 34, 70–89. [Google Scholar] [CrossRef]
- Toktay, L.B. Forecasting product returns. In Business Aspects of Closed-loop Supply Chains; Guide, V.G., Jr., Van Wassenhove, L.N., Eds.; Carnegie Mellon University Press: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Ratcliff, C. How Fashion Ecommerce Retailers Can Reduce Online Returns. 2014. Available online: https://econsultancy.com/how-fashion-ecommerce-retailers-can-reduce-online-returns (accessed on 24 June 2019).
- Kwon, K.; Kim, C. How to design personalization in a context of customer retention: Who personalizes what and to what extent? Electron. Commer. Res. Appl. 2012, 11, 101–116. [Google Scholar] [CrossRef]
- Stock, J.; Thomas, S.; Shear, H. Managing product returns for competitive advantage. MIT Sloan Manag. Rev. 2006, 48, 56–62. [Google Scholar]
- McWilliams, B. Money-Back Guarantees: Helping the Low-Quality Retailer. Manag. Sci. 2012, 58, 1521–1524. [Google Scholar] [CrossRef]
- Syam, N.; Krishnamurthy, P.; Hess, J.D. That’s What I Thought I Wanted? Miswanting and Regret for a Standard Good in a Mass-Customized World. Mark. Sci. 2008, 27, 379–397. [Google Scholar] [CrossRef]
- Gu, Y.; Hsee, C.K.; Yang, Y.; Chen, J. Specification Seeking: How Product Specifications Influence Consumer Preference. J. Consum. Res. 2009, 35, 952–966. [Google Scholar]
- Chiang, W.-Y.K.; Chhajed, D.; Hess, J.D. Direct Marketing, Indirect Profits: A Strategic Analysis of Dual-Channel Supply-Chain Design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef]
- Yan, R.; Pei, Z. Retail services and firm profit in a dual-channel market. J. Retail. Consum. Serv. 2009, 16, 306–314. [Google Scholar] [CrossRef]
- Yoo, W.S.; Lee, E. Internet Channel Entry: A Strategic Analysis of Mixed Channel Structures. Mark. Sci. 2011, 30, 29–41. [Google Scholar] [CrossRef]
- Soysal, G.; Krishnamurthi, L. How does adoption of the outlet channel impact customers’ spending in the retail stores: Conflict vs. synergy? Soc. Sci. Electron. Publ. 2015, 62, 2457–2764. [Google Scholar] [CrossRef]
- Peng, G.; Tian, X.; Chen, Q.; Erjiang, E. Online Cooperative Promotion and Cost Sharing Policy under Supply Chain Competition. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar]
- Baiman, S.; Fischer, P.E.; Rajan, M.V. Information, contracting, and quality costs. Manag. Sci. 2000, 46, 776–789. [Google Scholar] [CrossRef]
- Webster, S.; Weng, Z.K. A Risk-free Perishable Item Returns Policy. Manuf. Serv. Oper. Manag. 2000, 2, 100–106. [Google Scholar] [CrossRef]
- Davis, J. Minor adjustments, such as a simple return policy, can increase e-tail sales. InfoWorld 2001, 23, 78. [Google Scholar]
- Shi, J.; Xiao, T. Service investment and consumer returns policy in a vendor-managed inventory supply chain. J. Ind. Manag. Optim. 2015, 11, 439–459. [Google Scholar] [CrossRef]
- Franke, N.; Schreier, M. Why Customers Value Self-Designed Products: The Importance of Process Effort and Enjoyment*. J. Prod. Innov. Manag. 2010, 27, 1020–1031. [Google Scholar] [CrossRef]
- Kramer, T.; Spolter-Weisfeld, S.; Thakkar, M. The Effect of Cultural Orientation on Consumer Responses to Personalization. Mark. Sci. 2007, 26, 246–258. [Google Scholar] [CrossRef]
- Jiang, Y.; Shang, J.; Kemerer, C.F.; Liu, Y. Optimizing E-tailer Profits and Customer Savings: Pricing Multistage Customized Online Bundles. Mark. Sci. 2011, 30, 737–752. [Google Scholar] [CrossRef]
- Irmak, C.; Vallen, B.; Robinson, S.R. The Impact of Product Name on Dieters’ and Nondieters’ Food Evaluations and Consumption. J. Consum. Res. 2011, 38, 390–405. [Google Scholar] [CrossRef]
- Huang, X.; Dong, P.; Mukhopadhyay, A. Proud to Belong or Proudly Different? Lay Theories Determine Contrasting Effects of Incidental Pride on Uniqueness Seeking. J. Consum. Res. 2014, 41, 697–712. [Google Scholar] [CrossRef]
- Simonson, I. Determinants of Customers’ Responses to Customized Offers: Conceptual Framework and Research Propositions. J. Mark. 2005, 69, 32–45. [Google Scholar] [CrossRef]
- Hunt, D.M.; Radford, S.K.; Evans, K.R. Individual differences in consumer value for mass customized products. J. Consum. Behav. 2013, 12, 327–336. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J. When to introduce an online channel, and offer money back guarantees and personalized pricing? Eur. J. Oper. Res. 2017, 257, 614–624. [Google Scholar] [CrossRef]
| Return Strategies | NN | GN | NG | GG |
|---|---|---|---|---|
| K | NN | NG |
|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Li, J.; Huang, Z.; Liu, B. Return Strategies and Online Product Customization in a Dual-Channel Supply Chain. Sustainability 2019, 11, 3482. https://doi.org/10.3390/su11123482
Zhang R, Li J, Huang Z, Liu B. Return Strategies and Online Product Customization in a Dual-Channel Supply Chain. Sustainability. 2019; 11(12):3482. https://doi.org/10.3390/su11123482
Chicago/Turabian StyleZhang, Rong, Jiatong Li, Zongsheng Huang, and Bin Liu. 2019. "Return Strategies and Online Product Customization in a Dual-Channel Supply Chain" Sustainability 11, no. 12: 3482. https://doi.org/10.3390/su11123482
APA StyleZhang, R., Li, J., Huang, Z., & Liu, B. (2019). Return Strategies and Online Product Customization in a Dual-Channel Supply Chain. Sustainability, 11(12), 3482. https://doi.org/10.3390/su11123482





