Developing Fair Investment Plans to Enhance Supply Chain Visibility Using Cooperative Games
Abstract
:1. Introduction
2. Literature Review
3. Background of the Proposed Method
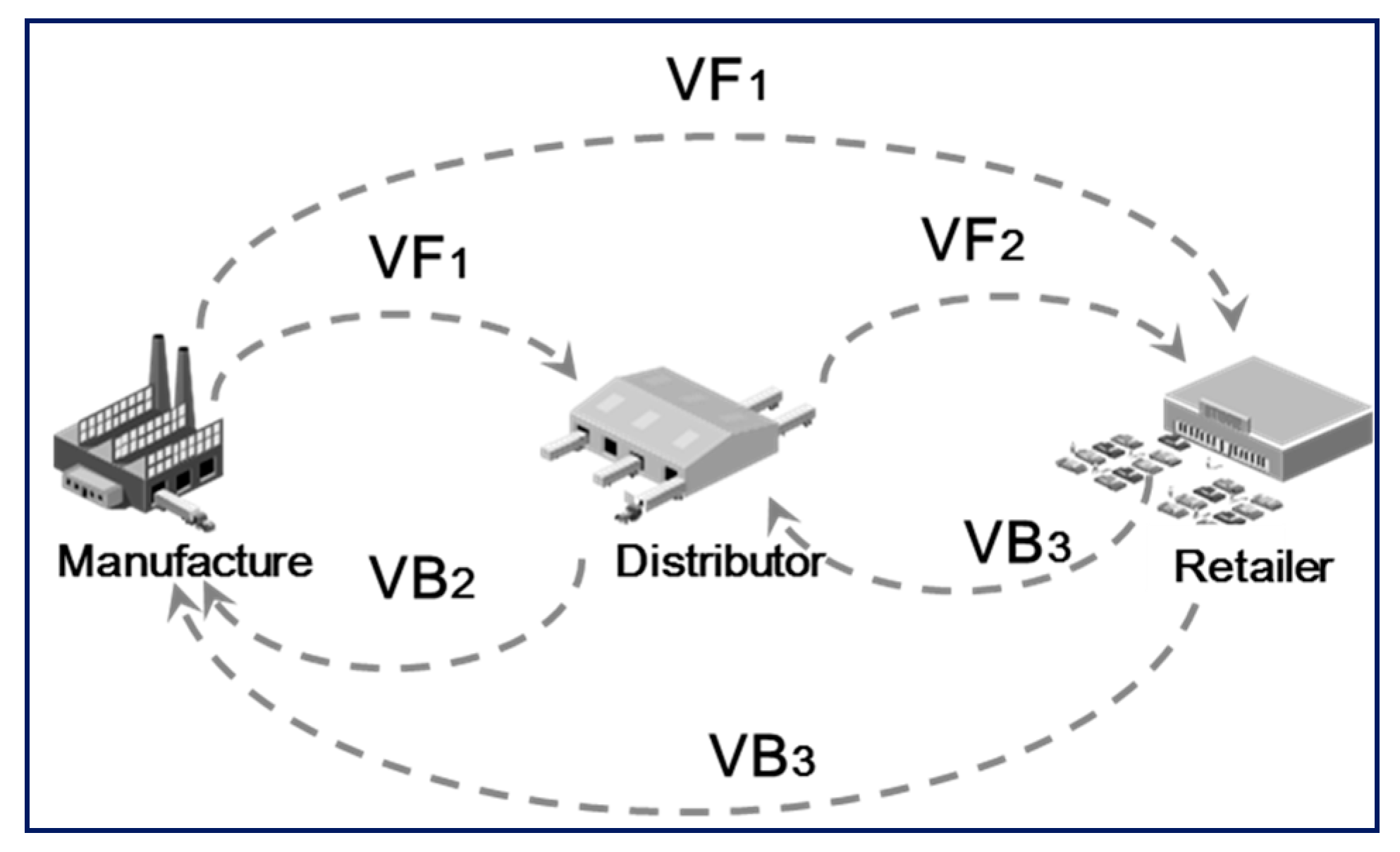
4. Model for Supply Chain Visibility Using the Collaborative Game Theoretical Model
4.1. Notations and Assumptions
4.2. Definition of Cost and Benefit and Allocation Rule
5. Illustrative Numerical Experiments
5.1. Design for the Experiment
5.2. Results and Discussion
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kashav, S.; Cerchione, R.; Centobelli, P.; Shabani, A. Sustainability Orientation, Supply Chain Integration, and SMEs Performance: A Causal Analysis. Benchmarking Int. J. 2018, 25, 3679–3701. [Google Scholar]
- Jin, Z.; Navare, J.; Lynch, R. The Relationship between Innovation Culture and Innovation Outcomes: Exploring the Effects of Sustainability Orientation and Firm Size. R D Manag. 2018. [Google Scholar] [CrossRef]
- Croom, S.; Vidal, N.; Spetic, W.; Marshall, D.; McCarthy, L. Impact of Social Sustainability Orientation and Supply Chain Practices on Operational Performance. Int. J. Oper. Prod. Manag. 2018, 38, 2344–2366. [Google Scholar] [CrossRef]
- Barratt, M.; Oke, A. Antecedents of Supply Chain Visibility in Retail Supply Chains: A Resource-Based Theory Perspective. J. Oper. Manag. 2007, 25, 1217–1233. [Google Scholar] [CrossRef]
- Tse, Y.K.; Tan, K.H. Managing Product Quality Risk and Visibility in Multi-Layer Supply Chain. Int. J. Prod. Econ. 2012, 139, 49–57. [Google Scholar] [CrossRef]
- Kang, Y.; Son, K.; Lee, Y.; Rhee, J. A Model-Based Performance Study of the EPCglobal Network. IE Interfaces 2011, 24, 139–150. [Google Scholar] [CrossRef]
- Ustundag, A. Evaluating RFID Investment on a Supply Chain using Tagging Cost Sharing Factor. Int. J. Prod. Res. 2010, 48, 2549–2562. [Google Scholar] [CrossRef]
- Kim, Y.; Chang, T.; Park, J. Gen2 RFID-Based System Framework for Resource Circulation in Closed-Loop Supply Chains. Sustainability 2017, 9, 1995. [Google Scholar] [CrossRef]
- Fan, T.; Tao, F.; Deng, S.; Li, S. Impact of RFID Technology on Supply Chain Decisions with Inventory Inaccuracies. Int. J. Prod. Econ. 2015, 159, 117–125. [Google Scholar] [CrossRef]
- Teucke, M.; Sommerfeld, D.; Freitag, M. Sharing Sensor Based Quality Data in Automotive Supply Chain Processes. IFAC-PapersOnLine 2018, 51, 770–775. [Google Scholar] [CrossRef]
- Joung, S.-I.; Kim, D.S. Case Study for RFID Applications from Business Model Perspective. J. Inf. Technol. Appl. Manag. 2013, 20, 197–216. [Google Scholar]
- Lee, S.; Jung, K. The Role of Community-Led Governance in Innovation Diffusion: The Case of RFID Waste Pricing System in the Republic of Korea. Sustainability 2018, 10, 3125. [Google Scholar] [CrossRef]
- Kim, J. ROI Model for the Adoption of RFID Technology in SCM. In Proceedings of the Korean Operations and Management Science Society Conference, Seoul, Korea, 13 May 2005; pp. 36–43. [Google Scholar]
- Melski, A.; Mueller, J.; Zeier, A.; Schumann, M. Assessing the Effects of Enhanced Supply Chain Visibility through Rfid. In AMCIS 2008 Proceedings; Association for Information Systems: New York, NY, USA, 2008; Volume 51. [Google Scholar]
- Xu, N. Improved Weighted Shapley Value Model for the Fourth Party Logistics Supply Chain Coalition. J. Control. Sci. Eng. 2013, 2013, 1. [Google Scholar] [CrossRef]
- Park, B.; Sung, S. Pricing the Seaport Service According to the Cost Allocation Rule of Game Theory. J. Korea Port. Econ. Assoc. 2012, 28, 257–274. [Google Scholar]
- Seong, S. A Game Theoretic Approach to the Container Quay Construction in Busan. J. Korea Port. Econ. Assoc. 2008, 24, 23–35. [Google Scholar]
- Otero, C.; Amaya, R. A Cost-Effective Collaborative Inventory Management Strategy between Non-Competitor Companies-A Case Study. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Bogota, Colombia, 25–26 October 2017; pp. 948–960. [Google Scholar]
- Hyun, C.L.; Ha, C. Sustainable Integrated Process Planning and Scheduling Optimization using a Genetic Algorithm with an Integrated Chromosome Representation. Sustainability 2019, 11, 502. [Google Scholar]
- Seok-jin, L. A Study on the Production and Distribution Problem in a Supply Chain Network using Algorithm. J. Korean Inst. Ind. Eng. 2003, 5, 263–270. [Google Scholar]
- Yeh, W.; Chuang, M. Using Multi-Objective Genetic Algorithm for Partner Selection in Green Supply Chain Problems. Expert Syst. Appl. 2011, 38, 4244–4253. [Google Scholar] [CrossRef]
- Nachiappan, S.P.; Jawahar, N. A Genetic Algorithm for Optimal Operating Parameters of VMI System in a Two-Echelon Supply Chain. Eur. J. Oper. Res. 2007, 182, 1433–1452. [Google Scholar] [CrossRef]
- Yokota, T.; Gen, M.; Li, Y. Genetic Algorithm for Non-Linear Mixed Integer Programming Problems and its Applications. Comput. Ind. Eng. 1996, 30, 905–917. [Google Scholar] [CrossRef]











| Contribution | RFID System | SCVisibility | Sharing Cost | Sharing Profit | Optimization SC Visibility |
|---|---|---|---|---|---|
| Kang, Y [6] Kim, Y [8] Joung, S [11] Lee, S [12] | O | ||||
| Fan, T. [9] Teucke [10] | O | ||||
| Ustundag [7] | O | ||||
| Kim, J [13] Melski, A [14] Xu, N [15] | O | ||||
| This study | O | O | O | O | O |
| Notations | Description |
|---|---|
| M | The set of visibility level, i ∈ M |
| N | The set of participants of the supply chain, j ∈ N |
| Xij | Decision variable which means the participant j install tags on the level i, Xij ∈ {0,1} |
| Kij | Binary variable which means the participant j may receive the benefit when tag is installed on visibility level i |
| CFij | Cost for operating and maintaining a RFID system |
| CTij | Cost for installing RFID tags |
| Cij | Total cost for installing and operating RFID systems |
| BSij | Benefit shared when participant j installs tags on level i |
| BTij | Benefit that only the participant j may have when installing RFID tags on level i |
| Bij | Total benefit that the participant j may have when installing RFID tags on level i |
| CSij | Cost when participant j installs RFID Tags on the visibility level i, which is shared by all participants |
| SVij | Sharing ratio of surplus benefit the participants j may receive surplus benefit from information sharing at the visibility level i. Σj VSij = 1. |
| fci | Characteristic function of participant i who installs RFID tag |
| VFij | The value of forward information flow |
| VBij | The value of backward information flow |
| BCOij | Net benefit of participant j which is adjusted by SVij |
| Level of Visibility | Manufacturer | Carrier | Buyer | |||
|---|---|---|---|---|---|---|
| Var. Cost | Benefit | Var. Cost | Benefit | Var. Cost | Benefit | |
| Container | 700 | 1875 | 500 | 3750 | 700 | 12,500 |
| Pallet | 336 | 5625 | 168 | 2500 | 336 | 25,000 |
| Box | 120 | 5625 | 181 | 2500 | 181 | 25,000 |
| Item | 2419 | 1875 | 3628 | 1250 | 2419 | 37,500 |
| Property Name | Value |
|---|---|
| Natural selector | Original rate: 0.9 |
| Crossover operator | Rate: 35% |
| Mutation operator | Desired rate: 12 |
| Stop condition | 200 executions |
| Population size | 200 |
| Algorithm: Optimization supply chain visibility using a cooperative game |
| Input: Set-up cost, surplus benefit, Shapley values, evolution limit, parameters of GA |
| create randomized initial chromosomes in the population pool |
| Define fitness function for GA: Production of the B/C ratio for each participant |
| Repeat |
| 1) Get parental chromosomes in the population pool |
| 2) Crossover chromosomes |
| 3) Mutate chromosomes |
| 4) Evaluate fitness-function value |
| 5) Replace survivor chromosomes in the population pool |
| Until evolution limit |
| Get the optimized chromosomes by repeated evolution limit |
| Print: all parameters, fitness-function value, optimized chromosomes, |
| B/C ratio of all participants |
| Level of Visibility | Net Profit of Whole Supply Chain | B/C Ratio of Whole Supply Chain | B/C Ratio Considering Cost Sharing | B/C Ratio Considering Benefit Sharing |
|---|---|---|---|---|
| Container | Manufacturer | Carrier | Manufacturer | Buyer |
| Pallet | Manufacturer | Carrier | Carrier | Carrier |
| Box | Manufacturer | Carrier | Manufacturer | Manufacturer |
| Item | Manufacturer | Manufacturer | Buyer | Manufacturer |
| Manufacturer’s Shapley Value | Distributor’s Shapley Value | Retailer’s Shapley Value | Number of Repetitions |
|---|---|---|---|
| 2 | 2 | 5 | 10 |
| 2 | 2 | 4 | 10 |
| 2 | 2 | 3 | 10 |
| 2 | 2 | 2 | 10 |
| 2 | 2 | 1 | 10 |
| 2 | 1 | 5 | 10 |
| 2 | 1 | 4 | 10 |
| 2 | 1 | 3 | 10 |
| 2 | 1 | 2 | 10 |
| 2 | 1 | 1 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Shin, K. Developing Fair Investment Plans to Enhance Supply Chain Visibility Using Cooperative Games. Sustainability 2019, 11, 3209. https://doi.org/10.3390/su11113209
Kim C, Shin K. Developing Fair Investment Plans to Enhance Supply Chain Visibility Using Cooperative Games. Sustainability. 2019; 11(11):3209. https://doi.org/10.3390/su11113209
Chicago/Turabian StyleKim, Changhyun, and KwangSup Shin. 2019. "Developing Fair Investment Plans to Enhance Supply Chain Visibility Using Cooperative Games" Sustainability 11, no. 11: 3209. https://doi.org/10.3390/su11113209
APA StyleKim, C., & Shin, K. (2019). Developing Fair Investment Plans to Enhance Supply Chain Visibility Using Cooperative Games. Sustainability, 11(11), 3209. https://doi.org/10.3390/su11113209






