1. Introduction
Train-based rapid transit systems—also known as tubes, underground, or metros—are a popular choice for high-capacity public transportation systems in urban areas. Rapid transit is used in urban areas typically for transporting large numbers of passengers over small distances, at high frequencies, and are usually preferred over other transportation modes due to its several advantages. Road transportation annually costs
million deaths and trillions of dollars to the global economy due to congestion [
1,
2]. Train-based rapid transit is the safest and most dependable mode of transportation due to lack of congestion, and a significantly lower chance of accidents and vehicle/system failure. It is the fastest forms of land transportation, is usually relatively inexpensive, and is good for economic and social sustainability.
Rapid transit systems are usually supported by other transportation modes such as trams, buses, ferries, vehicle park and ride stations, motorcycles, bike-sharing stations, and walking routes. Various topologies including lines, circle, grid and cross, are used for the railway structures. It is a complex system in itself due to an enormous number of passengers to be transported through a large number of stations connected through multiple train lines. Keeping track of the passengers, speedy issuance of tickets, enforcing the use of appropriate tickets, is one dimension of the system complexity. The routes need to be planned and the trains need to be scheduled in such a way to optimize passenger convenience and the overall throughput of the system. A more complex aspect of the rapid transit system design is to consider it a part of the larger urban transportation system, including complementary transportation resources and networks, and optimize it holistically, i.e., to consider the transportation routes and choices made by people, not only within the rapid transit system, but also outside the rapid transit, which includes, as mentioned before, trams, buses, bike-sharing stations, and walking routes. This optimization is a gigantic challenge, particularly if we consider cities such as London and its rapid transit, i.e., the London Metro, or the New York City Subway, Tokyo subway system, or the Beijing Subway. For brevity, from here on, we use “metro” to refer to rapid transit systems.
Many techniques have been proposed to model, analyze, and design metro systems. For instance, Hu et al. [
3] develop an operation plan for intercity passenger train and the ticket prices using a multi-objective model. They apply their model to the intercity rail between the Chongqing and Chengdu cities. Sun et al. [
4] provide an optimization method for train scheduling in a metro line including the terminal dwell time. The method, in optimizing the train schedule, takes into account the passenger preferences, plan robustness, and energy efficiency of the system. Escolano et al. [
5] use artificial neural networks (ANNs) to optimize the bus scheduling and dispatch system in Metro Manila. The aim of the ANN model is to reduce passenger waiting time on the bus stops and hence reduce the overall journey time. Wang at al. [
6] proposed two approaches for estimating train delays using historical and real-time data obtained from Amtrak US trains during 2011–2013.
Several researchers have tried to predict the number of passengers for metro systems using various techniques. Wang et al. [
7] propose a prediction model to predict passenger volume combining Radial Basis Function (RBF) neural network and Least Squares Support Vector Machines (LSSVM). They use flow data of passengers traveling through the Dongzhimen subway stations from 2012. Abadi et al. [
8] predict the number of train passengers in a selected region of Indonesia using a combination of a neuro-fuzzy model and singular value decomposition (SVD). Zhang et al. [
9] design a skip-stop strategy to optimize the journey time and the number of passengers traveling in Shenzhen Metro. Zhao et al. [
10] propose a probabilistic model to estimate the passenger flows through different trains and routes. The estimated passenger flows are useful in modeling passenger path choices. They use data from the Shenzhen Metro automated fare collection (AFC) system to evaluate their proposed technique. A detailed literature review of metro-based research is given in
Section 2.
The focus of our research in this paper is to address the metro system performance using a holistic approach whereby the transportation authorities can optimize the performance of the whole urban transportation network. We have mentioned earlier that an urban transportation system usually includes one or more metro systems and the complementary transportation network which consists of other transportation modes, e.g., buses, ferries, and bike-sharing stations. The aim of the transportation authorities in an urban area is to provide public personalized, convenient, speedy, multi-modal, and inexpensive travel options. A transportation authority, such as a city council, for this purpose, builds transportation facilities for people to travel to the nearest metro stations from their homes, offices, or other Points of Interests (PoIs), and vice versa. The current works in this domain have not studied the performance of urban metro systems in such details.
Secondly, the use of cutting-edge technologies has been limited in these studies. The last few decades have seen an increasing surge in the technological advancements. The penetration of these technologies to all spheres of everyday life has given rise to the smart cities, smart societies, and smart infrastructure developments [
11,
12]; smart transportation infrastructure is at the forefront of these developments [
13,
14,
15]. The use of GPS devices and mobile signals to collect vehicle location and congestion data [
16]; the use of big data [
17,
18,
19,
20] and high-performance computing (HPC) [
17,
19,
21,
22] technologies; mobile, cloud and fog computing [
16,
23,
24,
25,
26]; image processing, deep learning, and artificial intelligence (AI) for road traffic analysis and prediction [
27,
28,
29,
30]; urban logistics prototyping [
31]; vehicular ad hoc networks [
24,
32,
33,
34,
35]; autonomous driving [
27]; autonomic transportation systems [
36,
37,
38]; and the use of social media for traffic event detection [
39,
40,
41]; are but a few examples. There is a need for innovative uses of the cutting-edge technologies in transportation.
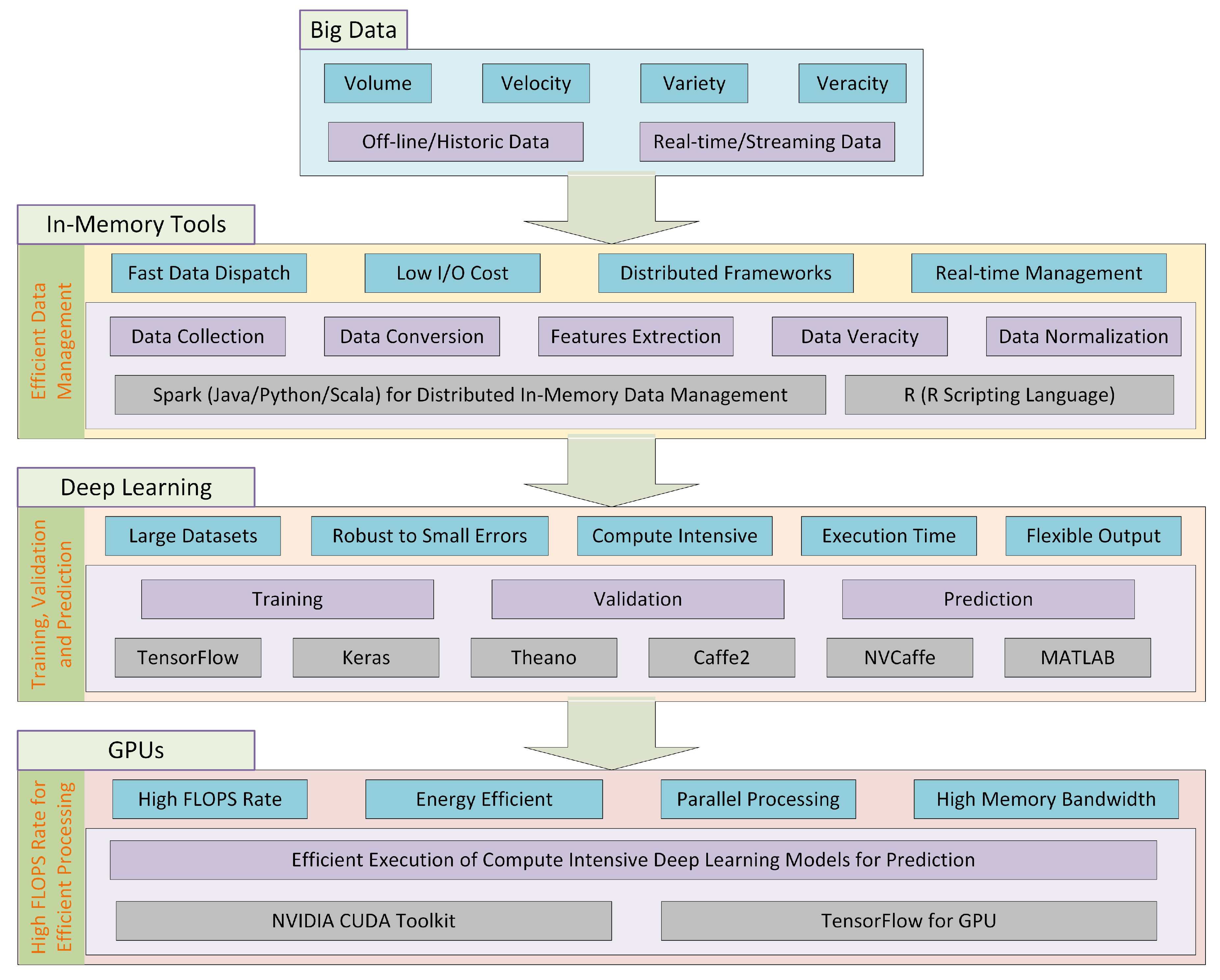
We focus on this paper on bringing four complementary cutting-edge technologies together—big data, in-memory computing, deep learning, and Graphics Processing Units (GPUs)—to address the challenges of holistically analyzing urban metro systems. The approach presented in this paper provides a novel and comprehensive approach toward large-scale urban metro systems analysis and design. GPUs provide massively parallel computing power to speed up computations. Big data leverages distributed and HPC technologies, such as GPUs, to manage and analyze data. Big data and HPC technologies are converging to address their individual limitations and exploit their synergies [
42,
43,
44,
45]. In-memory computing allows faster analysis of data using random-access memories (RAMs) as opposed to the secondary memories. Deep learning is used to predict various characteristics of urban metro systems.
We have used the London Metro system as a case study in this paper to demonstrate the effectiveness of our proposed approach. The London Metro, also called London Underground, is one of the oldest rapid transit systems in the world, indeed the first metro system in the world. It has 270 stations and 11 train lines covering 402 KM, serving 5 million passenger journeys daily [
46]. A map of the London Metro network is given in
Figure 1. The dataset we have used in this study is provided by Transport for London (TFL) under the Rolling Origin and Destination Survey (RODS) program [
47]. This data is collected by surveying the passengers traveling through the London Metro network in the United Kingdom. The purpose of this program is to collect the data of passengers traveling between different stations during different time intervals in a day. The data is available for the year 2015.
We use the RODS data to model the relationship between the number of passengers and (a) various access transportation modes used by the passengers to reach the train stations; (b) egress modes used to travel from the metro station to their next PoIs; (c) different origin-destination (OD) pairs of stations; and (d) the distance between the OD pairs of stations. Therefore, we predict, for six time intervals, the number of passengers using different access and egress modes to travel to, and travel from, each of the London Metro stations, respectively. We will see later in the paper that there are ten different types of access and egress transportation modes being used to complement the London Metro including buses and motorcycles. The information about the access and egress modes is valuable because it allows estimating the spatiotemporal use of various transportation modes, and could be used for planning and resource provisioning purposes. For example, if many passengers are using the access mode “car/van parked”, then the transportation authorities need to estimate whether the parking area reserved for the passengers to park their cars is sufficient to accommodate the vehicles. Similarly, the demand for buses and their time schedules could be estimated and planned for. We also predict for six time intervals the number of passengers that will be traveling between specific pairs of stations (OD pairs) at various time intervals, such as “PM Peak”. Moreover, we predict the number of passengers traveling between various OD station pairs to investigate the relationship between the number of passengers and the distance between those pairs of stations. This would be helpful in improving planning, resource provisioning, and quality of service of the urban transport system. This is the first study where the RODS data is used to model and predict various metro system characteristics.
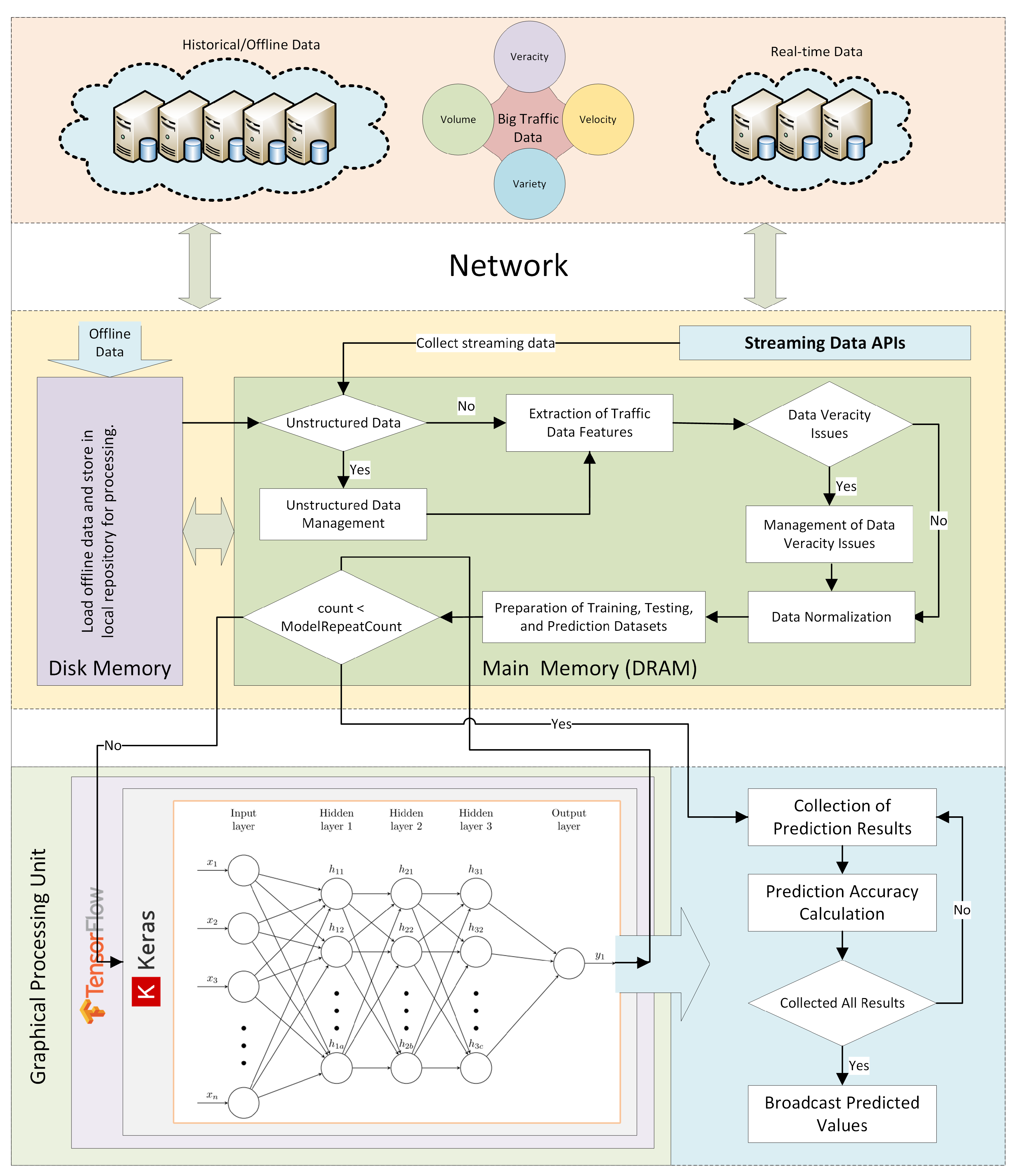
The RODS data described above is fed into the deep learning pipeline for training and prediction purposes. We have used Convolutional Neural Networks (CNNs) in our deep learning models. Firstly, the data is pre-processed to deal with the data veracity issues, and for data parsing and normalization. The data is processed in-memory using R [
48] and Spark [
49]. Subsequently, the data is fed to the deep learning engine, which is a compute intensive task. The use of GPUs provides a speedy deep learning training process. We have used two well-known evaluation metrics for the accuracy evaluation of our deep prediction models. These are mean absolute error (MAE) and mean absolute percentage error (MAPE). Additionally, we have provided the comparison of actual and predicted values of the metro characteristics. The results demonstrate a range of prediction accuracies, from high to fair. These are discussed in detail. The paper contributes novel deep learning models, algorithms, implementation, analytics methodology, and software tool for analysis of metro systems. The paper also serves as a preliminary investigation into the convergence of big data and HPC for the transportation sector, specifically for the rapid transit systems, incorporating London Metro as a case study. We would like to clarify here that HPC and big data convergence have been discussed by researchers in the literature for the last few years, such as in [
42,
43,
44,
45]. We are not suggesting that this is the first study on the convergence in general, rather it is the first study on the convergence that focuses specifically on the transportation and rapid transit application domains. The topic of HPC and big data convergence is in its infancy and will require many more efforts by the community across diverse applications domains before reaching its maturity. We will explore these convergence issues in the future with the aim to devise novel multidisciplinary technologies for transportation and other sectors. This is the first study of its kind where integration of leading-edge technologies—big data, in-memory computing, deep learning, and HPC—have been applied to holistic modeling and prediction of a real rapid transit system.
The rest of the paper is organized as follows. The literature review is provided in
Section 2. The proposed methodology is presented in
Section 3. The analysis and results are given in
Section 4.
Section 5 concludes the paper and gives directions for future work.
4. Performance Evaluation
4.1. Predicting Number of Passengers Reaching the Stations Using Different Access Modes
In this phase, we have used the dataset that gives the number of passengers who have been using different access modes to enter the stations while traveling through the underground train in UK during the year 2015. Access modes indicate the sources used by passengers to reach the stations and these have been divided into different categories based on the nature of transportation used by passengers. These include NR/DLR/Tram, Bus/Coach, Bicycle, Motorcycle, Car/Van Parked, Car/Van Driven Away, Walked, Taxi/Minicab, River Bus/Ferry. Another category “Other modes” describes the access modes other than those mentioned above. In addition to these categories, entry data collected for passengers who did not describe their means of transportation to reach the station is included by using the tag “Not stated”.
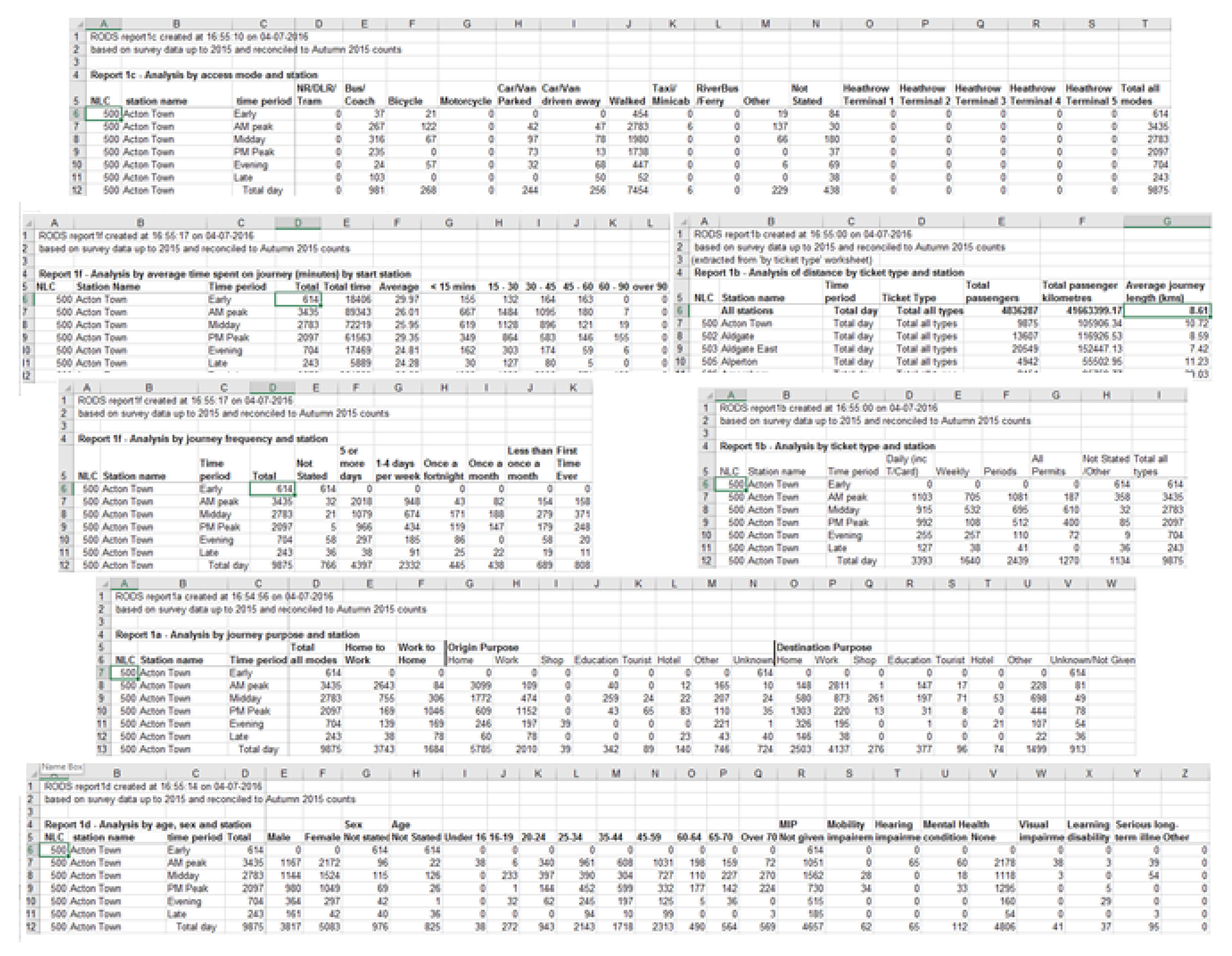
Passengers data entering the stations is collected at six different intervals in a day. These intervals are named as “early”, “a.m. peak”, “midday”, “p.m. peak”, “evening” and “late”. “Early” in this data represent the time interval before 7 a.m. in early morning, “a.m. peak” represents the time interval between 7 a.m. to 10 a.m., “midday” starts form 10 in morning and ends at 4 p.m., whereas the “p.m. peak” is the time interval between 4 p.m. to 7 p.m., from 7 p.m. to 10 p.m. it is considered “evening” and time slot from the 10 p.m. to late night is put in the category “late”. In addition to these time interval-based counts, passengers count for the entire day are also given. The data has been collected from 267 stations in UK and this provides information about 10 million people entering the stations using different modes. By using this data, we have modeled the relationship between the number of passengers at different time intervals and the access modes they are using to enter the stations. The purpose to model this relationship is to predict the expected number of passengers entering the stations at a specific time interval using those access modes. In this section, we are using the passengers count at different time intervals e.g., early, am peak, midday, evening, and late to estimate the number of passengers entering the station at “p.m. peak” time interval using these access modes. An overview of the data used in this section is given in
Table 3 which shows the access modes data during all the time intervals for one station and then goes on the same pattern for other stations.
For all the access modes, we have repeated the training, testing and prediction process 25 times. Each time, batch size 5 was used with the number of epochs 1000. i.e., the training procedure was repeated 1000 times while running the model. In addition to this, we have used 80% data for training purpose, 10% data for testing purpose and the remaining 10% data is used for prediction purposes. The purpose to run the model with same configurations and same data (access modes) multiple times was to see how much variation was there in the predicted number of passengers. As we executed the same model for each access mode 25 times, we have obtained different loss values.
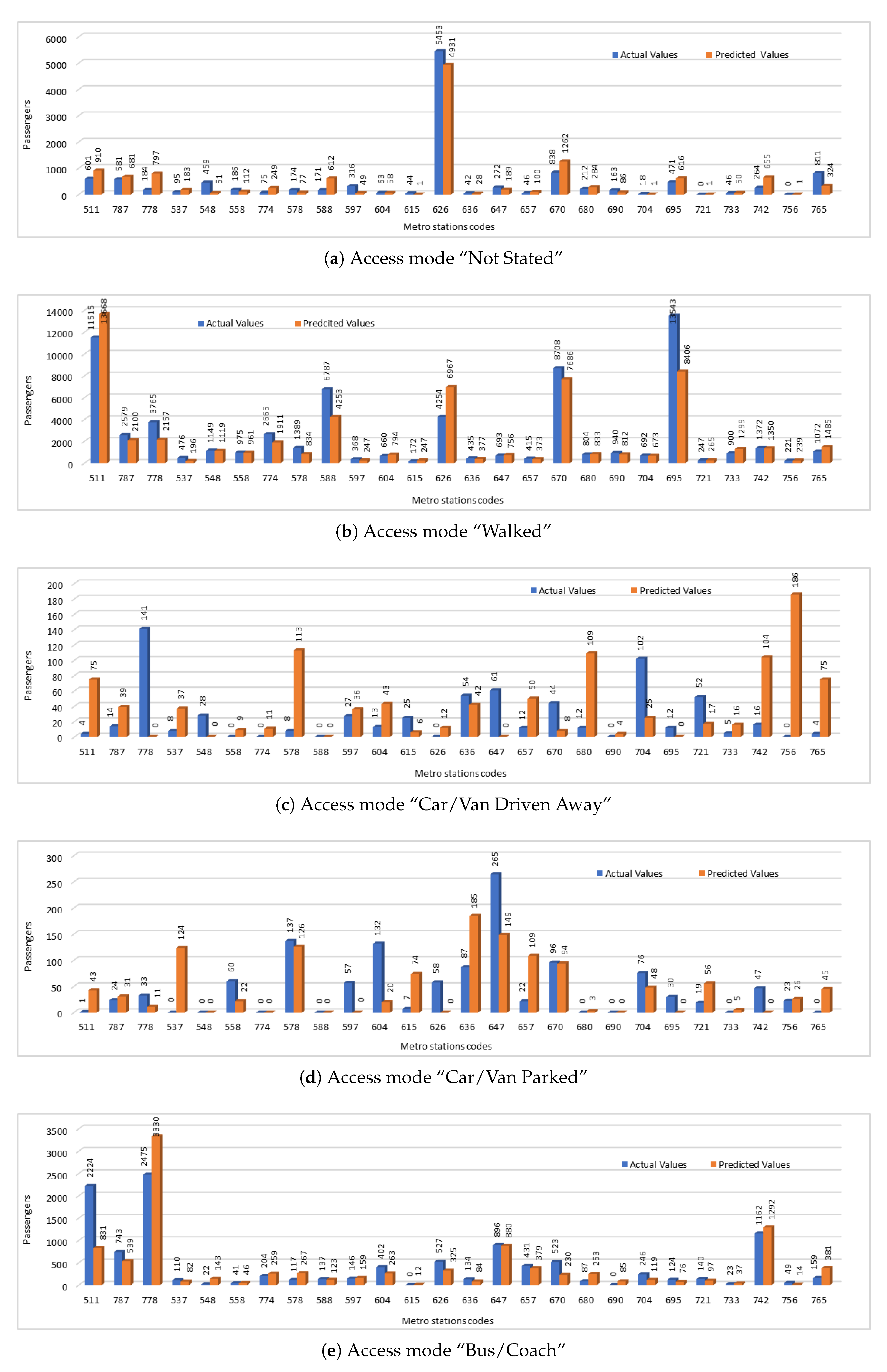
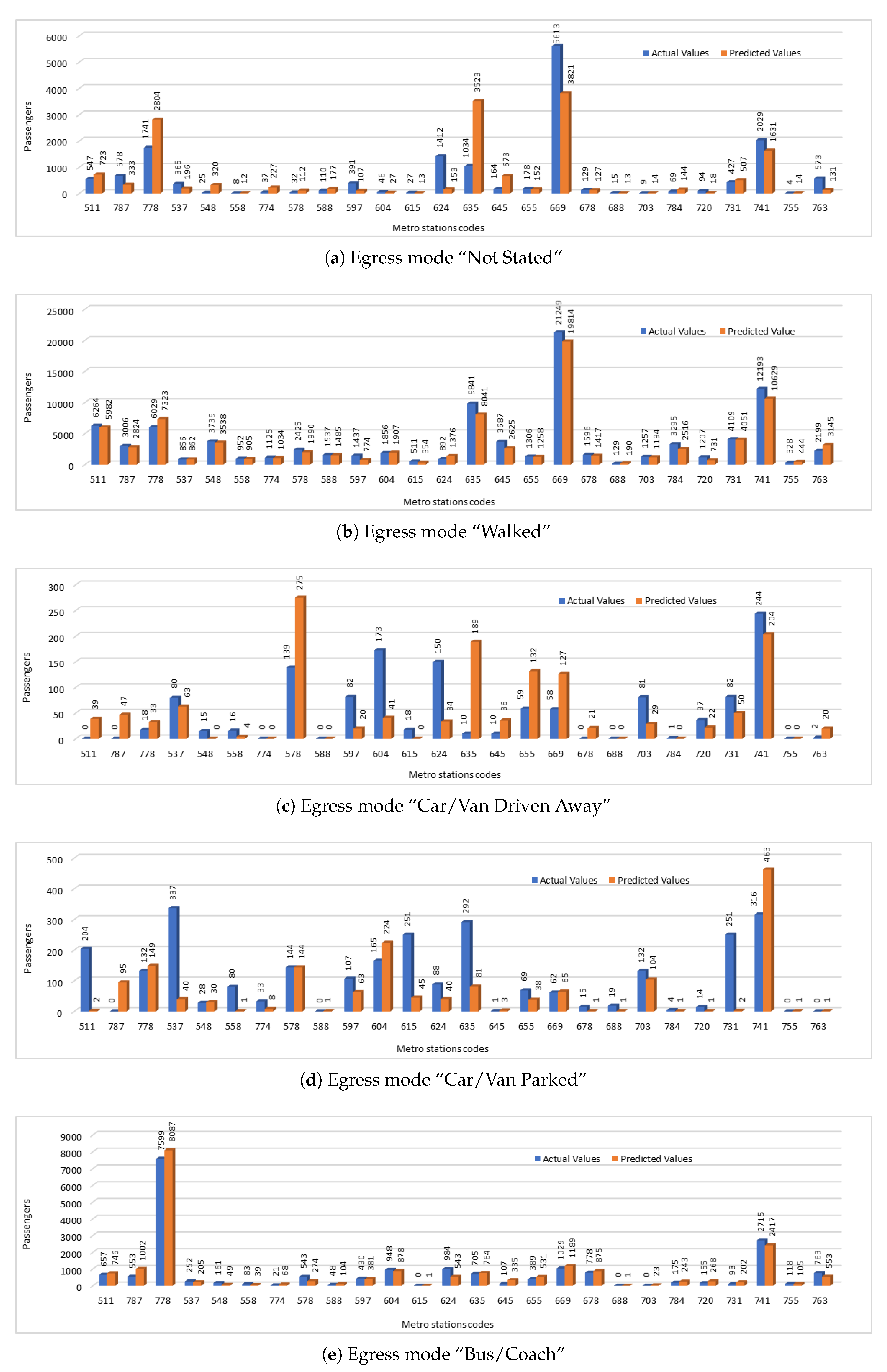
For evaluation of our predicted values, we have compared the predicted values with the actual values. We have presented the predicted passengers values that were entering the stations using five selected access modes including “not stated”, “walked”, “car/van driven away”, “car/van parked”, and “bus/coach”. The comparison of actual number of passengers entering the stations using different access modes and the number of passengers predicted by our deep model is shown in
Figure 6. We have used station codes (NLC) in this figure instead of station names. For corresponding station names, please refer to
Table 4. Comparison of actual and predicted values shows that in some cases prediction results were close to the actual values and predicted values were showing the same trends even if they were not very close in some cases. In
Figure 6a,b,e, we can see where both actual and predicted values are showing the similar trends, but in
Figure 6c,d are showing the trends that are not similar. One reason of this error could be the small amount of passenger data which shows the infrequent use of these access modes by the passengers.
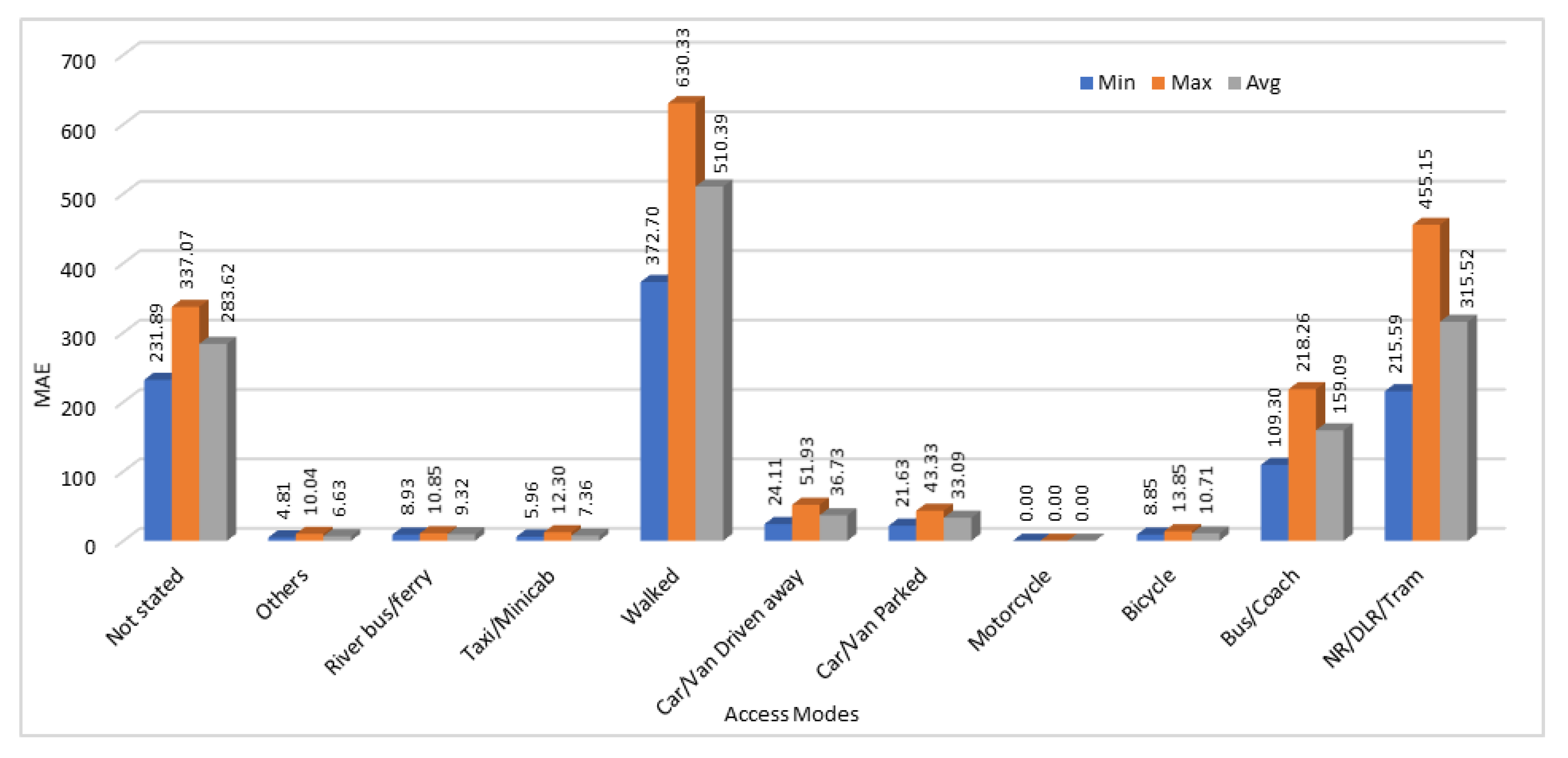
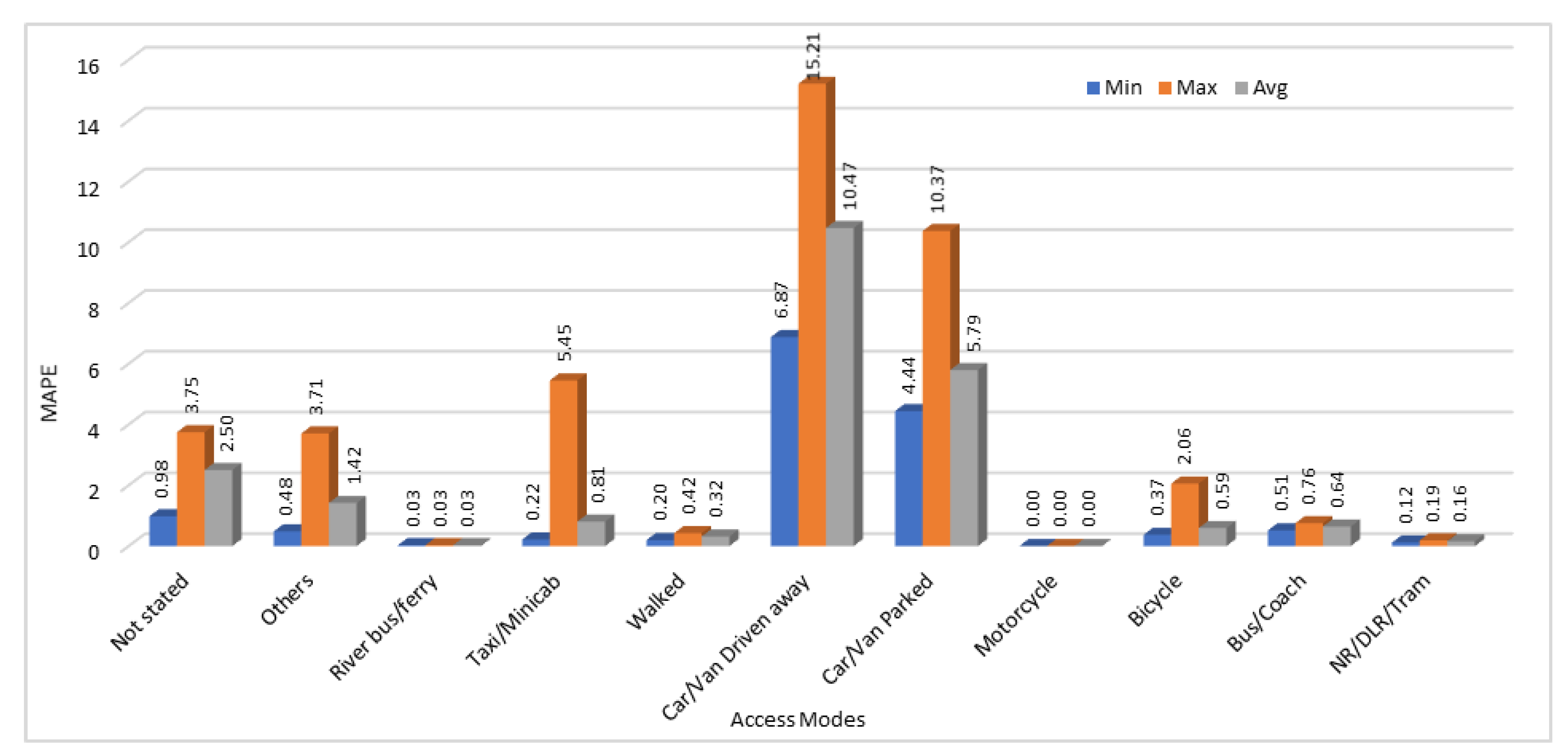
We have calculated MAE, and MAPE for all 25 executions of our model to test the accuracy of predicted results. From those 25 results, we have calculated the minimum errors (MAE and MAPE), maximum error and average error values among 25 generated results. Results obtained by calculating the MAE and MAPE values by comparing the actual and predicted passengers count values are shown in
Figure 7 and
Figure 8 respectively.
The prediction accuracy shows high variation due to the nature of the dataset. This is clear from the results and by showing minimum, maximum, and average error values for all the access modes. In some cases, there was no change in data across different stations, so the prediction accuracy is very high for those access modes. As shown in
Figure 7 and
Figure 8, both mean absolute error and mean absolute percentage error values are zero when motorcycle is used as an access mode. This is because the data patterns on all the stations for the number of passengers traveling through motorcycles were same. Therefore, the predicted values for number of passengers using motorcycles to reach the stations were also accurate. In some cases, absolute mean error value was high as compared to other access modes as we can see from
Figure 7. We can see that error value for the access mode “walked” is higher than all the other access modes which shows that the predicted values were much different from the actual values. However, if we see the
Figure 8, mean absolute percentage error values are very low for those passengers who mentioned the station access mode as “walked”. This is because of a lot of variation in data of passengers who entered the station by walking. In some stations, such passengers were in hundreds, on some stations they were in thousands, and on some stations those were in tens of thousands. Therefore, the MAE is very high because the predicted values are different from the actual values, but the MAPE is comparatively very low that shows that it is tolerable. Same is the case for the access modes “Car/Van driven away” and “Car/Van parked”. In some other cases, such as “Taxi/Minicab”, “River bus/ferry”, “Others”, and "Bicycle”, the error value calculated using MAE was low and it was not very high when using MAPE method as well.
4.2. Predicting Number of Passengers Exiting the Stations using Different Egress Modes
In this section, we have used the dataset that gives the number of passengers exiting the train stations after traveling from their origin stations to the destination stations. The data gives us the number of passengers using different egress modes when exiting the stations to reach their destinations. Same as access modes described above, egress modes have also been divided into different categories based on the nature of transportation means. These include NR/DLR/Tram, Bus/Coach, Bicycle, Motorcycle, Car/Van Parked, Car/Van Driven Away, Walked, Taxi/Minicab, River Bus/Ferry, and Others. In addition to these categories, exiting data collected for passengers who did not describe their means of transportation to reach the station is included by using the tag “Not stated”. This data has also been collected at six different intervals in a day. Same interval names and durations have been used to describe the egress modes as well. To predict the number of passengers using a specific egress mode while leaving the station, we have modeled the relationship between the passengers exiting the stations at different time intervals. We have used the five time intervals (early, am peak, midday, evening, and late) data as input to predict the passengers count at sixth time interval i.e., “p.m. peak”. An overview of the input dataset used in this work is shown in
Table 5. This table also shows the egress mode data for selected station (NLC 574) whereas the data for all the other stations is available on the same pattern. Again, we have used 80% data for training purpose, 10% data for testing purpose and the remaining 10% data is used for prediction purposes. For each egress mode, our deep model was executed for 25 times and therefore we collected 25 sets of predicted numbers of passengers for each egress mode.
We have compared the original number of passengers exiting the metro stations using selected egress modes with the passengers count predicted by our deep model. Same as we did in access modes, we have 10 different egress modes, but for the comparison of original and predicted values, we have selected five egress modes. The reason to compare the values with only selected egress modes is that some of the modes does not have a reasonable amount of data that could be used to make a meaningful comparison. In
Figure 9, we have shown the actual and predicted number of passengers leaving the stations using different egress modes. In these figures, we have used the station codes and number of passengers exiting at different times to predict the number of passengers exiting at “p.m. peak” time interval using different egress modes. To find the station names corresponding to the station codes used in this figure, please see
Table 4. If we compare the prediction results, we can say that in some cases, predicted values were very close to the actual values. For example, if we compare the results for egress mode “Walked”
Figure 9b, we can see that accuracy is very high in this egress mode. This egress mode also has highest number of passengers reported among other results shown in this figure. Also the predicted number of passengers are very close to the actual number of passengers in case of egress modes “Bus/Coach”
Figure 9e. However, if we see the results of “Car/Van Driven Away” or “Car/Van Parked” modes
Figure 9c,d we can say that the predicted values are bit different than the actual values and unfortunately the predicted values are not as good as these were in above two cases. One reason of this low accuracy in these two modes could be the high variation in the passenger data. Also, number of passengers in these two cases are very low as compared to the other modes discussed above.
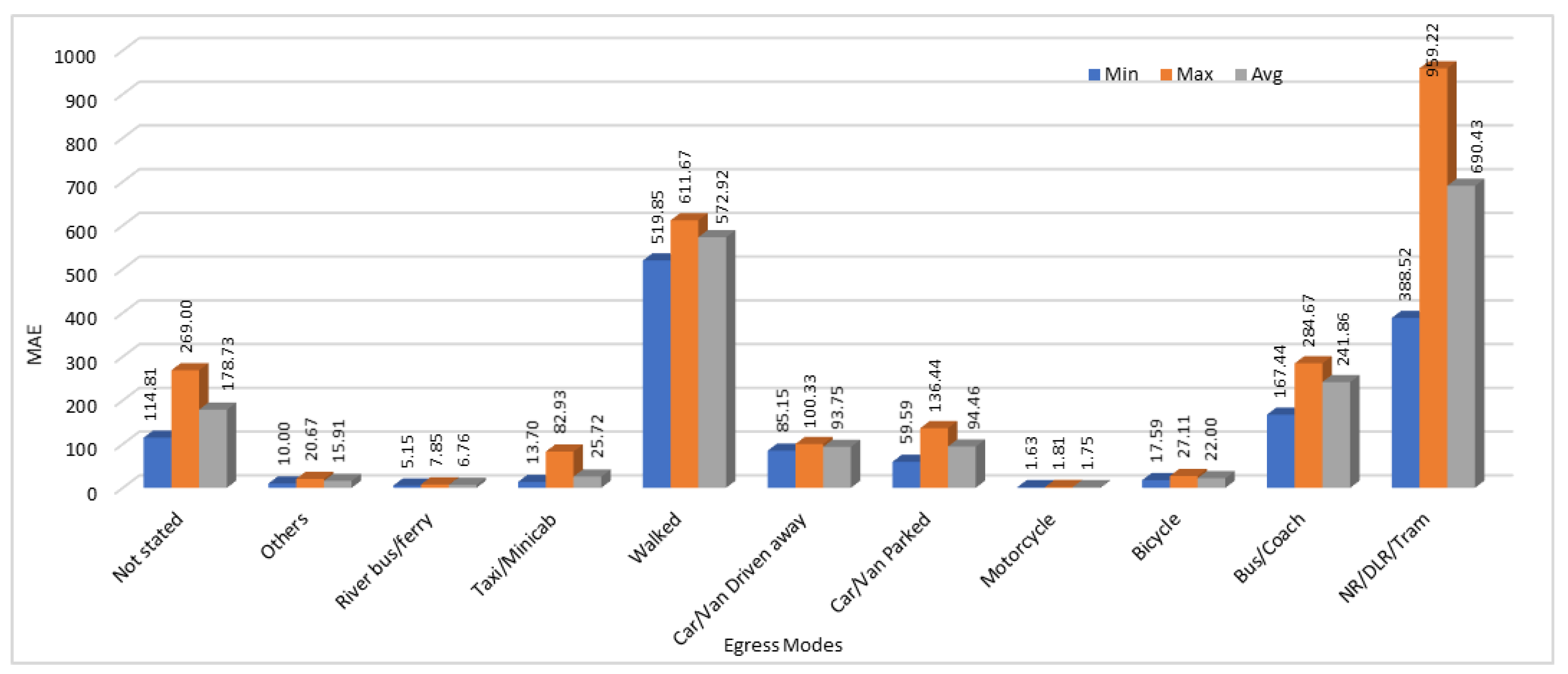
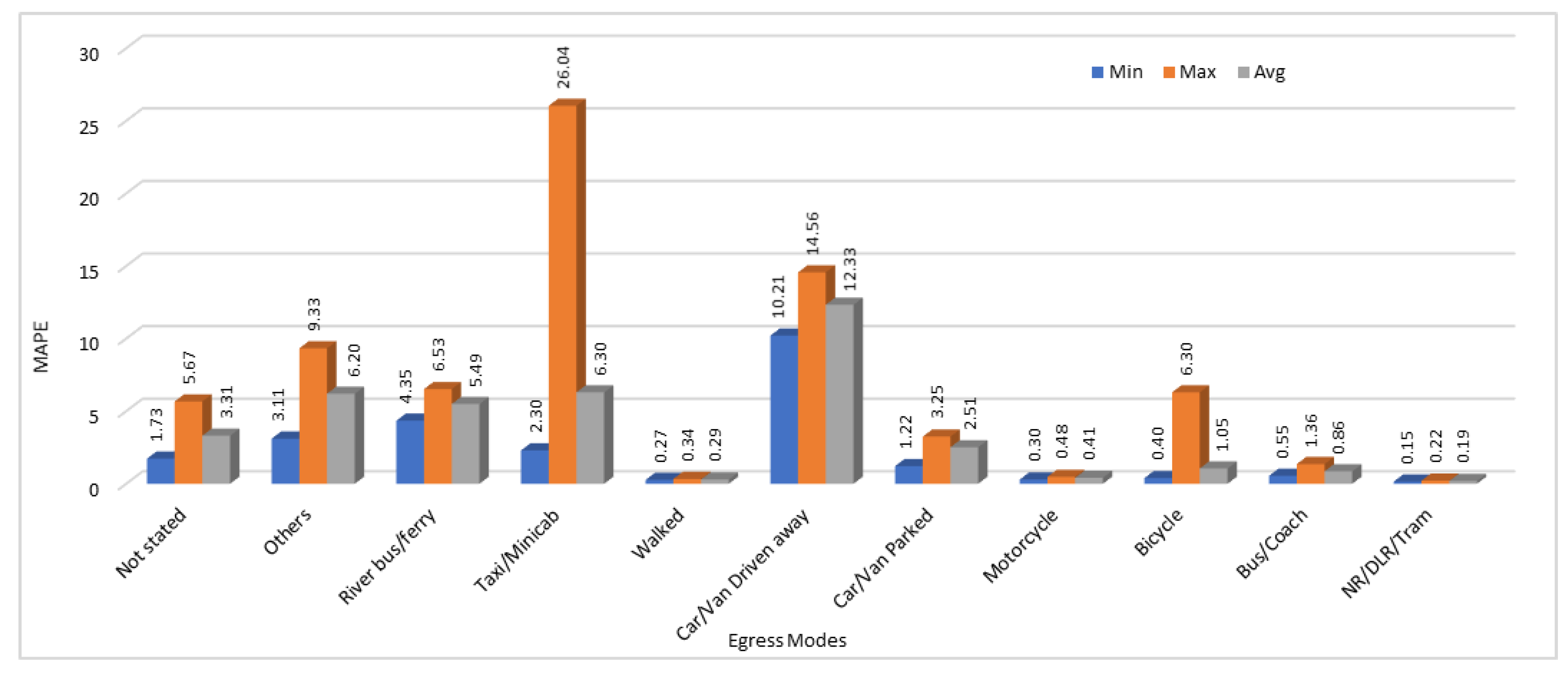
We have calculated the MAE, and MAPE in this section as well to test the accuracy of our model. For evaluation purpose and to compare the results, we have calculated the minimum, maximum, and average error values for all the 25 results obtained by running the same model with same configurations for 10 different egress modes. Minimum, Maximum, and Average MAE and MAPE values calculated by analyzing the all 25 execution results are shown in
Figure 10 and
Figure 11 respectively.
As we discussed before in access modes, prediction results show high variation in some cases in the egress modes data as well. For egress modes, MAE shows that the two egress modes “walked” and “NR/DLR/Tram” have very high loss values. This is because of the very high values (passengers count) in those two modes. If we see the MAPE calculated for both these modes, it is lowest among all the other egress modes. On the other hand, egress modes “Car/Van driven away” and “river bus/ferry” that show very low loss rate when using MAE, show very high error rate when MAPE is used as a performance metric.
4.3. Passenger Prediction for Specific Time Interval for Origin-Destination Station Pairs
In this section, we have used the dataset that gives the passenger count at different intervals of a day using OD matrix. In this dataset, we are given the number of passengers at six different time intervals (early, am peak, midday, pm peak, evening, and late) in a day. Therefore, OD matrix gives the number of passengers, who traveled from one station to another at different time intervals. There are 267 stations in this dataset and all the trips from one station to others via different routes have been considered in this data.
We have used the same DL model with the same model configurations as we have used before in the previous sections. Here the division of the dataset to be used as training, testing, and prediction has changed. In this case, dataset was divided into the ratio of 60, 30, and 10 percentage for training, testing and prediction, respectively. MAE and MAPE values have been calculated for analysis purpose in this case as well. Also, we are using ReLU as an activation function. The day time has been divided into six time intervals and we are using the number of passengers at five time intervals to predict the number of passengers at sixth time, so number of input features for our DL model is 5 and its output layer produces 1 feature to get a single estimated value. Due to the large amount of data, batch size is now 50 as compared to 5 which we have used previously in other models, but the number of epochs is same i.e., 1000 iterations per model. This model has also been executed 25 times to check the stability of our model and to see the variations.
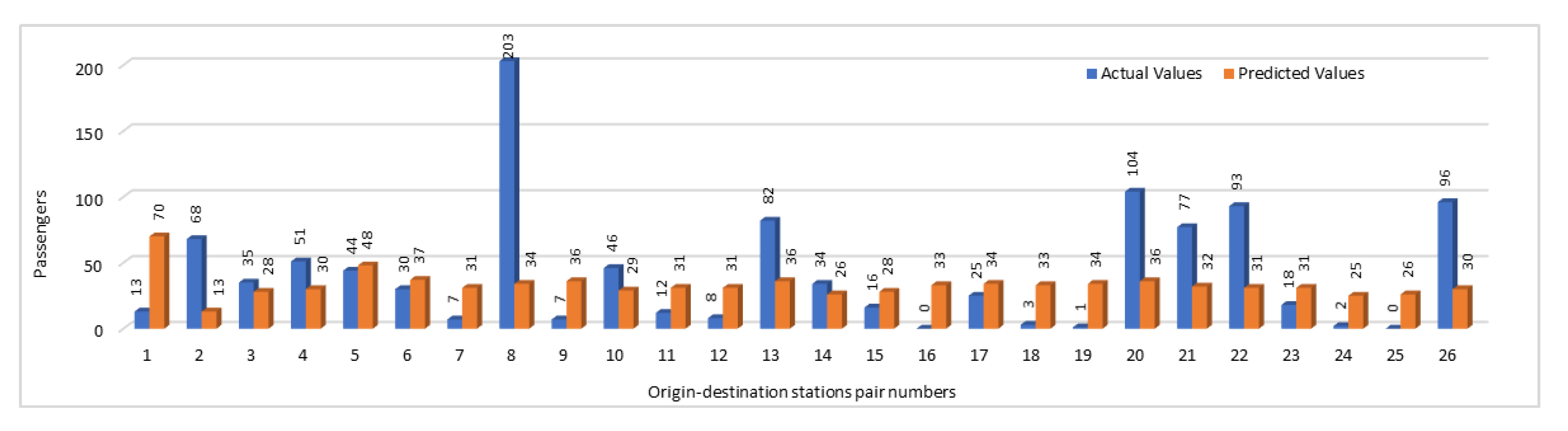
We have compared the predicted numbers of passengers traveling between the OD stations with the original values for selected pairs of OD stations pairs. In this comparison, we have shown the number of passengers traveling between two stations during the time interval “p.m. peak”.
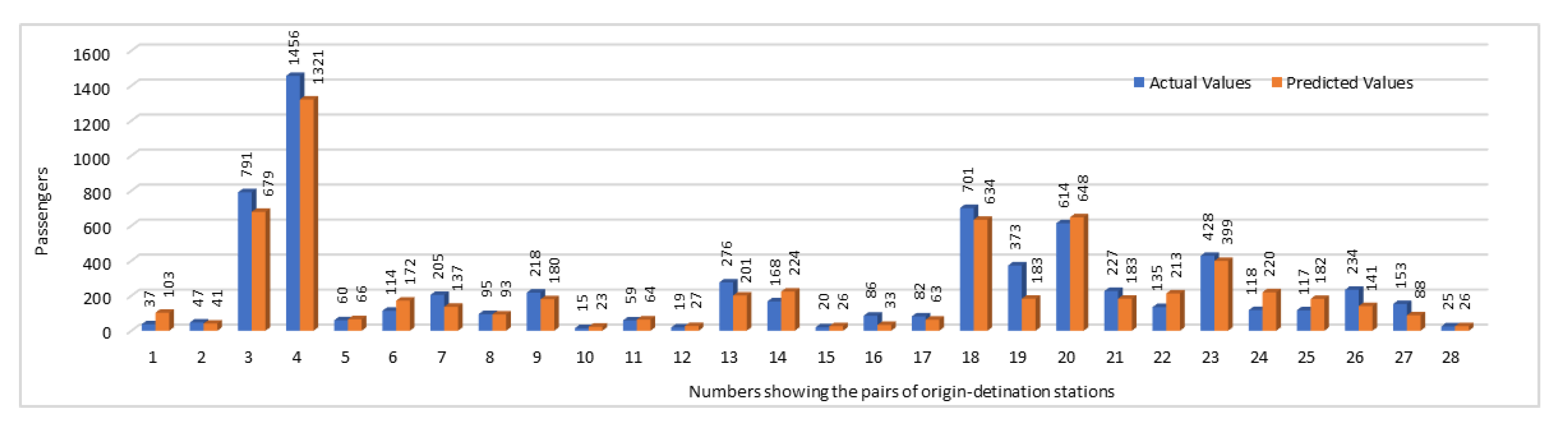
Figure 12 gives a comparison of actual and the predicted numbers of passengers. In this figure, instead of using the OD station pairs names, we have used the pairs numbers. To find the corresponding stations pairs names against a pair number shown in the graph, please refer to
Table 6. Comparison of actual and predicted values not only provides us the opportunity to analyze the accuracy of prediction results but it also enables us to analyze the OD pairs during that specific time interval based on the number of passengers traveling between them. As far it is concerned to the accuracy of our results, we can see that in most of the stations pairs, predicted values were predicting the accurate trend. Although in some cases, there were some fluctuations in results, but overall, the predicted values have predicted the same trend which was shown by plotting the actual values. This could help the authorities to identify which trains are overloaded with a large number of passengers and which have only a few passengers. They may take the decisions accordingly by reducing number of trips on the routes with less passengers count and can add more trains on the routes where passengers count is high. This way they may generate more revenue as well by saving fuel and other costs on low density routes and by earning more fairs on highly crowded routes.
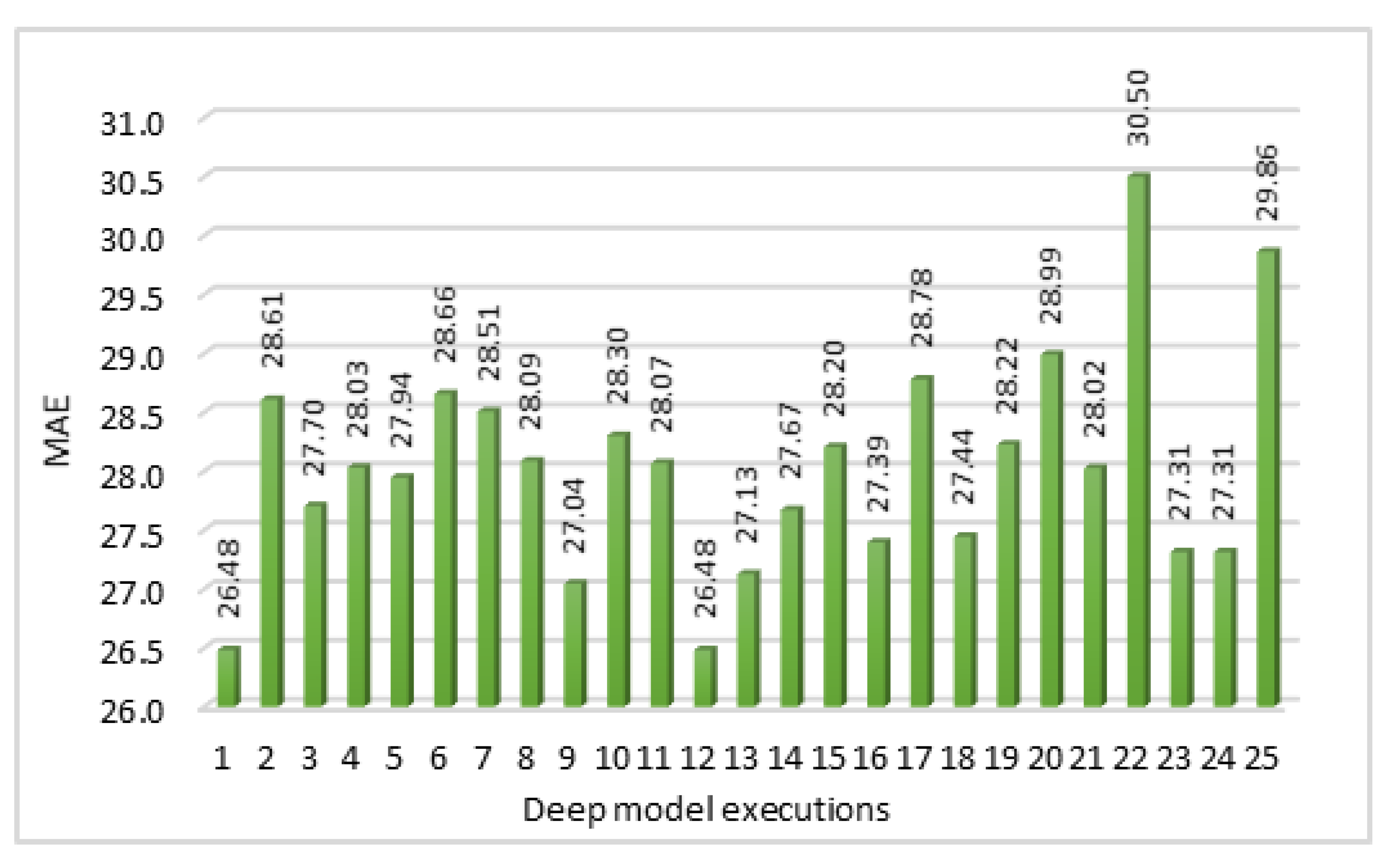
Also, as we are running the same model for 25 times, so we get 25 loss/error values. MAE values calculated by using the prediction values in all 25 executions of our model are shown in the
Figure 13. Here, instead of considering the minimum loss value among those results, we are taking the average loss values. We are mainly focusing on the MAE values instead of MAPE values for calculation of error rates. This is due to the reason that our actual data includes zeros as well and MAPE values cannot be calculated if actual value is zero.
4.4. Relationship between the Passenger Count and Distance between the Stations
In this section, we have modeled the relation between the distance between the origin and the destination stations and the number of passengers traveling between these OD pairs. Therefore, we are presenting the results of our deep learning model in which we have used the distance between the train stations and have estimated the number of passengers traveling from one station to another using the OD matrix. Our OD matrix contains the details of more than 34,000 journeys. Around 5 million passengers were surveyed to get the details about their journey on trains from one place/station to other. We have calculated the distance between all the pairs of stations given in the OD matrix and tried to find a relation between the distance between the stations and the number of passengers traveling between those stations at different time intervals in a day. In addition to this, by estimating the number of passengers traveling between any two stations on weekdays, we have tried to investigate if there is any relationship between the distance between the two stations and the number of passengers traveling on a week day. An overview of the dataset used in this section is given in
Table 7.
We have predicted the number of passengers traveling between the selected OD stations during the six different time intervals in a day. For this purpose, the deep model was executed with the same configurations set with a batch size of 5 and number of epochs were 1000. In this model, the input data was first changed by considering only the unique origin. The station codes (NLC) for OD stations, and the distance between the OD stations were also used as input parameters while predicting the number of passengers during weekdays.
Figure 14 compares the number of passengers traveling between different stations during “weekday”. In this figure, vertical axis shows the number of passengers traveling between the origin and destination stations. Horizontal axis shows the OD pair number as we have not given the names of stations to make it clear on graph. To see the corresponding origin-destination station names against an OD-pair number, please refer to
Table 8. In this table, we have given the distance between the ODs stations pairs used in this work to predict the number of passengers traveling between them on weekdays. Comparison of actual and predicted values shows that for small values, the predicted values were close to the actual values but for high data values, it was unable to predict accordingly and there was a big difference between the actual and the predicted values.
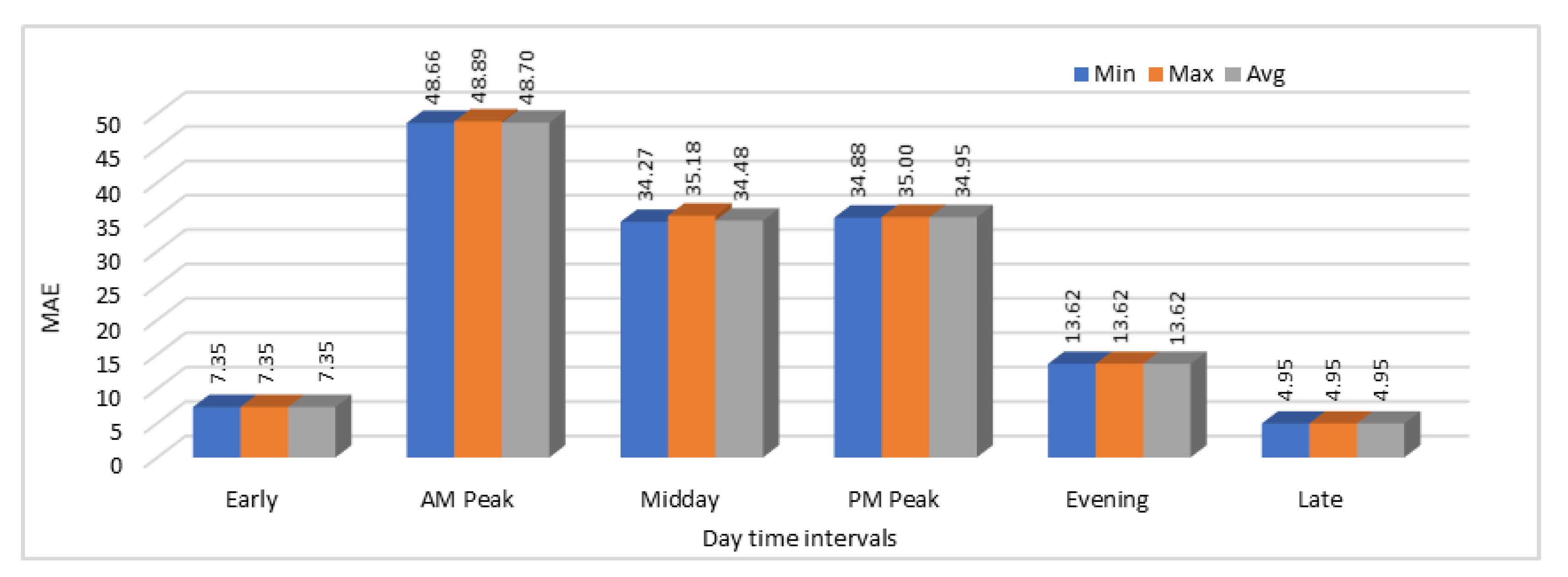
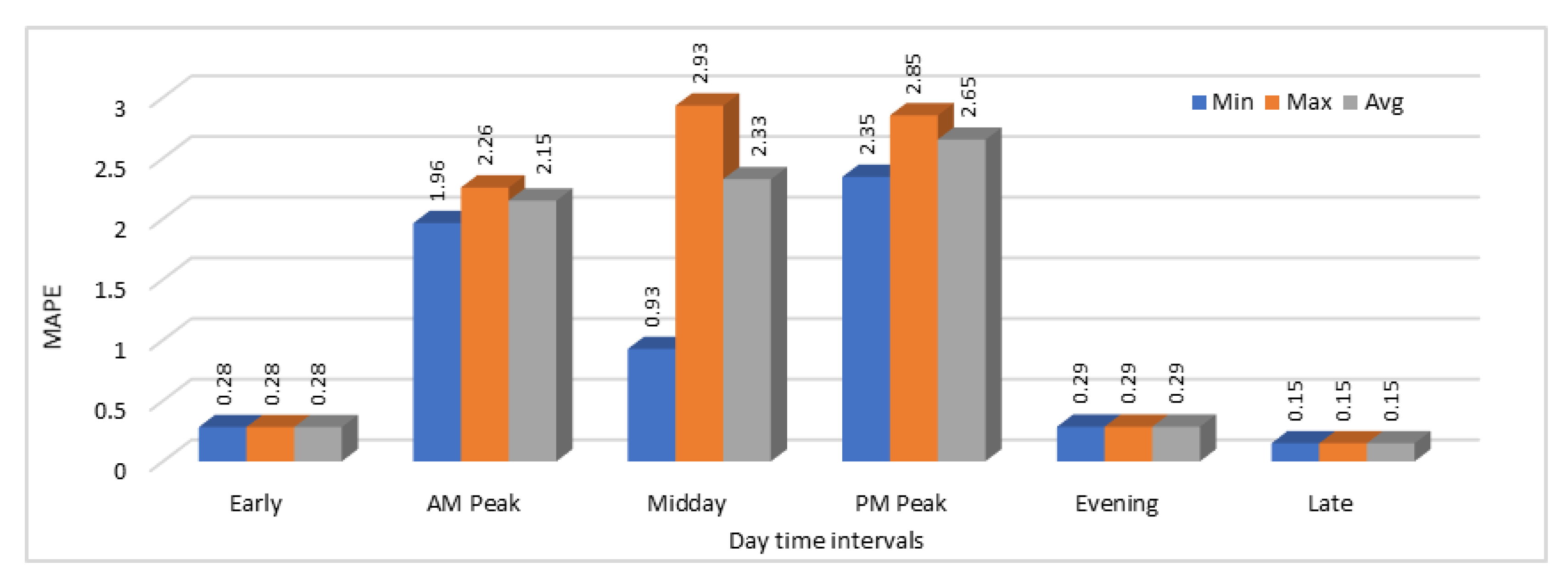
We have calculated both MAE and MAPE values in this case as well and again the model was executed for 25 time with the same configurations and input data to see the variations. MAE and MAPE values obtained by analyzing these results are shown in
Figure 15 and
Figure 16 respectively. Results show that during some time intervals, error rates were very high as shown for “AM Peak”, “Midday”, and “PM Peak” in
Figure 15. Same trend is shown in the MAPE values graph in
Figure 16. Another interesting thing about these results is that in all 25 executions of the same model with the same input data, prediction results were almost the same in all the executions because we can see that there are just minor differences in the minimum, maximum, and average MAE and MAPE values.
5. Conclusions and Future Work
Rapid transit systems or metros are a popular choice for high-capacity public transport in urban areas due to their several advantages including safety, dependability, speed, cost, and lower risk of accidents. It is a complex system in itself due to enormous numbers of passengers to be transported through many stations connected through multiple train lines. It becomes even more complex if we are to study and optimize a metro system along with its parent, larger, urban transportation system, including its complementary transportation resources and networks, e.g., trams, buses, ferries, vehicle park and ride stations, motorcycles, bike-sharing stations, and walking routes. This optimization is a gigantic challenge, particularly if we consider complex metro systems in mega-cities, such as the London Metro, the New York City Subway, Tokyo subway system, or the Beijing Subway. Many techniques have been proposed to model, analyze, and design metro systems and these were reviewed in detail in
Section 2. However, the current works in this domain have not studied the performance of urban metro systems in sufficiently holistic details. Moreover, existing studies have not adequately benefited from the use of emerging technologies. There is a need for innovative uses of cutting-edge technologies in transportation.
In this paper, we have proposed a comprehensive approach toward large-scale and faster prediction of metro system characteristics by employing the integration of four leading-edge technologies; big data, deep learning, in-memory computing, and GPUs. We have used the London Metro system as a case study to demonstrate the effectiveness of our proposed approach in this paper. We have used the RODS data to predict the number of passengers using different access and egress modes to travel to, and travel from, each of the London Metro stations, respectively. We have also predicted the number of passengers traveling between specific pairs of stations at various time intervals. Moreover, we have predicted the number of passengers traveling between various OD station pairs to investigate the relationship between the number of passengers and the distance between those pairs of stations. The prediction allows better spatiotemporal planning of the whole urban transport system, including the metro subsystem, and its various access and egress modes. We have used CNNs for prediction in our deep learning models. The prediction results were evaluated using MAE and MAPE, and by comparing actual and predicted values of the metro characteristics. A range of prediction accuracies were obtained, from high to fair, and were elaborated on. This is the first study of its kind where integration of leading-edge technologies has been applied to holistic modeling and prediction of a real rapid transit system.
The paper has contributed novel deep learning models, algorithms, implementation, analytics methodology, and software tool for analysis of metro systems. The paper also serves as a preliminary investigation into the convergence of big data and HPC for the transportation sector, specifically for the rapid transit systems, incorporating London Metro as a case study. The convergence has been discussed by researchers in the literature for the last few years (see e.g., [
42,
43,
44,
45]). We are not suggesting that this is the first study on the convergence in general, rather it is the first study on the convergence that focuses specifically on the transportation and rapid transit application domains. The topic of HPC and big data convergence is in its infancy and will require many more efforts by the community across diverse applications domains before reaching its maturity. We will explore these convergence issues in the future with the aim to devise novel multidisciplinary technologies for transportation and other sectors.
An important aspect of the work presented in this paper is data analysis and prediction using a distributed computing platform. We have used R [
48] and Spark [
49] for the purpose. Apache Spark is an improvement over the earlier Hadoop platform. Several other solutions are beginning to emerge for big data during the last few years. These include, among others, Apache Storm [
71] and Apache Flink [
72]. Apache Storm is a distributed real-time computation platform, particularly well suited toward streaming analytics applications. Apache Flink is another distributed processing engine for stateful computations over data streams [
72]. Both these platforms provide myriad of functionalities for distributed processing, particularly for streaming applications. In our case, we are interested in a high-performance, general-purpose, distributed computing platform for both streaming and batch processing of big data. Apache Spark excels in this respect because, compared to both Apache Storm and Apache Flink, it a stable platform with a relatively larger active community of developers. Moreover, Spark is relatively faster, and the development is easier in Spark compared to the other alternatives. Most importantly, Apache Spark is a general-purpose engine and allows integration of a much broader collection of functionalities, tools, and libraries. Future work will investigate the alternatives for the distributed big data computing platforms and consider incorporating cutting-edge technologies for smarter transportation.
Finally, we have integrated multiple technologies to develop in our lab the transportation prediction pipeline proposed in this paper. We manage a supercomputer called Aziz which provides both HPC and big data computational facilities. Aziz was ranked among the Top500 machines in June and November 2015 rankings [
73]. We hence have the facilities and motivation to develop in-house complex data processing pipelines. Accessing paid cloud computing resources have also been prohibitive for us due to the costs. This may be different for many researchers due to the lack of facilities and skilled force, and the availability of funds for cloud access. In such cases, or otherwise, similar pipelines can be easily developed and deployed in cloud computing environments. Major cloud vendors such as Amazon and Microsoft are already providing configurable big data analysis pipelines include access to GPUs and in-memory computing platforms. It is foreseen that ICT solutions will increasingly be delivered using the cloud, fog, and edge computing paradigms. We aim to do the same; i.e., to deliver the rapid transit software using cloud computing. This would form another topic for our future research.