1. Introduction
The Sustainable Development Goals (SDGs) are a set of 17 global goals adopted by all member states of the United Nations in September 2015 [
1]. They include areas such as economic inequality, environmental sustainability, innovation, peace and justice, sustainable consumption, among other priorities. The goals are structured in 169 broad and somewhat interdependent indicators, which are proposed to guide governments to achieve a sustainable development. As stated by [
2], these goals were designed to be applicable to all nations, regardless of gross domestic product or geographical location, which makes them a marked improvement on the previous Millennium Development Goals (MDGs).
SDGs can assist government officials, business and civil society to closely understand the key challenges that must be accomplished in order to achieve the SDGs by 2030. Even though the variety of indicators can help to accurately measure, monitor and control for different dimensions related with sustainable development, it can also impede timely accounting for a universal accomplishment measure. Academics have recently proposed the calculation of a composite index in order to compute a global sustainable development measure, as an effort to summarise the goals stated in the SDGs [
1,
3,
4]. Stakeholders can benefit from the advantages offered by a composite index [
5], e.g., it permits summarising complex and multi-dimensional realities to support decision-makers, it is easier to interpret than a broad range of different indicators, enables country comparison and country evolution assessment over time, and facilitates communication with the general public.
According to the current structure of SDGs, the composite index construction must be addressed in two consecutive steps:
- Step 1:
The combination of the indicators of every particular SDG to compute the corresponding estimated SDG. This way, we can summarise all the indicators regarding one SDG into a single variable.
- Step 2:
The combination of previously estimated SDGs to compute the composite SDG index.
Calculating such an index must take into account the complex relation between indicators. Potential synergies can favour the simultaneous accomplishment of some indicators by improving others. However, the existence of a trade-off between conflicting indicators has also been reported. Trade-offs are also referred to as negative synergies because of the adverse effect, i.e., the achievement of an indicator is obtained in such a way that it implies a negative impact on the achievement of another indicator [
6]. For example, a strong synergy among various SDGs indicators was reported by [
7]. The research was performed regarding six developing countries in South Asia and Sub-Saharan Africa, and a significant trade-off between the level of water stress and the rest of SDGs was found. In a similar way, it has been pointed out that SDGs relating to poverty, inequality, food security, economic development and life in water and on land, are potentially competing in most circumstances [
8]. Incompatibility between economic development and ecological sustainability has been recognised as a critical limitation to simultaneously achieve multiple SDGs [
9,
10].
Assuming the concerns regarding synergies and trade-offs between SDGs, emerging literature identifies three alternative ways to combine those into a global sustainable development index: (1) arithmetic mean, (2) geometric mean and (3) Leontief production function [
1,
4].
The arithmetic mean is the most widely used aggregation method for the calculation of a composite index because of its straightforward implementation and communication. As examples, we can refer to the Global Innovation Index [
11], the African Green Growth Index [
12] and the SDG Index and Dashboard for countries [
1,
4,
13]. The arithmetic average assumes equal weighting for all indicators corresponding to each SDG, and equal weighting for all computed SDGs in the construction of the index, which authors justify as a reflection of the commitment by policy makers to treat all SDGs as equally important. As stated by [
1], this method implies that the relative weight of every indicator in a particular goal is inversely proportional to the number of indicators in that goal. Thus, the relevance of an indicator can be artificially promoted by constraining the number of competitor indicators in its corresponding goal. Furthermore, the estimated SDGs can also be seriously affected by extreme values or outlier indicators. This situation worsens as highly correlated indicators (or SDGs) are combined because that way a double counting is introduced into the index [
5].
The geometric mean is less sensitive to the presence of extreme values. Furthermore, this method follows the economic concept of “limited substitutability” [
5], which states that being strong on one goal does not fully substitute for being weak in another. As stated by [
1], progress on one goal cannot offset lack of progress on another, which translates in the necessity of countries to progress towards every goal. Despite geometric mean is mostly preferred by academics, recent evidence suggests that differences in results are actually negligible [
1]. In the following section, we discuss some relevant issues that limit the applicability of the geometric mean.
Finally, the Leontief production function over-weights the worst case elements. This way, the score for each goal is obtained by the indicator on which the country performs worst. Regarding the composite SDG index, the country value is obtained by only considering the worst performing SDG for that country. Such a pessimistic approach has the disadvantage of focusing on a single attribute, thus discarding the remainder elements on the sustainable development of the country.
Thus, limitations of traditional aggregation methods are related with the weighting process of indicators and goals. The arithmetic mean assumes equal weighting, even though there is no clear reason for considering all indicators and goals equally important. The geometric and Leontief aggregation methods over-weight the worst performer indicators and goals, which, as showed in the next section, can cause some countries to remain as the worst SDG performers regardless of how well they perform in other indicators.
The aim of this paper is to propose a new weighting scheme for the calculation of the Sustainable Development Goal Index by considering Goal Programming (GP), thus filling the above-mentioned gap regarding traditional aggregation methods. In the scope of our study, this translates into an index that allows the simultaneous consideration of different dimensions that make up the sustainable development. The model extends the range of the aforementioned aggregation methods and overcomes some of their limitations.
Recent papers illustrate the use of GP for the ranking of alternatives in different contexts. For example, a GP model for ranking commercial firms is proposed in [
14] and the results are compared with previous approaches based on CRITIC and a modified version of TOPSIS. Spanish saving banks were ranked in [
15] according to different accounting and financial variables related with its productivity, credit risk and size. A social performance index was computed for a wide range of microfinance institutions in Ecuador [
16]. Although these organizations operate in a different way to traditional banks, some financial variables were considered for ranking microfinance institutions. A multicriteria Corporate Social Responsibility (CSR) performance over 212 European companies was estimated by [
17], who considered different criteria, subcriteria and indicators. Some recent applications of multi-criteria decision-making methods on ranking alternatives include AHP, Dematel or rough BWM-MAIRCA [
18,
19,
20,
21].
2. Material and Methods
This section serves to draw some limitations of popular aggregation methods in the computation of a composite index (
Section 2.1), and subsequently introduce a GP model to address those highlighted issues and compute a consensus solution (
Section 2.2).
2.1. Developing a Composite Index: Some Limitations Regarding Classical Methods
Following the recommendation of the UNDP Reports [
22], the most extended way to aggregate both indicators and estimated SDGs and construct the SDG index is by using the arithmetic average, although the geometric average and the Leontief production function are often referenced. This section is intended to discuss some limitations of the above-mentioned methods in the construction of an index based on the SDG indicators.
Table 1 comprises six indicators measured in the No poverty SDG for the EU-28 countries, which serves to illustrate some issues regarding the three aggregation methods. The first step is to normalise the data because the measurement unit can be different among them. The normalisation is usually performed by scaling the data to have values between 0 and 1 (Equation (
1)). It is important to remark that the sign of some variables must be inverted before the aggregation process because their direction can be opposite to the SDG. In the case of
Table 1, the SDG is No poverty, but the six indicators express the poverty of the countries in a direct way; i.e., the higher the value, the higher the poverty level. Thus, the last columns of
Table 1 include the normalised values for the six indicators
related to poverty as
. A country with a normalised value of 1 indicates the best performance value against poverty, while a 0 value indicates the worst position regarding poverty:
Once the normalisation process has been carried out, the above-mentioned aggregation methods can be computed.
Table 2 presents the results of the arithmetic, geometric and Leontief aggregations. Because the result of such aggregation can compress the 0–1 limits, we have also performed a post-normalisation process to ensure that these limits are strictly observed (the last three columns of
Table 2). This is not required for the ranking of the countries, but helps to compare relative distances in terms of the aggregation method.
The best positioned country is Czech Republic, regardless of the aggregation method. However, if we inspect the worst positioned country, the result depends on the aggregation method used. Regarding the arithmetic aggregation, the normalised column shows that the worst positioned country is Greece. However, both geometric and Leontief normalised columns indicate that five countries share the last position regarding the No poverty SDG: Bulgaria, Greece, Ireland, Portugal and Romania. Due to the way that these aggregation methods are calculated, a sufficient condition a country must meet to be eligible with a 0 value is to be the worst positioned country in—at least—one indicator. For example, in the case of Bulgaria, the country obtains a 0 value in the normalised indicator. After applying the geometric or the Leontief aggregation methods, the estimated SDG also gets a 0 value. In addition, the same situation applies for other countries. The reason is that each country is the worst positioned in at least one indicator.
This situation can potentially worsen when more indicators are involved in the estimation of the SGD. The number of different countries occupying the worst position in a generic indicator can increase as more indicators are considered. In addition, once a country is positioned as the worst one in an indicator, its SDG value becomes 0 regardless of how well or bad it performs in other indicators.
These limitations, along with those mentioned for the arithmetic average, suggest the research of new approaches to widen the bundle of alternatives in the composition of a SDG index.
2.2. The Goal Programming Approach
GP is a multicriteria technique that enables building mathematical programming models consisting of linear or nonlinear functions, where all functions have been transformed into goals and the decision-maker is interested in minimising the non-achievement of the corresponding goals [
23]. GP seeks a Simonian satisficing solution, in contrast with the inflexible concept of optimisation attached to the mathematical models with a single-objective function. According to [
24], the satisficing choice, or to accept the ‘good enough’, is generally more realistic than the choice to optimise the satisfaction or utility of the decision-maker. To the best knowledge of the authors, the paper from Linares and Romero [
25] on an environmental economics context is the first one to propose the use of GP for the aggregation of preferences.
Our research proposes the aggregation of indicators and SDGs by using different GP models. In the first step, the GP approach is applied over those indicators linked to each single SDG, as many times as different SDGs are included in the database. The output of this step is a bundle of estimated multicriteria SDGs. These values are used as inputs in the second step, when the GP model is run again to obtain the estimated multicriteria SDG index.
Depending on the norm used in the GP model, the solution can be interpreted either as one in which the consensus between all the indicators is maximised (penalising the more conflicting indicator in favour of those that are more representative of the majority trend in the corresponding SDG) or as one where preference is given to the most conflicting indicators (thereby penalising the indicators that share the most information with the rest in the common SDG). Considering the case of aggregating indicators, in the first case, the absolute difference between the obtained multicriteria SDG and the associated indicators is minimised (norm ); in the second case, it is the greatest difference between the computed multicriteria SDG and single indicators which is minimised (norm ).
In the following, we assume the case of aggregating indicators (step 1), but the same models hold adequately for the aggregation of SDGs (step 2).
The model in norm
is shown in Equation (
2):
where
is the weight computed for the
j-th indicator;
is the value of the
j-th indicator in the
i-th country;
is the estimated multicriteria SDG for the
i-th country, which is obtained as a weighted average of the corresponding indicators;
and
are the negative and positive deviation variables which quantify the differences by excess and deficiency, respectively, between the observed
j-th indicator of the
i-th country and the estimated multicriteria SDG for the
i-th country;
accounts for the disagreement between the
j-th indicator and the estimated multicriteria SDG; finally,
Z is the sum of the overall disagreement, which in the case of the
is the variable to be minimised in the objective function of model (
2).
The constraint labelled as goals is composed by a total of equations. For each SDG i, so many equations are created as indicators have been considered; that is, m equations. In each of these equations, the estimated multicriteria SDG is compared to the corresponding j-th indicator. The estimated SDG is computed as a weighted average of the indicators , and is summarised as in the first equation of the accounting rows constraints. The difference between this value and each value of the different j indicators, , is computed by the deviation variables and . In other words, .
The hard constraint determines that the sum of the weights must be one. The last two accounting rows compute the value of and Z, respectively. A high value in indicates that there is a high disagreement between the j-th indicator and its corresponding estimated multicriteria SDG. On the other hand, small values indicate that countries’ behavior in that indicator is very close to the estimated multicriteria SDG. Finally, a model with a low value of Z indicates that the estimated SDG is in line with all related indicators, while a high value means that there are large differences between the observed indicators and the consensus SDG. The last situation occurs in case indicators is very dissimilar to each other.
Model (
2) serves to highlight the difference between the weighting scheme of the arithmetic average (all indicators are equally-weighted) and the weighting approach followed by GP (higher weight to those indicators aligned with the consensus trend).
Another variant of GP allows an alternative approach in the calculation of multicriteria SDG. This model implements the
norm and is known as the MINMAX or Chebyshev GP model [
26]. The aim of the model is minimising the maximum difference between the estimated multicriteria SDG and its corresponding indicators (
3):
All variables in model (
3) have been previously defined in model (
2). There are only two differences regarding that model. The first one is the addition of a new
hard constraint,
. This new constraint makes
D to be larger than any other deviation
. The second difference is the change in the objective function, which is the minimisation of the maximum deviation
D indeed. The rest of the constraints remain the same as in the
norm model.
The solutions from both models represent extreme cases in which two contrasting strategies are set against one another, giving an advantage to the general consensus between indicators,
norm, or to the conflicting indicators,
norm [
17]. This way, we can establish a similarity between these two models and those represented by the arithmetic and the geometric averages discussed in the previous subsection. However, there is an alternative to find a compromise between the two GP models: the so-called extended GP model [
26]. The objective function and constraints of this model are presented in Equation (
4):
The
parameter fluctuates between 0 and 1, which enables more balanced solutions between models (
2) and (
3). This parameter widens the range of alternatives, giving compromise solutions between the extreme cases represented by both models [
17]. Note that
gives the same solution as the
norm model, while
gives the solution of the
model. Therefore, it can be concluded that the first two GP models are special cases of the extended GP model (
4).
Thus, our proposal is to compute the SDG index by considering a wide range of values for
, comparing the results with those obtained using classical aggregation alternatives, and analysing the robustness of the results. As stated by [
25], the consensus attached to the solution with
norm is statistically defined by the median weight. The arithmetic mean is related with the
norm, so that the extended GP model can be seen as a generalisation of any possible norm, including the arithmetic mean.
3. Results
This section presents the result of applying the GP methodology to construct a SDG index based on the SDGs dataset for the EU-28 countries provided by the European Commission [
27]. The database is comprised of 17 SDGs, each one composed of different indicators (The database can be downloaded from Eurostat [
28]). The total number of indicators is 169. However, some countries do not report information for all these indicators, which impedes the numerical aggregation of data. We have decided to remove those indicators where three or more countries have reported no information. This reduces the number of indicators to 154 (
Appendix A). We have filled with its median those countries with no information on a specific indicator.
Once the database has been refined, the extended GP model (
4) has been applied in two consecutive steps. (The Goal Programming model was solved using the R software [
29]. We have used the
lpSolve package for the calculation of the weights of the mathematical programming model. Those readers interested in more details about solving mathematical programming models (please consult [
30]).)
The first step consists of the aggregation of indicators corresponding to each individual SDG. This step considers the different sign of the indicators relative to its SDG. The aggregation model has been performed by considering ; that is, the model searches for the maximum consensus between all the indicators—the values for are very similar to those obtained with and are not reported for brevity. The output consists of 17 estimated multicriteria SDGs, which serve as input for the second step related with the computation of the SDG index.
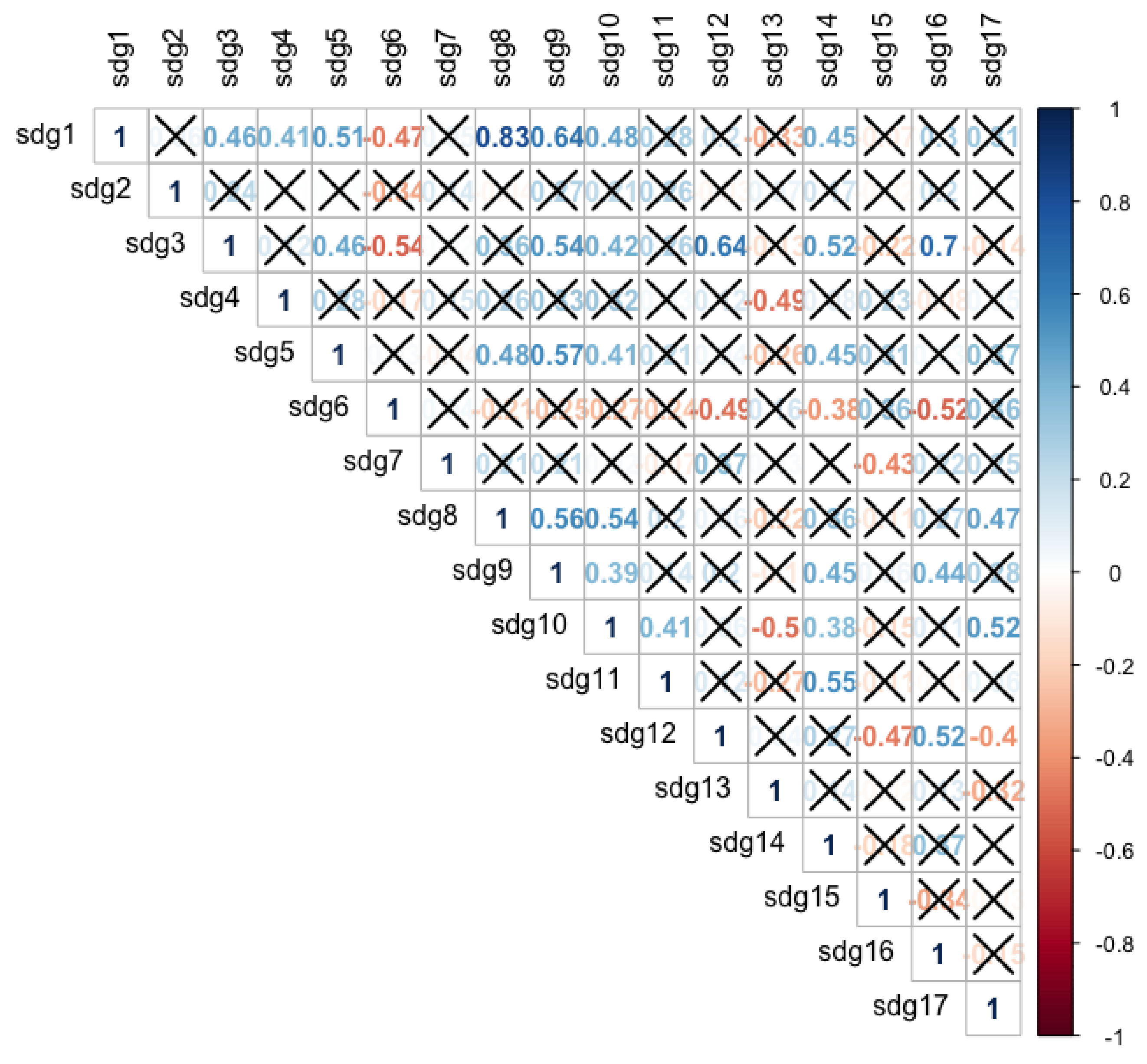
Figure 1 presents the correlation coefficients between the 17 estimated SDGs. Most of the pairwise correlation coefficients are not statistically significant, which confirms that in general terms the SDGs are capturing different dimensions of sustainable development. In addition, some of the SDGs are positive related to others. For example, the
No poverty goal (sdg1) is highly correlated with the
Good jobs and economic growth goal (sdg8) and the
Innovation and infrastructure goal (sdg9). Another significant relation is between the
Good health goal (sdg3) and the
Peace and justice goal (sdg16). As expected, some of the SDG correlation coefficients are negative, which means that the improvement of some dimension can worsen the performance of another dimension. The most significant cases are the −0.54 correlation coefficient between the
Good health goal (sdg3) and the
Clean water and sanitation goal (sdg6), the −0.52 correlation coefficient between the
Clean water and sanitation goal (sdg6) and the
Peace and justice goal (sdg16), and the −0.5 correlation coefficient between the
Reduce inequalities goal (sdg10) and the
Protect the planet goal (sdg13).
Once the correlation analysis has verified that some SDGs can be in competition with others and that the trade-off between them can exist, a wide range of values for has been considered in the second step. The value of has ranged from 0 to 1 by increasing 0.01. Thus, 101 different models have been computed, ranging from norm to norm. Any of these models reports different weights for each SDG and consequently the SDG index and the ranking of each country vary.
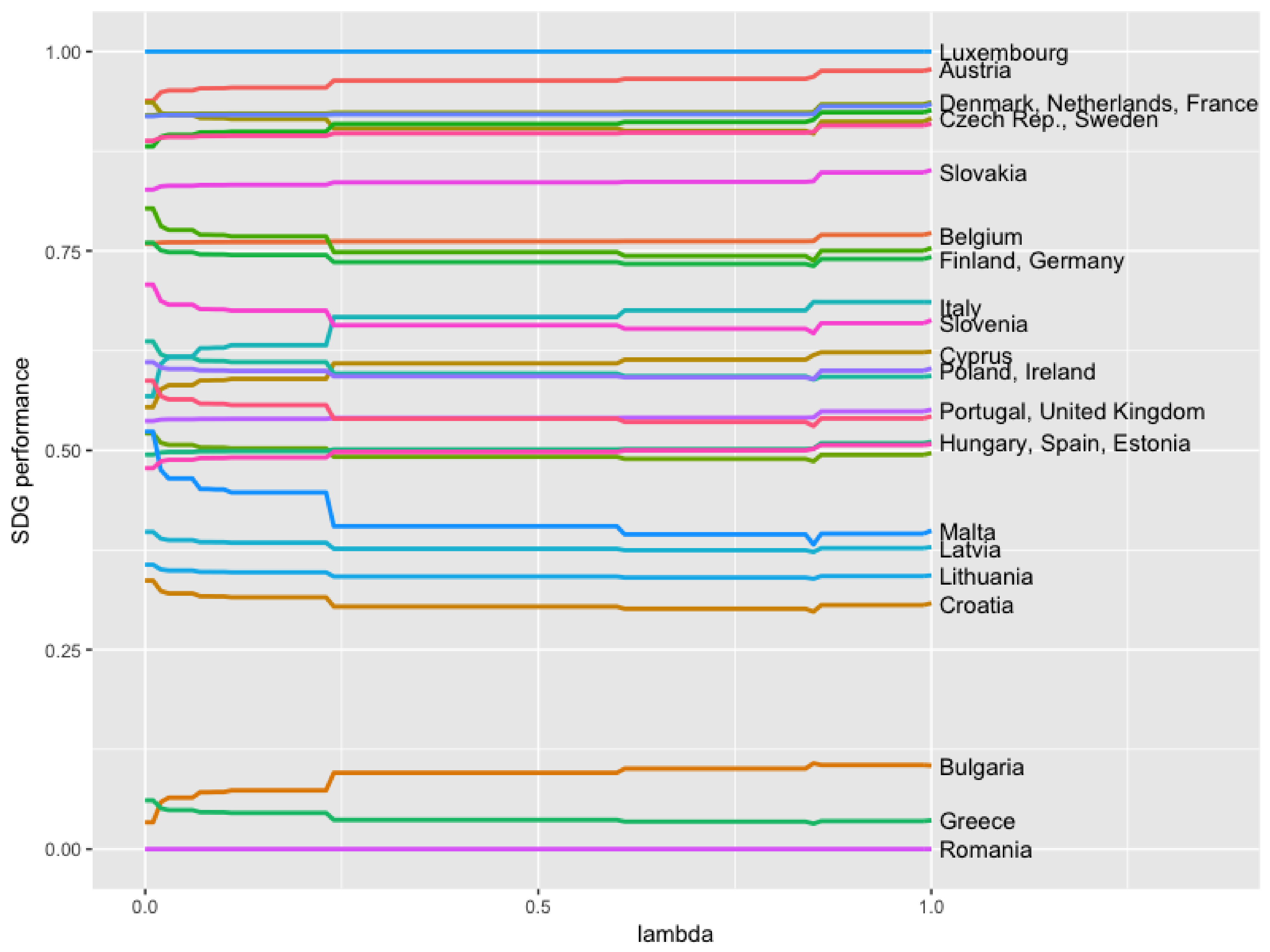
Figure 2 presents the variation of the SDG index estimation for each country in the EU-28. The
y-axis represents the SDG index value of each country as a percentage of the total, whereas the
x-axis stands for the value of
considered in each case. Hence, a bigger area means a higher SDG index value, while a smaller one implies a poor SDG performance. Slight differences regarding the value of
can be observed, and the sustainable development performance of each country is mainly constant through the whole range of
values considered. This supports the robustness of the GP model. In this case, and before calculating some statistics to examine more closely the relation between different rankings, the results confirm that the SDG index is primarily independent of the
-approach considered in the GP model.
As a result, Greece and Romania are the worst SDG performers, followed by Bulgaria. On the other side, the best performers are Luxembourg and Austria, followed by the Czech Republic, Denmark, France, Netherlands and Sweden, which obtain a very similar SDG value.
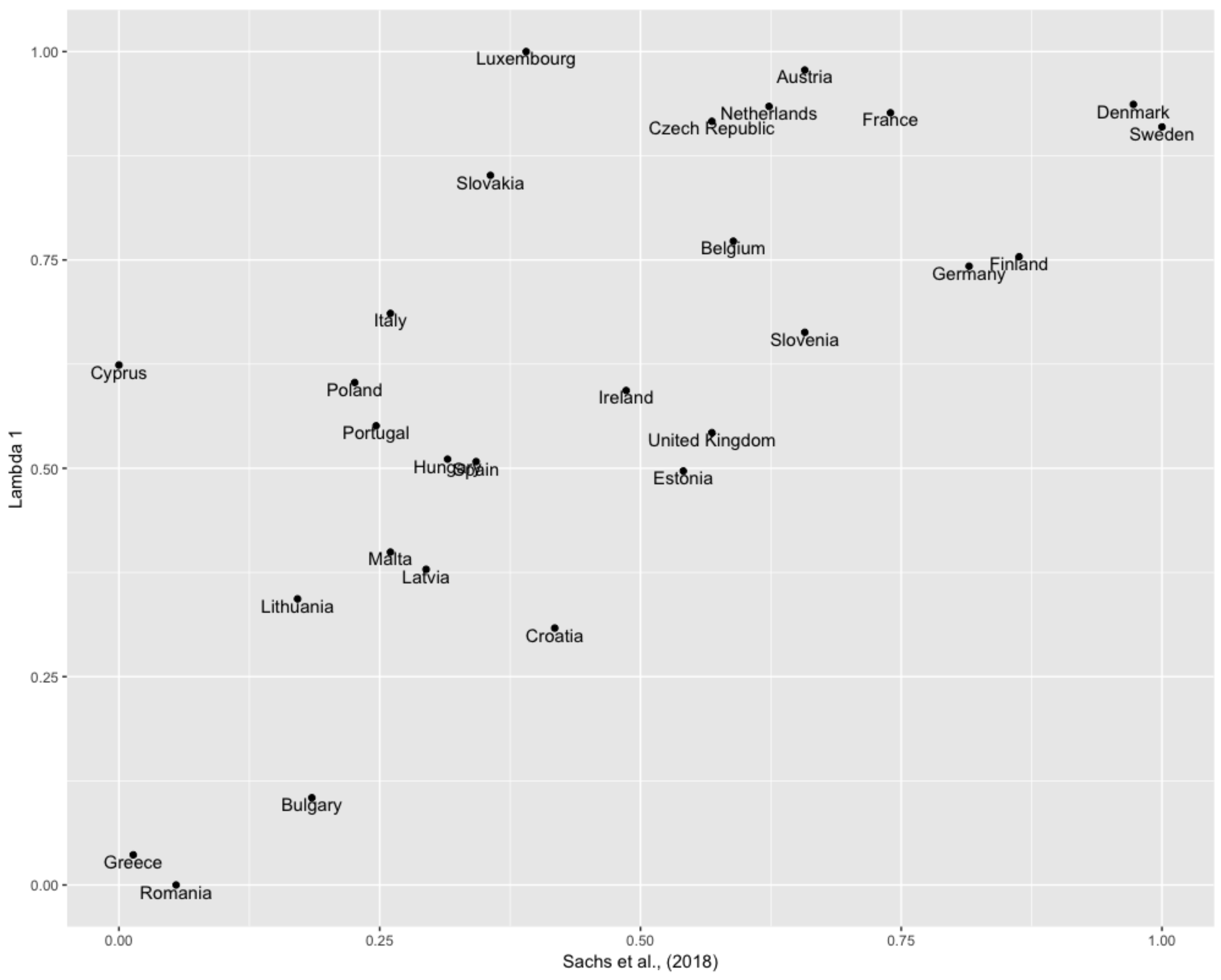
Figure 3 compares the ranking according to
GP model (Although we have not represented the
case, the picture is very similar to the one depicted in
Figure 3) and the arithmetic average method from [
1]. We can see that both rankings are positively related, but remarkable differences are observed regarding some countries of the EU-28. For example, Cyprus obtains the worst score (0) according to the arithmetic average method, whilst its score in the case of the GP model is 0.6; and a similar situation is observed for Luxembourg.
The GP model emphasises the gap between best and worst performers. For example, we can observe in the GP model that only three countries (i.e., Bulgary, Greece and Romania) obtain a score below 0.25. In the case of the arithmetic average, there are seven countries (i.e., Bulgary, Cyprus, Greece, Lithuania, Poland, Portugal and Romania) with a score below that threshold. On the side of the best performers, the GP model reports 10 countries with a score higher than 0.75, whilst the arithmetic average only identifies four countries. We can observe that the GP model spreads the countries by isolating the worst performers in a small group compared with the best performers. In the case of the arithmetic average, countries are spread following a more homogeneous pattern.
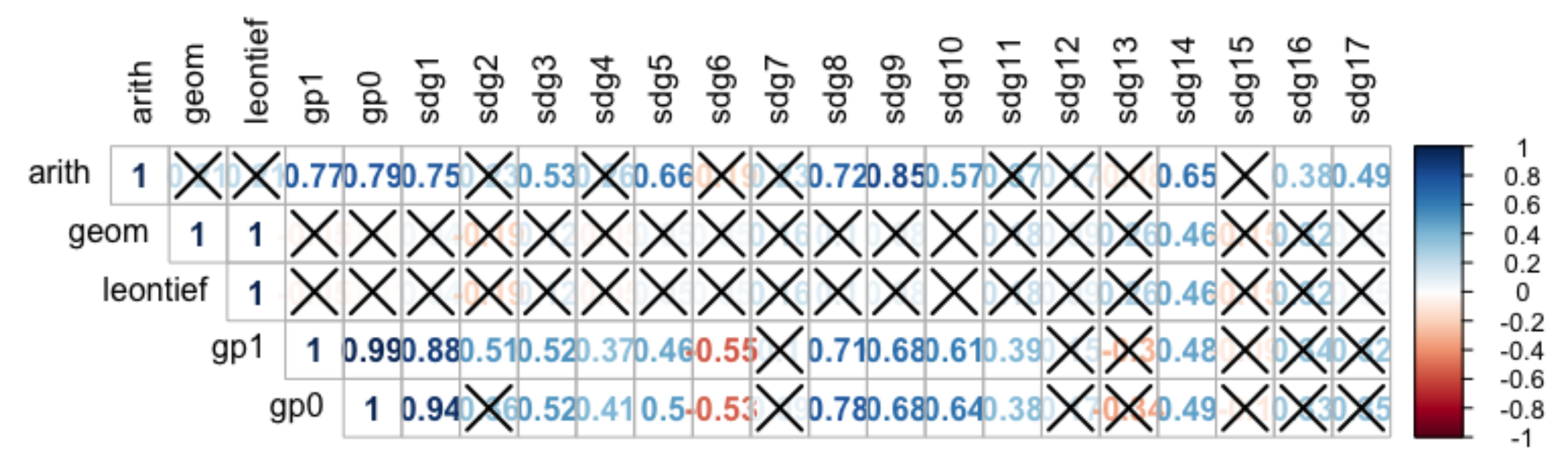
Figure 4 shows the Pearson correlation between the estimated SDGs of step 1 and the computed SDG indexes of step 2. In order to compare our results with those obtained through previous approaches, the matrix includes the index estimation for the arithmetic average, the geometric average, the Leontief production function, and the two extreme versions of the extended GP model:
and
. As suggested in
Figure 2, we can observe that both variants of the GP model obtain very similar solutions. The correlation coefficient between these two SDG index estimations based on GP is 0.99. This way, we can assert that, in the case of the SDG index composition for the EU-28 countries, the GP methodology proves to be robust. Regardless of the approach—favouring the majority, or favouring the most conflicting SDGs—the results remain primarily stable.
We must also note that the geometric and the Leontief solutions are the same, and both of them are uncorrelated with 16 out of 17 estimated SDGs. Thus, we can conclude that these aggregation methods are not representative of the trend of SDG behaviour. According to these aggregation methods, the best performance country is United Kingdom, while the rest of the countries obtains the same index value: 0. This is because all the remaining 27 countries occupy the last position in at least one of the 154 indicators considered in the experiment. This translates into a zero value on at least one SDG estimation and, consequently, a zero value for the index estimation. As previously stated, this is an important limitation of both aggregation methods that must be considered by academics in the computation of an SDG composite index. Hence, we can conclude that the positive and significant correlation reported in previous studies between the arithmetic, geometric and Leontief approaches is due to the sample characteristics and does not hold in a bigger case as the one reported here.
4. Discussion
The correlation analysis performed on the 17 estimated SDGs has confirmed that several goals are statistically related to others. This finding supports the existence of trade-offs and synergies between goals, as stated by previous researchers [
7,
8,
9,
10]. The proposed GP model can balance indicators and goals in conflict in a way that all relevant elements are considered. The two extremes regarding the parameter
enable balancing the solution according to decision-maker preferences. However, in the case of the EU-28 countries, our results suggest that the optimal solution for the weighting of the goals and the ranking of the countries is highly independent of the
value.
Compared with the arithmetic average, it must be highlighted that this aggegation method is based on the assumption that all SDGs are equally weighted and thus equally important. Observing the commitment with the “no-one left behind” principle does not necessarily translate into a constraint, i.e., considering all SDGs equally important.
As previously stated, literature has confirmed that there exists a trade-off between several SDGs, as the significant correlation coefficients of
Figure 1 also suggest. This way, the arithmetic average can actually over-weight some dimensions and under-weight others. This is the reason why this paper proposes the use of the GP methodology, a more complex framework that takes into account the relation between the indicators and the SDGs, and between the SDGs and the SDG index.
Although in the case of EU-28 countries the correlation between the arithmetic and the GP models is fairly strong, the use of the GP approach fulfills the need of considering the underlined relation between some SDGs. Furthermore,
Figure 3 reveals that a consensus between GP models is much stronger than the one exhibited by other classical approaches. This enables us to show that the ranking of countries can be robust regardless on the approach followed by the
parameter, and the EU-28 example is a good case in point.
We must also note that there is no negative, statistically significant correlation between the estimated SDG index by using the arithmetic average and any of the SDGs. However, in the case of the two GP models, both correlation coefficients are negative and statistically significant regarding the
Clean water and sanitation goal (sdg6). All significant correlation coefficients of this variable in
Figure 1 are negative, which implies that the estimated SDG index should be negatively correlated with this SDG. This is true in the case of the GP models, but not in the case of the arithmetic average. Thus, the arithmetic average does not properly capture the relation between the
Clean water and sanitation goal and the majority of the SDGs.
Finally, our research can give decision-makers useful insights about the relative position regarding other countries in the EU-28 group, and how a country can improve its performance by reinforcing some indicators and goals. We have not performed a sensitivity analysis for the countries considered, but the model suggests that small improvements in some dimensions can benefit the ranking of worst performer countries in a significant way. Furthermore, the European Commission should support this approach aligned with the “no-one left behind” principle.
5. Conclusions
The Sustainable Development Goals define priorities and aspirations to mobilise global efforts among governments, business and civil society. They cover a broad range of indicators related with the end of poverty, quality of education, gender equality, peace and justice, among others. Some recent research has focused on the composition of a global SDG index to summarise the performance of each country regarding the achievement of the goals, considering that some of them are in conflict with others.
Despite the widespread use of the different average procedures to aggregate the goal variables, this paper highlights some limitations that must be addressed to properly measure the sustainable development of the countries. Our paper shows through a simple example some shortcomings of traditional aggregation methods. In the case of the arithmetic average, this approach follows the principle of equally-weighting, which obviously not necessarily apply in the case of SDGs where some goals can be considered more important than others. Regarding the geometric average and the Leontief production function, both approaches over-weight the most unfavourable measures. This way, several countries can be ranked as the worst performers by fulfilling the following condition: be the worst performer in at least one indicator/goal. No matter how brilliant they are in other dimensions, these aggregation methods only considered the poorest performance measures.
These limitations can be overcome by using a mathematical programming model. The Goal Programming methodology enables the decision-maker to consider two extreme approaches in the aggregation of the goals: favouring the majority or favouring the most conflicting SDGs. Using a extended GP model, we have found that the ranking of EU-28 countries is primarily independent of the parameterisation of the GP model, and also overcomes the above-mentioned limitations reported for the arithmetic, geometric and Leontief aggregation methods. According to our results, the best SDG performers in the EU-28 are Luxembourg and Austria, whilst the worst performers are Greece and Romania.
We must also highlight some limitations of the proposed Goal Programming model. Although we have observed a robust solution regardless of the parameter used in the extended model, a statistical approach could help to deeply analyse other issues in the aggregation procedure. For example, in the classical regression analysis, we can compute the statistical significance and importance of independent variables, or the explanatory power of the model through the coefficient of determination. As in the case of traditional aggregation methods, the mathematical programming approach does not include similar measures to compute the significance of the model.