Observation of the Effect of Gender on Children’s Concept of Motion; Sustainability Issue

Abstract

Determination of the parameters of motion of the surrounding objects, and in particular their speed, is one of the basic skills of a human being. Studies on the development of basic concepts of motion have been carried out for years, exploiting various methods and in different contexts. In our research, we analyzed the effect of school education on the understanding of the phenomenon of motion. We tried to determine its possible short- and long-term cognitive consequences. To achieve this goal, we used the survey method. Our studies show that children differentiate two specific concepts: average speed and instantaneous velocity. In the present work we present how the gender context is superimposed on the general picture. We found that the initial, genuine pre-school concept of speed is different for girls and boys. Our analysis shows also that this gender effect vanishes quickly along with the introduction of physical definitions of kinematical quantities by physics/science curricula. We discuss the methodological aspect of the statistical gender gap measure and we calculate the gender effect chance probability, p-value, to be slightly less than 0.001. The importance of the observed effect for the sustainable science teaching processes is discussed.

1. Introduction

As mentioned by Vincent-Ruz and Schunn [1], the number of women studying STEM and pursuing graduate degrees has not changed substantially in the last decade [2]. Although some progress has been made in narrowing the gender gap in science over the last 30 years, girls and women continue to be underrepresented and marginalized in fields such as physics, engineering, and technology. As noticed by Brotman and Moore [3], there have been a myriad of approaches, evolving and growing over time, where researchers continue to investigate strategies for engaging girls in science. In all likelihood, the observed gender gaps are due to a combination of many gendered factors rather than any one that can be easily modified [4]. Our work is devoted to one particular factor observed in the process of the development of a basic concept of physics, the spatio-temporal relations of moving objects.

The age at which sex differences in spatial skills emerge is a matter of debate. As noticed by Coluccia and Louse, “results concerning gender differences in spatial orientation skills are mixed, ranging from marked differences to no-differences” [5]. Some authors [6,7,8,9,10,11,12] claim that the differences emerge with the onset of adolescence and thus it is a relatively late development phenomenon, but other studies report sex differences on spatial tasks as early as the preschool years. Boys as young as 4 years of age performed better than girls on spatio-temporal problems. Some studies confirmed that this situation remains constant until 10 years of age [13,14]. Extensive studies on mental rotation abilities [15] show clear and robust gender differences [16,17] which appear at the age of about 8 years and remain as adults, as presented clearly in the review of 14 independent studies by Masters and Sanders [18]. However, in recent years, the magnitude, consistency, and stability across time, of cognitive sex differences, have been questioned [17]. In the present work, we examine these issues in the context of spatial abilities and we add some arguments to the ongoing debate.

Alexander, Johnson and Kelley suggest [19] that from a very early age (ages 4–6), science interests are strong predictors of later opportunities to engage in informal science learning. School science fails to engage a wide range of students, and the “swing away from science” is a challenging problem in Sweden, England, and Australia [20]. These studies were performed by interviewing high school students (ages ranging from 10 to 16) and several reasons for the mentioned situation were identified and discussed.

Our research on forming primary ideas of physics in the elementary education follows the model of learning as conceptual change [21]. The work of Hewson investigates the conditions under which an individual holding a set of conceptions of natural phenomena, when confronted by new experiences, will either keep his or her conceptions substantially unaltered in the process of incorporating these experiences, or have to replace them because of their inadequacy. Such a process obviously leads to some misconceptions, which are very stable. Changing misconceptions is not simply adding new information to an individual’s mind. Interaction of new knowledge with the existing knowledge is necessary if the new needs to replace the old [22]. Detailed examination of these replacements and, in particular, their gender distinctions, is the main aim of the present work.

The problem of studying gender-related differences in cognitive processes been a topic of discussion for more than a hundred years. According to Halpern [23], Mrs. Helen Bradford Thompson at the beginning of the 20th century began her doctoral dissertation “The Mental Traits of Sex” with the opinion: ‘The object of the present monograph is to furnish some accurate information on the much discussed question of the psychology of the sexes’. Further detailed analysis of the problem appeared in literature later, in the mid-1970s [6].

An evolutionary account of sex differences in science can be inferred just from Darwin’s concept that many sex differences have evolved by means of sexual selection, as well in the case of the human as of other species [24]. However, two foundations of sexual selection: male competition and female choice are more complex and abstruse in humans by the existence of female competition and male choice. This can diminish the expected sex differences, but certainly not entirely [23]. In some aspects the situation is rather clear. For example, studies that used “time to collision” estimates that also involve spatiotemporal abilities, found that males made more accurate estimates [25]. Maintaining group territorial borders, tribal warfare, and large-game hunting are all almost exclusively male activities [26]. Male activities of hunting and warfare, which involve the construction and use of projectile weapons, obviously require the ability to track movements, sometimes even in 3D space.

From the neuro-biological point of view the proximate expression of many of the traits that have evolved by means of sexual selection are influenced by prenatal and postnatal exposure to sex hormones, particularly androgens in mammals, see, e.g., [27,28]. The processes that are at work in sexual selection can also exaggerate within-sex variation. Selection that favors extreme traits can result in quite unexpected gender difference [29,30,31].

From an evolutionary perspective, nature and nurture are integrally and reciprocally linked and cannot be separated. The developmental process (e.g., length of infancy) and the responsiveness of the developing trait to experiences are evolved phenotypes [32]. It is particularly important to consider the developmental patterns of slowly developing and highly social species; these species tend to have large brains and may be the most “plastic” in terms of learning and social behavior (e.g., [33,34]). Sex differences are often small early in development and become larger as individuals approach reproductive maturation—a finding that was originally noted by Darwin [24].

Of course, there are plenty of varied evidences for social and cultural influences of sex differences in science performance. Numerous studies have confirmed the existence of the parents’ expectations in correlation with their children’s abilities and successes [35,36], but still more specifically, studies are needed to determine whether parents showing sex-differentiated treatment of their children is important.

Neighborhood effects—that is, the effects outside of home that have an impact on children—were studied (e.g., [37]). For example, moving to low-poverty neighborhoods had positive effects on boys’ achievements as compared with those of their peers living in high-poverty neighborhoods. The gender effect has also been seen for adolescents in high-poverty neighborhoods. Children and adolescents are also strongly influenced by peers, but this is not limited to childhood and adolescence.

Schools may exert influence on children in multiple ways, including teachers’ attitudes and behaviors, curricula, ability groupings, and sex composition of classrooms [38].

The ability grouping in science tends to benefit high-ability students [39]. Experiences are especially important for learning of physical sciences in middle and high school. It is interesting that, although laboratory experiences do not improve much of the science achievement for boys, they do improve the achievement of girls, helping to close the gender gap [40,41].

Out-of-school learning, informal learning, contributes also to the general education process. The quality of students’ informal learning environments correlates with their performance on tests of scientific reasoning ability. For example, the presence of a computer in the home and use of a home computer for educational purposes leads to better performance on standardized tests. Compared with high-school girls, high-school boys are more likely to have computers in their homes and they are more likely to use them for educational purposes [42]. High-school boys are also more likely to have participated in a science fair [42].

The stereotype-threat effect on males’ and females’ performance is another factor of the gender gap. Although there has been a major shift over the last several decades toward equalizing men’s and women’s roles in the home, employed women still spend significantly more time with their children than men do and it is known that achieving high levels of success in science careers requires substantially more than 40 h of work per week. Additionally, women who choose nontraditional careers, for example in science, may be penalized in the marriage market: women engineers are less likely to be married and more likely to be childless than men engineers, etc.

We should mention here that there are also other ‘sociocultural influences on occupational choice’ aspects, which could be introduced and explained [23] with the Eccles model [43].

As we see, the number of factors which could influence gender difference in children’s understanding and developing basic concepts of physics, is significant. In the next sections, we should at least partially elucidate the problem of sex difference in a very small area of physics, and we will explain why this problem is important and what general recommendations can be derived from this explanation.

We present below our results of examining the way children understand the concept of velocity. Velocity is the basic concept of kinematics, from which physics, school physics, begins its quantitative approach. It is the key to further progress, to new concepts and eventually the laws of physics such as, for example Newton’s three laws of motion, on which the entire technical civilization of mankind has been based for several centuries. On the other hand, it is known that before Galileo began to study free falling and the general movement of bodies in a modern way, this subject had also been considered for at least two thousand years by ancient scholars. Probably even earlier, as our ancestors already understood in their own pre-human way what speed (velocity) was, trying to escape a chasing lion or hunting an antelope. The understanding of speed has evolved over the course of mankind’s history. In our research, we examine how it changes during the lifespan of an individual man, a child, from the moment before the shaping of his/her mind begins in the process of school education. Also, how these changes affect the learning process in the short- and long-term. We have found that these changes are quite fundamental and universal [44]. In this work, we present results related to the analysis of the issue of whether children understanding the concept of velocity is conditioned by his/her gender. Do girls and boys (women and men) perceive the notion of velocity identically, and if the changes mentioned above occur in the same way. This knowledge could help to create physics/science curricula which maximize learning outcomes. We believe that they should be initially consistent with the natural understanding of basic ideas, and introduce more complex physical concepts in a balanced manner resulting from comparing the currently observed situation and the desired image in the final state.

Contemporary research on motion perception has an origin in Piaget’s classical work [45]. He investigated children’s understanding of movement of objects in one-dimensional (usually uniform) motion and found that speed, the relation of faster/slower, appears as a result of observing the difference between the initial and final position of the considered object. In current physical terminology, this leads to speed being understood as an ‘average’. The average speed is the object’s motion attribute, not the attribute of the moving object itself. Piaget conducted his research in the 1940s. Since then, much has changed in the world where children interact with moving things. The speedometer in dad’s car or a computer speed indicator in computer games where cars race on race tracks has become natural. Both of these examples relate to instantaneous speed, quite different from the average one. Regardless of changes in the environment affecting the perception of motion by children, in this work we do not limit our studies to one-dimensional movements. Most movements around children are actually two-dimensional, only trains running (from station A to station B) are examples of one-dimensional motion in real life. In addition, in the vast majority of cases, we actually deal with variable speed motions. School questions about the speed at which the train traveled, if it covered the distance of 100 km in one hour, are unrealistic. The train did not consistently travel at the speed of 100 km/h, but rather, sometimes faster and sometimes slower. Everyone knows this fact, and the considered questions in school physics lessons have not been changed for years. The studies of today’s children’s perception of velocity is a general topic of our research. In this paper, though, we would like to add another aspect to our investigations: the gender dependence.

Many current studies [23,46,47] point to the existence of gender differences in various aspects of human intellectual activity, and these days nobody has any doubts about them, also in the area of exact and physical sciences, e.g., [48,49] and seventeen papers in the 12th volume 2nd special issue of Physical Review Physics Education Research (and hundreds of papers concerning the subject cited in them). Therefore, one could expect that the understanding of basic kinematic concepts will show trends depending on the sex of the respondents.

2. Methods

Our research was based on a (somewhat) open test. Our test was planned to show the understanding of motion by children (who have not started their education of physics yet) as well as the perception of physics by youngsters and adults at the subsequent teaching stages.

2.1. The Form

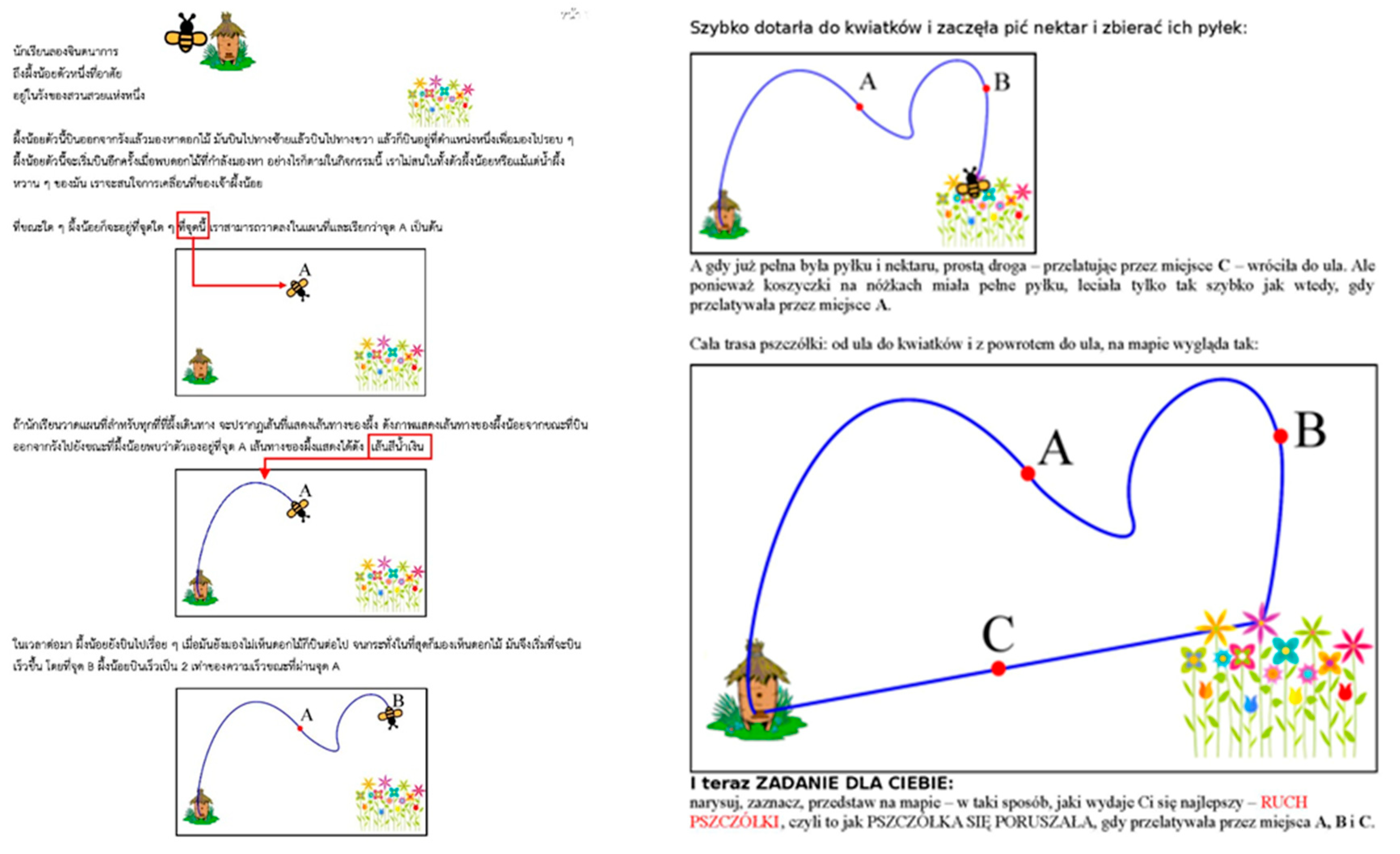
In order to ensure the intelligibility and attractiveness of the test also for the youngest children, we enclosed it with a kind of a short story. An illustrated tale of a bee that flew out of a hive looking for flowers in a meadow introduced the movement path to children, described verbally where and when the bee accelerated (twice), where she stopped and nibbled, and, finally, also her slow rectilinear return to the hive. At the end, a form of question/command was formulated: “Please draw, mark, depict on the provided situation map THE MOTION OF THE BEE when she flew through the places marked by ‘A’, ‘B’ and ‘C’, as shown in Figure 1.

It seems that the content and the command did not cause much trouble even for the youngest. The word “speed” or “velocity” has not been used anywhere, even though it was really the concept of main interest. Our intention was that the older children and high school students would not mechanically reference the known (to any extent) textbook definition and, we have to say, that we actually succeeded.

This task turned out to be so complex that the range of received responses and ways of performances was very large and could be analyzed in many ways. With a lack of any suggestions from our co-workers, teachers forced children (and adult respondents) to formulate their own ideas about the motion of material objects in their own, specific way and to depict them in their own, special graphical way. Surely, if we would ask about the speed of the bee, the answers of people, who met this concept in physics lessons at school, would correspond to what has been repeatedly tested by various tests of knowledge and that which has been tested for the ‘gender gap effect’ many times. The correct answer would be a textbook answer and we would check what percentage of respondents remember what they had once learned in physics lessons. The lack of the precision of our question allowed us to get to know how the motion, and therefore also, in a sense, the concept of velocity is understood by the participants of our research. In this work, we analyze only one aspect of the broad concept of motion, namely the one, which Galileo [50] already named when describing the speed. He distinguished between ‘average speed’ that requires observation of moving objects for a finite time, from ‘instantaneous velocity’ precisely defined later by Newton using the derivative concept, the limit of the path quotient by the time when the denominator seeks zero, the mean in infinitively short time.

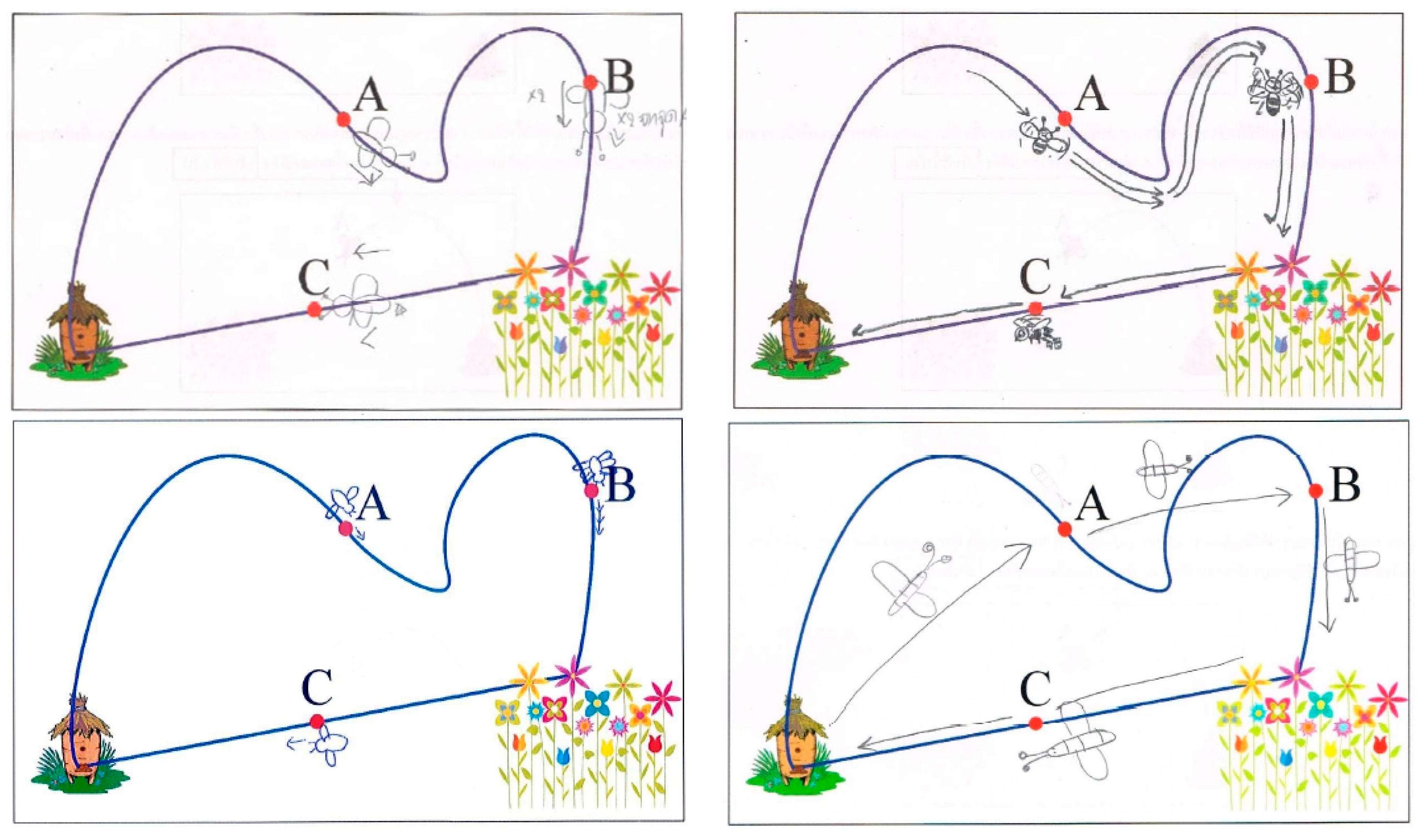
Among the answers to our test, we were able to distinguish those in which the respondents tried to visualize what was happening to the bee at a particular moment (‘intuitive’, ‘instantaneous’ case) and those where longer sections of the bee path were marked and velocity was marked on these sections (‘average’, ‘operational’ case). Examples are shown in Figure 2. The frequency of appearance of both is the subject of our analysis.

2.2. The Data

The test was carried out on almost 1000 participants of all ages, from pre-schoolers aged 6 to adults, students and teachers. The research was carried out in two countries: in Poland and in Thailand (statistics in both were similar). No significant differences were found. Fortunately, curricula for the kinematic studies in Poland and in Thailand are similar and similarly spread over student age.

When conducting a test among children in Thailand, each answer was marked whether it was given by a girl or a boy. Among children in Poland only in some groups they were asked for such information, encouraging children to sign their tests with their first name. The reluctance to identify on any forms, unjustified, in spite of everything, meant that the statistics of answers in which sex was possible to determine in Poland were significantly smaller than in Thailand. Therefore, we will focus on the data collected in Thailand, later on.

The tests were carried out in whole classes (groups) of children and students through teachers’ lessons with them. We asked everyone in the class to complete the forms and refusals were absolute exceptions. For some we received empty, unfilled forms. This number was also recorded and included in the statistics.

We tested children who were just preparing to go to school, as well as university and post-graduate students. The tests were attended by students of mathematics and science classes, as well as students of humanities. Among the university students we tested students of computer science, physics, geography, engineering, as well as medicine.

Classes and test groups were selected, to a large extent, randomly, although we certainly did not conduct research to show a statistically representative picture of society (societies). On the other hand, our research was devoid of the element of “volunteering”, which may lead to a difficult-to-determine shifting in emphasis.

Statistics ~1000 responses are the collection of approximately 40 groups of respondents. In each of these groups, the test was carried out simultaneously and it was practically impossible to isolate completely every respondent, especially the younger ones, as well as in each case, the test person, or other circumstances which could mean (and sometimes did mean) that not all answers were given independently. Nevertheless, their number is so large that the conclusions drawn are statistically valid.

2.3. Statistical Tool

The gender differences in relation to the educational achievements describes the observed differences in the results achieved by girls and boys in tests and various comparisons evaluating knowledge and skills in various fields of both humanities and science disciplines. As we have already said, it has been established beyond any doubt that such differences exist and in fact the object of studies is to determine their size in specific areas. To do this, it became necessary to define an appropriate, objective measure of the gender difference and use it in practical applications.

It has been widely accepted [51], to take as the measure of the “gender gap”, the value of the difference in the observed average of the evaluated value (assessments, number of correct answers, number of points, etc.) received by boys and girls divided by the square root of the variance of the observed value:

$$d=\left({\overline{X}}_m-{\overline{X}}_f\right)/\sigma$$

(1)

Usually when variance (σ²) is not known it is replaced by the square root of the arithmetic mean of the squares of standard deviations observed in the study of these values in the boys’ and girls’ sub-population,

$$d=\left({\overline{X}}_m-{\overline{X}}_f\right)/\sqrt{\left(S{D}_m{}^2+S{D}_f{}^2\right)/\left(2n\right)} ,$$

(2)

where ${\overline{X}}_m$ and ${\overline{X}}_f$ are the mean (average) values of $X$, the value under consideration calculated for subpopulations of men and women, and $S{D}_m$ and $S{D}_f$ are standard deviations of variable $X$ measured in both subpopulations, each consists of $n$ individuals. A positive value of $d$ means male predominance, negative, vice versa. It is worth noting that the word “dominance” here means only a larger average value of the measured variable and nothing more. Recognizing it as positive, is an external act, assuming that, for example, specific answers considered right or wrong.

If we know that the average values $\overline{X}$ have a normal (Gaussian) distribution (which is evident if the $X$ variables themselves is known to have such a distribution, or using the Central Limit Theorem, when the statistics are large enough) then the value of $d$ calculated from the Equation (2) can be used to test the hypothesis about the equality of $X$ distribution means in both sub-populations. If $\overline{X}$ distributions are identical, the variable $d$ has a normal (Gaussian) distribution with 0 mean and the square root of variance equal to $\sqrt{2}$, and thus unambiguously determines the value of the so-called p-value, which is the probability that the observed test result appeared as an “unfortunate coincidence”, by accident, while, in real, in the full subpopulations “M” and “F” there are no any difference in the mean value of the variable $X$ being tested.

It can be added here that a statistically justified measure of the inequality of mean values in two (large) populations with different statistics is:

$$d^{\prime }=\left({\overline{X}}_m-{\overline{X}}_f\right)/\sqrt{\frac{S{D}_m{}^2\times (n_m-1)+S{D}_f{}^2\times (n_f-1)}{n_m+n_f-2}\times \frac{1}{2}\left(\frac{1}{n_m}+\frac{1}{n_f}\right)},$$

(3)

where $n_m$ and $n_f$ are numbers of individuals in both sub-populations.

Equations (1) and (2) and the modification Equation (3) are convenient if the variable in question, X, can be expressed numerically (as an average rating, number of points, etc.). In some studies, particularly in the present analysis, the answer to the one test question is only a YES/NO, the binary response. It happens often in cases of closed tests, where the analysis of the answer includes specific item belongs (‘true’ or 1) or it does not belong (‘false’ or 0) to some class. With binary answers: 0/1, the concept of ‘mean value’, $\overline{X}$, does not make sense. In this case, the notion of probability should be used instead. The proper term is the probability that the answer of a randomly selected individual from a given subpopulation will be “1” (or “0”): the probability in the Bernoulli trial. For large subpopulations and reasonable (not very large and not very small probabilities, i.e., studies with a relatively big number of responses of “1” as well as “0”) the respective binomial distribution can be approximated by a normal distribution with a clearly defined mean ($np$) and variance ($p\left(1-p\right)$). It does not depend on the nature of the examined quantity of course. Corresponding formula, for the proper “gender gap” measure is in this case:

$$d^{″}=\left(p_m-p_f\right)/\sqrt{\frac{n_m{p}_m+n_f{p}_f}{n_m+n_f}\left(1-\frac{n_m{p}_m+n_f{p}_f}{n_m+n_f}\right)\times \frac{1}{2}\left(\frac{1}{n_m}+\frac{1}{n_f}\right)},$$

(4)

where $p_m$ $p_f$ are the observed frequencies of the one type response (“YES”, “true”, or “1”) in the subpopulation of men and women respectively.

The value of $d^{″}$ calculated using Equation (4) for large statistics has again the Gaussian distribution and uniquely determines the p-value defining the statistical significance of the obtained result. In the

Table 1. p-Values (in %) corresponding to the observed d′′ difference measure.

d″	p-Value (%)
0.0	50
0.2	45
0.5	36
0.8	29
1.0	24
1.81	10
2.0	8
3.0	2
3.3	1
3.6	0.5
4.4	0.1
5.3	0.01
10	10−10

we show the p-values which correspond to observed $d^{″}$ value. They can be interpreted classically as a chance of obtaining the same or even bigger value, if we repeat the same test in the same conditions. A simpler and more understandable Bayesian interpretation is that the p-values are the probabilities that both populations in the studied context have the same mean.

According to Johnson [52] statistically significant test results are associated with p-values that are less than 0.005 ($d^{″}$ ≈ 3.6). Make 0.005 the default level of significance. Highly significant test results are associated with p-values that are less than 0.001 ($d^{″}$ ≈ 4.4).

3. Results

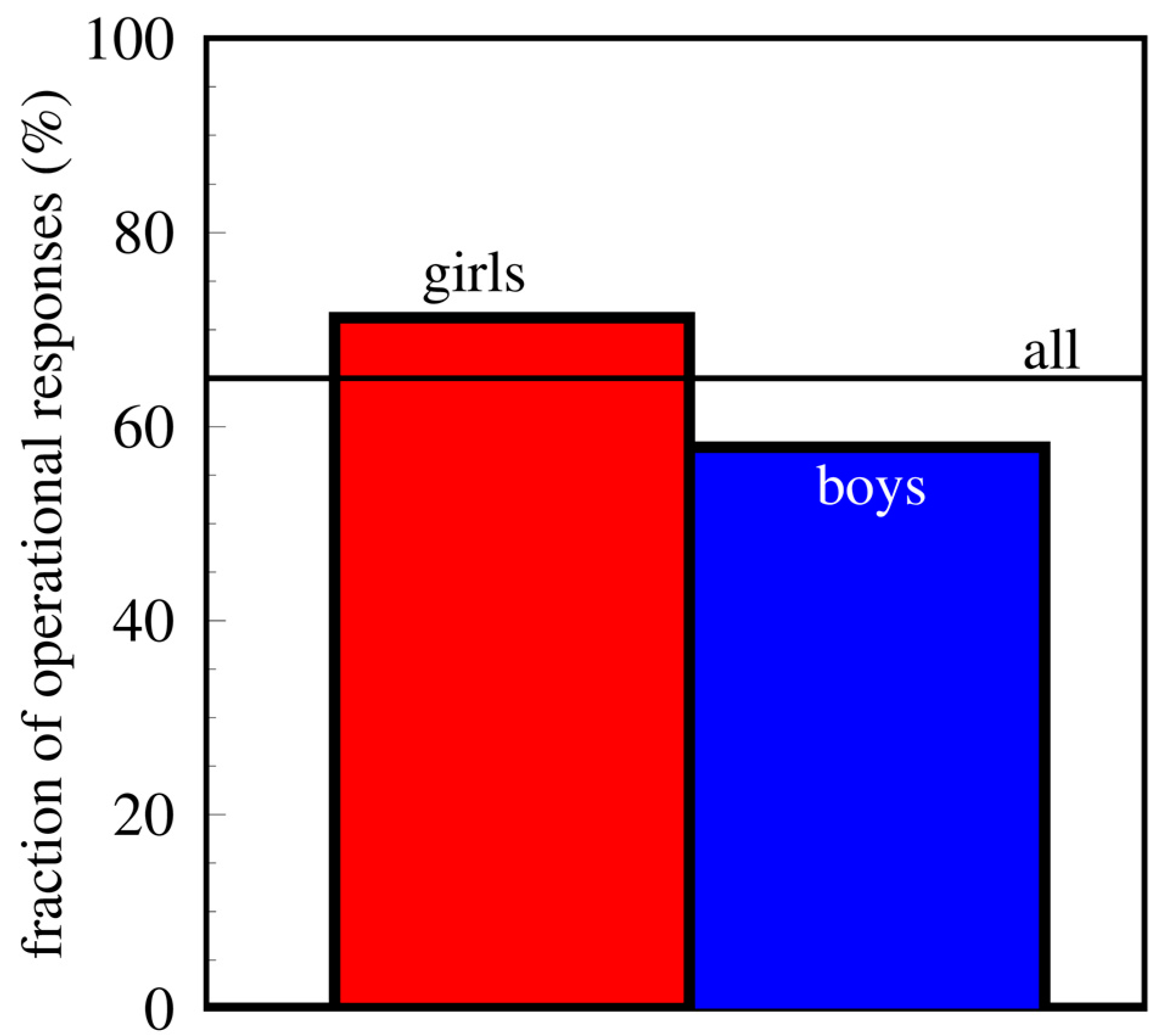
In this work, we present results of only one aspect of the problem of understanding motion, distinguishing cases where the speed of the bee was treated by the respondents as ‘operational’: on a finite section of the path, in contrast to the concept of ‘intuitive’: speed at a specific point of the path. First, we counted both types of answers. Results are presented in Figure 3.

Heights of rectangles (boxes) in the Figure 3 correspond to a fraction of answers indicating the understanding of velocity as the ‘operational’ among girls (red) and boys (blue). The surprising disproportion between the frequency observed in the group of girls and the group of boys is clearly visible. Girls clearly more readily (more often) understand the velocity of the bee’s motion, observing how it moves along the finite road section. For boys there are more answers in which the velocity is determined and marked at a precisely determined point (place, time).

The measure of the size of the gender difference $d^{″}$ according to Equation (4), considering that all girls/women participating in our test in Thailand were 271, and men/boys 233 we obtained the value of 4.41. Using the definitions given in Equations (2) and (3) the respective values of $d$ and $d^{\prime }$ are 4.42, and 4.45, respectively. The differences are not big, which means that the approximations do not change the significance of the effect. According Cohen [51], the value of effect size difference greater than 0.8 already suggests the large effect size, the values of about 4 are beyond the range of tables in the paper of Cohen [51], so one can say that the effect size in exceptionally big. To determined exactly the statistical significance of the observed effect we calculated the p-value for the hypothesis of the equality of the response type rates of boys and girls. This value was slightly less than 0.001 (Table 1), so the observed difference can definitely not be accidental. It is highly statistically significant.

For additional confirmation of this result, we tried to set the same frequencies for children tested in Poland (whom we were able to assign gender based on completed tests). The rates were 71% and 53%, respectively for girls and for boys. With a much smaller (almost ten times) statistic obtained for these frequencies, the p-value equals to 0.2, which is not a statistically significant result. The surprising coincidence with the frequencies calculated for Thai children therefore does not mean anything, although it must be noted that it is not contradictory to them, but rather on the contrary. At this point, it should be added that the classification of data from Poland and Thailand was carried out independently by different groups, possibly subjectively conditioned, to some extent.

After observing the correlation of the results of understanding the concepts of kinematic and sex of the tested persons, we made a more detailed breakdown of groups of girls and boys from Thailand, considering their level of advancement in the school physical education process.

Previous studies on the variability of the interpretation of kinematics concepts [44] have shown that together with the children’s presentation of a textbook, classic picture of elementary physics, which takes place in the 12–13 age group and after intense training in the classroom changes drastically seeing the surrounding physical children reality. This is the goal of the standard teaching process. Figure 3 shows this change. To a large extent, children abandon the intuitive understanding of the concept of speed we study in favor of the Galilean operational way enabling the quantitative solution of textbook problems associated with the concept of the average velocity.

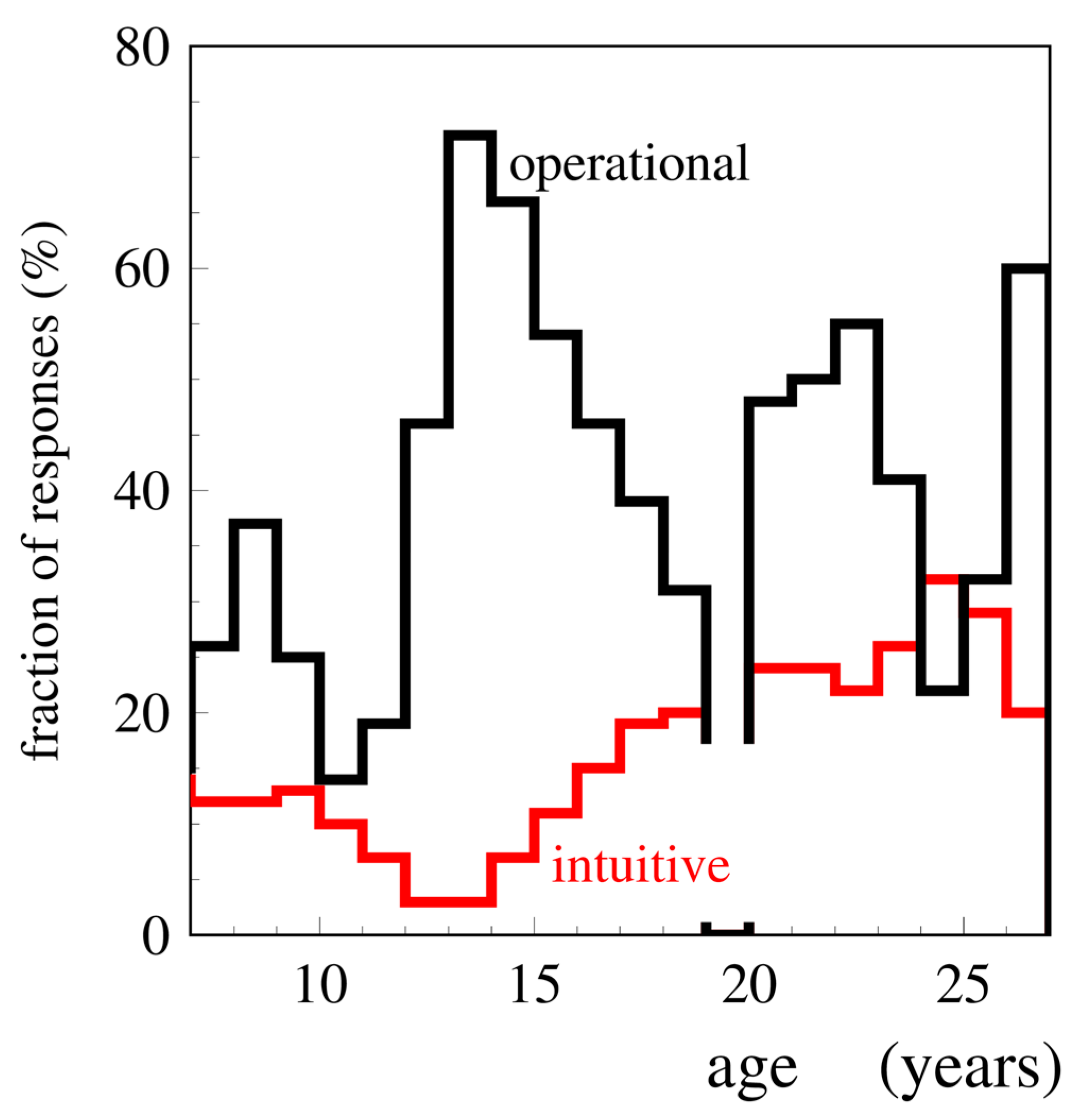
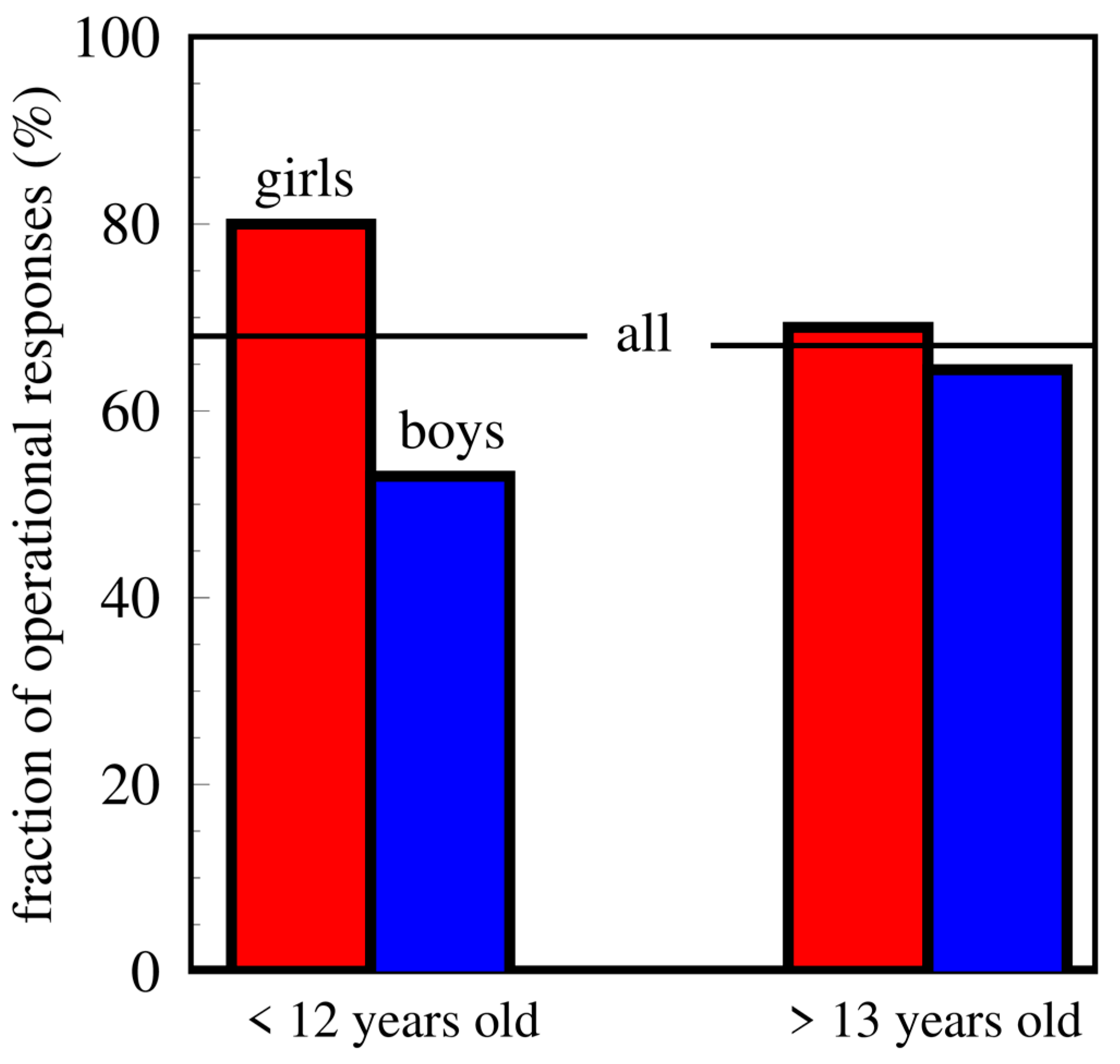
The analysis of the whole of data presented in Figure 4 shows that the clear effects of physics teaching at school in relation to the way of understanding the concepts of kinematics appear in children aged 12–13. We have adopted this line by dividing children as young as 12 and older than 13 years old.

Figure 5 shows the results of this analysis.

4. Discussion

The existence of a large disparity between the number of males and females who pursue careers in the areas of science, mathematics, computer science and engineering, is well-known and it was discussed, for example in [53,54]. Searches for biological and sociocultural causation are still not conclusive.

Our studies of gender differences concerning the understanding of basic physical ideas show that at very early childhood stage girls more frequently than boys naturally accept the initial school ‘operational’ (Galilean) concept of velocity. This could be the explanation of the findings of Gafoor [55] who examined the misconceptions in concept of velocity. Boys identified more likely the distance with the displacement, thus understand velocity as the instantaneous one, while girls clearly see the relation of the speed and direction of motion and have no problems with units of speed and velocity.

This initial girls’ ‘advantage’ diminishes fast during the education process by enforcing unitary way of understanding and describing motion. Before the school physics turns to ‘modern’, Newtonian, concept of instantaneous velocity the ‘gender gap’ disappears completely. The transition from Galilean (‘operational’) to modern (‘intuitive’, instantaneous) concepts in physical concept of motion forced by school education around the age of 17–18 is, however, more profound for girls than for boys. The change: pre-school → ‘operational’, and then next subsequent change ‘operational’ → Newtonian, ‘intuitive’ introduces a kind of cognitive confusion, building space for successive misconceptions, perturbations and muddle, physical, scientific image of the world.

For boys it is (on average, of course) the return to their initial concept: ‘intuitive’. For girls, more frequently, it is the reversal of their initial concept which was ‘operational’ from the beginning. The eventual ‘civilized’, ‘educated’ way of understanding the parameters of motion could be considered as a manifestation of the ‘masculine culture’ of physics, or modern science, STEM, in general. This concept works in favour of the factor (a) in the model with three overarching factors to explain larger gender gaps in participation in STEM fields proposed by Cheryan [53]: “a masculine culture of physics that signals to women a lower sense of belonging than to men.” But the observed gender-difference evolution can also favour the factor (c) “gender gaps in self-efficacy”. This problem is discussed in a case of introductory physics course by Nissen and Shemwell, [56]. We can say that the girls’ self-efficacy may be reduced by the discussed school enforced transition of concepts.

On the other hand, such homogeneous and scientifically justified approach undoubtedly facilitates educated youth to move in a world built on the basis of modern science. However, it still remains to examine what has simultaneously disappeared in the school teaching process. It is not known whether this is an irreversible disappearance or whether, after passing all levels of education, the ‘natural’ understanding of phenomena is back. As our results show, one way to verify whether it is, or it is not, is to check if people who left the school walls long ago do recover the difference in the approach to the concept of speed between women and men.

Blickenstaff mentioned in his work [57] nine possible important issues concerning ‘gender gap’ for science and engineering. Of course, all of them are important, but one, the 5th, is particularly related to our present work. It reads: “Science curricula are irrelevant to many girls”. We have shown that, on average, girls have natural understanding of the more ‘operational’, Galilean velocity concept. Possibly some discouragement could appear when the ‘modern’, Newtonian, ‘instantaneous’ concept is introduced during physics lessons instead of the natural one they understood well.

The curricula at least for the essential kinematic part that we studied should be made more sustainable, in accordance with natural sense of basic ideas. This suggestion, if taken into account, could reduce the problem of the ‘gender gap’ in physics and science at least to some extent.

5. Conclusions

The problem of early understanding of basic concepts of kinematics has obvious significance for further courses of physics education. The goal of education, teaching, learning and understanding, cannot be achieved without a diagnosis of students’ initial understanding of relevant content knowledge. Without proper determination of speed and velocity one cannot speak about correct teaching not only of dynamics, but also of thermodynamics, electricity, astronomy and virtually any of the branches of physics. The presented results show, not only that the understanding of the basic concepts is not good enough, but also indicate that, from the very beginning, following the schemes well established for more than a hundred years, we are moving away from reality, natural understandings of concepts and coherent images of the surrounding world. Taking velocity as an example, we have shown that these schemes require fundamental revision, because otherwise, they only serve the purpose of being a fun school puzzle, rather than having any real impact on the development of children’s minds or on their future successes and achievements. A proper change, bringing school physics closer to the intuition of children, would also induce positive attitudes towards physics, which is otherwise a generally disliked subject.

Finally, as we have already mentioned, it seems necessary to modify current physics curricula, and at least in terms of kinematics, to become more sustainable and more appropriate. This, in view of the presented results and considerations, would certainly help to reduce the problem of the ‘gender gap’, not only in physics, but also in STEM subjects in general.